Abstract
A piecewise frequency control (PFC) strategy is proposed in this paper for coordinating vibration isolation and positioning of supporting systems under complex disturbance conditions, such as direct and external disturbances. This control strategy is applied in an active-passive parallel supporting system, where relative positioning feedback for positioning and absolute velocity feedback for active vibration isolation. The analysis of vibration and deformation transmissibility shows that vibration control increases low-frequency position error while positioning control amplifies high-frequency vibration amplitude. To overcome this contradiction across the whole control bandwidth, a pair of Fractional-Order Filters (FOFs) is adopted in the PFC system, which increases the flexibility in the PFC design by introducing fraction orders. The system stability analysis indicates that the FOFs can provide a better stability margin than the Integral-Order Filters (IOFs), so the control gains are increased to get a better performance on the AVI and positioning. The PFC based on FOFs can suppress the peak amplitude at the natural frequency which cannot be avoided when using the IOFs. The constrained nonlinear multivariable function is formed by the required performance and the stability of the system, then the controller parameters are optimized effectively. Lastly, the effectiveness of the proposed method is verified by experiments.
1. Introduction
Sensitive units of precision instruments such as atomic force microscopes [1], photolithography [2], electro-optical systems [3] need to maintain their stable positions under complex disturbances. The spring-damper supporting system is the most commonly used technique for suppressing disturbances. This technique can isolate high-frequency disturbances from the base, but the vibration amplitude is amplified around the inherent frequency. Moreover, due to the low supporting stiffness [4,5], the passive supporting system is easily deformed by disturbances, which leads to the leveling problem. As the counterpart, the active vibration isolation (AVI) system can make up for these deficiencies [6,7].
The dynamic characteristics of the AVI system can be adjusted through various feedback controls. The virtual supporting stiffness can be reduced by the positive relative position feedback (RPF) control [5] and the virtual mass can be increased by the acceleration or force feedback control [8]. Thus, the inherent frequency of the supporting system can be reduced to improve vibration isolation bandwidth [9]. The relative damping can be obtained through the relative velocity control, which attenuates the vibration around the inherent frequency with the cost of weakening the ability of the high-frequency vibration isolation [10]. Using the absolute velocity feedback (AVF) control or the integral force feedback control [11], the absolute damping can be obtained to address this problem. In addition, by increasing the virtual stiffness, the position accuracy, and the resistance to direct disturbances are improved [12]. However, if the support system experiences complex disturbances, it is necessary to effectively synthesize multiple types of feedback controls.
To enhance the positional stability of the supporting system, multiple types of feedback control composed of the absolute motion feedback and the RPF are widely used. To ensure the AVI performance and the position stability, Liao et al. [13] used the AVF and the RPF to obtain the sky-hook damping and improve the relative position stability, respectively. Beijen et al. [14] added the virtual mass and skyhook damping using the proportional and integral (PI) acceleration feedback control and contributed to the virtual stiffness through the RPF for a soft-mounted vibration isolator. In microgravity environments, the acceleration feedback and the RPF are also employed simultaneously. Zhang et al. [15] employed the position control loop to keep the contactless actuator from crashing and employed the acceleration control loop to eliminate the vibration of the payload for the MAIS (Microgravity active vibration isolation system). The g-limit (Glovebox Integrated Microgravity Isolation Technology) [16] was also controlled by these two control loops to cancel the inertial motion and keep the platform centered. Similarly, the force feedback combined with the RPF also has the same control effect. In a flexible stewart platform, Yang et al. [17] compensated for the stiffness of the flexure hinge using the position feedback control and employed the PI force feedback to broaden the vibration isolation bandwidth and add to the absolute damping. To resist the disturbances during the positioning process, Yun et al. [18] combined the position control loop and acceleration control loop in the compliant parallel manipulator to achieve vibration attenuation and micro-positioning. As shown in Figure 1, it is worth considering the fact that the RPF tightens the connection between the payload and the base, which weakens vibration isolation. Setting the relative position regulation as the secondary control objective, a low-frequency RPF was adopted in the micro-gravity vibration isolation system [19] and the advanced LIGO (laser interferometer gravitational-wave observatory) [20], while the low-frequency RPF with the cut-off frequency of 1 Hz was used in the HT (Hood Technology Corporation)/UW (University of Washington) hexapod [21]. However, the performance of the AVI and positioning was discussed separately or only one of these factors was discussed by the above scholars. The interaction between the AVI and positioning is still lacking the in-depth research needed to achieve effective coordination.
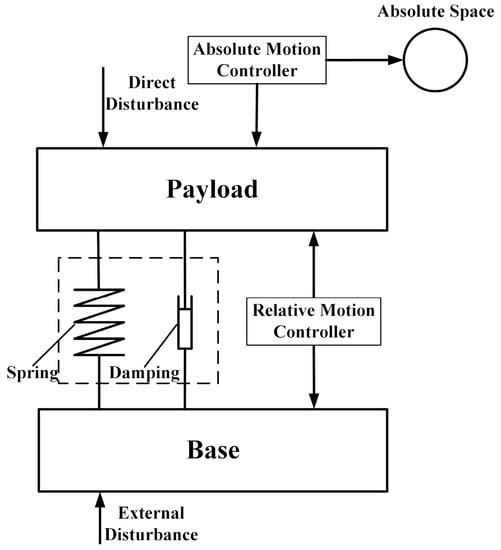
Figure 1.
The theory of active vibration isolation (AVI) and positioning.
To avoid the undesired effects of the feedback controllers on the frequency range, the Integral-Order Filter (IOF) is adopted to limit the bandwidth of the feedback signals. However, the magnitude and phase margin may be reduced by inserting the IOF into the control system, which means that the system tends to be unstable. In recent years, the Fractional-Order Filter (FOF) has been increasingly used in dynamic systems [22,23,24], which provides greater flexibility to optimize both the magnitude and phase responses in comparison with the IOF [25]. Though the analysis of the mutual restriction between vibration and deformation transmissibility, a novel piecewise frequency control (PFC) system based on FOFs is presented in this paper to effectively weaken the contradiction between the AVI and positioning of the supporting system. The FOFs can provide a larger stability margin than the IOFs, so the control gains can be increased to get a better performance on the AVI and positioning. In Section 2, the PFC strategy for the vibration isolation and positioning (VIP) system is described and the interaction between the AVI and positioning is explained. In Section 3, the influence of the AVF and RPF on the supporting system is analyzed. In Section 4, the PFC based on FOFs is analyzed and optimized. In Section 5, the experimental setup is described, and the proposed control approach is verified by the experimental results. In Section 6, the conclusions are presented.
2. Description of PFC Strategy for VIP
As shown in Section 1, the complex disturbances affect the sensitive units of precision instruments, resulting in loss of accuracy. The VIP system is applied to restrain the disturbances to an acceptable level and enhance the positional stability, which can commonly be described as an active-passive parallel supporting system. The active component of the VIP system consists of actuators, sensors, and a control system. The signals collected from relative position sensors and absolute motion sensors are transmitted to the actuator for the AVI and positioning in the VIP system. To focus on the essence of the coordinated control problem, the analysis presented in this paper is limited to a single degree of freedom (DOF) VIP system.
As shown in Figure 2, the VIP system is composed of a passive supporting unit and an active control system. The payload and the base are modeled as two rigid bodies, i.e., the masses m2 and m1, respectively. They are interconnected by the passive supporting unit consisting of the stiffness k2 and the damping c2. The disturbance is transmitted from the ground to the mass m1 through the stiffness k1 to produce the external disturbance x1. The payload position x2 is disturbed by an external disturbance x1 and a direct disturbance Fd. The passive supporting unit can sufficiently attenuate high-frequency external disturbances x1, but this amplifies the vibrations around its inherent frequency and limits its ability to suppress the direct disturbance Fd. In the active control system, a velocity sensor located on the payload is used to measure the absolute velocity of the payload, and an eddy-current sensor positioned in parallel with the supporting unit is used to obtain the relative position δD between the payload and the base. The actuator M is a voice coil motor (VCM) that is used to produce a force Fa according to the AVI and positioning control. As shown in Figure 3, to attenuate the absolute velocity x2 and maintain the relative motion δD, the PFC is composed of the AVI controller Hv(s), the positioning controller Hd(s), and the filters ωv(s) and ωd(s).
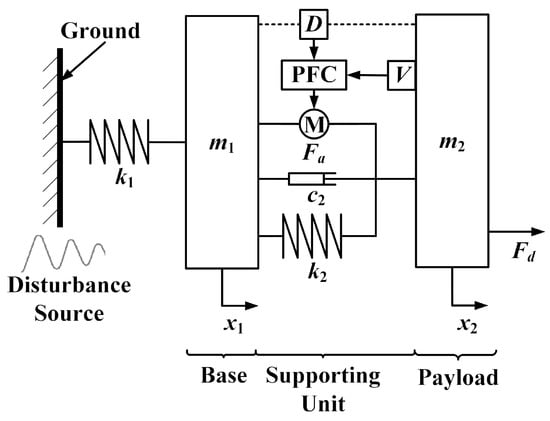
Figure 2.
Single-degree of freedom (DOF) supporting systems with a piecewise frequency control (PFC) strategy for vibration isolation and positioning (VIP).
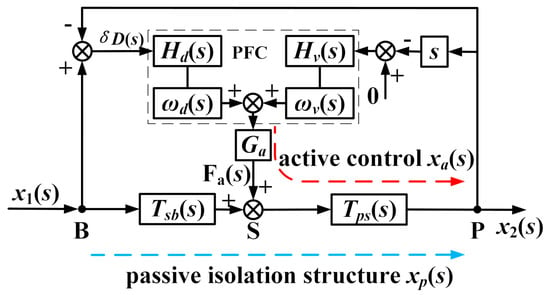
Figure 3.
Block diagram of the PFC strategy for VIP. The PFC is shown in the dotted box. The external disturbance x1 is transmitted to point P by the active control loop, shown as the red dotted line, for which the response motion is xa; by the passive isolation structure, shown as the blue dotted line, for which the response motion is xp.
To describe the PFC strategy, the transfer function of the passive isolation structure is written as
where xp(s) is the payload motion caused by the passive isolation structure transmitting the base motion x1(s). As the connection stiffness k1 can be considered infinite, the transfer function Tps(s) can be obtained by
where xa is the payload motion caused by the actuator force Fa. Thus, the transfer function Tsb(s) can be expressed as
From Figure 3, the motion equation of the VIP system resisting the external disturbance x1 can be represented by
Because the AVI is the negative feedback of the velocity x2s, which is used to suppress the vibration velocity. And the positioning control is used to maintain the relative position δD between m1 and m2. Considering the VCM as a gain Ga, the actuator force Fa is given as
Then, by substituting the value of Fa from Equation (5) into Equation (4), the performance of the AVI and positioning can be evaluated by the vibration transmissibility Tiso (s):
and by the deformation transmissibility Tpos(s):
Hence, the effects of Hv(s) and Hd(s) can be described by a sensitivity matrix E, which is given as follows
where
From Equation (9) to Equation (12), one can obtain ∂Tiso/∂Hd = −∂Tpos/∂Hd and ∂Tpos/∂Hv = −∂Tiso/∂Hv. It means that the controllers have opposite effects on the AVI and positioning. The basic idea of the PFC is to shape the Hd(s) and Hv(s) with suitable ωd(s) and ωv(s), thus weakening the contradiction between the AVI and positioning in the frequency range.
3. Effects of AVI and Positioning Controls
Understanding the interaction law between the absolute velocity feedback (AVF) and the relative position feedback (RPF) is the basis for the design and optimization of PFC. To evaluate the effects of AVF and RPF, both the values of the ωd(s) and ωv(s) are firstly taken as 1, and the controllers are set as
where kdp, kdi,, and kdd are the gains of Hd(s), while kvp and kvd are the gains of Hv(s). The parameters of the VIP system are listed in Table 1, which is consistent with the experimental setup described in Section 5.

Table 1.
Parameters of single-DOF supporting system.
3.1. Effect of AVF on AVI
The AVF is used to resist the external disturbance x1. When only the AVF is used, according to Equation (4) and Equation (5), the motion equation can be expressed as
Substituting Equation (13) into Equation (14), the vibration transmissibility can be written as
From the vibration transmissibility shown in Figure 4, it can be seen that the effect of kvp is equivalent to adding absolute damping to the supporting system, which attenuates the vibration amplitude around the inherent frequency. The effect of kvd is equivalent to the added virtual mass, which moves the inherent frequency forward and broadens the vibration isolation bandwidth, however, the vibration amplitude is amplified at the peak.
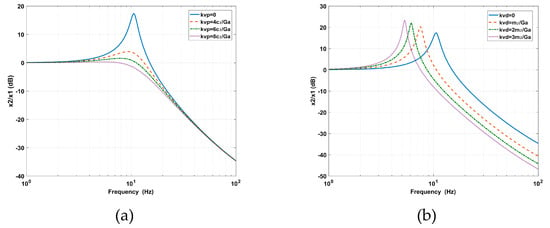
Figure 4.
Effect of (a) the proportion kvp and (b) the derivative kvd of the absolute velocity feedback (AVF) on vibration transmissibility.
3.2. Effect of RPF on Positioning
When only the RPF is used, according to Equation (4) and Equation (5), the motion equation can be written as
Because the base position cannot be obtained directly, the base acceleration is set as the input. Substituting Equation (13) into Equation (16), the deformation transmissibility is rewritten as
The influence of RPF on the deformation transmissibility is shown in Figure 5. The effect of kdp is equivalent to the mechanical stiffness parallel to k2, which can be used to increase the supporting stiffness. The addition of kdp increases the natural frequency and decreases the amplitude at low frequencies and the peak. The effect of kdi is equivalent to eliminating the steady-state error of the position and solving the leveling problem for the supporting system [26]. The amplitude is decreased at ultra-low frequencies with the addition of kdi. The effect of kdd is equivalent to adding relative damping between the base and the payload. With the addition of kdd, the amplitude around the inherent frequency is decreased gradually.
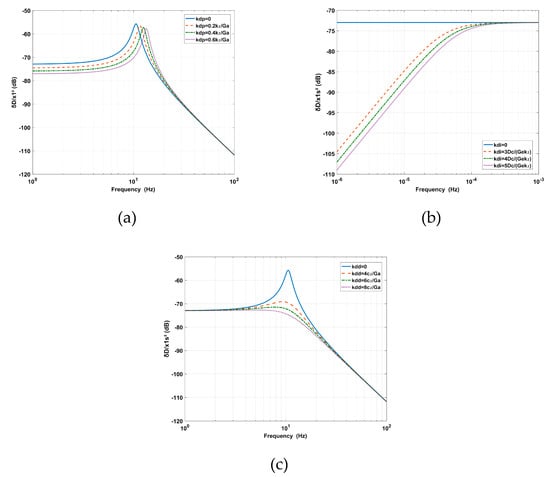
Figure 5.
The effects of (a) the proportion kdp, (b) the integration kdi where Ge = 0.421 mm/V is the eddy-current sensor gain and Dc = 1 mm is the relative position between the payload and the base, (c) the effect of the derivative kdd of the relative position feedback (RPF) on the deformation transmissibility.
Additionally, it should be noted that the compliance is a way to evaluate the ability to resist the internal disturbance Fd. As such, the compliance with the RPF is described as
The above equation has the same expression as . This shows that the deformation transmissibility has a similar meaning to the compliance .
3.3. Interaction of AVI and Positioning
When the AVF and the RPF are used simultaneously, the vibration transmissibility and the deformation transmissibility of the closed-loop system are
As shown in Figure 6a, the RPF adds the stiffness and relative damping between the base and the payload. The added stiffness increases the natural frequency, which narrows the vibration isolation bandwidth, while the relative damping decreases the maximum value of vibration transmissibility at the cost of amplifying the vibration amplitude at high frequencies. In Figure 6b, the AVF adds the mass and absolute damping to the payload, which weakens the connection between the base and the payload, so that the amplitude of the deformation transmissibility at low frequencies is amplified, which in turn deteriorates the positioning performance; that is, the interaction between the AVI and positioning leads to a reduction of the vibration isolation performance at high frequencies and a reduction of the positioning accuracy at low frequencies.
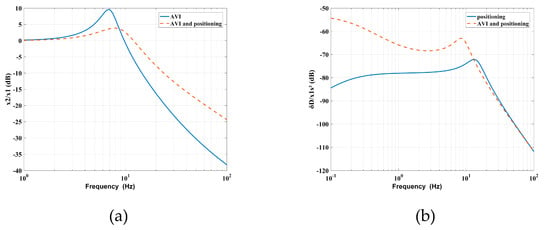
Figure 6.
Contradictions between the AVF and RPF related to the (a) vibration transmissibility and (b) deformation transmissibility.
4. Analysis and Optimization of PFC
To suppress the effects of the interaction between the AVI and positioning on the frequency range, as shown in Figure 7, the ωv(s) and ωd(s) of the PFC adopt a low-pass filter Hlp(s) and a high-pass filter Hhp(s), respectively; that is, the PFC carries out the positioning at low frequencies and the AVI at high frequencies.
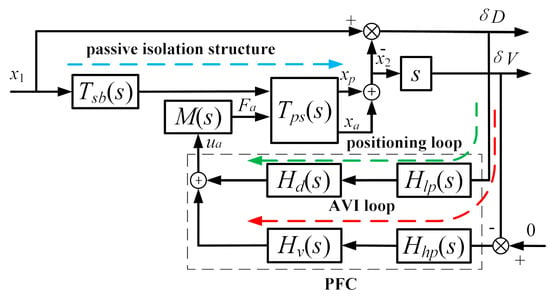
Figure 7.
Block diagram of the PFC with the filter pair. The blue dotted line is the transfer path of the passive isolation structure, the green dotted line is the positioning loop, and the red dotted line is the AVI loop.
4.1. PFC Based on IOFs
To obtain a higher signal attenuation rate beyond the control band of the AVF or RPF, the conventional second-order IOFs are selected. The filters are as follows:
where ζ is the damping ratio of the filters, which is selected as 0.7. Here, flp and fhp are the cut-off frequency value for Hlp(s) and Hhp(s), respectively. As the control bandwidth of the AVF and RPF is limited by the sensor noise, the sensor bandwidth is firstly determined by the correlation function of the actuator and the sensor signals. In this paper, the relative position and the absolute velocity are measured by the XS4P18AB120 eddy-current position sensor and the GS-11D absolute velocity sensor, respectively. By exciting the VCM with white noise, the coherence values are obtained as shown in Figure 8. When the coherence values are greater than 0.7, the traditional control can be considered as a special PFC, with flp = 29 Hz and fhp = 1.6 Hz.
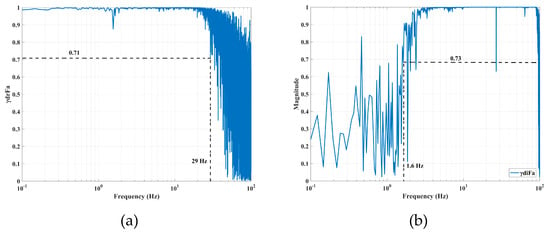
Figure 8.
Coherence values between the signals of the actuator and the sensors: (a) XS4P18AB120 eddy-current sensor and (b) GS-11D-H velocity sensor.
To ensure the stability of the closed-loop system, the parameters of the controller are restricted by the gain margin and phase margin of the open-loop system. In practice, the phase margin should be greater than about 30° to prevent the system instability caused by the time delay, while the gain margin should be larger than 6 dB [27]. As shown in Figure 7, xp and xa are the payload movements caused by the passive isolation structure disturbance and the active control input, respectively. The relation between xp as the input and xa as the output is described as
Then, according to Equation (1) and Equation (23), the open-loop transfer function can be written as
The gains of Hv(s) and Hd(s) are taken with moderate values as kvd = 2 m2/Ga, kvp = 8 c2/Ga, kdp = 0.5 k2/Ga, kdi = 3 Dc/(Gek2), kdd = 8 c2/Ga. As shown in Figure 9, it can be seen that the adjustment of the cut-off frequencies will impact the gain margin and phase margin, meaning the gains of Hv(s) and Hd(s) should be reduced to ensure the system stability. The gain margins and phase margins according to different cut-off frequencies are listed in Table 2.
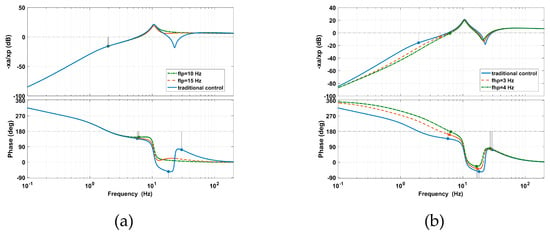
Figure 9.
Open-loop system performance with the movement of (a) flp and (b) fhp caused by the PFC based on IOFs.

Table 2.
Gain margins and phase margins by different cut-off frequencies.
Furthermore, to evaluate the performance of the AVI and positioning, the vibration transmissibility and the deformation transmissibility of the closed-loop system are described as
As shown in Figure 10a, the decrease of flp leads to the increase of the vibration transmissibility at the peak, the decease of the vibration transmissibility at high frequencies, and the enlargement of the AVI bandwidth. In Figure 10b, the amplitude of the deformation transmissibility at the peak is enlarged. This means that the virtual stiffness and relative damping are decreased.
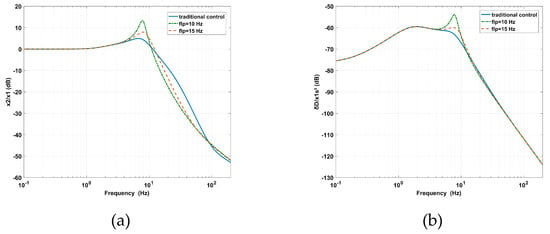
Figure 10.
The effects of flp on the PFC based on IOFs for (a) vibration transmissibility and (b) deformation transmissibility.
As shown in Figure 11a, with an increasing fhp, the amplitude of the vibration transmissibility at the peak is significantly amplified, and the AVI bandwidth is slightly narrowed. Due to the lower virtual mass and absolute damping, the effect of the AVF on the AVI is gradually reduced. In Figure 11b, by using a smaller virtual mass and less absolute damping, the position accuracy is strengthened at low frequencies. However, the amplitude of deformation transmissibility at the peak is enlarged due to the loss of absolute damping.
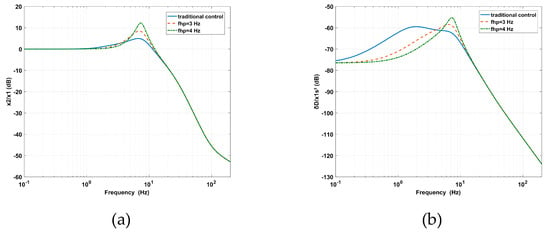
Figure 11.
The effects of fhp on the PFC based on IOFs for (a) vibration transmissibility and (b) deformation transmissibility.
4.2. PFC Based on FOFs
The above analysis shows that the PFC based on IOFs can decrease the vibration transmissibility amplitude at high frequencies and improves the position accuracy at low frequencies; however, it amplifies the amplitude of the vibration and deformation transmissibility at the peak because of the loss of relative and absolute damping. Although the damping can be compensated by adding the gain from kvp and kdd, this results in system instability. Considering that FOFs can provide greater flexibility in optimizing both the magnitude and phase response than the IOF, a pair of FOFs is introduced into the PFC. The FOFs are considered as the generalized case of IOFs [28,29], for which are more flexible as they introduce more variables of fraction order, but also more complicated. To reduce the additional unknown parameters, the FOFs are formed by replacing the integral order of the IOFs with the fractional order, which can be described as
where α1, α2, β1, and β2∈R represent the fractional order.
The design specifications required for the system stability and performance are as follows:
- (1)
- Phase margin = PM ≥ 40°;
- (2)
- Gain margin = GM ≥ 15 dB;
- (3)
- Vibration transmissibility: max() ≤ 5 dB and the amplitude crossover frequency is close to 10 Hz;
- (4)
- Positioning transmissibility: max() ≤ −75 dB when the frequency is smaller than 2 Hz, otherwise max () ≤ −60 dB.
To simplify the parameter searching process for the optimization of controllers and filters, the damping ratios of filters ζα and ζβ are set as 0.7; both the variation range of α2 and β2 is from 0 to 2 and the relations between α1 and α2, and between β1 and β2 are set as α1 = 2α2 and β1 = 2β2, respectively. Because kdi affects the deformation transmissibility at ultralow frequencies, it is not considered in the optimization process. The Matlab optimization toolbox is applied to find the minimum of the constrained nonlinear multivariable function. The optimized controller gains and the Fractional-Order Filters are
The FOF provides more flexibility and insight in the filter design, but the ideal FOF can only be realized by proper approximation with the IOF [30]. The Oustaloup filter approximation is widely used in fractional calculus [31], and it is adopted in the implementation of FOFs in Equations (30) and (31). An Oustaloup filter can be designed as
where γ is the order of the derivative and N is the order of the filter. The poles, zeros, and gains are calculated from
with , where ωb and ωh are the lower and upper limits of the frequency range for the Oustaloup filter.
The designed FOFs can be approximated more accurately with a higher-order filter. However, this costs more computing time and may distort the input signal. Therefore, the fractional-order derivatives s0.5 and s0.8 are approximated by the 4-order and 2-order Oustaloup filters, respectively, as ωb and ωh are determined using the related AVI and positioning bandwidth range, i.e., 1 Hz to 50 Hz. From ωb = 0.314 rad/sec and ωa = 2.51 × 103 rad/sec, and are obtained as follows:
In Figure 12, it can be seen that the approximations of the fractional-order derivatives s0.5 and s0.8 are suitable through comparing the theoretical and approximated bode diagrams. Moreover, as shown in Figure 12a, the PFC based on FOFs results in a phase margin of 179° at 3.21 Hz and provides more stability than the traditional control. As shown in Figure 12b,c, the PFC based on FOFs can simultaneously decrease the amplitude of the vibration transmissibility at high frequencies and the deformation transmissibility at low frequencies. This shows that the amplitudes of the vibration and deformation at the peak are restrained because the FOFs provide a larger gain range for Hv(s) and Hd(s) to coordinate the AVI and positioning.
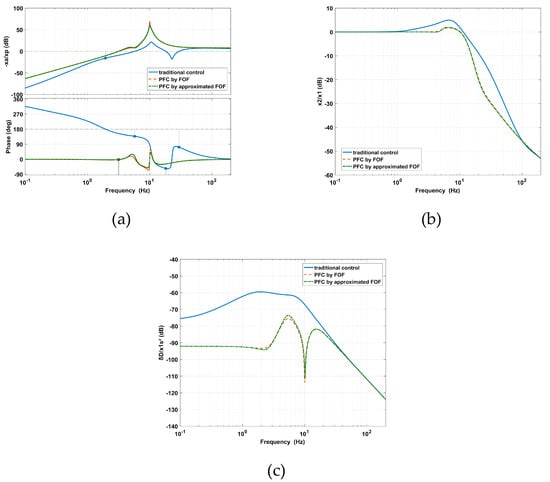
Figure 12.
Comparisons between the traditional control and PFC based on FOFs regarding the (a) open-loop system, (b) vibration transmissibility, and (c) deformation transmissibility.
5. Experimental Verification
5.1. Experimental Setup
As shown in Figure 13, the experimental system was established to verify the PFC. It can be seen that the single-DOF VIP system and the exciter are hung on the frame to avoid additional stiffness and damping along the motion direction. The two mass blocks corresponding to the payload and the base are connected by the supporting unit through two flexure hinges. This ensures that the experimental system is only affected by the axial force. The NI (National Instruments) PXI (Peripheral Component Interconnection extensions for Instrumentation) real-time system collects the feedback signals from the velocity sensor and eddy-current sensor through the PXI-6123 acquisition card and controls the VCM to actuate the VIP system. The LMS (Leuven Measurement & System) SCADAS (Supervisory Control And Data Acquisition) system controls the MB Dynamic MODAL110 instrument to simulate the base excitation and analyzes the control performance according to the vibration signals of the base and the payload, which are collected by the PCB356A17 acceleration sensor.
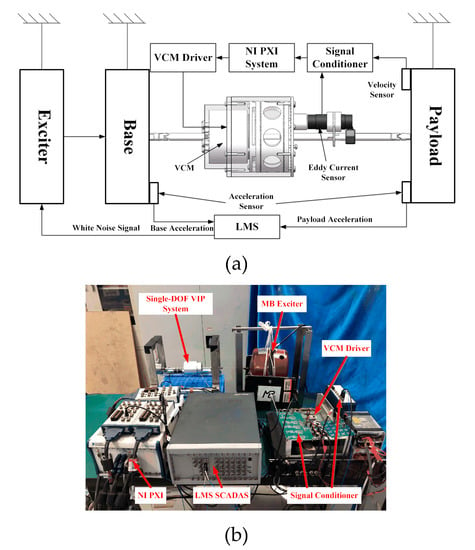
Figure 13.
The experimental setup: (a) schematic diagram and (b) photograph.
5.2. Experimental Results
The experimental analyses of fhp and flp were carried out. The decrease of flp from 29 to 10 Hz due to the effect of flp on the AVI is shown in Figure 14a. The maximum value of the vibration transmissibility increased from 3.93 dB at 7.91 Hz to 10.84 dB at 7.03 Hz. The cross-frequency (where the amplitude of vibration transmissibility is 0 dB) decreased from 11.23 to 9.57 Hz. The performance was improved at high frequencies but deteriorated from 3.32 to 8.7 Hz as flp is equal to 10 Hz and from 3.5 to 9.3 Hz as flp is equal to 15 Hz. In Figure 14b, as the same tendency for flp changes, the maximum value of the deformation transmissibility is enlarged from −58.37 dB at 7.72 Hz to −48.7 dB at 7.23 Hz. The amplitude amplified in the frequency range of 3.6 to 10.45 Hz as flp is equal to 10 Hz, while the amplitude amplified in the frequency range of 3.9 to 10.84 Hz as flp is equal to 15 Hz. The experimental results are consistent with Figure 10.
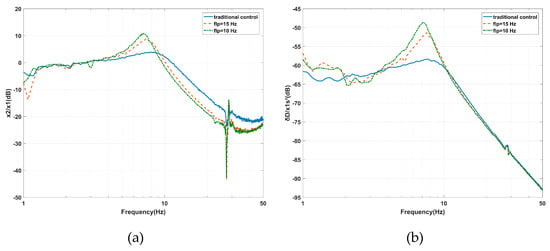
Figure 14.
Experimental results of the effects of the flp effects on the PFC based on IOFs regarding the (a) vibration transmissibility and (b) deformation transmissibility.
The increase of fhp from 1.6 to 4 Hz due to the effect of fhp on the AVI is shown in Figure 15a. The maximum value of the vibration transmissibility is amplified from 3.93 dB at 7.91 Hz to 10.06 dB at 13.07 Hz, while the cross-frequency moves from 11.23 to 13.57 Hz. The amplitudes are amplified in the frequency range of 5.47 to 27.05 Hz because fhp is equal to 3 Hz and from 4.2 to 27.05 Hz because fhp is equal to 4 Hz. The variation trend is consistent with Figure 11a. The influence of fhp on positioning is shown in Figure 15b. The maximum value of the deformation transmissibility is amplified from –58.37 dB at 7.72 Hz to –52.15 dB at 10.06 Hz. The amplitude decreases before 6.64 Hz as fhp is equal to 3 Hz and before 8.11 Hz as fhp is equal to 4 Hz. The amplitude is amplified around the inherent frequency and diminished at low frequencies, similar to that shown in Figure 11b. The results of flp and fhp in terms of the effects on the performance of the AVI and positioning are listed in Table 3.
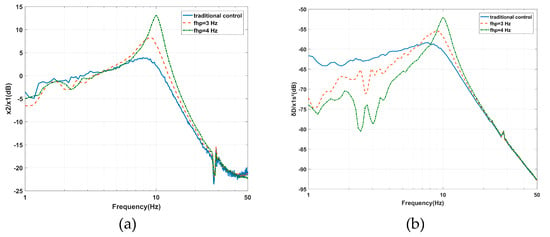
Figure 15.
Experimental results of the effects of the fhp on the PFC based on IOFs regarding the (a) vibration transmissibility and (b) deformation transmissibility.

Table 3.
The performance of AVI and positioning with different flp and fhp values.
The performance of the AVI at high-frequencies and the positioning at low frequencies can be improved by the PFC based on IOFs, however, both the amplitudes of the vibration transmissibility and deformation transmissibility are undesirably amplified around the inherent frequency. To solve this problem, the and filters of the PFC based on FOFs are introduced and the corresponding experiments are carried out. By setting flp as 10 Hz and fhp as 5 Hz, as calculated in Section 4.2, the PFC based on FOFs is compared with the traditional control and the PFC based on IOFs.
As shown in Figure 16a, the PFC based on FOFs moves the cross-frequency to 8.6 Hz and diminishes the maximum value to 3.3 dB at 6.93 Hz for the vibration transmissibility. Compared with the traditional control and the PFC based on IOFs with a fhp value equal to 4 Hz, the PFC based on FOFs improves the AVI performance from 6.54 Hz to the end of the frequency range. It seems that the vibration transmissibility at high frequencies is moved forward. The PFC based on IOFs with an flp value equal to 10 Hz can also achieve this effect at the cost of amplifying the amplitude around the inherent frequency. The AVI performance is improved by the limited control bandwidth of the positioning and the increased gains of kvp and kvd. These targets can be realized by the PFC based on FOFs simultaneously, which is not possible with the PFC based on IOFs.
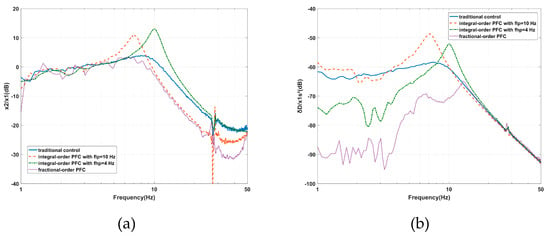
Figure 16.
Experimental results of the effects of the PFC based on FOFs on the: (a) vibration transmissibility and (b) deformation transmissibility.
As shown in Figure 16b, the PFC based on FOFs restrains the maximum value to –64.96 dB at 12.79 Hz for the deformation transmissibility. Compared with the traditional control and the PFC based on IOFs with an flp value equal to 10 Hz, the deformation performance is significantly improved when the frequency is less than 12.7 Hz. The PFC based on IOFs with an fhp value equal to 4 Hz can also enhance the positional stability at low frequencies; however, not to the same degree as with the PFC based on FOFs. The amplitude around the inherent frequency is also amplified. The PFC based on FOFs improves the positioning performance by limiting the control bandwidth of the AVI and increasing the gains of kdp and kdd. The deformation transmissibility starts to increase from about 10 Hz due to the control bandwidth of positioning being limited by the filter.
Significantly, the PFC based on FOFs suppresses the peak amplitude obviously in the natural frequency area, which cannot be avoided when using the IOFs, while the performance of AVI at high frequencies and positioning at low frequencies is also guaranteed.
5.3. Discussion
Three different control strategies are presented in this section, and the control effects are evaluated based on the vibration transmissibility and deformation transmissibility. Compared with the traditional control, the low-frequency positioning using the PFC based on IOFs improves the AVI performance obviously at high frequencies. Both the amplitudes of the vibration transmissibility and deformation transmissibility around the inherent frequency are increased. The attenuation of the RPF via low-frequency positioning is the primary cause of this change. The high-frequency AVI by the PFC based on IOFs improves the positioning performance notably at low frequencies. This introduces the same adverse effects for the peak amplitudes of the vibration transmissibility and deformation transmissibility as the low-frequency positioning does. The requirements for the AVI and positioning are not satisfied by the PFC based on IOFs.
The PFC based on FOFs can overcome the above limitation. The performance of the AVI at low frequencies and the positioning at high frequencies is improved, and both of the peak amplitudes are decreased. The FOFs provide more parameters that can be adjusted, which increases the flexibility of the controller. This gives more choices for the cut-off of the low-frequency positioning and high-frequency AVI, and higher feedback gains for coordination of the AVI and positioning performance.
6. Conclusions
This paper proposes a novel PFC strategy based on FOFs. The PFC can weaken the interaction between the AVI and positioning by using low-frequency positioning and high-frequency AVI. The PFC is verified using a single-DOF supporting system. Compared with the traditional control, the PFC based on IOFs can decrease the amplitude of the vibration transmissibility at high frequencies and the deformation transmissibility at low frequencies. However, both of the amplitudes around the inherent frequency are amplified and the adjustment of the cut-off frequency decreases the stability margin. Thus, the performance of the AVI and positioning cannot be further improved by the limited control gains. The PFC based on FOFs is optimized to overcome this contradiction between the system stability and the VIP performance. Compared with the traditional control, both the maximum value of the vibration and deformation transmissibility are restrained, while the performance of the AVI and positioning is improved in the frequency range from 6.54 Hz to the end and at less than 12.7 Hz, respectively.
Author Contributions
Y.T. conceived and designed the experiment; Y.T. performed the experiment; L.Z. analyzed the data; B.H., X.L., and W.J. contributed materials and supervised the research; Y.T. wrote the original draft preparation. L.Z. and Y.L. reviewed and edited the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number No.51675195, No.51721092 and the National Science and Technology Major Project of China, grant number No.2017ZX02101007-002.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ito, S.; Schitter, G. Comparison and classification of high-precision actuators based on stiffness influencing vibration isolation. IEEE-Asme Trans. Mech. 2015, 21, 1169–1178. [Google Scholar] [CrossRef]
- Butler, H. Position control in lithographic equipment. IEEE Contr. Syst. Mag. 2011, 31, 28–47. [Google Scholar] [CrossRef]
- Kienholz, D.A. Active alignment and vibration control system for a large airborne optical system. In Proceedings of the SPIE-The International Society for Optical Engineering, Newport Beach, CA, USA, 6–8 March 2000; pp. 464–472. [Google Scholar] [CrossRef]
- Heertjes, M.; de Graaff, K.; van der Toorn, J.G. Active vibration isolation of metrology frames; a modal decoupled control design. J. Vib. Acoust. 2005, 127, 223–233. [Google Scholar] [CrossRef]
- Tjepkema, D.; Dijk, J.V.; Soemers, H.M.J.R. Sensor fusion for active vibration isolation in precision equipment. J. Sound. Vib. 2012, 331, 735–749. [Google Scholar] [CrossRef]
- Gong, Z.P.; Ding, L.; Yue, H.H.; Gao, H.B.; Liu, R.Q.; Deng, Z.Q.; Lu, Y.F. System integration and control design of a maglev platform for space vibration isolation. J. Vib. Control 2019, 25, 1720–1736. [Google Scholar] [CrossRef]
- Ma, K.; Ghasemi-Nejhad, M.N. Frequency-weighted adaptive control for simultaneous precision positioning and vibration suppression of smart structures. Smart Mater Struct. 2004, 13, 1143–1154. [Google Scholar] [CrossRef]
- van Dijk, J. Mechatronic design of hard-mount concepts for precision equipment. In Motion and Vibration Control; Springer: Dordrecht, The Netherlands, 2009; pp. 315–324. [Google Scholar]
- Pu, H.Y.; Li, J.M.; Wang, M.; Huang, Y.N.; Sun, Y. Optimum design of an eddy current damper considering the magnetic congregate effect. J. Phys. D Appl. Phys. 2019, 53, 115002. [Google Scholar]
- Pu, H.Y.; Yuan, S.J.; Peng, Y.; Meng, K.; Zhao, J.L.; Xie, R.Q.; Huang, Y.N.; Sun, Y.; Yang, Y.; Xie, S.R.; et al. Multi-layer electromagnetic spring with tunable negative stiffness for semi-active vibration isolation. Mech. Syst. Signal Pr. 2019, 121, 942–960. [Google Scholar]
- Hanieh, A.A. Active isolation and damping of vibrations via Stewart platform. Ph.D. Thesis, Universit’e Libre de Bruxelles, Brussels, Belgium, 2003. [Google Scholar]
- van der Poel, G.W. An exploration of active hard mount vibration isolation for precision equipment. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2010. [Google Scholar]
- Liao, F.H.; Li, X.P.; Yuan, Z.Y. Self-tuning of position feedback and velocity feedback of active vibration isolation system with 6 dofs. Mechanika 2012, 17, 630–636. [Google Scholar] [CrossRef]
- Beijen, M.A.; Heertjes, M.F.; Butler, H.; Steinbuch, M. Practical tuning guide to mixed feedback and feedforward control of soft-mounted vibration isolators. IFAC-PapersOnLine 2016, 49, 163–169. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Dong, W.B.; Liu, W.; Li, Z.F.; Lv, S.M.; Sang, X.R.; Yang, Y. Verification of the microgravity active vibration isolation system based on parabolic flight. Microgravity Sci. Technol. 2017, 29, 415–426. [Google Scholar] [CrossRef]
- Jackson, M.; Kim, Y.; Whorton, M. Design and Analysis of the g-LIMIT Baseline Vibration Isolation Control System. In Proceedings of the AiAA Guidance, Navigation, & Control Conference & Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 5019. [Google Scholar] [CrossRef]
- Yang, X.L.; Wu, H.T.; Chen, B.; Kang, S.Z.; Cheng, S.L. Dynamic modeling and decoupled control of a flexible stewart platform for vibration isolation. J. Sound Vib. 2019, 439, 398–412. [Google Scholar] [CrossRef]
- Yun, Y.; Li, Y. Modeling and control analysis of a 3-pupu dual compliant parallel manipulator for micro positioning and active vibration isolation. J. Dyn. Syst-T. Asme. 2012, 134, 021001. [Google Scholar] [CrossRef]
- Zhu, W.H.; Tryggvason, B.; Piedboeuf, J.C. On active acceleration control of vibration isolation systems. Control Eng. Pract. 2006, 14, 863–873. [Google Scholar] [CrossRef]
- Matichard, F.; Lantz, B.; Mason, K.; Mittleman, R.; Abbott, B.; Abbott, S.; Allwine, E.; Barnum, S.; Birch, J.; Biscans, S.; et al. Advanced LIGO two-stage twelve-axis vibration isolation and positioning platform. Part 1: Design and production overview. Precis. Eng. 2015, 40, 273–286. [Google Scholar]
- Thayer, D.; Campbell, M.; Flotow, A.V.; Vagners, J. Six-axis vibration isolation system using soft actuators and multiple sensors. J. Spacecr. Rocket. 2012, 39, 206–212. [Google Scholar] [CrossRef]
- Coopmans, C.; Jensen, A.M.; Chen, Y.Q. Fractional-order complementary filters for small unmanned aerial system navigation. J. Intell. Robot Syst. 2014, 73, 429–453. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, T.; Zhou, L.; Chen, Y.Q. Pre-filtering and head-dependent adaptive feed-forward compensation for translation vibration in hard-disc-drive. Mechatronics 2015, 27, 13–19. [Google Scholar] [CrossRef]
- Charef, M.; Charef, A. Fractional order controller based on the fractionalization of PID controller. In Proceedings of the 2017 5th International Conference on Electrical Engineering-Boumerdes (ICEE-B), Boumerdes, Algeria, 29–31 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Zheng, W.J.; Luo, Y.; Wang, X.H.; Pi, Y.G.; Chen, Y.Q. Fractional order piλdμ controller design for satisfying time and frequency domain specifications simultaneously. ISA Trans. 2017, 68, 212–222. [Google Scholar] [CrossRef]
- Fleming, A.J. Nanopositioning system with force feedback for high-performance tracking and vibration control. IEEE-Asme. T. Mech. 2010, 15, 433–447. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Soltan, A.; Radwan, A.G.; Soliman, A.M. Fractional order filter with two fractional elements of dependent orders. Microelectron. J. 2012, 43, 818–827. [Google Scholar] [CrossRef]
- Radwan, A.G.; Elwakil, A.S.; Soliman, A.M. On the generalization of second-order filters to the fractional-order domain. J. Circuit Syst. Comp. 2009, 18, 361–386. [Google Scholar] [CrossRef]
- Ma, C.; Hori, Y. Fractional-order control: Theory and applications in motion control [past and present]. IEEE Ind. Electron. Mag. 2007, 1, 6–16. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. I 2002, 47, 25–39. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).