An Evaluation of Three Kinematic Methods for Gait Event Detection Compared to the Kinetic-Based ‘Gold Standard’
Abstract
1. Introduction
2. Materials and Methods
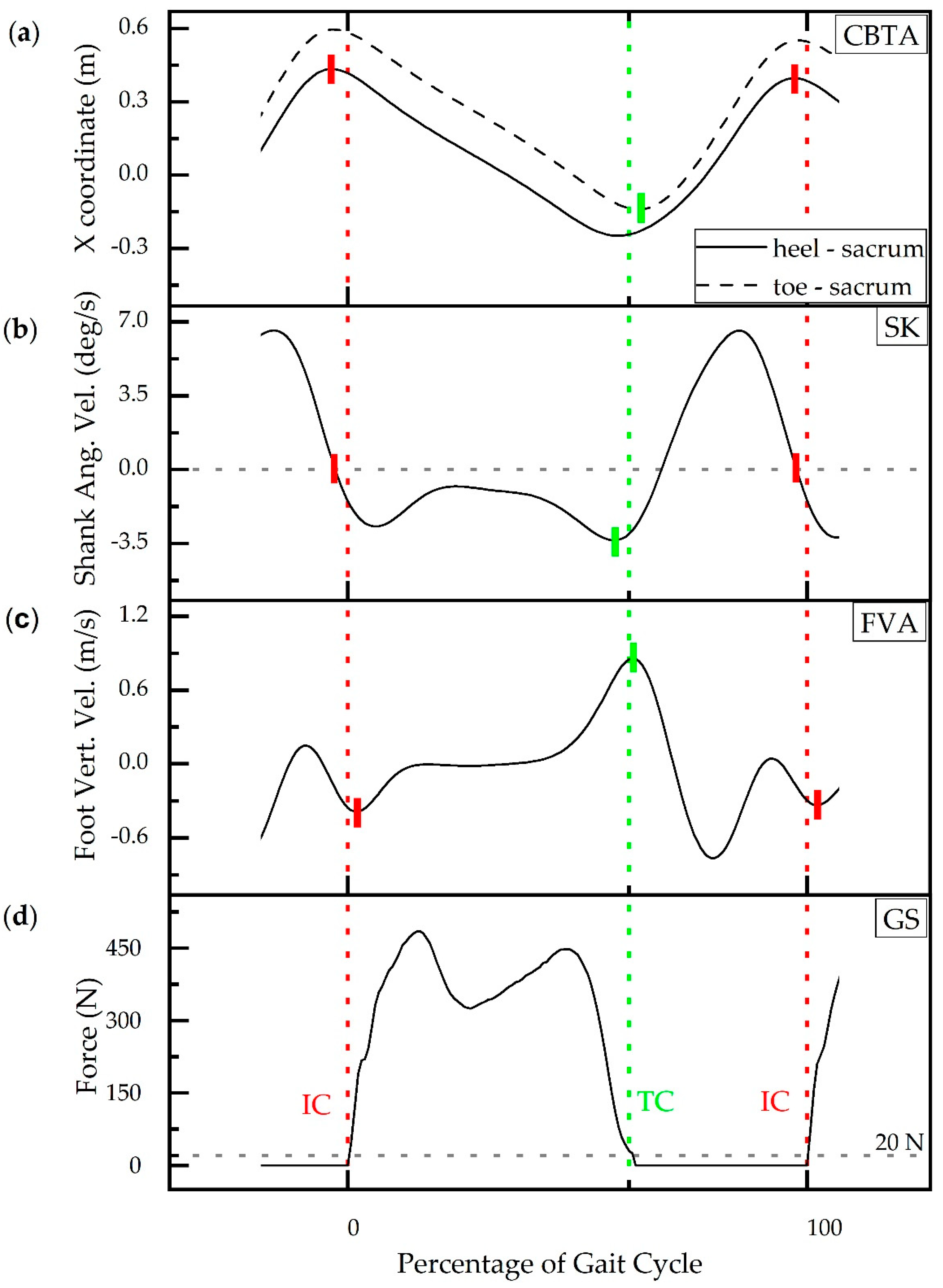
2.1. Gait Event Detection Methods (GEDM)
2.2. Experimental Protocol
2.3. Statistical Analysis
2.3.1. Overall Performance
2.3.2. Covariates
2.3.3. Statistical Modeling
3. Results
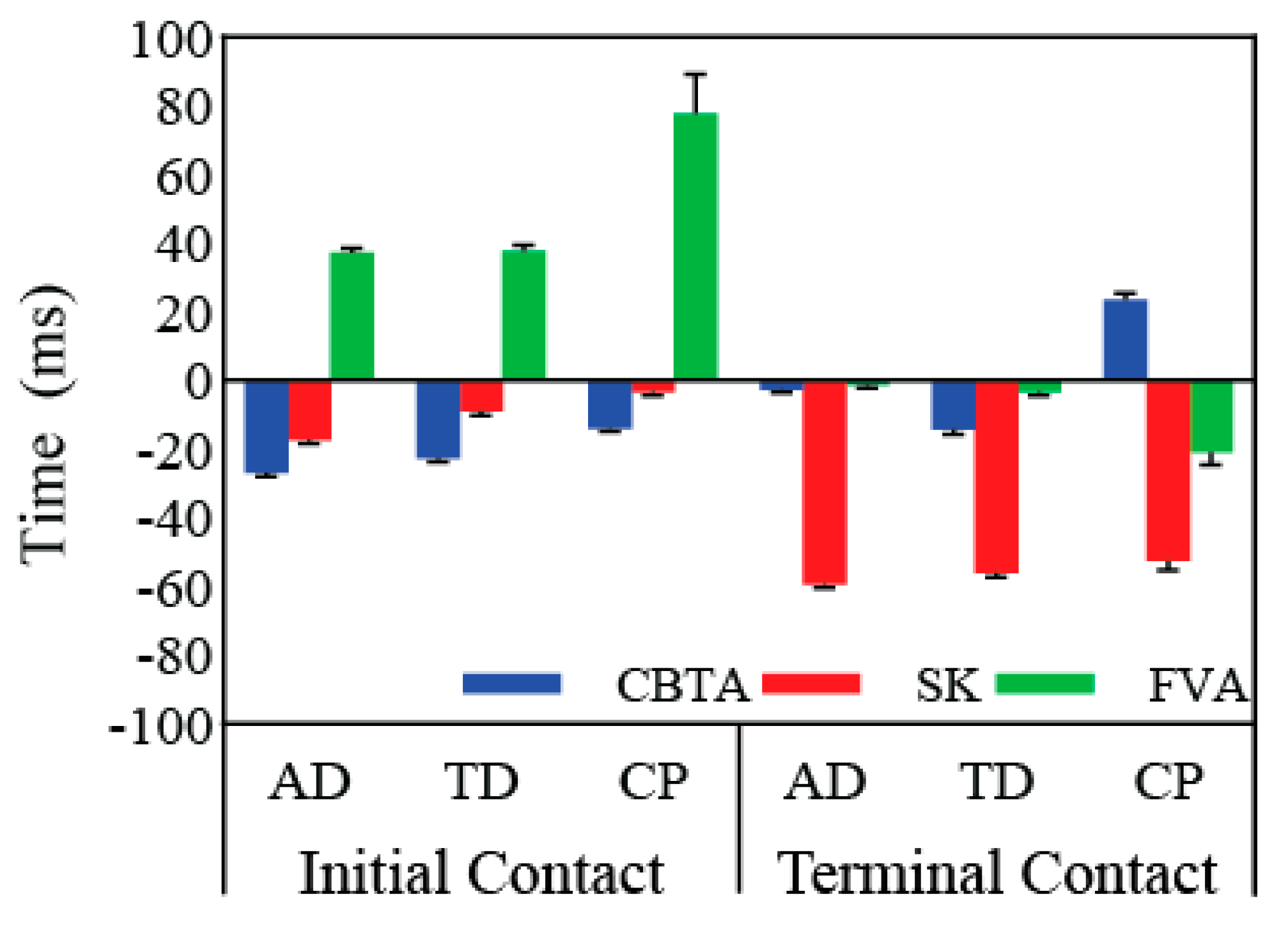
3.1. Overall Performance
3.2. Statistical Modeling
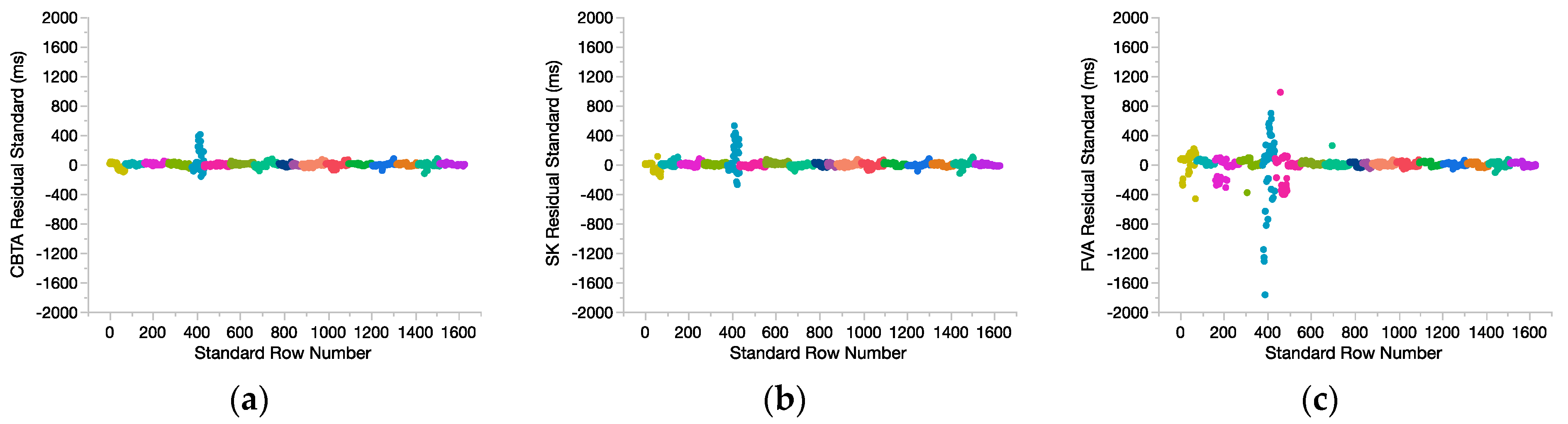
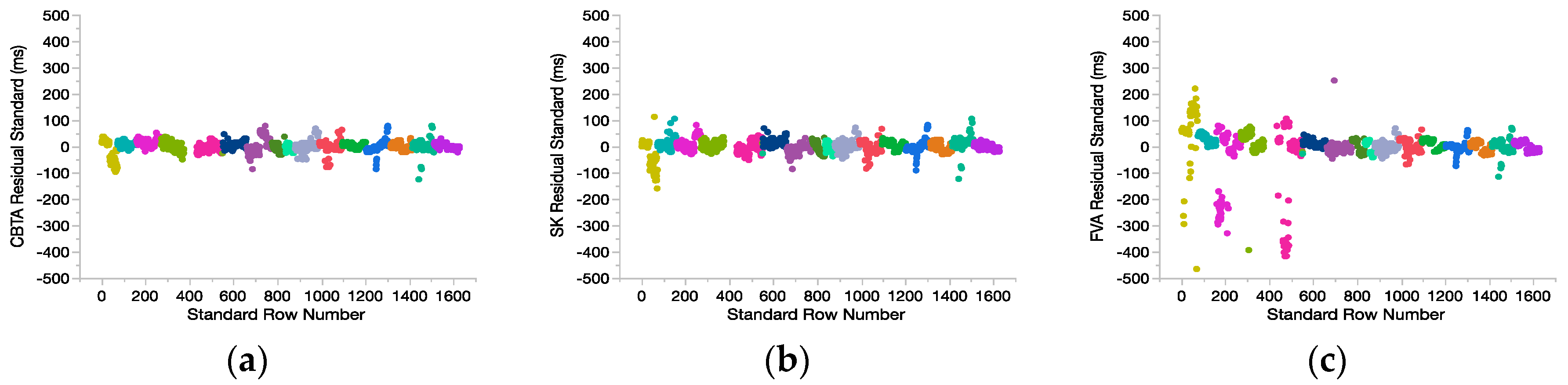
3.2.1. Fit Diagnostics: Data Reduction
3.2.2. Model Development
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Raccagni, C.; Gaßner, H.; Eschlboeck, S.; Boesch, S.; Krismer, F.; Seppi, K.; Poewe, W.; Eskofier, B.M.; Winkler, J.; Wenning, G.; et al. Sensor-based gait analysis in atypical parkinsonian disorders. Brain Behav. 2018, 8, e00977. [Google Scholar] [CrossRef] [PubMed]
- Bello, O.; Fernandez-Del-Olmo, M. How Does the Treadmill Affect Gait in Parkinsons Disease? Curr. Aging Sci. 2012, 5, 28–34. [Google Scholar] [CrossRef]
- Pistacchi, M.; Gioulis, M.; Sanson, F.; de Giovannini, E.; Filippi, G.; Rossetto, F.; Marsala, S.Z. Gait analysis and clinical correlations in early Parkinson’s disease. Funct. Neurol. 2017, 32, 28–34. [Google Scholar] [CrossRef] [PubMed]
- Sloot, L.H.; Harlaar, J.; van der Krogt, M.M. Self-paced versus fixed speed walking and the effect of virtual reality in children with cerebral palsy. Gait Posture 2015, 42, 498–504. [Google Scholar] [CrossRef]
- Behboodi, A.; Zahradka, N.; Wright, H.; Alesi, J.; Lee, S.C.K. Real-time detection of seven phases of gait in children with cerebral palsy using two gyroscopes. Sensors 2019, 19, 2517. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, H.; Awad, L.N.; Palmer, J.A.; Higginson, J.S.; Binder-Macleod, S.A. Contribution of Paretic and Nonparetic Limb Peak Propulsive Forces to Changes in Walking Speed in Individuals Poststroke. Neurorehabil. Neural Repair 2015, 30, 743–752. [Google Scholar] [CrossRef]
- Mulroy, S.; Gronley, J.A.; Weiss, W.; Newsam, C.; Perry, J. Use of cluster analysis for gait pattern classification of patients in the early and late recovery phases following stroke. Gait Posture 2003, 18, 114–125. [Google Scholar] [CrossRef]
- Palmer, J.A.; Hsiao, H.Y.; Wright, T.; Binder-Macleod, S.A. Single session of functional electrical stimulation-assisted walking produces corticomotor symmetry changes related to changes in poststroke walking mechanics. Phys. Ther. 2017, 97, 550–560. [Google Scholar] [CrossRef]
- Chen, G.; Patten, C.; Kothari, D.H.; Zajac, F.E. Gait deviations associated with post-stroke hemiparesis: Improvement during treadmill walking using weight support, speed, support stiffness, and handrail hold. Gait Posture 2005, 22, 57–62. [Google Scholar] [CrossRef]
- Whittle, M.W. Gait Analysis: An Introduction, 4th ed.; Elsevier Ltd.: Philadelphia, PA, USA, 2007; ISBN 9780750688833. [Google Scholar]
- O’Connor, C.M.; Thorpe, S.K.; O’Malley, M.J.; Vaughan, C.L. Automatic detection of gait events using kinematic data. Gait Posture 2007, 25, 469–474. [Google Scholar] [CrossRef]
- Zeni, J.A.; Richards, J.G.; Higginson, J.S. Two simple methods for determining gait events during treadmill and overground walking using kinematic data. Gait Posture 2008, 27, 710–714. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Zheng, J.; Wang, Y.; Song, Z.; Zhan, E. Adaptive method for real-time gait phase detection based on ground contact forces. Gait Posture 2015, 41, 269–275. [Google Scholar] [CrossRef]
- Zheng, E.; Vitiello, N.; Wang, Q. Gait phase detection based on non-contact capacitive sensing: Preliminary results. In Proceedings of the IEEE International Conference on Rehabilitation Robotics, Singapore, 11–14 August 2015; Nanyang Technological University: Singapore, 2015; Volume 2015, pp. 43–48. [Google Scholar]
- Senanayake, C.M.; Senanayake, S.M.N.A.N.A. Computational intelligent gait-phase detection system to identify pathological gait. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 1173–1179. [Google Scholar] [CrossRef] [PubMed]
- Tong, K.; Granat, M.H. A practical gait analysis system using gyroscopes. Med. Eng. Phys. 1999, 21, 87–94. [Google Scholar] [CrossRef]
- Halliday, S.E.; Winter, D.A.; Frank, J.S.; Patla, A.E.; Prince, F. The initiation of gait in young, elderly, and Parkinson’s disease subjects. Gait Posture 1998, 8, 8–14. [Google Scholar] [CrossRef]
- Holsbeeke, L.; Ketelaar, M.; Schoemaker, M.M.; Gorter, J.W. Capacity, Capability, and Performance: Different Constructs or Three of a Kind? Arch. Phys. Med. Rehabil. 2009, 90, 849–855. [Google Scholar] [CrossRef] [PubMed]
- Smits, D.W.; Gorter, J.W.; Van Schie, P.E.; Dallmeijer, A.J.; Ketelaar, M. How do changes in motor capacity, motor capability, and motor performance relate in children and adolescents with cerebral palsy? Arch. Phys. Med. Rehabil. 2014, 95, 1577–1584. [Google Scholar] [CrossRef] [PubMed]
- Van Eck, M.; Dallmeijer, A.J.; Voorman, J.M.; Becher, J.G. Longitudinal study of motor performance and its relation to motor capacity in children with cerebral palsy. Dev. Med. Child Neurol. 2009, 51, 303–310. [Google Scholar] [CrossRef]
- Catalfamo, P.; Ghoussayni, S.; Ewins, D. Gait event detection on level ground and incline walking using a rate gyroscope. Sensors 2010, 10, 5683–5702. [Google Scholar] [CrossRef]
- Taborri, J.; Scalona, E.; Palermo, E.; Rossi, S.; Cappa, P. Validation of inter-subject training for hidden markov models applied to gait phase detection in children with Cerebral Palsy. Sensors 2015, 15, 24514–24529. [Google Scholar] [CrossRef]
- Gouwanda, D.; Gopalai, A.A. A robust real-time gait event detection using wireless gyroscope and its application on normal and altered gaits. Med. Eng. Phys. 2015, 37, 219–225. [Google Scholar] [CrossRef] [PubMed]
- Aminian, K.; Najafi, B.; Büla, C.; Leyvraz, P.F.; Robert, P. Spatio-temporal parameters of gait measured by an ambulatory system using miniature gyroscopes. J. Biomech. 2002, 35, 689–699. [Google Scholar] [CrossRef]
- Zeni, J.A.; Higginson, J.S. Gait parameters and stride-to-stride variability during familiarization to walking on a split-belt treadmill. Clin. Biomech. 2010, 25, 383–386. [Google Scholar] [CrossRef] [PubMed]
- Monaghan, C.C.; van Riel, W.J.B.M.; Veltink, P.H. Control of triceps surae stimulation based on shank orientation using a uniaxial gyroscope during gait. Med. Biol. Eng. Comput. 2009, 47, 1181–1188. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.K.; Park, E.J. Quasi real-time gait event detection using shank-attached gyroscopes. Med. Biol. Eng. Comput. 2011, 49, 707–712. [Google Scholar] [CrossRef] [PubMed]
- Rueterbories, J.; Spaich, E.G.; Larsen, B.; Andersen, O.K. Methods for gait event detection and analysis in ambulatory systems. Med. Eng. Phys. 2010, 32, 545–552. [Google Scholar] [CrossRef]
- Rueterbories, J.; Spaich, E.G.; Andersen, O.K. Gait event detection for use in FES rehabilitation by radial and tangential foot accelerations. Med. Eng. Phys. 2014, 36, 502–508. [Google Scholar] [CrossRef]
- Senanayake, C.M.N.A.; Senanayake, S.M.N.A.; Jasiewicz, J.M.; Allum, J.H.J.; Middleton, J.W.; Barriskill, A.; Condie, P.; Purcell, B.; Li, R.C.T.; Skelly, M.M.; et al. BIONic WalkAide for correcting foot drop. Gait Posture 2005, 15, 242–246. [Google Scholar] [CrossRef]
- Yang, C.C.; Hsu, Y.L. A review of accelerometry-based wearable motion detectors for physical activity monitoring. Sensors 2010, 10, 7772–7788. [Google Scholar] [CrossRef]
- Lauer, R.T.; Smith, B.T.; Coiro, D.; Betz, R.R.; McCarthy, J. Feasibility of gait event detection using intramuscular electromyography in the child with cerebral palsy. Neuromodulation 2004, 7, 205–213. [Google Scholar] [CrossRef]
- Lauer, R.T.; Smith, B.T.; Betz, R.R. Application of a neuro-fuzzy network for gait event detection using electromyography in the child with cerebral palsy. IEEE Trans. Biomed. Eng. 2005, 52, 1532–1540. [Google Scholar] [CrossRef]
- Skelly, M.M.; Chizeck, H.J. Real-time gait event detection for paraplegic FES walking. IEEE Trans. Neural Syst. Rehabil. Eng. 2001, 9, 59–68. [Google Scholar] [CrossRef]
- Smith, B.T.; Coiro, D.J.; Finson, R.; Betz, R.R.; McCarthy, J. Evaluation of force-sensing resistors for gait event detection to trigger electrical stimulation to improve walking in the child with cerebral palsy. IEEE Trans. Neural Syst. Rehabil. Eng. 2002, 10, 22–29. [Google Scholar] [CrossRef] [PubMed]
- Kotiadis, D.; Hermens, H.J.; Veltink, P.H. Inertial Gait Phase Detection for control of a drop foot stimulator. Inertial sensing for gait phase detection. Med. Eng. Phys. 2010, 32, 287–297. [Google Scholar] [CrossRef] [PubMed]
- Sale, P.; Franceschini, M.; Waldner, A.; Hesse, S. Use of the robot assisted gait therapy in rehabilitation of patients with stroke and spinal cord injury. Eur. J. Phys. Rehabil. Med. 2012, 48, 111–121. [Google Scholar] [PubMed]
- Awad, L.N.; Awad, L.N.; Awad, L.N.; Esquenazi, A.; Francisco, G.E.; Nolan, K.J.; Nolan, K.J.; Jayaraman, A.; Jayaraman, A. The ReWalk ReStoreTM soft robotic exosuit: A multi-site clinical trial of the safety, reliability, and feasibility of exosuit-augmented post-stroke gait rehabilitation. J. Neuroeng. Rehabil. 2020, 17, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Esquenazi, A.; Talaty, M.; Packel, A.; Saulino, M. The Rewalk powered exoskeleton to restore ambulatory function to individuals with thoracic-level motor-complete spinal cord injury. Am. J. Phys. Med. Rehabil. 2012, 91, 911–921. [Google Scholar] [CrossRef]
- Zahradka, N.; Behboodi, A.; Wright, H.; Bodt, B.; Lee, S. Evaluation of gait phase detection delay compensation strategies to control a gyroscope-controlled functional electrical stimulation system during walking. Sensors 2019, 19, 2471. [Google Scholar] [CrossRef]
- Behboodi, A.; Zahradka, N.; Alesi, J.; Wright, H.; Lee, S.C.K. Use of a Novel Functional Electrical Stimulation Gait Training System in 2 Adolescents With Cerebral Palsy: A Case Series Exploring Neurotherapeutic Changes. Phys. Ther. 2019, 99, 739–747. [Google Scholar] [CrossRef]
- Fitzmaurice, G.M.; Laird, N.M.; Ware, J.H. Applied Longitudinal Analysis, 2nd ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Teufl, W.; Lorenz, M.; Miezal, M.; Taetz, B.; Fröhlich, M.; Bleser, G. Towards inertial sensor based mobile gait analysis: Event-detection and spatio-temporal parameters. Sensors 2018, 1, 38. [Google Scholar] [CrossRef]
- Park, S.; Ryu, K.; Kim, J.; Son, J.; Kim, Y. Verification of accuracy and validity of gait phase detection system using motion sensors for applying walking assistive FES. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 1129–1135. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Wang, Z.; Gao, Q.; Hassan, M.M.; Alelaiwi, A. Smooth estimation of human foot motion for zero-velocity-update-aided inertial pedestrian navigation system. Sens. Rev. 2015, 35, 389–400. [Google Scholar] [CrossRef]
- Alvarez, J.C.; González, R.C.; Alvarez, D.; López, A.M.; Rodríguez-Uría, J. Multisensor approach to walking distance estimation with foot inertial sensing. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology—Proceedings, Lyon, France, 22–26 August 2007; pp. 5719–5722. [Google Scholar]
- Zhao, H.; Wang, Z.; Qiu, S.; Shen, Y.; Zhang, L.; Tang, K.; Fortino, G. Heading Drift Reduction for Foot-Mounted Inertial Navigation System via Multi-Sensor Fusion and Dual-Gait Analysis. IEEE Sens. J. 2019, 19, 8514–8521. [Google Scholar] [CrossRef]
- Desailly, E.; Daniel, Y.; Sardain, P.; Lacouture, P. Foot contact event detection using kinematic data in cerebral palsy children and normal adults gait. Gait Posture 2009, 29, 76–80. [Google Scholar] [CrossRef] [PubMed]
- Jasiewicz, J.M.; Allum, J.H.J.; Middleton, J.W.; Barriskill, A.; Condie, P.; Purcell, B.; Li, R.C.T. Gait event detection using linear accelerometers or angular velocity transducers in able-bodied and spinal-cord injured individuals. Gait Posture 2006, 24, 502–509. [Google Scholar] [CrossRef]
- Behboodi, A.; Wright, H.; Zahradka, N.; Lee, S.C.K. Seven phases of gait detected in real-time using shank attached gyroscopes. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Milan, Italy, 25–29 August 2015; Volume 2015, pp. 5529–5532. [Google Scholar]
- Schuy, J.; Stech, N.; Harris, G.; Beckerle, P.; Zahedi, S.; Rinderknecht, S. A Prosthetic Shank with Adaptable Torsion Stiffness and Foot Alignment. Front. Neurorobot. 2020, 14. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.T.; Novak, A.C.; Brouwer, B.; Li, Q. Estimation of spatio-temporal parameters for post-stroke hemiparetic gait using inertial sensors. Gait Posture 2013, 37, 354–358. [Google Scholar] [CrossRef]
| Gait Event | CBTA | SK | FVA | |||
|---|---|---|---|---|---|---|
| Mean | SE | Mean | SE | Mean | SE | |
| Initial contact | −21.54 | 0.66 | −10.45 | 0.74 | 49.50 | 3.43 |
| Terminal contact | 2.47 | 0.96 | −56.20 | 1.02 | −6.88 | 1.33 |
| Gait Event | Group | CBTA | SK | FVA |
|---|---|---|---|---|
| Initial contact | AD | 33.10 | 26.53 | 42.06 |
| TD | 27.53 | 22.55 | 44.13 | |
| CP | 20.43 | 17.06 | 182.03 | |
| Terminal contact | AD | 14.98 | 62.44 | 14.76 |
| TD | 27.79 | 58.69 | 15.82 | |
| CP | 35.09 | 66.73 | 61.91 |
| Kinetic | Kinematic | ||||
|---|---|---|---|---|---|
| Gait Event | Group | GS | CBTA | SK | FVA |
| Initial contact | AD | 100.0 | 95.3 | 95.9 | 96.6 |
| TD | 99.5 | 97.3 | 95.5 | 95.0 | |
| CP | 99.2 | 94.8 | 94.8 | 87.1 | |
| Terminal contact | AD | 99.7 | 95.6 | 97.5 | 96.2 |
| TD | 100.0 | 96.8 | 97.2 | 95.9 | |
| CP | 100.0 | 95.1 | 95.5 | 95.1 | |
| Model | Marginal Coefficient | Standard Error | p-Value | Marginal RMSE (ms) | Conditional RMSE (ms) |
|---|---|---|---|---|---|
| Full (CBTA) | 20.00 | 18.93 | |||
| CBTA | 0.99999 | 0.00006 | <0.0001 | ||
| Intercept | 7.78694 | 4.82735 | 0.1262 | ||
| Reduced (CBTA+IC) | 22.49 | 19.16 | |||
| CBTA | 0.99998 | 0.00006 | <0.0001 | ||
| IC | 24.0017 | 0.99473 | <0.0001 | ||
| Intercept | −2.98337 | 3.40686 | 0.3985 | ||
| Final (CBTA) | 25.50 | 22.61 | |||
| CBTA | 1.00001 | 0.00007 | <0.0001 | ||
| Intercept | 8.63979 | 3.41579 | 0.0298 | ||
| Full(SK) | 24.14 | 21.82 | |||
| SK | 0.99994 | 0.00005 | <0.0001 | ||
| Intercept | 55.0062 | 5.34258 | <0.0001 | ||
| Reduced (SK+IC) | 24.52 | 21.87 | |||
| SK | 0.99994 | 0.00005 | <0.0001 | ||
| IC | −45.7127 | 1.12596 | <0.0001 | ||
| Intercept | 56.2336 | 2.89395 | <0.0001 | ||
| Final (SK) | 33.53 | 32.03 | |||
| SK | 0.99996 | 0.00008 | <0.0001 | ||
| Intercept | 33.3328 | 2.91872 | <0.0001 | ||
| Full (FVA) | 70.02 | 65.07 | |||
| FVA | 0.99989 | 0.00024 | <0.0001 | ||
| Intercept | 13.4269 | 13.7265 | 0.3442 | ||
| Reduced (FVA+IC) | 70.10 | 65.10 | |||
| FVA | 0.99989 | 0.00024 | <0.0001 | ||
| IC | −57.4868 | 3.41134 | <0.0001 | ||
| Intercept | 10.7528 | 7.46160 | 0.1689 | ||
| Final (FVA) | 75.56 | 71.19 | |||
| FVA | 0.99994 | 0.00026 | <0.0001 | ||
| Intercept | −18.3814 | 7.15659 | 0.0222 |
| Gait Event | Group | Sensor | Motion Capture |
|---|---|---|---|
| Initial contact | AD | 32 | 27 |
| TD | 52 | 23 | |
| CP | 63 | 17 | |
| Terminal contact | AD | 33 | 62 |
| TD | 70 | 59 | |
| CP | 81 | 67 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zahradka, N.; Verma, K.; Behboodi, A.; Bodt, B.; Wright, H.; Lee, S.C.K. An Evaluation of Three Kinematic Methods for Gait Event Detection Compared to the Kinetic-Based ‘Gold Standard’. Sensors 2020, 20, 5272. https://doi.org/10.3390/s20185272
Zahradka N, Verma K, Behboodi A, Bodt B, Wright H, Lee SCK. An Evaluation of Three Kinematic Methods for Gait Event Detection Compared to the Kinetic-Based ‘Gold Standard’. Sensors. 2020; 20(18):5272. https://doi.org/10.3390/s20185272
Chicago/Turabian StyleZahradka, Nicole, Khushboo Verma, Ahad Behboodi, Barry Bodt, Henry Wright, and Samuel C. K. Lee. 2020. "An Evaluation of Three Kinematic Methods for Gait Event Detection Compared to the Kinetic-Based ‘Gold Standard’" Sensors 20, no. 18: 5272. https://doi.org/10.3390/s20185272
APA StyleZahradka, N., Verma, K., Behboodi, A., Bodt, B., Wright, H., & Lee, S. C. K. (2020). An Evaluation of Three Kinematic Methods for Gait Event Detection Compared to the Kinetic-Based ‘Gold Standard’. Sensors, 20(18), 5272. https://doi.org/10.3390/s20185272








