A Review on Electrical Impedance Tomography Spectroscopy
Abstract
1. Introduction
2. Physical Principles of EITS
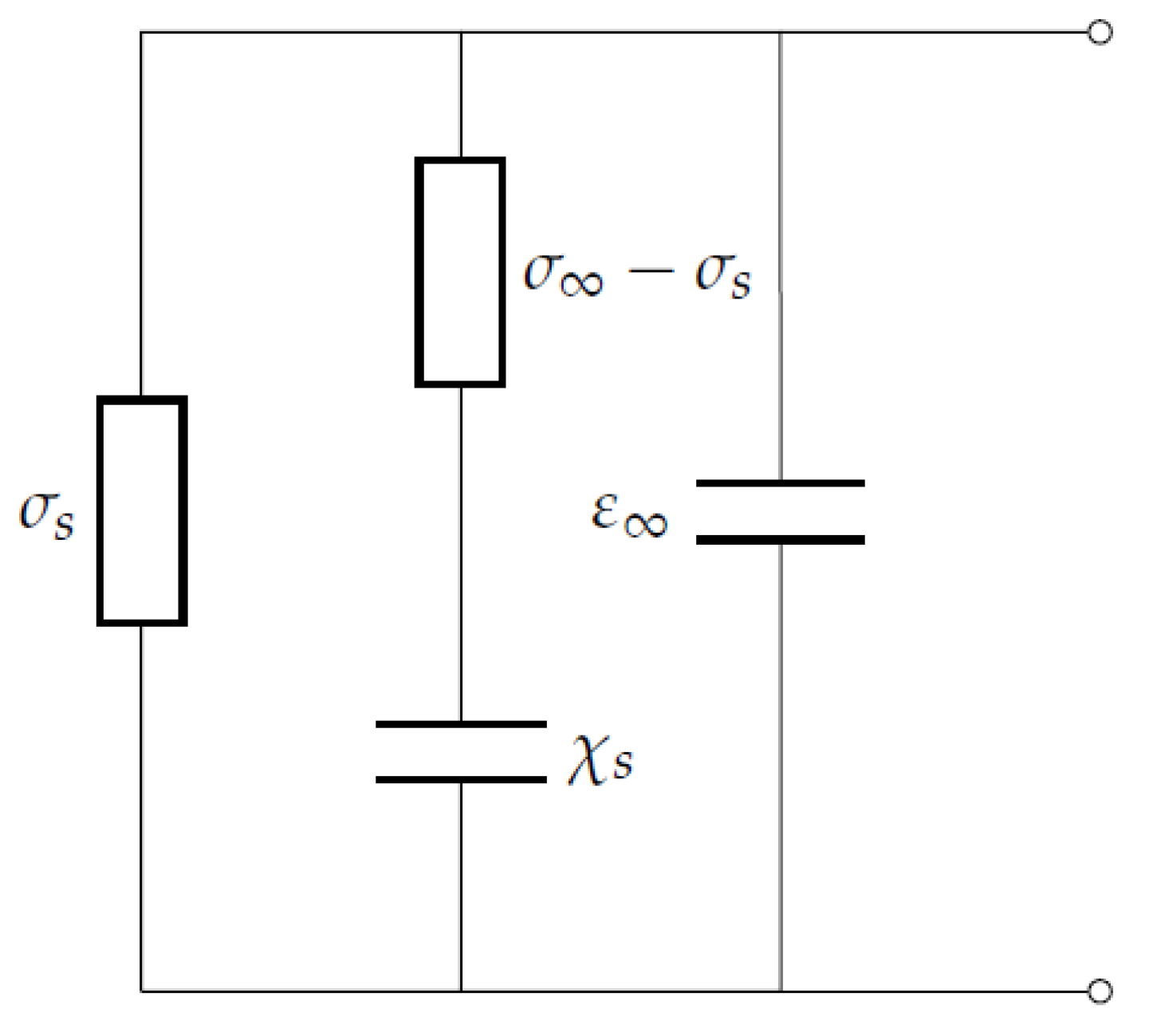
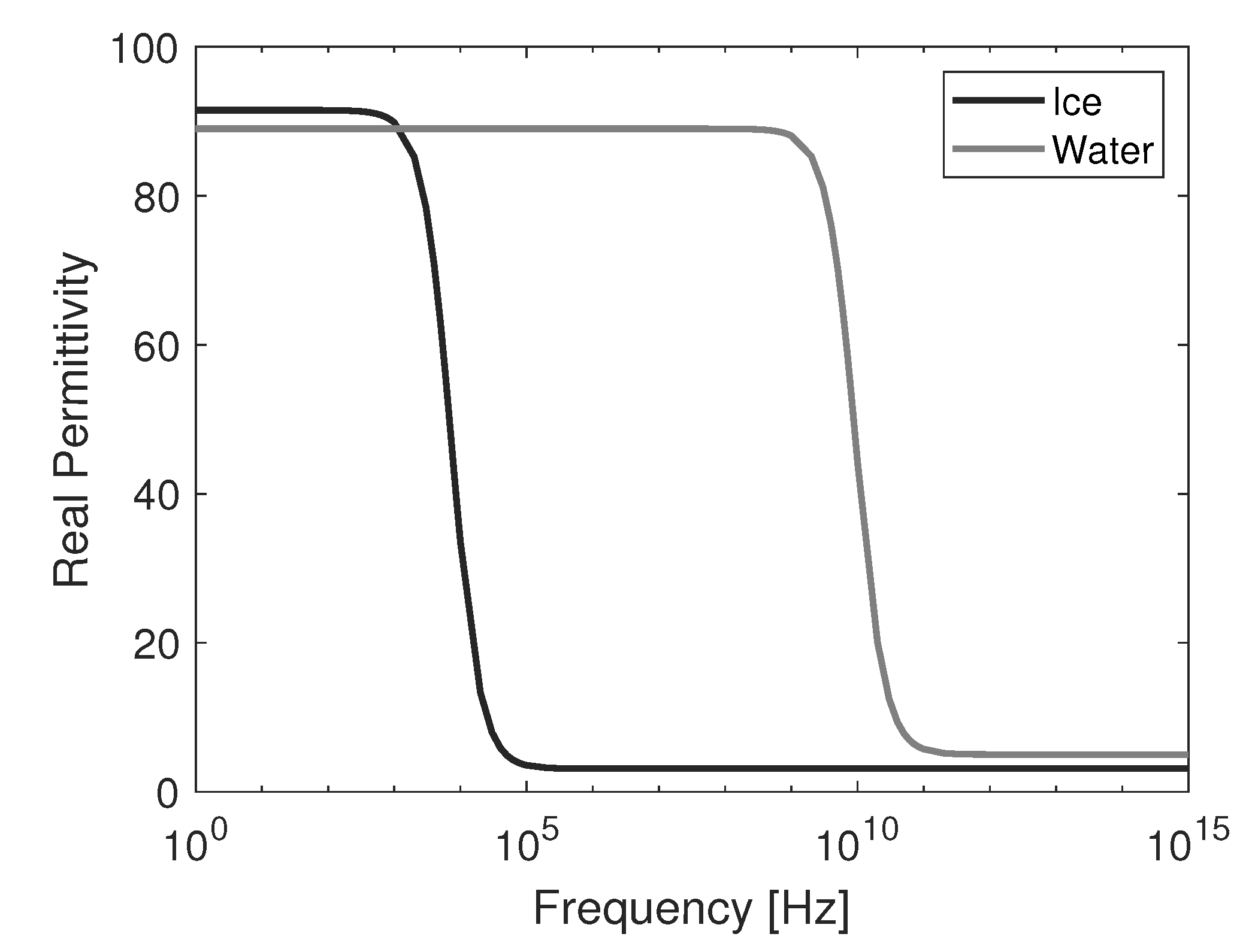
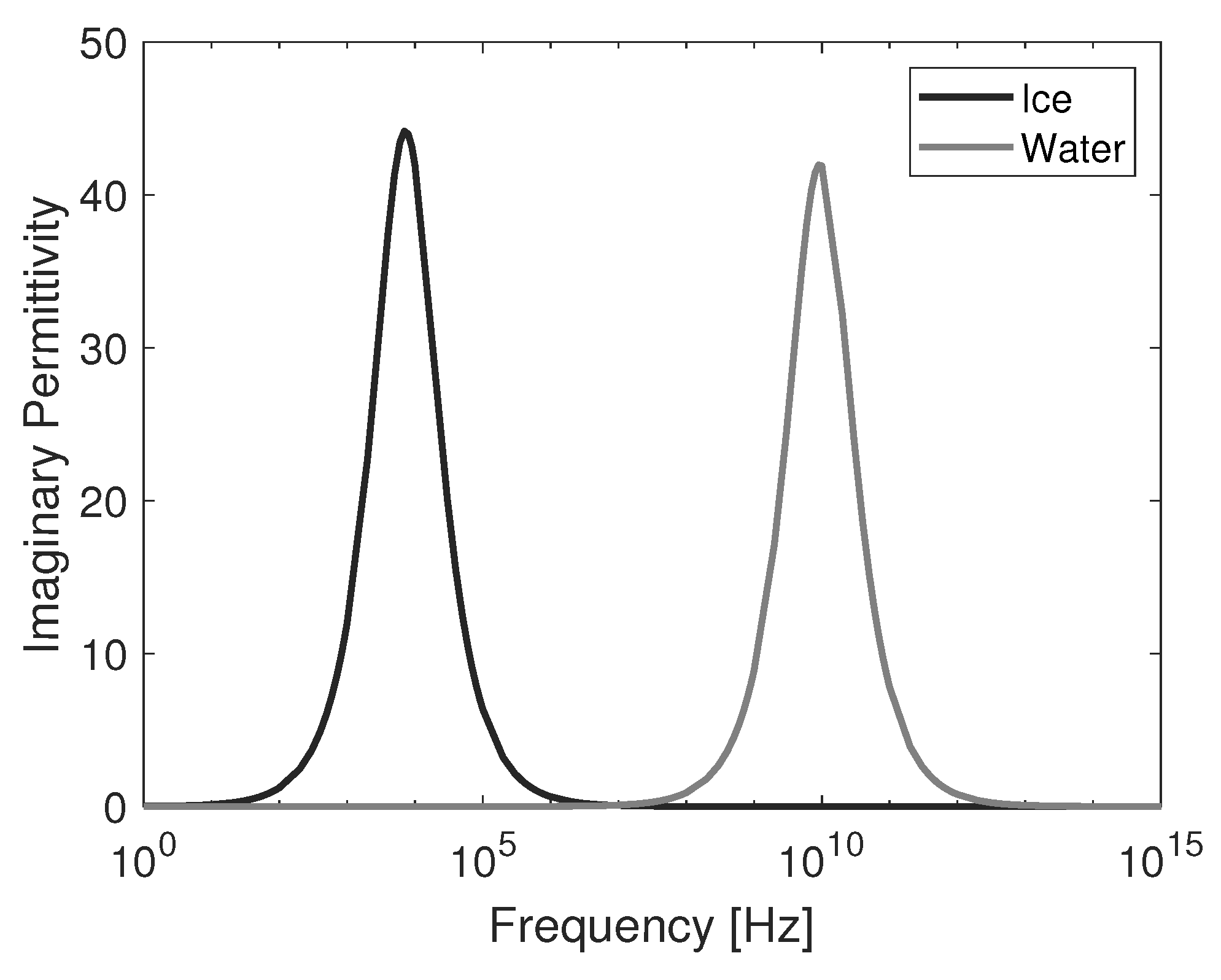
3. Electrical Characteristics of Materials
4. Sensing Methods
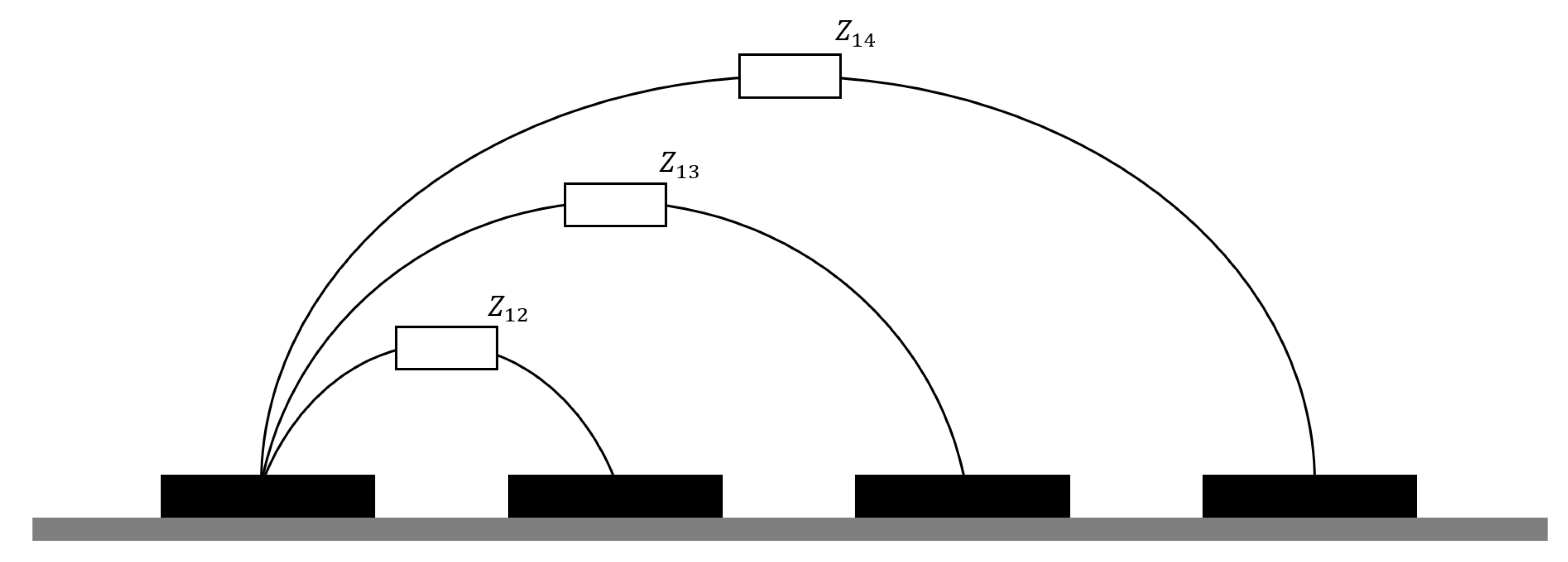
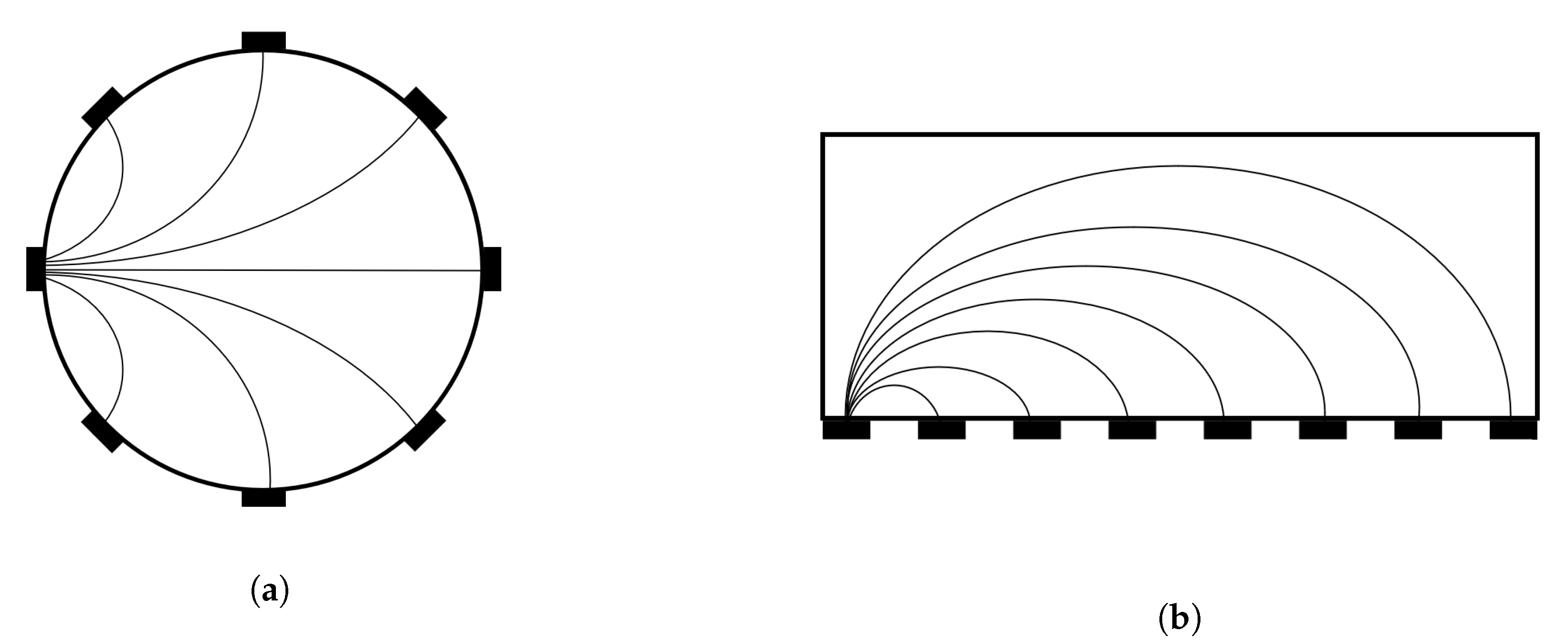
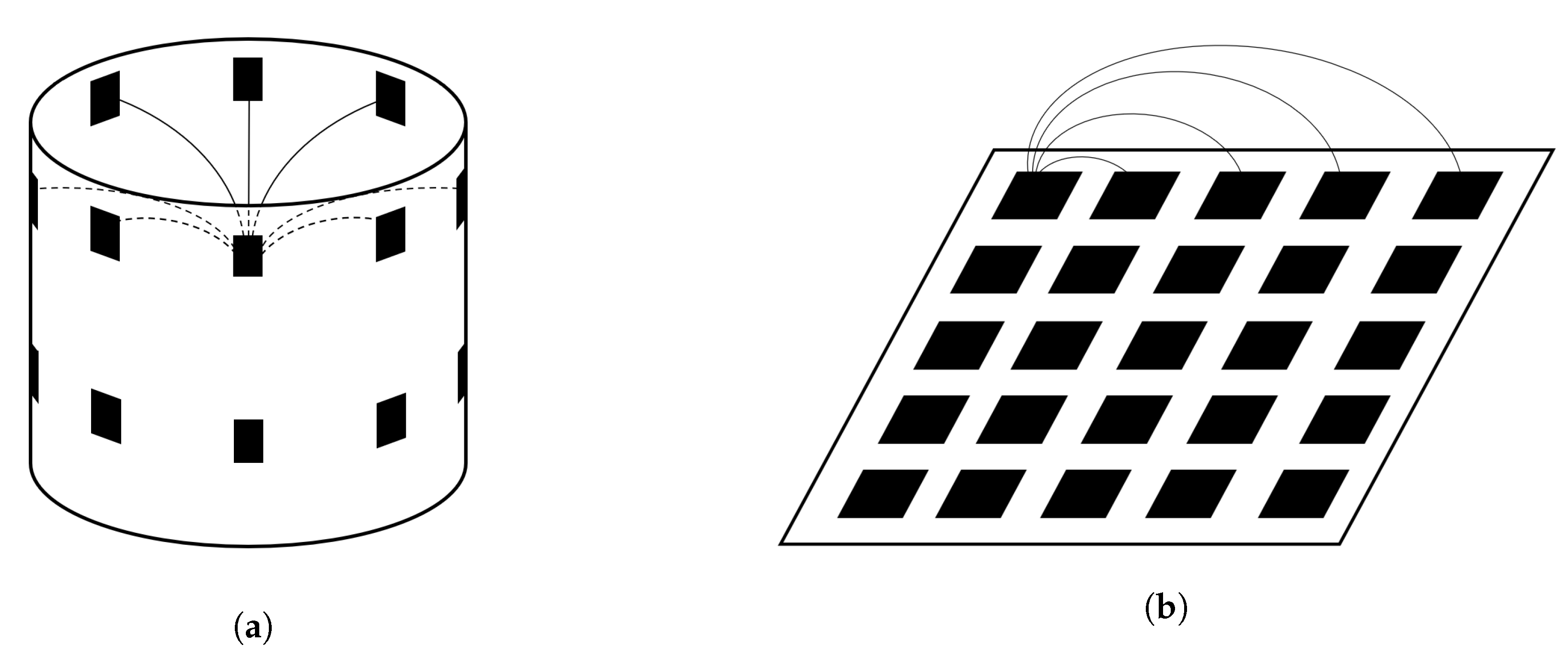
4.1. Electrode Geometry
4.1.1. Two-Dimensional EITS
4.1.2. Three-Dimensional EITS
4.2. Measurement Systems
4.3. Measurement Noise and Error
5. Image Reconstruction Algorithm
5.1. Main Algorithms Used for EITS
5.2. Recent Developments
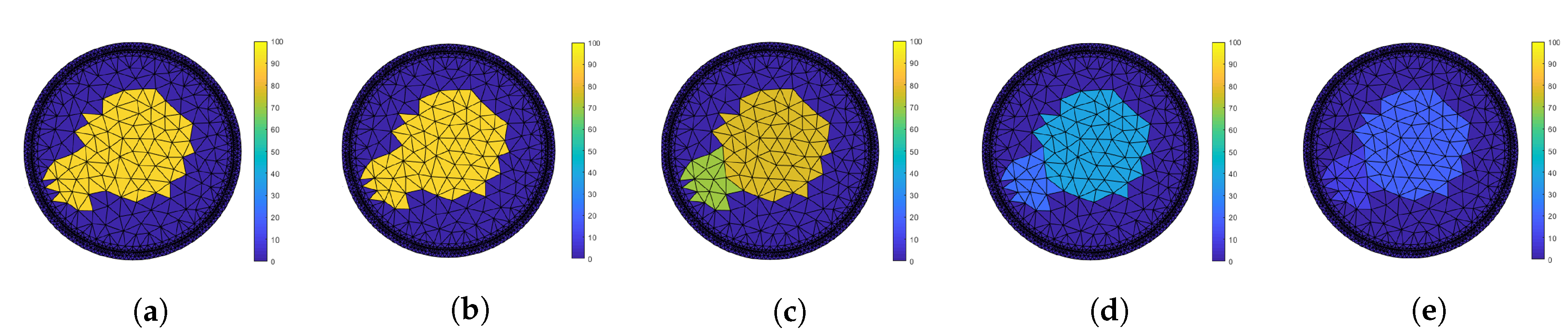
6. Image Representation
6.1. Absolute
6.2. Time Difference
6.3. Frequency Difference
6.3.1. Traditional Frequency Difference
6.3.2. Relative Frequency Difference
6.3.3. Weighted Frequency Difference
6.3.4. Adjacent Frequency Difference
6.4. Frequency-Time Difference
6.4.1. Traditional Frequency-Time Difference
6.4.2. Relative Frequency-Time Difference
6.5. Material Fraction
6.6. Model Based Representation
6.7. 3D Imaging
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. List of Symbols
| Symbol | Description | Unit |
|---|---|---|
| Electric Field | ||
| Electric Potential | V | |
| Current Density | ||
| Conductivity | ||
| Admittivity | ||
| Permittivity | ||
| Polarization | ||
| Susceptibility | 1 | |
| Angular Frequency | ||
| Relaxation Time | s |
References
- Borcea, L. Electrical impedance tomography. Inverse Probl. 2002, 18, R99. [Google Scholar] [CrossRef]
- Brown, B.H. Electrical impedance tomography (EIT): A review. J. Med. Eng. Technol. 2003, 27, 97–108. [Google Scholar] [CrossRef]
- Wang, M. Industrial Tomography: Systems and Applications; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Tan, J. Medical Informatics: Concepts, Methodologies, Tools, and Applications: Concepts, Methodologies, Tools, and Applications; IGI Global: Hershey, PA, USA, 2008. [Google Scholar]
- Yang, W.; Peng, L. Image reconstruction algorithms for electrical capacitance tomography. Meas. Sci. Technol. 2003, 14, R1–R13. [Google Scholar] [CrossRef]
- Lionheart, W.R. EIT reconstruction algorithms: Pitfalls, challenges and recent developments. Physiol. Meas. 2004, 25, 125. [Google Scholar] [CrossRef] [PubMed]
- Neumayer, M.; Zangl, H.; Watzenig, D.; Fuchs, A. Current Reconstruction Algorithms in Electrical Capacitance Tomography. In New Developments and Applications in Sensing Technology; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2011; Volume 83, pp. 65–106. [Google Scholar] [CrossRef]
- Rymarczyk, T. Tomographic Imaging in Environmental, Industrial and Medical Applications; Monographs of the Faculty of Transport and Computer Science of WSEI; Innovatio Press Publishing House: Lublin, Poland, 2019. [Google Scholar]
- Macdonald, J.R.; Barsoukov, E. Impedance Spectroscopy: Theory, Experiment, and Applications; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Griffiths, H.; Ahmed, A. A dual-frequency applied potential tomography technique: Computer simulations. Clin. Phys. Physiol. Meas. 1987, 8, 103. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, H.; Zhang, Z. A dual-frequency electrical impedance tomography system. Phys. Med. Biol. 1989, 34, 1465. [Google Scholar] [CrossRef] [PubMed]
- Brown, B.; Barber, D.; Wang, W.; Lu, L.; Leathard, A.; Smallwood, R.; Hampshire, A.; Mackay, R.; Hatzigalanis, K. Multi-frequency imaging and modelling of respiratory related electrical impedance changes. Physiol. Meas. 1994, 15, A1. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, H.; Jossinet, J. Bioelectrical spectroscopy from multi-frequency EIT. Physiol. Meas. 1994, 15, A59. [Google Scholar] [CrossRef]
- Yerworth, R.J.; Bayford, R.; Brown, B.; Milnes, P.; Conway, M.; Holder, D.S. Electrical impedance tomography spectroscopy (EITS) for human head imaging. Physiol. Meas. 2003, 24, 477. [Google Scholar] [CrossRef]
- Gehre, M.; Kluth, T.; Sebu, C.; Maass, P. Sparse 3D reconstructions in electrical impedance tomography using real data. Inverse Probl. Sci. Eng. 2014, 22, 31–44. [Google Scholar] [CrossRef][Green Version]
- Yang, Y.; Jia, J. A multi-frequency electrical impedance tomography system for real-time 2D and 3D imaging. Rev. Sci. Instruments 2017, 88, 085110. [Google Scholar] [CrossRef] [PubMed]
- Soni, N.K.; Hartov, A.; Kogel, C.; Poplack, S.P.; Paulsen, K.D. Multi-frequency electrical impedance tomography of the breast: New clinical results. Physiol. Meas. 2004, 25, 301. [Google Scholar] [CrossRef] [PubMed]
- Halter, R.J.; Hartov, A.; Paulsen, K.D. A Broadband High-Frequency Electrical Impedance Tomography System for Breast Imaging. IEEE Trans. Biomed. Eng. 2008, 55, 650–659. [Google Scholar] [CrossRef] [PubMed]
- Gregory, W.; Marx, J.; Gregory, C.; Mikkelson, W.; Tjoe, J.; Shell, J. The Cole relaxation frequency as a parameter to identify cancer in breast tissue. Med. Phys. 2012, 39, 4167–4174. [Google Scholar] [CrossRef]
- Aberg, P.; Nicander, I.; Hansson, J.; Geladi, P.; Holmgren, U.; Ollmar, S. Skin cancer identification using multifrequency electrical impedance—A potential screening tool. IEEE Trans. Biomed. Eng. 2004, 51, 2097. [Google Scholar] [CrossRef]
- Romsauerova, A.; McEwan, A.; Horesh, L.; Yerworth, R.; Bayford, R.; Holder, D.S. Multi-frequency electrical impedance tomography (EIT) of the adult human head: Initial findings in brain tumours, arteriovenous malformations and chronic stroke, development of an analysis method and calibration. Physiol. Meas. 2006, 27, S147. [Google Scholar] [CrossRef]
- Hampshire, A.; Smallwood, R.; Brown, B.; Primhak, R. Multifrequency and parametric EIT images of neonatal lungs. Physiol. Meas. 1995, 16, A175. [Google Scholar] [CrossRef]
- Leitzke, J.P.; Zangl, H. Low-power electrical impedance tomography spectroscopy. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2019, 38, 1480. [Google Scholar] [CrossRef]
- Leitzke, J.P.; Mitterer, T.; Zangl, H. Sensing of Icing under Vacuum and Cryogenic Temperatures. Sensors 2019, 19, 3574. [Google Scholar] [CrossRef]
- Holder, D.S. Electrical Impedance Tomography, 1st ed.; Institute of Physics Publishing: Bristol, UK; Philadelphia, PA, USA, 2005. [Google Scholar]
- Cheney, M.; Isaacson, D.; Newell, J.C. Electrical impedance tomography. SIAM Rev. 1999, 41, 85–101. [Google Scholar] [CrossRef]
- Debye, P.J.W. Polar Molecules; Chemical Catalog Company, Inc.: New York, NY, USA, 1929. [Google Scholar]
- Bain, A.K.; Chand, P. Ferroelectrics: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Petrenko, V.F.; Whitworth, R.W. Physics of Ice; Oxford University Press Inc.: New York, NY, USA, 1999. [Google Scholar]
- von Hippel, A. The dielectric relaxation spectra of water, ice, and aqueous solutions, and their interpretation. III Proton organization and proton transfer in ice. IEEE Trans. Electr. Insul. 1988, 23, 825–840. [Google Scholar] [CrossRef]
- Artemov, V.; Volkov, A. Water and ice dielectric spectra scaling at 0 C. Ferroelectrics 2014, 466, 158–165. [Google Scholar] [CrossRef]
- Ammari, H.; Garnier, J.; Giovangigli, L.; Jing, W.; Seo, J.K. Spectroscopic imaging of a dilute cell suspension. J. De Math. Pures Et Appl. 2016, 105, 603–661. [Google Scholar] [CrossRef]
- Ammari, H.; Triki, F. Identification of an inclusion in multifrequency electric impedance tomography. Commun. Partial. Differ. Equ. 2017, 42, 159–177. [Google Scholar] [CrossRef][Green Version]
- Ammari, H.; Giovangigli, L.; Nguyen, L.H.; Seo, J.K. Admittivity imaging from multi-frequency micro-electrical impedance tomography. J. Math. Anal. Appl. 2017, 449, 1601–1618. [Google Scholar] [CrossRef][Green Version]
- McEwan, A.; Romsauerova, A.; Yerworth, R.; Horesh, L.; Bayford, R.; Holder, D. Design and calibration of a compact multi-frequency EIT system for acute stroke imaging. Physiol. Meas. 2006, 27, S199. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.; Milnes, P.; Waterworth, A.; Smallwood, R.; Brown, B. Mk3. 5: A modular, multi-frequency successor to the Mk3a EIS/EIT system. Physiol. Meas. 2001, 22, 49. [Google Scholar] [CrossRef]
- Zhu, Q.; McLeod, C.; Denyer, C.; Lidgey, F.; Lionheart, W. Development of a real-time adaptive current tomograph. Physiol. Meas. 1994, 15, A37. [Google Scholar] [CrossRef]
- Yue, X.; McLeod, C. FPGA design and implementation for EIT data acquisition. Physiol. Meas. 2008, 29, 1233. [Google Scholar] [CrossRef]
- Oh, T.I.; Woo, E.J.; Holder, D. Multi-frequency EIT system with radially symmetric architecture: KHU Mark1. Physiol. Meas. 2007, 28, S183. [Google Scholar] [CrossRef] [PubMed]
- Oh, T.I.; Wi, H.; Kim, D.Y.; Yoo, P.J.; Woo, E.J. A fully parallel multi-frequency EIT system with flexible electrode configuration: KHU Mark2. Physiol. Meas. 2011, 32, 835. [Google Scholar] [CrossRef]
- Wi, H.; Sohal, H.; McEwan, A.L.; Woo, E.J.; Oh, T.I. Multi-frequency electrical impedance tomography system with automatic self-calibration for long-term monitoring. IEEE Trans. Biomed. Circuits Syst. 2014, 8, 119–128. [Google Scholar]
- Baidillah, M.; Iman, A.A.; Sun, Y.; Takei, M. Electrical Impedance Spectro-Tomography based on Dielectric Relaxation Model. IEEE Sens. J. 2017, 17, 8251–8262. [Google Scholar] [CrossRef]
- Khan, S.; Manwaring, P.; Borsic, A.; Halter, R.J. FPGA-based voltage and current dual drive system for high frame rate electrical impedance tomography. IEEE Trans. Med. Imaging 2015, 34, 888–901. [Google Scholar] [CrossRef]
- Xu, Z.; Yao, J.; Wang, Z.; Liu, Y.; Wang, H.; Chen, B.; Wu, H. Development of a Portable Electrical Impedance Tomography System for Biomedical Applications. IEEE Sens. J. 2018, 18, 8117–8124. [Google Scholar] [CrossRef]
- Tan, C.; Liu, S.; Jia, J.; Dong, F. A Wideband Electrical Impedance Tomography System Based on Sensitive Bioimpedance Spectrum Bandwidth. IEEE Trans. Instrum. Meas. 2019, 69, 144–154. [Google Scholar] [CrossRef]
- McEwan, A.; Cusick, G.; Holder, D. A review of errors in multi-frequency EIT instrumentation. Physiol. Meas. 2007, 28, S197. [Google Scholar] [CrossRef]
- Schlappa, J.; Annese, E.; Griffiths, H. Systematic errors in multi-frequency EIT. Physiol. Meas. 2000, 21, 111. [Google Scholar] [CrossRef]
- Bayford, R.H. Bioimpedance tomography (electrical impedance tomography). Annu. Rev. Biomed. Eng. 2006, 8, 63–91. [Google Scholar] [CrossRef]
- Adler, A.; Lionheart, W. Uses and abuses of EIDORS: An extensible software base for EIT. Physiol. Meas. 2006, 27, 25–42. [Google Scholar] [CrossRef] [PubMed]
- Kuen, J.; Woo, E.J.; Seo, J.K. Multi-frequency time-difference complex conductivity imaging of canine and human lungs using the KHU Mark1 EIT system. Physiol. Meas. 2009, 30, S149. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, S.J.; Herrera, C.; Mueller, J.; Von Herrmann, A. A direct D-bar reconstruction algorithm for recovering a complex conductivity in 2D. Inverse Probl. 2012, 28, 095005. [Google Scholar] [CrossRef] [PubMed]
- Leitzke, J.P.; Zangl, H. Electrical Impedance Tomography Spectroscopy for Ice and Water Mixtures. In Proceedings of the XXII IMEKO World Congress, IMEKO 2018, Belfast, UK, 3–6 September 2018. [Google Scholar]
- Alberti, G.S.; Ammari, H.; Jin, B.; Seo, J.K.; Zhang, W. The linearized inverse problem in multifrequency electrical impedance tomography. SIAM J. Imaging Sci. 2016, 9, 1525–1551. [Google Scholar] [CrossRef]
- Malone, E.; dos Santos, G.S.; Holder, D.; Arridge, S. A reconstruction-classification method for multifrequency electrical impedance tomography. IEEE Trans. Med. Imaging 2015, 34, 1486–1497. [Google Scholar] [CrossRef] [PubMed]
- Golub, G.H.; Reinsch, C. Singular value decomposition and least squares solutions. Numer. Math. 1970, 14, 403–420. [Google Scholar] [CrossRef]
- Hansen, P.C. The truncatedsvd as a method for regularization. BIT Numer. Math. 1987, 27, 534–553. [Google Scholar] [CrossRef]
- Hansen, P.C. Truncated singular value decomposition solutions to discrete ill-posed problems with ill-determined numerical rank. SIAM J. Sci. Stat. Comput. 1990, 11, 503–518. [Google Scholar] [CrossRef]
- Tikhonov, A.N. On the Solution of Ill-Posed Problems and the Method of Regularization; Doklady Akademii Nauk; Russian Academy of Sciences: Moscow, Russia, 1963; Volume 151, pp. 501–504. [Google Scholar]
- Tikhonov, A.N.; Glasko, V.B. Use of the regularization method in non-linear problems. USSR Comput. Math. Math. Phys. 1965, 5, 93–107. [Google Scholar] [CrossRef]
- Vauhkonen, M.; Vadasz, D.; Karjalainen, P.A.; Somersalo, E.; Kaipio, J.P. Tikhonov regularization and prior information in electrical impedance tomography. IEEE Trans. Med. Imaging 1998, 17, 285–293. [Google Scholar] [CrossRef]
- Avery, J.; Dowrick, T.; Faulkner, M.; Goren, N.; Holder, D. A versatile and reproducible multi-frequency electrical impedance tomography system. Sensors 2017, 17, 280. [Google Scholar] [CrossRef] [PubMed]
- Francini, E. Recovering a complex coefficient in a planar domain from the Dirichlet-to-Neumann map. Inverse Probl. 2000, 16, 107. [Google Scholar] [CrossRef]
- Barber, D.C.; Seagar, A.D. Fast reconstruction of resistance images. Clin. Phys. Physiol. Meas. 1987, 8, 47. [Google Scholar] [CrossRef] [PubMed]
- Avis, N.; Barber, D. Incorporating a priori information into the Sheffield filtered backprojection algorithm. Physiol. Meas. 1995, 16, A111. [Google Scholar] [CrossRef] [PubMed]
- Watzenig, D.; Fox, C. A review of statistical modelling and inference for electrical capacitance tomography. Meas. Sci. Technol. 2009, 20, 052002. [Google Scholar] [CrossRef]
- Kaipio, J.P.; Kolehmainen, V.; Somersalo, E.; Vauhkonen, M. Statistical inversion and Monte Carlo sampling methods in electrical impedance tomography. Inverse Probl. 2000, 16, 1487. [Google Scholar] [CrossRef]
- Zangl, H.; Mühlbacher-Karrer, S. Artefact reduction in fast Bayesian inversion in electrical tomography. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2015, 34, 1381–1391. [Google Scholar] [CrossRef]
- Malone, E.; dos Santos, G.S.; Holder, D.; Arridge, S. Multifrequency electrical impedance tomography using spectral constraints. IEEE Trans. Med. Imaging 2014, 33, 340–350. [Google Scholar] [CrossRef]
- Malone, E.; Jehl, M.; Arridge, S.; Betcke, T.; Holder, D. Stroke type differentiation using spectrally constrained multifrequency EIT: Evaluation of feasibility in a realistic head model. Physiol. Meas. 2014, 35, 1051. [Google Scholar] [CrossRef]
- Martin, S.; Choi, C.T. Nonlinear electrical impedance tomography reconstruction using artificial neural networks and particle swarm optimization. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Packham, B.; Koo, H.; Romsauerova, A.; Ahn, S.; McEwan, A.; Jun, S.; Holder, D. Comparison of frequency difference reconstruction algorithms for the detection of acute stroke using EIT in a realistic head-shaped tank. Physiol. Meas. 2012, 33, 767. [Google Scholar] [CrossRef] [PubMed]
- Nahvi, M.; Hoyle, B. Wideband electrical impedance tomography. Meas. Sci. Technol. 2008, 19, 094011. [Google Scholar] [CrossRef]
- Oh, T.I.; Koo, H.; Lee, K.H.; Kim, S.M.; Lee, J.; Kim, S.W.; Seo, J.K.; Woo, E.J. Validation of a multi-frequency electrical impedance tomography (mfEIT) system KHU Mark1: Impedance spectroscopy and time-difference imaging. Physiol. Meas. 2008, 29, 295. [Google Scholar] [CrossRef] [PubMed]
- McEwan, A.; Tapson, J.; van Schaik, A.; Holder, D.S. Code-division-multiplexed electrical impedance tomography spectroscopy. IEEE Trans. Biomed. Circuits Syst. 2009, 3, 332–338. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Xu, C.; Dai, M.; Fu, F.; Shi, X.; Dong, X. A novel multi-frequency electrical impedance tomography spectral imaging algorithm for early stroke detection. Physiol. Meas. 2016, 37, 2317. [Google Scholar] [CrossRef]
- Riu, P.; Rosell, J.; Lozano, A.; Pallà-Areny, R. Multi-frequency static imaging in electrical impedance tomography: Part 1 instrumentation requirements. Med. Biol. Eng. Comput. 1995, 33, 784–792. [Google Scholar] [CrossRef]
- Seo, J.K.; Lee, J.; Kim, S.W.; Zribi, H.; Woo, E.J. Frequency-difference electrical impedance tomography (fdEIT): Algorithm development and feasibility study. Physiol. Meas. 2008, 29, 929. [Google Scholar] [CrossRef]
- Goren, N.; Avery, J.; Dowrick, T.; Mackle, E.; Witkowska-Wrobel, A.; Werring, D.; Holder, D. Multi-frequency electrical impedance tomography and neuroimaging data in stroke patients. Sci. Data 2018, 5, 180112. [Google Scholar] [CrossRef]
- Brown, B.; Leathard, A.; Lu, L.; Wang, W.; Hampshire, A. Measured and expected Cole parameters from electrical impedance tomographic spectroscopy images of the human thorax. Physiol. Meas. 1995, 16, A57. [Google Scholar] [CrossRef]

| Publication | Year | System | Technology | Source | Frequency Range | Frequency Signal | Drive Pattern/Sensing Strategy | Total of Electrodes | Electrode Geometry | Average SNR |
|---|---|---|---|---|---|---|---|---|---|---|
| [37] | 2001 | Sheffield Mk 3.5 | DSP | Single | 2 kHz to MHz | Discrete Sinusoidal (30 frequencies), up to 10 simultaneous frequencies | Adjacent | 8 | 2D Circular | 40 dB |
| [14] | 2003 | UCLH Mk 2 | DSP | Single | 20 Hz to 1 MHz | Discrete Sinusoidal (30 frequencies), up to 10 simultaneous frequencies | Opposite | 64 | 3D Circular | 40 dB |
| [36] | 2006 | UCLH Mk 2.5 | DSP | Single | 20 Hz to 1 MHz | Discrete Sinusoidal (30 frequencies), up to 10 simultaneous frequencies | Opposite | 32 | 2D Circular | 40 dB |
| [18] | 2008 | - | DSP/FPGA | Multiple | 10 kHz to 10 MHz | Discrete Sinusoidal (20 frequencies) | Adjacent | 64 | 3D Circular | 84 dB |
| [39] | 2008 | OXBACT-5 | FPGA | Multiple | 1 kHz to 100 kHz | Discrete Sinusoidal (16 frequencies) | - | 64 | 2D or 3D Circular | - |
| [42] | 2014 | KHUMark2.5 | DSP/FPGA | Multiple | 10 Hz to 500 kHz | Discrete Sinusoidal (9 frequencies), up to 6 simultaneous frequencies | Adjacent or Opposite | 16 | 2D Circular | 90 dB |
| [44] | 2015 | - | FPGA | Single | 100 Hz to 10 MHz | Discrete Sinusoidal (47 frequencies) | Adjacent | 32 | 2D or 3D Circular | 90 dB |
| [46] | 2019 | SWEIT | FPGA | Single | 1 kHz to MHz | Continuous Chirp | Adjacent | 16 | 2D Circular | 56 dB |
| Algorithm | Type | Classification | Publications |
|---|---|---|---|
| Singular Value Decomposition | Non-iterative | Regularization-Based | [21,42,51] |
| Newton-Raphson | Iterative | Regularization-Based | [17] |
| Gauss-Newton | Iterative | Regularization-Based | [43] |
| D-Bar | Non-iterative | Direct | [52] |
| Optimal First Order Approximation | Non-iterative | Statistical | [23,53] |
| Group Sparse Reconstruction Algorithm | Iterative | Regularization-Based | [54] |
| Reconstruction-Classification | Non-iterative | Machine Learning | [55] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Padilha Leitzke, J.; Zangl, H. A Review on Electrical Impedance Tomography Spectroscopy. Sensors 2020, 20, 5160. https://doi.org/10.3390/s20185160
Padilha Leitzke J, Zangl H. A Review on Electrical Impedance Tomography Spectroscopy. Sensors. 2020; 20(18):5160. https://doi.org/10.3390/s20185160
Chicago/Turabian StylePadilha Leitzke, Juliana, and Hubert Zangl. 2020. "A Review on Electrical Impedance Tomography Spectroscopy" Sensors 20, no. 18: 5160. https://doi.org/10.3390/s20185160
APA StylePadilha Leitzke, J., & Zangl, H. (2020). A Review on Electrical Impedance Tomography Spectroscopy. Sensors, 20(18), 5160. https://doi.org/10.3390/s20185160





