Pattern Synthesis of Linear Antenna Array Using Improved Differential Evolution Algorithm with SPS Framework
Abstract
1. Introduction
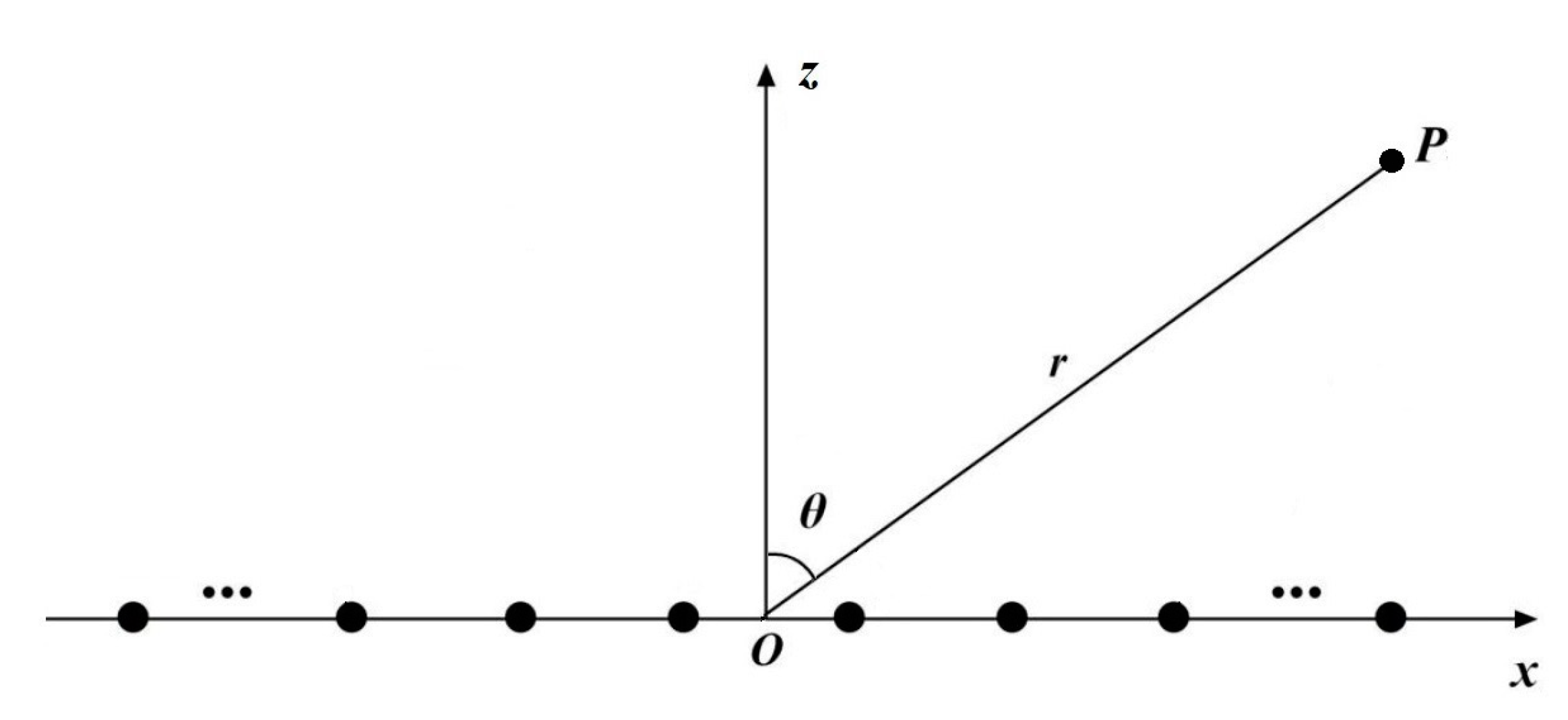
2. Pattern Synthesis of Linear Antenna Array
3. SPS-JADE Algorithm
3.1. Classic DE Algorithm
- 1.
- “DE/rand/1”
- 2.
- “DE/best/1”
3.2. JADE Algorithm
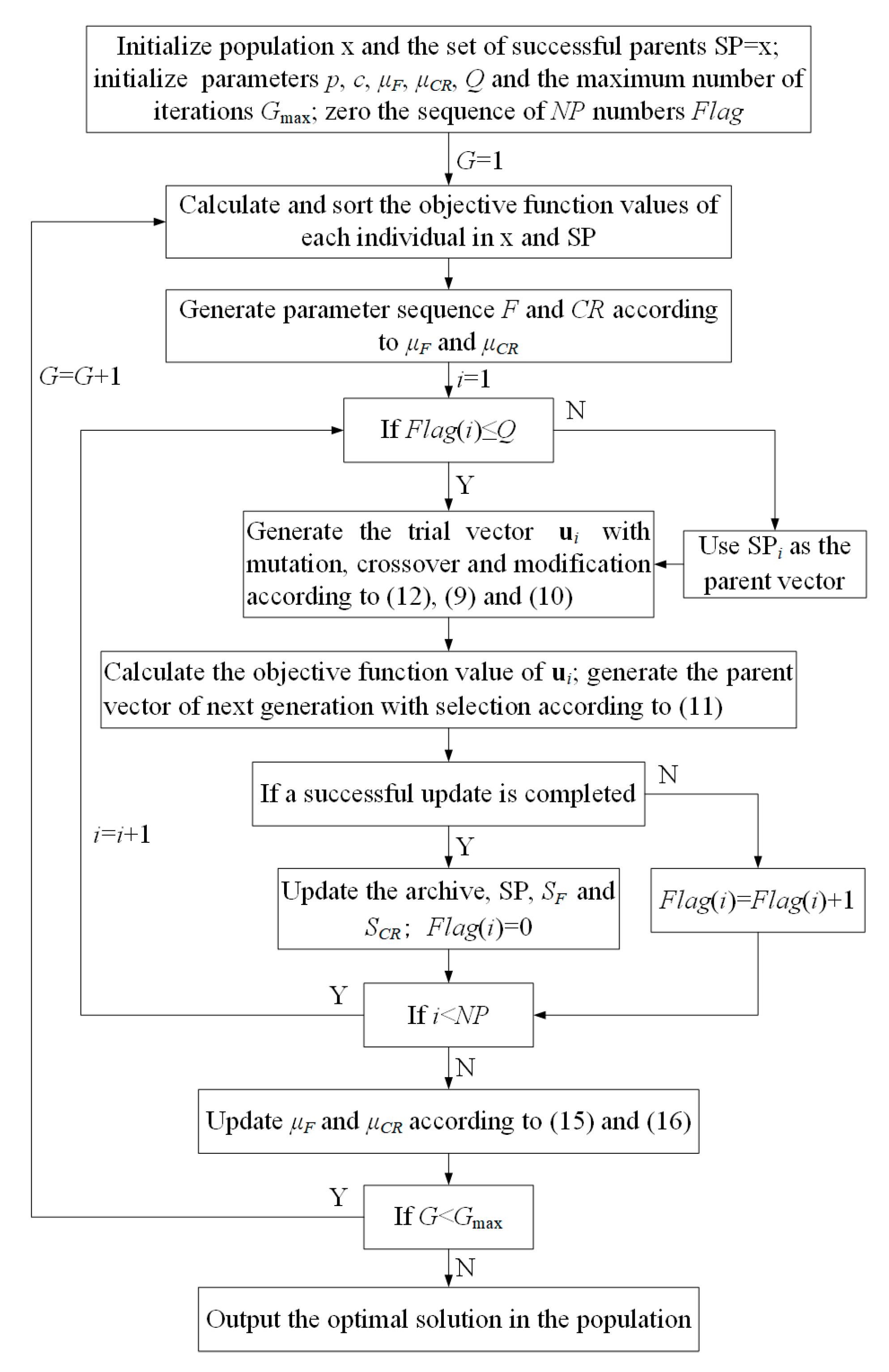
3.3. SPS-JADE Algorithm with SPS Framework
4. Numerical Analysis and Results
4.1. Parameter Settings
4.2. Simulation Experiments Results
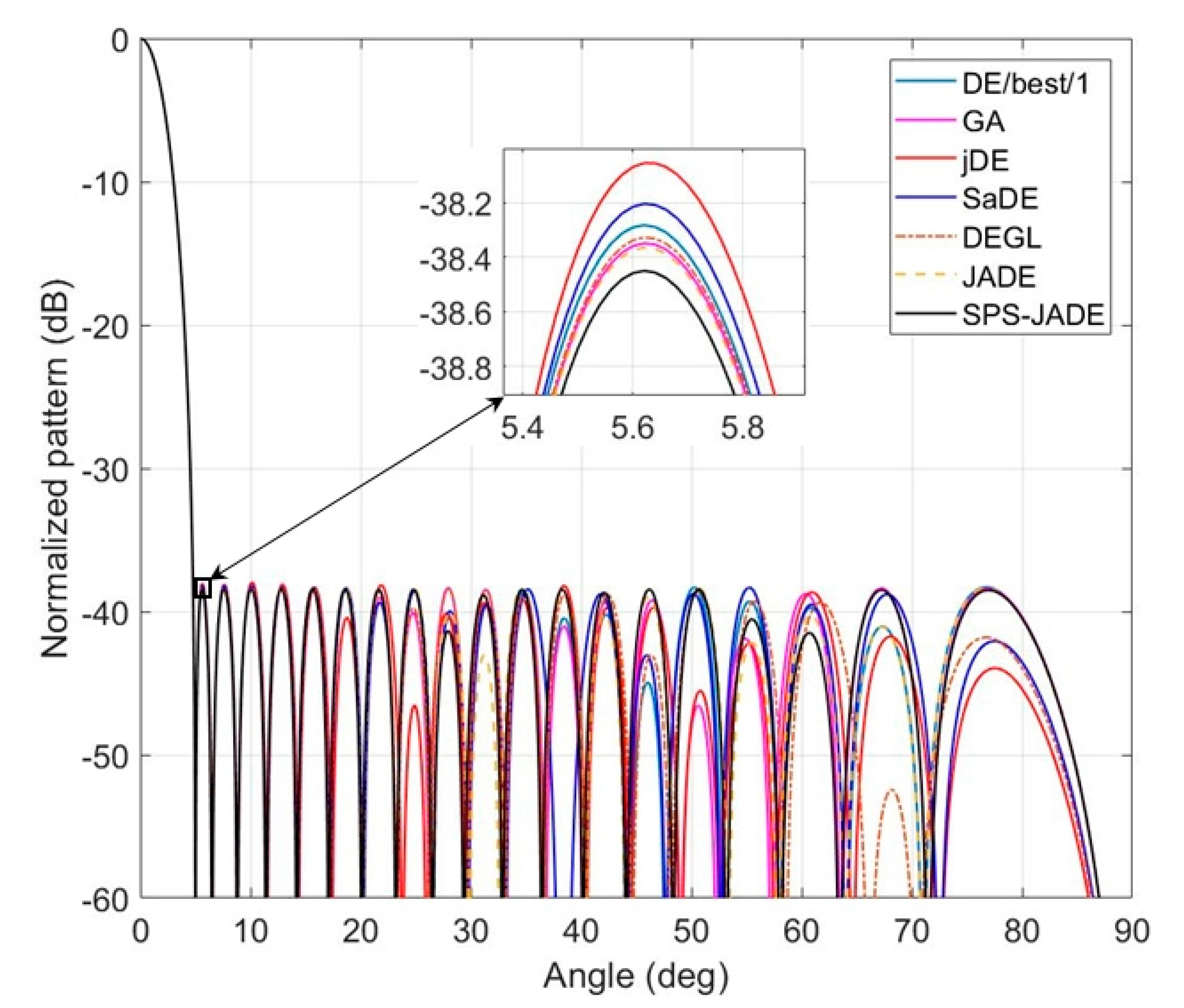
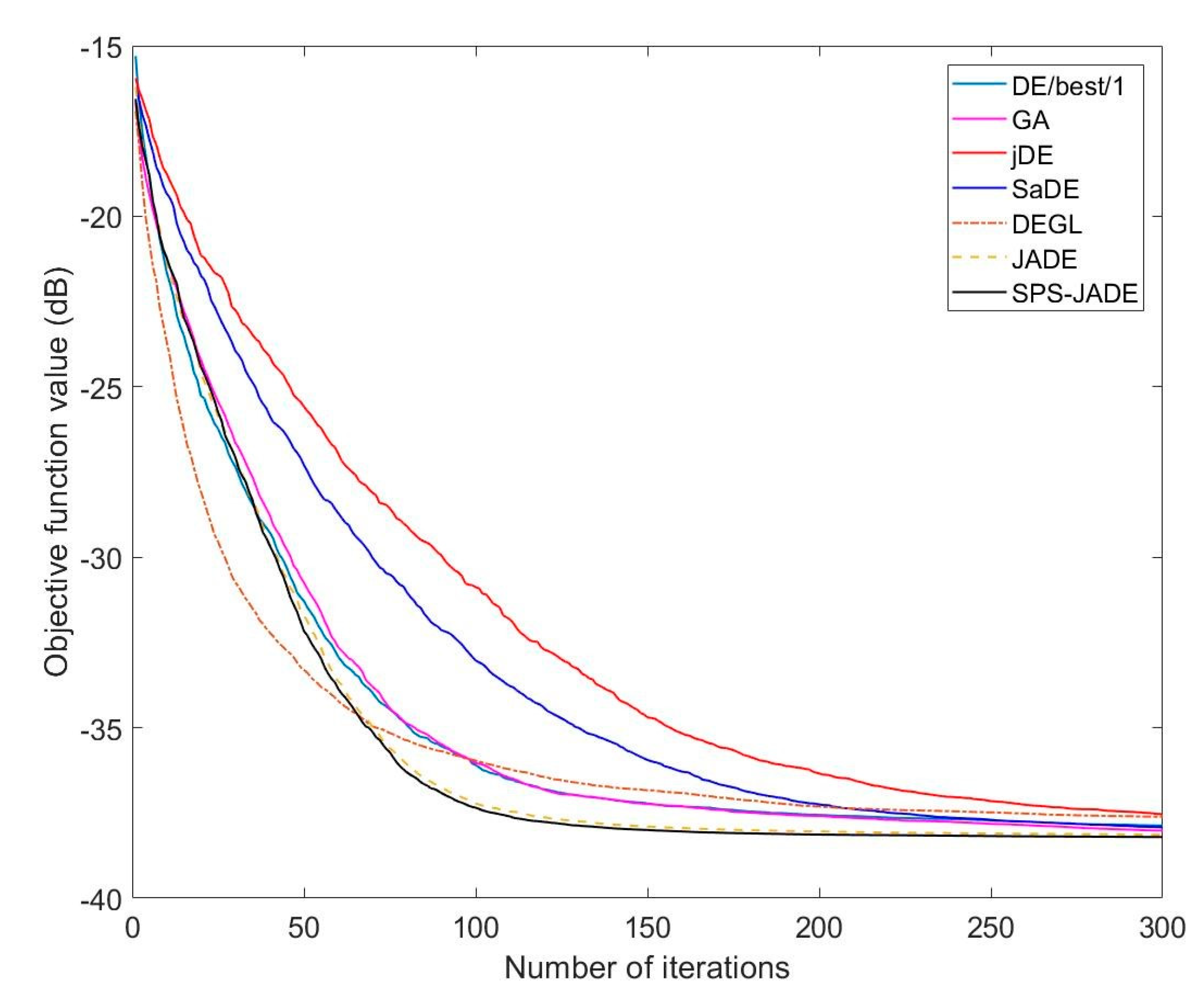
4.2.1. Experiment A
4.2.2. Experiment B
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Caputo, F.; De Luca, A.; Greco, A.; Maietta, S.; Bellucci, M. FE simulation of a SHM system for a large radio-telescope. Int. Rev. Model. Simul. 2018, 11, 5–14. [Google Scholar] [CrossRef]
- Balanis, C. Antenna Theory—Analysis and Design; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Holland, J. Genetic algorithms. Sci. Amer. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Yan, K.K.; Lu, Y. Sidelobe reduction in array pattern synthesis using genetic algorithm. IEEE Trans. Antennas Propagat. 1997, 27, 1117–1121. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 1942–1948. [Google Scholar]
- Jin, N.; Rahmat-Samii, Y. Advances in particle swarm optimization for antenna designs: Real-number, binary, single-objective and multiobjective implementations. IEEE Trans. Antennas Propag. 2007, 55, 556–567. [Google Scholar] [CrossRef]
- Singh, U.; Salgotra, R. Pattern synthesis of linear antenna arrays using enhanced flower pollination algorithm. Int. J. Antennas Propag. 2017, 2017, 7158752. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Liang, W.; Jiao, Y.; Zhang, L. Sideband suppression in time-modulated linear array by modified differential evolution algorithm. In Proceedings of the IEEE International Conference Communication on Problem-Solving (ICCP), Guilin, China, 16–18 October 2015; IEEE: New York, NY, USA, 2015; pp. 399–401. [Google Scholar]
- Qing, A. Dynamic differential evolution strategy and applications in electromagnetic inverse scattering problems. IEEE Trans. Geosci. Remote Sens. 2006, 44, 116–125. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhang, Q. Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans. Evol. Comput. 2011, 15, 55–66. [Google Scholar] [CrossRef]
- Reddy, S.S. Optimal power flow using hybrid differential evolution and harmony search algorithm. Int. J. Mach. Learn. Cyber. 2019, 10, 1077–1091. [Google Scholar] [CrossRef]
- Li, X.; Li, W.T.; Shi, X.W.; Yang, J.; Yu, J.F. Modified differential evolution algorithm for pattern synthesis of antenna arrays. Prog. Electromagn. Res. 2013, 137, 371–388. [Google Scholar] [CrossRef]
- Mandal, A.; Zafar, H.; Das, S.; Vasilakos, A. A modified differential evolution algorithm for shaped beam linear array antenna design. Prog. Electromagn. Res. 2012, 125, 439–457. [Google Scholar] [CrossRef]
- Blackman, S.S.; Popoli, R. Design and analysis of modern tracking systems. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1834–1854. [Google Scholar]
- Lin, C.; Qing, A.; Feng, Q. Synthesis of unequally spaced antenna arrays by using differential evolution. IEEE Trans. Antennas Propag. 2010, 58, 2553–2561. [Google Scholar]
- Li, X.; Yin, M. Hybrid differential evolution with artificial bee colony and its application for design of a reconfigurable antenna array with discrete phase shifters. IET Microw. Antennas Propag. 2012, 6, 1573–1582. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Guo, S.-M.; Yang, C.-C.; Hsu, P.-H.; Tsai, J.S.-H. Improving differential evolution with a successful-parent-selecting framework. IEEE Trans. Evol. Comput. 2015, 19, 717–730. [Google Scholar] [CrossRef]
- Guney, K.; Durmus, A.; Basbug, S. Antenna array synthesis and failure correction using differential search algorithm. Int. J. Antennas Propag. 2014, 2014, 276754. [Google Scholar] [CrossRef]
- Guney, K.; Onay, M. Optimal synthesis of linear antenna arrays using a harmony search algorithm. Expert Syst. Appl. 2011, 38, 15455–15462. [Google Scholar] [CrossRef]
- Saxena, P.; Kothari, A. Optimal pattern synthesis of linear antenna array using grey wolf optimization algorithm. Int. J. Antennas Propag. 2016, 2016, 1205970. [Google Scholar] [CrossRef]
- Khan, S.U.; Qureshi, I.M.; Zaman, F.; Naveed, A. Null placement and sidelobe suppression in failed array using symmetrical element failure technique and hybrid heuristic computation. Prog. Electromagn. Res. B 2013, 52, 165–184. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, X.; Leo, L.; Peng, S.; Xie, M. Synthesis of broadside linear aperiodic arrays with sidelobe suppression and null steering using whale optimization algorithm. IEEE Antennas Wireless Propag. Lett. 2018, 17, 347–350. [Google Scholar] [CrossRef]
- Boeringer, D.W.; Werner, D.H. Particle swarm optimization versus genetic algorithms for phased array synthesis. IEEE Trans. Antennas Propag. 2004, 52, 771–779. [Google Scholar] [CrossRef]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 647–657. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Das, S.; Abraham, A.; Chakraborty, U.K.; Konar, A. Differential evolution using a neighborhood-based mutation operator. IEEE Trans. Evol. Comput. 2009, 13, 526–553. [Google Scholar] [CrossRef]
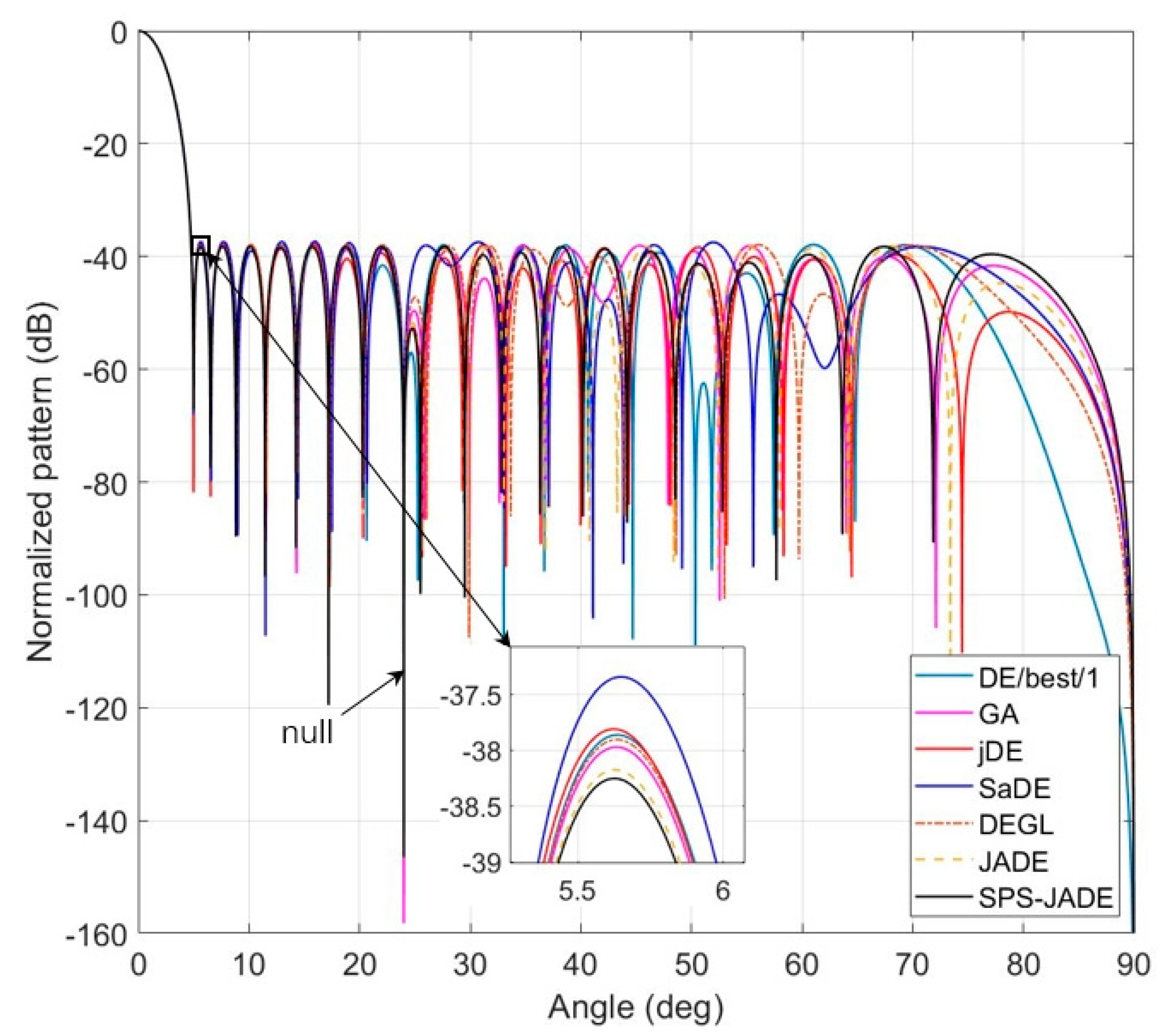
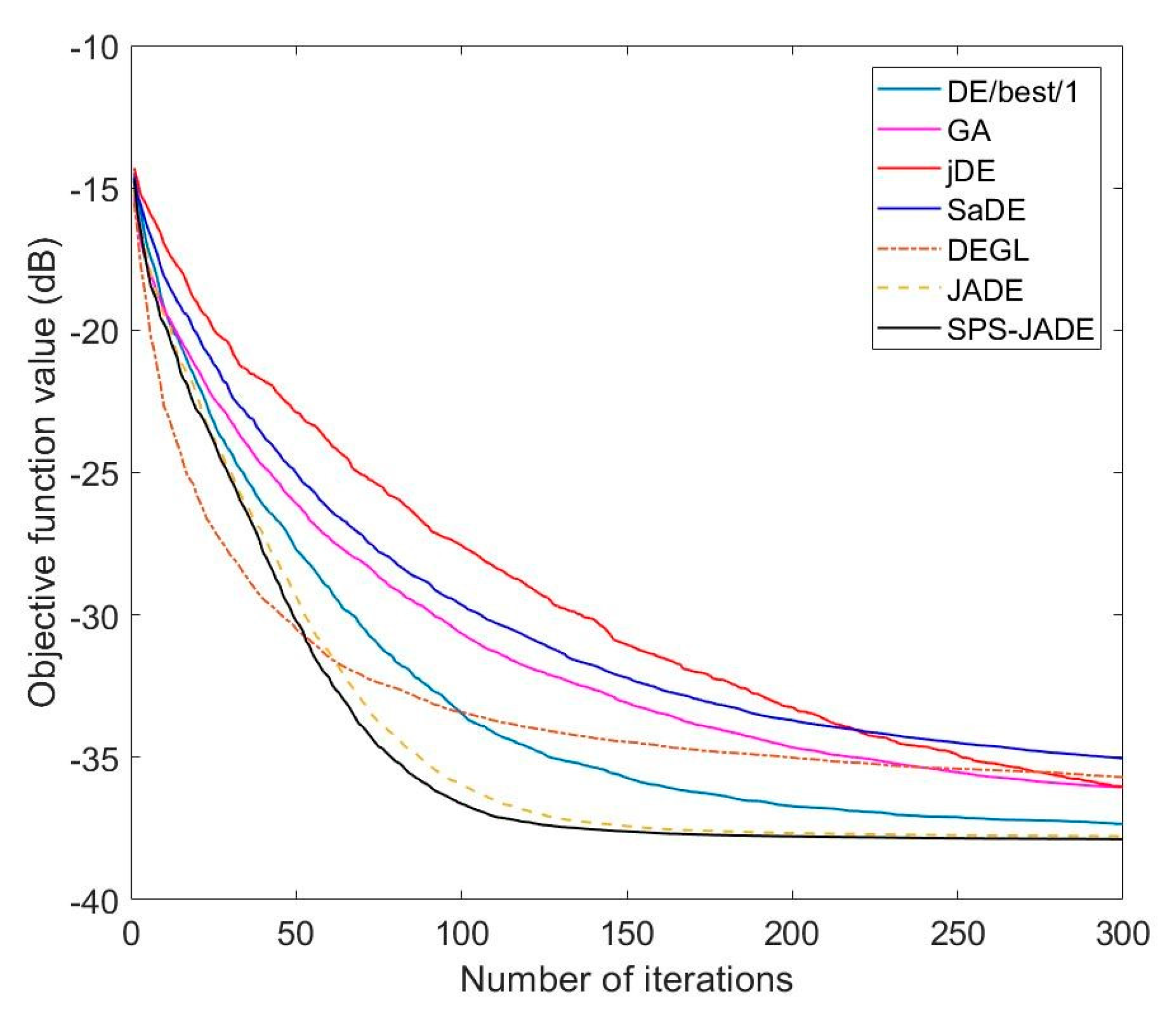
| Algorithm | Best (dB) | Worst (dB) | Average (dB) | Std. (dB) |
|---|---|---|---|---|
| DE/best/1 | −38.2821 | −37.3611 | −37.8710 | 0.2084 |
| GA | −38.3459 | −37.6051 | −38.0196 | 0.1887 |
| jDE | −37.9625 | −36.7904 | −37.5397 | 0.2577 |
| SaDE | −38.2037 | −37.4546 | −37.9220 | 0.1622 |
| DEGL | −38.3228 | −36.1336 | −37.6120 | 0.5901 |
| JADE | −38.3639 | −37.4839 | −38.1391 | 0.1811 |
| SPS-JADE | −38.4496 | −37.7394 | −38.2081 | 0.1468 |
| Element Number | Excitation Amplitude | Element Number | Excitation Amplitude |
|---|---|---|---|
| 1, 40 | 0.1853 | 11, 30 | 0.6274 |
| 2, 39 | 0.1326 | 12, 29 | 0.6941 |
| 3, 38 | 0.1679 | 13, 28 | 0.7436 |
| 4, 37 | 0.2156 | 14, 27 | 0.8028 |
| 5, 36 | 0.2614 | 15, 26 | 0.8496 |
| 6, 35 | 0.3085 | 16, 25 | 0.9015 |
| 7, 34 | 0.3830 | 17, 24 | 0.9325 |
| 8, 33 | 0.4332 | 18, 23 | 0.9580 |
| 9, 32 | 0.5012 | 19, 22 | 0.9771 |
| 10, 31 | 0.5561 | 20, 21 | 0.9916 |
| VTR (dB) | SPS-JADE | JADE | ||||||
|---|---|---|---|---|---|---|---|---|
| −37.4 | 100% | 4030 | 7065 | 5060 | 100% | 4242 | 14,332 | 5470 |
| −37.6 | 100% | 4583 | 8535 | 5563 | 96.7% | 4504 | 9530 | 5742 |
| −37.8 | 96.7% | 4865 | 9952 | 6132 | 96.7% | 5001 | 13,147 | 6773 |
| −38.0 | 90% | 5552 | 12,236 | 7252 | 83.3% | 5754 | 11,430 | 7810 |
| Algorithm | Best (dB) | Worst (dB) | Average (dB) | Std. (dB) |
|---|---|---|---|---|
| DE/best/1 | −37.8559 | −35.9365 | −37.3418 | 0.3833 |
| GA | −37.9721 | −30.5613 | −36.0488 | 1.7067 |
| jDE | −37.6730 | −33.7738 | −36.0254 | 0.9156 |
| SaDE | −37.3390 | −31.9234 | −35.0410 | 1.2500 |
| DEGL | −37.8964 | −29.9828 | −35.6964 | 2.1167 |
| JADE | −38.1666 | −37.3229 | −37.7729 | 0.2104 |
| SPS-JADE | −38.2521 | −37.3910 | −37.8737 | 0.1703 |
| Algorithm | Best (dB) | Worst (dB) | Average (dB) |
|---|---|---|---|
| DE/best/1 | −130.4027 | −74.6508 | −92.1970 |
| GA | −167.9265 | −103.7220 | −118.4906 |
| jDE | −103.5643 | −61.3954 | −73.6811 |
| SaDE | −112.0015 | −73.8613 | −98.3941 |
| DEGL | −142.5442 | −77.2106 | −106.6899 |
| JADE | −166.6318 | −111.3316 | −131.7949 |
| SPS-JADE | −162.1386 | −105.3397 | −130.8599 |
| Element Number | Excitation Amplitude | Element Number | Excitation Amplitude |
|---|---|---|---|
| 1, 40 | 0.1736 | 11, 30 | 0.6040 |
| 2, 39 | 0.1271 | 12, 29 | 0.6776 |
| 3, 38 | 0.1710 | 13, 28 | 0.7447 |
| 4, 37 | 0.2173 | 14, 27 | 0.8021 |
| 5, 36 | 0.2607 | 15, 26 | 0.8358 |
| 6, 35 | 0.2948 | 16, 25 | 0.8740 |
| 7, 34 | 0.3699 | 17, 24 | 0.9205 |
| 8, 33 | 0.4366 | 18, 23 | 0.9613 |
| 9, 32 | 0.4954 | 19, 22 | 0.9698 |
| 10, 31 | 0.5573 | 20, 21 | 0.9682 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Zhang, Y.; Sun, J.; Li, Q. Pattern Synthesis of Linear Antenna Array Using Improved Differential Evolution Algorithm with SPS Framework. Sensors 2020, 20, 5158. https://doi.org/10.3390/s20185158
Zhang R, Zhang Y, Sun J, Li Q. Pattern Synthesis of Linear Antenna Array Using Improved Differential Evolution Algorithm with SPS Framework. Sensors. 2020; 20(18):5158. https://doi.org/10.3390/s20185158
Chicago/Turabian StyleZhang, Ruimeng, Yan Zhang, Jinping Sun, and Qing Li. 2020. "Pattern Synthesis of Linear Antenna Array Using Improved Differential Evolution Algorithm with SPS Framework" Sensors 20, no. 18: 5158. https://doi.org/10.3390/s20185158
APA StyleZhang, R., Zhang, Y., Sun, J., & Li, Q. (2020). Pattern Synthesis of Linear Antenna Array Using Improved Differential Evolution Algorithm with SPS Framework. Sensors, 20(18), 5158. https://doi.org/10.3390/s20185158





