Empirical and Comparative Validation for a Building Energy Model Calibration Methodology
Abstract
1. Introduction
- White box models are based on a physical models with exclusively physically meaningful parameters. This can provide the most detailed building performance characteristics that can be applied in energy prediction for demand response applications or establishing baseline models for ECM performance, among others.
- Black-box models are mathematical models constructed from training data. They typically lack physical meaning in their mapping of input parameters. This models can be developed in short time although frequent re-training can be required to adjust small changes in a building.
2. Empirical Validation and Comparative Test Methodology
2.1. Selection of Data Provided by Annex 58 for Empirical Validation
- In the area of windows, Window 6.3 software was used. We used publicly available computer software that provides a versatile heat transfer analysis method consistent with the updated rating procedure developed by the National Fenestration Rating Council (NFRC), which is consistent with the ISO 15099 standard. With Window 6.3, the optical properties of house glass were calculated. The Fraunhofer IBP Institute (Institute for Construction Physics) calculated the absorption capacity of the blinds.
- The transmittance values of the thermal bridges were calculated using TRISCO and THERM software. The latter is state-of-the-art computer software that performs a two-dimensional conduction heat transfer analysis based on the finite element methodology. The Fraunhofer IBP Institute provided the U values of the thermal bridge for windows similar to those built in the houses.
- For ventilation, apart from the sensors used, the PHluft program of the Passive House Institute was used. This is a free program that calculates the heat transfer between the ventilation ducts and the indoor environment.
- The infiltration of the houses was obtained by the use of blower doors. A blower door is a machine used to measure the hermeticism (air tightness) of buildings. It can also be used to measure the flow between built areas, to test the tightness of air conductors, or to help physically locate air escape sites in the building envelope. A total of five blower doors were used between the two houses. They were applied throughout the house and in the rooms that were part of the experiment.
- For the ground, the reflection of the short wave ground was measured. Reflectivity measurements were recorded on both asphalt and gravel and the ground temperature was recorded at various depths: 0, 0.05, 0.1, and 0.2 m.
2.2. The Buildings
2.3. Experimental Design and Calibration Process
- Period 1: In this first period, the aim was to achieve identical and well-defined starting conditions for both houses. To do this, they were heated to 30 C for three days.
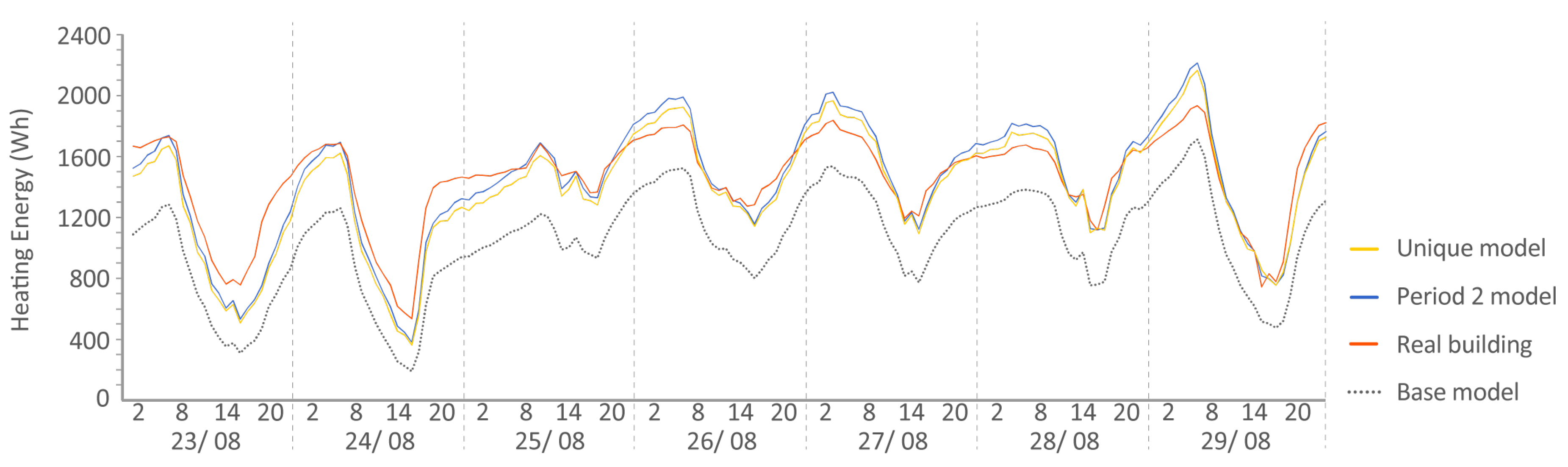
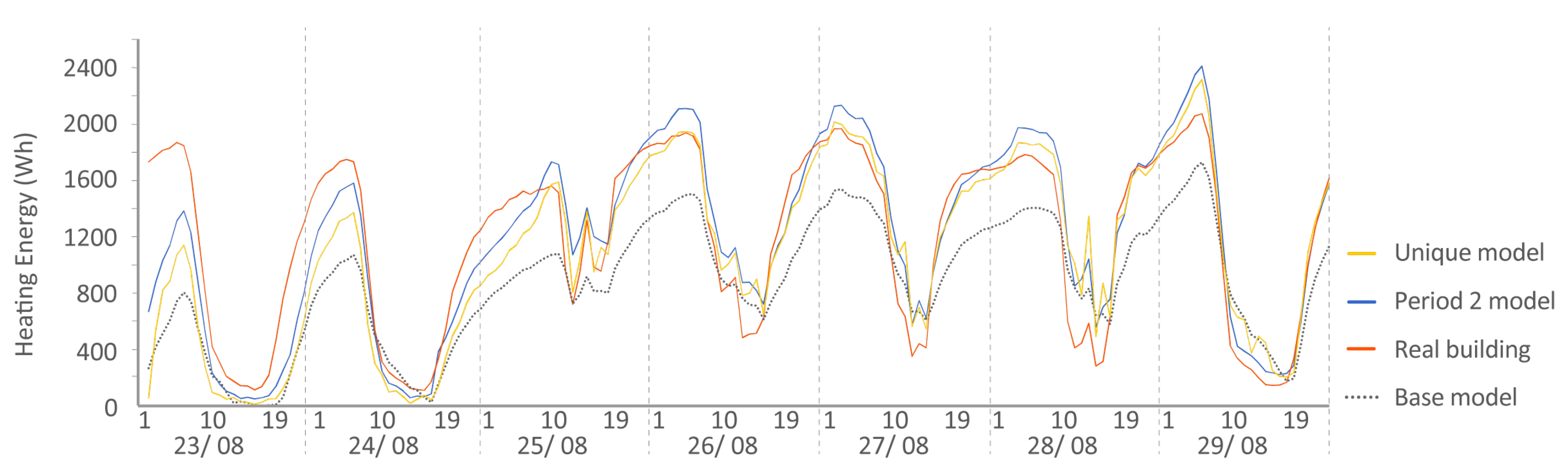
- Period 2: During the following seven days, the interior temperatures were kept constant at 30 C using the building’s control system. For the experiment, indoor temperatures were provided as inputs to the mode, and the energy needed by the HVAC system to achieve those temperatures was requested.
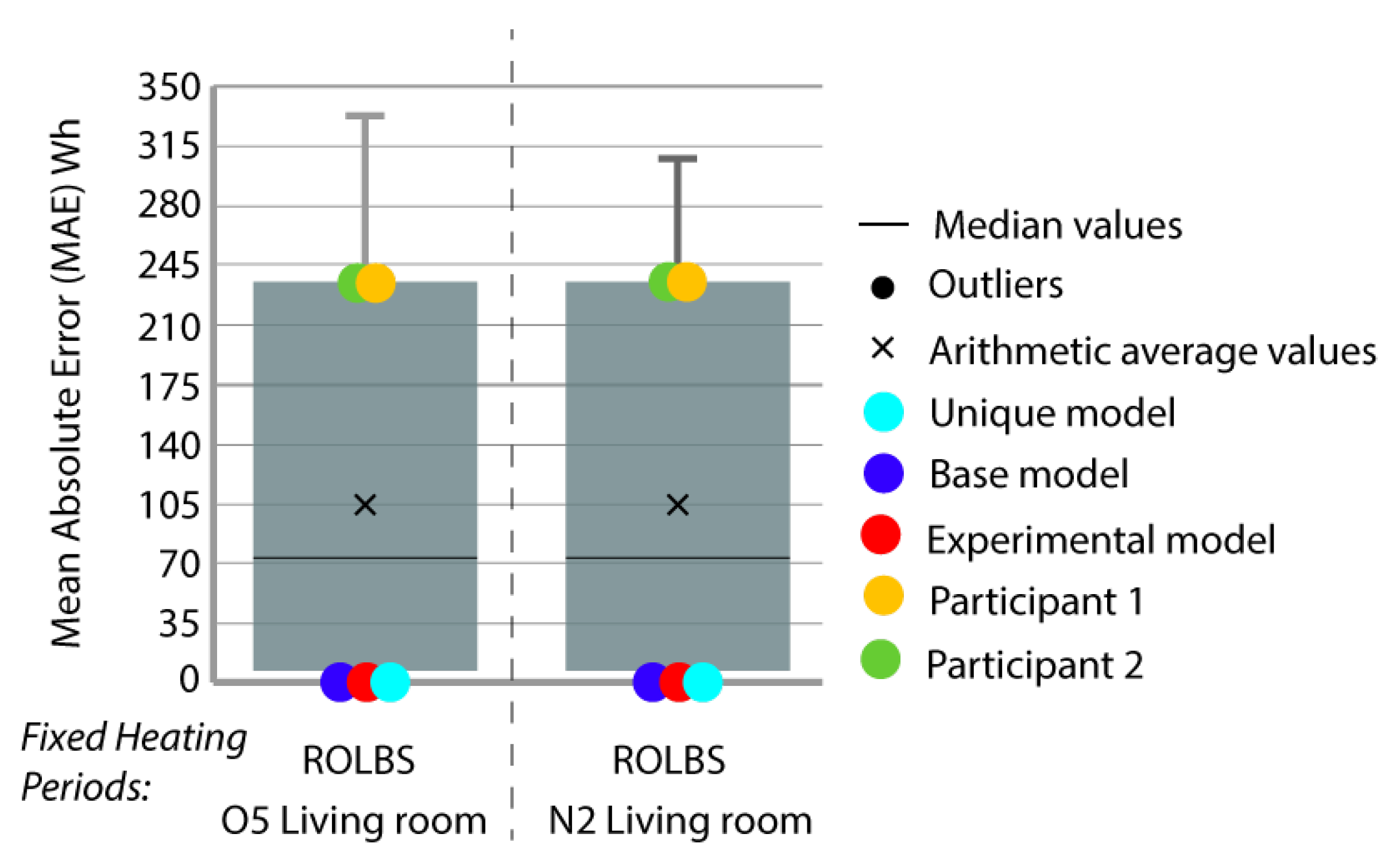
- Period 3: In this period, a Randomly-Ordered Logarithmic Binary Sequence (ROLBS) was implemented for the activation of the living room radiator (the rest of the radiators in the rooms were turned off, thus increasing the interaction between the units). This sequence was developed in the EC COMPASS project. The ROLBS, which aims to cover all relevant frequencies with the same weight, is a signal in which the on and off periods are chosen at logarithmically equal intervals and shuffled in a quasi-random order. This random sequence ensures that there is no relationship between the heat input by the HVAC system and the solar gains. This phase lasted two weeks with heat inputs ranging from 1 to 90 h. The power of the radiator was limited to 500 W. During this stage, the energy consumed by the radiator was offered and the energy model was asked to predict the interior temperatures of the rooms.
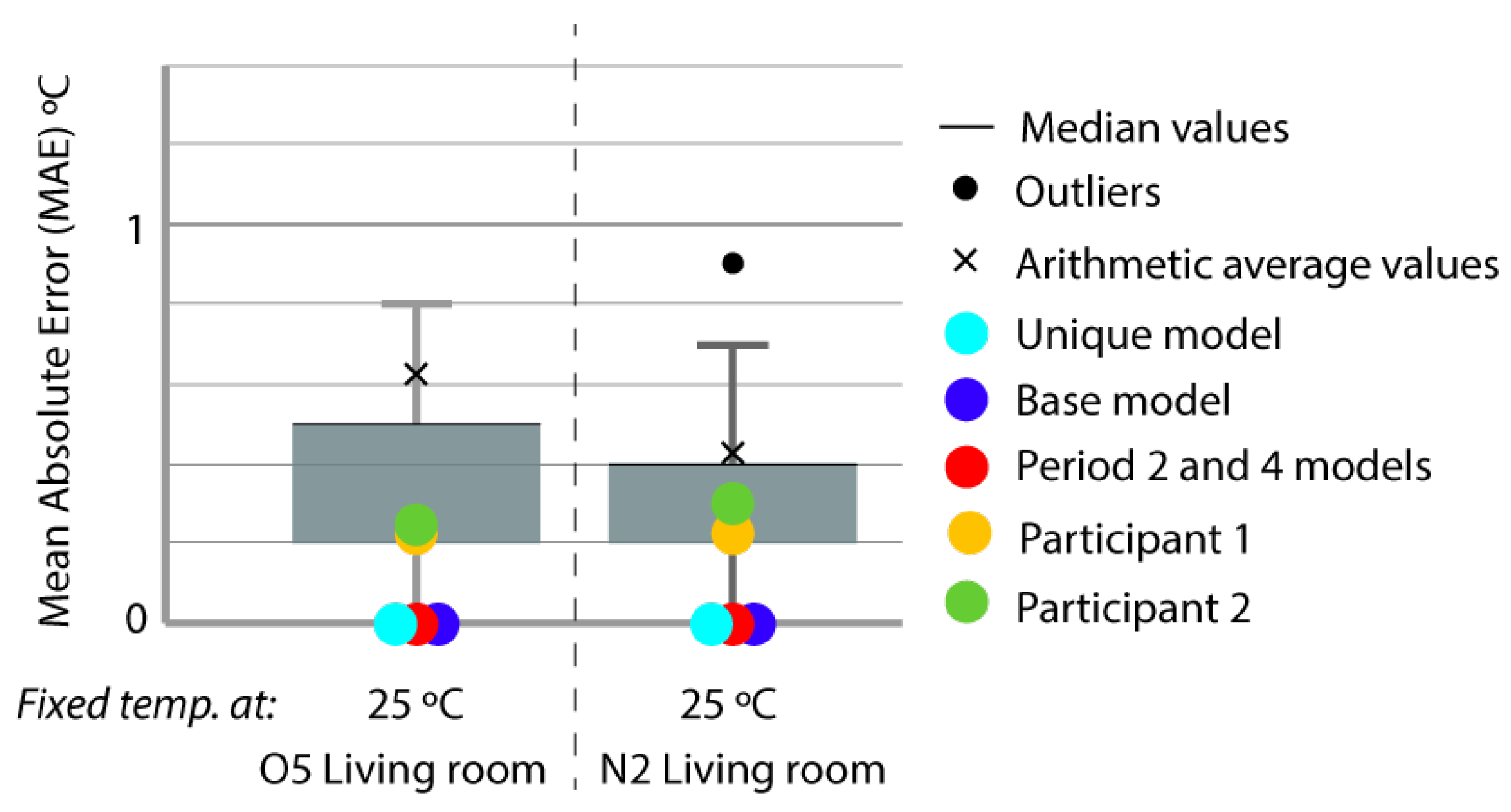
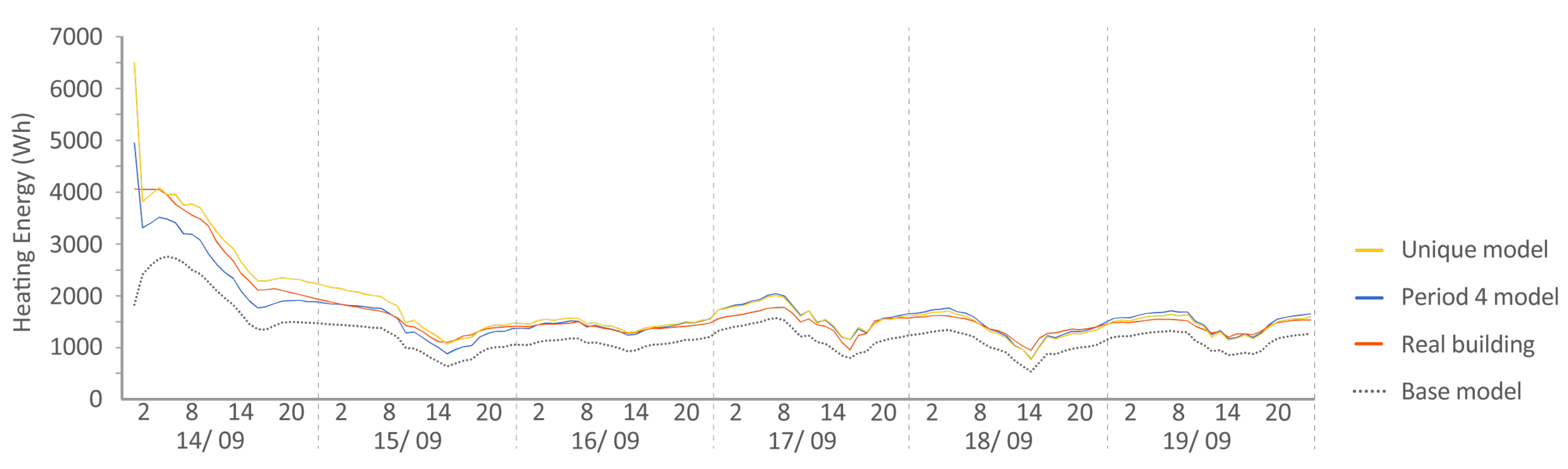
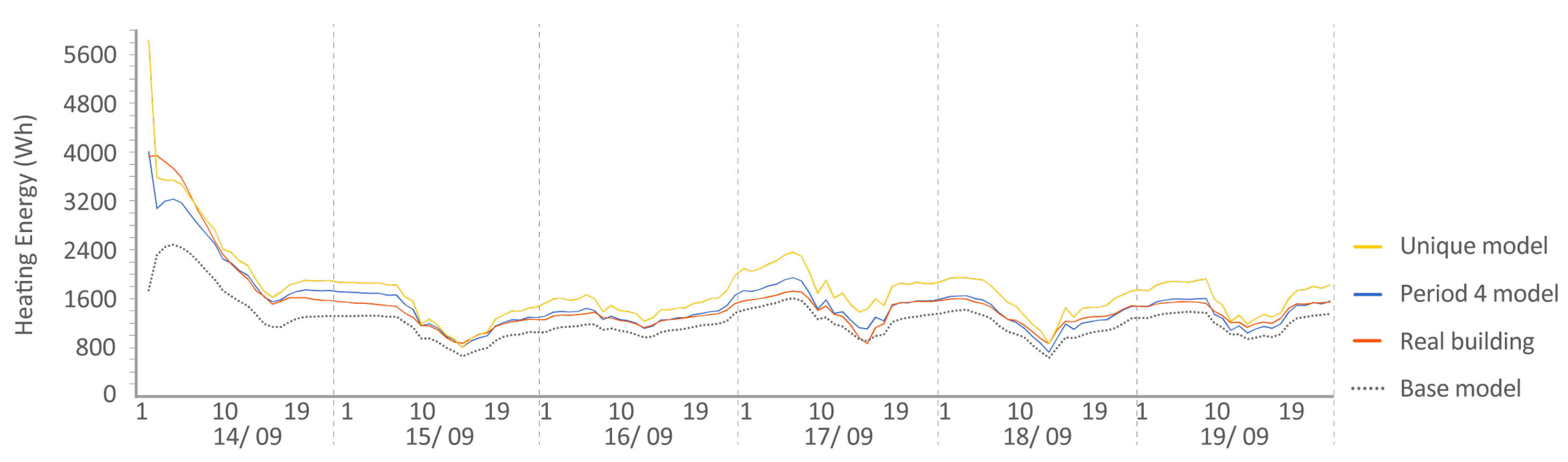
- Period 4: After Period 3, the thermal load of the houses was reset so that in the following period, both houses started with the same temperature and internal energy conditions. To achieve this, over 7 days, a constant temperature of 25 C was introduced. As in Period 2, the indoor temperatures were provided so that they could be entered into the energy model and were asked to predict the energy involved in raising the indoor temperature to 25 C.
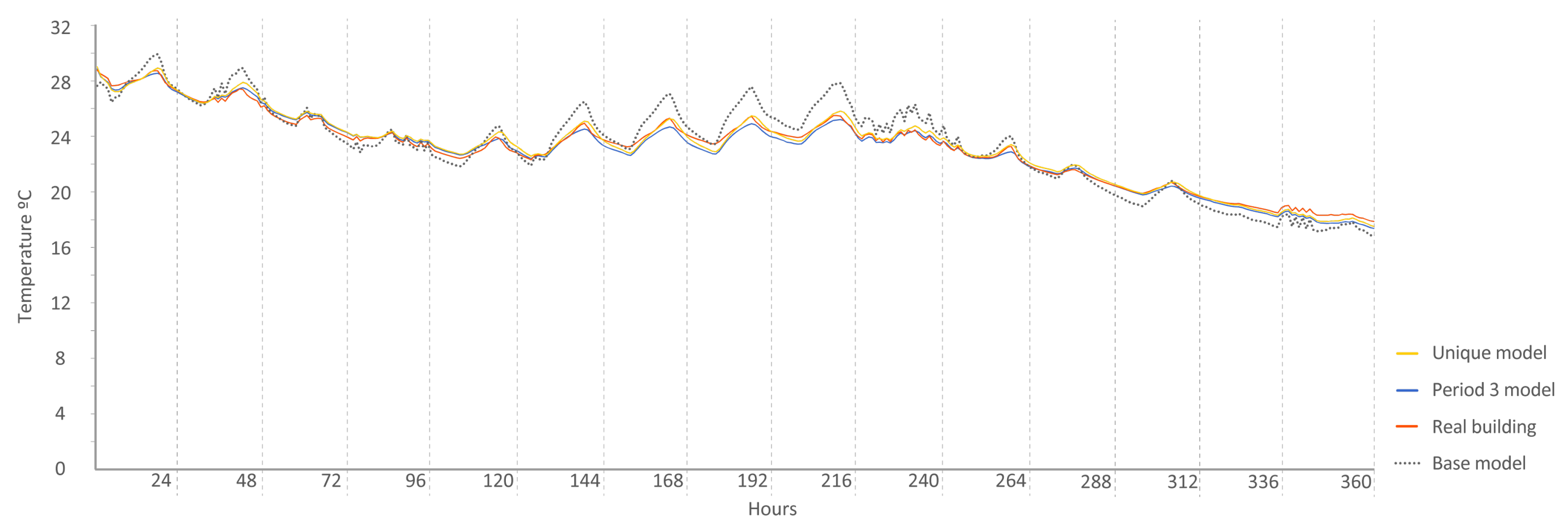
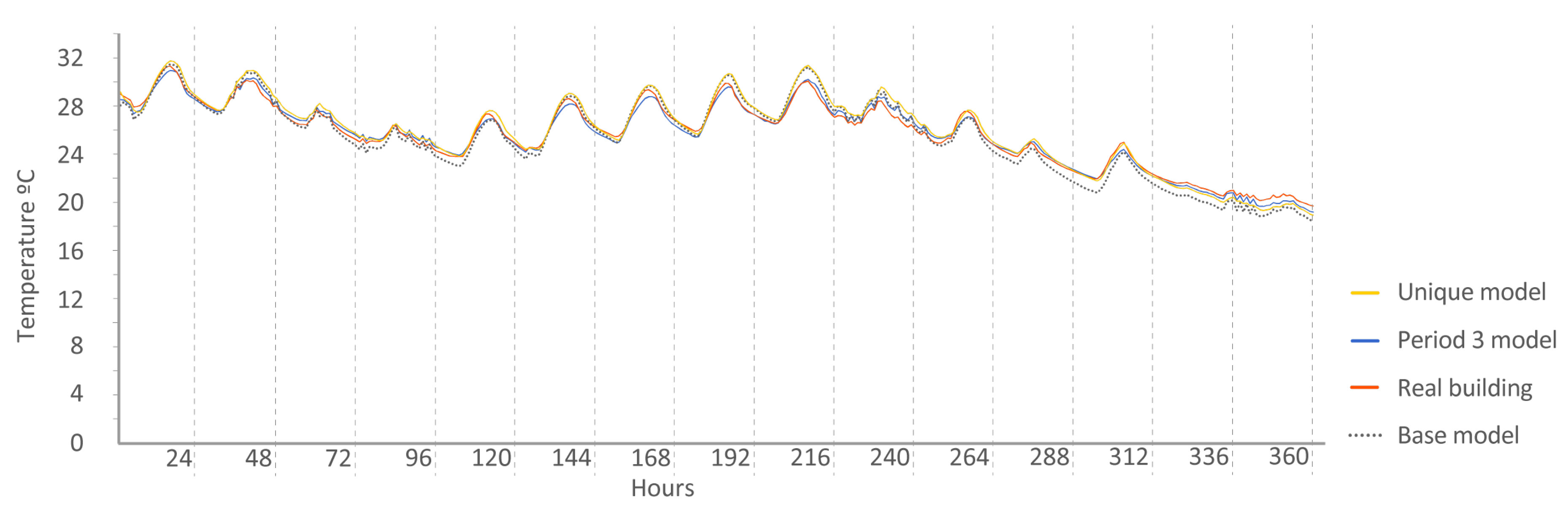
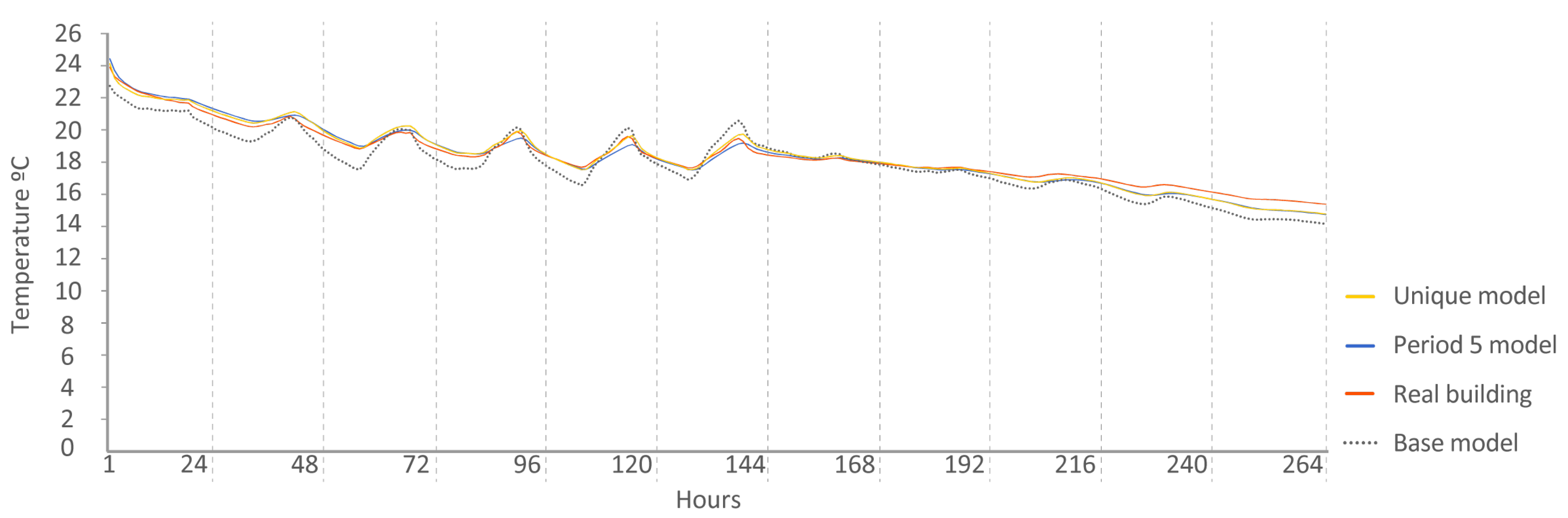
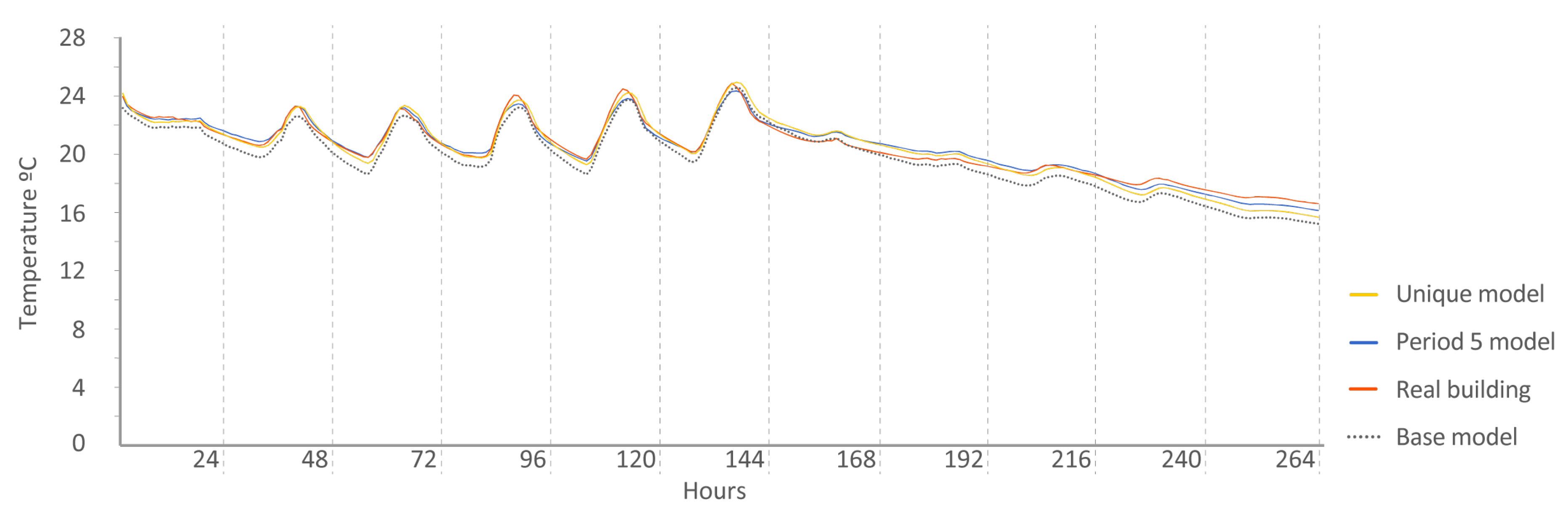
- Period 5: This was the last stage of the experiment. During this time, no energy was introduced into the buildings; they were left in free oscillation. The energy model was asked to reproduce the indoor temperatures using only input of energy provided by the external weather.
- To measure the magnitude adjustment, we used mean absolute error (MAE) in Equation (1), which is the measurement of the difference between two continuous variables, considering the two sets of data (some calculated and others measured) related to the same phenomenon:where and are the real and simulated values, respectively, and n is the number of values in the test sample.
- To assess the level of correspondence of the form, we used Spearman’s rank correlation coefficient, , using Equation (2). This coefficient is a measure of linear association that uses the ranges and the order number of each group of subjects and compares these ranges:
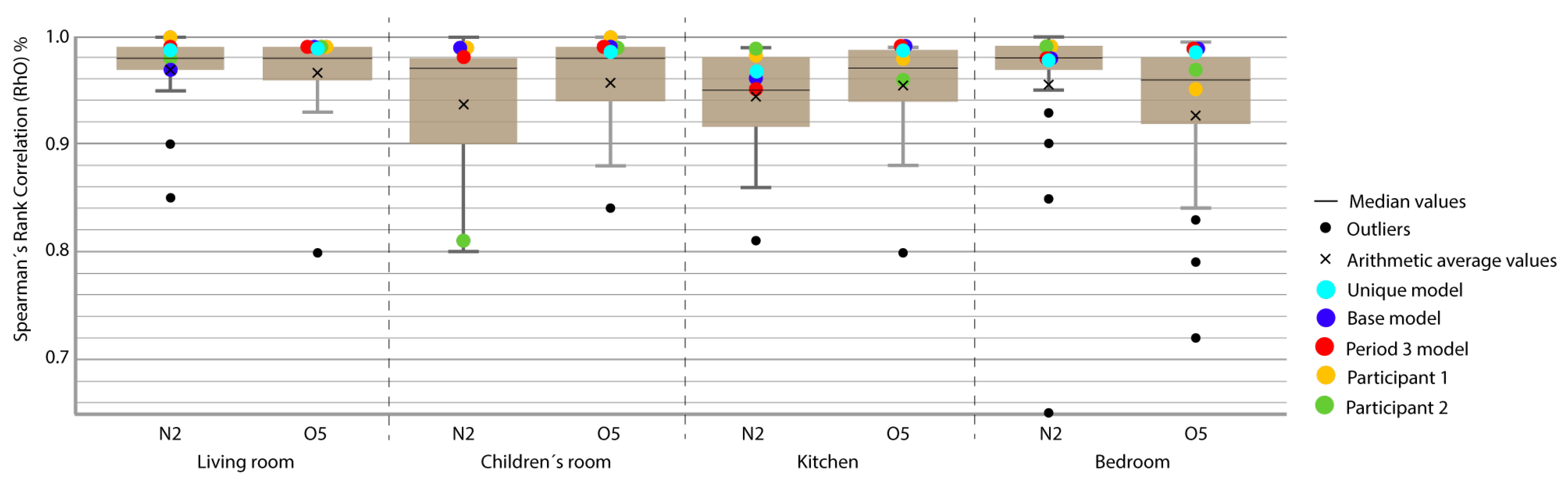
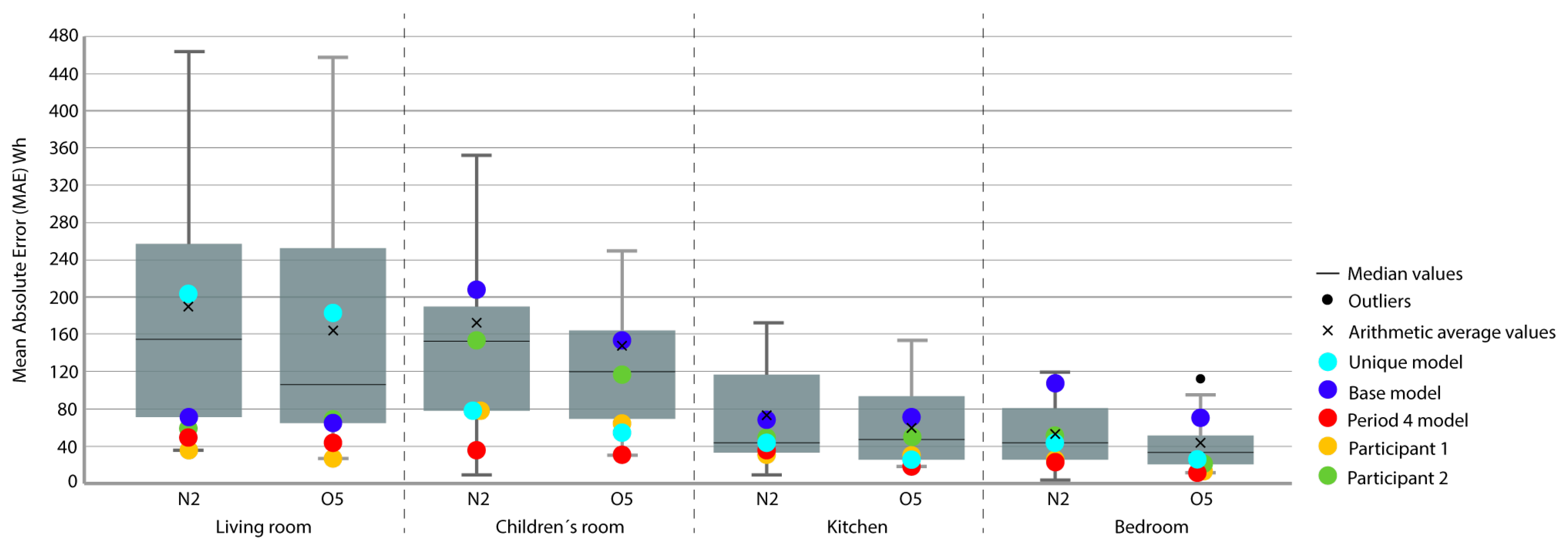
3. Analysis of Results and Discussion
- P 3-4 5: model adjusted in Periods 3, 4, and 5 and checked in Period 2.
- P 3-4: model adjusted in Periods 3 and 4 and checked in Period 2.
- P 2-4-5: model adjusted in Periods 2, 4, and 5 and checked in Period 3.
- P 2-3-5: model adjusted at Periods 2, 3, and 5 and checked at Period 4.
- P 2-3-4: model fitted at Periods 2, 3, and 4 and checked at Period 5.
- P 3-4: model fitted in Periods 3 and 4 and checked in Period 5.
- P 3-4 5: model adjusted in Periods 3, 4, and 5 and checked in Period 2.
- P 3-5: model adjusted in Periods 3 and 4 and checked in Period 2.
- P 2-4-5: model adjusted in Periods 2, 4, and 5 and checked in Period 3.
- P 2-3-5: model adjusted at Periods 2, 3, and 5 and checked at Period 4.
- P 3-5: model adjusted in Periods 3 and 4 and checked in Period 4.
- P 2-3-4: model fitted in Periods 2, 3, and 4 and checked in Period 5.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| IEA | International Energy Agency |
| SABINA | SmArt BI-directional multi eNergy gAteway |
| NFRC | National Fenestration Rating Council |
| EU | European Union |
| DOE | Department of Energy |
| BEM | Building Energy Model |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm |
| IBP | Institute for Building Physics |
| HVAC | Heating Ventilation Air Conditioning |
| ROLBS | Randomly Ordered Logarithmic Binary Sequence |
| MAE | Mean Absolute Error |
| Spearman’s Rank Correlation Coefficient | |
| ASHRAE | American Society of Heating, Refrigerating and Air-Conditioning Engineers |
| IPMVP | International Performance Measurement and Verification Protocol |
| FEMP | Federal Energy Management Program |
| CV(RMSE) | Coefficient of Variation of Mean Square Error |
| RMSE | Root Mean Square Error |
| r | Pearson Correlation Coefficient |
| R2 | Square Pearson Correlation Coefficient |
| NMBE | Normalize Mean Bias Error |
| BE | Bias Error |
| h | Height |
| BL1 | Boundary layer between insulation and brick wall rendering |
| ES | External Surface |
| IS | Internal Surface |
| SUA | Supply Air |
| ODA | Fresh Air |
| EHA | Exhaust Air |
| VFR | Volume flow rate |
| tpH | Thermal power |
| rH | Relative humidity |
| S | South |
| Temp. | Temperature |
| C | Celsius degrees |
| W | Watt |
| % | Percentage |
| m3/h | Cubic meters per hour |
| w/m2 | watt to square meter |
| m/s | meter per second |
| cm | centimeter |
| m | meter |
| Q | quartile |
| BMS | Building Management System |
References
- Navigant, Energy Efficiency Retrofits for Commercial and Public Buildings. 2014. Available online: http://www.navigantresearch.com/research/energy-efficiency-retrofits-for-commercial-and-public-buildings (accessed on 10 June 2014).
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Mustafaraj, G.; Marini, D.; Costa, A.; Keane, M. Model calibration for building energy efficiency simulation. Appl. Energy 2014, 130, 72–85. [Google Scholar] [CrossRef]
- Privara, S.; Cigler, J.; Váňa, Z.; Oldewurtel, F.; Sagerschnig, C.; Žáčeková, E. Building modeling as a crucial part for building predictive control. Energy Build. 2013, 56, 8–22. [Google Scholar] [CrossRef]
- Harish, V.; Kumar, A. Reduced order modeling and parameter identification of a building energy system model through an optimization routine. Appl. Energy 2016, 162, 1010–1023. [Google Scholar] [CrossRef]
- Henze, G.P.; Kalz, D.E.; Felsmann, C.; Knabe, G. Impact of forecasting accuracy on predictive optimal control of active and passive building thermal storage inventory. HVAC R. Res. 2004, 10, 153–178. [Google Scholar] [CrossRef]
- Ruiz, G.R.; Segarra, E.L.; Bandera, C.F. Model Predictive Control Optimization via Genetic Algorithm Using a Detailed Building Energy Model. Energies 2018, 12, 34. [Google Scholar] [CrossRef]
- Fernández Bandera, C.; Pachano, J.; Salom, J.; Peppas, A.; Ramos Ruiz, G. Photovoltaic Plant Optimization to Leverage Electric Self Consumption by Harnessing Building Thermal Mass. Sustainability 2020, 12, 553. [Google Scholar] [CrossRef]
- Reynolds, J.; Rezgui, Y.; Kwan, A.; Piriou, S. A zone-level, building energy optimisation combining an artificial neural network, a genetic algorithm, and model predictive control. Energy 2018, 151, 729–739. [Google Scholar] [CrossRef]
- Li, X.; Wen, J. Review of building energy modeling for control and operation. Renew. Sustain. Energy Rev. 2014, 37, 517–537. [Google Scholar] [CrossRef]
- Hong, T.; Langevin, J.; Sun, K. Building simulation: Ten challenges. Build. Simul. 2018, 11, 871–898. [Google Scholar] [CrossRef]
- Monge-Barrio, A.; Sánchez-Ostiz, A. Energy efficiency and thermal behaviour of attached sunspaces, in the residential architecture in Spain. Summer Conditions. Energy Build. 2015, 108, 244–256. [Google Scholar] [CrossRef]
- Sánchez-Ostiz, A.; Monge-Barrio, A.; Domingo-Irigoyen, S.; González-Martínez, P. Design and experimental study of an industrialized sunspace with solar heat storage. Energy Build. 2014, 80, 231–246. [Google Scholar] [CrossRef]
- Monge-Barrio, A.; Gutiérrez, A.S.O. Passive Energy Strategies for Mediterranean Residential Buildings: Facing the Challenges of Climate Change and Vulnerable Populations; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Carlos Gamero-Salinas, J.; Monge-Barrio, A.; Sanchez-Ostiz, A. Overheating risk assessment of different dwellings during the hottest season of a warm tropical climate. Build. Environ. 2020, 171, 106664. [Google Scholar] [CrossRef]
- Fernández Bandera, C.; Muñoz Mardones, A.F.; Du, H.; Echevarría Trueba, J.; Ramos Ruiz, G. Exergy As a Measure of Sustainable Retrofitting of Buildings. Energies 2018, 11, 3139. [Google Scholar] [CrossRef]
- Domingo-Irigoyen, S.; Sánchez-Ostiz, A.; San Miguel-Bellod, J. Cost-effective Renovation of a Multi-residential Building in Spain through the Application of the IEA Annex 56 Methodology. Energy Procedia 2015, 78, 2385–2390. [Google Scholar] [CrossRef]
- Hensen, J.L.; Lamberts, R. Building Performance Simulation for Design and Operation; Routledge: Abingdon, UK, 2012. [Google Scholar]
- Braun, J.E.; Chaturvedi, N. An inverse gray-box model for transient building load prediction. HVAC R. Res. 2002, 8, 73–99. [Google Scholar] [CrossRef]
- Lebrun, J. Simulation of a HVAC system with the help of an engineering equation solver. In Proceedings of the Seventh International IBPSA Conference, Rio de Janeiro, Brazil, 13–15 August 2001; pp. 13–15. [Google Scholar]
- ASHRAE. 2009 ASHRAE Handbook Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2009. [Google Scholar]
- Coakley, D.; Raftery, P.; Keane, M. A review of methods to match building energy simulation models to measured data. Renew. Sustain. Energy Rev. 2014, 37, 123–141. [Google Scholar] [CrossRef]
- Farhang, T.; Ardeshir, M. Monitoring-based optimization-assisted calibration of the thermal performance model of an office building. In Proceedings of the International Conference on Architecture and Urban Design, Tirana, Albania, 19–21 April 2012. [Google Scholar]
- ASHRAE. ASHRAE Guideline 14-2002, Measurement of Energy and Demand Savings; American Society of Heating, Ventilating, and Air Conditioning Engineers, Inc.: Atlanta, GA, USA, 2002. [Google Scholar]
- Lucas Segarra, E.; Du, H.; Ramos Ruiz, G.; Fernández Bandera, C. Methodology for the quantification of the impact of weather forecasts in predictive simulation models. Energies 2019, 12, 1309. [Google Scholar] [CrossRef]
- Ruiz, G.R.; Bandera, C.F. The importance of climate in building energy simulation. In International Conference on Architectural Research: Housing: Past, present and Future: Abstracts and Records; Institute of Eduardo Torroja: Madrid, Spain, 2013. (In Spanish) [Google Scholar]
- Du, H.; Bandera, C.F.; Chen, L. Nowcasting methods for optimising building performance. In Proceedings of the 16th Conference of International Building Performance Simulation Association, Rome, Italy, 2–4 September 2019. [Google Scholar]
- Li, H.; Hong, T.; Sofos, M. An inverse approach to solving zone air infiltration rate and people count using indoor environmental sensor data. Energy Build. 2019, 198, 228–242. [Google Scholar] [CrossRef]
- Martínez, S.; Eguía, P.; Granada, E.; Hamdy, M. A performance comparison of Multi-Objective Optimization-based approaches for calibrating white-box Building Energy Models. Energy Build. 2020, 216, 109942. [Google Scholar] [CrossRef]
- Reddy, T.A.; Maor, I.; Panjapornpon, C. Calibrating detailed building energy simulation programs with measured data—Part II: Application to three case study office buildings (RP-1051). HVAC R. Res. 2007, 13, 243–265. [Google Scholar] [CrossRef]
- Carroll, W.; Hitchcock, R. Tuning simulated building descriptions to match actual utility data: Methods and implementation. ASHRAE-Trans. Soc. Heat. Refrig. Air-Conditioning Engine 1993, 99, 928–934. [Google Scholar]
- Cowan, J. International performance measurement and verification protocol: Concepts and Options for Determining Energy and Water Savings-Vol. I. In International Performance Measurement & Verification Protocol; The U.S. Department of Energy: Springfield, VA, USA, 2002; Volume 1. [Google Scholar]
- Hong, T.; Lee, S.H. Integrating physics-based models with sensor data: An inverse modeling approach. Build. Environ. 2019, 154, 23–31. [Google Scholar] [CrossRef]
- Soebarto, V.I. Calibration of hourly energy simulations using hourly monitored data and monthly utility records for two case study buildings. Proc. Build. Simul. 1997, 97, 411–419. [Google Scholar]
- Wei, G.; Liu, M.; Claridge, D. Signatures of Heating and Cooling Energy Consumption for Typical AHUs. 1998. Available online: https://oaktrust.library.tamu.edu/handle/1969.1/6752 (accessed on 10 June 2020).
- Heo, Y.; Choudhary, R.; Augenbroe, G. Calibration of building energy models for retrofit analysis under uncertainty. Energy Build. 2012, 47, 550–560. [Google Scholar] [CrossRef]
- Manfren, M.; Aste, N.; Moshksar, R. Calibration and uncertainty analysis for computer models–a meta-model based approach for integrated building energy simulation. Appl. Energy 2013, 103, 627–641. [Google Scholar] [CrossRef]
- O’Neill, Z.; Eisenhower, B. Leveraging the analysis of parametric uncertainty for building energy model calibration. Build. Simul. 2013, 6, 365–377. [Google Scholar] [CrossRef]
- EN ISO 13790: Energy Performance of Buildings: Calculation of Energy Use for Space Heating and Cooling (ISO 13790: 2008). 2008. Available online: https://www.iso.org/obp/ui/#iso:std:iso:13790:ed-2:en (accessed on 10 June 2020).
- Kim, D.; Braun, J.E. A general approach for generating reduced-order models for large multi-zone buildings. J. Build. Perform. Simul. 2015, 8, 435–448. [Google Scholar] [CrossRef]
- Crawley, D.B.; Hand, J.W.; Kummert, M.; Griffith, B.T. Contrasting the capabilities of building energy performance simulation programs. Build. Environ. 2008, 43, 661–673. [Google Scholar] [CrossRef]
- U.S. DoE. EnergyPlus Engineering Reference: The Reference to EnergyPlus Calculations; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2009. [Google Scholar]
- Lee, S.H.; Hong, T.; Piette, M.A.; Taylor-Lange, S.C. Energy retrofit analysis toolkits for commercial buildings: A review. Energy 2015, 89, 1087–1100. [Google Scholar] [CrossRef]
- Lee, S.H.; Hong, T.; Piette, M.A.; Sawaya, G.; Chen, Y.; Taylor-Lange, S.C. Accelerating the energy retrofit of commercial buildings using a database of energy efficiency performance. Energy 2015, 90, 738–747. [Google Scholar] [CrossRef]
- Hong, T.; Piette, M.A.; Chen, Y.; Lee, S.H.; Taylor-Lange, S.C.; Zhang, R.; Sun, K.; Price, P. Commercial building energy saver: An energy retrofit analysis toolkit. Appl. Energy 2015, 159, 298–309. [Google Scholar] [CrossRef]
- SABINA H2020 EU Program. Available online: http://sindominio.net/ash (accessed on 10 June 2020).
- Kohlhepp, P.; Hagenmeyer, V. Technical potential of buildings in Germany as flexible power-to-heat storage for smart-grid operation. Energy Technol. 2017, 5, 1084–1104. [Google Scholar] [CrossRef]
- Bloess, A.; Schill, W.P.; Zerrahn, A. Power-to-heat for renewable energy integration: A review of technologies, modeling approaches, and flexibility potentials. Appl. Energy 2018, 212, 1611–1626. [Google Scholar] [CrossRef]
- Neymark, J.; Judkoff, R.; Knabe, G.; Le, H.T.; Dürig, M.; Glass, A.; Zweifel, G. Applying the building energy simulation test (BESTEST) diagnostic method to verification of space conditioning equipment models used in whole-building energy simulation programs. Energy Build. 2002, 34, 917–931. [Google Scholar] [CrossRef]
- ASHRAE. 2013 ASHRAE Handbook Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2013. [Google Scholar]
- Judkoff, R.; Wortman, D.; O’doherty, B.; Burch, J. Methodology for Validating Building Energy Analysis Simulations; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2008. [Google Scholar]
- Judkoff, R.; Polly, B.; Bianchi, M.; Neymark, J. Building Energy Simulation Test for Existing Homes (BESTEST-EX) Methodology; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2011. [Google Scholar]
- Judkoff, R.; Neymark, J. Model Validation and Testing: The Methodological Foundation of ASHRAE Standard 140; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2006. [Google Scholar]
- Zweifel, G.; Achermann, M. RADTEST—The extension of program validation towards radiant heating and cooling. In Proceedings of the Eighth International IBPSA Conference, Eindhoven, The Netherlands, 11–14 August 2003; pp. 1505–1511. [Google Scholar]
- Purdy, J.; Beausoleil-Morrison, I. Building Energy Simulation Test and Diagnostic Method for Heating, Ventilation, and Air-Conditioning Equipment Models (HVAC BESTEST): Fuel-Fired Furnace Test Cases. In Natural Resources Canada; CANMET Energy Technology Centre: Ottawa, ON, Canada, 2003; Available online: http://www.iea-shc.org/task22/deliverables.htm (accessed on 10 June 2020).
- Yuill, G.; Haberl, J. Development of Accuracy Tests for Mechanical System Simulation. Final Report for ASHRAE. 2002. Available online: https://technologyportal.ashrae.org/report/detail/154 (accessed on 10 June 2020).
- Ruiz, G.R.; Bandera, C.F.; Temes, T.G.A.; Gutierrez, A.S.O. Genetic algorithm for building envelope calibration. Appl. Energy 2016, 168, 691–705. [Google Scholar] [CrossRef]
- Fernández Bandera, C.; Ramos Ruiz, G. Towards a new generation of building envelope calibration. Energies 2017, 10, 2102. [Google Scholar] [CrossRef]
- Raftery, P. Calibrated Whole Building Energy Simulation: An Evidence-Based Methodology. PhD Thesis, National University of Ireland, Galway, Ireland, January 2011. [Google Scholar]
- Chaudhary, G.; New, J.; Sanyal, J.; Im, P.; O’Neill, Z.; Garg, V. Evaluation of “Autotune” calibration against manual calibration of building energy models. Appl. Energy 2016, 182, 115–134. [Google Scholar] [CrossRef]
- Strachan, P.; Svehla, K.; Heusler, I.; Kersken, M. Whole model empirical validation on a full-scale building. J. Build. Perform. Simul. 2016, 9, 331–350. [Google Scholar] [CrossRef]
- Ruiz, G.; Bandera, C. Validation of calibrated energy models: Common errors. Energies 2017, 10, 1587. [Google Scholar] [CrossRef]
- González, V.G.; Colmenares, L.Á.; Fidalgo, J.F.L.; Ruiz, G.R.; Bandera, C.F. Uncertainy’s Indices Assessment for Calibrated Energy Models. Energies 2019, 12, 2096. [Google Scholar] [CrossRef]
- Ruiz, G.R.; Bandera, C.F. Analysis of uncertainty indices used for building envelope calibration. Appl. Energy 2017, 185, 82–94. [Google Scholar] [CrossRef]
- Vogt, M.; Remmen, P.; Lauster, M.; Fuchs, M.; Müller, D. Selecting statistical indices for calibrating building energy models. Build. Environ. 2018, 144, 94–107. [Google Scholar] [CrossRef]
- Verbeke, S.; Audenaert, A. Thermal inertia in buildings: A review of impacts across climate and building use. Renew. Sustain. Energy Rev. 2018, 82, 2300–2318. [Google Scholar] [CrossRef]
- Lee, S.H.; Hong, T. Validation of an inverse model of zone air heat balance. Build. Environ. 2019, 161, 106232. [Google Scholar] [CrossRef]
- Johra, H.; Heiselberg, P. Influence of internal thermal mass on the indoor thermal dynamics and integration of phase change materials in furniture for building energy storage: A review. Renew. Sustain. Energy Rev. 2017, 69, 19–32. [Google Scholar] [CrossRef]
- Zeng, R.; Wang, X.; Di, H.; Jiang, F.; Zhang, Y. New concepts and approach for developing energy efficient buildings: Ideal specific heat for building internal thermal mass. Energy Build. 2011, 43, 1081–1090. [Google Scholar] [CrossRef]
- Wang, S.; Xu, X. Parameter estimation of internal thermal mass of building dynamic models using genetic algorithm. Energy Convers. Manag. 2006, 47, 1927–1941. [Google Scholar] [CrossRef]
- Han, G.; Srebric, J.; Enache-Pommer, E. Different modeling strategies of infiltration rates for an office building to improve accuracy of building energy simulations. Energy Build. 2015, 86, 288–295. [Google Scholar] [CrossRef]
- Zhang, Y.; Korolija, I. Performing complex parametric simulations with jEPlus. In Proceedings of the SET2010—9th International Conference on Sustainable Energy Technologies, Shanghai, China, 24–27 August 2010; pp. 24–27. [Google Scholar]
- Annex 58: Reliable Building Energy Performance Characterisation Based on Full Scale Dynamic Measurement. 2016. Available online: https://bwk.kuleuven.be/bwf/projects/annex58/index.htm (accessed on 10 June 2020).
- Guglielmetti, R.; Macumber, D.; Long, N. OpenStudio: An Open Source Integrated Analysis Platform; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2011. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]



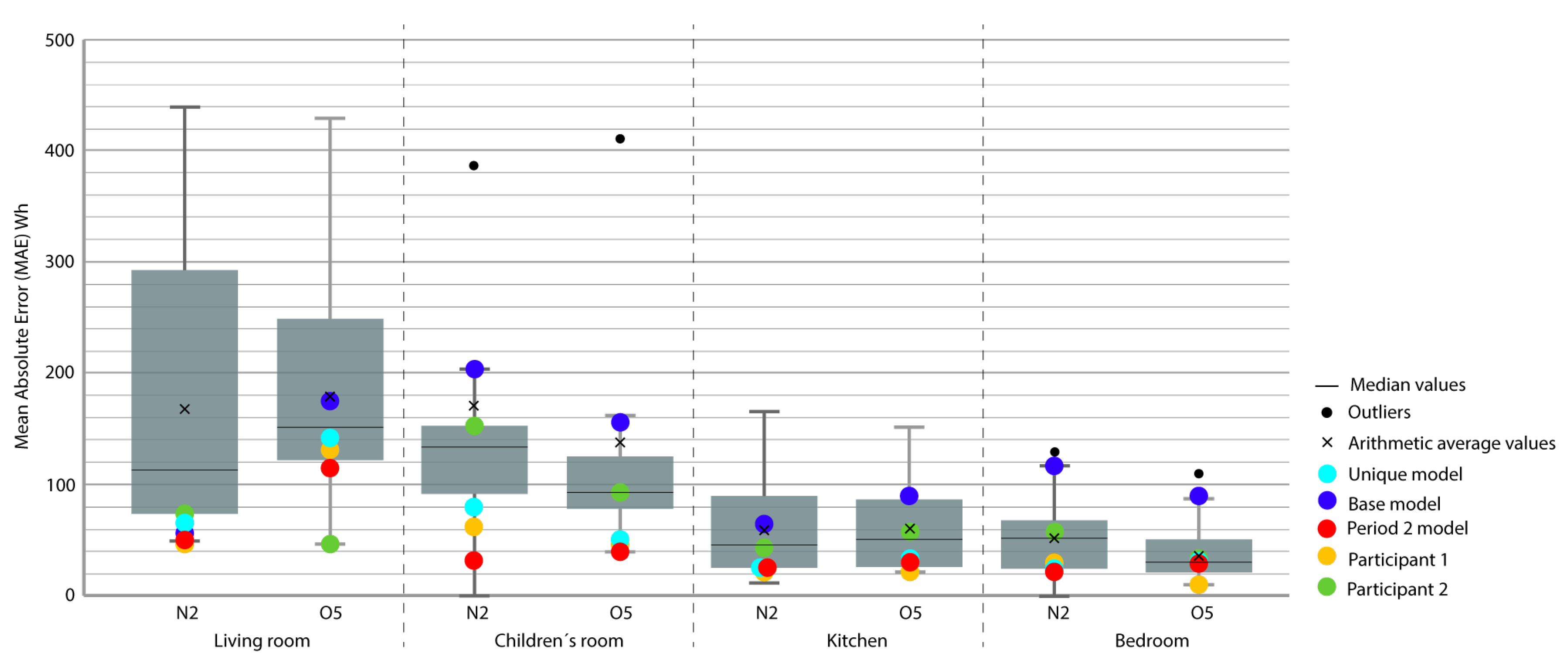
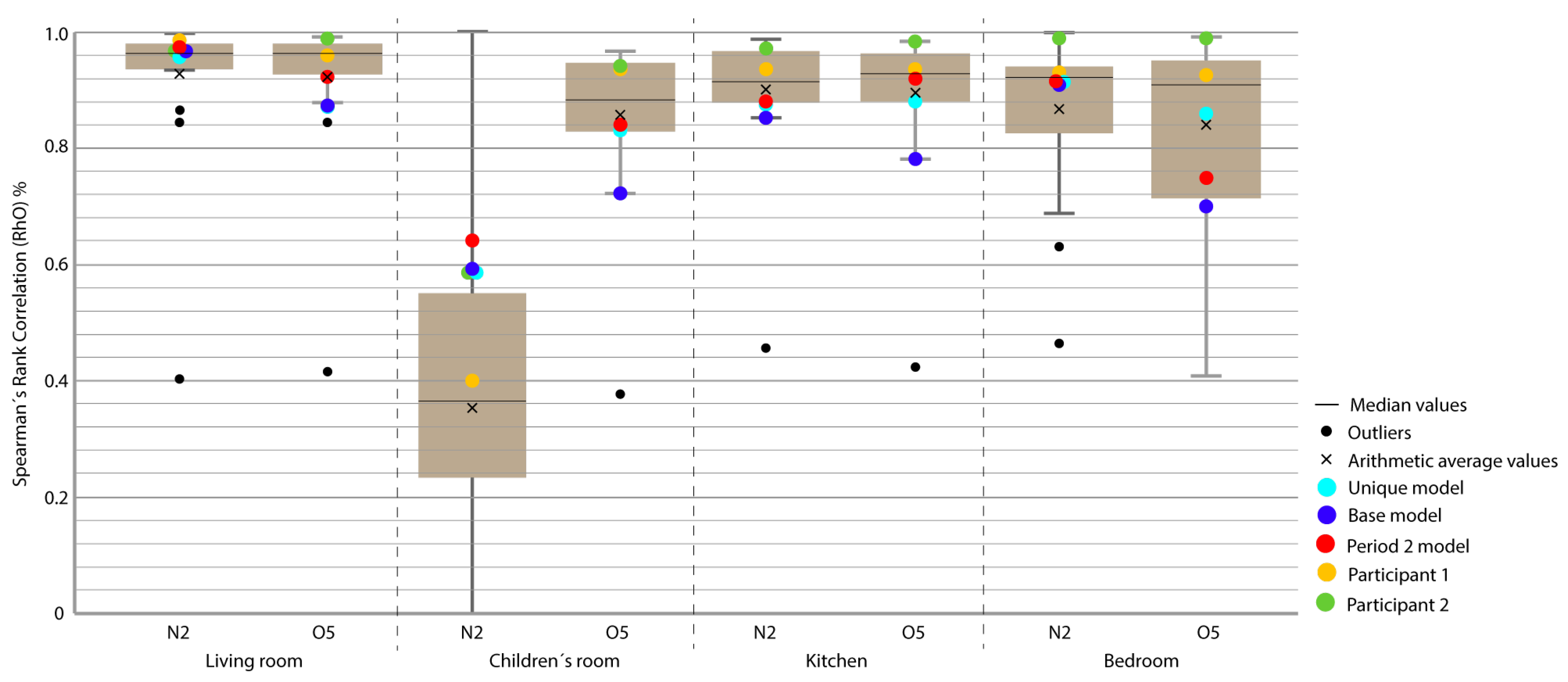
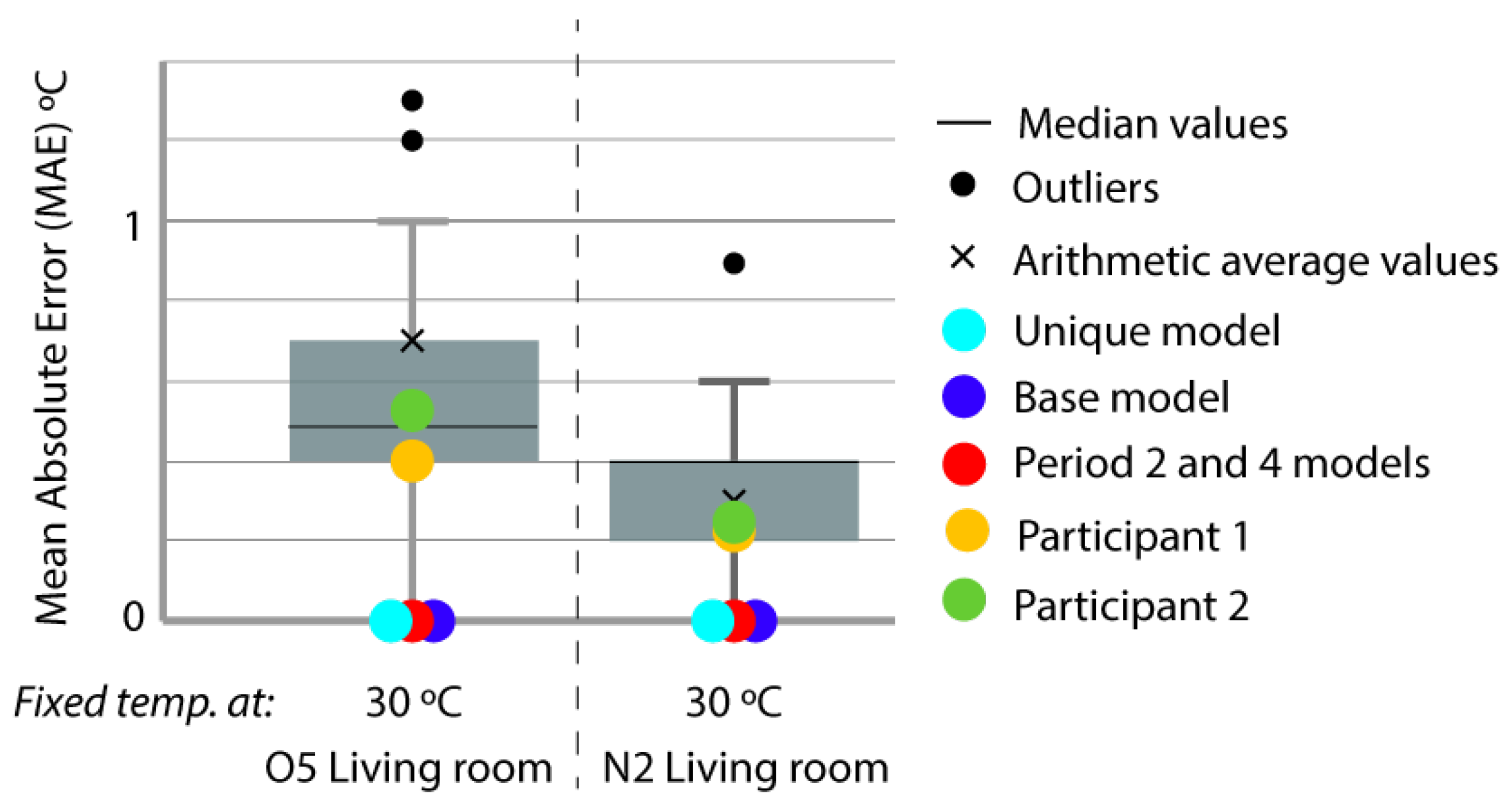
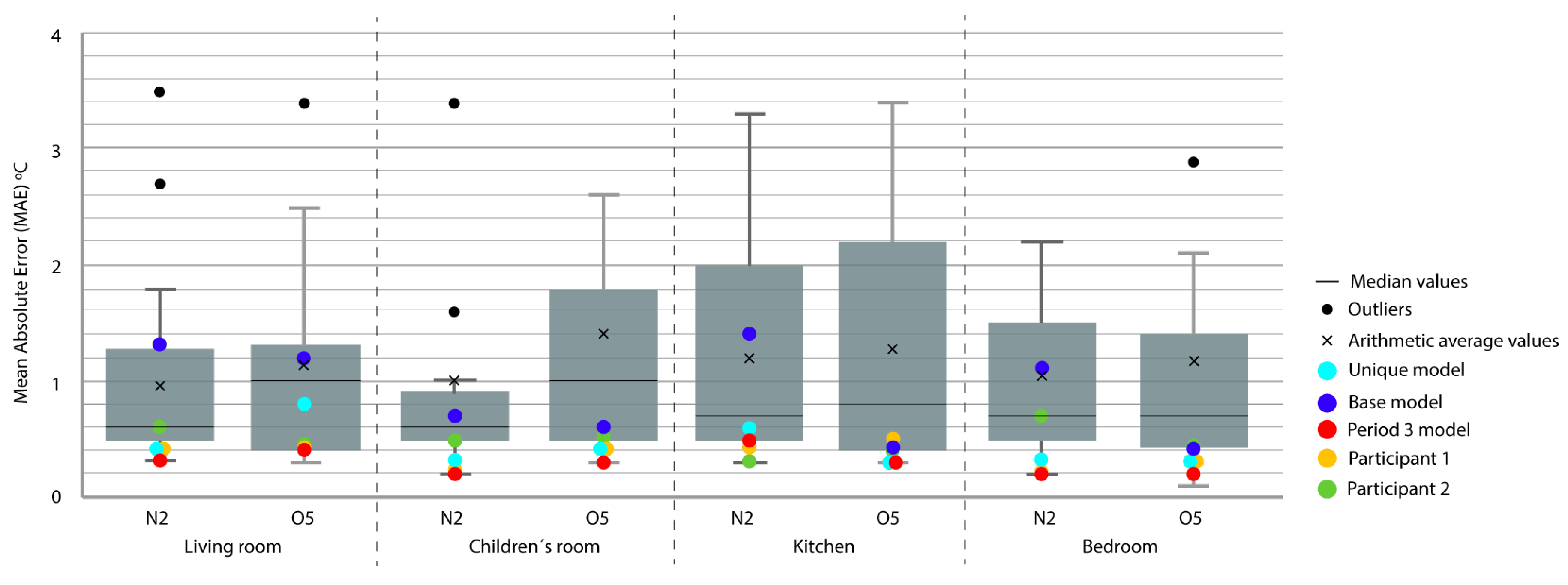


| House | Location | Sensor | Units | Measured |
|---|---|---|---|---|
| N2/O5 | doorway | Temperature | C | Indoor air |
| N2/O5 | bedroom | Temperature | C | Indoor air |
| N2/O5 | bath | Temperature | C | Indoor air |
| N2/O5 | child room | Temperature | C | Indoor air |
| N2/O5 | living h125 cm | Temperature | C | Indoor air |
| N2/O5 | kitchen | Temperature | C | Indoor air |
| N2/O5 | corridor | Temperature | C | Indoor air |
| N2/O5 | living h67 cm | Temperature | C | Indoor air |
| N2/O5 | living h187 cm | Temperature | C | Indoor air |
| N2/O5 | west facade S BL1 | Temperature | C | Surface temperature |
| N2/O5 | west facade S ES | Temperature | C | Surface temperature |
| N2/O5 | west facade S IS | Temperature | C | Surface temperature |
| N2/O5 | attic east | Temperature | C | Indoor temperature |
| N2/O5 | attic west | Temperature | C | Indoor air |
| N2/O5 | vent SUA | Temperature | C | Ventilation temperature |
| N2/O5 | vent ODA | Temperature | C | Ventilation temperature |
| N2/O5 | vent EHA | Temperature | C | Ventilation temperature |
| N2/O5 | cellar | Temperature | C | Indoor air |
| N2/O5 | child’s room | Electrical power | W | Heating power |
| N2/O5 | living room | Electrical power | W | Heating power |
| N2/O5 | kitchen | Electrical power | W | Heating power |
| N2/O5 | bathroom | Electrical power | W | Heating power |
| N2/O5 | bedroom | Electrical power | W | Heating power |
| N2/O5 | doorway | Electrical power | W | Ventilation power |
| N2/O5 | vent EHA fan | Electrical power | W | Ventilation power |
| N2/O5 | vent SUA fan | Electrical power | W | Ventilation power |
| N2/O5 | vent EHA VFR | Air speed | m3/h | Ventilation air speed |
| N2/O5 | vent SUA VFR | Air speed | m3/h | Ventilation air speed |
| N2/O5 | vent thP | Electrical power | W | Thermal power |
| N2 | west facade S BL1 | Heat flux | W/m2 | Heat flux |
| N2 | west facade S IS | Heat flux | W/m2 | Heat flux |
| O5 | west facade S BL1 | Heat flux | W/m2 | Heat flux |
| O5 | west facade S IS | Heat flux | W/m2 | Heat flux |
| N2 | N2 living rH h 125 cm | Humidity | % | Relative humidity |
| O5 | N2 living rH h 125 cm | Humidity | % | Relative humidity |
| N2/O5 | Weather station | Wind speed | m/s | Wind speed |
| N2/O5 | Weather station | Wind direction | º | Wind direction |
| N2/O5 | Weather station | Relative humidity | % | Relative humidity |
| N2/O5 | Weather station | Radiation | W/m2 | Vertical radiation south |
| N2/O5 | Weather station | Radiation | W/m2 | Global radiation |
| N2/O5 | Weather station | Radiation | W/m2 | Diffuse radiation |
| N2/O5 | Weather station | Radiation | W/m2 | Vertical radiation north |
| N2/O5 | Weather station | Radiation | W/m2 | Vertical radiation east |
| N2/O5 | Weather station | Radiation | W/m2 | Vertical radiation west |
| N2/O5 | Weather station | Temperature | C | Ambient temperature |
| N2/O5 | Weather station | Temperature | C | Ground temperature 0 cm. |
| N2/O5 | Weather station | Temperature | C | Ground temperature 50 cm. |
| N2/O5 | Weather station | Temperature | C | Ground temperature 100 cm. |
| N2/O5 | Weather station | Temperature | C | Ground temperature 200 cm. |
| N2/O5 | Weather station | Radiation | W/m2 | Long-wave radiation horizontal |
| N2/O5 | Weather station | Radiation | W/m2 | Long-wave radiation west |
| Period | Date | Configuration | Data Provided | Data Requested |
|---|---|---|---|---|
| Period 1 | 2013/8/21 to 2013/8/23 | Initialization (constant temperature) | Temperature and heat inputs | - |
| Period 2 | 2013/8/23 to 2013/8/30 | Constant temperature (nominal 30 C) | Temperature and heat inputs | Heat outputs |
| Period 3 | 2013/8/30 to 2013/9/14 | ROLBS heat inputs in living room | Temperature and heat inputs | Temperature outputs |
| Period 4 | 2013/9/14 to 2013/9/20 | Re-initialization Constant temp. | Temperature and heat inputs | Heat outputs |
| Period 5 | 2013/9/20 to 2013/9/30 | (nominal 25 C) Free float | Temperature inputs | Temp. outputs |
| Data Type | Index | FEMP 3.0 Criteria | ASHRAE G14-2002 | IPMVP |
|---|---|---|---|---|
| Calibration Criteria | ||||
| Monthly Criteria % | NMBE | |||
| CV(RMSE) | - | |||
| Hourly Criteria % | NMBE | |||
| CV(RMSE) |
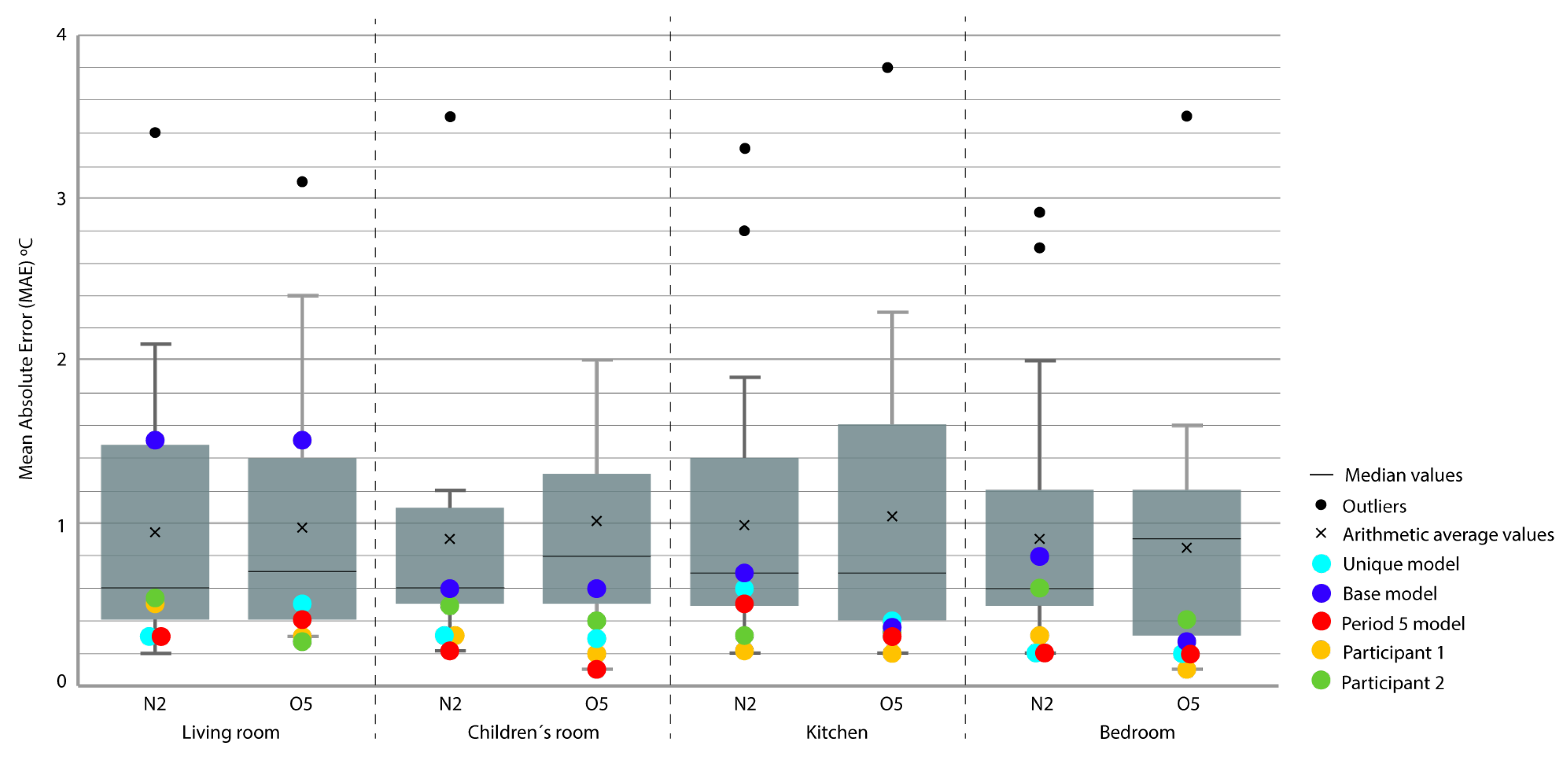
| MAE Index | Index | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| House | Calibrated Period | Checking Period | Living Room | Children’s Room | Bedroom | Kitchen | Living Room | Children’s Room | Bedroom | Kitchen |
| W/h | W/h | W/h | W/h | % | % | % | % | |||
| N2 | Period 2 | Period 2 | 51 | 29 | 21 | 25 | 97.3 | 63.9 | 91.7 | 87.9 |
| N2 | Period 4 | Period 2 | 52 | 35 | 22 | 30 | 97.2 | 55.8 | 91.9 | 87.6 |
| N2 | Unique model | Period 2 | 69 | 81 | 24 | 25 | 96.2 | 58.9 | 91.1 | 87.7 |
| N2 | P 3-4 | Period 2 | 52 | 112 | 48 | 26 | 97.2 | 59.4 | 91.5 | 87.5 |
| N2 | Period 5 | Period 2 | 85 | 132 | 22 | 81 | 96.2 | 56.1 | 91.2 | 74.1 |
| N2 | P 3-4-5 | Period 2 | 81 | 101 | 37 | 26 | 96.3 | 59.4 | 91.6 | 87.5 |
| N2 | Period 3 | Period 2 | 211 | 194 | 45 | 102 | 96.3 | 58.1 | 91.3 | 71.6 |
| N2 | Period 4 | Period 4 | 56 | 37 | 37 | 34 | 97.8 | 59.7 | 85.7 | 82.2 |
| N2 | Period 2 | Period 4 | 67 | 169 | 32 | 41 | 94.8 | 81.5 | 86.9 | 85.1 |
| N2 | Unique model | Period 4 | 209 | 77 | 43 | 40 | 94.6 | 67.8 | 85.4 | 86.1 |
| N2 | P 2-3-5 | Period 4 | 209 | 91 | 43 | 47 | 92.3 | 94.0 | 55.1 | 85.1 |
| N2 | Period 3 | Period 4 | 318 | 153 | 46 | 80 | 94.4 | 62.4 | 86.9 | 67.2 |
| N2 | Period 5 | Period 4 | 242 | 352 | 45 | 170 | 94.8 | 32.8 | 87.7 | 37.2 |
| C | C | C | C | % | % | % | % | |||
| N2 | Period 3 | Period 3 | 0.32 | 0.23 | 0.22 | 0.55 | 98.5 | 97.5 | 97.6 | 91.7 |
| N2 | Unique model | Period 3 | 0.40 | 0.33 | 0.26 | 0.58 | 98.9 | 95.6 | 97.3 | 96.7 |
| N2 | Period 5 | Period 3 | 0.36 | 0.27 | 0.34 | 0.59 | 98.5 | 97.2 | 97.3 | 92.0 |
| N2 | P 2-4-5 | Period 3 | 0.54 | 0.97 | 0.29 | 0.58 | 98.9 | 86.6 | 97.1 | 96.6 |
| N2 | Period 4 | Period 3 | 1.02 | 1.04 | 1.04 | 0.86 | 98.4 | 97.3 | 95.4 | 95.5 |
| N2 | Period 2 | Period 3 | 1.20 | 1.05 | 0.91 | 0.79 | 97.6 | 85.8 | 95.4 | 96.4 |
| N2 | Period 5 | Period 5 | 0.34 | 0.22 | 0.21 | 0.51 | 99.5 | 99.9 | 99.0 | 94.6 |
| N2 | Unique model | Period 5 | 0.30 | 0.26 | 0.21 | 0.59 | 99.7 | 99.9 | 99.1 | 95.4 |
| N2 | Period 3 | Period 5 | 0.40 | 0.28 | 0.23 | 0.51 | 99.6 | 99.8 | 99.1 | 94.8 |
| N2 | P 3-4 | Period 5 | 1.11 | 0.25 | 0.26 | 0.65 | 97.0 | 99.8 | 98.6 | 95.7 |
| N2 | P 2-3-4 | Period 5 | 1.14 | 0.22 | 0.32 | 0.73 | 96.1 | 99.6 | 98.1 | 88.9 |
| N2 | Period 4 | Period 5 | 1.31 | 0.52 | 0.88 | 0.86 | 96.7 | 99.5 | 97.0 | 95.1 |
| N2 | Period 2 | Period 5 | 1.42 | 1.55 | 0.78 | 0.81 | 94.6 | 98.8 | 96.8 | 95.3 |
| MAE Index | Index | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| House | Calibrated Period | Checking Period | Living Room | Children’s Room | Bedroom | Kitchen | Living Room | Children’s Room | Bedroom | Kitchen |
| W/h | W/h | W/h | W/h | % | % | % | % | |||
| O5 | Period 2 | Period 2 | 117 | 40 | 26 | 29 | 92.4 | 84.1 | 73.8 | 92.1 |
| O5 | Period 4 | Period 2 | 117 | 42 | 27 | 30 | 92.0 | 83.5 | 72.3 | 91.6 |
| O5 | Unique model | Period 2 | 146 | 53 | 33 | 34 | 87.1 | 82.8 | 86.1 | 88.3 |
| O5 | P 3-4-5 | Period 2 | 154 | 82 | 35 | 43 | 85.8 | 79.2 | 83.9 | 85.2 |
| O5 | P 3-5 | Period 2 | 199 | 109 | 38 | 38 | 87.6 | 78.1 | 82.5 | 89.1 |
| O5 | Period 5 | Period 2 | 219 | 87 | 29 | 59 | 88.8 | 76.5 | 84.1 | 87.4 |
| O5 | Period 3 | Period 2 | 197 | 122 | 63 | 66 | 84.4 | 78.8 | 75.3 | 82.6 |
| O5 | Period 4 | Period 4 | 51 | 31 | 13 | 19 | 97.4 | 51.9 | 97.0 | 96.2 |
| O5 | Unique model | Period 4 | 182 | 48 | 31 | 26 | 97.3 | 37.5 | 96.3 | 96.8 |
| O5 | Period 3 | Period 4 | 128 | 70 | 52 | 42 | 95.8 | 29.1 | 96.9 | 95.5 |
| O5 | P 2-3-5 | Period 4 | 294 | 55 | 50 | 65 | 96.4 | 33.7 | 95.0 | 95.7 |
| O5 | P 3-5 | Period 4 | 399 | 99 | 38 | 65 | 96.2 | 41.5 | 90.5 | 95.7 |
| O5 | Period 2 | Period 4 | 143 | 70 | 112 | 31 | 94.1 | 16.8 | 68.5 | 89.9 |
| O5 | Period 5 | Period 4 | 457 | 76 | 43 | 126 | 96.1 | 36.9 | 82.3 | 91.3 |
| C | C | C | C | % | % | % | % | |||
| O5 | Period 3 | Period 3 | 0.45 | 0.29 | 0.19 | 0.28 | 98.5 | 99.0 | 98.8 | 98.7 |
| O5 | Unique model | Period 3 | 0.79 | 0.36 | 0.22 | 0.35 | 98.6 | 98.4 | 98.4 | 98.8 |
| O5 | P 2-4-5 | Period 3 | 0.90 | 0.44 | 0.22 | 0.35 | 98.6 | 98.2 | 98.4 | 98.7 |
| O5 | Period 5 | Period 3 | 0.46 | 0.53 | 0.30 | 0.47 | 97.9 | 98.8 | 99.3 | 95.8 |
| O5 | Period 4 | Period 3 | 0.64 | 0.92 | 0.54 | 0.48 | 97.7 | 92.9 | 95.5 | 98.8 |
| O5 | Period 2 | Period 3 | 1.78 | 1.12 | 1.22 | 1.25 | 98.3 | 98.2 | 88.4 | 96.2 |
| O5 | Period 5 | Period 5 | 0.39 | 0.13 | 0.18 | 0.27 | 98.3 | 99.5 | 99.4 | 98.6 |
| O5 | Period 3 | Period 5 | 0.66 | 0.34 | 0.20 | 0.30 | 98.3 | 99.6 | 99.1 | 99.3 |
| O5 | Unique model | Period 5 | 0.52 | 0.27 | 0.19 | 0.35 | 98.1 | 99.2 | 99.3 | 98.6 |
| O5 | P 2-3-4 | Period 5 | 0.81 | 0.25 | 0.24 | 0.42 | 97.9 | 98.9 | 98.9 | 98.2 |
| O5 | Period 4 | Period 5 | 0.60 | 1.23 | 0.58 | 0.41 | 97.9 | 96.4 | 99.4 | 97.6 |
| O5 | Period 2 | Period 5 | 1.60 | 0.63 | 1.35 | 1.24 | 97.3 | 97.8 | 99.5 | 93.4 |
| MAE | CV(RMSE) | NMBE | R2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Houses | Periods | Models | Temp. °C | Energy W/h | Temp. % | Energy % | Temp. % | Energy % | Temp. % | Energy % | Temp. % | Energy % |
| N2 | Period 2 (Set point 30 C) | Period 2 model | 0 | 104 | 0% | 9.06% | 0% | 0.02% | 100% | 92.70% | 100% | 96.89% |
| N2 | Period 2 (Set point 30 C) | Unique model | 0 | 111 | 0% | 9.65% | 0% | 0.04% | 100% | 91.80% | 100% | 96.12% |
| N2 | Period 2 (Set point 30 C) | Base model | 0 | 410 | 0% | 29.05% | 0% | 0.21% | 100% | 91.93% | 100% | 96.58% |
| O5 | Period 2 (Set point 30 C) | Period 2 model | 0 | 197 | 0% | 21.75% | 0% | 0.02% | 100% | 83.78% | 100% | 92.24% |
| O5 | Period 2 (Set point 30 C) | Unique model | 0 | 230 | 0% | 28.41% | 0% | 0.02% | 100% | 74.18% | 100% | 87.64% |
| O5 | Period 2 (Set point 30 C) | Base model | 0 | 396 | 0% | 39.77% | 0% | 0.24% | 100% | 69.18% | 100% | 86.92% |
| N2 | Period 3 (ROLBS) | Period 3 model | 0.23 | 0 | 1.24% | 0% | 0.49% | 0% | 99.09% | 0% | 98.79% | 100% |
| N2 | Period 3 (ROLBS) | Unique model | 0.24 | 0 | 1.23% | 0% | −0.38% | 0% | 99.07% | 0% | 98.97% | 100% |
| N2 | Period 3 (ROLBS) | Base model | 0.69 | 0 | 3.71% | 0% | −0.93% | 0% | 95.45% | 0% | 97.84% | 100% |
| O5 | Period 3 (ROLBS) | Period 3 model | 0.28 | 0 | 1.26% | 0% | 0.13% | 0% | 98.69% | 0% | 99.09% | 100% |
| O5 | Period 3 (ROLBS) | Unique model | 0.45 | 0 | 2.19% | 0% | −0.97% | 0% | 98.59% | 0% | 99.02% | 100% |
| O5 | Period 3 (ROLBS) | Base model | 0.55 | 0 | 2.51% | 0% | 0.83% | 0% | 98.73% | 0% | 99.13% | 100% |
| N2 | Period 4 (Set point at 25 C) | Period 4 model | 0 | 131 | 0% | 11.76% | 0% | −0.05% | 100% | 91.70% | 100% | 96.30% |
| N2 | Period 4 (Set point at 25 C) | Unique model | 0 | 122 | 0% | 14.46% | 0% | −0.03% | 100% | 92.77% | 100% | 96.90% |
| N2 | Period 4 (Set point at 25 C) | Base model | 0 | 432 | 0% | 30.98% | 0% | 0.11% | 100% | 90.01% | 100% | 96.70% |
| O5 | Period 4 (Set point at 25 C) | Period 4 model | 0 | 86 | 0% | 9.30% | 0% | −0.01% | 100% | 94.36% | 100% | 96.35% |
| O5 | Period 4 (Set point at 25 C) | Unique model | 0 | 256 | 0% | 21.12% | 0% | −0.13% | 100% | 87.70% | 100% | 96.93% |
| O5 | Period 4 (Set point at 25 C) | Base model | 0 | 276 | 0% | 25.78% | 0% | 0.09% | 100% | 86.36% | 100% | 97.24% |
| N2 | Period 5 (Free oscillation) | Period 5 model | 0.25 | — | 1.67% | — | 0.37% | — | 99.01% | — | 99.60% | — |
| N2 | Period 5 (Free oscillation) | Unique model | 0.24 | — | 1.63% | — | 0.11% | — | 98.66% | — | 99.80% | — |
| N2 | Period 5 (Free oscillation) | Base model | 0.61 | — | 3.84% | — | 2.52% | — | 92.43% | — | 96.50% | — |
| O5 | Period 5 (Free oscillation) | Period 5 model | 0.27 | — | 1.57% | — | -0.11% | — | 97.52% | — | 99.00% | — |
| O5 | Period 5 (Free oscillation) | Unique model | 0.35 | — | 2.12% | — | 0.36% | — | 97.25% | — | 98.60% | — |
| O5 | Period 5 (Free oscillation) | Base model | 0.65 | — | 3.64% | — | 3.06% | — | 97.75% | — | 98.80% | — |
| Houses | Object | Room | Period 2 Model | Period 3 Model | Period 4 Model | Period 5 Model | Unique Model | Base Model | Base Model | Unique Model | Period 5 Model | Period 4 Model | Period 3 Model | Period 2 Model | Room | Object | Houses |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N2 | Capacitance (Temp. capacity multiplayer) | Living room | 10 | 10 | 10 | 20 | 10 | - | - | 10 | 10 | 10 | 2 | 0 | Living room | Capacitance (Temp. capacity multiplayer) | O5 |
| Children’s room | 20 | 1 | 40 | 10 | 20 | - | - | 20 | 1 | 20 | 5 | 1 | Children’s room | ||||
| Kitchen | 20 | 140 | 1 | 130 | 10 | - | - | 20 | 20 | 10 | 5 | 1 | Kitchen | ||||
| Bedroom | 10 | 40 | 1 | 50 | 50 | - | - | 40 | 60 | 10 | 15 | 5 | Bedroom | ||||
| N2 | Infiltrations (cm2) | Living room | 0 | 0 | 0 | 0 | 1 | - | - | 70 | 100 | 0 | 0 | 10 | Living room | Infiltrations (cm2) | O5 |
| Children’s room | 25 | 25 | 25 | 0 | 25 | - | - | 40 | 50 | 40 | 10 | 75 | Children’s room | ||||
| Kitchen | 0 | 0 | 0 | 0 | 0 | - | - | 0 | 20 | 0 | 0 | 1 | Kitchen | ||||
| Bedroom | 0 | 0 | 1 | 0 | 0 | - | - | 0 | 20 | 0 | 10 | 20 | Bedroom | ||||
| N2 | Thermal bridge Partition/Floor (m2K/W) | Living room | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 2.940 | 2.940 | 2.940 | 2.940 | 2.940 | 2.940 | 2.940 | Living room | Thermal bridge Partition/Floor (m2K/W) | O5 |
| Children’s room | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 2.940 | 2.940 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | Children’s room | ||||
| Kitchen | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 2.940 | 2.940 | 2.940 | 2.940 | 2.940 | 2.940 | 2.940 | Kitchen | ||||
| Bedroom | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 2.940 | 2.940 | 0.200 | 0.200 | 0.200 | 0.200 | 0.200 | Bedroom | ||||
| N2 | Thermal bridge Partition/Ceiling (m2K/W) | Living room | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 2.940 | 2.940 | 2.940 | 2.940 | 2.940 | 2.940 | 2.940 | Living room | Thermal bridge Partition/Ceiling (m2K/W) | O5 |
| Children’s room | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 2.940 | 2.940 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | Children’s room | ||||
| Kitchen | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 2.940 | 2.940 | 2.940 | 2.940 | 2.940 | 2.940 | 2.940 | Kitchen | ||||
| Bedroom | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 2.940 | 2.696 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | Bedroom | ||||
| N2 | Thermal bridge Wall/Ceiling (m2K/W) | Living room | 3.000 | 0.001 | 3.000 | 1.000 | 3.000 | 2.696 | 2.696 | 1.000 | 0.001 | 5.000 | 2.000 | 1.000 | Living room | Thermal bridge Wall/Ceiling (m2K/W) | O5 |
| Children’s room | 0.001 | 2.500 | 0.001 | 2.000 | 0.001 | 2.696 | 2.696 | 0.001 | 5.000 | 0.001 | 0.001 | 1.000 | Children’s room | ||||
| Kitchen | 0.001 | 0.001 | 0.001 | 0.001 | 0.500 | 2.696 | 2.696 | 1 | 0.001 | 0.001 | 1.000 | 0.001 | Kitchen | ||||
| Bedroom | 0.001 | 0.500 | 0.100 | 1.000 | 0.001 | 2.696 | 2.450 | 0.001 | 1.000 | 0.001 | 1.000 | 0.001 | Bedroom | ||||
| N2 | Thermal bridge Wall/Floor (m2K/W) | Living room | 2.000 | 0.001 | 2.000 | 0.100 | 2.000 | 2.450 | 2.450 | 1.000 | 0.001 | 5.000 | 0.001 | 0.001 | Living room | Thermal bridge Wall/Floor (m2K/W) | O5 |
| Children’s room | 0.001 | 1.500 | 0.100 | 2.000 | 0.100 | 2.450 | 2.450 | 1.000 | 2.000 | 5.000 | 5.000 | 0.001 | Children’s room | ||||
| Kitchen | 0.100 | 0.001 | 0.100 | 0.001 | 0.100 | 2.450 | 2.450 | 0.001 | 0.001 | 0.001 | 0.001 | 1.000 | Kitchen | ||||
| Bedroom | 0.100 | 1.500 | 0.100 | 0.100 | 0.100 | 2.450 | 2.261 | 0.001 | 0.001 | 1.000 | 1.000 | 5.000 | Bedroom | ||||
| N2 | Thermal bridge Wall/Wall (m2K/W) | Living room | 1.500 | 0.500 | 1.500 | 1.500 | 0.100 | 2.261 | 2.261 | 1.000 | 0.001 | 5.000 | 5.000 | 0.001 | Living room | Thermal bridge Wall/Wall (m2K/W) | O5 |
| Children’s room | 0.001 | 1.000 | 0.001 | 0.001 | 0.500 | 2.261 | 2.261 | 0.001 | 5.000 | 5.000 | 5.000 | 1.000 | Children’s room | ||||
| Kitchen | 0.500 | 0.001 | 1.000 | 0.001 | 0.500 | 2.261 | 2.261 | 0.001 | 0.001 | 1.000 | 5.000 | 0.001 | Kitchen | ||||
| Bedroom | 0.100 | 0.001 | 0.100 | 0.001 | 0.500 | 2.261 | 2.261 | 1.000 | 1.000 | 1.000 | 1.000 | 5.000 | Bedroom | ||||
| N2 | Internal mass (m2) | Living room | 10 | 80 | 1 | 70 | 70 | - | - | 30 | 80 | 20 | 43 | 0 | Living room | Internal mass (m2) | O5 |
| Children’s room | 10 | 1 | 90 | 1 | 10 | - | - | 20 | 0 | 50 | 0 | 0 | Children’s room | ||||
| Kitchen | 0 | 0 | 0 | 0 | 0 | - | - | 10 | 30 | 5 | 5 | 0 | Kitchen | ||||
| Bedroom | 0 | 0 | 0 | 0 | 0 | - | - | 10 | 5 | 20 | 1 | 70 | Bedroom |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez González, V.; Ramos Ruiz, G.; Fernández Bandera, C. Empirical and Comparative Validation for a Building Energy Model Calibration Methodology. Sensors 2020, 20, 5003. https://doi.org/10.3390/s20175003
Gutiérrez González V, Ramos Ruiz G, Fernández Bandera C. Empirical and Comparative Validation for a Building Energy Model Calibration Methodology. Sensors. 2020; 20(17):5003. https://doi.org/10.3390/s20175003
Chicago/Turabian StyleGutiérrez González, Vicente, Germán Ramos Ruiz, and Carlos Fernández Bandera. 2020. "Empirical and Comparative Validation for a Building Energy Model Calibration Methodology" Sensors 20, no. 17: 5003. https://doi.org/10.3390/s20175003
APA StyleGutiérrez González, V., Ramos Ruiz, G., & Fernández Bandera, C. (2020). Empirical and Comparative Validation for a Building Energy Model Calibration Methodology. Sensors, 20(17), 5003. https://doi.org/10.3390/s20175003






