A Multiscale Recognition Method for the Optimization of Traffic Signs Using GMM and Category Quality Focal Loss
Abstract
1. Introduction
- The road environment is complicated, which leads to the complicated background of the traffic signs. Even, the traffic signs are partially obscured by other objects.
- The complexity of lighting conditions (including the influence of weather conditions) may cause color distortion of the traffic sign images [7].
- Different shooting angles may cause different degrees of geometric distortion during the collection of traffic sign images [8].
- The color and shape of the traffic signs will change when they are polluted and damaged in nature.
- To the best of the authors’ knowledge, this is the first time that the Gaussian Mixture Model (GMM) [11] is used in prior anchor clustering, which significantly reduces the clustering error and thus improves the recognition accuracy of the neural network and reduces the computational time.
- This paper innovatively adds a category proportion factor in Quality Focal Loss [12] and solves the problem of the poor recognition effect caused by the lack of training samples, which leads to performance improvement.
- The five-scale recognition network and the corresponding prior anchor allocation strategy are proposed, which significantly improves the ability of small target recognition without many extra computing costs.
2. Related Work
2.1. Traditional Traffic Sign Recognition Algorithm
2.2. The State-of-the-Art Traffic Sign Recognition Algorithm
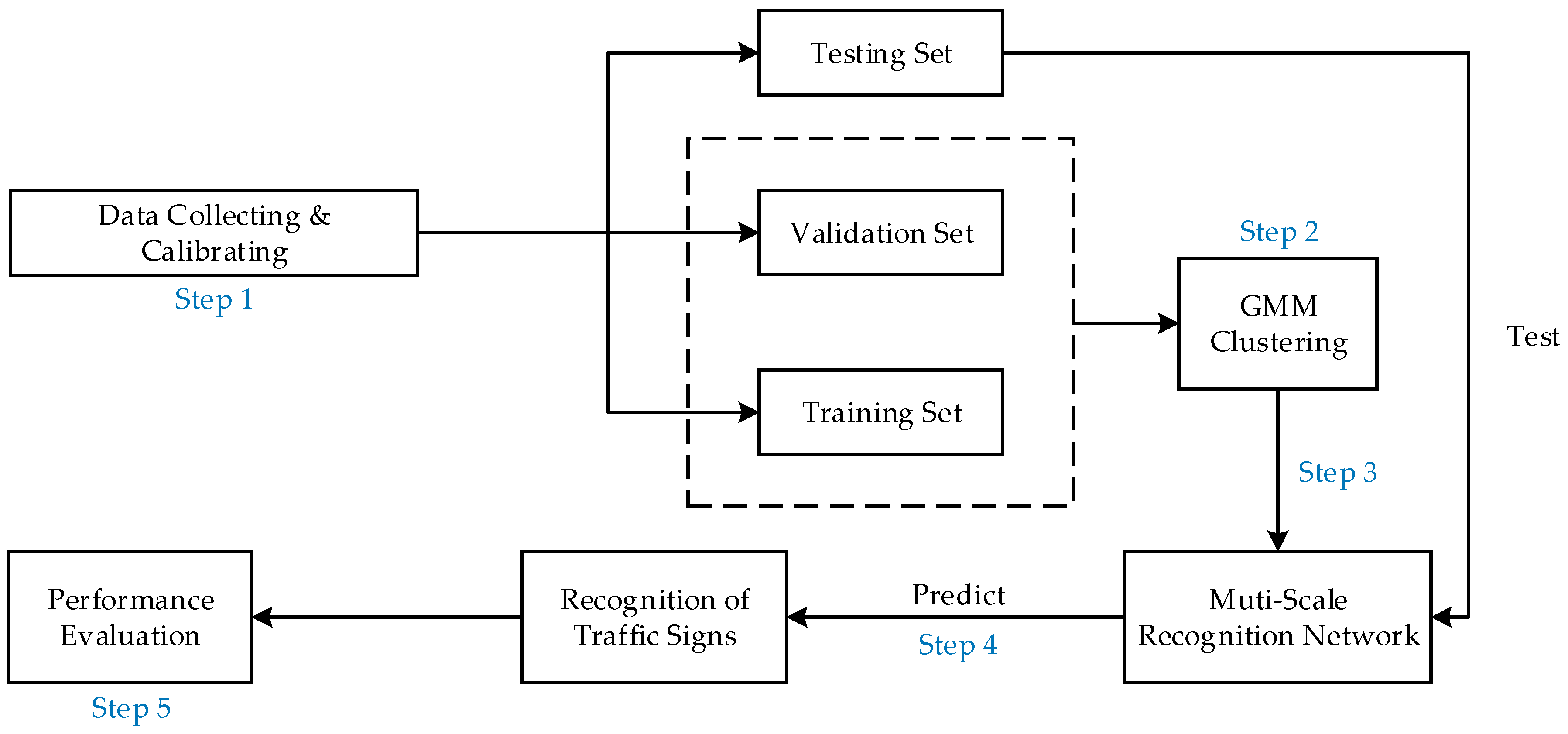
3. Proposed Traffic Sign Recognition Algorithm
- Step 1
- Data collecting and calibrating: We collect 10,000 images of traffic lights and traffic signs and divide them into the training set, validation set and testing set. The testing set does not participate in the model training. The calibration task of images is realized by the visual image calibration tool (labelImg).
- Step 2
- GMM clustering: We cluster all the samples in the training set and the validation set through the GMM to obtain the size of the prior anchors. Details of GMM clustering can be found in Section 5.1.
- Step 3
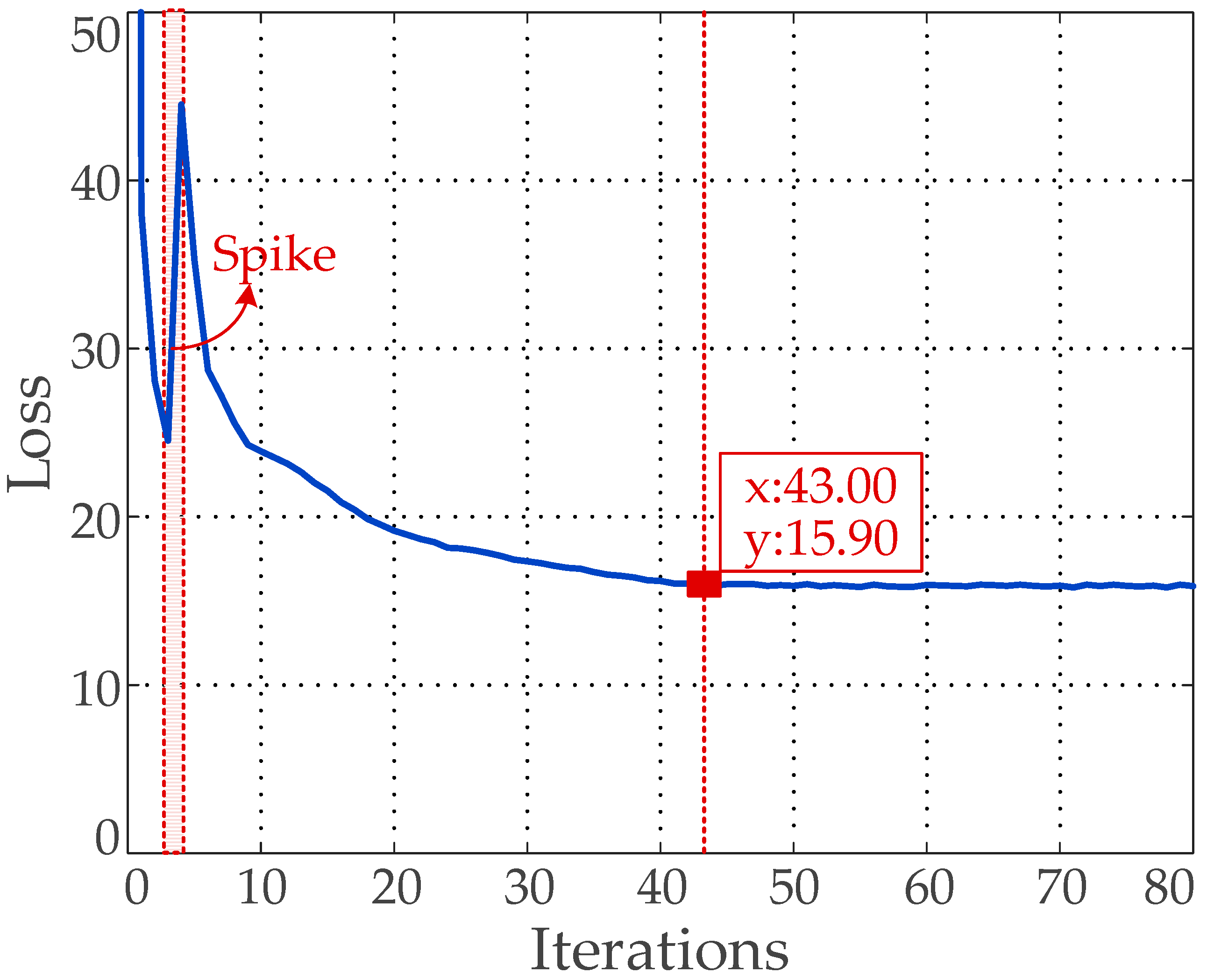
- Training the multi-scale recognition network: We take the size of the prior anchors obtained in Step 2 as the parameter of the multi-scale recognition network training, and we add the prior anchor allocation strategy and Category Quality Focal Loss proposed in this paper, as well as some existing effective tricks, to our five-scale recognition network. We train all the training samples and validation samples. The number of training iterations is set to 100. The network parameters are iteratively updated by training. The final training model is obtained once the number of iterations reaches the preset value or the change value of loss function is less than the threshold value.
- Step 4
- Model testing: Test the final training model obtained in Step 3 on the test set. This model can mark the category and confidence of traffic signs in the correct position of the test image.
- Step 5
- Performance testing: Objective evaluation of the performance of different traffic sign recognition algorithms (mAP, AP50, AP75, APS, APM, APL, recall rate, FPS and size of the networks) is calculated and compared. mAP refers to the mean Average Precision when the IoU is constrained to 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9 and 0.95. It is an important metric for judging the accuracy of recognition. The larger its value is, the higher the recognition accuracy is. AP50 and AP75 is the Average Precision when the threshold of IoU is greater than 0.5 and 0.75. APS, APM and APL are the Average Precision of the recognition network in identifying small, medium and large targets. Recall rate is the ratio of the number of positive samples (TP) correctly judged by the recognition network to the number of all positive samples (TP + FN) in the data set. FPS (Frames Per Second) is the number of images that can be recognized by the recognition network per second and is the metric for judging the recognition speed of the network. The larger its value, the faster the speed of recognition [13,23]. Figure 1 presents the holistic process of the traffic sign recognition algorithm.
4. Strong Baseline
- To avoid over-fitting, the labeling results are processed by Label Smoothing [28]. The mathematical expression of the Label Smoothing can be written by [28]:where, y_new denotes the new labeling value after Label Smoothing, y denotes the original labeling value, δ is a preset coefficient (in general, δ = 0.01 [28]) and NoC is the number of categories.Taking the dichotomies as an example (NoC = 2), if the original labeling value y = (0, 1), the new labeling value y_new is equal to (0.005, 0.995). In other words, Label Smoothing can penalize the labeling results and the baseline uses these penalized labeling results for model training, so that the model cannot be accurately classified during the training process which can avoid overfitting.
- The Mosaic data enhancement strategy [29] captures four training images which have ground truth bounding boxes at a time and clip the four training images. Then, the trimmed training images can be stitched together according to the preset position. In this process, the four training images and the ground truth bounding box in the training images are combined into one training image. Baseline transforms all the training images according to the Mosaic data enhancement strategy, and it trains the transformed training images. Due to the Mosaic data enhancement strategy, the background of the training samples is enriched. This method is equivalent to increasing the batch size which can improve the recognition accuracy to a certain extent.
- To solve the divergence problem that may be caused by IoU and GIoU in the training process, we introduce CIoU Loss [30] to measure the gap between the position information of the predicted bounding box and the actual position information. Therefore, CIoU Loss is used as part of the loss function to participate in the training process of baseline. The mathematical expression of the CIoU Loss can be written by [30]:Among them:
- IoU is the Intersection over Union between the predicted bounding box and the ground truth bounding box
- ρ2 (b, bgt) is the Euclidean Distance between the center of the predicted bounding box and the ground truth bounding box
- c is the diagonal distance of the smallest closure region that can contain both the predicted bounding box and the ground truth bounding box
- v denotes the parameter used to measure the consistency of aspect ratio, which is defined as
- α is the parameter used for trade-off, which is defined as
CIoU Loss takes into account the distance, overlap rate, scale and penalty terms between the predicted bounding box and the ground truth bounding box, which makes the bounding box regression more stable. As a result, CIoU Loss can achieve better convergence speed and accuracy on the bounding box regression problem. - Cosine annealing scheduler [31] is a strategy to adjust the learning rate. After setting the initial learning rate, the maximum learning rate and the number of steps to increase or decrease the learning rate, the value of learning rate first increases linearly and then decreases in line with the cosine function. This pattern of change in learning rate occurs periodically. Cosine annealing scheduler is used to adjust the learning rate of the baseline during training, which helps the model to escape the local minimum during training and find the path to the global minimum by instantly increasing the learning rate.
5. Proposed Methodology
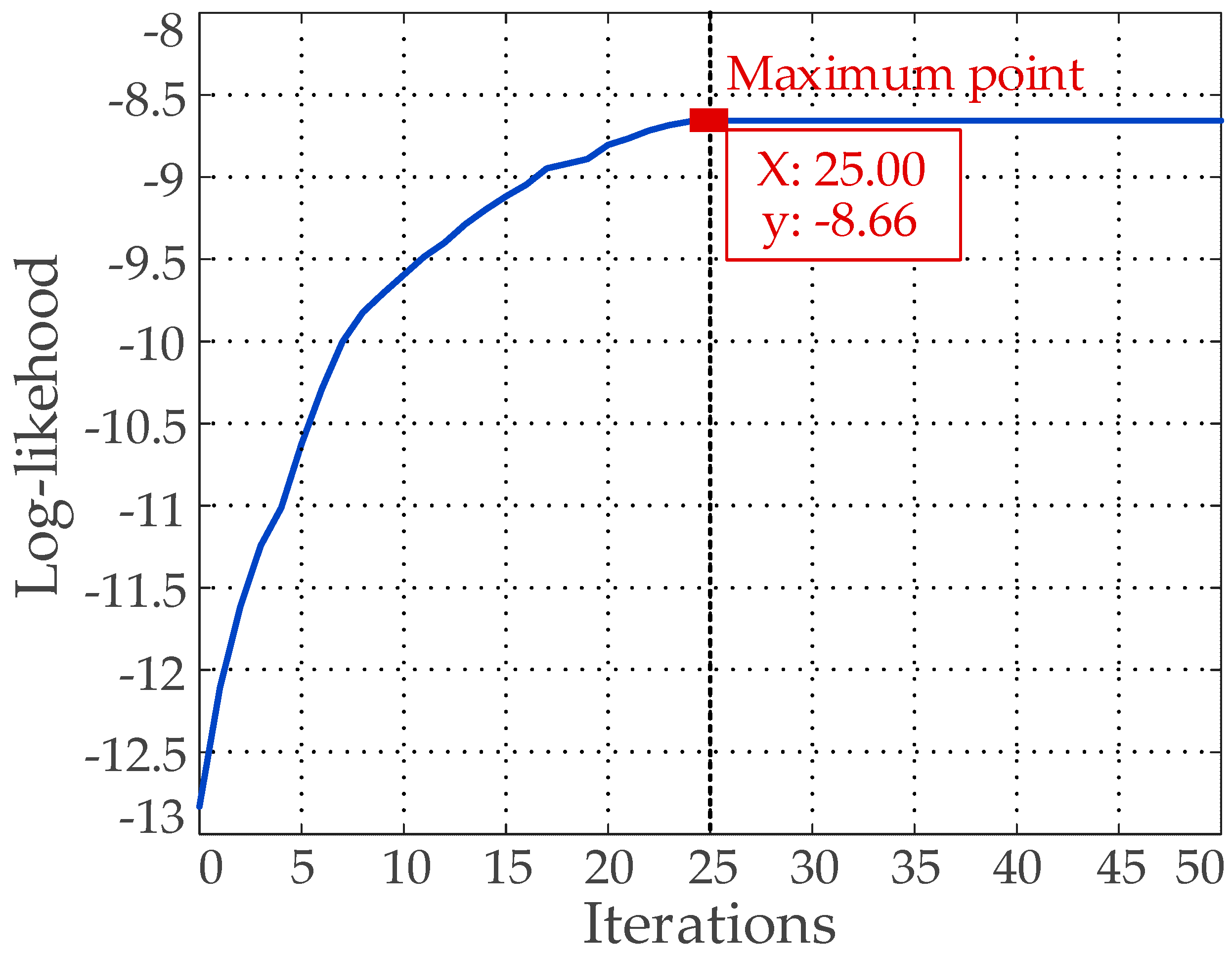
5.1. Prior Anchors Clustering Based on Gaussian Mixture Model
- N is the number of single Gaussian Models in the GMM
- πm is the proportion of each single Gaussian Model
- P(Xi|μm, Varm) is the probability density function of the sample Xi in the mth single Gaussian Model.
- Step 1:
- Initialize the mean (μ), variance (Var), and proportion (π) of each single Gaussian Model.
- Step 2:
- Calculate the contribution coefficient (Wi,m) of the sample Xi and the initial value of the likelihood function (LW), respectively:
- Step 3:
- After obtaining Wi,m, the proportion, mean, and variance of each single Gaussian Model in sequence can be updated by Equations (7)–(9) [32]:
5.2. Category Quality Focal Loss
- , p∈[0, 1] represents the category prediction probability, and y is the label value
- CE(pt) = −log(pt) is the cross-entropy function
- (1 − pt)γ is a factor used to control the influencing ability of difficult-to-train samples and easy-to-train samples, γ is used to adjust the steepness of the curve
- α∈[0, 1] is a parameter to adjust the influencing ability of positive samples and negative samples.
5.3. Five-Scale Recognition Network with a Prior Anchor Allocation Strategy
6. Experimental Results and Analysis
6.1. Traffic Sign Data Set
6.2. Experimental Environment and Parameter Settings
- 128 × 128: (9 × 10), (17 × 20), (21 × 30), (26 × 29), (29 × 47), (25 × 25)
- 64 × 64: (28 × 32), (33 × 34), (36 × 48), (40 × 42), (33 × 43), (46 × 49)
- 32 × 32: (48 × 104), (53 × 61), (65 × 68)
- 16 × 16: (87 × 110), (76 × 82), (100 × 153)
- 8 × 8: (113 × 134), (162 × 192), (368 × 389)
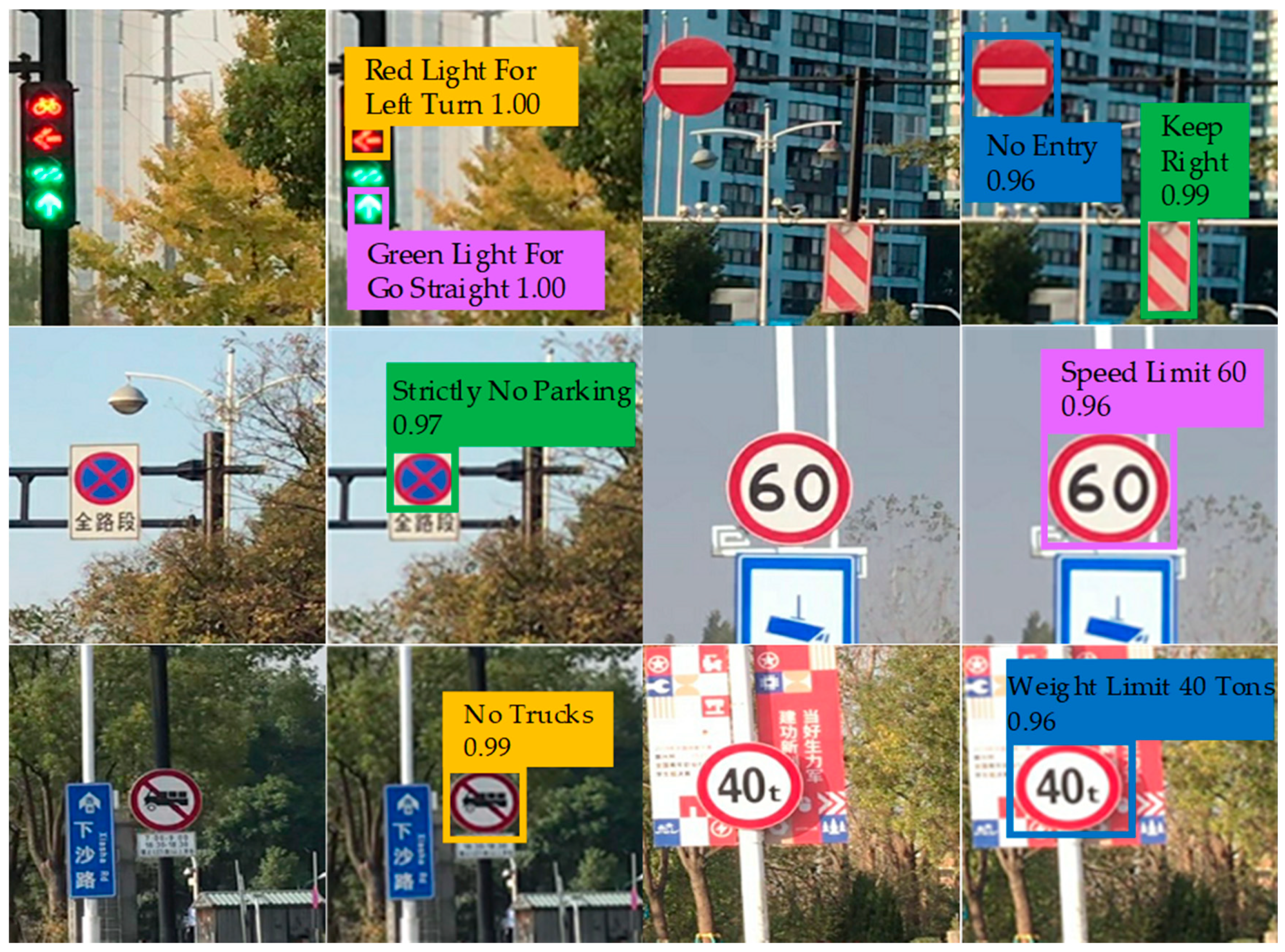
6.3. Traffic Sign Recognition Results and Analysis
- Using GMM for prior anchor clustering. The clustering results can have an arbitrary ellipse shape in the coordinate system, which is more in line with the actual clustering distribution. Therefore, the flexibility of clustering is improved, and the clustering error is obviously reduced, which can improve the overall recognition accuracy and speed of the network.
- Using CQFL can make the neural network pay more attention to the categories with small sample size in the training process. Taking its value as a measure of the difference between the predicted category result and the label value, participating in the training of the neural network. It can improve the recognition accuracy of the neural network for the category with small sample size and, therefore, solve the problem of poor recognition effect caused by the small number of samples.
- Based on the proposed recognition network, the resolution of the feature map is increased to 128 × 128, so that the recognition network has a better performance for small objects in the image. Besides, we assign more anchors to 128 × 128 and 64 × 64 feature map, which improves the probability of small target objects being covered by anchors manually. Therefore, the recognition accuracy of the recognition network is further improved, and the problem of small target recognition is solved by our tricks.
7. Conclusions
- A scientific traffic sign recognition framework is proposed. The framework is proved by the traffic sign data set containing 30 common traffic sign categories.
- Based on the existing tricks, we build a baseline with a better performance than the origin. In this paper, the GMM algorithm is used for prior anchor clustering, and a new loss function (CQFL) is proposed based on QFL. Besides, a five-scale recognition network with a prior anchor allocation strategy is proposed. By using the above tricks, the recognition accuracy and recognition speed of the baseline can be significantly improved. Particularly, it has an excellent recognition effect for small target objects.
- Compared with the state-of-the-art algorithms, the proposed algorithm has certain advantages in recognition accuracy and recognition speed.
Author Contributions
Funding
Conflicts of Interest
References
- Cao, Z.; Xu, X.; Hu, B.; Zhou, M. Rapid Detection of Blind Roads and Crosswalks by Using a Lightweight Semantic Segmentation Network. IEEE Trans. Intell. Transp. Syst. 2020, 16, 1–10. [Google Scholar] [CrossRef]
- Gao, K.; Zhang, Y.; Su, R.; Yang, F.; Suganthan, P.; Zhou, M. Solving Traffic Signal Scheduling Problems in Heterogeneous Traffic Network by Using Meta-Heuristics. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3272–3282. [Google Scholar] [CrossRef]
- Qi, L.; Zhou, M.C.; Luan, W.J. A Two-level Traffic Light Control Strategy for Preventing Incident-Based Urban Traffic Congestion. IEEE Trans. Intell. Transp. Syst. 2018, 19, 13–24. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Liu, W.; Wu, W.; Lim, S.J. An Asynchronous Clustering and Mobile Data Gathering Schema Based on Timer Mechanism in Wireless Sensor Networks. Comput. Mater. Contin. 2019, 58, 711–725. [Google Scholar] [CrossRef]
- Noskov, A.; Zipf, A. Open-data-driven embeddable quality management services for map-based web applications. Big Earth Data 2018, 2, 395–422. [Google Scholar] [CrossRef]
- Keil, J.; Edler, D.; Kuchinke, L.; Dickmann, F. Effects of visual map complexity on the attentional processing of landmarks. PLoS ONE 2020, 15, e0229575. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, X.; Sun, J.; Wang, J.; Li, K. Dual Model Learning Combined With Multiple Feature Selection for Accurate Visual Tracking. IEEE Access 2019, 7, 43956–43969. [Google Scholar] [CrossRef]
- Cao, D.; Jiang, Y.; Wang, J.; Ji, B.; Alfarraj, O.; Tolba, A.; Ma, X.; Liu, Y. ARNS: Adaptive Relay-Node Selection Method for Message Broadcasting in the Internet of Vehicles. Sensors 2020, 20, 1338. [Google Scholar] [CrossRef]
- Wu, L.; Li, H.; He, J.; Chen, X. Traffic sign detection method based on Faster R-CNN. J. Phys. Conf. Ser. 2019, 1176, 032045. [Google Scholar] [CrossRef]
- Branislav, N.; Velibor, I.; Bogdan, P. YOLOv3 Algorithm with additional convolutional neural network trained for traffic sign recognition. In Proceedings of the 2020 Zooming Innovation in Consumer Technologies Conference, Novi Sad, Serbia, 26–27 May 2020; pp. 165–168. [Google Scholar] [CrossRef]
- Tsuji, T.; Ichinobe, H.; Fukuda, O.; Kaneko, M. A maximum likelihood neural network based on a log-linearized Gaussian mixture model. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 304–316. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Wu, L.; Chen, S.; Hu, X.; Li, J.; Tang, J.; Yang, J. Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection. arXiv 2020, arXiv:2006.04388. Available online: https://arxiv.org/abs/2006.04388 (accessed on 31 July 2020).
- Redmon, J.; Farhadi, A. YOLOv3: An incremental improvement. arXiv 2018, arXiv:1804.02767. Available online: https://arxiv.org/abs/1804.02767 (accessed on 31 July 2020).
- Liu, X.; Zhu, S.; Chen, K. Method of Traffic Signs Segmentation Based on Color-Standardization. In Proceedings of the International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2009; pp. 193–197. [Google Scholar] [CrossRef]
- Li, H.; Sun, F.; Liu, L.; Wang, L. A Novel Traffic Sign Detection Method via Color Segmentation and Robust Shape Matching. Neurocomputing 2015, 169, 77–88. [Google Scholar] [CrossRef]
- Ellahyani, A.; Ansari, M.E.; Jaafari, I.E. Traffic Sign Detection and Recognition Based on Random Forests. Appl. Soft Comput. 2016, 46, 805–815. [Google Scholar] [CrossRef]
- Keser, T.; Ivan, D. Traffic sign shape detection and classification based on the segment surface occupancy analysis and correlation comparisons. Teh. Vjesn. Tech. Gaz. 2018, 25 (Suppl. S1), 23–31. [Google Scholar]
- Charette, R.D.; Nashashibi, F. Real time visual traffic lights recognition based on spot light detection and adaptive traffic lights templates. In Proceedings of the Intelligent Vehicles Symposium, Xian, China, 3–5 June 2009; pp. 358–363. [Google Scholar] [CrossRef]
- Kim, Y.K.; Kim, K.W.; Yang, X. Real time traffic light recognition system for color vision deficiencies. In Proceedings of the International Conference on Mechatronics and Automation, Harbin, China, 5–8 August 2007; pp. 76–81. [Google Scholar] [CrossRef]
- Jensen, M.B.; Philipsen, M.P.; Møgelmose, A.; Moeslund, T.B.; Trivedi, M.M. Vision for looking at traffic lights: Issues, survey, and perspectives. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1800–1815. [Google Scholar] [CrossRef]
- He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. arXiv 2015, arXiv:1406.47294. Available online: https://arxiv.org/abs/1406.47294 (accessed on 31 July 2020). [CrossRef] [PubMed]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar] [CrossRef]
- Jin, Y.; Fu, Y.; Wang, W.; Guo, J.; Ren, C.; Xiang, X. Multi-Feature Fusion and Enhancement Single Shot Detector for Traffic Sign Recognition. IEEE Access 2020, 8, 38931–38940. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Dollar, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 936–944. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, X.; Sun, J.; Wang, J.; Sangaiah, A.K. Spatial and semantic convolutional features for robust visual object tracking. Multimed. Tools Appl. 2020, 79, 15095–15115. [Google Scholar] [CrossRef]
- Zhang, S.; Wen, L.; Bian, X.; Lei, Z.; Li, S.Z. Single-shot refinement neural network for object detection. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4203–4212. [Google Scholar] [CrossRef]
- Diganta, M. Mish: A Self Regularized Nonmonotonic Neural Activation Function. arXiv 2019, arXiv:1908.08681. Available online: https://arxiv.org/abs/1908.08681 (accessed on 31 July 2020).
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar] [CrossRef]
- Alexey, B.; Chien, Y.W.; Hong, Y.M.L. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. Available online: https://arxiv.org/abs/2004.10934 (accessed on 31 July 2020).
- Zheng, Z.; Wang, P.; Liu, W.; Li, J.; Ye, R.; Ren, D. Distance-IoU Loss: Faster and better learning for bounding box regression. arXiv 2020, arXiv:1911.08287. Available online: https://arxiv.org/abs/1911.08287 (accessed on 31 July 2020). [CrossRef]
- Ilya, L.; Frank, H. SGDR: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. Available online: https://arxiv.org/abs/1608.03983 (accessed on 31 July 2020).
- Xu, L.; Jordan, M. On Convergence Properties of the EM Algorithm for Gaussian Mixtures. Neural Comput. 1996, 8, 129–151. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conferenceon Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar] [CrossRef]
- Sergey, I.; Christian, S. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. Available online: https://arxiv.org/abs/1502.03167 (accessed on 31 July 2020).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Luo, Y.; Qin, J.; Xiang, X.; Tan, Y.; Liu, Q.; Xiang, L. Coverless real-time image information hiding based on image block matching and dense convolutional network. J. Real-Time Image Process. 2019, 17, 125–135. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, J.; Weng, L.; Yang, Y. Rotated region based CNN for ship detection. In Proceedings of the International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 900–904. [Google Scholar] [CrossRef]
- Traffic lights and traffic signs test set. Available online: https://github.com/KeyPisces/Test-Set (accessed on 26 August 2020).
- Zhang, J.; Wang, W.; Lu, C.; Wang, J.; Sangaiah, A.K. Lightweight deep network for traffic sign classification. Ann. Telecommun. 2019, 75, 369–379. [Google Scholar] [CrossRef]
- Wang, J.J.; Kumbasar, T. Parameter optimization of interval Type-2 fuzzy neural networks based on PSO and BBBC methods. IEEE/CAA J. Autom. Sin. 2019, 6, 247–257. [Google Scholar] [CrossRef]
- Gao, S.; Zhou, M.; Wang, Y.; Cheng, J.; Yachi, H.; Wang, J. Dendritic Neuron Model With Effective Learning Algorithms for Classification, Approximation, and Prediction. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 601–614. [Google Scholar] [CrossRef]
- Rajendran, S.P.; Shine, L.; Pradeep, R.; Vijayaraghavan, S. Fast and Accurate Traffic Sign Recognition for Self Driving Cars using RetinaNet based Detector. In Proceedings of the 2019 International Conference on Communication and Electronics Systems, Coimbatore, India, 17–19 July 2019; pp. 784–790. [Google Scholar] [CrossRef]




| Mish | Label Smoothing | Mosaic | CIoU Loss | Cosine Annealing Scheduler | FPS | mAP | AP50 | AP75 |
|---|---|---|---|---|---|---|---|---|
| 12 | 33.1% | 57.7% | 34.1% | |||||
| ✓ | 11 | 34.2% | 59.0% | 35.2% | ||||
| ✓ | ✓ | 11 | 34.4% | 59.2% | 35.5% | |||
| ✓ | ✓ | ✓ | 11 | 34.6% | 59.4% | 35.9% | ||
| ✓ | ✓ | ✓ | ✓ | 11 | 36.3% | 59.7% | 38.4% | |
| ✓ | ✓ | ✓ | ✓ | ✓ | 11 | 37.0% | 60.3% | 39.2% |
| Category | Percentage of the Number of Ground-Truth Labels | AP | |
|---|---|---|---|
| Small sample size | Yield Ahead | 0.05% | 1.8% |
| One-way Road | 0.52% | 11.9% | |
| No U-Turn | 1.24% | 33.7% | |
| Bus-only Lane | 1.02% | 18.8% | |
| Speed Limit 80 | 2.06% | 35.8% | |
| Speed Limit 30 | 1.74% | 31.5% | |
| Large sample size | Speed Limit 60 | 9.95% | 82.4% |
| No Trucks | 8.86% | 80.3% | |
| Keep Right | 8.69% | 74.7% | |
| No Entry | 9.08% | 81.6% | |
| No Motor Vehicles | 8.14% | 72.4% | |
| Stop | 7.94% | 70.9% |
| Method | FPS | mAP | AP50 | AP75 | APS | APM | APL |
|---|---|---|---|---|---|---|---|
| baseline | 11 | 37.0% | 60.3% | 39.2% | 20.1% | 38.2% | 48.7% |
| baseline + FL | 11 | 37.6% | 60.6% | 39.9% | 20.3% | 39.0% | 49.5% |
| baseline + QFL | 11 | 37.8% | 60.8% | 40.3% | 20.3% | 39.4% | 49.8% |
| baseline + CQFL | 11 | 38.4% | 61.2% | 40.9% | 20.5% | 40.9% | 50.5% |
| Category | ||||
|---|---|---|---|---|
| Traffic Lights | Traffic Signs | |||
| Red Light for Go Straight | Go Straight Slot | No Entry | Bus-only Lane | Speed Limit 120 |
| Green Light for Go Straight | Left Turn Slot | No Trucks | One-way Road | Weight Limit 15 Tons |
| Red Light for Left Turn | Right Turn Slot | No U-Turn | Motor Vehicles Only | Weight Limit 40 Tons |
| Green Light for Left Turn | Strictly No Parking | Yield Ahead | Speed Limit 30 | Weight Limit 60 Tons |
| Red Light for Right Turn | No Left or Right Turn | Keep Right | Speed Limit 60 | School Crossing Ahead |
| Green Light for Right Turn | No Motor Vehicles | Stop | Speed Limit 80 | Pedestrian Crossing Ahead |
| GMM | CQFL | Anchor Allocation Strategy | Five-Scale Network | FPS | mAP | AP50 | AP75 | APS | APM | APL |
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 37.0% | 60.3% | 39.2% | 20.1% | 38.2% | 48.7% | ||||
| ✓ | 16 | 37.6% | 60.9% | 40.6% | 20.8% | 39.8% | 50.1% | |||
| ✓ | ✓ | 16 | 38.9% | 61.6% | 42.1% | 21.1% | 42.1% | 51.6% | ||
| ✓ | ✓ | ✓ | 16 | 39.4% | 61.9% | 42.5% | 22.4% | 42.3% | 51.7% | |
| ✓ | ✓ | ✓ | ✓ | 15 | 40.1% | 63.1% | 43.8% | 24.1% | 43.1% | 52.2% |
| Method | Size | FPS | Recall Rate | mAP | AP50 | AP75 | APS | APM | APL |
|---|---|---|---|---|---|---|---|---|---|
| Method A [9] | 109.3M | 4 | 68.9% | 39.1% | 59.8% | 42.7% | 18.4% | 43.2% | 50.0% |
| Method B [23] | 100.4M | 9 | 60.3% | 29.4% | 49.4% | 30.6% | 10.5% | 34.1% | 43.6% |
| Method C [26] | 78.1M | 8 | 66.3% | 33.2% | 53.9% | 36.3% | 15.4% | 38.3% | 44.9% |
| Method D [42] | 145.6M | 6 | 64.1% | 33.6% | 52.6% | 35.1% | 14.4% | 37.1% | 47.8% |
| Method E [42] | 212.9M | 6 | 67.2% | 35.2% | 53.9% | 37.8% | 14.9% | 38.7% | 49.7% |
| Method F [10] | 237.4M | 13 | 66.4% | 34.7% | 59.8% | 36.4% | 18.6% | 39.7% | 43.8% |
| Ours | 245.3M | 15 | 69.5% | 40.1% | 63.1% | 43.8% | 24.1% | 43.1% | 52.2% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Chen, C.; Shi, J.; Lai, C.S.; Yang, Y.; Dong, Z. A Multiscale Recognition Method for the Optimization of Traffic Signs Using GMM and Category Quality Focal Loss. Sensors 2020, 20, 4850. https://doi.org/10.3390/s20174850
Gao M, Chen C, Shi J, Lai CS, Yang Y, Dong Z. A Multiscale Recognition Method for the Optimization of Traffic Signs Using GMM and Category Quality Focal Loss. Sensors. 2020; 20(17):4850. https://doi.org/10.3390/s20174850
Chicago/Turabian StyleGao, Mingyu, Chao Chen, Jie Shi, Chun Sing Lai, Yuxiang Yang, and Zhekang Dong. 2020. "A Multiscale Recognition Method for the Optimization of Traffic Signs Using GMM and Category Quality Focal Loss" Sensors 20, no. 17: 4850. https://doi.org/10.3390/s20174850
APA StyleGao, M., Chen, C., Shi, J., Lai, C. S., Yang, Y., & Dong, Z. (2020). A Multiscale Recognition Method for the Optimization of Traffic Signs Using GMM and Category Quality Focal Loss. Sensors, 20(17), 4850. https://doi.org/10.3390/s20174850








