Quantitative Long-Term Monitoring of the Circulating Gases in the KATRIN Experiment Using Raman Spectroscopy
Abstract
1. Introduction
2. Concepts of the KATRIN Experiment
3. Setup and Methods
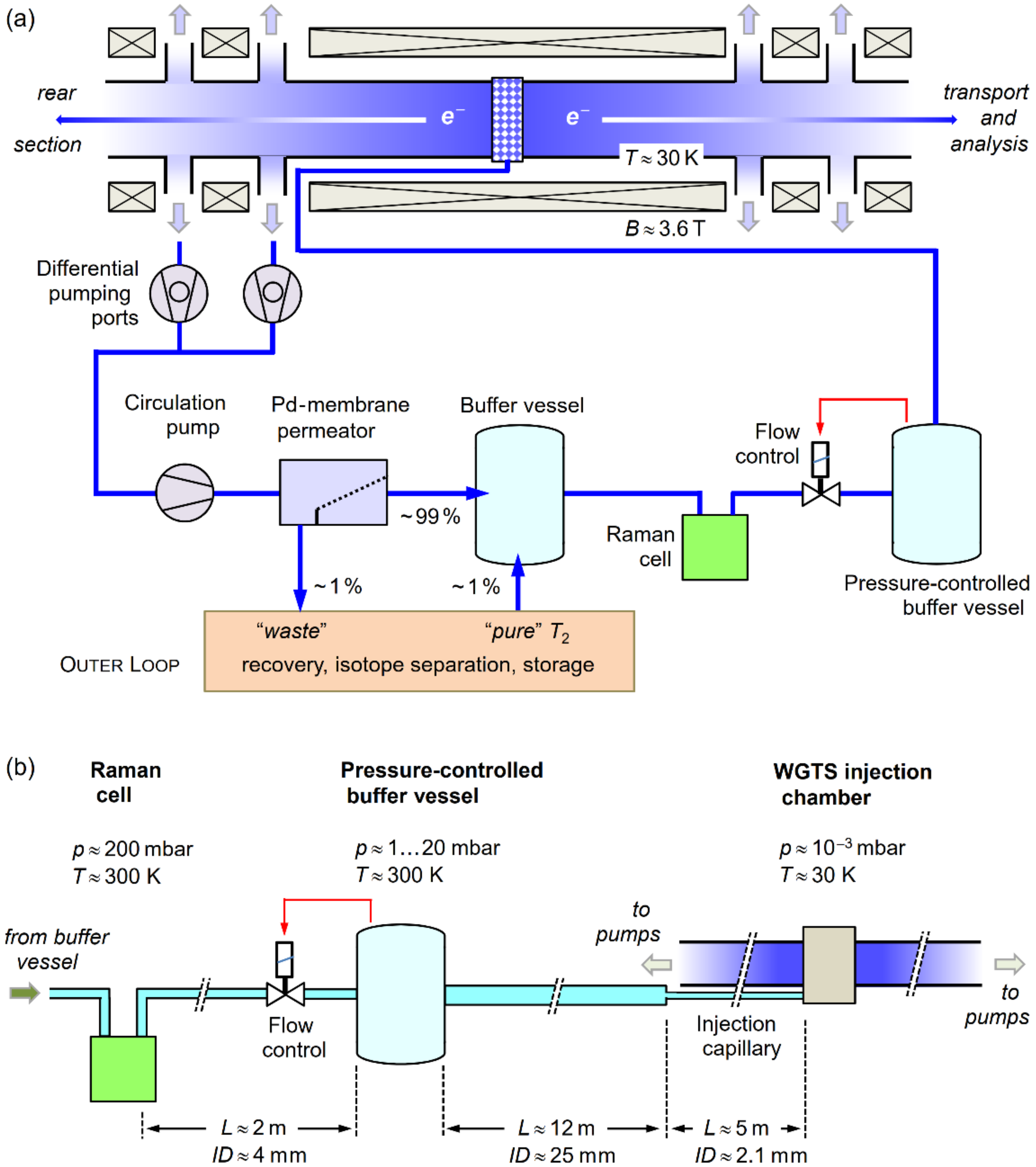
3.1. Gas Circulation within the WGTS Loop
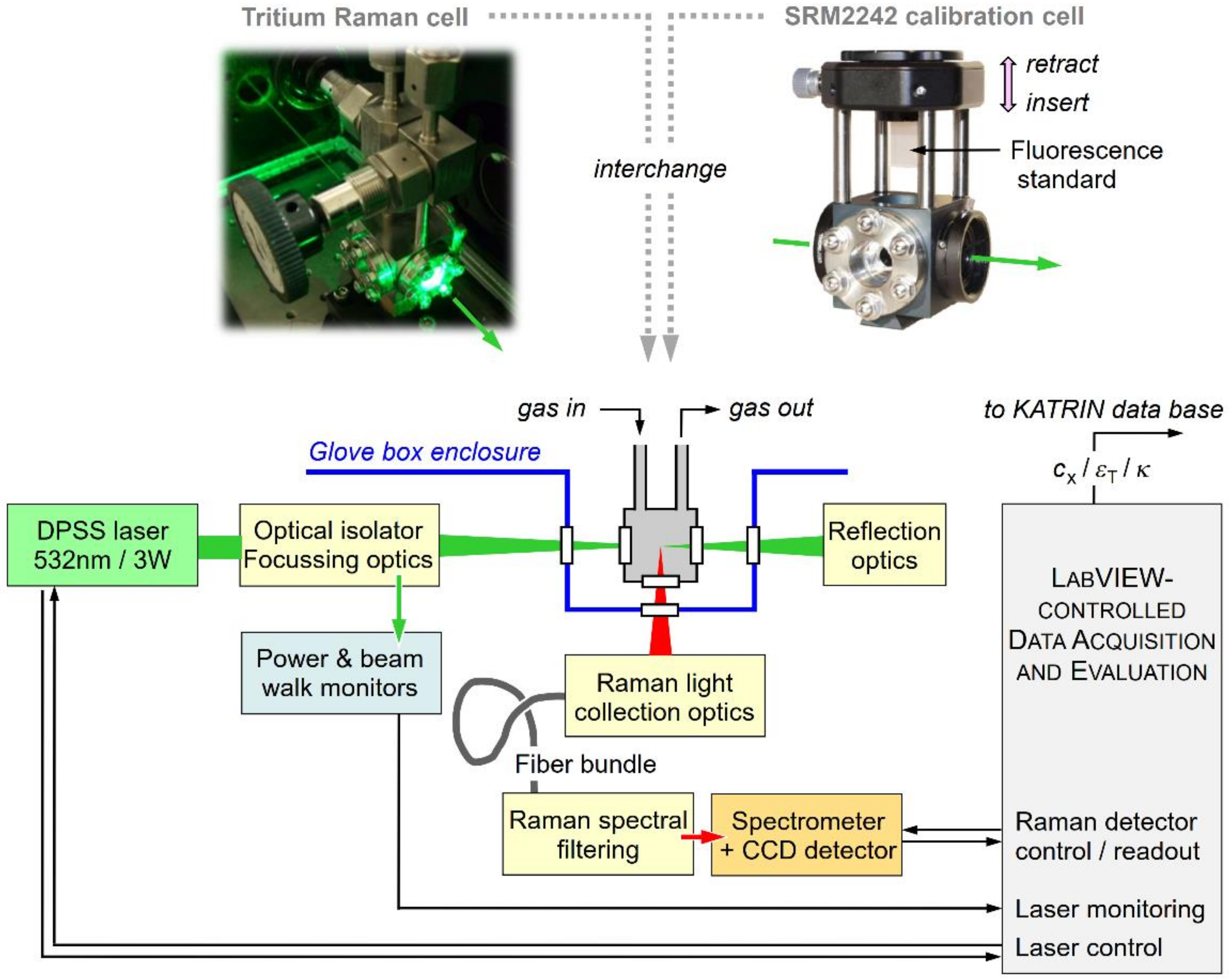
3.2. The Laser Raman System
3.3. Aspects of Calibration
- = unit normalization constant
- = laser wavelength
- = Raman line wavelength
- = spectral sensitivity of the LARA system at the Raman line position
- = transition probability function for Raman line, for initial rotational level J″
- = number of molecules, in their initial energy state, at gas temperature T
- = incident laser power density
3.3.1. Wavelength Calibration for λs
3.3.2. Spectral Intensity Response Function, η(λs)
3.3.3. Linking the Measured Raman signal to the Particle Density
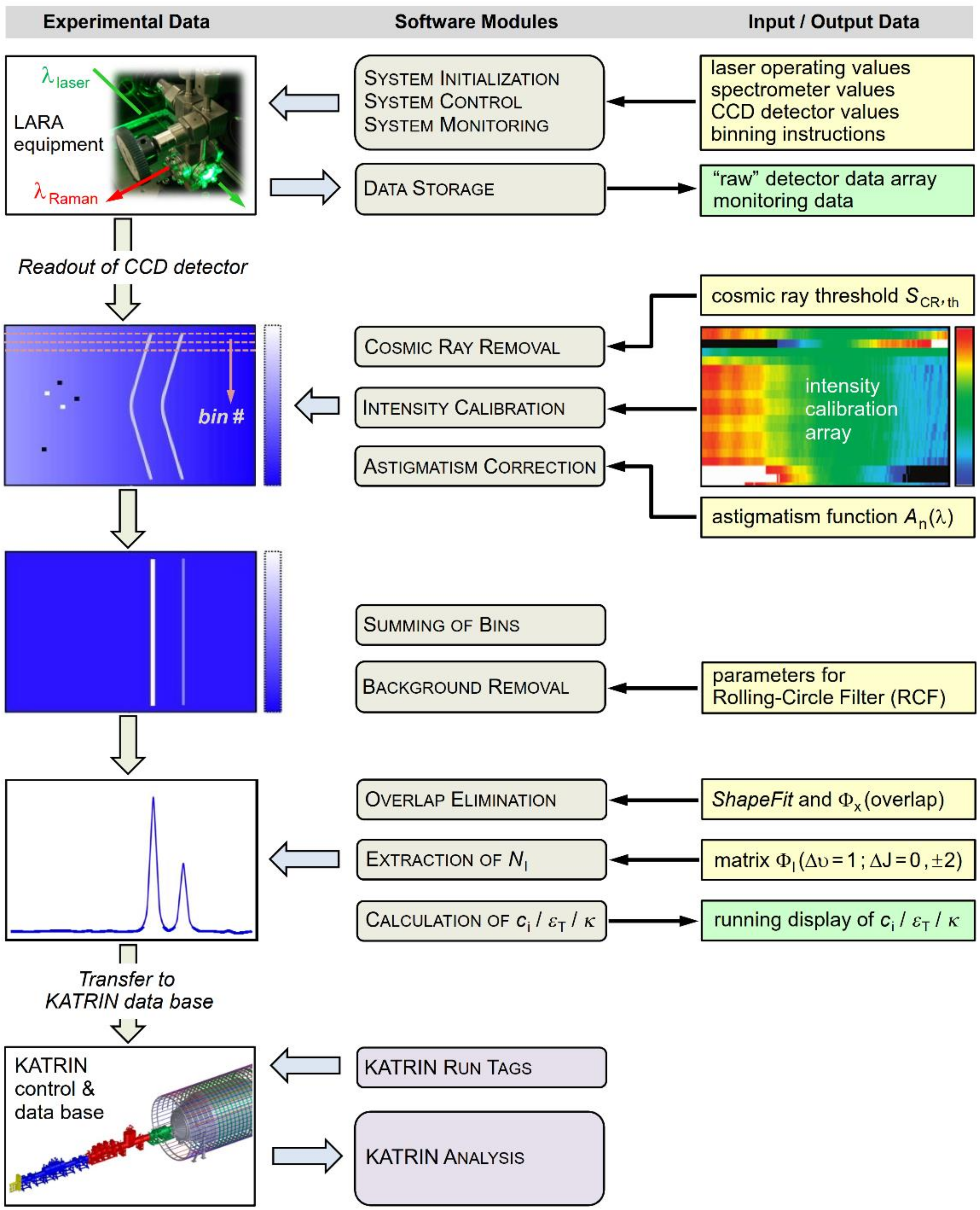
3.4. Automated Data Processing
3.4.1. LARA System Control
3.4.2. Detector Readout, Sensitivity Calibration and Spectrum Generation
3.4.3. Spectrum Evaluation
3.4.4. Calculation of Parameter Values for the KATRIN Experiment
4. Results
4.1. Spectra for the Different T2 Circulation Scenarios
4.1.1. LOOPINO Spectra
4.1.2. First Tritium (FT) Spectra
4.1.3. KATRIN (KNM1) Spectra
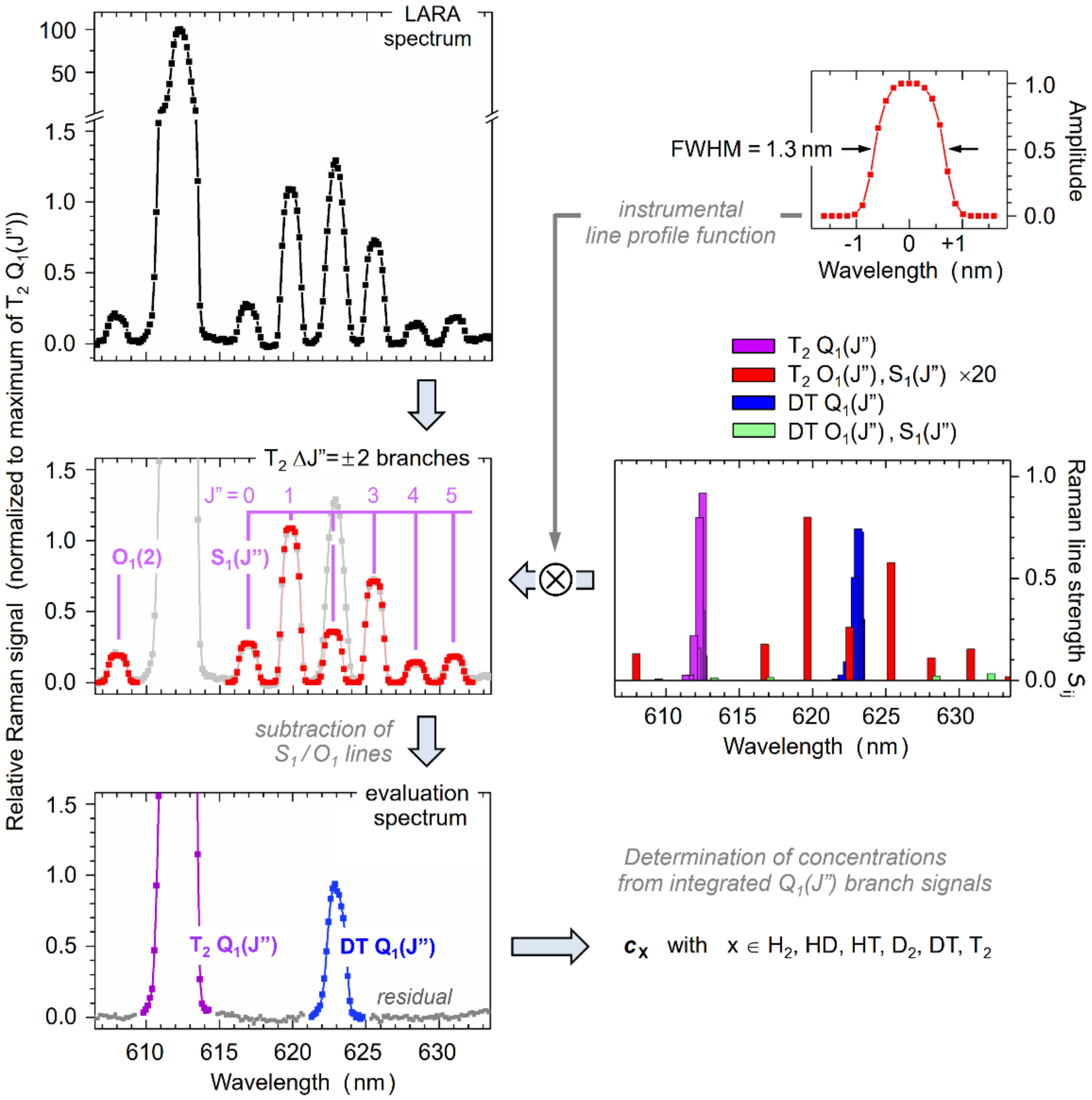
4.2. Disentangling Spectral Overlap Features
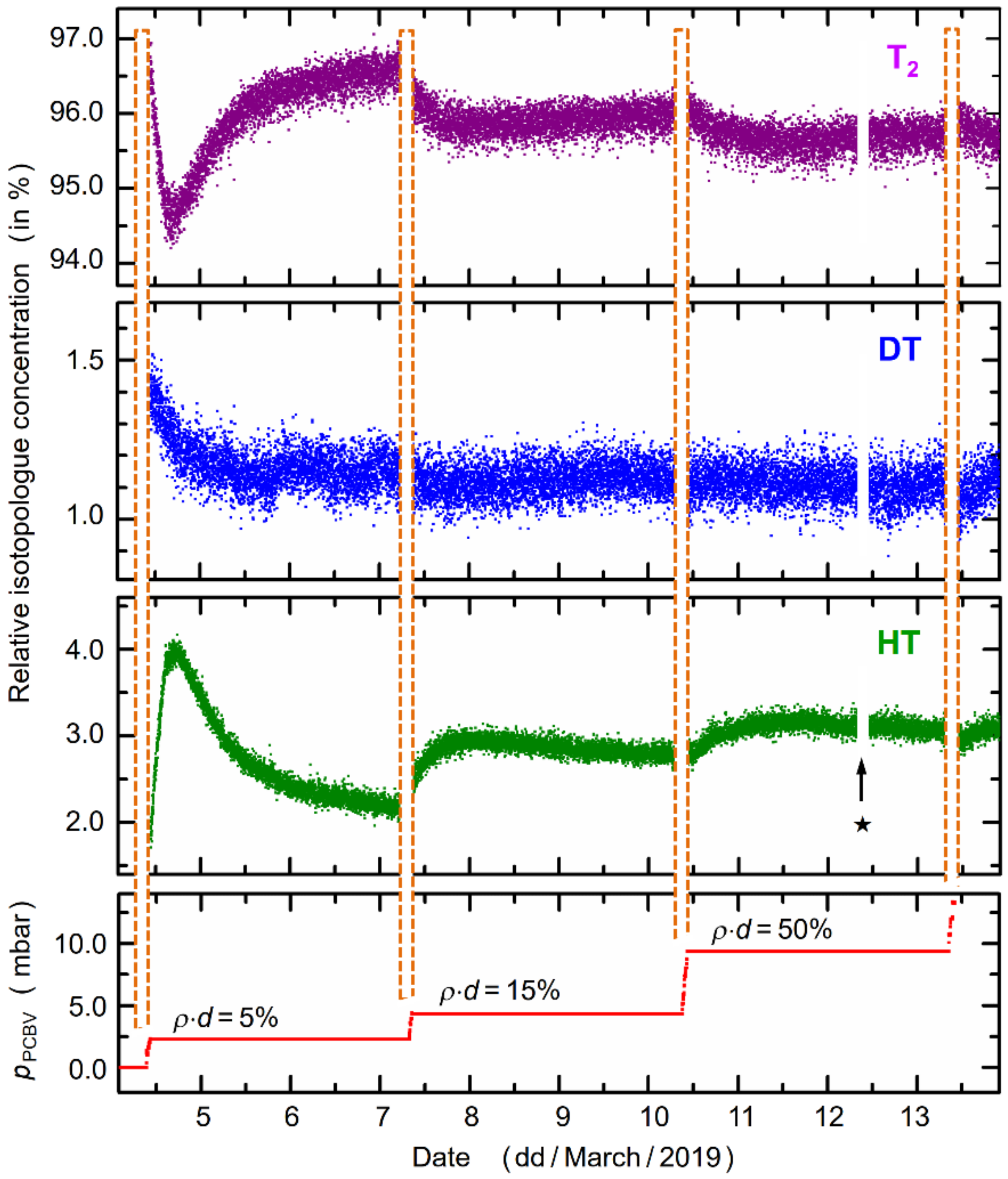
4.3. Temporal Evolution of the Concentrations of T2/DT/HT
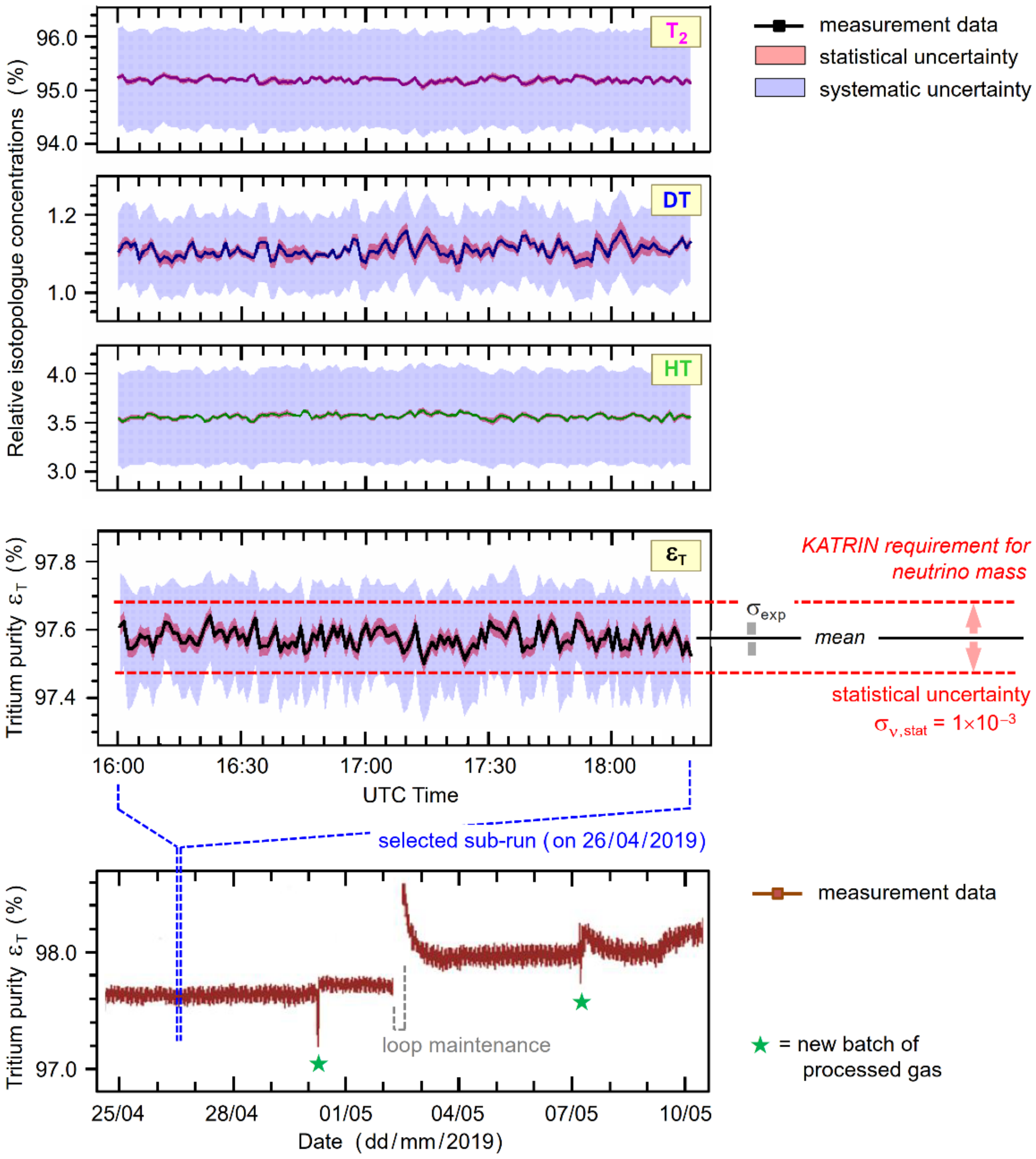
4.4. Precision and Stability
- (i)
- Statistical (σstat); directly associated with the determination of the Nx (Sx) including
- -
- shot noise (variations of the Raman signal amplitude);
- -
- background noise (from shot noise of the fluorescence background);
- -
- readout noise (from CCD, in general negligible in our LARA measurements);
- -
- laser noise (short-term fluctuation of the Finesse laser, of the order <2 × 10−4).
- (ii)
- Systematics I (σcal); associated with calibration processes, including
- -
- uncertainty of SRM spectral intensity calibration (ηx);
- -
- uncertainty from calculation of transition probabilities ().
- (iii)
- Systematics II (σana); associated with analysis procedures, including
- -
- uncertainty from ShapeFit, which encompasses effects from the SCARF background removal and other implicit analysis steps as well (Sx).
4.5. Remarks on Chemical and Radio-Chemical Reaction Products
4.5.1. Products Associated with the β-decay of Tritium—Hydrogen and 3He Atoms
4.5.2. HT and Tritium-Substituted Methane from Surface-Mediated Reactions
4.5.3. Reactions Observed during the FT Campaign
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brown, L.M. The idea of the neutrino. Phys. Today 1978, 31, 23–28. [Google Scholar] [CrossRef]
- Mößbauer, R.L. History of Neutrino Physics: Pauli’s Letters. In Proceedings of the Fourth SFB-375 Ringberg Workshop Neutrino Astrophysics. 1998, pp. 3–5. Available online: https://arxiv.org/pdf/astro-ph/9801320.pdf#page=11 (accessed on 10 July 2020).
- Cowan, C.L., Jr.; Reines, F.; Harrison, F.B.; Kruse, H.W.; McGuire, A.D. Detection of the free neutrino: A confirmation. Science 1956, 124, 103–104. [Google Scholar] [CrossRef] [PubMed]
- Gaillard, M.K.; Grannis, P.D.; Sciulli, F.J. The standard model of particle physics. Rev. Mod. Phys. 1999, 71, S96–S111. [Google Scholar] [CrossRef]
- Fukuda, Y.; Hayakawa, T.; Ichihara, E.; Inoue, K.; Ishihara, K.; Ishino, H.; Itow, Y.; Kajita, T.; Kameda, J.; Kasuga, S.; et al. Evidence for oscillation of atmospheric neutrinos. Phys. Rev. Lett. 1998, 81, 1562–1567. [Google Scholar] [CrossRef]
- Capozzi, F.; Lisi, E.; Marrone, A.; Montanino, D.; Palazzo, A. Neutrino masses and mixings: Status of known and unknown 3ν parameters. Nucl. Phys. B 2016, 908, 218–234. [Google Scholar] [CrossRef]
- Soler, F.J.P.; Froggatt, C.D.; Muheim, F. Neutrinos in Particle Physics, Astronomy and Cosmology; CRC Press: Boca Raton, FL, USA, 2019; ISBN 9780367386498. [Google Scholar]
- Drexlin, G.; Hannen, V.; Mertens, S.; Weinheimer, C. Current direct neutrino mass experiments. Adv. High Energy Phys. 2013, 2013, 293986. [Google Scholar] [CrossRef]
- Picard, A.; Backe, H.; Barth, H.; Bonn, J.; Degen, B.; Edling, T.; Haid, R.; Hermanni, A.; Leiderer, P.; Loeken, T.; et al. A solenoid retarding spectrometer with high resolution and transmission for keV electrons. Nucl. Instrum. Methods Phys. Res. B 1992, 63, 345–358. [Google Scholar] [CrossRef]
- Kraus, C.; Bornschein, B.; Bornschein, L.; Bonn, J.; Flatt, B.; Kovalik, A.; Ostrick, B.; Otten, E.W. Final results from phase II of the Mainz neutrino mass search in tritium β-decay. Eur. Phys. J. C 2005, 40, 447–468. [Google Scholar] [CrossRef]
- Aseev, V.N.; Belesev, A.I.; Berlev, A.I.; Geraskin, E.V.; Golubev, A.A.; Likhovid, N.A.; Lobashev, V.M.; Nozik, A.A.; Pantuev, V.S.; Parfenov, V.I.; et al. Upper limit on the electron antineutrino mass from the Troitsk experiment. Phys. Rev. D 2011, 84, 112003. [Google Scholar] [CrossRef]
- Lobashev, V.M. The search for the neutrino mass by direct method in the tritium beta-decay and perspectives of study it in the project KATRIN. Nucl. Phys. A 2003, 719, C153–C160. [Google Scholar] [CrossRef]
- Angrik, J.; Armbrust, T.; Beglarian, A.; Besserer, U.; Blumer, J.; Bonn, J.; Carr, R.; Bornschein, B.; Bornschein, L.; Burritt, T.; et al. (the KATRIN collaboration). KATRIN Design Report 2004. FZKA Scientific Report 2005, 7090. Available online: http://inspirehep.net/record/680949/files/FZKA7090.pdf (accessed on 10 July 2020).
- Arenz, M.; Baek, W.-J.; Beck, M.; Beglarian, A.; Behrens, J.; Bergmann, T.; Berlev, A.; Besserer, U.; Blaum, K.; Bode, T.; et al. The KATRIN superconducting magnets: Overview and first performance results. JINST 2018, 13, T08005. [Google Scholar] [CrossRef]
- Babutzka, M.; Bahr, M.; Bonn, J.; Bornschein, B.; Dieter, A.; Drexlin, G.; Eitel, K.; Fischer, S.; Glück, F.; Grohmann, S.; et al. Monitoring of the operating parameters of the KATRIN Windowless Gaseous Tritium Source. New J. Phys. 2012, 14, 103046. [Google Scholar] [CrossRef]
- Doss, N.; Tennyson, J.; Saenz, A.; Jonsell, S. Molecular effects in investigations of tritium molecule β-decay endpoint experiments. Phys. Rev. C 2006, 73, 025502. [Google Scholar] [CrossRef]
- Bodine, L.I.; Parno, D.S.; Robertson, R.G.H. Assessment of molecular effects on neutrino mass measurements from tritium β-decay. Phys. Rev. C 2015, 91, 035505. [Google Scholar] [CrossRef]
- Matsuyama, M.; Watanabe, K.; Hasegawa, K. Tritium assay in materials by the bremsstrahlung counting method. Fusion Eng. Des. 1997, 39–40, 929–936. [Google Scholar] [CrossRef]
- Ellinger, E.; Haußmann, N.; Helbing, K.; Hickford, S.; Klein, M.; Naumann, U. Monitoring the KATRIN source properties within the beamline. J. Phys. Conf. Series 2017, 888, 012229. [Google Scholar] [CrossRef]
- Kleesiek, K.; Behrens, J.; Drexlin, G.; Eitel, K.; Erhard, M.; Formaggio, J.A.; Glück, F.; Groh, S.; Hötzel, M.; Mertens, S.; et al. β-decay spectrum, response function and statistical model for neutrino mass measurements with the KATRIN experiment. Eur. Phys. J. C 2019, 79, 204. [Google Scholar] [CrossRef]
- Aker, M.; Altenmüller, K.; Arenz, M.; Baek, W.-J.; Barrett, J.; Beglarian, A.; Behrens, J.; Berlev, A.; Besserer, U.; Blaum, K.; et al. First operation of the KATRIN experiment with tritium. Eur. Phys. J. C 2020, 80, 264. [Google Scholar] [CrossRef]
- Aker, M.; Altenmüller, K.; Arenz, M.; Babutzka, M.; Barrett, J.; Bauer, S.; Beck, M.; Beglarian, A.; Behrens, J.; Bergmann, T.; et al. An improved upper limit on the neutrino mass from a direct kinematic method by KATRIN. Phys. Rev. Lett. 2019, 123, 221802. [Google Scholar] [CrossRef]
- Dörr, L.; Besserer, U.; Bekris, N.; Bornschein, B.; Caldwell-Nichols, C.; Demange, D.; Cristescu, I.; Cristescu, I.R.; Glugla, M.; Hellriegel, G.; et al. A decade of tritium technology development and operation at the Tritium Laboratory Karlsruhe. Fusion Sci. Technol. 2008, 54, 143–148. [Google Scholar] [CrossRef]
- Priester, F.; Sturm, M.; Bornschein, B. Commissioning and detailed results of KATRIN inner loop tritium processing system at Tritium Laboratory Karlsruhe. Vacuum 2015, 116, 42–47. [Google Scholar] [CrossRef]
- Grohmann, S.; Bode, T.; Hötzel, M.; Schön, H.; Süßer, M.; Wahl, T. The thermal behaviour of the tritium source in KATRIN. Cryogenics 2013, 55–56, 5–11. [Google Scholar] [CrossRef]
- Rahimpour, M.R.; Samimi, F.; Babapoor, A.; Tohidian, T.; Mohebi, S. Palladium membranes applications in reaction systems for hydrogen separation and purification: A review. Chem. Eng. Process. 2017, 121, 24–49. [Google Scholar] [CrossRef]
- Kuckert, L.; Heizmann, F.; Drexlin, G.; Glück, F.; Hötzel, M.; Kleesiek, M.; Sharipov, F.; Valerius, K. Modelling of gas dynamical properties of the KATRIN tritium source and implications for the neutrino mass measurement. Vacuum 2018, 158, 195–205. [Google Scholar] [CrossRef]
- Lewis, R.J.; Telle, H.H.; Bornschein, B.; Kazachenko, O.; Kernert, N.; Sturm, M. Dynamic Raman spectroscopy of hydrogen isotopomer mixtures in-line at TILO. Laser Phys. Lett. 2008, 5, 522–531. [Google Scholar] [CrossRef]
- Schlösser, M.; Rupp, S.; Brunst, T.; James, T.M. Relative intensity correction of Raman systems with National Institute of Standards and Technology Standard Reference Material 2242 in 90°-scattering geometry. Appl. Spectrosc. 2015, 69, 597–607. [Google Scholar] [CrossRef] [PubMed]
- James, T.M.; Schlösser, M.; Lewis, R.J.; Fischer, S.; Bornschein, B.; Telle, H.H. Automated quantitative spectroscopic analysis combining background subtraction, cosmic ray removal, and peak fitting. Appl. Spectrosc. 2013, 67, 949–959. [Google Scholar] [CrossRef]
- Taylor, D.J.; Glugla, M.; Penzhorn, R.D. Enhanced Raman sensitivity using an actively stabilized external resonator. Rev. Sci. Instrum. 2001, 72, 1970–1976. [Google Scholar] [CrossRef]
- Zeller, G. Development of a Calibration Procedure and Calculation of the Uncertainty Budget for the KATRIN Laser Raman system. Master’s Thesis, KIT/ETP, Karlsruhe, Germany, 2017. Available online: https://www.katrin.kit.edu/publikationen/mth-Zeller.pdf (accessed on 10 July 2020).
- LeRoy, R.J. (Department of Chemistry, University of Waterloo, ON, Canada). Recalculation of Raman transition matrix elements of all hydrogen isotopologues for 532 nm laser excitation. Personal communication, 2011. [Google Scholar]
- Allemand, C.D. Depolarization Ratio Measurements in Raman Spectrometry. Appl. Spectrosc. 1970, 24, 348–353. [Google Scholar] [CrossRef]
- James, T.M.; Schlösser, M.; Fischer, S.; Sturm, M.; Bornschein, B.; Lewis, R.J.; Telle, H.H. Accurate depolarization ratio measurements for all diatomic hydrogen isotopologues. J. Raman Spectrosc. 2013, 44, 857–865. [Google Scholar] [CrossRef]
- Schlösser, M.; Rupp, S.; Seitz, H.; Fischer, S.; Bornschein, B.; James, T.M.; Telle, H.H. Accurate calibration of the laser Raman system for the Karlsruhe Tritium Neutrino experiment. J. Mol. Struct. 2013, 1044, 61–66. [Google Scholar] [CrossRef]
- Schlösser, M.; Seitz, H.; Rupp, S.; Herwig, P.; Alecu, C.G.; Sturm, M.; Bornschein, B. In-line calibration of Raman systems for analysis of gas mixtures of hydrogen isotopologues with sub-percent accuracy. Anal. Chem. 2013, 85, 2739–2745. [Google Scholar] [CrossRef] [PubMed]
- Niemes, S.; Zeller, G. Calibration strategy and status of tritium purity monitoring for KATRIN. In Proceedings of the Neutrino 2018—28th International Conference Neutrino Physics and Astrophysics, Heidelberg, Germany, 4–9 June 2018. [Google Scholar] [CrossRef]
- Schulze, H.G.; Jirasek, A.; Yu, M.M.L.; Lim, A.; Turner, R.F.B.; Blades, M.W. Optimization and quantification of the systematic effects of a rolling circle filter for spectral pre-processing. Appl. Spectrosc. 2005, 59, 545–574. [Google Scholar] [CrossRef] [PubMed]
- Mirz, S.; Größle, R.; Kraus, A. Optimization and quantification of the systematic effects of a rolling circle filter for spectral pre-processing. Analyst 2019, 144, 4281–4287. [Google Scholar] [CrossRef] [PubMed]
- Fischer, S.; Sturm, M.; Schlösser, M.; Bornschein, B.; Drexlin, G.; Priester, F.; Lewis, R.J.; Telle, H.H. Monitoring of tritium purity during long-term circulation in the KATRIN test experiment LOOPINO using laser Raman spectroscopy. Fusion Sci. Technol. 2011, 60, 925–930. [Google Scholar] [CrossRef]
- Fischer, S. Commissioning of the KATRIN Raman System and Durability Studies of Optical Coatings in Glove Box and Tritium Atmospheres. Ph.D. Thesis, KIT/IEKP, Karlsruhe, Germany, 2014. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology. International Vocabulary of Metrology—Basic and General Concepts and Associated Terms (VIM), JCGM 200:2008; Bureau International des Poids et Mesures (BIPM): Sèvres, France, 2008; Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_200_2008.pdf (accessed on 10 July 2020).
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. JCGM 100:2008; Bureau International des Poids et Mesures (BIPM): Sèvres, France, 2008; Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 10 July 2020).
- Wexler, S. Dissociation of TH and T2 by β-decay. J. Inorg. Nucl. Chem. 1959, 10, 8–16. [Google Scholar] [CrossRef]
- Kramida, A.E. A critical compilation of experimental data on spectral lines and energy levels of hydrogen, deuterium, and tritium. Atom. Data Nucl. Data 2010, 96, 586–644. [Google Scholar] [CrossRef]
- Schlösser, M.; Pakari, O.; Rupp, S.; Mirz, S.; Fischer, S. How to make Raman-inactive helium visible in Raman spectra of tritium-helium gas mixtures. Fusion Sci. Technol. 2015, 67, 559–562. [Google Scholar] [CrossRef]
- Morris, G.A. Methane Formation in Tritium Gas Exposed to Stainless Steel; Report UCRL-52262, LLNL; University of California: Livermore, CA, USA, 1977. [Google Scholar] [CrossRef][Green Version]
- Dawson, P.T. Methane Impurity Production in the Fusion Reactor. Report CFFTP-G-85038, Ontario Hydro, Mississauga, ON, Canada, 1985. Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/19/034/19034135.pdf (accessed on 10 July 2020).
- Dickson, R.S. Tritium Interactions with Steel and Construction Materials in Fusion Devices: A literature Review; Report No. CFFTP G-9039; Chalk River Laboratories: Chalk River, ON, Canada, 1990; Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/24/009/24009449.pdf (accessed on 10 July 2020).
- Croudace, I.W.; Warwick, P.E.; Kim, D. Using thermal evolution profiles to infer tritium speciation in nuclear site metals: An aid to decommissioning. Anal. Chem. 2014, 86, 9177–9185. [Google Scholar] [CrossRef]
- Smialowski, M. Hydrogen in Steel: Effect of Hydrogen on Iron and Steel during Production, Fabrication, and Use; Pergamon Press: London, UK, 1962; ISBN 9781483213712. [Google Scholar]
- Grabke, H.J. Evidence on the surface concentration of carbon on gamma iron from the kinetics of the carburization in CH4-H2. Metall. Trans. 1970, 1, 2972–2975. [Google Scholar] [CrossRef]

| Device | Model | Manufacturer | Specifications |
|---|---|---|---|
| Laser | Finesse | Laser Quantum, UK | Nd:YVO4 2nd harmonic (TEM00); λL = 532 nm; PL = 5 W (CW) |
| Raman filter | RazorEdge LP03-532RU | Semrock, USA | T > 0.97 for λRaman > 537.nm; T < 10−6 for λL = 532 nm |
| Fiber bundle | Custom “slit-to-slit” | CeramOptec, Germany | 48 individual fibers, core = 100 μm; Bundle height = 6 mm |
| Spectrometer | HTS | PI Acton, USA | f = 85 mm, with f/# = 1.8; λrange = 500–750 nm (fixed); Δλ ≈ 1 nm (for slit = 100 μm) |
| CCD array detector | Pixis 2KB | Princeton Instruments, USA | Back illuminated; 2048 × 512 pixel (27.6 × 6.9 mm); TCCD-chip ≤ −70 °C; Dark noise ≈ 10−3 e−·s−1·pixel−1 |
| Acquisition software | LARAsoft | TLK in-house | Device control; Data acquisition; Spectrum analysis (written in LabVIEW) |
| Parameter/Setting | Units | LOOPINO | FT | KNM1 | |
|---|---|---|---|---|---|
| Pressure in LARA Cell, pRC | mbar | 149 | 190 | 190 | |
| Tritium content in the gas mixture, εT | ~0.93 | ~5 × 10−3 | >0.97 | ||
| Column density, ρd (fraction of nominal ρdmax) | % | n/a | ~100 | 25 | |
| Laser power, PL | W | 1.5 | 4.0 | 3.0 | |
| Spectral line resolution (FWHM), | nm | 1.15 | 1.15 | 1.15 | |
| cm−1 | 28.2 | 28.2 | 28.2 | ||
| CCD acquisition time (single spectrum), tSS | s | 58.5 | 58.5 | 58.5 | |
| cx for | T2 | DT | D2 | HT | HD | H2 |
|---|---|---|---|---|---|---|
| LOOPINO (1) | 89.4 | 5.4 | <0.1 | 5.0 | <0.1 | <0.1 |
| FT (2) | <0.1 | 1.2 | 97.6 | <0.1 | 0.9 | <0.1 |
| KNM1 (2) | 96.8 | 1.6 | <0.1 | 1.2 | <0.1 | 0.1 |
| T2 Raman Line | S1(0) | S1(1) | S1(2) | S1(3) | S1(4) | S1(5) |
|---|---|---|---|---|---|---|
| Sij (1) | 0.00889 | 0.03990 | 0.01302 | 0.02841 | 0.00540 | 0.00737 |
| ARS,theory (2) | 0.241 | 1.094 | 0.355 | 0.785 | 0.151 | 0.209 |
| ARS,exp | 0.253 | 1.094 | --- | 0.770 | 0.154 | 0.200 |
| KATRIN Requirements (1) | Achieved during KNM1 (2) | ||||||
|---|---|---|---|---|---|---|---|
| Parameter | Value | Precision | Trueness | Value | Precision | Trueness | |
| Concentrations, cx | for T2 | 0.95193 | 4.7 × 10−4 | 9.7 × 10−3 | |||
| for DT | 0.01109 | 1.5 × 10−2 | 9.2 × 10−2 | ||||
| for HT | 0.03562 | 6.4 × 10−3 | 1.3 × 10−1 | ||||
| Tritium purity, εT | >0.95 | 1 × 10−3 | 3 × 10−2 | 0.97576 | 2.8 × 10−4 | 1.6 × 10−3 | |
| Ratio of impurities HT/DT, κ | --- | --- | 10 × 10−2 | 3.212 | 2.5 × 10−2 | 3.3 × 10−2 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aker, M.; Altenmüller, K.; Beglarian, A.; Behrens, J.; Berlev, A.; Besserer, U.; Bieringer, B.; Blaum, K.; Block, F.; Bornschein, B.; et al. Quantitative Long-Term Monitoring of the Circulating Gases in the KATRIN Experiment Using Raman Spectroscopy. Sensors 2020, 20, 4827. https://doi.org/10.3390/s20174827
Aker M, Altenmüller K, Beglarian A, Behrens J, Berlev A, Besserer U, Bieringer B, Blaum K, Block F, Bornschein B, et al. Quantitative Long-Term Monitoring of the Circulating Gases in the KATRIN Experiment Using Raman Spectroscopy. Sensors. 2020; 20(17):4827. https://doi.org/10.3390/s20174827
Chicago/Turabian StyleAker, Max, Konrad Altenmüller, Armen Beglarian, Jan Behrens, Anatoly Berlev, Uwe Besserer, Benedikt Bieringer, Klaus Blaum, Fabian Block, Beate Bornschein, and et al. 2020. "Quantitative Long-Term Monitoring of the Circulating Gases in the KATRIN Experiment Using Raman Spectroscopy" Sensors 20, no. 17: 4827. https://doi.org/10.3390/s20174827
APA StyleAker, M., Altenmüller, K., Beglarian, A., Behrens, J., Berlev, A., Besserer, U., Bieringer, B., Blaum, K., Block, F., Bornschein, B., Bornschein, L., Böttcher, M., Brunst, T., Caldwell, T. C., Chilingaryan, S., Choi, W., Díaz Barrero, D. D., Debowski, K., Deffert, M., ... Zeller, G. (2020). Quantitative Long-Term Monitoring of the Circulating Gases in the KATRIN Experiment Using Raman Spectroscopy. Sensors, 20(17), 4827. https://doi.org/10.3390/s20174827







