Analysis on the Radial Vibration of Longitudinally Polarized Radial Composite Tubular Transducer
Abstract
:1. Introduction
2. Theoretical Analysis of Radial Composite Tubular Transducer
2.1. Equivalent Circuit of the Piezoelectric Ceramic Tube
2.2. Electromechanical Equivalent Circuit of the Metal Tube
3. Effects of Radial Geometric Dimension and Load Mechanical Resistance of the Radial Composite Tubular Transducer on the Vibration Characteristics
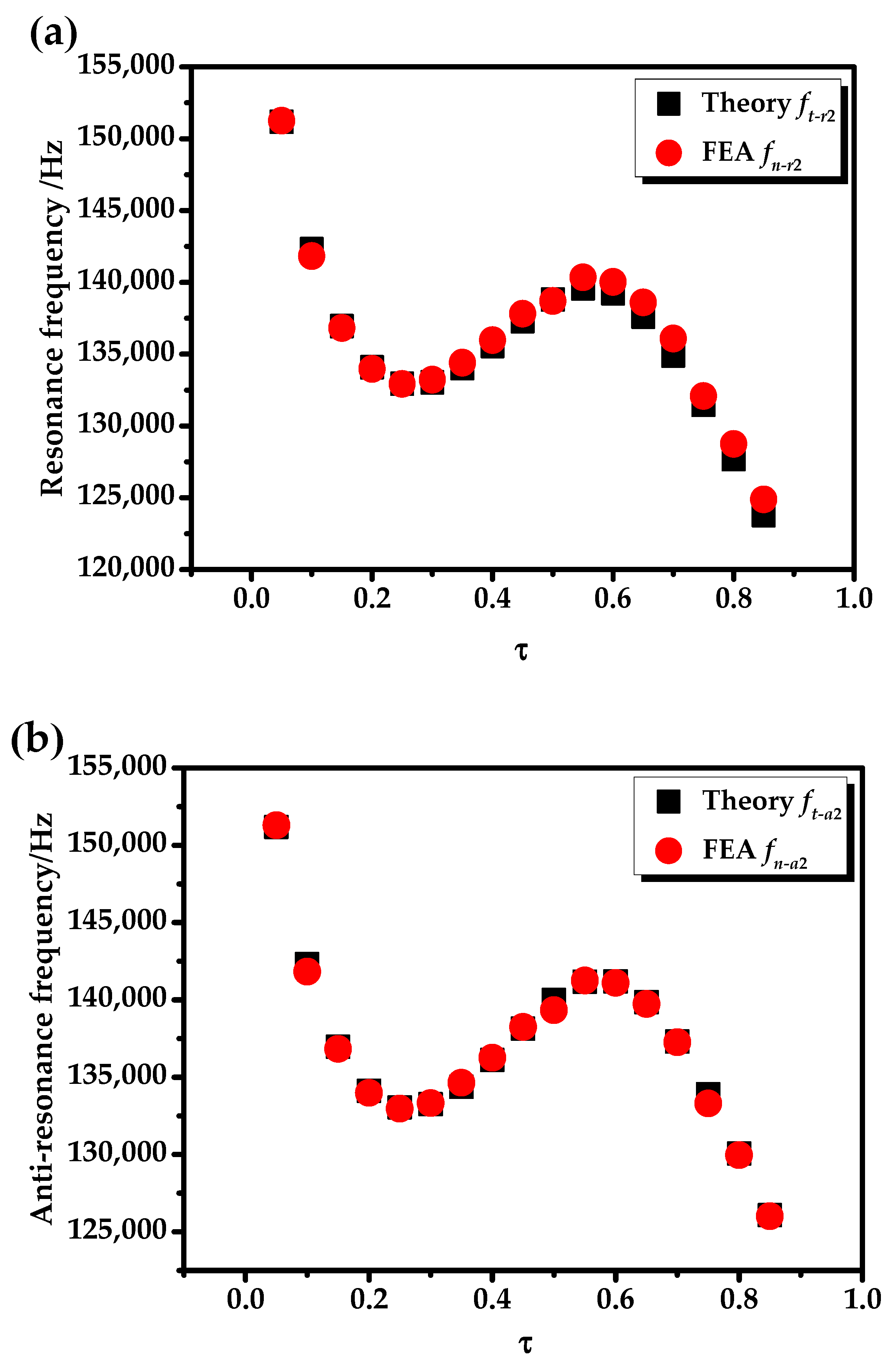
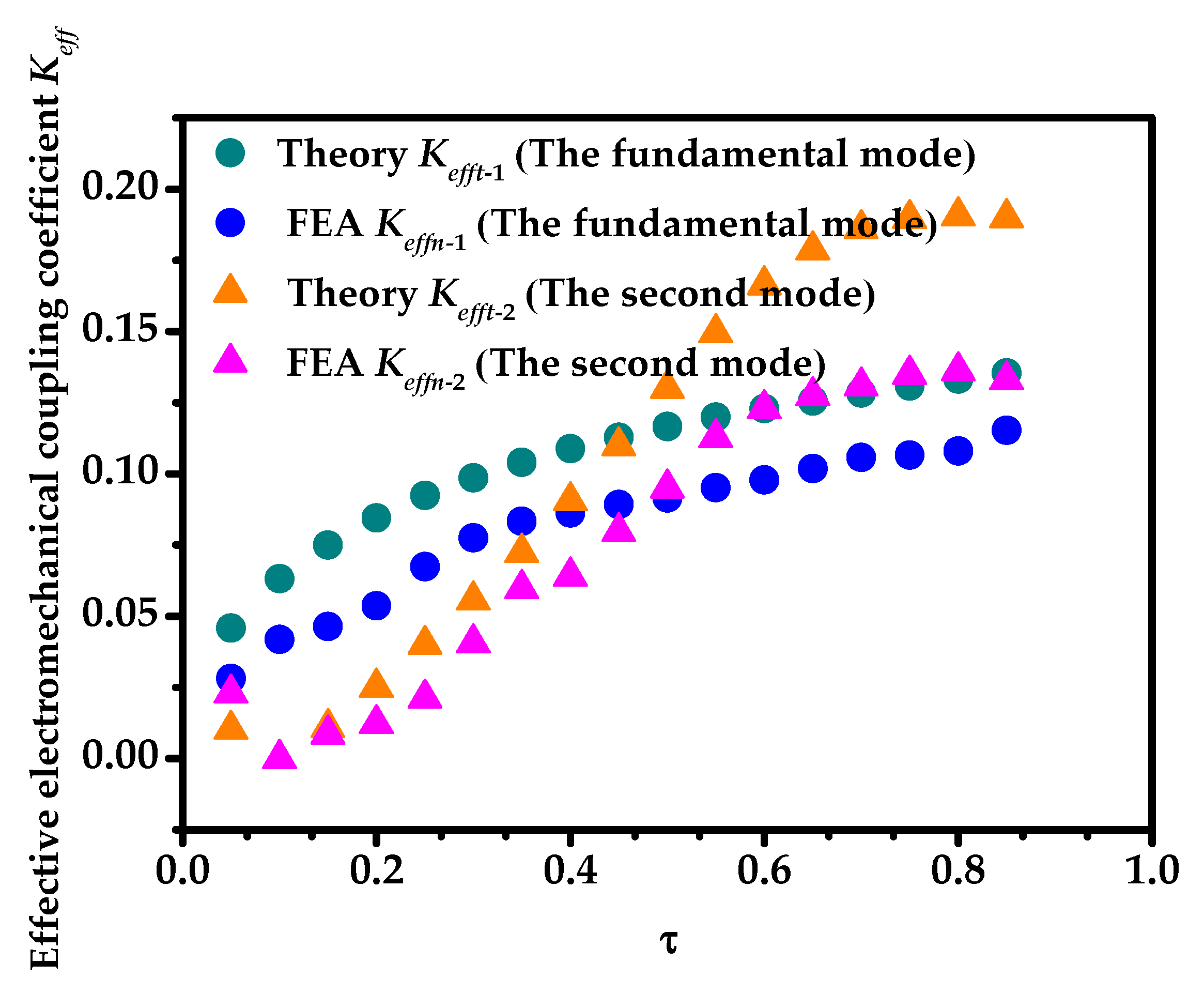
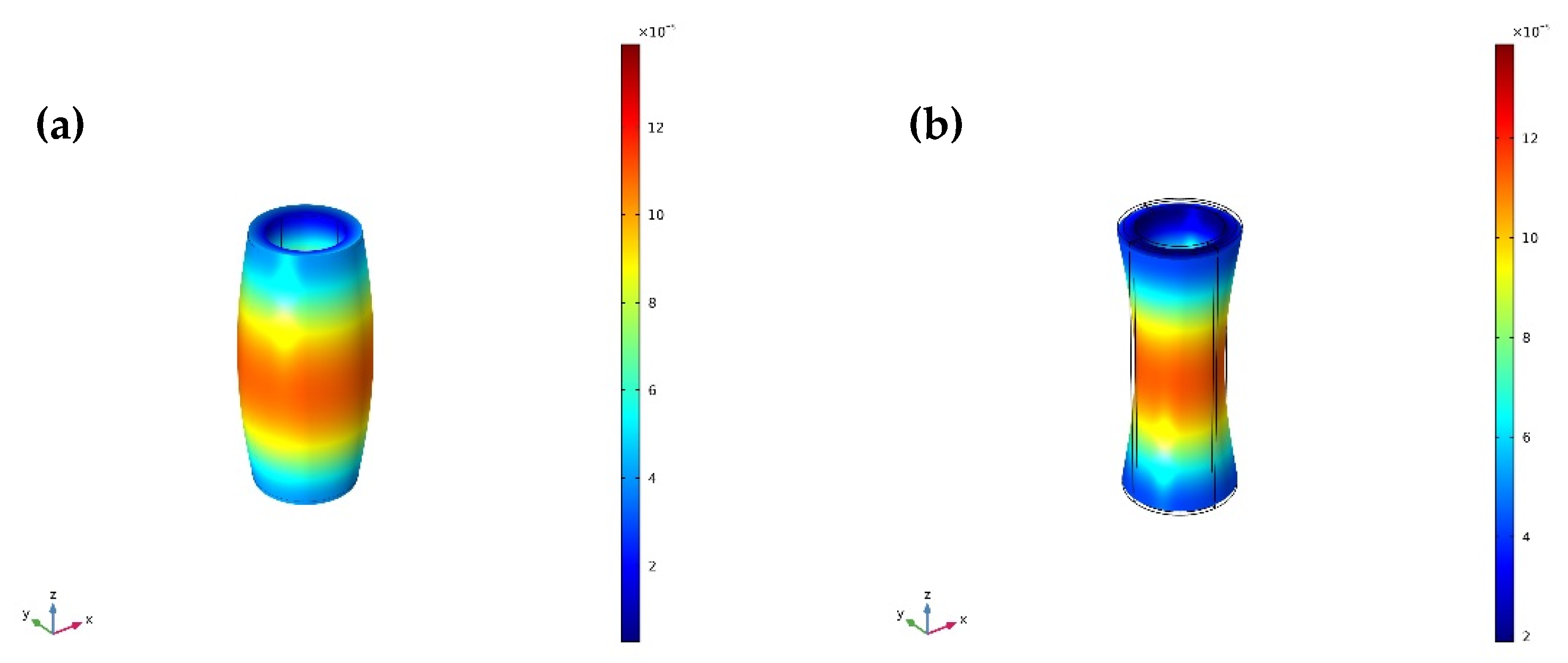
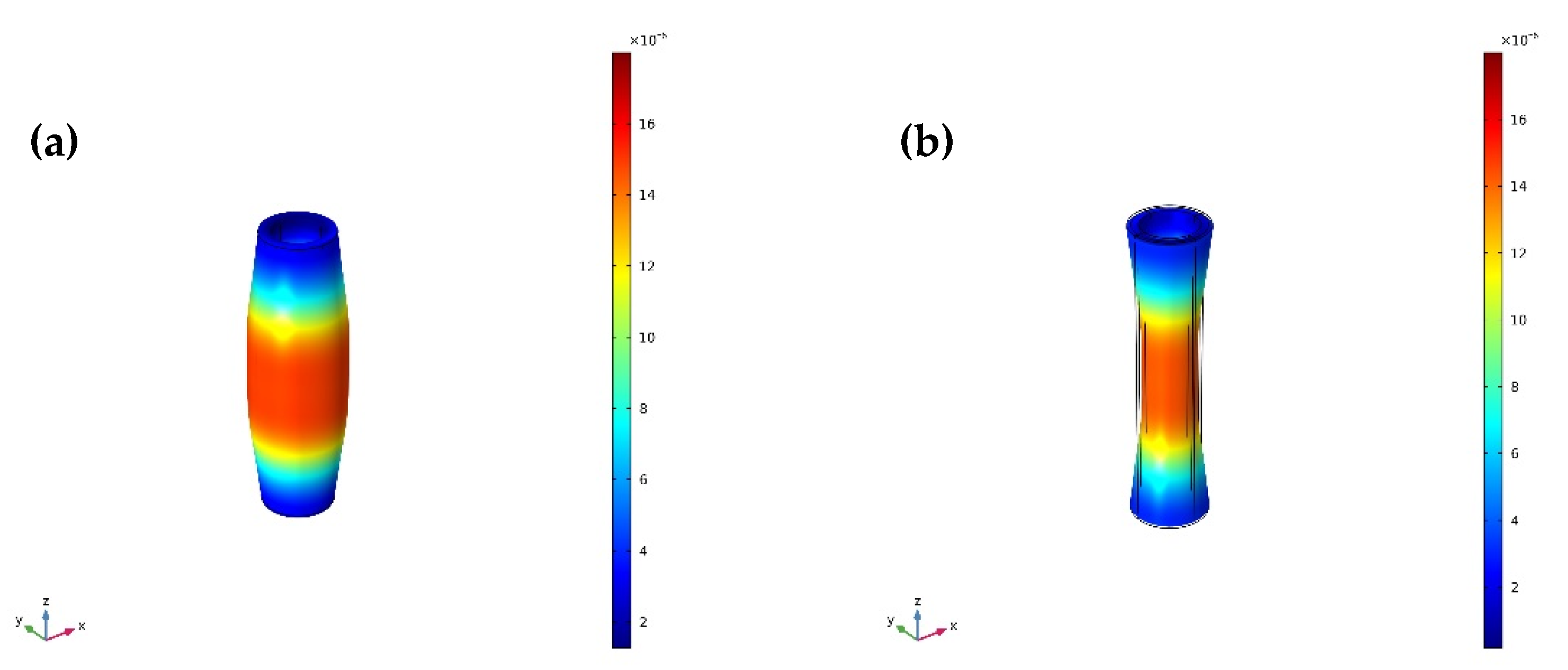
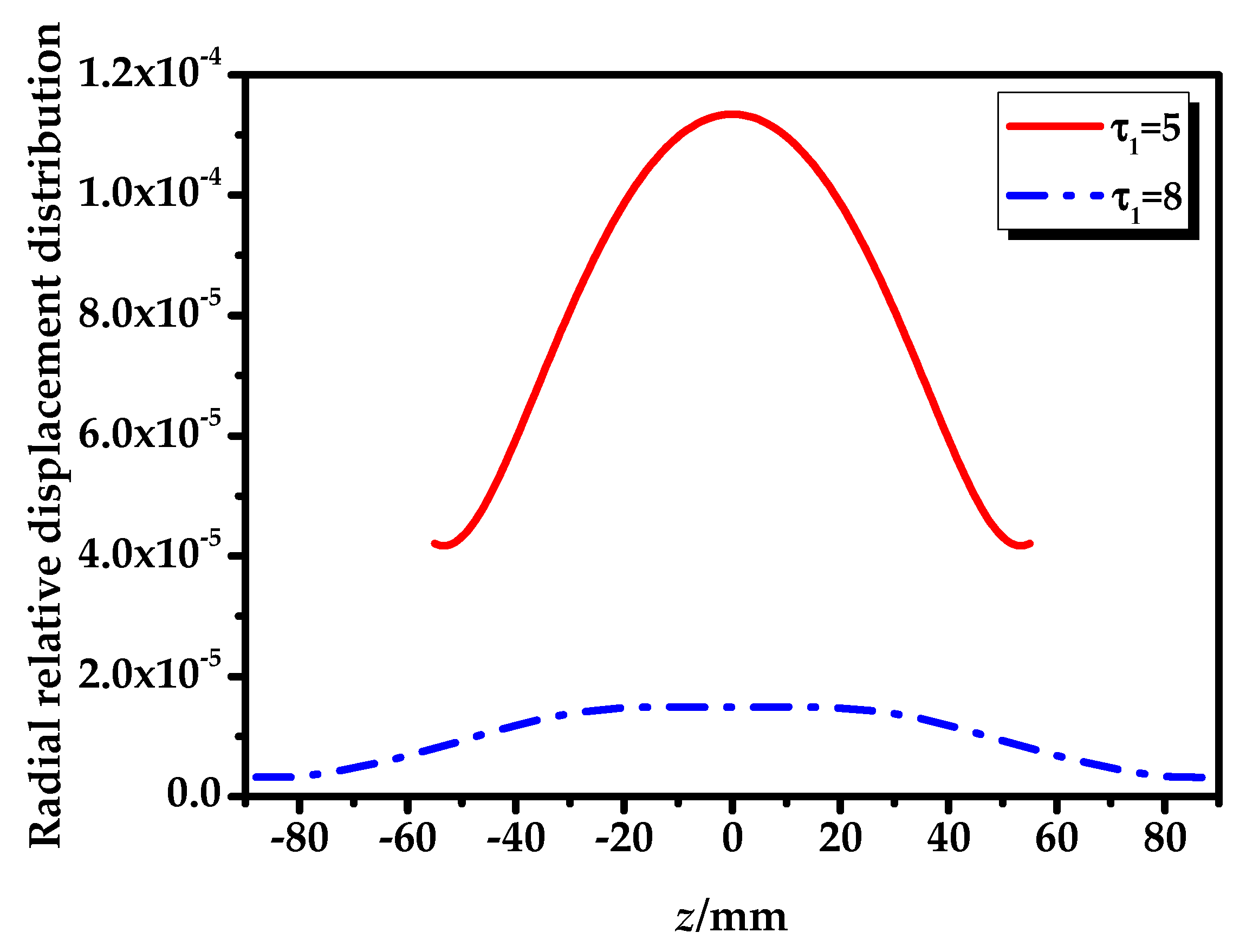
4. Finite Element Analysis of the Radial Composite Tubular Transducer
5. Conclusions
- (1)
- Under the no-load state, when the overall size of the transducer is unchanged, as the proportion of piezoelectric ceramics increases, there are two inflection points on the variation curves of the radial resonance frequency and anti-resonance frequency at the second mode.
- (2)
- The resonance/anti-resonance frequencies of the No. 1 and No. 2 transducers under different ratios of length to radius are obtained using COMSOL. After comparison, the analytical theoretical results and COMSOL results are in good agreement.
- (3)
- In the present work, the vibration characteristics of the transducer at the fundamental mode and the second mode are analyzed. In future work, the higher vibrational order and the effects of the dielectric and load losses on the vibration characteristics will be studied.
- (4)
- The derivation of the electromechanical equivalent circuit of the radial vibration of a longitudinally polarized piezoelectric ceramic tube completes the equivalent circuit theory. The tubular transducer with a large radiation range and power capacity has certain application prospects in the fields of high-power ultrasonic wastewater treatment, ultrasonic degradation, and underwater acoustics.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chilibon, I. Underwater flextensional piezoceramic sandwich transducer. Sens. Actuators A Phys. 2002, 100, 287–292. [Google Scholar] [CrossRef]
- Chilibon, I. High power ultrasonic piezoceramic vibratory sandwich transducers. In Proceedings of the Tenth International Congress on Sound and Vibration, Stockholm, Sweden, 7–10 July 2003; pp. 1035–1042. [Google Scholar]
- Loveday, P.W. Numerical comparison of patch and sandwich piezoelectric transducers for transmitting ultrasonic waves. In Proceedings of the SPIE the International Society for Optical Engineering, San Diego, CA, USA, 16 March 2006. [Google Scholar]
- Lin, S.Y.; Tian, H. Study on the sandwich piezoelectric ceramic ultrasonic transducer in thickness vibration. Smart Mater. Struct. 2008, 17, 015034. [Google Scholar] [CrossRef]
- Wang, J.J.; Qin, L.; Song, W.B.; Shi, Z.; Song, G. Electromechanical Characteristics of Radially Layered Piezoceramic/Epoxy Cylindrical Composite Transducers: Theoretical Solution, Numerical Simulation, and Experimental Verification. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 1643–1656. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.O.; Hwang, K.K.; Jeong, H.G. Radial vibration characteristics of piezoelectric cylindrical transducers. J. Sound Vib. 2004, 276, 1135–1144. [Google Scholar] [CrossRef]
- Li, G.; Gong, J.; Wang, T.; Qiu, C.; Xu, Z. Study on the broadband piezoelectric ceramic transducer based on radial enhanced composite structure. Ceram. Int. 2018, 44, S250–S253. [Google Scholar] [CrossRef]
- Jia, L.Y.; Zhang, G.B.; Zhang, X.F.; Yao, Y.; Lin, S. Study on tangentially polarized composite cylindrical piezoelectric transducer with high electro-mechanical coupling coefficient. Ultrasonics 2017, 74, 204–210. [Google Scholar] [CrossRef] [PubMed]
- Iula, A.; Lamberti, N.; Carotenuto, R.; Pappalardo, M. Analysis of the radial symmetrical modes of thin piezoceramic rings. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 1047–1049. [Google Scholar] [CrossRef]
- Iula, A.; Lamberti, N.; Pappalardo, M. A model for the theoretical characterization of thin piezoceramic rings. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1996, 43, 370–375. [Google Scholar] [CrossRef]
- Ganilova, O.; Lucas, M.; Cardoni, A. Analytical model of the cymbal transducer dynamics, radial vibration of the piezoelectric disc. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 1077–1086. [Google Scholar] [CrossRef]
- Guo, N.; Cawley, P.; Hitchings, D. The finite element analysis of the vibration characteristics of piezoelectric discs. J. Sound Vib. 1992, 159, 115–138. [Google Scholar] [CrossRef]
- Lin, S.Y.; Hu, J.; Fu, Z.Q. Electromechanical characteristics of piezoelectric ceramic transformers in radial vibration composed of concentric piezoelectric ceramic disk and ring. Smart Mater. Struct. 2013, 22, 45018. [Google Scholar] [CrossRef]
- Lin, S.Y. Study on a new type of radial composite piezoelectric ultrasonic transducers in radial vibration. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 1671–1678. [Google Scholar] [PubMed]
- Lin, S.Y. Electro-mechanical equivalent circuit of a piezoelectric ceramic thin circular ring in radial vibration. Sens. Actuators A Phys. 2007, 134, 505–512. [Google Scholar] [CrossRef]
- Lin, S.Y. Study on the equivalent circuit and coupled vibration for the longitudinally polarized piezoelectric ceramic hollow cylinders. J. Sound Vib. 2004, 275, 859–875. [Google Scholar] [CrossRef]
- Aronov, B. Coupled vibration analysis of the thin-walled cylindrical piezoelectric ceramic transducers. J. Acoust. Soc. Am. 2009, 125, 803. [Google Scholar] [CrossRef]
- Hongwei, W. Finite element analysis and testing of the stacked piezoelectric composite ring array transducer. J. Funct. Mater. 2016, 47, 5084–5090. [Google Scholar]
- Tolliver, L.; Xu, T.B.; Jiang, X. Finite element analysis of the piezoelectric stacked-HYBATS transducer. Smart Mater. Struct. 2013, 22, 035015. [Google Scholar] [CrossRef]
- Nantawatana, W.; Seemann, W. Dynamic response analysis of the two stators hybrid transducer type piezoelectric ultrasonic motor using finite element simulation. Proc. Appl. Math. Mech. 2008, 8, 10393–10394. [Google Scholar] [CrossRef]
- Lin, S.Y.; Wang, S.J.; Fu, Z.Q. Electro-mechanical equivalent circuit for the radial vibration of the radially poled piezoelectric ceramic long tubes with arbitrary wall thickness. Sens. Actuators A Phys. 2012, 180, 87–96. [Google Scholar] [CrossRef]
- Tsysar, S.A.; Sinelnikov, Y.D.; Sapozhnikov, O.A. Characterization of cylindrical ultrasonic transducers using acoustic holography. Acoust. Phys. 2011, 57, 94–105. [Google Scholar] [CrossRef]
- Aronov, B. The energy method for analyzing the piezoelectric electroacoustic transducers. J. Acoust. Soc. Am. 2005, 117, 210. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.H.; Ma, C.C. Experimental measurements and finite element analysis of the coupled vibrational characteristics of piezoelectric shells. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 785–798. [Google Scholar] [CrossRef] [PubMed]
- Grigorenko, A.Y.; Loza, I.A. Solution of the problem of nonaxisymmetric free vibrations of piezoceramic hollow cylinders with axial polarization. J. Math. Sci. 2012, 184, 69–77. [Google Scholar] [CrossRef]
- Mason, W.P. Electro-Mechanical Transducers and Wave Filters, 2nd ed.; D. Van Nostrand Co., Inc.: New York, NY, USA, 1948; pp. 399–404. [Google Scholar]
- Martin, G.E. Vibrations of Longitudinally Polarized Ferroelectric Cylindrical Tubes. J. Acoust. Soc. Am. 1963, 35, 510. [Google Scholar] [CrossRef]
- Bybi, A.; Mouhat, O.; Garoum, M.; Drissi, H.; Grondel, S. One-dimensional equivalent circuit for ultrasonic transducer arrays. Appl. Acoust. 2019, 156, 246–257. [Google Scholar] [CrossRef]
- Silva, T.M.; Clementino, M.A.; Erturk, A.; De Marqui, C., Jr. Equivalent electrical circuit framework for nonlinear and high-quality factor piezoelectric structures. Mechatronics 2018, 54, 133–143. [Google Scholar] [CrossRef]
- Feng, F.L.; Shen, J.Z.; Deng, J.J. A 2D equivalent circuit of piezoelectric ceramic ring for transducer design. Ultrasonics 2007, 44, e723–e726. [Google Scholar] [CrossRef]
- Jalili, H.; Goudarzi, H. Modeling the hollow cylindrical piezo-ceramics with axial polarization using equivalent electro-mechanical admittance matrix. Sens. Actuators A Phys. 2009, 149, 266–276. [Google Scholar] [CrossRef]
- Luan, J.D.; Zhang, J.Q.; Wang, R.Q. Piezoelectric Transducers and Arrays; Peking University Press: Beijing, China, 2005; pp. 119–121. [Google Scholar]
- Liu, S.Q.; Lin, S.Y. The analysis of the electro-mechanical model of the cylindrical radial composite piezoelectric ceramic transducer. Sens. Actuators A Phys. 2009, 155, 175–180. [Google Scholar] [CrossRef]
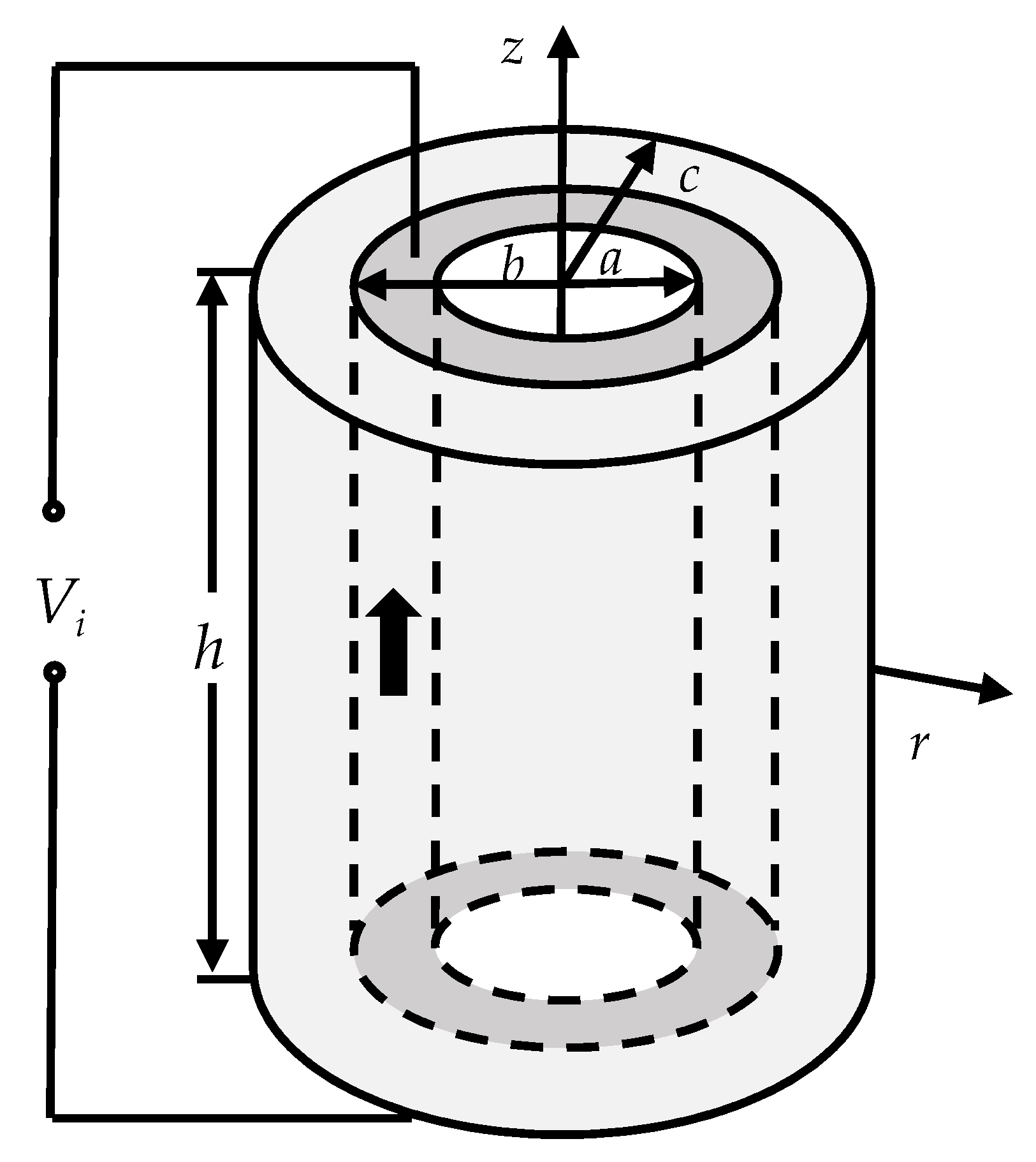
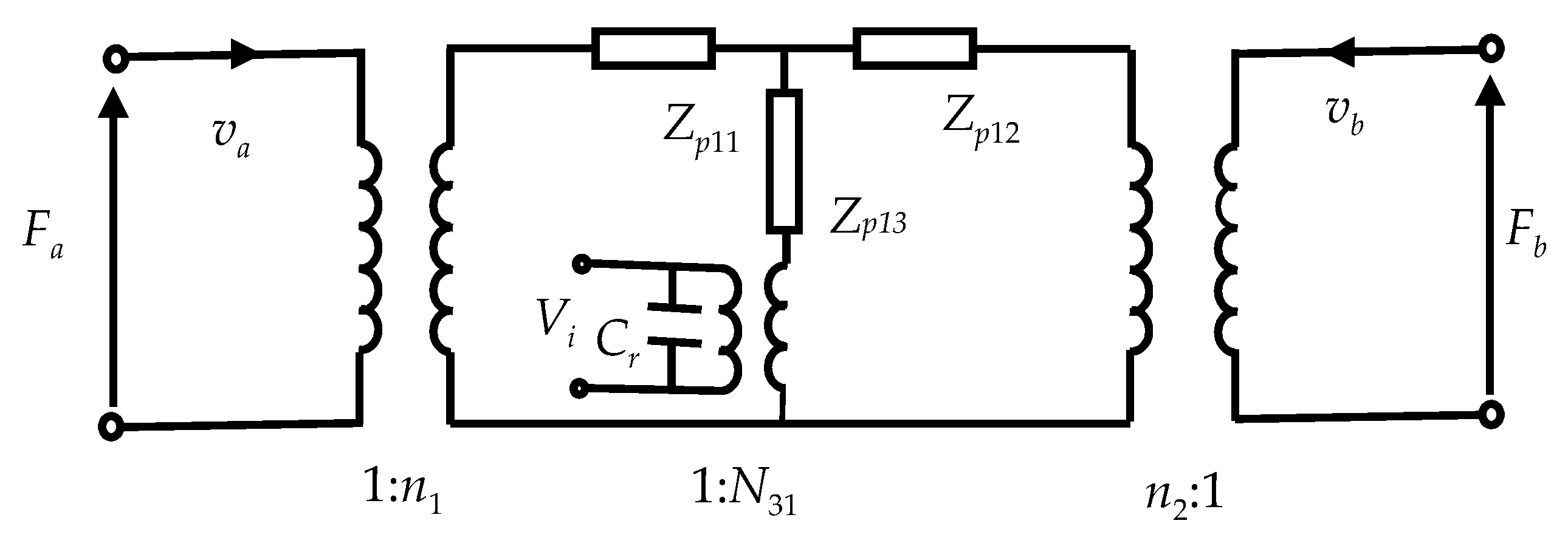

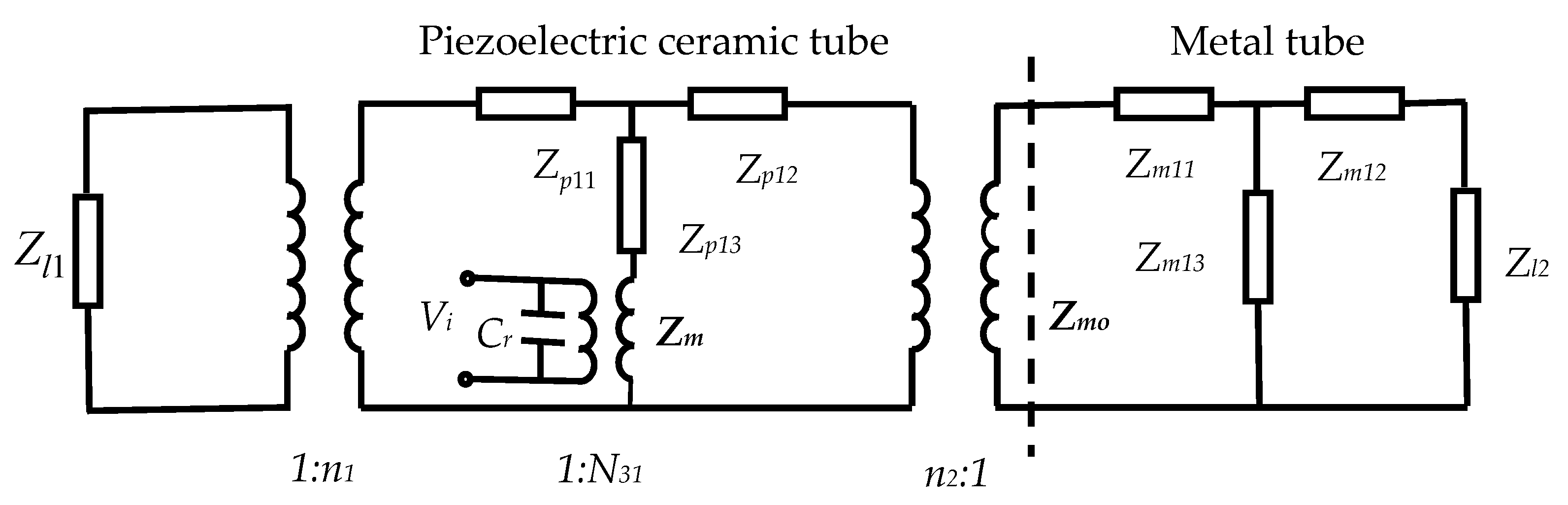
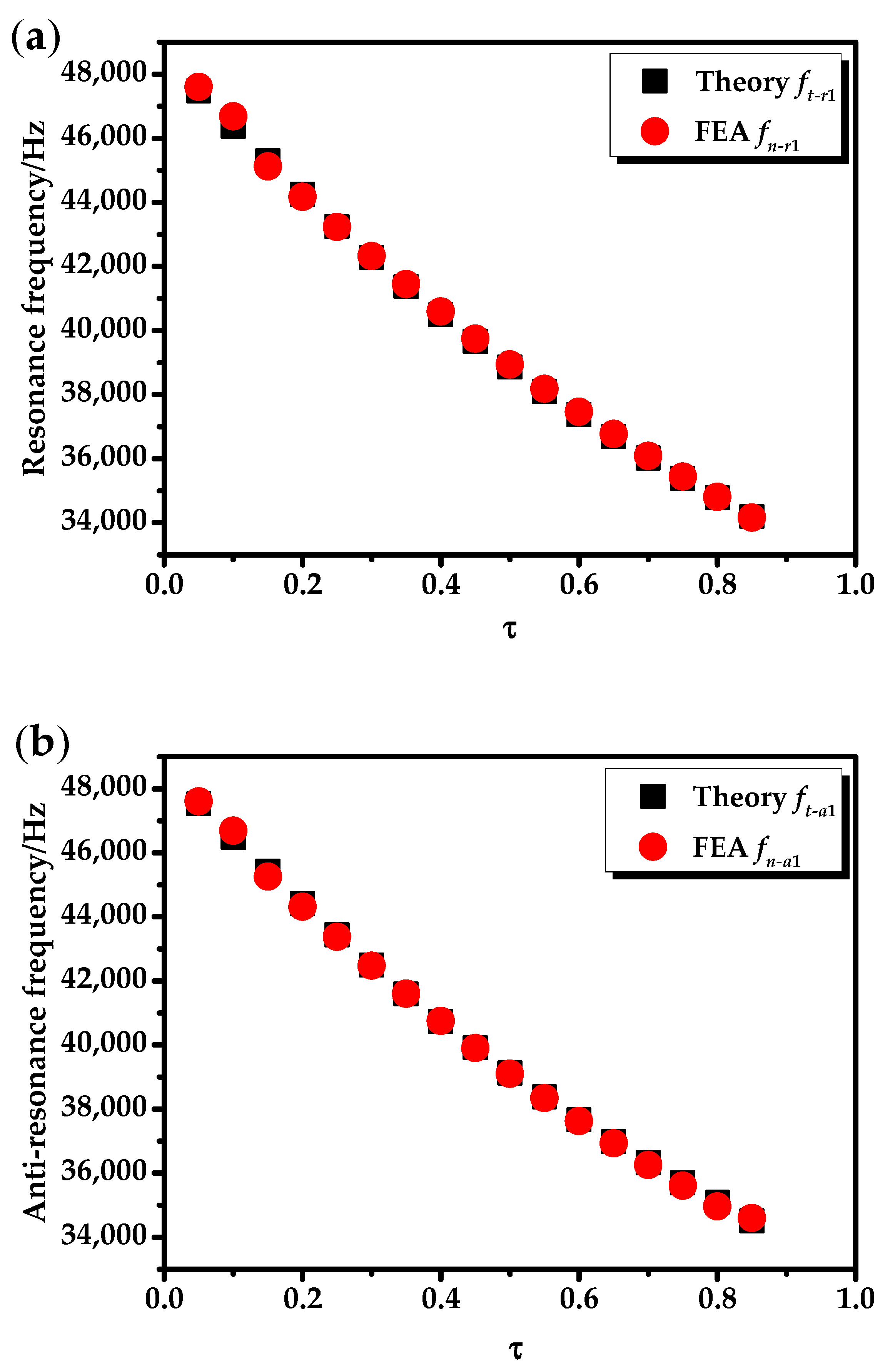

| No. | a/m | b/m | c/m |
|---|---|---|---|
| 1 | 0.016 | 0.020 | 0.022 |
| 2 | 0.010 | 0.016 | 0.030 |
| ft−r1/Hz | fn−r1/Hz | % | ft−a1/Hz | fn−a1/Hz | % | |
|---|---|---|---|---|---|---|
| 5 | 33,286 | 33,997 | 2.09 | 33,465 | 34,007 | 1.59 |
| 8 | 33,286 | 33,541 | 0.76 | 33,465 | 33,583 | 0.35 |
| ft−r1/Hz | fn−r1/Hz | % | ft−a1/Hz | fn−a1/Hz | % | |
|---|---|---|---|---|---|---|
| 5 | 42,288 | 42,495 | 0.49 | 42,495 | 42,622 | 0.30 |
| 8 | 42,288 | 42,338 | 0.11 | 42,495 | 42,456 | 0.09 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Lin, S. Analysis on the Radial Vibration of Longitudinally Polarized Radial Composite Tubular Transducer. Sensors 2020, 20, 4785. https://doi.org/10.3390/s20174785
Wang X, Lin S. Analysis on the Radial Vibration of Longitudinally Polarized Radial Composite Tubular Transducer. Sensors. 2020; 20(17):4785. https://doi.org/10.3390/s20174785
Chicago/Turabian StyleWang, Xiaoyu, and Shuyu Lin. 2020. "Analysis on the Radial Vibration of Longitudinally Polarized Radial Composite Tubular Transducer" Sensors 20, no. 17: 4785. https://doi.org/10.3390/s20174785
APA StyleWang, X., & Lin, S. (2020). Analysis on the Radial Vibration of Longitudinally Polarized Radial Composite Tubular Transducer. Sensors, 20(17), 4785. https://doi.org/10.3390/s20174785





