Selecting the Best Image Pairs to Measure Slope Deformation
Abstract
1. Introduction
2. Materials and Methods
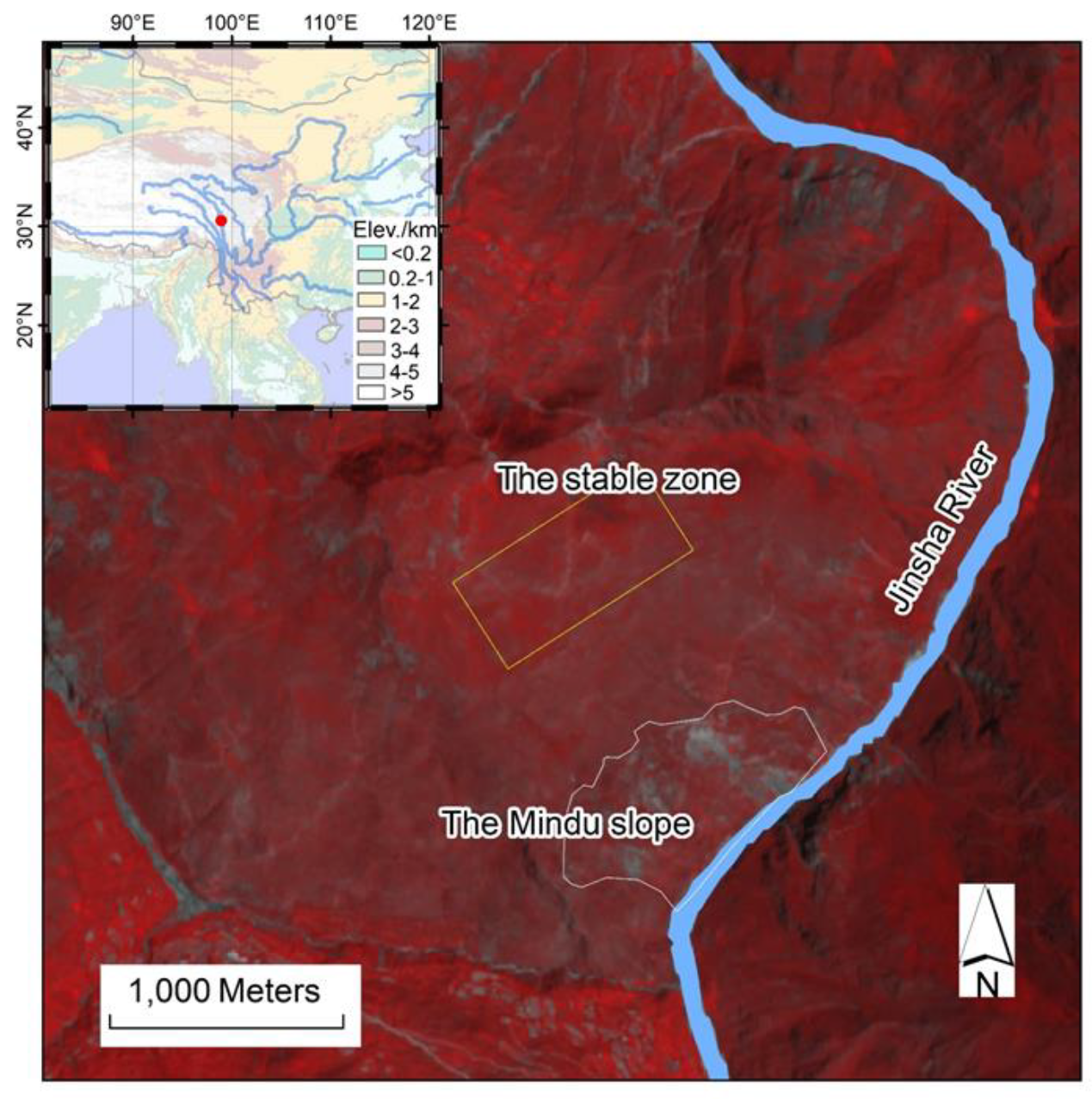
2.1. Study Area
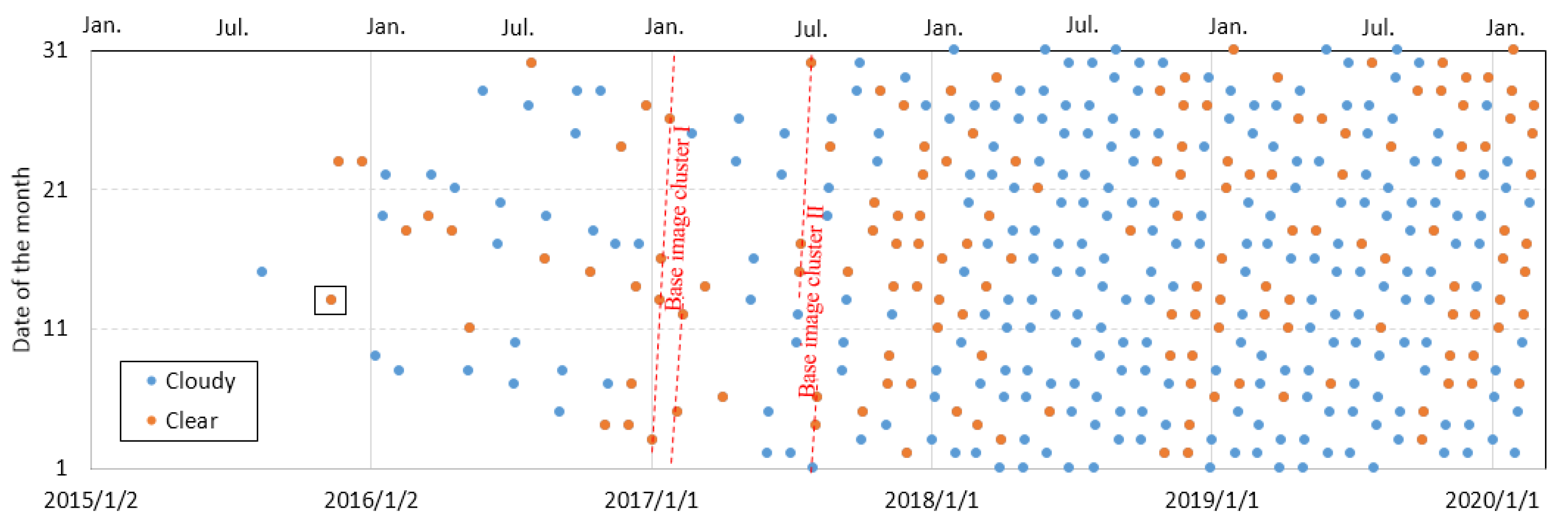
2.2. Data
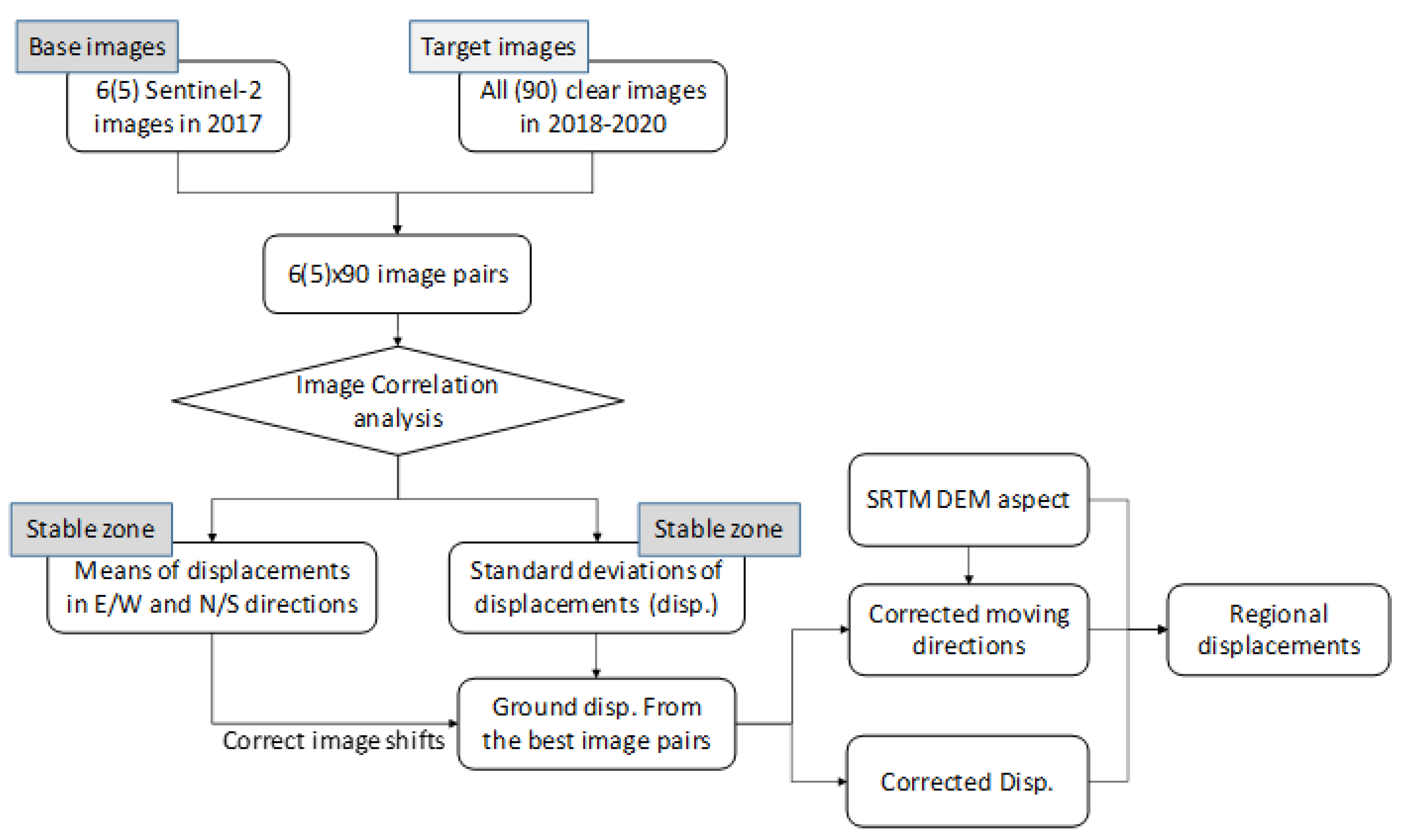
2.3. Time Series of Standard Deviations in E/W and N/S Displacements
2.4. Estimated Slope Displacements in 2019 and 2020
3. Results
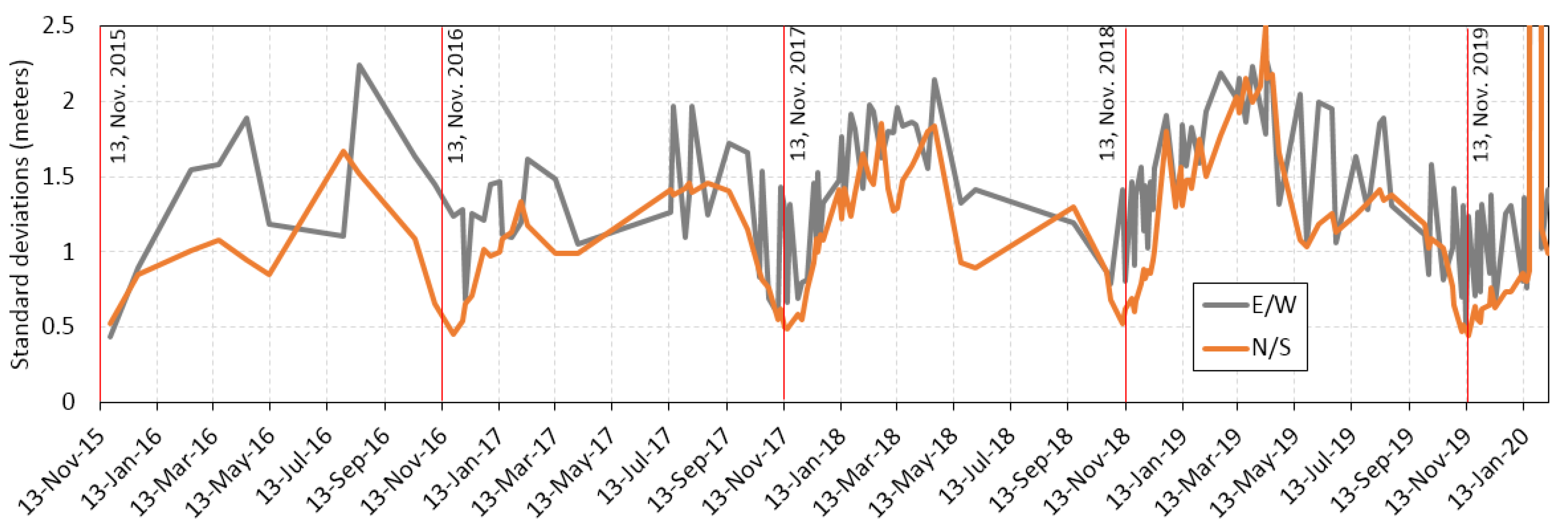
3.1. Uncertainty Analysis
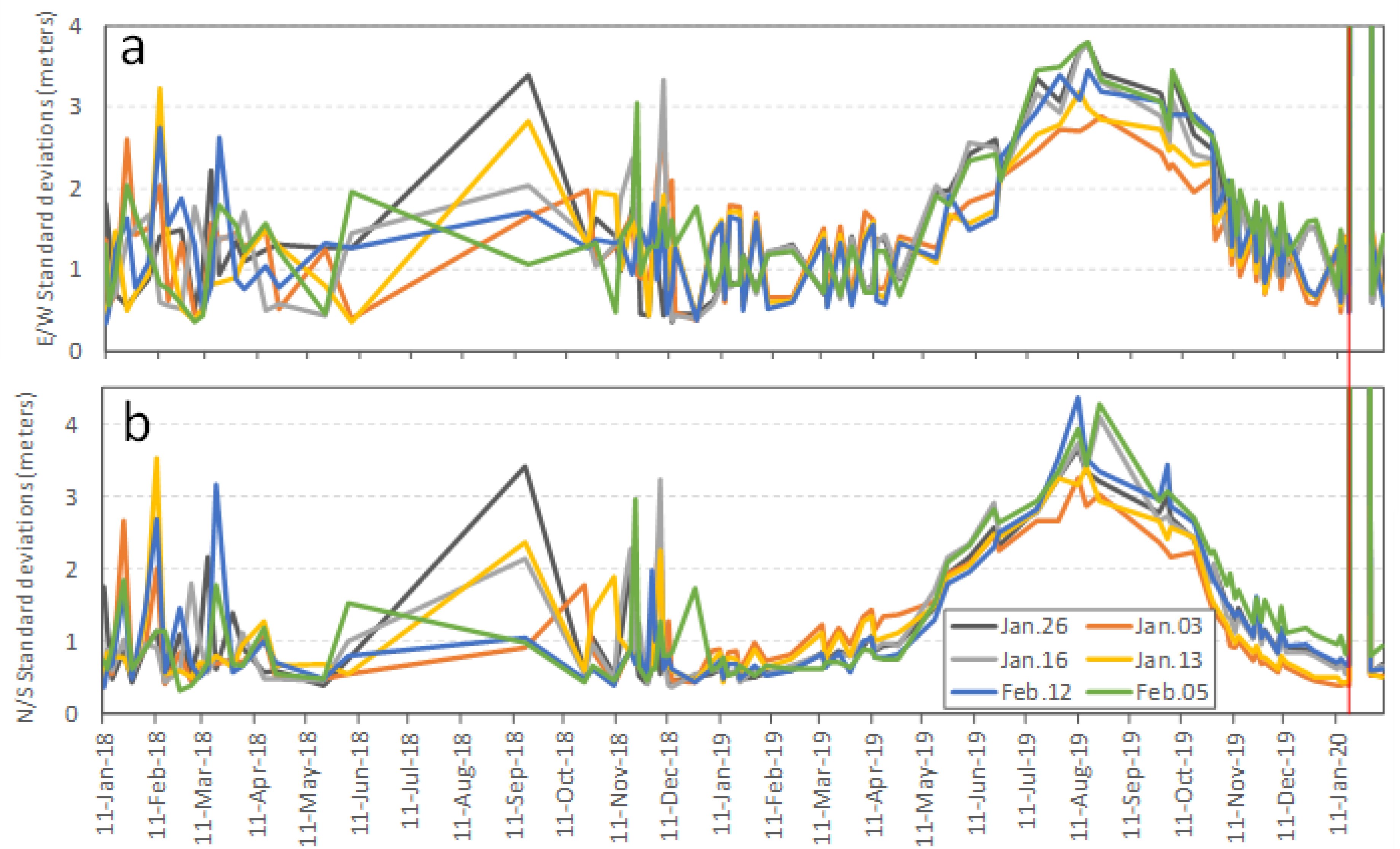
3.1.1. Time Series of Standard Deviations in the Stable Zone Using the Base Image from 13 November 2015
3.1.2. Time Series of Standard Deviations Using the First Base Image Cluster from January and February 2017
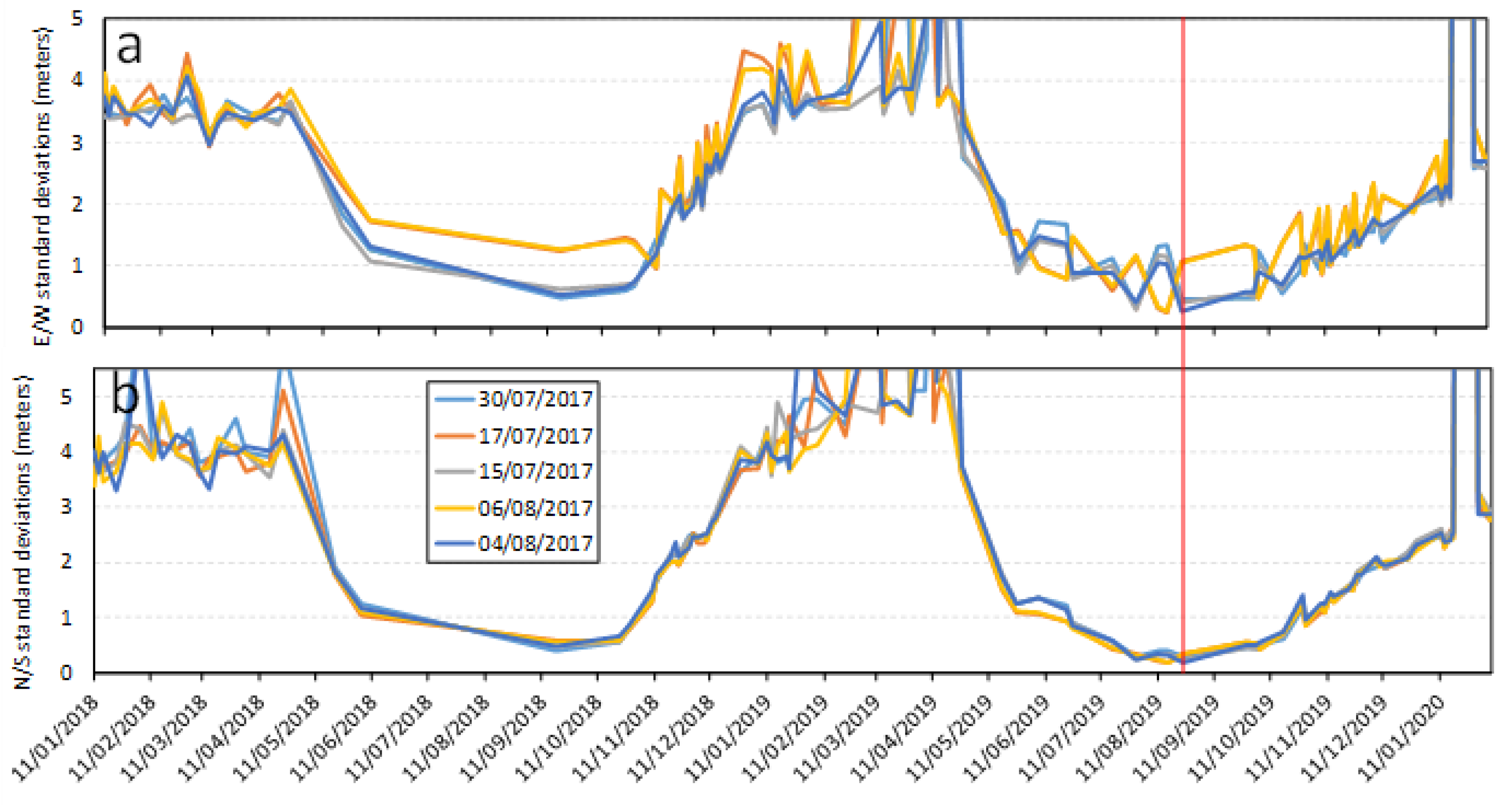
3.1.3. Time Series of Standard Deviations Using the Second Base Image Cluster from July and August 2017
3.2. Cross-Checks of Derived Displacements
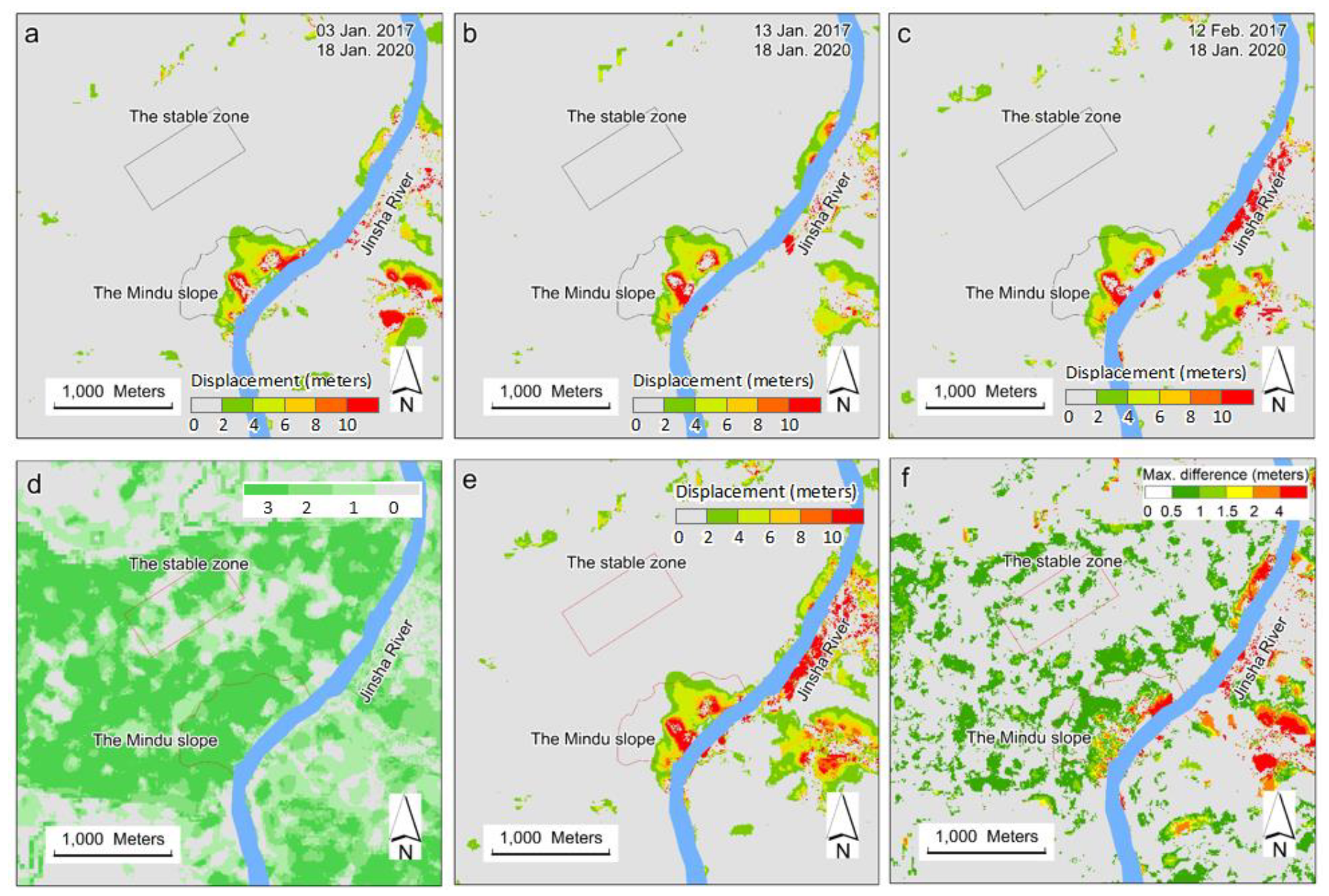
3.2.1. Cross-Checks of the Derived Displacement on 18 January 2020
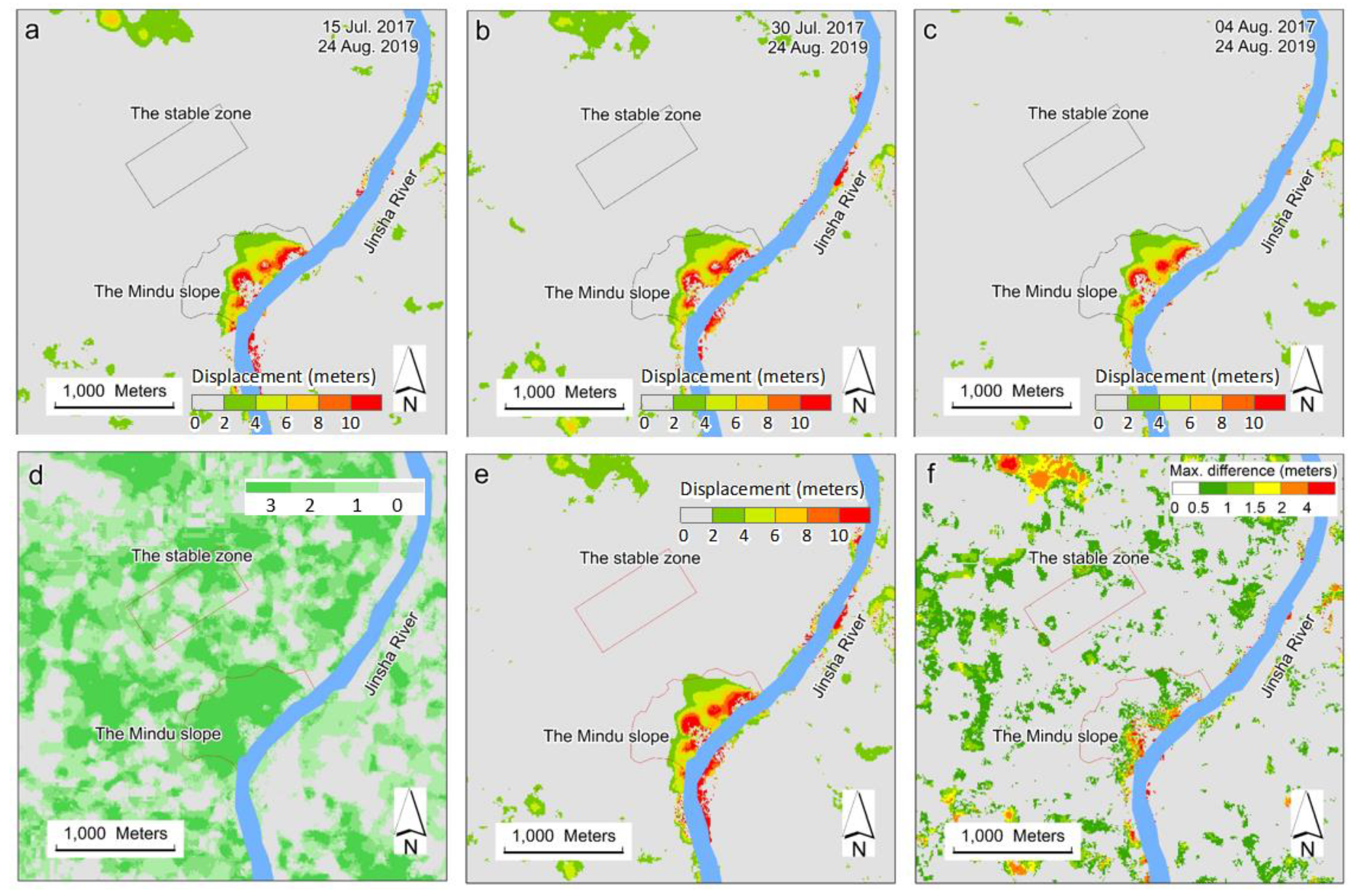
3.2.2. Cross-Checks of Derived Displacement from 24 August 2019
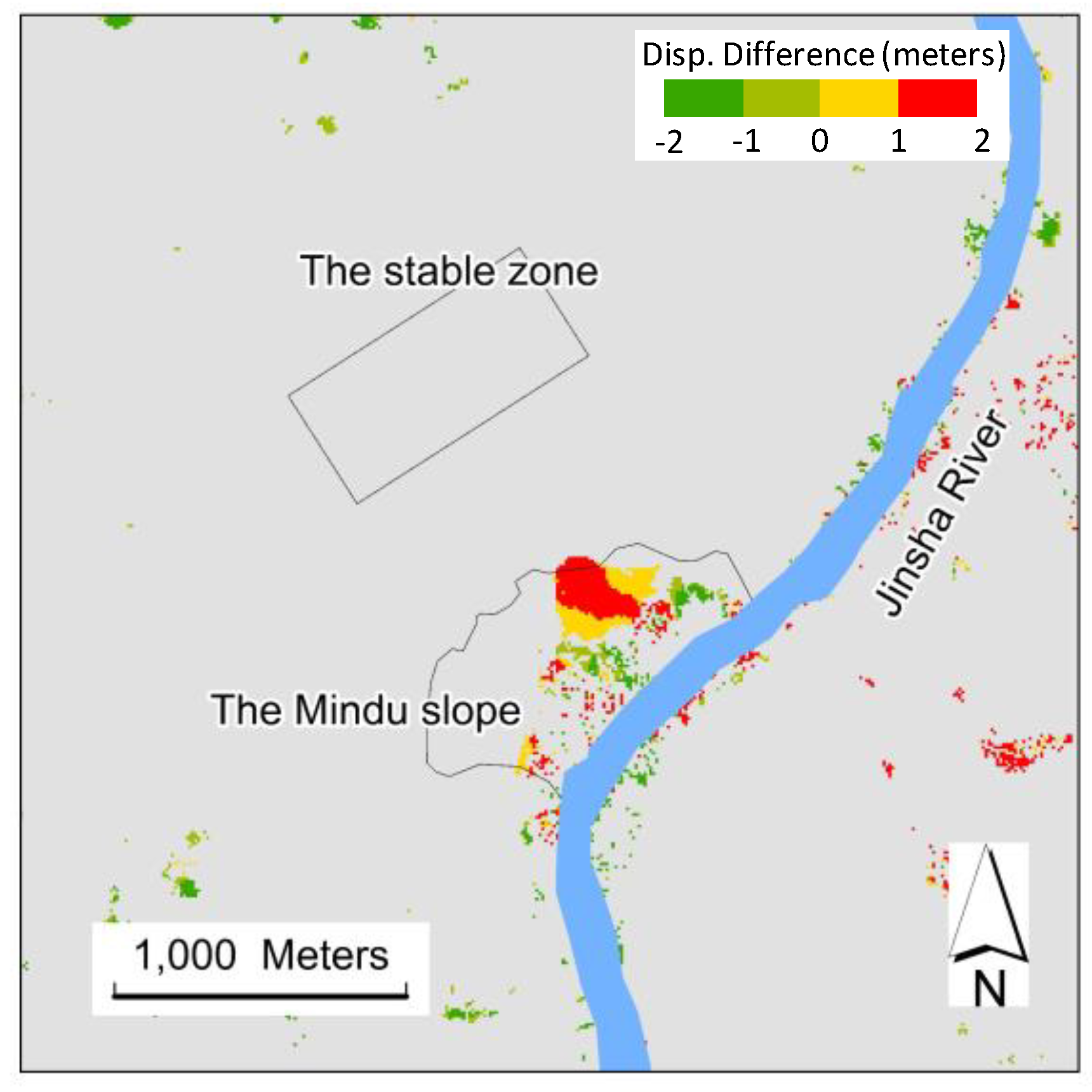
3.2.3. Comparison of Displacement between August 2019 and January 2020
4. Discussion
4.1. Temporal Patterns of Uncertainties in Slope Deformation Detection Using Optical Images
4.2. Limitations
5. Conclusions
Funding
Conflicts of Interest
References
- Lin, Q.; Wang, Y. Spatial and temporal analysis of a fatal landslide inventory in China from 1950 to 2016. Landslides 2018, 15, 2357–2372. [Google Scholar] [CrossRef]
- Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Kirschbaum, D.; Stanley, T.; Zhou, Y. Spatial and temporal analysis of a global landslide catalog. Geomorphology 2015, 249, 4–15. [Google Scholar] [CrossRef]
- Zhang, S.; Li, C.; Zhang, L.; Peng, M.; Zhan, L.; Xu, Q. Quantification of human vulnerability to earthquake-induced landslides using Bayesian network. Eng. Geol. 2020, 265, 105436. [Google Scholar] [CrossRef]
- Bradley, K.; Mallick, R.; Andikagumi, H.; Hubbard, J.; Meilianda, E.; Switzer, A.; Du, N.; Brocard, G.; Alfian, D.; Benazir, B.; et al. Earthquake-triggered 2018 Palu Valley landslides enabled by wet rice cultivation. Nat. Geosci. 2019, 12, 935–939. [Google Scholar] [CrossRef]
- Lacroix, P.; Dehecq, A.; Taipe, E. Irrigation-triggered landslides in a Peruvian desert caused by modern intensive farming. Nat. Geosci. 2020, 13, 56–60. [Google Scholar] [CrossRef]
- Stumpf, A.; Malet, J.P.; Delacourt, C. Correlation of satellite image time-series for the detection and monitoring of slow-moving landslides. Remote Sens. Environ. 2017, 189, 40–55. [Google Scholar] [CrossRef]
- Yang, W.; Wang, Y.; Wang, Y.; Ma, C.; Ma, Y. Retrospective deformation of the Baige landslide using optical remote sensing images. Landslides 2020, 17, 659–668. [Google Scholar] [CrossRef]
- Lacroix, P.; Berthier, E.; Maquerhua, E.T. Earthquake-driven acceleration of slow-moving landslides in the Colca valley, Peru, detected from Pléiades images. Remote Sens. Environ. 2015, 165, 148–158. [Google Scholar] [CrossRef]
- Lacroix, P.; Bièvre, G.; Pathier, E.; Kniess, U.; Jongmans, D. Use of Sentinel-2 images for the detection of precursory motions before landslide failures. Remote Sens. Environ. 2018, 215, 507–516. [Google Scholar] [CrossRef]
- Bontemps, N.; Lacroix, P.; Doin, M.-P. Inversion of deformation fields time-series from optical images, and application to the long term kinematics of slow-moving landslides in Peru. Remote Sens. Environ. 2018, 210, 144–158. [Google Scholar] [CrossRef]
- Leprince, S.; Barbot, S.; Ayoub, F.; Avouac, J. Automatic and precise orthorectification, coregistration, and subpixel correlation of satellite images, application to ground deformation measurements. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1529–1558. [Google Scholar] [CrossRef]
- Fan, X.; Xu, Q.; Alonso-Rodriguez, A.; Siva Subramanian, S.; Li, W.; Zheng, G.; Dong, X.; Huang, R. Successive landsliding and damming of the Jinsha River in eastern Tibet, China: Prime investigation, early warning, and emergency response. Landslides 2019, 16, 1003–1020. [Google Scholar] [CrossRef]
- Handwerger, A.L.; Fielding, E.J.; Huang, M.H.; Bennett, G.L.; Liang, C.; Schulz, W.H. Widespread initiation, reactivation, and acceleration of landslides in the Northern California Coast Ranges due to extreme rainfall. J. Geophys. Res. Earth Surf. 2019, 124, 1782–1797. [Google Scholar] [CrossRef]
- Hu, X.; Bürgmann, R. Rheology of a debris slide from the joint analysis of UAVSAR and LiDAR data. Geophys. Res. Lett. 2020, 47, e2020GL087452. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, X.; Dijkstra, T.A.; Jordan, C.J.; Chen, G.; Zeng, R.Q.; Novellino, A. Forecasting the magnitude of potential landslides based on InSAR techniques. Remote Sens. Environ. 2020, 241, 111738. [Google Scholar] [CrossRef]
- Zeng, R.Q.; Meng, X.M.; Wasowski, J.; Dijkstra, T.; Bovenga, F.; Xue, Y.T.; Wang, S.Y. Ground instability detection using PS-InSAR in Lanzhou, China. Q. J. Eng. Geol. Hydrogeol. 2014, 47, 307–321. [Google Scholar] [CrossRef]
- Intrieri, E.; Raspini, F.; Fumagalli, A.; Lu, P.; Del Conte, S.; Farina, P.; Allievi, J.; Ferretti, A.; Casagli, N. The Maoxian landslide as seen from space: Detecting precursors of failure with Sentinel-1 data. Landslides 2018, 15, 123–133. [Google Scholar] [CrossRef]
- Yin, Y.; Zheng, W.; Liu, Y.; Zhang, J.; Li, X. Integration of GPS with InSAR to monitoring of the Jiaju landslide in Sichuan, China. Landslides 2010, 7, 359–365. [Google Scholar] [CrossRef]
- Stumpf, A.; Malet, J.P.; Puissant, A.; Travelletti, J. Monitoring of earth surface motion and geomorphologic processes by optical image correlation. Land Surf. Remote Sens. 2016, 147–190. [Google Scholar] [CrossRef]
- Gascon, F.; Bouzinac, C.; Thépaut, O.; Jung, M.; Francesconi, B.; Louis, J.; Lonjou, V.; Lafrance, B.; Massera, S.; Gaudel-Vacaresse, A.; et al. Copernicus Sentinel-2A Calibration and Products Validation Status. Remote Sens. 2017, 9, 584. [Google Scholar] [CrossRef]
- Yang, W.; Liu, L.; Shi, P. A downstream landslide along the Jinsha river initiated by the 2018 Baige floods. Nat. Hazards Earth Syst. Sci. Discuss. 2020. under review. [Google Scholar]
- Yu, C.; Li, Z.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W. Selecting the Best Image Pairs to Measure Slope Deformation. Sensors 2020, 20, 4721. https://doi.org/10.3390/s20174721
Yang W. Selecting the Best Image Pairs to Measure Slope Deformation. Sensors. 2020; 20(17):4721. https://doi.org/10.3390/s20174721
Chicago/Turabian StyleYang, Wentao. 2020. "Selecting the Best Image Pairs to Measure Slope Deformation" Sensors 20, no. 17: 4721. https://doi.org/10.3390/s20174721
APA StyleYang, W. (2020). Selecting the Best Image Pairs to Measure Slope Deformation. Sensors, 20(17), 4721. https://doi.org/10.3390/s20174721




