Joint Demosaicing and Denoising Based on Interchannel Nonlocal Mean Weighted Moving Least Squares Method
Abstract
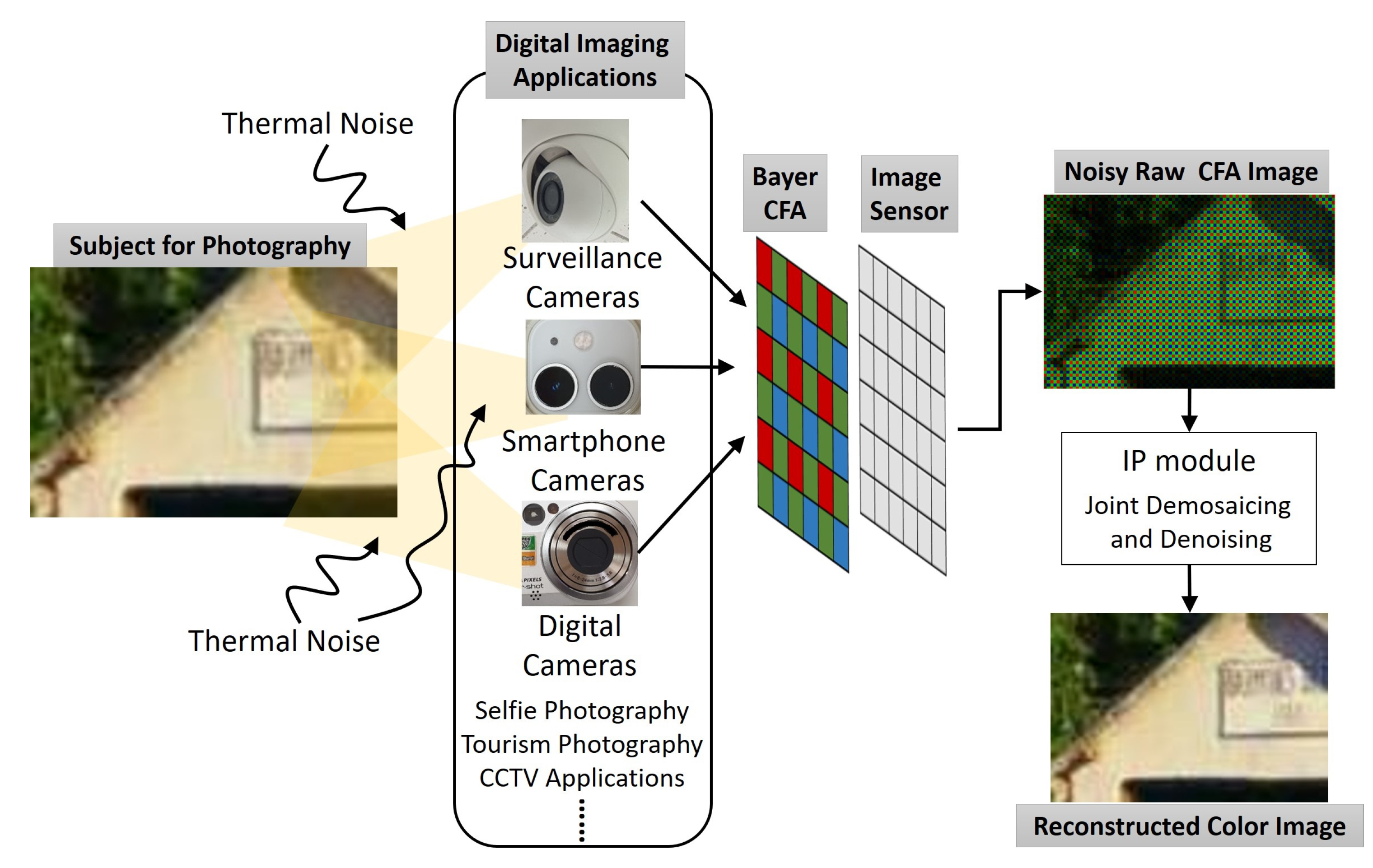
1. Introduction
- For the first time, we applied a two-dimensional polynomial-approximation-based denoising on noisy CFA patterns.
- Compared with nonlocal-mean-based methods, e,g., the BM3D denoising, the proposed method incorporates an extra reproducing constraint into the denoising scheme. This guarantees an approximation accuracy to a desired order.
- We incorporate interchannel information into the polynomial approximation by determining the nonlocal weights directly from the noisy raw CFA image.
2. Relation of the Proposed Work to Sensors
3. Related Works
3.1. Residual Interpolation
3.2. Moving Least Square Methods with Total Variation Minimization
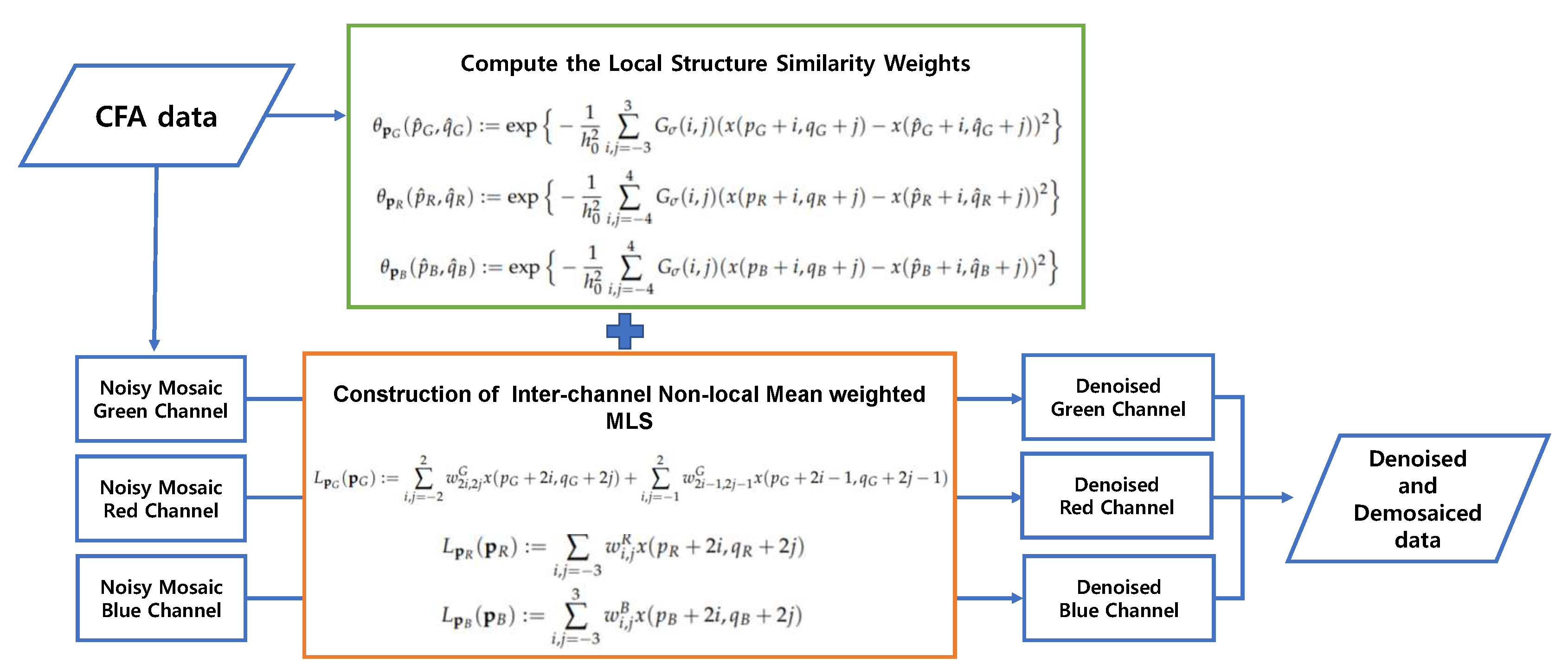
4. Proposed Method
4.1. Problem Formulation
4.2. Interchannel Data Weighted Least Squares Reconstruction
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MLS-TV | Moving least squares methods with total variation minimization |
| RI | Residual interpolation |
References
- Bayer, B. Color Imaging Array. U.S. Patent 3971065 A, 20 July 1976. [Google Scholar]
- Wu, J.; Anisetti, M.; Wu, W.; Damiani, E.; Jeon, G. Bayer demosaicing with polynomial interpolation. IEEE Trans. Image Process. 2016, 25, 5369–5382. [Google Scholar] [CrossRef] [PubMed]
- Buades, A.; Coll, B.; Morel, J.; Sbert, C. Self-similarity driven demosaicing. IEEE Trans. Image Process. 2009, 18, 1192–1202. [Google Scholar] [CrossRef] [PubMed]
- Kiku, D.; Monno, Y.; Tanaka, M.; Okutomi, M. Residual interpolation for color image demosaicing. In Proceedings of the 2013 IEEE International Conference on Image Processing(ICIP), Melbourne, Australia, 15–18 September 2013; pp. 2304–2308. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided Image Filtering. IEEE Trans. Pattern Anal. 2013, 53, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Pekkucuksen, I.; Altunbasak, Y. Gradient based threshold free color filter array interpolation. In Proceedings of the 2010 IEEE International Conference on Image Processing(ICIP), Hong Kong, China, 12–15 September 2010; pp. 137–140. [Google Scholar] [CrossRef]
- Akiyama, H.; Tanaka, M.; Okutomi, M. Pseudo four-channel image denoising for noisy CFA raw data. In Proceedings of the 2015 IEEE International Conference on Image Processing(ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 4778–4782. [Google Scholar] [CrossRef]
- Danielyan, A.; Vehvilainen, M.; Foi, A.; Katkovnik, V.; Egiazarian, K. Cross-color BM3D filtering of noisy raw data. In Proceedings of the 2009 International Workshop on Local and Non-Local Approximation in Image Processing, Tuusalu, Finland, 19–21 August 2009; pp. 125–129. [Google Scholar] [CrossRef]
- Tan, H.; Zeng, X.; Lai, S.; Liu, Y.; Zhang, M. Joint demosaicing and denoising of noisy bayer images with ADMM. In Proceedings of the 2017 IEEE International Conference on Image Processing(ICIP), Beijing, China, 17–20 September 2017; pp. 2951–2955. [Google Scholar] [CrossRef]
- Huang, T.; Wu, F.F.; Dong, W.; Guangming, S.; Li, X. Lightweight deep residue learning for joint color image demosaicking and denoising. In Proceedings of the 2018 International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 127–132. [Google Scholar]
- Ehret, T.; Davy, A.; Arias, P.; Facciolo, G. Joint Demosaicking and denoising by fine-tuning of bursts of raw images. In Proceedings of the 2019 International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 8868–8877. [Google Scholar]
- Kokkinos, F.; Lefkimmiatis, S. Iterative joint image demosaicking and denoising wsing a residual denoising network. IEEE Trans. Image Process. 2019, 28, 4177–4188. [Google Scholar] [CrossRef] [PubMed]
- Klatzer, T.; Hammernik, K.; Knobelreiter, P.; Pock, T. Learning joint demosaicing and denoising based on sequential energy minimization. In Proceedings of the 2016 IEEE International Conference on Computational Photography (ICCP), Evanston, IL, USA, 13–15 May 2016; pp. 1–11. [Google Scholar]
- Gharbi, M.; Chaurasia, G.; Paris, S.; Durand, F. Deep Joint Demosaicking and Denoising. ACM Trans. Graph. 2016, 35, 1–12. [Google Scholar] [CrossRef]
- Luo, J.; Wang, J. Image Demosaicing based on generative adversarial network. Math. Probl. Eng. 2020, 2020, 7367608. [Google Scholar] [CrossRef]
- Fu, H.; Bian, L.; Cao, X.; Zhang, J. Hyperspectral imaging from a raw mosaic image with end-to-end learning. Opt. Express 2020, 28, 314–324. [Google Scholar] [CrossRef]
- Schwartz, E.; Giryes, R.; Bronstein, A.M. DeepISP: Toward kearning an end-to-end image processing pipeline. IEEE Trans. Image Process. 2019, 28, 912–923. [Google Scholar] [CrossRef]
- Choi, W.; Park, H.; Kyung, C. Color reproduction pipeline for an RGBW color filter array sensor. Opt. Express 2020, 28, 15678–15690. [Google Scholar] [CrossRef]
- Kwan, C.; Larkin, J. Demosaicing of bayer and CFA 2.0 patterns for low lighting images. Electronics 2019, 8, 1444. [Google Scholar] [CrossRef]
- Lee, S.; Choi, D.; Song, B. Hardware-efficient color correlation-adaptive demosaicing with multifiltering. J. Electron. Imaging 2019, 28, 013018. [Google Scholar] [CrossRef]
- Szczepanski, M.; Giemza, F. Noise removal in the developing process of digital negatives. Sensors 2020, 20, 902. [Google Scholar] [CrossRef] [PubMed]
- Thomas, J.; Farup, I. Demosaicing of periodic and random color filter arrays by linear anisotropic diffusion. J. Imaging Sci. Technol. 2018, 62, 050401. [Google Scholar] [CrossRef]
- Mihoubi, S.; Lapray, P.; Bigue, L. Survey of demosaicking methods for polarization filter array images. Sensors 2018, 18, 3688. [Google Scholar] [CrossRef]
- Sober, B.; Levin, D. Manifold approximation by moving least-squares projection (MMLS). Constr. Approx. 2019. [Google Scholar] [CrossRef]
- Ji, L.; Guo, Q.; Zhang, M. Medical image denoising based on biquadratic polynomial with minimum error constraints and low-rank approximation. IEEE Access 2020, 8, 84950–84960. [Google Scholar] [CrossRef]
- Novosadova, M.; Rajmic, P.; Sorel, M. Orthogonality is superiority in piecewise-polynomial signal segmentation and denoising. EURASIP J. Adv. Signal Process. 2019, 2019, 6. [Google Scholar] [CrossRef]
- Takeda, H.; Farsiu, S.; Milanfar, P. Kernel regression for image processing and reconstruction. IEEE Trans. Image Process. 2007, 16, 349–366. [Google Scholar] [CrossRef]
- Bose, N.K.; Ahuja, N.A. Superresolution and noise filtering using moving least squares. IEEE Trans. Image Process. 2006, 15, 2239–2248. [Google Scholar] [CrossRef]
- Lee, Y.; Yoon, J. Nonlinear image upsampling method based on radial basis function interpolation. IEEE Trans. Image Process. 2010, 19, 2682–2692. [Google Scholar] [CrossRef]
- MatinFar, M.; Pourabd, M. Modified moving least squares method for two-dimensional linear and nonlinear systems of integral equations. Appl. Math. 2018, 37, 5857–5875. [Google Scholar] [CrossRef]
- Fujita, Y.; Ikuno, S.; Itoh, T.; Nakamura, H. Modified Improved Interpolating Moving Least Squares Method for Meshless Approaches. IEEE Trans. Magn. 2019, 55, 7203204. [Google Scholar] [CrossRef]
- Hwang, J.; Lee, J.; Kweon, I.; Kim, S. Probabilistic moving least squares with spatial constraints for nonlinear color transfer between images. Comput. Vis. Image Underst. 2019, 180, 1–12. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, S.; Yoon, J. A framework for moving least squares method with total variation minimizing regularization. J Math. Imaging Vis. 2013, 48, 566–582. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The split bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Levin, D. The approximation power of moving least-squares. Math. Comput. 1998, 67, 1517–1531. [Google Scholar] [CrossRef]





| McMaster Dataset Images | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Noise Level | Methods | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RI | 25.4925 | 29.7198 | 27.4230 | 28.7656 | 28.7352 | 30.2073 | 30.3072 | 31.3710 | 30.3286 | |
| ADMM | 24.0986 | 28.7480 | 25.8632 | 27.1826 | 27.4595 | 28.9430 | 28.9478 | 30.1183 | 29.2356 | |
| BM3D | 25.5562 | 30.3227 | 28.5314 | 30.5665 | 28.9093 | 30.6146 | 31.2559 | 32.7216 | 30.9308 | |
| Proposed | 25.4436 | 29.5762 | 27.3741 | 28.8772 | 28.6393 | 29.9254 | 29.4552 | 31.4400 | 30.5131 | |
| RI | 24.7643 | 28.1071 | 26.3138 | 27.3294 | 27.2902 | 28.3014 | 28.4306 | 29.4504 | 28.4691 | |
| ADMM | 23.9313 | 28.4944 | 25.7016 | 26.9503 | 27.3179 | 28.7975 | 28.7118 | 29.5892 | 29.0134 | |
| BM3D | 25.0413 | 29.3712 | 27.2120 | 29.2910 | 28.0784 | 29.6043 | 29.7767 | 31.4700 | 29.8660 | |
| Proposed | 25.0890 | 29.0947 | 26.8136 | 28.2796 | 28.1961 | 29.5057 | 29.1555 | 30.7407 | 29.9819 | |
| McMaster Dataset Images | ||||||||||
| Noise Level | Methods | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| RI | 31.4582 | 32.0506 | 31.5159 | 32.7740 | 32.1560 | 32.3301 | 28.2429 | 27.5546 | 29.3230 | |
| ADMM | 30.2806 | 31.4607 | 30.8019 | 33.7572 | 32.2113 | 32.4052 | 26.7781 | 25.8872 | 28.5202 | |
| BM3D | 32.0903 | 32.7758 | 33.0493 | 35.1113 | 33.5730 | 33.4575 | 28.2952 | 27.4109 | 30.2682 | |
| Proposed | 31.2061 | 31.8866 | 32.2402 | 34.4451 | 32.7570 | 32.8573 | 27.7978 | 27.1630 | 29.1151 | |
| RI | 29.2452 | 29.6592 | 29.0120 | 29.6388 | 29.6244 | 29.8651 | 27.0536 | 26.5489 | 27.7879 | |
| ADMM | 29.8837 | 30.9067 | 30.5479 | 33.4766 | 31.8245 | 31.9279 | 26.5367 | 25.7544 | 28.2356 | |
| BM3D | 30.9424 | 31.6128 | 31.7795 | 34.1728 | 32.6172 | 32.4932 | 27.3090 | 26.6519 | 29.2443 | |
| Proposed | 30.7439 | 31.4394 | 31.4415 | 33.7712 | 32.2474 | 32.3134 | 27.3533 | 26.8395 | 28.6549 | |
| McMaster Dataset Images | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Noise Level | Methods | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RI | 0.9709 | 0.9694 | 0.9740 | 0.9752 | 0.9724 | 0.9710 | 0.9702 | 0.9768 | 0.9700 | |
| ADMM | 0.9607 | 0.9570 | 0.9637 | 0.9750 | 0.9668 | 0.9599 | 0.9559 | 0.9705 | 0.9665 | |
| BM3D | 0.9820 | 0.9823 | 0.9859 | 0.9859 | 0.9838 | 0.9837 | 0.9829 | 0.9859 | 0.9829 | |
| Proposed | 0.9732 | 0.9672 | 0.9774 | 0.9804 | 0.9738 | 0.9635 | 0.9647 | 0.9770 | 0.9723 | |
| RI | 0.9618 | 0.9528 | 0.9605 | 0.9493 | 0.9572 | 0.9550 | 0.9511 | 0.9472 | 0.9473 | |
| ADMM | 0.9599 | 0.9572 | 0.9626 | 0.9734 | 0.9671 | 0.9610 | 0.9567 | 0.9681 | 0.9654 | |
| BM3D | 0.9709 | 0.9694 | 0.9740 | 0.9752 | 0.9724 | 0.9710 | 0.9702 | 0.9768 | 0.9700 | |
| Proposed | 0.9663 | 0.9607 | 0.9703 | 0.9715 | 0.9655 | 0.9561 | 0.9582 | 0.9692 | 0.9650 | |
| McMaster Dataset Images | ||||||||||
| Noise Level | Methods | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| RI | 0.9753 | 0.9646 | 0.9739 | 0.9773 | 0.9773 | 0.9714 | 0.9672 | 0.9595 | 0.9725 | |
| ADMM | 0.9687 | 0.9606 | 0.9692 | 0.9780 | 0.9759 | 0.9712 | 0.9497 | 0.9538 | 0.9697 | |
| BM3D | 0.9857 | 0.9795 | 0.9854 | 0.9859 | 0.9857 | 0.9820 | 0.9832 | 0.9776 | 0.9844 | |
| Proposed | 0.9730 | 0.9615 | 0.9779 | 0.9791 | 0.9766 | 0.9738 | 0.9597 | 0.9652 | 0.9725 | |
| RI | 0.9491 | 0.9493 | 0.9397 | 0.8805 | 0.9334 | 0.9355 | 0.9695 | 0.9640 | 0.9614 | |
| ADMM | 0.9673 | 0.9598 | 0.9685 | 0.9768 | 0.9740 | 0.9709 | 0.9493 | 0.9526 | 0.9692 | |
| BM3D | 0.9753 | 0.9646 | 0.9739 | 0.9773 | 0.9773 | 0.9714 | 0.9672 | 0.9595 | 0.9725 | |
| Proposed | 0.9662 | 0.9533 | 0.9706 | 0.9719 | 0.9700 | 0.9672 | 0.9537 | 0.9574 | 0.9658 | |
| McMaster Dataset Images | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Noise Level | Methods | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RI | 0.9281 | 0.9163 | 0.8833 | 0.8713 | 0.9124 | 0.8964 | 0.8386 | 0.8447 | 0.9571 | |
| ADMM | 0.9026 | 0.9033 | 0.8655 | 0.8743 | 0.9025 | 0.8786 | 0.7760 | 0.8383 | 0.9550 | |
| BM3D | 0.9318 | 0.9319 | 0.9222 | 0.9234 | 0.9259 | 0.9067 | 0.8786 | 0.9218 | 0.9674 | |
| Proposed | 0.9245 | 0.9152 | 0.9018 | 0.8995 | 0.9165 | 0.8907 | 0.7963 | 0.8897 | 0.9620 | |
| RI | 0.9116 | 0.8763 | 0.8234 | 0.7795 | 0.8667 | 0.8475 | 0.7578 | 0.7365 | 0.9293 | |
| ADMM | 0.8991 | 0.8954 | 0.8541 | 0.8663 | 0.8966 | 0.8730 | 0.7629 | 0.7856 | 0.9497 | |
| BM3D | 0.9203 | 0.9167 | 0.9005 | 0.9032 | 0.9115 | 0.8866 | 0.8298 | 0.9041 | 0.9588 | |
| Proposed | 0.9188 | 0.9052 | 0.8824 | 0.8758 | 0.9058 | 0.8782 | 0.7844 | 0.8572 | 0.9564 | |
| McMaster Dataset Images | ||||||||||
| Noise Level | Methods | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| RI | 0.9602 | 0.9548 | 0.9833 | 0.9832 | 0.9445 | 0.9613 | 0.9495 | 0.9318 | 0.9313 | |
| ADMM | 0.9644 | 0.9539 | 0.9834 | 0.9874 | 0.9608 | 0.9691 | 0.9346 | 0.9088 | 0.9299 | |
| BM3D | 0.9734 | 0.9645 | 0.9894 | 0.9904 | 0.9685 | 0.9747 | 0.9527 | 0.9328 | 0.9496 | |
| Proposed | 0.9674 | 0.9570 | 0.9868 | 0.9886 | 0.9625 | 0.9703 | 0.9449 | 0.9266 | 0.9365 | |
| RI | 0.9312 | 0.9257 | 0.9687 | 0.9660 | 0.8988 | 0.9333 | 0.9266 | 0.9095 | 0.8960 | |
| ADMM | 0.9576 | 0.9453 | 0.9818 | 0.9864 | 0.9540 | 0.9621 | 0.9276 | 0.9034 | 0.9208 | |
| BM3D | 0.9670 | 0.9554 | 0.9859 | 0.9883 | 0.9628 | 0.9697 | 0.9400 | 0.9184 | 0.9370 | |
| Proposed | 0.9600 | 0.9508 | 0.9842 | 0.9868 | 0.9546 | 0.9644 | 0.9382 | 0.9183 | 0.9262 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Ryu, H.; Lee, S.; Lee, Y.J. Joint Demosaicing and Denoising Based on Interchannel Nonlocal Mean Weighted Moving Least Squares Method. Sensors 2020, 20, 4697. https://doi.org/10.3390/s20174697
Kim Y, Ryu H, Lee S, Lee YJ. Joint Demosaicing and Denoising Based on Interchannel Nonlocal Mean Weighted Moving Least Squares Method. Sensors. 2020; 20(17):4697. https://doi.org/10.3390/s20174697
Chicago/Turabian StyleKim, Yeahwon, Hohyung Ryu, Sunmi Lee, and Yeon Ju Lee. 2020. "Joint Demosaicing and Denoising Based on Interchannel Nonlocal Mean Weighted Moving Least Squares Method" Sensors 20, no. 17: 4697. https://doi.org/10.3390/s20174697
APA StyleKim, Y., Ryu, H., Lee, S., & Lee, Y. J. (2020). Joint Demosaicing and Denoising Based on Interchannel Nonlocal Mean Weighted Moving Least Squares Method. Sensors, 20(17), 4697. https://doi.org/10.3390/s20174697








