A Challenge-Response Assisted Authorisation Scheme for Data Access in Permissioned Blockchains
Abstract
1. Introduction
- Unlike many mainstream designs [10,12,16] that cannot protect users’ private information in the authorisation, CRA3 can realise authorisation without revealing the access permissions and other private information of users to nodes in the consensus network and keep users anonymous in the permissioned blockchain because we consider the consensus network as untrusted.
- A theoretical security model and proof are illustrated formally to show that CRA3 can achieve the confidentiality of indistinguishability under chosen-ciphertext attacks (IND-CCA) [17] to avoid privacy leakage during the authorised data access in a permissioned blockchain.
- Most of the computing work for authorising the data access request is executed by the data requester and provider to decrease the transaction cost and the burden on the consensus network.
2. Related Work
3. Preliminaries
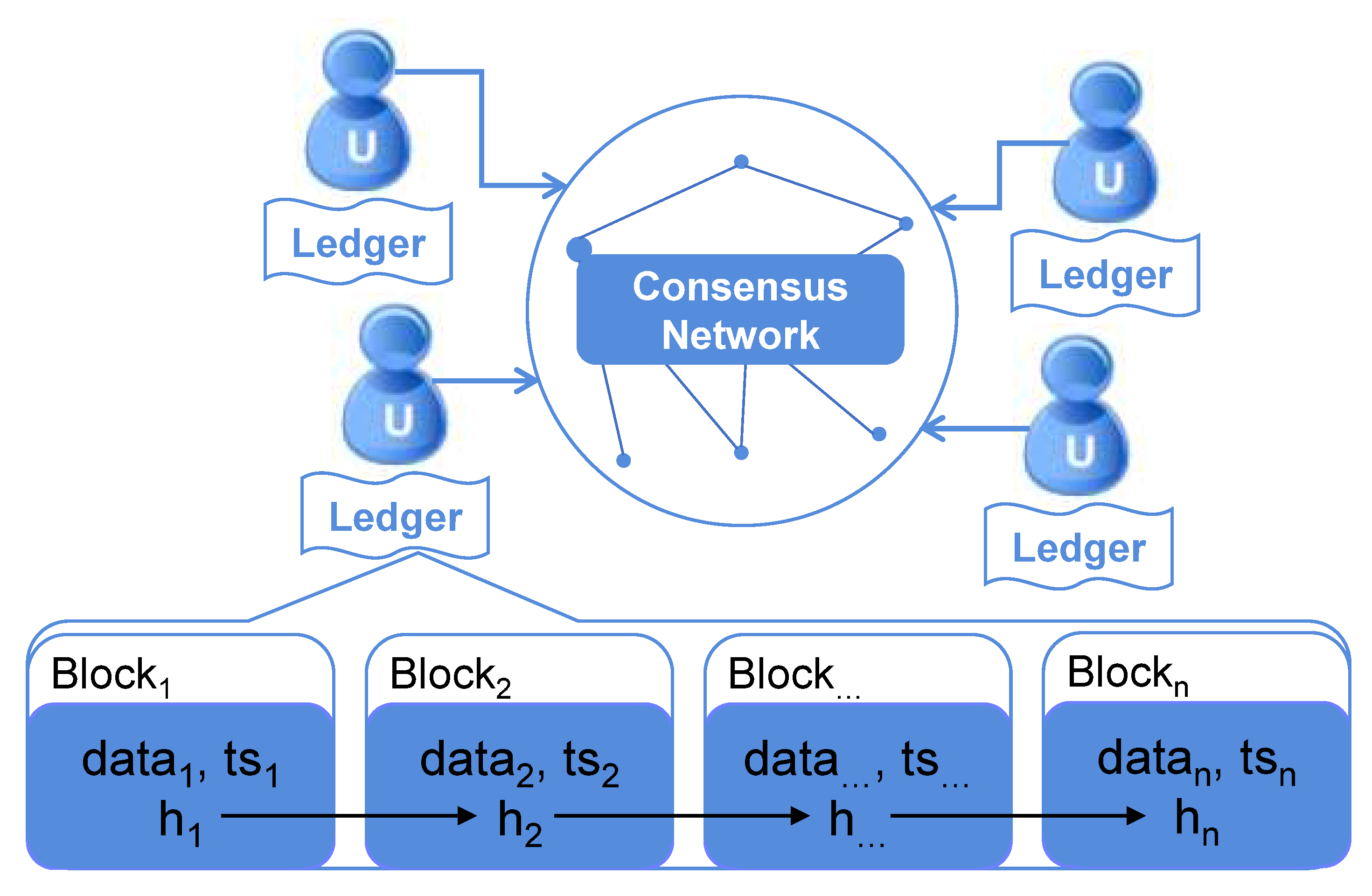
3.1. Permissioned Blockchain Networks
3.2. Lagrange Interpolating Polynomial
4. Problem and Definitions
4.1. Problem Statement
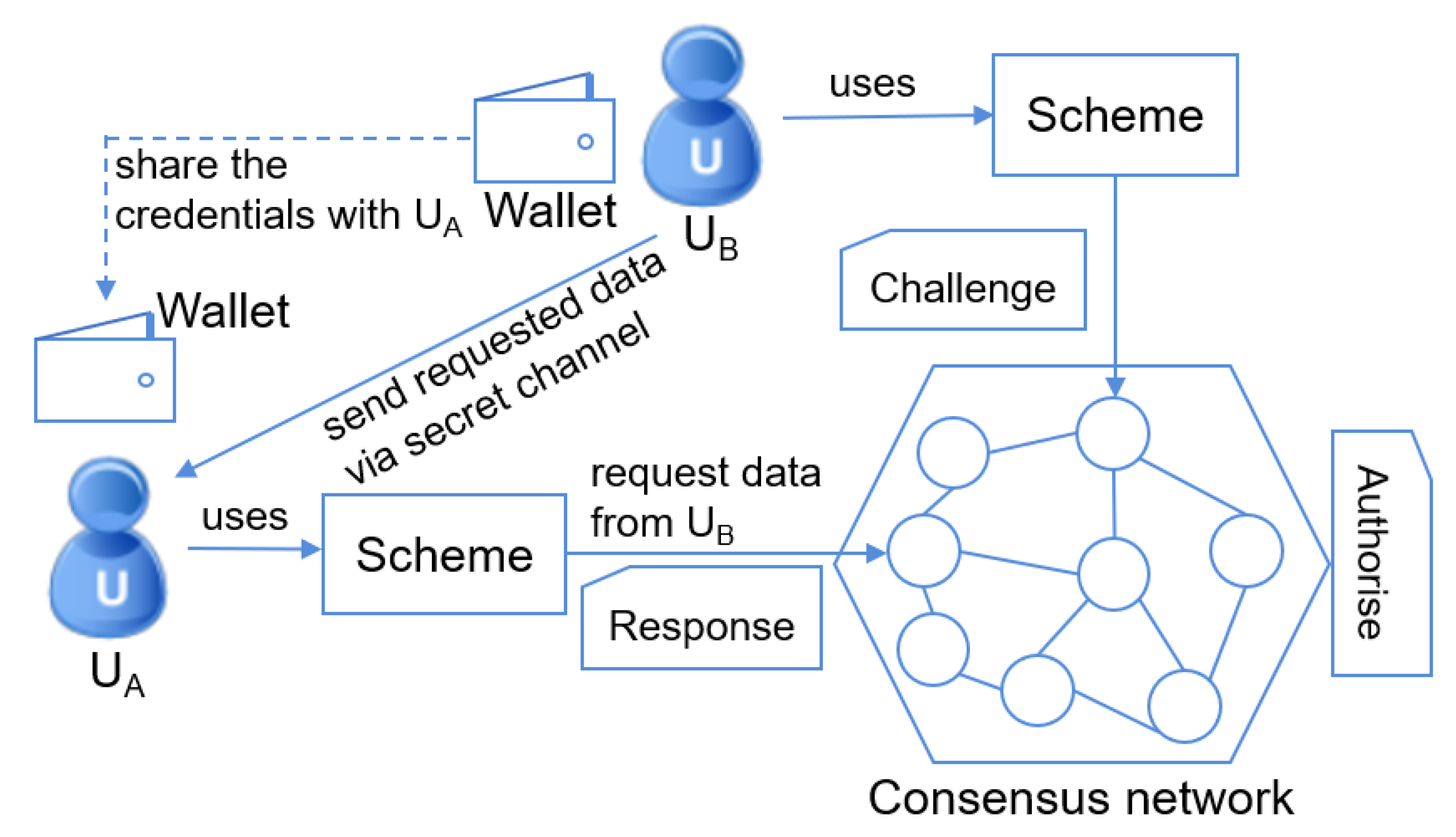
4.2. Scheme Definitions
- Setup (): This algorithm takes the security parameter and generates the public parameter .
- Request (): uses the algorithm to send a data access request Q to via .
- Challenge (): constructs and sends the challenge to with the identity attributes sequence .
- Response (): uses its own sequence to calculate and send the response to the .
- Authorise (, ): validates the correctness of the response based upon the challenge .
- Encrypt (): uses this algorithm to encrypt the requested data M then return the ciphertext C and a point P (for decryption use) to .
- Decrypt (, P, ): decrypts the encrypted data C to retrieve the requested data M with the given point P.
4.3. Security Definition
4.3.1. Correctness
4.3.2. Confidentiality (IND-CCA Security)
- Initialise:first generates the public parameter via running the algorithm . Then, generates n data providers (key-value pairs) and the target data provider is . The generated and all are given to the adversary .
- Queries:The following queries can be requested by for polynomial times in the game:
- Identity attributes query : responds with the sequence of the random identity attributes ;
- Encrypt query: outputs the ciphertext and the point P on the constructed polynomial in the Encrypt phase;
- Decrypt query: decrypts C via running the algorithm Decrypt, then responds with the plain message.
- Challenge:submits two equal-length messages and . picks , and then computes and returns the challenge ciphertext .
- Constraints:
- and are not allowed to appear in the above Encrypt query;
- The target data provider’s index t and the challenge ciphertext are not allowed to appear in the above Decrypt query.
- Guess:can win the game if its output satisfies the condition .Now, the advantage of could be defined as:
5. Proposed Scheme CRA3
- Setup ():This procedure outputs public parameters with the security parameter using the following steps.
- Generate a big prime q ();
- Select one secure cryptographic hash function ;
- Select a symmetric encryption algorithm, e.g., (Advanced Encryption Standard);
- Output the public parameters .
- Request ():The user (data inquirer) prepares the query Q via the following steps.
- Decide on the data to be requested. Note that should have the corresponding identity attributes (a sequence, ) and the unique reference number ( that is shared by . For illustrating the remaining parts of the proposed scheme, we assume the requested data is in one block ;
- Prepare the unique reference number then send the request to through .
- Challenge (): generates the challenge based upon the request Q from via the following steps.
- Prepare the sequence of the identity attributes (values): based upon the unique reference number ;
- Calculate the hash value of each element in the sequence to get the sequence ;
- Construct a polynomial , then pick n random points on the polynomial as a set: ;
- Construct two sequences and of all the and all the in P: and ;
- Calculate the hash value of the sequence : ;
- Send the challenge to through . Note that should keep the to execute the following Authorise phase.
- Response ():generates the response to the challenge from via the following steps.
- Prepare the sequence of the identity attributes (shared by ) based upon ;
- Construct a new polynomial ;
- Take to calculate the sequence and then hash the sequence : ;
- Send the response to the consensus network .
- Authorise ():The consensus network validates the two hash values in and . If holds (consensus check point), it means that the user can be authorised to access the requested data and the next phases are conducted; otherwise, the agent layer should deny the access request from .
- Encrypt ():encrypts the requested data via the following steps.
- Acquire the requested data M based upon from and then calculate the hash value of the data M: ;
- Generate a secure key for the symmetric encryption;
- Use to encrypt M with key k to get the ciphertext . For decrypting to recover the plain data M, is defined as the decryption process: ;
- Generate a random integer and calculate a point ;
- Return to through a secret channel.
- Decrypt ():can decrypt the ciphertext C after passing the Authorise phase via the following steps.
- Use the sequence organised in the former Response phase to construct a polynomial : . Note that is an unknown coefficient;
- Follow the Lagrange interpolation polynomial in the Section 3.2 to reconstruct the polynomial fully, and then recover the key for decryption with the point : ;
- Decrypt C to retrieve the plaintext ;
- If holds, this algorithm outputs M; otherwise, it outputs ⊥.
6. Theoretical Analysis of CRA3
6.1. Correctness
6.2. Confidentiality (IND-CCA Security)
- Initialisefirst generates the public parameter and then sends to . After that, generates n data providers (key-value pairs) and the target data provider is denoted by . Note that all the generated are given to the adversary . Finally, initialises one empty lists and updates it continuously in the random oracle query Identity attributes query. If the same input is asked multiple times, the same answer will be returned.
- Queriescan respond to the queries requested by polynomial times in the following ways.
- Identity attributes query : generates the sequence of the identity attributes randomly and saves in if it is the first time that i is queried. Then respond with the sequence . Otherwise, should retrieve the sequence from directly then return it to .
- Encrypt query: uses the algorithm Encrypt to output the ciphertext and the point P (P should be on the polynomial constructed with in the algorithm Encrypt).
- Decrypt query: tries to decrypt C via running then responds with the plain message. Note that there is a conditional branch caused by i to be discussed.
If , for each item in , executes the operations.- −
- Reconstruct the Lagrange interpolating polynomial with and P to determine the secret key for AES decryption.
- −
- Recover by computing .
- −
- If holds, returns M to . If there is no item in the that satisfies the condition, returns ⊥ to .If , runs the algorithm directly and then sends the output to as the answer.
- Challengesubmits two messages with the same length to , then picks one random bit from the set . Finally, computes the ciphertext of via the following steps:
- Choose a secret key for AES encryption and decryption;
- Determine ;
- Pick a random point on ;
- Compute .
Finally, sends the ciphertext and the point to the adversary . - Constraints
- and are not allowed to appear in the above Encrypt query;
- The target data provider’s index t and the challenge ciphertext are not allowed to appear in the above Decrypt query.
- Guessoutputs one bit from the set . At the same time, picks a random element from as the answer to the above given instance of the Lagrange interpolating polynomial.
- Probability analysisAn event is defined as that the adversary requests a query for the target sequence in the Identity attributes query during the described game above. If the event has happened, occurs in at least one item of at the end of this game.
6.3. Data Integrity
6.4. Comparison of Security Features
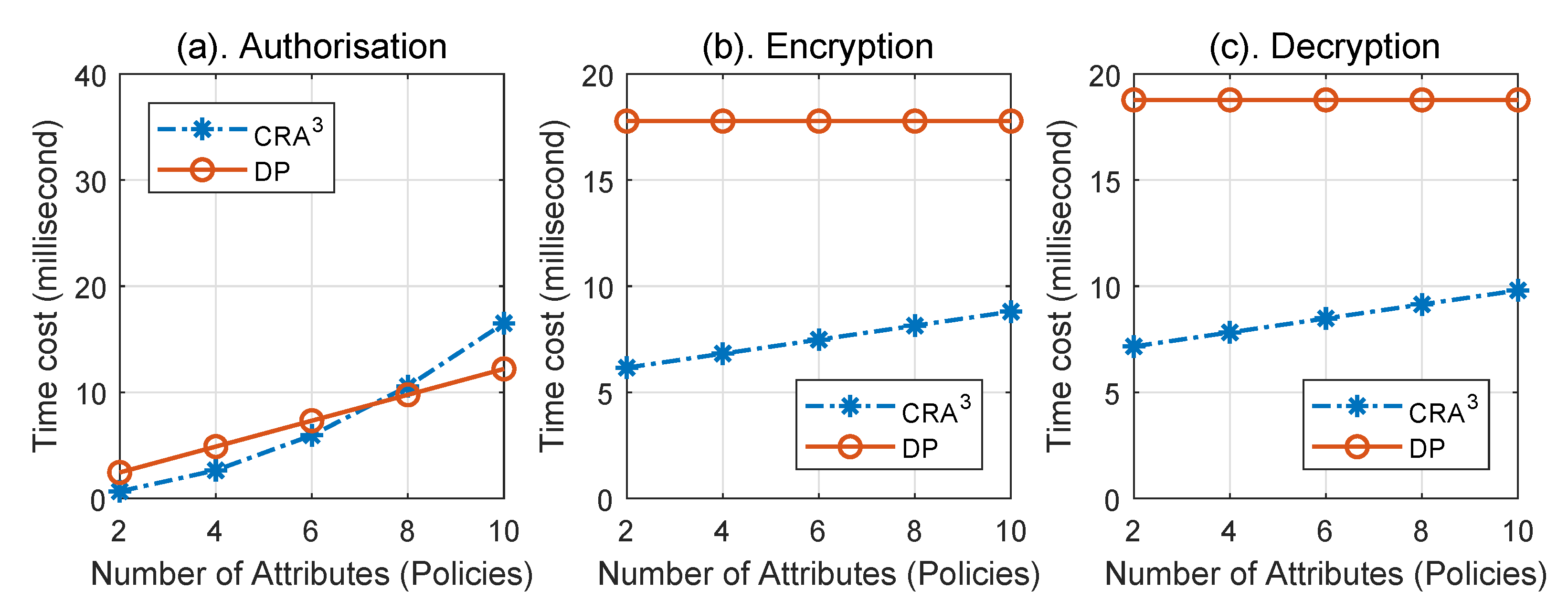
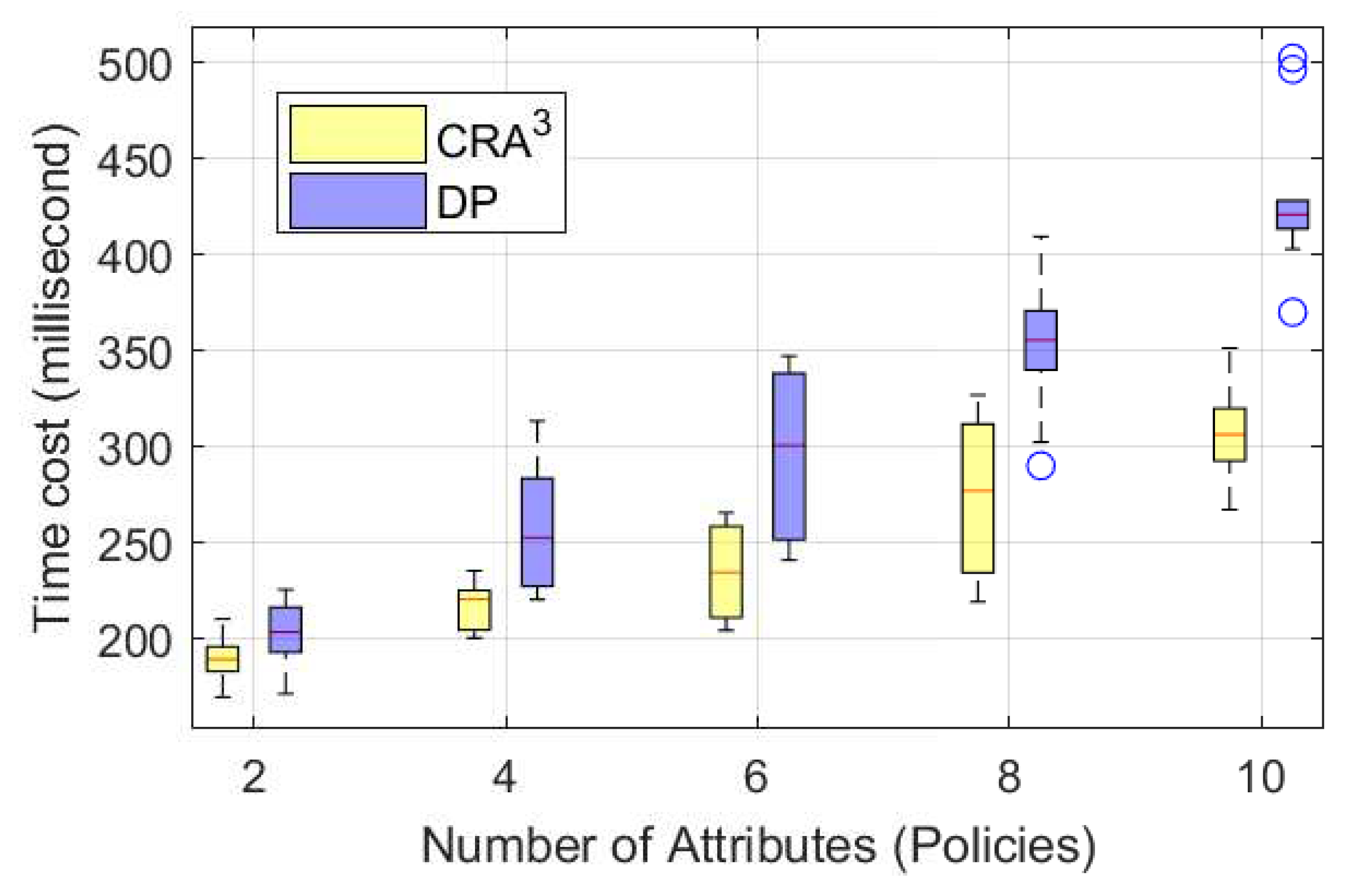
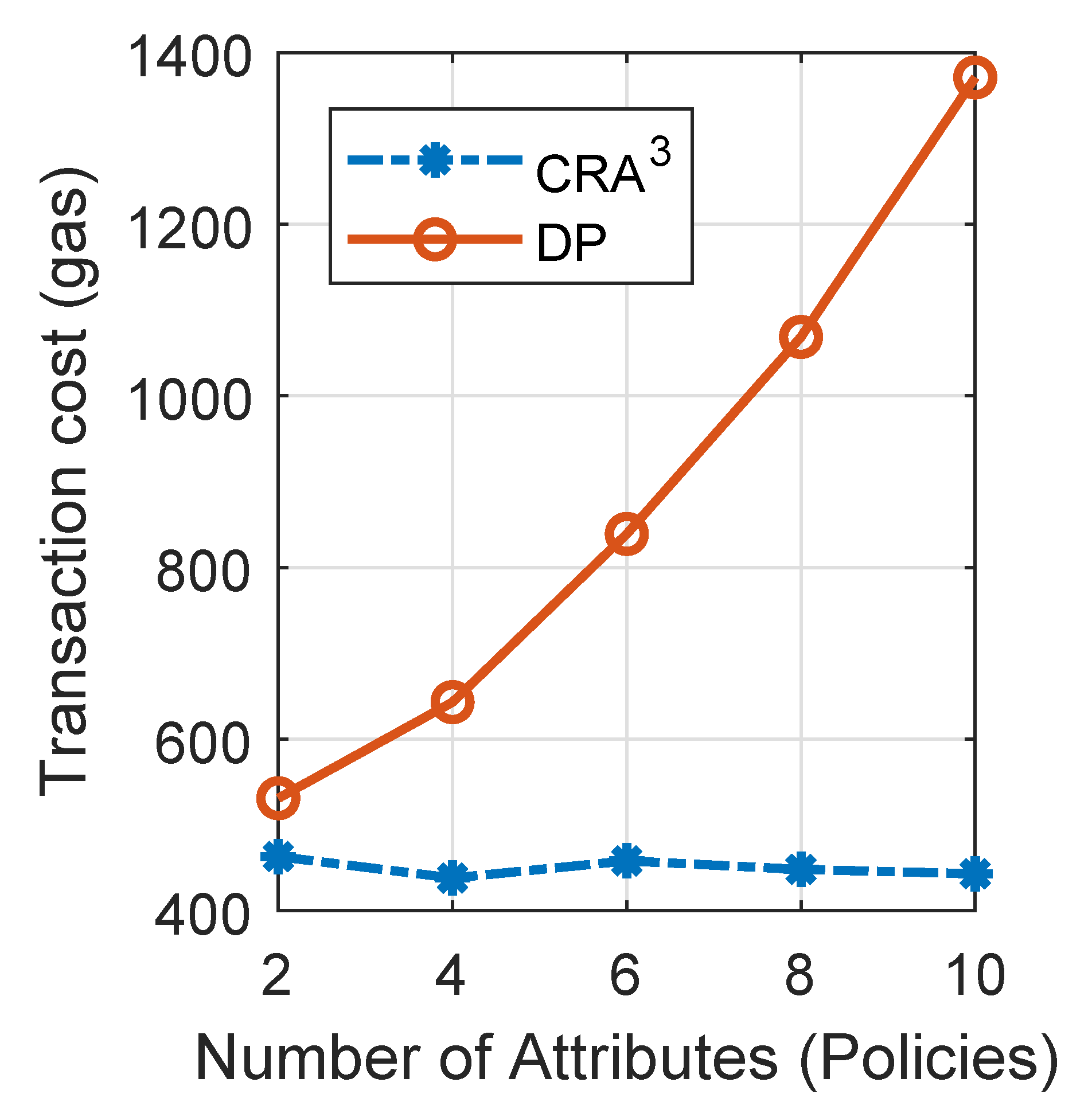
7. Performance Evaluation and Results
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nakamoto, S. Bitcoin: A Peer-to-peer Electronic Cash System. Available online: https://nakamotoinstitute.org/bitcoin/ (accessed on 31 October 2008).
- Sukhwani, H.; Martínez, J.M.; Chang, X.; Trivedi, K.S.; Rindos, A. Performance modeling of pbft consensus process for permissioned blockchain network (hyperledger fabric). In Proceedings of the 2017 IEEE 36th Symposium on Reliable Distributed Systems (SRDS), Hong Kong, China, 26–29 September 2017; pp. 253–255. [Google Scholar]
- Noyes, C. Bitav: Fast anti-malware by distributed blockchain consensus and feedforward scanning. arXiv 2016, arXiv:1601.01405. [Google Scholar]
- Kopp, H.; Mödinger, D.; Hauck, F.; Kargl, F.; Bösch, C. Design of a privacy-preserving decentralized file storage with financial incentives. In Proceedings of the 2017 IEEE European Symposium on Security and Privacy Workshops (EuroS&PW), Paris, France, 26–28 April 2017; pp. 14–22. [Google Scholar]
- Zhang, Y.; Wen, J. An IoT electric business model based on the protocol of bitcoin. In Proceedings of the 2015 18th International Conference on Intelligence in Next Generation Networks (ICIN), Paris, France, 14 June 2015; pp. 184–191. [Google Scholar]
- Zhang, X.; Poslad, S. Blockchain support for flexible queries with granular access control to electronic medical records (EMR). In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, KC, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Sharples, M.; Domingue, J. The blockchain and kudos: A distributed system for educational record, reputation and reward. In European Conference on Technology Enhanced Learning; Springer: Berlin/Heidelberg, Germany, 2016; pp. 490–496. [Google Scholar]
- Liu, C.; Chai, K.K.; Zhang, X.; Chen, Y. Peer-to-peer electricity trading system: Smart contracts based proof-of-benefit consensus protocol. Wirel. Netw. 2019, 25, 1–12. [Google Scholar] [CrossRef]
- Buterin, V. On Public and Private Blockchains. Available online: https://blog.ethereum.org/2015/08/07/on-public-and-private-blockchains/ (accessed on 7 August 2015).
- Androulaki, E.; Barger, A.; Bortnikov, V.; Cachin, C.; Christidis, K.; De Caro, A.; Enyeart, D.; Ferris, C.; Laventman, G.; Manevich, Y.; et al. Hyperledger fabric: A distributed operating system for permissioned blockchains. In Proceedings of the Thirteenth EuroSys Conference, Porto, Portugal, 23–26 April 2018; p. 30. [Google Scholar]
- Smetanin, S.; Ometov, A.; Komarov, M.; Masek, P.; Koucheryavy, Y. Blockchain Evaluation Approaches: State-of-the-Art and Future Perspective. Sensors 2020, 20, 3358. [Google Scholar] [CrossRef] [PubMed]
- Zyskind, G.; Nathan, O. Decentralizing privacy: Using blockchain to protect personal data. In Proceedings of the Security and Privacy Workshops (SPW), San Jose, CA, USA, 21–22 May 2015; pp. 180–184. [Google Scholar]
- Quirós-Tortós, J.; Ochoa, L.F.; Lees, B. A statistical analysis of EV charging behavior in the UK. In Proceedings of the 2015 IEEE PES Innovative Smart Grid Technologies Latin America (ISGT LATAM), Montevideo, Uruguay, 5 October 2015; pp. 445–449. [Google Scholar]
- Hafez, O.; Bhattacharya, K. Queuing analysis based PEV load modeling considering battery charging behavior and their impact on distribution system operation. IEEE Trans. Smart Grid 2016, 9, 261–273. [Google Scholar] [CrossRef]
- Gai, K.; Wu, Y.; Zhu, L.; Xu, L.; Zhang, Y. Permissioned blockchain and edge computing empowered privacy-preserving smart grid networks. IEEE Internet Things J. 2019, 6, 7992–8004. [Google Scholar] [CrossRef]
- Yue, X.; Wang, H.; Jin, D.; Li, M.; Jiang, W. Healthcare data gateways: Found healthcare intelligence on blockchain with novel privacy risk control. J. Med. Syst. 2016, 40, 218. [Google Scholar] [CrossRef] [PubMed]
- Wenbo, M. Modern Cryptography: Theory and Practice; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Dorri, A.; Steger, M.; Kanhere, S.S.; Jurdak, R. Blockchain: A distributed solution to automotive security and privacy. IEEE Commun. Mag. 2017, 55, 119–125. [Google Scholar] [CrossRef]
- Min, X.; Li, Q.; Liu, L.; Cui, L. A permissioned blockchain framework for supporting instant transaction and dynamic block size. In Proceedings of the 2016 IEEE Trustcom/BigDataSE/ISPA, Tianjin, China, 23 August 2016; pp. 90–96. [Google Scholar]
- Pop, C.; Cioara, T.; Antal, M.; Anghel, I.; Salomie, I.; Bertoncini, M. Blockchain based decentralized management of demand response programs in smart energy grids. Sensors 2018, 18, 162. [Google Scholar] [CrossRef] [PubMed]
- Ateniese, G.; Camenisch, J.; Joye, M.; Tsudik, G. A practical and provably secure coalition-resistant group signature scheme. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2000; pp. 255–270. [Google Scholar]
- Boneh, D.; Shacham, H. Group signatures with verifier-local revocation. In Proceedings of the 11th ACM Conference on Computer and Communications Security, Washington, DC, USA, 25–29 October 2004; pp. 168–177. [Google Scholar]
- Ling, S.; Nguyen, K.; Roux-Langlois, A.; Wang, H. A lattice-based group signature scheme with verifier-local revocation. Theor. Comput. Sci. 2018, 730, 1–20. [Google Scholar] [CrossRef]
- Perera, M.N.S.; Nakamura, T.; Hashimoto, M.; Yokoyama, H. Traceable and Fully Anonymous Attribute Based Group Signature Scheme with Verifier Local Revocation from Lattices. In International Conference on Network and System Security; Springer: Berlin/Heidelberg, Germany, 2019; pp. 675–684. [Google Scholar]
- Dawson, E.; Donovan, D. The breadth of Shamir’s secret-sharing scheme. Comput. Secur. 1994, 13, 69–78. [Google Scholar] [CrossRef]
- Daemen, J.; Rijmen, V. Reijndael: The Advanced Encryption Standard. Dobb J. Softw. Tools Prof. Program. 2001, 26, 137–139. [Google Scholar]
- Monk, S. Programming the Raspberry Pi: Getting Started with Python; Mcgraw-Hill: New York, NY, USA, 2013. [Google Scholar]
- Barker, E.; Barker, W.; Burr, W.; Polk, W.; Smid, M. Recommendation for key management part 1: General (revision 3). Nist Spec. Publ. 2012, 800, 1–147. [Google Scholar]
- Wood, G. Ethereum: A secure decentralised generalised transaction ledger. Ethereum Proj. Yellow Pap. 2014, EIP-151, 1–32. [Google Scholar]
- Ekparinya, P.; Gramoli, V.; Jourjon, G. The attack of the clones against proof-of-authority. arXiv 2019, arXiv:1902.10244. [Google Scholar]

| Scheme | Blockchain Type | Consensus Network Type | Security Features | ||
|---|---|---|---|---|---|
| Authorisation | Confidentiality | Integrity | |||
| [12] | Public/Permissioned | Trusted | √ | × 1 | × 1 |
| [16] | Public | Trusted | √ | × | × |
| [19] | Permissioned | Trusted | × | × | × |
| [15] | Permissioned | Trusted | √ | × | √ |
| CRA3 * | Permissioned | Trusted/Untrusted | √ | √ | √ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Liu, C.; Chai, K.K.; Poslad, S. A Challenge-Response Assisted Authorisation Scheme for Data Access in Permissioned Blockchains. Sensors 2020, 20, 4681. https://doi.org/10.3390/s20174681
Zhang X, Liu C, Chai KK, Poslad S. A Challenge-Response Assisted Authorisation Scheme for Data Access in Permissioned Blockchains. Sensors. 2020; 20(17):4681. https://doi.org/10.3390/s20174681
Chicago/Turabian StyleZhang, Xiaoshuai, Chao Liu, Kok Keong Chai, and Stefan Poslad. 2020. "A Challenge-Response Assisted Authorisation Scheme for Data Access in Permissioned Blockchains" Sensors 20, no. 17: 4681. https://doi.org/10.3390/s20174681
APA StyleZhang, X., Liu, C., Chai, K. K., & Poslad, S. (2020). A Challenge-Response Assisted Authorisation Scheme for Data Access in Permissioned Blockchains. Sensors, 20(17), 4681. https://doi.org/10.3390/s20174681






