The CMOS Highly Linear Current Amplifier with Current Controlled Gain for Sensor Measurement Applications
Abstract
1. Introduction
- (a)
- low total harmonic distortion of the processed current signal as the most considered parameter (<1%)
- (b)
- wide and linear input range (about ±200 µA)
- (c)
- very low input resistance (<10 Ω)
- (d)
- high output impedance (>1 MΩ)
- (e)
- adjustability of current gain (theoretically 0–2)
- (f)
- high linearity of the gain control for current gain B < 0.8
- (g)
- acceptable power consumption (comparing to the process signal current) below 5 mW
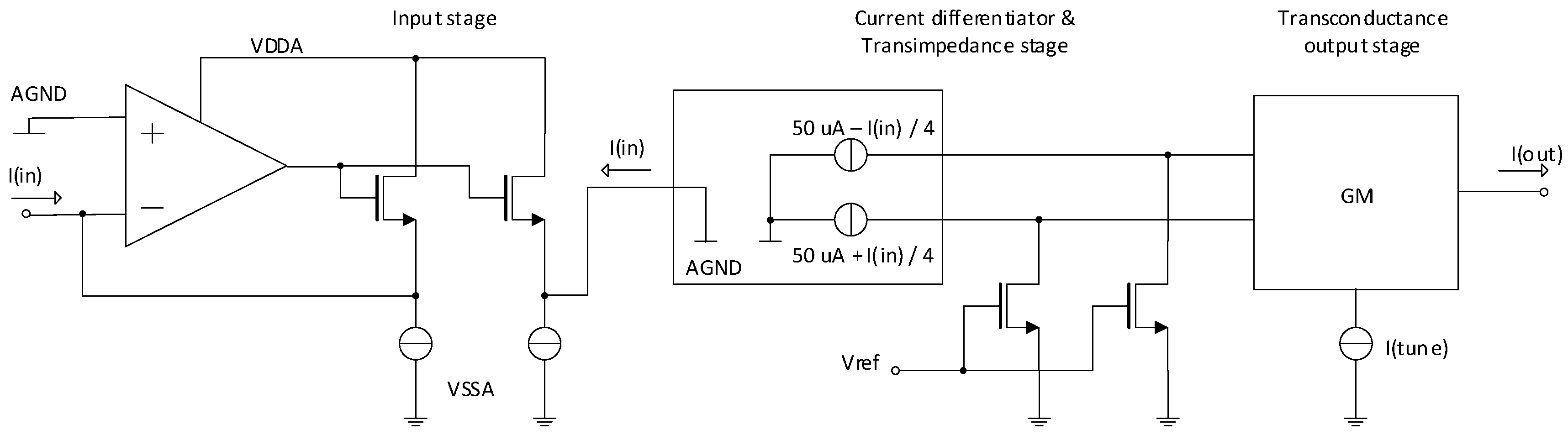
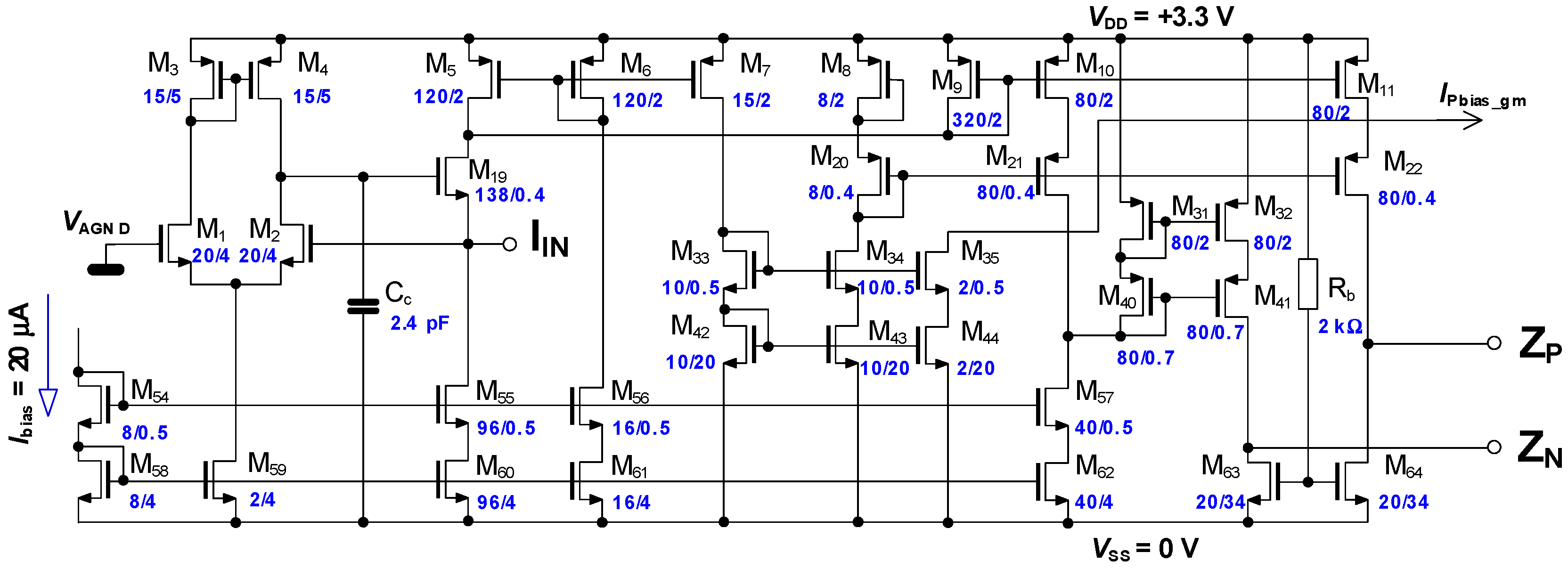
2. Circuit Principle and Design
2.1. Input Stage and Transimpedance Stage in Detail
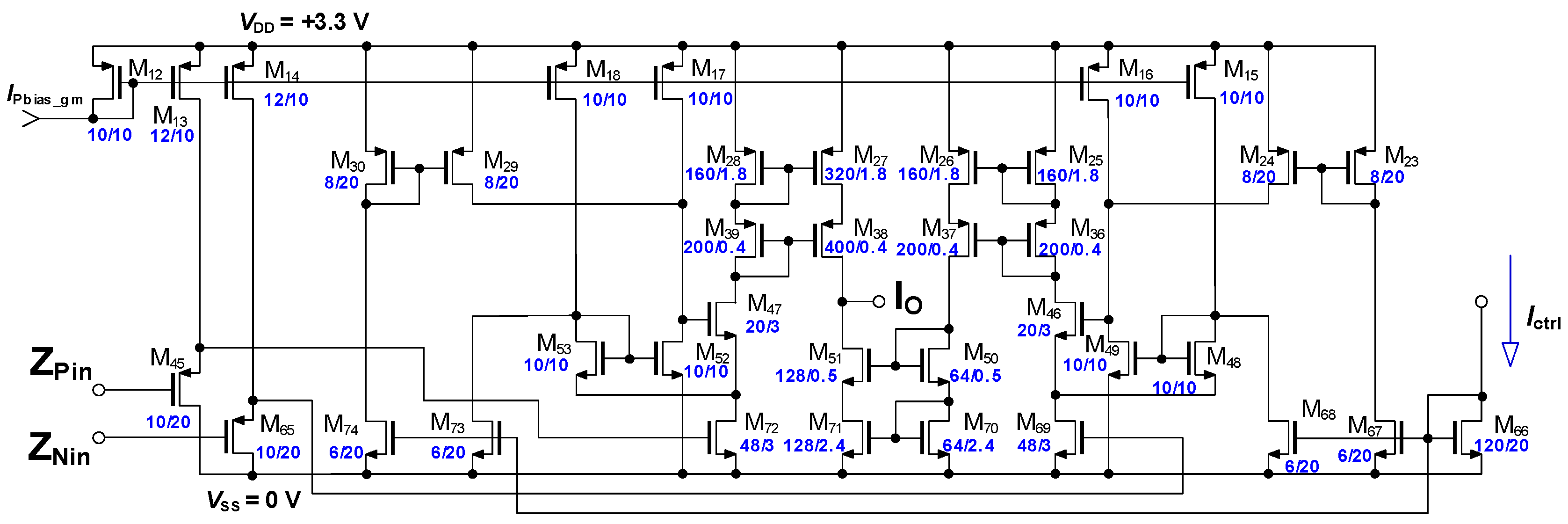
2.2. Tunable Transconductance Stage
 | ||
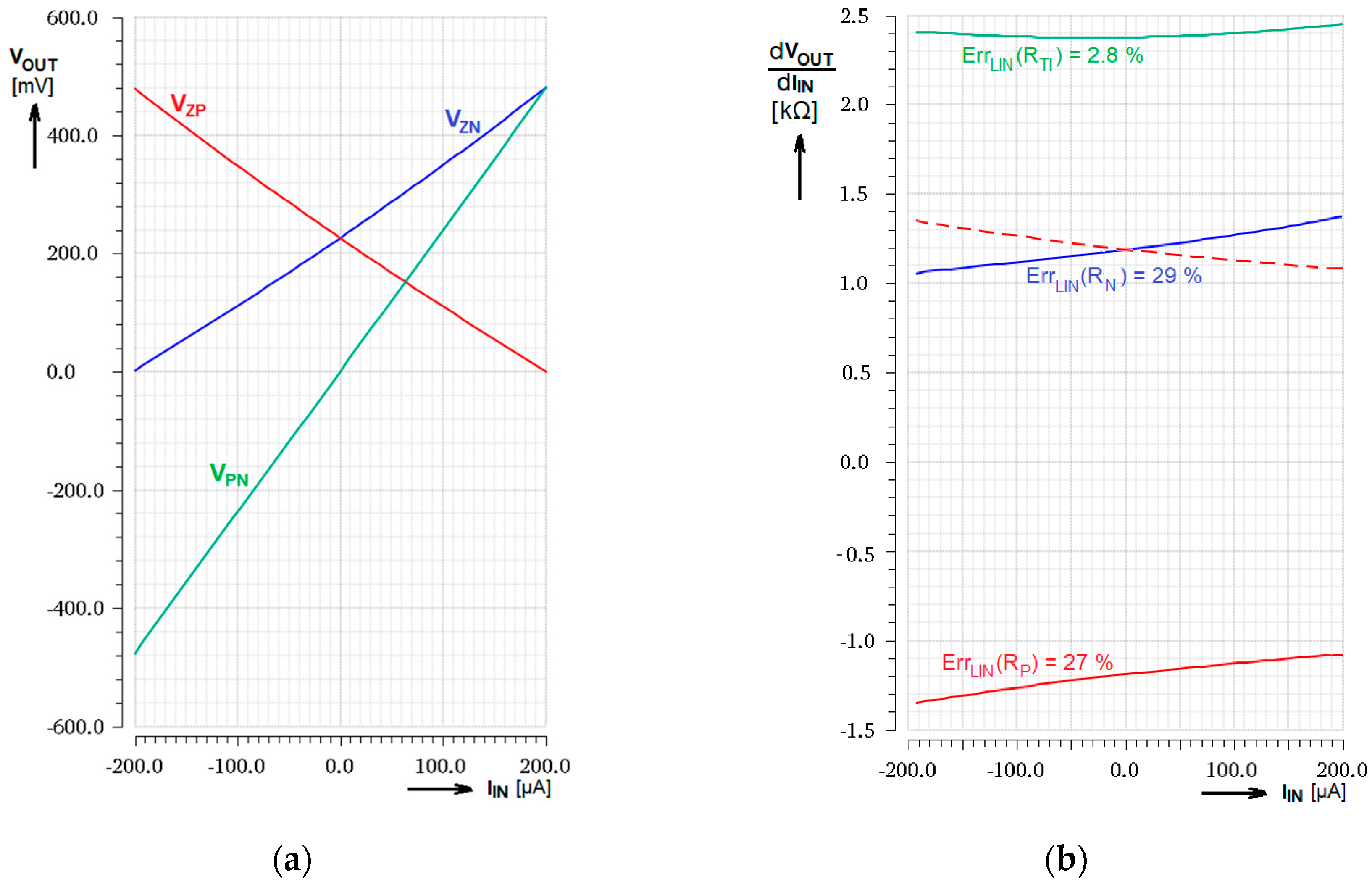
| Linearity error |
3. Results
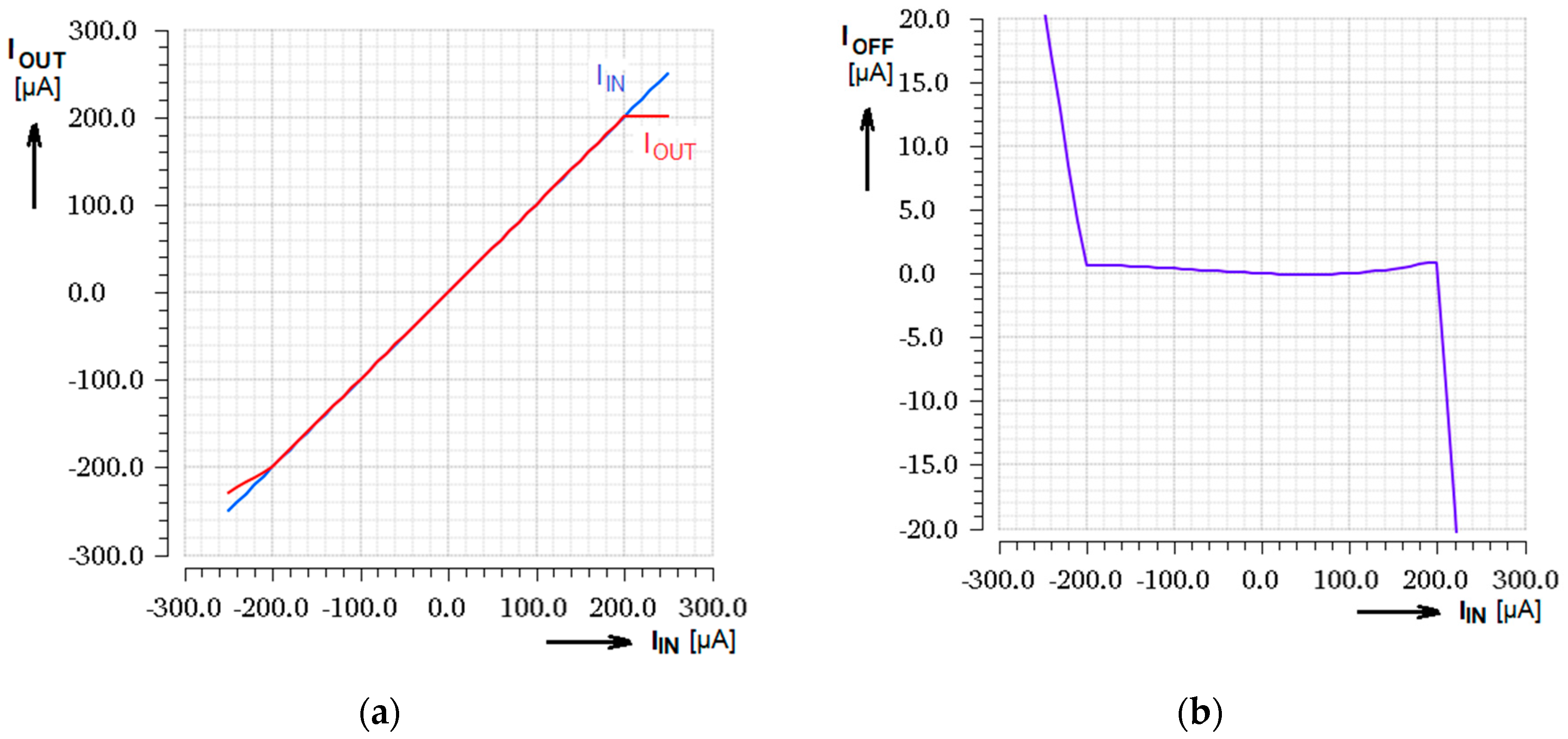
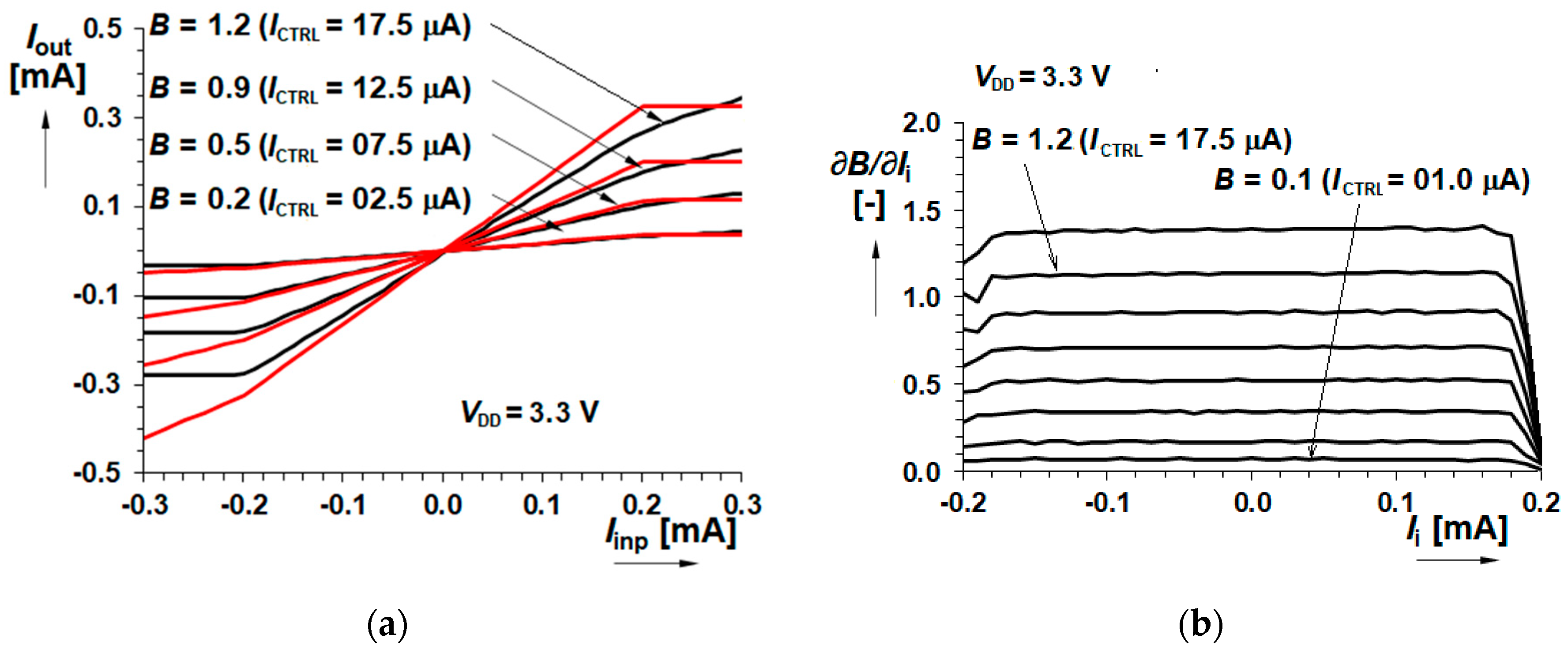
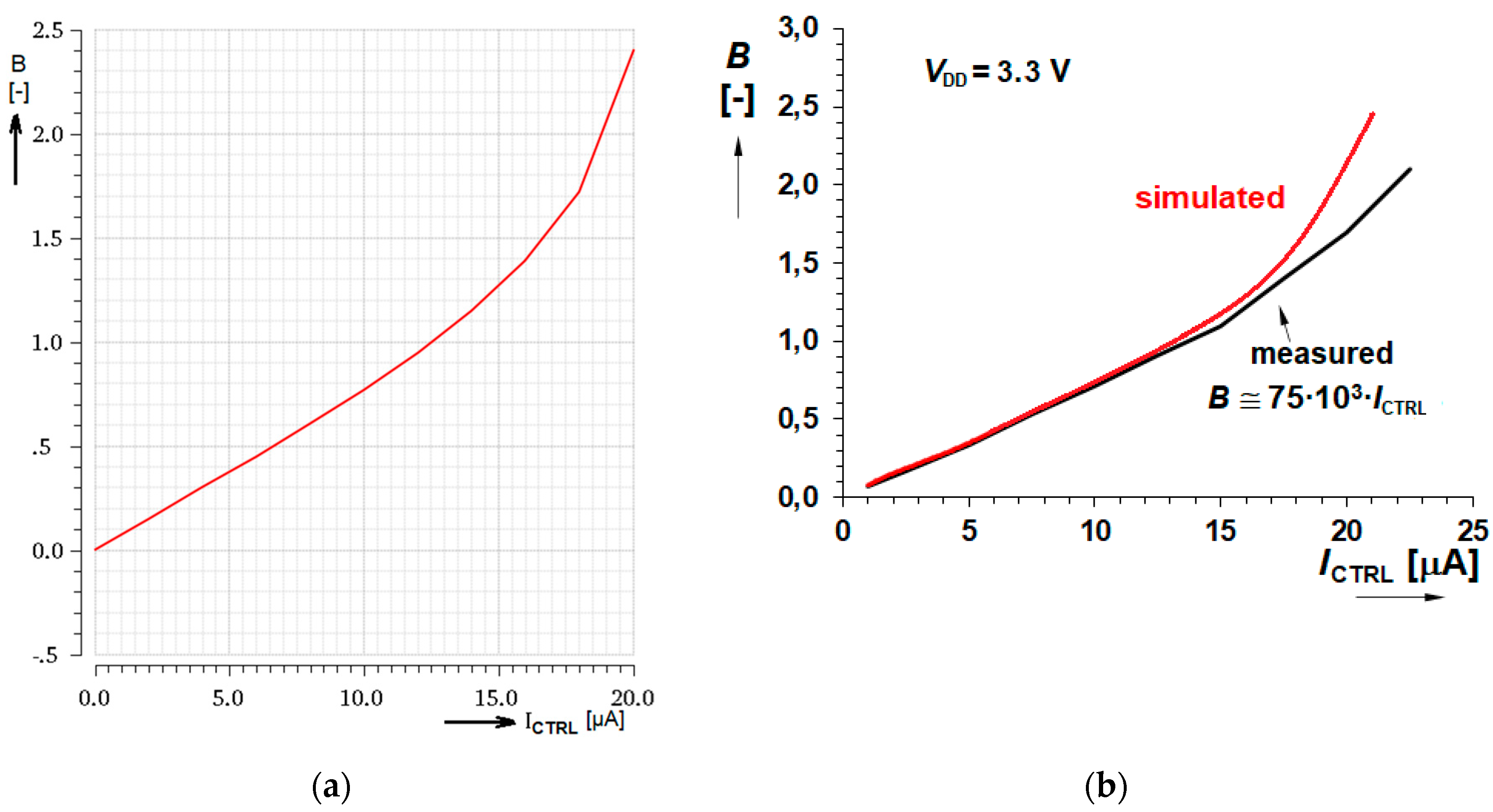
3.1. DC Transfer Characteristics
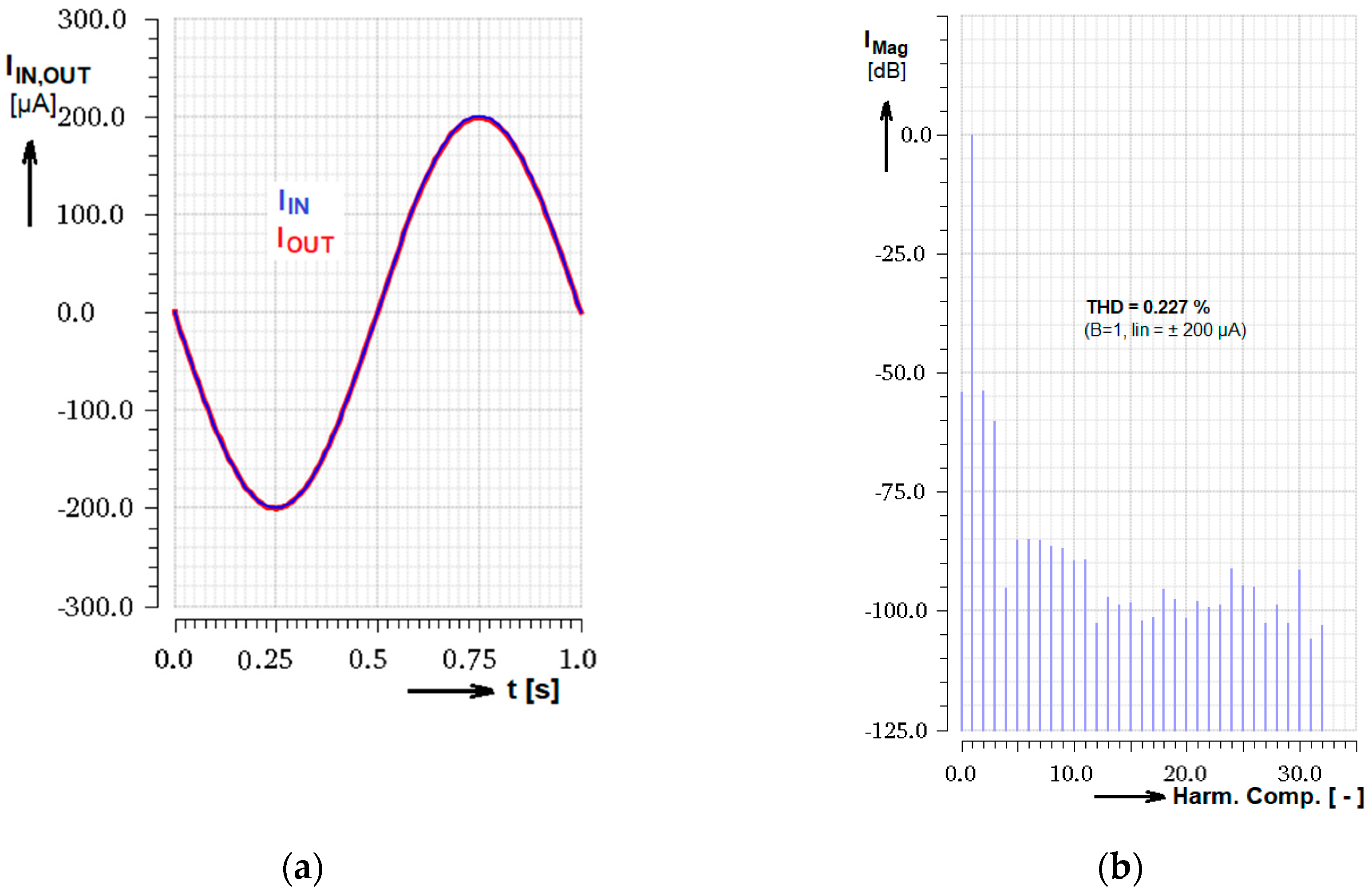
3.2. Input Signal Linearity and THD
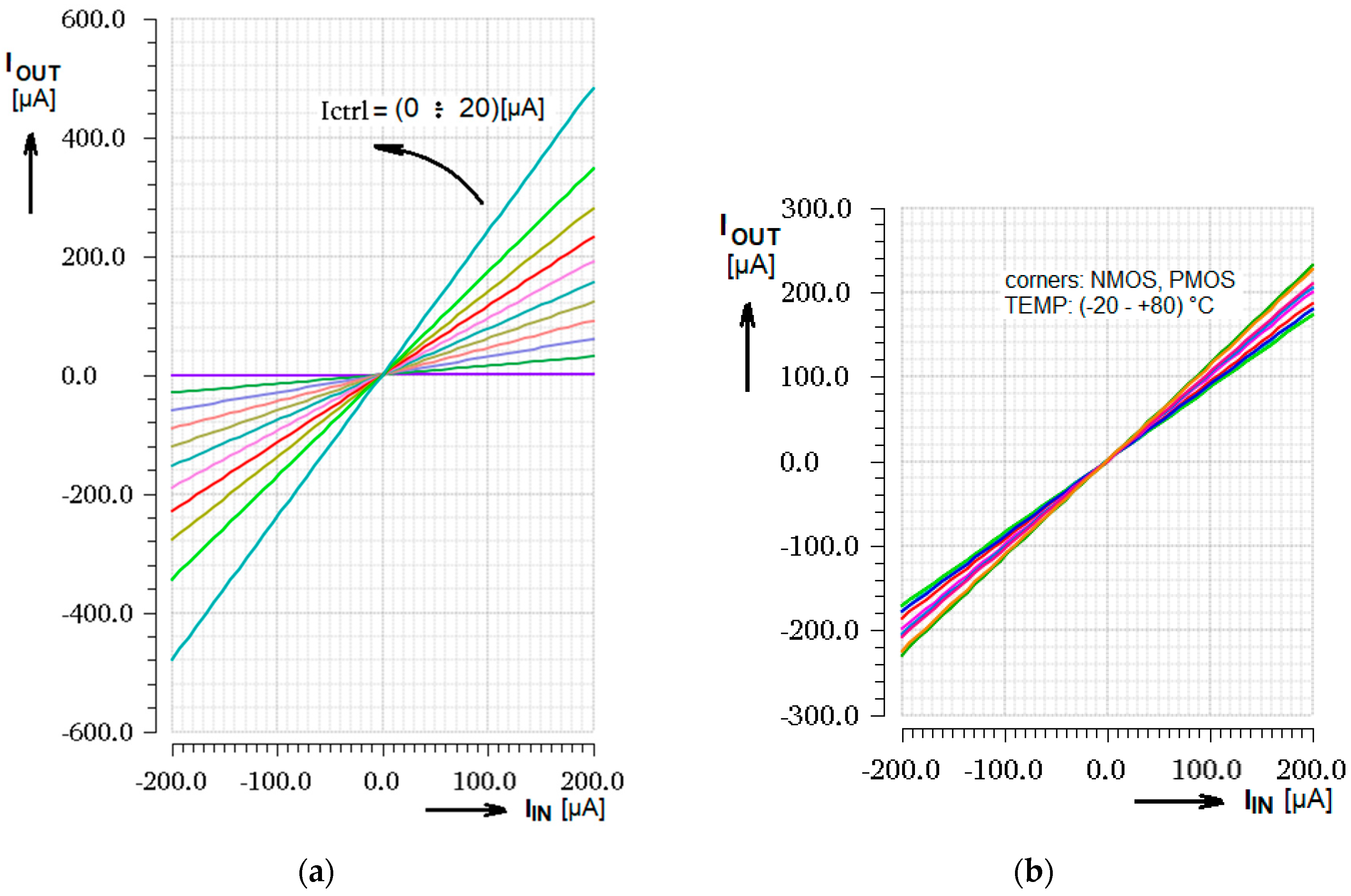
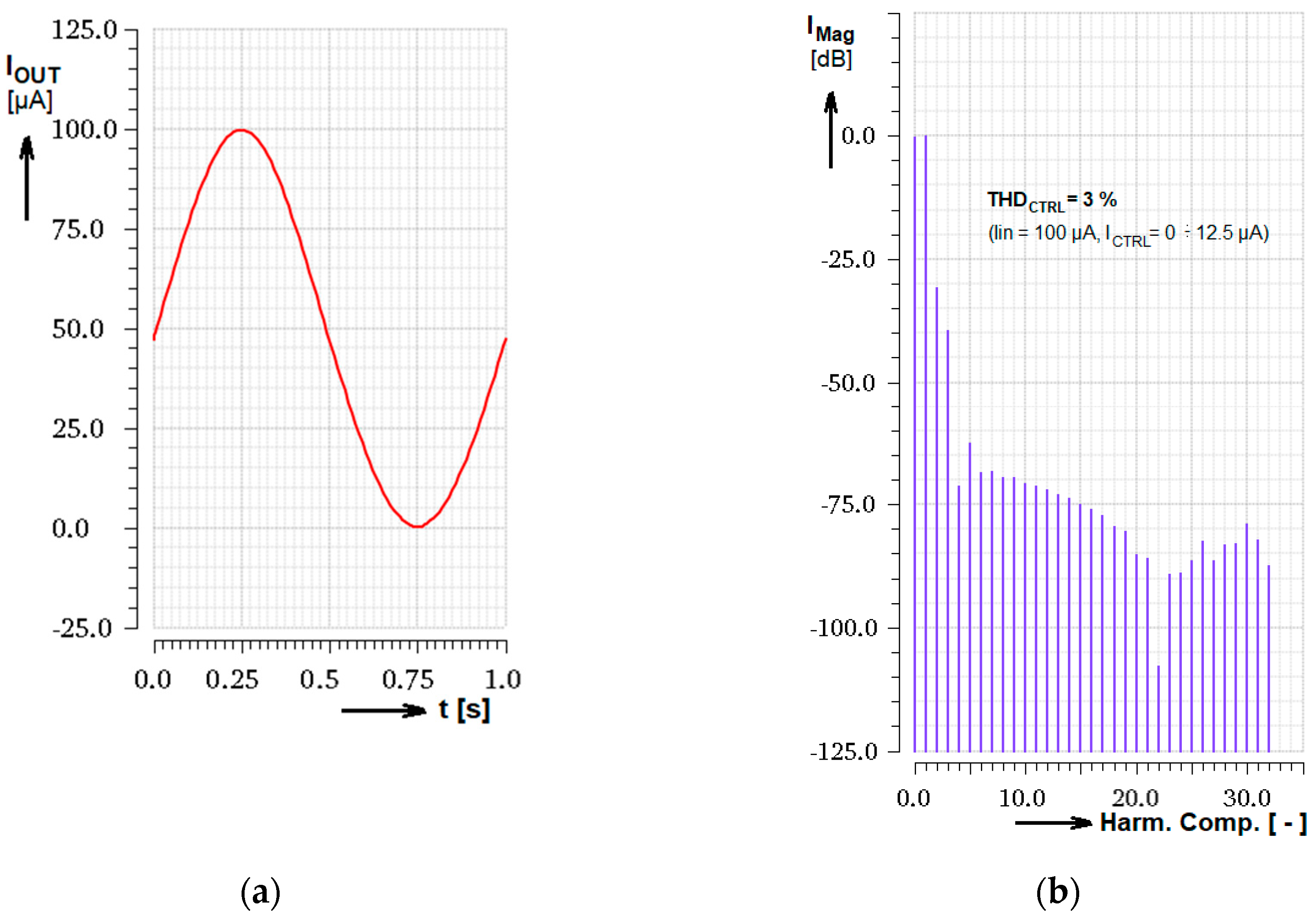
3.3. Linearity of the Control and Control Input THD
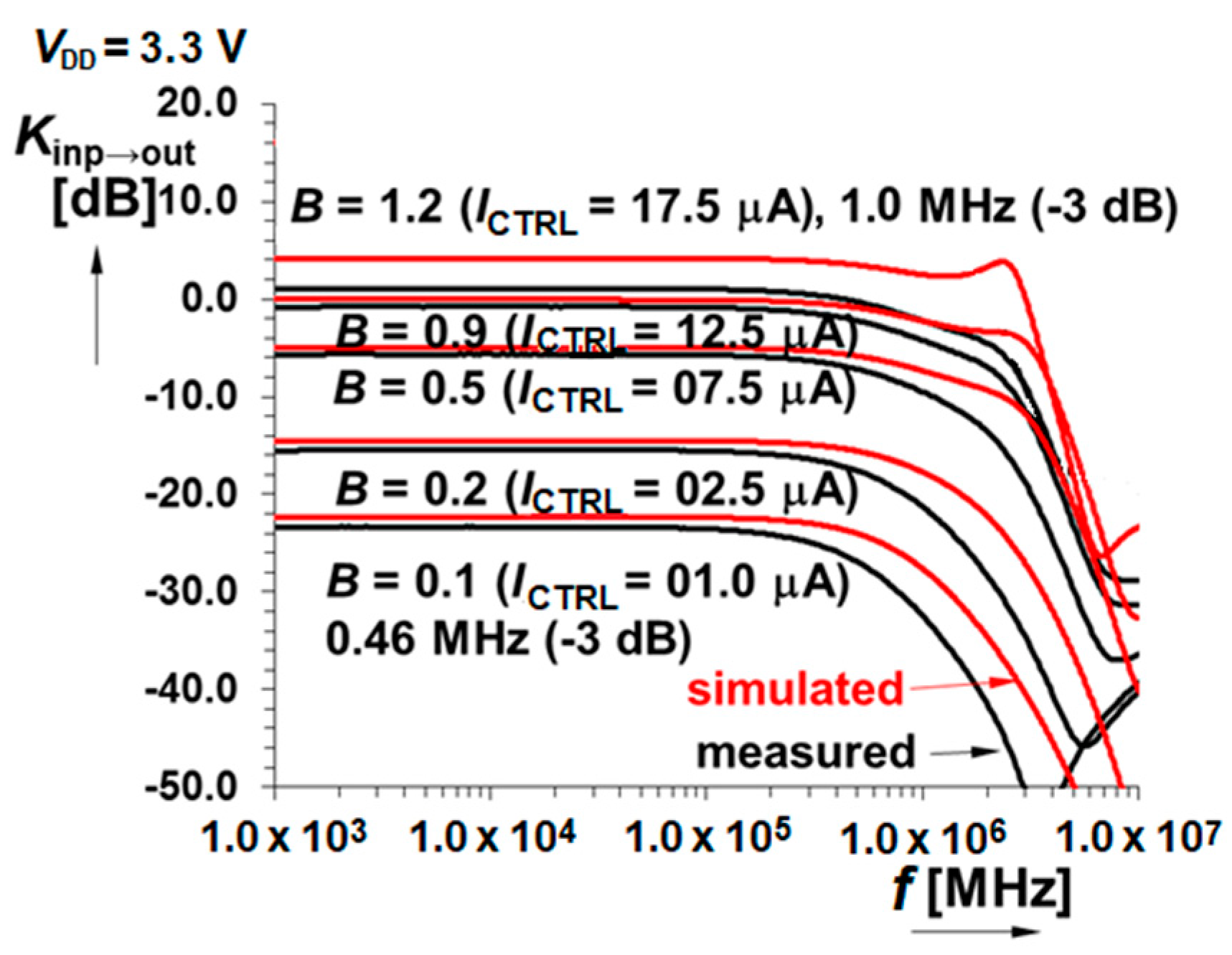
3.4. Frequency Response and Bandwidth
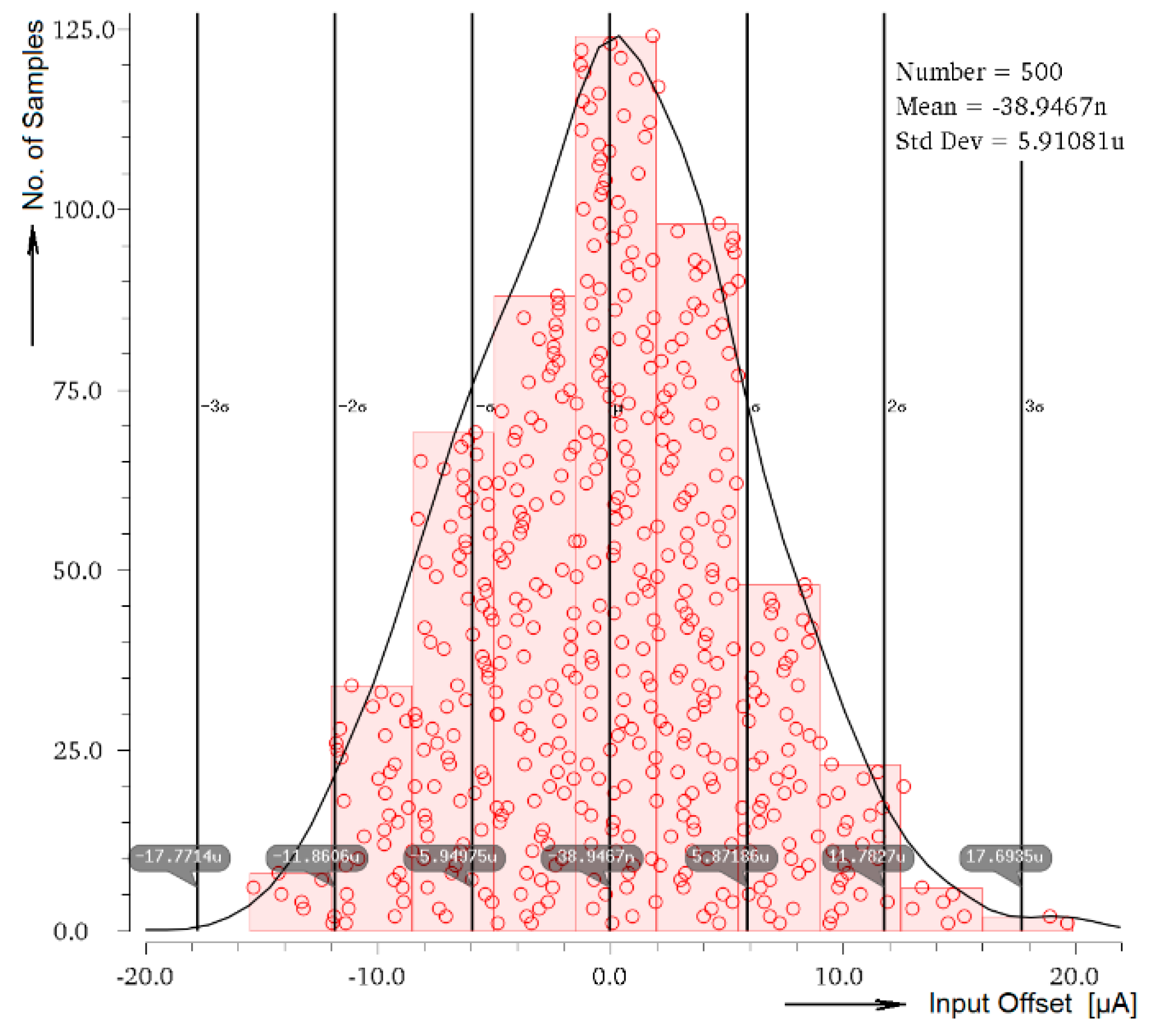
3.5. Input Current Offset
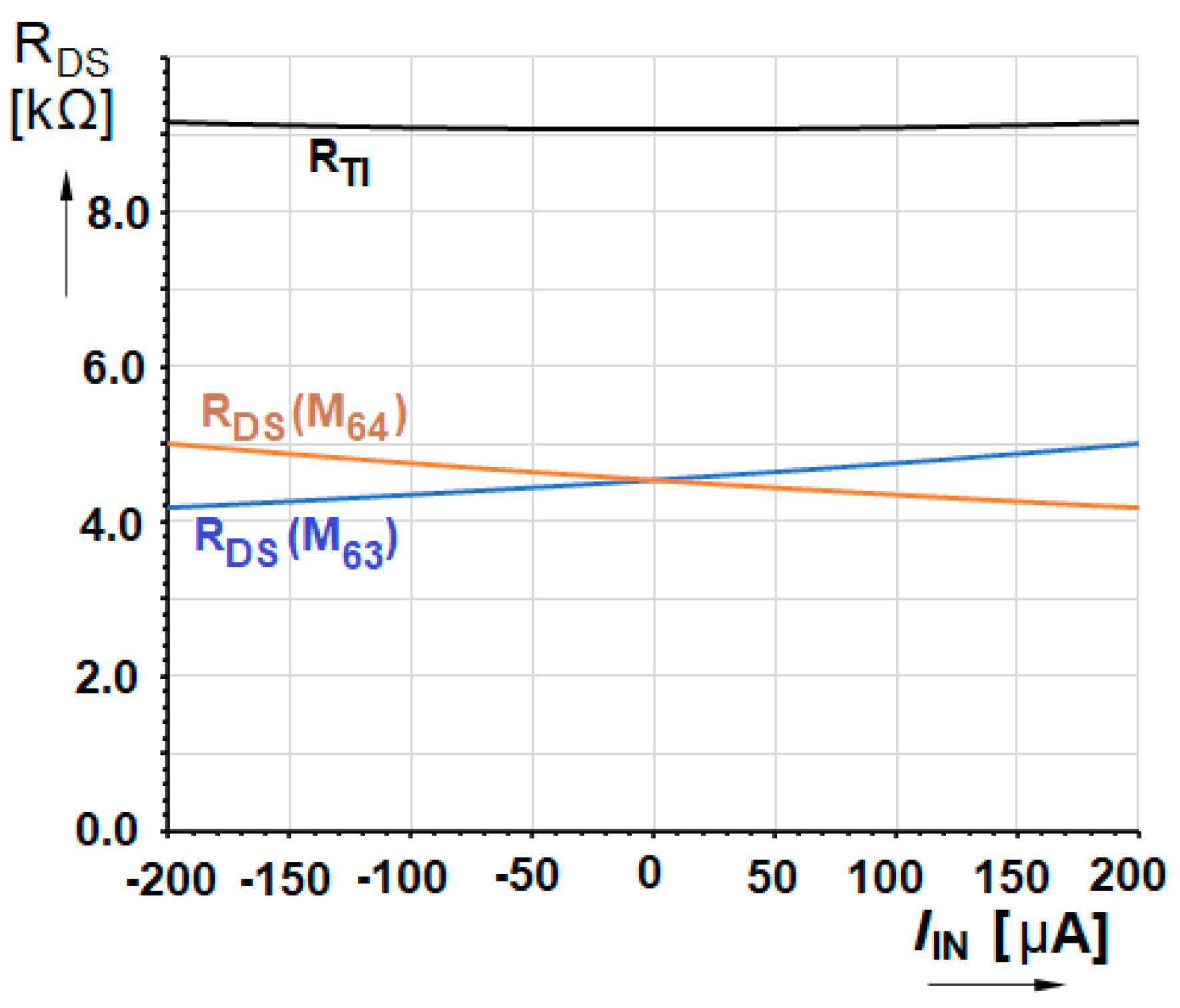
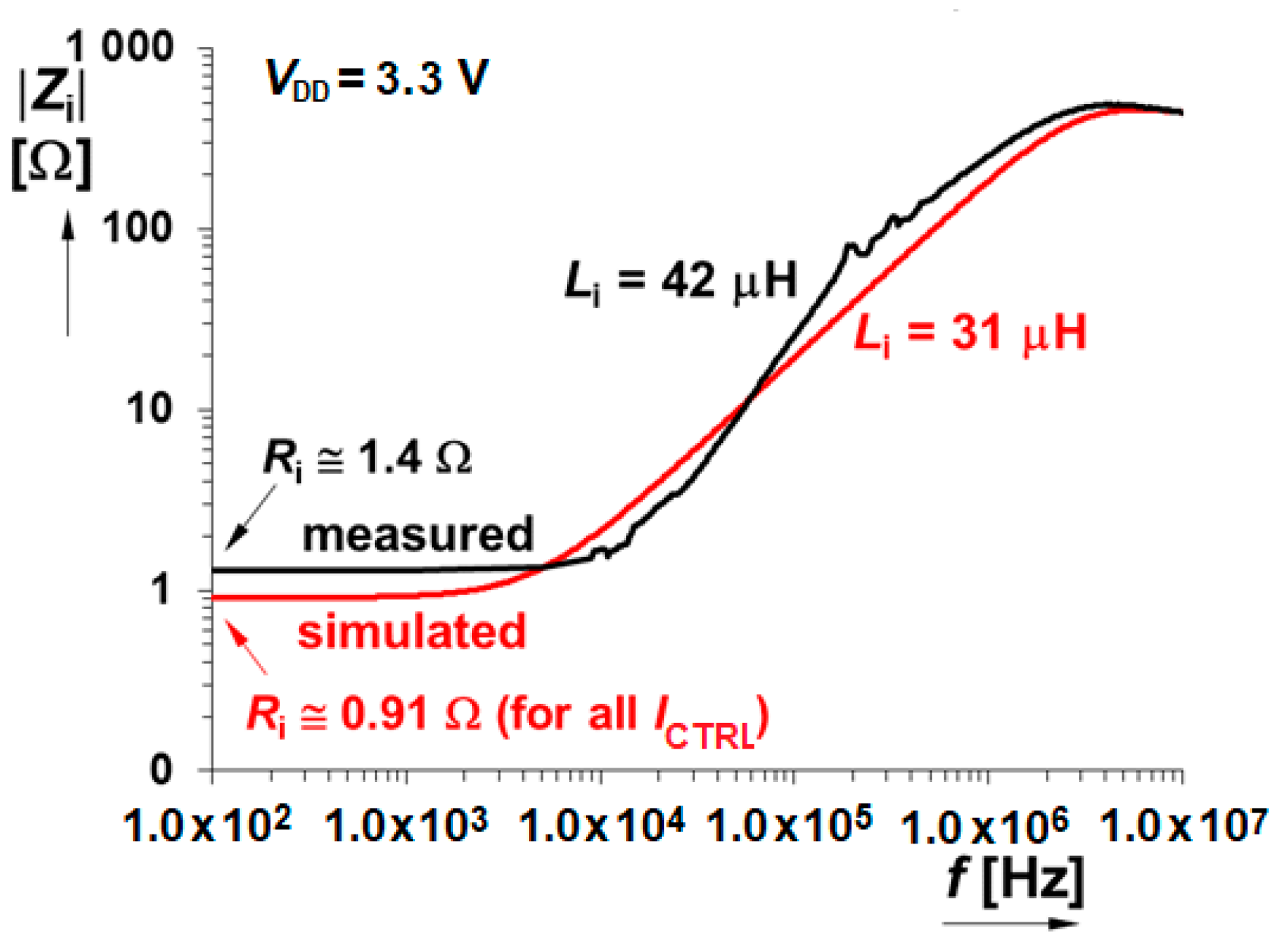
3.6. Input and Output Impedance
3.7. Result Overview
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Biolek, D.; Senani, R.; Biolkova, V.; Kolka, Z. Active elements for analog signal processing: Classification, Review, and New Proposals. Radioengineering 2008, 17, 15–32. [Google Scholar]
- Senani, R.; Bhaskar, D.R.; Singh, A.K. Current Conveyors: Variants, Applications and Hardware Implementations; Springer: Berlin, Germany, 2015. [Google Scholar]
- Surakampontorn, W.; Thitimajshima, W. Integrable electronically tunable current conveyors. IEE Proc. G 1988, 135, 71–77. [Google Scholar] [CrossRef]
- Fabre, A.; Mimeche, N. Class A/AB Second-generation Current Conveyor with Controlled Current Gain. Electron. Lett. 1994, 30, 1267–1268. [Google Scholar] [CrossRef]
- El-Adawy, A.; Soliman, A.M.; Elwan, H.O. Low Voltage Digitally Controlled CMOS Current Conveyor. AEU Int. J. Electron. Commun. 2002, 56, 137–144. [Google Scholar] [CrossRef]
- Minaei, S.; Sayin, O.K.; Kuntman, H. A new CMOS electronically tunable current conveyor and its application to current-mode filters. IEEE Trans. Circuits Syst. I 2006, 53, 1448–1457. [Google Scholar] [CrossRef]
- Tangsrirat, W. Electronically Tunable Multi-Terminal Floating Nullor and its Applications. Radioengineering 2008, 17, 3–7. [Google Scholar]
- Marcellis, A.; Ferri, G.; Guerrini, N.C.; Scotti, G.; Stornelli, V.; Trifiletti, A. The VGC-CCII: A novel building block and its application to capacitance multiplication. Analog Integr. Circuits Signal Process. 2009, 58, 55–59. [Google Scholar] [CrossRef]
- Biolek, D.; Bajer, J.; Biolkova, V.; Kolka, Z.; Kubicek, M. Z Copy-Controlled Gain-Current Differencing Buffered Amplifier and its applications. Int. J. Circuit Theory Appl. 2010, 39, 257–274. [Google Scholar] [CrossRef]
- Kumngern, M.; Chanwutium, J.; Dejhan, K. Electronically tunable multiphase sinusoidal oscillator using translinear current conveyors. Analog Integr. Circuits Signal Process. 2010, 65, 327–334. [Google Scholar] [CrossRef]
- Herencsar, N.; Lahiri, A.; Vrba, K.; Koton, J. An electronically tunable current-mode quadrature oscillator using PCAs. Int. J. Electron. 2012, 99, 609–621. [Google Scholar] [CrossRef]
- Sotner, R.; Kartci, A.; Jerabek, J.; Herencsar, N.; Dostal, T.; Vrba, K. An Additional Approach to Model Current Followers and Amplifiers with Electronically Controllable Parameters from Commercially Available ICs. Meas. Sci. Rev. 2012, 12, 255–265. [Google Scholar] [CrossRef]
- Sotner, R.; Jerabek, J.; Herencsar, N.; Dostal, T.; Vrba, K. Electronically Adjustable Modification of CFA: Double Current Controlled CFA (DCC-CFA). In Proceedings of the 35th International Conference on Telecommunications and Signal Processing (TSP), Prague, Czech Republic, 3–4 July 2012; pp. 401–405. [Google Scholar]
- Alzaher, H.; Tasadduq, N.; Al-Ees, O.; Al-Ammari, F. A complementary metal–oxide semiconductor digitally programmable current conveyor. Int. J. Circuit Theory Appl. 2013, 41, 69–81. [Google Scholar] [CrossRef]
- Jerabek, J.; Koton, J.; Sotner, R.; Vrba, K. Adjustable band-pass filter with current active elements: Two fully-differential and single-ended solutions. Analog Integr. Circuits Signal Process. 2013, 74, 129–139. [Google Scholar] [CrossRef]
- Langhammer, L.; Jeřábek, J.; Polák, J.; Pánek, D. A Single-Ended and Fully-Differential Universal Current-Mode Frequency Filter with MO-CF and DACA Elements. Adv. Electr. Comput. Eng. 2016, 16, 43–48. [Google Scholar] [CrossRef]
- Dual Wide-Bandwidth Digitally Adjustable Current Amplifier (DACA). Available online: http://www.utko.feec.vutbr.cz/~jerabekj/daca.pdf (accessed on 15 June 2020).
- Šotner, R.; Herencsár, N.; Jeřábek, J.; Koton, J.; Dostál, T.; Vrba, K. Electronically controlled oscillator with linear frequency adjusting for four-phase or differential quadrature output signal generation. Int. J. Circuit Theory Appl. 2013, 42, 1264–1289. [Google Scholar] [CrossRef]
- Sotner, R.; Herencsar, R.; Jerabek, J.; Langhammer, L.; Polak, J. On practical construction of electronically controllable compact current amplifier based on commercially available elements and its application. AEU Int. J. Electron. Commun. 2017, 81, 56–66. [Google Scholar] [CrossRef]
- Sotner, R.; Langhammer, L.; Petržela, J.; Domanský, O.; Dostál, T. Applications of Novel Behavioral Implementation of a Controllable Generalized Current Conveyor. In Proceedings of the 28th International Conference Radioelektronika 2018, Prague, Czech Republic, 19–20 April 2018. [Google Scholar]
- Esparza-Alfaro, F.; Lopez-Martin, A.J.; Palumbo, G.; Permisi, S. CMOS Class-AB Tunable Voltage-Feedback Current Operational Amplifier. In Proceedings of the 21st IEEE International Conference on Electronics, Circuits and Systems (ICECS), Marseille, France, 7–10 December 2014; pp. 140–143. [Google Scholar]
- Esparza-Alfaro, F.; Permisi, S.; Palumbo, G.; Lopez-Martin, A.J. Low-Power Class-AB CMOS Voltage Feedback Current Operational Amplifier with Tunable Gain and Bandwidth. IEEE Trans. Circuits Syst. II 2014, 61, 574–578. [Google Scholar] [CrossRef]
- Safari, L.; Minaei, S. New ECCII-Based Electronically Controllable Current-Mode Instrumentation Amplifier with High Frequency Performance. In Proceedings of the 2017 European Conference on Circuit Theory and Design (ECCTD), Catania, Italy, 4–6 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Agrawal, D.; Maheshwari, S. Low Voltage Current Mode Instrumentation Amplifier. In Proceedings of the 2019 International Conference on Computing, Communication, and Intelligent Systems (ICCCIS), Greater Noida, India, 19–20 February 2019; pp. 20–23. [Google Scholar] [CrossRef]
- Altuner, M.S.; Momen, H.G.; Yazgi, M.; Toker, A.; Zeki, A. A Linear-in-dB-Control Variable Gain Amplifier Using a New Approach. In Proceedings of the 2017 10th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 30 November–2 December 2017; pp. 1207–1211. [Google Scholar]
- Di Cataldo, G.; Mita, R.; Pennisi, S. High-Speed CMOS Unity-Gain Current Amplifier. Microelectron. J. 2006, 37, 1086–1091. [Google Scholar] [CrossRef]
- Alzaher, H. Current follower based reconfigurable integrator/differentiator circuits with passive and active components׳ reuse. Microelectron. J. 2015, 46, 135–142. [Google Scholar] [CrossRef]
- Tanno, K.; Ishizuka, O.; Tang, Z. Four-quadrant CMOS current-mode multiplier independent of device parameters. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 2000, 47, 473–477. [Google Scholar] [CrossRef]
- Wasaki, H.; Horio, Y.; Nakamura, S. Current multiplier/divider circuit. Electron. Lett. 1991, 27, 504–506. [Google Scholar] [CrossRef]
- Naderi, A.; Mojarrad, H.; Ghasemzadeh, H.; Khoei, A.; Hadidi, K. Four-Quadrant CMOS Analog Multiplier Based on New Current Squarer Circuit with High-Speed. In Proceedings of the IEEE Eurocon 2009, St.-Petersburg, Russia, 21 July 2009; pp. 282–287. [Google Scholar]
- Narksarp, W.; Pawarangkoon, P.; Kiranon, W.; Wadkien, P. A Four-Quadrant Current-Mode Multiplier/Divider Building Block. In Proceedings of the 6th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Pattaya, Thailand, 18–21 July 2009; pp. 574–577. [Google Scholar]
- Festila, L.; Cirlugea, M.; Szolga, L.; Groza, R. Current-Mode Multiplier Models Based on FF−1 Functions. In Proceedings of the 15th International Conference on Mixed Design of Integrated Circuits and Systems, Poznan, Poland, 19–21 June 2008; pp. 401–406. [Google Scholar]
- Yuce, E. Design of a Simple Current-Mode Multiplier Topology Using a Single CCCII+. IEEE Trans. Instrum. Meas. 2008, 57, 631–637. [Google Scholar] [CrossRef]
- Jaikla, W.; Siripruchyanun, M. A Novel Current-Mode Multiplier/Divider Employing only Single Dual-Output Current Controlled CDTA. In Proceedings of the International Symposium on Communications and Information Technologies, Sydney, Australia, 17–19 October 2007; pp. 106–109. [Google Scholar]
- Prommee, P.; Somdunyakanok, M.; Kumngern, M.; Dejhan, K. Single Low-Supply Current-mode CMOS Analog Multiplier Circuit. In Proceedings of the International Symposium on Communications and Information Technologies, Bangkok, Thailand, 18 October–20 September 2006; pp. 1101–1104. [Google Scholar]
- Gravati, M.; Valle, M.; Ferri, G.; Guerrini, N.; Reyes, N. A Novel Current-Mode very Low Power Analog CMOS Four Quadrant Multiplier. In Proceedings of the 31st European Solid-State Circuits Conference, ESSCIRC 2005, Grenoble, France, 12–16 September 2005; pp. 495–498. [Google Scholar]
- Hashiesh, M.A.; Mahmoud, S.A.; Soliman, A.M. New Current-Mode and Voltage-Mode CMOS Analog Multipliers. In Proceedings of the International Conference on Electrical, Electronic and Computer Engineering, ICEEC ’04, Cairo, Egypt, 5–7 September 2004; pp. 435–438. [Google Scholar] [CrossRef]
- Vlassis, S.; Siskos, S. Design of voltage-mode and current-mode computational circuits using floating-gate MOS transistors. IEEE Trans. Circuits Syst. I 2004, 51, 329–341. [Google Scholar] [CrossRef]
- Kaewdang, K.; Fongsamut, C.; Surakampontorn, W. A Wide-Band Current-Mode OTA-Based Analog Multiplier-Divider. In Proceedings of the 2003 International Symposium on Circuits and Systems, ISCAS ’03, Bangkok, Thailand, 25–28 May 2003; pp. 349–352. [Google Scholar] [CrossRef]
- El-Atta, M.A.; El-Ela, M.A.; El Said, M.K. Four-Quadrant Current Multiplier and its Application as a Phase-Detector. In Proceedings of the Nineteenth National Radio Science Conference, Alexandria, Egypt, 19–21 March 2002; pp. 502–508. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, M.-L.; Liu, S.-I. CMOS current-mode exponential-control variable-gain amplifier. Electron. Lett. 2001, 37, 868–869. [Google Scholar] [CrossRef]
- Ravindran, A.; Ramarao, K.; Vidal, E.; Ismail, M. Compact low voltage four quadrant CMOS current multiplier. Electron. Lett. 2001, 37, 1428–1429. [Google Scholar] [CrossRef]
- Lopez-Martin, A.J.; Carlosena, A. Geometric-Mean Based Current-Mode CMOS Multiplier/Divider. In Proceedings of the 1999 IEEE International Symposium on Circuits and Systems (ISCAS), Orlando, FL, USA, 30 May–2 June 1999; Volume 1, pp. 342–345. [Google Scholar] [CrossRef]
- Kongpoon, M. Ultra-Low-Power, Modular, Class-AB Current Multiplier. In Proceedings of the 5th International Conference on Engineering, Applied Sciences and Technology (ICEAST), 2019, Luang Prabang, Laos, 2–5 July 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Vlassis, S.; Souliotis, G.; Plessas, F. Ultra Low-Voltage Current Squaring and Multiplier. In Proceedings of the 8th 2019 International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 13–15 May 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Danesh, M.; Jayaraj, A.; Chandrasekaran, S.T.; Sanyal, A. Ultra-Low Power Analog Multiplier Based on Translinear Principle. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Parveen, T. Electronically Tunable Current Mode Temperature Insensitive Active Only Analog Multiplier/Divider. In Proceedings of the 3rd International Conference and Workshops on Recent Advances and Innovations in Engineering (ICRAIE), Jaipur, India, 22–25 November 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Aloui, I.; Hassen, N.; Besbes, K. ±0.75V Four Quadrant Analog Multiplier in Current Mode. In Proceedings of the 15th International Multi-Conference on Systems, Signals & Devices (SSD), Hammamet, Tunisia, 19–22 March 2018; pp. 1045–1050. [Google Scholar] [CrossRef]
- Aloui, I.; Hassen, N.; Besbes, K. Low-Voltage Low-Power Four-Quadrant Analog Multiplier in Current-Mode. In Proceedings of the 18th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 21–23 December 2017; pp. 163–167. [Google Scholar] [CrossRef]
- Tijare, A.; Dakhole, P. CMOS Current Mode Analog Multiplier. In Proceedings of the International Conference on Signal and Information Processing (IConSIP), Nanded, Maharashtra, 6–8 October 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Renge, A.; Tijare, A.; Dakhole, P. CMOS Current-Mode Analog Multiplier. In Proceedings of the International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 6–8 April 2016; pp. 823–826. [Google Scholar] [CrossRef]
- Baharmast, A.; Azhari, S.J.; Mowlavi, S. A New Current Mode High Speed Four Quadrant CMOS Analog Multiplier. In Proceedings of the 24th Iranian Conference on Electrical Engineering (ICEE), Shiraz, Iran, 10–12 May 2016; pp. 1371–1376. [Google Scholar] [CrossRef]
- Tangjit, J.; Tangsrirat, W.; Satansup, J.; Surakampontorn, W. Simple Design Technique for Realizing Low-Voltage Low-Power CMOS Current Multiplier. In Proceedings of the 7th International Conference on Information Technology and Electrical Engineering (ICITEE), Chiang Mai, Thailand, 29–30 October 2015; pp. 110–113. [Google Scholar] [CrossRef]
- Borkar, B.D.; Tijare, A.D. VLSI Implementation of Current Mode Analog Multiplier. In Proceedings of the International Conference on Communications and Signal Processing (ICCSP), Melmaruvathur, India, 2–4 April 2015; pp. 531–534. [Google Scholar] [CrossRef]
- Saatlo, A.N.; Ozoguz, S.; Minaei, S. Applications of a CMOS Current Squaring Circuit in Analog Signal Processing. In Proceedings of the 38th International Conference on Telecommunications and Signal Processing (TSP), Prague, Czech Republic, 9–11 July 2015; pp. 339–343. [Google Scholar] [CrossRef]
- Dos Santos, R.B.; Rizol, P.M.S.R.; Mesquita, L. Design of CMOS Current-Mode Multiplier-Divider Circuit for Type-2 FLC Applications. In Proceedings of the IEEE 6th Latin American Symposium on Circuits & Systems (LASCAS), Montevideo, Uruguay, 24–27 February 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Kumngern, M.; Chanwutitum, J. 0.75-V Four-Quadrant Current Multiplier Using Floating Gate-MOS Transistors. In Proceedings of the International Electrical Engineering Congress (iEECON), Chonburi, Thailand, 19–21 March 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Popa, C. Improved Accuracy Current-Mode Analog Function Synthesizer. In Proceedings of the 37th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 26–30 May 2014; pp. 64–67. [Google Scholar] [CrossRef]
- Popa, C. Improved Accuracy Current-Mode Multiplier Circuits with Applications in Analog Signal Processing. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2013, 22, 443–447. [Google Scholar] [CrossRef]
- Kumngern, M.; Junnapiya, S. A CMOS Four-Quadrant Current Multiplier Using Electronically Tunable CCII. In Proceedings of the International Conference on Advanced Technologies for Communications (ATC 2013), Ho Chi Minh City, Vietnam, 16–18 October 2013; pp. 366–369. [Google Scholar] [CrossRef]
- Kumngern, M.; Torteanchai, U. A CMOS Current-Mode Multiplier/Divider Using a Current Amplifier. In Proceedings of the IEEE 7th International Power Engineering and Optimization Conference (PEOCO), Langkawi, Malaysia, 3–4 June 2013; pp. 742–745. [Google Scholar] [CrossRef]
- Kaedi, S.; Farshidi, E. A New Low Voltage Four-Quadrant Current Mode Multiplier. In Proceedings of the 20th Iranian Conference on Electrical Engineering (ICEE2012), Tehran, Iran, 15–17 May 2012; pp. 160–164. [Google Scholar] [CrossRef]
- Al-Absi, M.A.; Hussein, A.; Abuelma’atti, M.Y. A Novel Current-Mode Ultra Low Power Analog CMOS Four Quadrant Multiplier. In Proceedings of the International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 3–5 July 2012; pp. 13–17. [Google Scholar] [CrossRef]
- Mongkolwai, P.; Tangsrirat, W. CFTA-Based Current Multiplier/Divider Circuit. In Proceedings of the International Symposium on Intelligent Signal Processing and Communications Systems (ISPACS), Chiang Mai, Thailand, 7–9 December 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Algueta Miguel, J.M.A.; De La Cruz Blas, C.A.; Lopez-Martin, A.J. Fully Differential Current-Mode CMOS Triode Translinear Multiplier. IEEE Trans. Circuits Syst. II Express Briefs 2010, 58, 21–25. [Google Scholar] [CrossRef]
- Lopez-Martin, A.J.; De La Cruz Blas, C.A.; Ramirez-Angulo, J.; Carvajal, R.G. Compact Low-Voltage CMOS Current-Mode Multiplier/Divider. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 1583–1586. [Google Scholar] [CrossRef]
- Petchakit, W.; Kiranon, W.; Wardkien, P.; Petchakit, S. A Current-Mode CCCII-Based Analog Multiplier/Divider. In Proceedings of the ECTI-CON2010–The 2010 ECTI International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Chiang Mai, Thailand, 19–21 May 2010; pp. 221–224. [Google Scholar]
- Pisutthipong, N.; Siripruchyanun, M. A Novel Simple Current-Mode Multiplier/Divider Employing Only Single Multiple-Output Current Controlled CTTA. In Proceedings of the TENCON 2009—2009 IEEE Region 10 Conference, Singapore, 23-26 November 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Datta, D.; Chaudhuri, A.; Bhanja, M.; Ray, B.; Banerjee, A. Series Realization of Non-Linear Analog Functions using Current Mode Device. In Proceedings of the 4th International Conference on Information Systems and Computer Networks (ISCON), Mathura, India, 21–22 November 2019; pp. 694–699. [Google Scholar] [CrossRef]
- Fujcik, L.; Vrba, R.; Prokop, R. CMOS Auto-Tunable Low-Pass Filter for Harmonic Signal Generator. In Proceedings of the 33rd International Conference on Telecommunications and Signal Processing (TSP 2010), Budapest, Hungary, 17–20 August 2010; pp. 31–34. [Google Scholar]
- Gatti, U.; Maloberti, F.; Torelli, G. A Novel CMOS Linear Transconductance Cell for Continuous-Time Filters. In Proceedings of the 1990 IEEE International Symposium on Circuits and Systems (ISCAS), New Orleans, LA, USA, 1–3 May 1990; pp. 1173–1176. [Google Scholar]


| Reference Year of Publication | Adjustment (Analog, Dig., Res., Feedback) | Bandwidth [MHz] | Tested Current Gain Range [–] | Input Linearity Range [µA] | The Highest DC Input Resistance [Ω] | The Lowest DC Output Resistance [MΩ] | Power Consumption [mW] | THD [%] | Technology | Fabricated and Tested Experimentally |
|---|---|---|---|---|---|---|---|---|---|---|
| [3] 1988 | A | 30 | 0→30 | N/A | N/A | N/A | N/A | N/A | BJT | Yes |
| [4] 1994 | A | 175 | 0.1→10 | N/A | N/A | N/A | N/A | <1.9 | BJT | Yes |
| [5] 2002 | D | <100 | 0.12→1 | N/A | N/A | N/A | N/A | N/A | CMOS AMI (1.2 µm) | No |
| [6] 2006 | A | <100 | 1→3 | ±50 | 46 | 73 | 6.6 | <2.5 | CMOS TSMC (0.35 µm) | No |
| [7] 2008 | A | <100 | 0.5→1 | N/A | 27000 | 0.175 | N/A | N/A | BJT | No |
| [8] 2009 | A | <10 | 0→20 | N/A | <50 | <31 | N/A | N/A | CMOS (0.35 µm) | No |
| [9] 2010 | A | <100 | 0.25→1 | ±5000 | 11 | 0.055 | N/A | <0.6 | BJT | Yes |
| [10] 2010 | A | N/A | N/A | N/A | N/A | N/A | 3.5 | N/A | BJT | No |
| [11] 2012 | A | <200 | 0.1→10 | N/A | 70 | 0.014 | 5.9 | N/A | BJT | No |
| [12] * 2012 | A | <100 | 0.1→8 | ±5000 | adjust | 0.055 | N/A | <5 | BJT | Yes |
| [13] * 2012 | A | <40 | 0.5→3.5 | ±300 | adjust | 0.300 | N/A | N/A | BJT + CMOS (ON 0.5 µm) | No |
| [14] 2013 | D | <100 | 0.02→64 | N/A | N/A | N/A | 0.5 | <0.15 | CMOS (0.18 µm) | No |
| [15]* 2013 [17] 2016 | D | <300 | 0.8→8 | ±300 | 5 | 0.1 | 10 | N/A | CMOS ON (0.35 µm) | Yes |
| [18]* 2014 | A | <25 | 0.36→3.61 | ±200 | 700 | 0.044 | 8.5 | N/A | CMOS TSMC (0.18 µm) | No |
| [19]* 2017 | A | <20 | 0→3.5 | ±1000 | adjust | 0.5 | N/A | N/A | BJT | Yes |
| [20]* 2018 | A | <70 | 0→1 | ±1400 | adjust | 0.055 | N/A | N/A | BJT | No |
| [21,22] 2014 | R | <1 | 1→16 | N/A | 50 | 10 | 0.28 | <1 | 0.5 µm | Yes |
| [23] 2017 | A | <68 | 1→23 | N/A | 624 | 0.060 | 1.73 | 5.9 | CMOS TSMC (0.18 µm) | No |
| [24] 2019 | R | <10 | 2.4→9.4 | N/A | 105 | 0.301 | 0.88 | N/A | CMOS TSMC (0.25 µm) | No |
| [25] 2017 | A | <300 | 0.1→6.3 | ±15 | N/A | N/A | < 3 | <1.8 | CMOS (0.35 µm) | No |
| [26], 2006 [27] 2015 | F | <500 | N/A | ±60 | 1 | N/A | N/A | N/A | CMOS (0.8 µm) | No Yes |
| Prop. 2020 | A | <0.5 | 0.00→1.7 | ±200 | 1.4 | 3.3 | 3.6 | <0.35 | CMOS ON (0.35 µm) | Yes |
| Reference Year of Publication | No. of Quadrants | Approximately Declared (Shown) Processed Input Levels [µA] | Ready for Immediate Practical Implementation without Additional Parts | Bandwidth [MHz] | Maximal THD [%] | Input Linearity Error [%] | The Highest DC Input Resistance [Ω] | The Lowest DC Output Resistance [MΩ] | Power Consumption [mW] | Technology (or Model) | Fabricated and Tested Experimentally |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [28] 2000 | 4 | ±20 | No | 23 | 1.5 | 1.2 | 7000 | N/A | 0.93 | CMOS 4007 | Yes |
| [29] 1991 | 4 | 0–100 | Yes | N/A | N/A | N/A | N/A | N/A | N/A | SPICE3C1 | No |
| [30] 2009 | 4 | ±10 | No | 45 | 1.8 | 1.2 | N/A | N/A | 0.24 | 0.35 µm std. CMOS | No |
| [31] 2009 | 4 | ±200 | No | 3 | N/A | N/A | N/A | N/A | N/A | SPICE BJT 2N2222+ +2N2907 | No |
| [32] 2008 | 4 | ±10 | No | N/A | N/A | N/A | N/A | N/A | N/A | SPICE BJT | No |
| [33] 2008 | 2/4 | ±60 | Yes | 114 | 5 | N/A | N/A | N/A | 3.8 | AD844 + BJT | Yes |
| [34] 2007 | 4 | ±150 | Yes | 26 | 5.6 | N/A | N/A | N/A | 1.4 | BJT AT&T | No |
| [35] 2006 | 4 | ±200 | No | 154 | 4 | 0.8 | N/A | N/A | N/A | 0.25 µm CMOS | No |
| [36] 2005 | 4 | ±0.25 | No | 0.2 | 0.9 | 5 | N/A | N/A | 0.006 | 0.35 µm CMOS | Yes |
| [37] 2004 | 4 | ±60 | No | 31 | 4.5 | N/A | N/A | N/A | 0.72 | 0.25 µm CMOS | No |
| [38] 2004 | 4 | ±25 | No | N/A | 0.5 | 0.4 | N/A | N/A | N/A | 2 µm MIETEC CMOS | No |
| [39] 2003 | 4 | ±1000 | Yes | 160 | 0.25 | N/A | N/A | N/A | N/A | BJT 2N3904 2N3906 | No |
| [40] 2002 | 4 | ±200 | No | 11 | 2 | N/A | 416 | N/A | N/A | 2 µm MOSIS SCNA | No |
| [41] 2001 | 4 | ±30 | No | N/A | N/A | 5 | N/A | N/A | N/A | 0.5 µm CMOS | Yes |
| [42] 2001 | 4 | ±50 | Yes | 33 | N/A | 0.9 | N/A | N/A | 0.6 | 0.5 µm CMOS | No |
| [43] 1999 | 2/4 | 0–200 | No | 16 | 0.9 | N/A | N/A | N/A | N/A | 0.7 µm MIETEC CMOS | No |
| [44] 2019 | 4 | ±0.02 | No | 0.16 | 3 | N/A | N/A | N/A | N/A | 0.35 µm AMS CMOS | No |
| [45] 2019 | 4 | ±0.5 | No | 0.1 | N/A | N/A | N/A | N/A | 0.018 | 0.18 µm standard CMOS | No |
| [46] 2019 | 4 | ±0.2 | No | 3.5 | 6 | N/A | N/A | N/A | 0.0005 | 0.065 µm std. CMOS | No |
| [47] 2018 | 4 | ±100 | Yes | 31 | N/A | N/A | N/A | N/A | N/A | 0.5 µm CMOS | No |
| [48] 2018 | 4 | ±10 | Yes | 460 | 1.2 | N/A | N/A | N/A | 0.8 | 0.18 µm CMOS | No |
| [49] 2017 | 4 | ±20 | No | 33 | 2.0 | N/A | N/A | N/A | 0.6 | 0.18 µm CMOS | No |
| [50] 2016 | 4 | ±10 0–200 | No | 75, 493 | N/A | N/A | N/A | N/A | 0.15 | 0.18 + 0.8 µm CMOS | No |
| [51] 2016 | 4 | ±10 | No | 493 | N/A | N/A | N/A | N/A | 0.15 | 0.18 µm CMOS | No |
| [52] 2016 | 4 | ±20 | No | 840 | 6 | N/A | 7200 | N/A | 0.09 | 0.18 µm std. CMOS | No |
| [53] 2015 | 4 | ±10 | No | 1320 | 1.1 | 1.0 | N/A | N/A | 0.09 | 0.25 µm CMOS | No |
| [54] 2015 | 1 | 0–10 | No | N/A | N/A | N/A | N/A | N/A | 0.32 | 0.18 µm CMOS | No |
| [55] 2015 | 4 | ±10 | No | N/A | N/A | N/A | N/A | N/A | N/A | 0.35 µm standard CMOS | No |
| [56] 2015 | 1 | 0–100 | No | N/A | N/A | 2 | N/A | N/A | N/A | 0.35 µm AMS CMOS | |
| [57] 2014 | 4 | ±8 | No | 180 | 1.3 | 1.5 | 7600 | N/A | 0.025 | 0.18 µm TSMC CMOS | No |
| [58] 2014 | 1 | 0–20 | No | N/A | N/A | 0.013 | N/A | N/A | N/A | 0.18 µm CMOS | No |
| [59] 2014 | 1 | 0–10 | No | 80 | N/A | 0.9 | N/A | N/A | 0.075 | 0.18 µm CMOS | No |
| [60] 2013 | 4 | ±20 | No | N/A | 2.5 | 3.5 | N/A | N/A | 6.4 | 0.5 µm CMOS | No |
| [61] 2013 | 2 | ±25 | No | N/A | N/A | 0.3 | N/A | N/A | 6.3 | 0.5 µm MIETEC CMOS | No |
| [62] 2012 | 4 | unreadable | No | 31 | 2.6 | N/A | N/A | N/A | 0.21 | 0.18 µm CMOS | No |
| [63] 2012 | 4 | ±30 | No | 3 | 1.1 | 0.3 | N/A | N/A | 0.0023 | 0.35 µm TSMC CMOS | No |
| [64] 2011 | 4 | ±100 | Yes | N/A | 4 | N/A | N/A | N/A | N/A | BJT AT&T | No |
| [65] 2011 | 2 | ±25 | No | 3 | 0.2 | N/A | N/A | N/A | 2.0 | 0.5 µm CMOS | Yes |
| [66] 2010 | 2 | ±8 | No | 18 | N/A | N/A | N/A | N/A | 0.13 | 0.5 µm CMOS | Yes |
| [67] 2010 | 4 | ±200 | Yes | N/A | N/A | N/A | N/A | N/A | N/A | BJT AT&T | No |
| [68] 2009 | 4 | ±150 | Yes | 53 | 4.3 | N/A | N/A | N/A | 1.8 | BJT AT&T | No |
| Prop 2020 | 2 | ±200 | Yes | 0.5 | 0.35 | 5.4 | 1.4 | 3 | 3.6 | ON I3T25/035 CMOS | Yes |
| Parameter | Simulated (Nominal) | Measured (Selected Prototype) |
|---|---|---|
| small-signal gain and AC transfer bandwidth (−3 dB) | ||
| B(i) for ICTRL = 1 µA | 0.076 [–], −22.3 dB (0.69 MHz) | 0.067 [–], −23.4 dB (0.46 MHz) |
| B(i) for ICTRL = 2.5 µA | 0.189 [–], −14.5 dB (0.95 MHz) | 0.169 [–], −15.5 dB (0.64 MHz) |
| B(i) for ICTRL = 7.5 µA | 0.566 [–], −4.9 dB (1.24 MHz) | 0.519 [–], −5.7 dB (0.83 MHz) |
| B(i) for ICTRL = 12.5 µA | 0.994 [–], −0.05 dB (1.51 MHz) | 0.912 [–], −0.8 dB (0.90 MHz) |
| B(i) for ICTRL = 17.5 µA | 1.632 [–], 4.3 dB (2.89 MHz) | 1.122 [–], 1.0 dB (0.94 MHz) |
| B(i) for ICTRL = 20.0 µA | 2.405 [–], 7.6 dB (3.00 MHz) | 1.73 [–], 4.76 dB (1.00 MHz) |
| BW for ICTRL = 1→20 µA | 0.69→3.00 MHz | 0.46→1.0 MHz |
| input DC dynamic range | ||
| for ICTRL= 1→20 µA | −200→200 µA | −190→180 µA |
| input signal distortion (full input signal range) | ||
| Linearity (ICTRL = 1→20 µA) | 1.8% | 6% |
| THD (ICTRL = 1→20 µA) | 0.227% | 0.35% |
| gain control input linearity (IIN = 100 µA) | ||
| Linearity (ICTRL = 1→12.5 µA) | 10% | N/A |
| THD (ICTRL = 1→12.5 µA) | 3% | N/A |
| input DC offset (IIN→0 A) | ||
| systematic (ICTRL = 1→20 µA) | 5.4 nA→60 nA | N/A |
| MC matching offset | σ = 5.9 µA | N/A |
| measured | N/A | 4→−7 µA |
| input/output impedances | ||
| Ri, (Li) | 0.91 Ω (31 µH) | 1.4 Ω (42 µH) |
| Ro, (Co) | 8.8 MΩ (3.9 pF) | 4 MΩ (14.1 pF] |
| consumption | ||
| IVDD (IOUT = −200, 0, +200 µA) | 1.35 mA, 1.1 mA, 0.87 mA | N/A * |
| Pd (for VDD = 3.3 V) | 4.45 mW, 3.63 mW, 2.88 mW | N/A * |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prokop, R.; Sotner, R.; Kledrowetz, V. The CMOS Highly Linear Current Amplifier with Current Controlled Gain for Sensor Measurement Applications. Sensors 2020, 20, 4653. https://doi.org/10.3390/s20164653
Prokop R, Sotner R, Kledrowetz V. The CMOS Highly Linear Current Amplifier with Current Controlled Gain for Sensor Measurement Applications. Sensors. 2020; 20(16):4653. https://doi.org/10.3390/s20164653
Chicago/Turabian StyleProkop, Roman, Roman Sotner, and Vilem Kledrowetz. 2020. "The CMOS Highly Linear Current Amplifier with Current Controlled Gain for Sensor Measurement Applications" Sensors 20, no. 16: 4653. https://doi.org/10.3390/s20164653
APA StyleProkop, R., Sotner, R., & Kledrowetz, V. (2020). The CMOS Highly Linear Current Amplifier with Current Controlled Gain for Sensor Measurement Applications. Sensors, 20(16), 4653. https://doi.org/10.3390/s20164653






