A Polynomial-Exponent Model for Calibrating the Frequency Response of Photoluminescence-Based Sensors
Abstract
:1. Introduction
2. Limitations of the Classical Calibration Models
2.1. Photoluminescence Response with Modulated Excitation
2.1.1. The Stern–Volmer Equation
2.1.2. Frequency Response of the Stern–Volmer Model
2.1.3. Analyte Determination with Modulated Illumination Sources
2.2. Limitations of the Stern–Volmer Model
2.3. Limitations of the Demas Model
3. The Polynomial-Exponent Model
4. Experimental Design
5. Results and Discussion
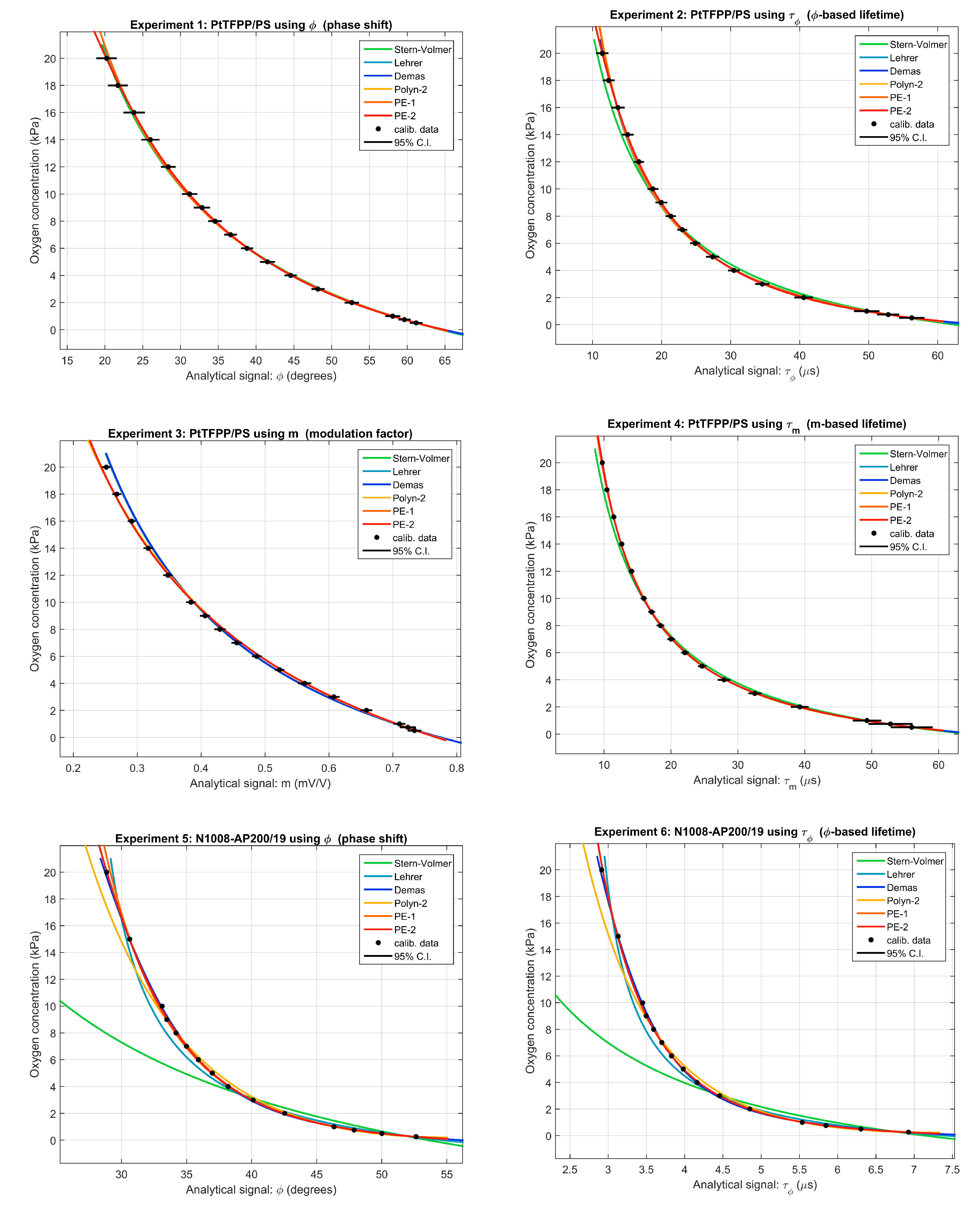
5.1. Calibration Curves
5.2. Error of the Calibration Models
5.3. Response at Null Concentration and Sensitivity
5.4. Influence of the Instrumental Bias
5.5. Primary Measurements vs. Apparent Lifetimes
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SV | Stern–Volmer model |
| L | Lehrer model |
| D | Demas model |
| PE | Polynomial-Exponent model |
| PE1 | 1st Degree Polynomial-Exponent model |
| PE2 | 2nd Degree Polynomial-Exponent model |
| LIA | Lock-in Amplifier |
| PtTFPP/PS | Platinum(II) 5,10,15,20-meso-tetrakis-(2,3,4,5,6-pentafluorophenyl)-porphyrin |
| immobilized in polystyrene | |
| N1008-AP200/19 | Ir(2-(2,2964-difluorophenyl) pyridine) 2(4,7-diphenyl-1, 10-phenanthroline) immobilized |
| into AP200/19, a nanostructured aluminium oxide-hydroxide solid support |
References
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: New York, NY, USA, 2006; pp. 278–327. [Google Scholar]
- Medina-Rodríguez, S.; de la Torre-Vega, A.; Medina-Rodríguez, C.; Fernández-Sánchez, J.F.; Fernández-Gutiérrez, A. On the calibration of chemical sensors based on photoluminescence: Selecting the appropriate optimization criterion. Sens. Actuators Chem. 2015, 212, 278–286. [Google Scholar] [CrossRef]
- Papkovsky, D.B. Methods in Optical Oxygen Sensing. In Methods in Enzymology; Sen, C.K., Semenza, G.L., Eds.; Academic Press: Cambridge, MA, USA, 2004; Volume 381, pp. 715–735. [Google Scholar]
- Wolfbeis, O.S. Fiber-Optic Chemical Sensors and Biosensors; CRC Press: Boca Raton, MA, USA, 1991. [Google Scholar]
- Ogurtsov, V.I.; Papkovsky, D.B. Modelling of phase-fluorometric oxygen sensors: Consideration of temperature effects and operational requirements. Sens. Actuators Chem. 2006, 113, 917–929. [Google Scholar] [CrossRef]
- Demas, J.N.; DeGraff, B.A.; Xu, W. Modeling of Luminescence Quenching-Based Sensors: Comparison of Multisite and Nonlinear Gas Solubility Models. Anal. Chem. 1995, 67, 1377–1380. [Google Scholar] [CrossRef]
- Demas, J.N.; DeGraff, B.A. Luminescence-based sensors: Microheterogeneous and temperature effects. Sens. Actuators Chem. 1993, 11, 35–41. [Google Scholar] [CrossRef]
- Ogurtsov, V.I.; Papkovsky, D.B.; Papkovskaia, N.Y. Approximation of calibration of phase-fluorimetric oxygen sensors on the basis of physical models. Sens. Actuators Chem. 2001, 81, 17–24. [Google Scholar] [CrossRef]
- Lehrer, S. Solute perturbation of protein fluorescence. Quenching of the tryptophyl fluorescence of model compounds and of lysozyme by iodide ion. Biochemistry 1971, 10, 3254–3263. [Google Scholar] [CrossRef]
- Eftink, M.R.; Ghiron, C.A. Exposure of tryptophanyl residues in proteins. Quantitative determination by fluorescence quenching studies. Biochemistry 1976, 15, 672–680. [Google Scholar] [CrossRef]
- Carraway, E.R.; Demas, J.N.; DeGraff, B.A.; Bacon, J.R. Photophysics and photochemistry of oxygen sensors based on luminescent transition-metal complexes. Anal. Chem. 1991, 63, 337–342. [Google Scholar] [CrossRef]
- Mills, A. Optical sensors for oxygen: A log-gaussian multisite-quenching model. Sens. Actuators Chem. 1998, 51, 69–76. [Google Scholar] [CrossRef]
- Bossi, M.L.; Daraio, M.E.; Aramendía, P.F. Luminescence quenching of Ru(II) complexes in polydimethylsiloxane sensors for oxygen. J. Photochem. Photobiol. Chem. 1999, 120, 15–21. [Google Scholar] [CrossRef]
- Ogurtsov, V.I.; Papkovsky, D.B. Modeling of luminescence-based oxygen sensors with non-uniform distribution of excitation and quenching characteristics inside active medium. Sens. Actuators Chem. 2003, 88, 89–100. [Google Scholar] [CrossRef]
- Draxler, S.; Lippitsch, M.E.; Klimant, I.; Kraus, H.; Wolfbeis, O.S. Effects of Polymer Matrixes on the Time-Resolved Luminescence of a Ruthenium Complex Quenched by Oxygen. J. Phys. Chem. 1995, 99, 3162–3167. [Google Scholar] [CrossRef]
- Mills, A. Response characteristics of optical sensors for oxygen: Models based on a distribution in tau0 or kq. Analyst 1999, 124, 1301–1307. [Google Scholar] [CrossRef]
- Badocco, D.; Mondin, A.; Fusar, A.; Pastore, P. Calibration Models under Dynamic Conditions for Determining Molecular Oxygen with Optical Sensors on the Basis of Luminescence Quenching of Transition-Metal Complexes Embedded in Polymeric Matrixes. J. Phys. Chem. 2009, 113, 20467–20475. [Google Scholar] [CrossRef]
- Trettnak, W.; Gruber, W.; Reininger, F.; Klimant, I. Recent progress in optical oxygen sensor instrumentation. Sens. Actuators Chem. 1995, 29, 219–225. [Google Scholar] [CrossRef]
- Hawkins, D.M. The Problem of Overfitting. J. Chem. Inf. Comput. Sci. 2004, 44, 1–12. [Google Scholar] [CrossRef]
- Faber, N.M.; Rajkó, R. How to avoid over-fitting in multivariate calibration—The conventional validation approach and an alternative. Anal. Chim. Acta 2007, 595, 98–106. [Google Scholar] [CrossRef]
- Fletcher, R. Practical Methods of Optimization, 2nd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2008. [Google Scholar]
- Torre-Vega, A.; Medina-Rodríguez, S.; Medina-Rodríguez, C.; Fernández-Sánchez, J.F. Chapter 6: Progress in Phosphorescence Lifetime Measurement Instrumentation for Oxygen Sensing. In Quenched-Phosphorescence Detection of Molecular Oxygen: Applications in Life Sciences; Papkovsky, D.B., Dmitriev, R.I., Eds.; RSC Detection Science Series No. 11; The Royal Society of Chemistry: London, UK, 2018; pp. 117–144. [Google Scholar]
- Medina-Rodríguez, S.; de la Torre-Vega, A.; Sainz-Gonzalo, F.J.; Marín-Suárez, M.; Elosúa, C.; Arregui, F.J.; Matias, I.R.; Fernández-Sánchez, J.F.; Fernández-Gutiérrez, A. Improved Multifrequency Phase-Modulation Method That Uses Rectangular-Wave Signals to Increase Accuracy in Luminescence Spectroscopy. Anal. Chem. 2014, 86, 5245–5256. [Google Scholar] [CrossRef]
- Schäferling, M. The Art of Fluorescence Imaging with Chemical Sensors. Angew. Chem. Int. Ed. Engl. 2012, 51, 3532–3554. [Google Scholar] [CrossRef]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing—Principles, Algorithms and Applications, 4th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Sundararajan, D. The Discrete Fourier Transform: Theory, Algorithms and Applications; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2001. [Google Scholar]
- Cajlakovic, M.; Bizzarri, A.; Konrad, C.; Voraberger, H. Optochemical Sensors Based on Luminescence. In Encyclopedia of Sensors; Grimes, C.A., Dickey, E.C., Pishko, M.V., Eds.; American Scientific Publishers: Valencia, CA, USA, 2006; Volume 7, pp. 291–313. [Google Scholar]
- Langer, P.; Müller, R.; Drost, S.; Werner, T. A new method for filter-free fluorescence measurements. Sens. Actuators Chem. 2002, 82, 1–6. [Google Scholar] [CrossRef]
- Medina-Rodríguez, S.; Medina-Rodríguez, C.; de la Torre-Vega, A.; Segura-Luna, J.C.; Mota-Fernández, S.; Fernández-Sánchez, J.F. Real-time optimal combination of multifrequency information in phase-resolved luminescence spectroscopy based on rectangular-wave signals. Sens. Actuators Chem. 2017, 238, 221–225. [Google Scholar] [CrossRef]
- Medina-Rodríguez, C.; Medina-Rodríguez, S.; de la Torre-Vega, A.; Fernández-Gutiérrez, A.; Fernández-Sánchez, J.F. Direct estimation of the standard error in phase-resolved luminescence measurements: Application to an oxygen measuring system. Sens. Actuators Chem. 2016, 224, 521–528. [Google Scholar]
- Medina-Rodríguez, S.; de la Torre-Vega, A.; Fernández-Sánchez, J.F.; Fernández-Gutiérrez, A. An open and low-cost optical-fiber measurement system for the optical detection of oxygen using a multifrequency phase-resolved method. Sens. Actuators Chem. 2013, 176, 1110–1120. [Google Scholar] [CrossRef]
- Medina-Rodríguez, S.; de la Torre-Vega, A.; Fernández-Sánchez, J.F.; Fernández-Gutiérrez, A. Evaluation of a simple PC-based quadrature detection method at very low SNR for luminescence spectroscopy. Sens. Actuators Chem. 2014, 192, 334–340. [Google Scholar] [CrossRef]
- Marín-Suarez del Toro, M.; Fernández-Sánchez, J.F.; Baranoff, E.; Nazeeruddin, M.K.; Graetzel, M.; Fernández-Gutiérrez, A. Novel luminescent Ir(III) dyes for developing highly sensitive oxygen sensing films. Talanta 2010, 82, 620–626. [Google Scholar] [CrossRef]
- Medina-Rodríguez, S.; Marín-Suárez, M.; Fernández-Sánchez, J.F.; de la Torre-Vega, A.; Baranoff, E.; Fernández-Gutiérrez, A. High performance optical sensing nanocomposites for low and ultra-low oxygen concentrations using phase-shift measurements. Analyst 2013, 138, 4607–4617. [Google Scholar] [CrossRef]

| (A) RMS Relative Error (%) for Average Calibration Data | ||||||||
|---|---|---|---|---|---|---|---|---|
| Experiment | ||||||||
| Model | 1 | 2 | 3 | 4 | 5 | 6 | Average | |
| SV | (2) | 1.94 | 6.66 | 5.77 | 4.58 | 36.2 | 38.5 | 15.6 |
| L | (3) | 1.65 | 2.97 | 5.77 | 1.55 | 12.2 | 13.0 | 6.19 |
| P2 | (3) | 1.64 | 2.56 | 4.12 | 1.56 | 6.48 | 8.10 | 4.08 |
| PE1 | (3) | 1.56 | 1.97 | 3.70 | 1.84 | 2.54 | 1.66 | 2.21 |
| D | (4) | 1.34 | 1.25 | 5.79 | 1.55 | 2.17 | 2.30 | 2.40 |
| PE2 | (4) | 0.79 | 0.86 | 3.64 | 1.51 | 1.41 | 1.66 | 1.65 |
| (B) RMS Relative Error (%) for Individual Evaluation Data | ||||||||
| Experiment | ||||||||
| Model | 1 | 2 | 3 | 4 | 5 | 6 | Average | |
| SV | (2) | 5.19 | 8.57 | 7.51 | 8.60 | 36.1 | 38.5 | 17.4 |
| L | (3) | 5.04 | 5.85 | 7.51 | 6.76 | 12.2 | 12.9 | 8.38 |
| P2 | (3) | 5.03 | 5.57 | 6.74 | 6.71 | 6.51 | 8.13 | 6.45 |
| PE1 | (3) | 4.98 | 5.20 | 6.66 | 6.61 | 2.56 | 1.72 | 4.62 |
| D | (4) | 4.81 | 4.76 | 7.55 | 6.76 | 2.18 | 2.31 | 4.73 |
| PE2 | (4) | 4.61 | 4.62 | 6.63 | 6.74 | 1.47 | 1.72 | 4.30 |
| Response at Null Concentration | Sensitivity at Null Concentration | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Experiment | Experiment | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | |
| Model | (o) | (s) | (mV/V) | (s) | (o) | (s) | (kPa) | |||||
| SV | 64.5 | 62.5 | 0.775 | 64.5 | 53.5 | 7.14 | 0.109 | 0.244 | 0.100 | 0.308 | 0.108 | 0.198 |
| L | 64.6 | 64.0 | 0.775 | 66.1 | 54.6 | 7.41 | 0.112 | 0.285 | 0.100 | 0.351 | 0.178 | 0.343 |
| P2 | 64.6 | 64.3 | 0.770 | 66.2 | 55.0 | 7.13 | 0.112 | 0.296 | 0.090 | 0.355 | 0.248 | 0.383 |
| PE1 | 64.6 | 64.9 | 0.768 | 66.8 | 56.5 | 8.31 | 0.113 | 0.317 | 0.086 | 0.376 | 0.348 | 1.111 |
| D | 64.9 | 66.0 | 0.775 | 66.1 | 56.1 | 7.84 | 0.121 | 0.359 | 0.099 | 0.350 | 0.291 | 0.596 |
| PE2 | 64.9 | 66.2 | 0.768 | 66.1 | 57.0 | 8.32 | 0.121 | 0.365 | 0.086 | 0.350 | 0.406 | 1.122 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torre, A.d.l.; Medina-Rodríguez, S.; Segura, J.C.; Fernández-Sánchez, J.F. A Polynomial-Exponent Model for Calibrating the Frequency Response of Photoluminescence-Based Sensors. Sensors 2020, 20, 4635. https://doi.org/10.3390/s20164635
Torre Adl, Medina-Rodríguez S, Segura JC, Fernández-Sánchez JF. A Polynomial-Exponent Model for Calibrating the Frequency Response of Photoluminescence-Based Sensors. Sensors. 2020; 20(16):4635. https://doi.org/10.3390/s20164635
Chicago/Turabian StyleTorre, Angel de la, Santiago Medina-Rodríguez, Jose C. Segura, and Jorge F. Fernández-Sánchez. 2020. "A Polynomial-Exponent Model for Calibrating the Frequency Response of Photoluminescence-Based Sensors" Sensors 20, no. 16: 4635. https://doi.org/10.3390/s20164635
APA StyleTorre, A. d. l., Medina-Rodríguez, S., Segura, J. C., & Fernández-Sánchez, J. F. (2020). A Polynomial-Exponent Model for Calibrating the Frequency Response of Photoluminescence-Based Sensors. Sensors, 20(16), 4635. https://doi.org/10.3390/s20164635







