Wind Tunnel Measurement Systems for Unsteady Aerodynamic Forces on Bluff Bodies: Review and New Perspective
Abstract
1. Introduction
2. Conventional Wind Tunnel Test Techniques
2.1. HFBB Test
2.2. SMPSS Test
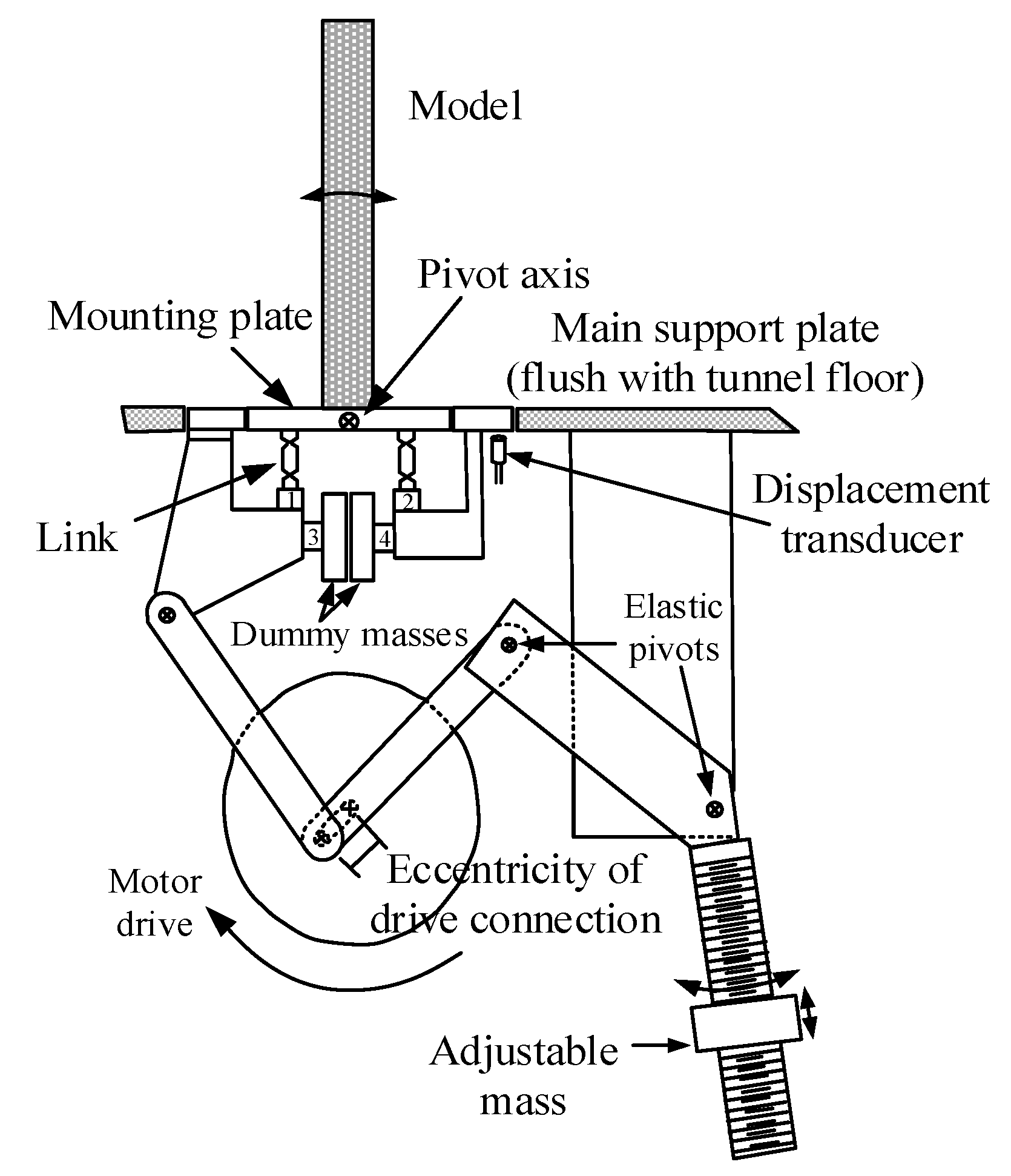
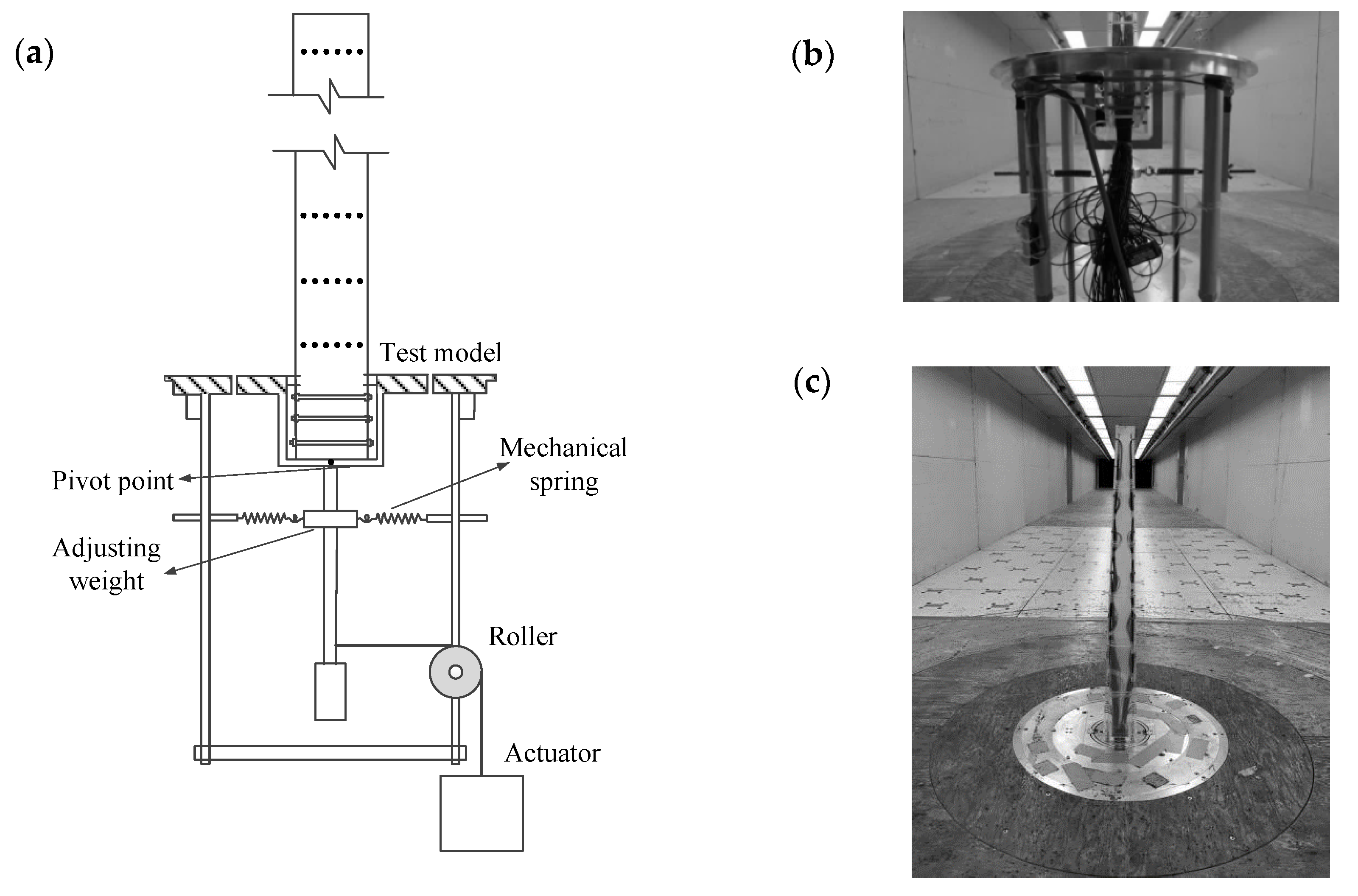
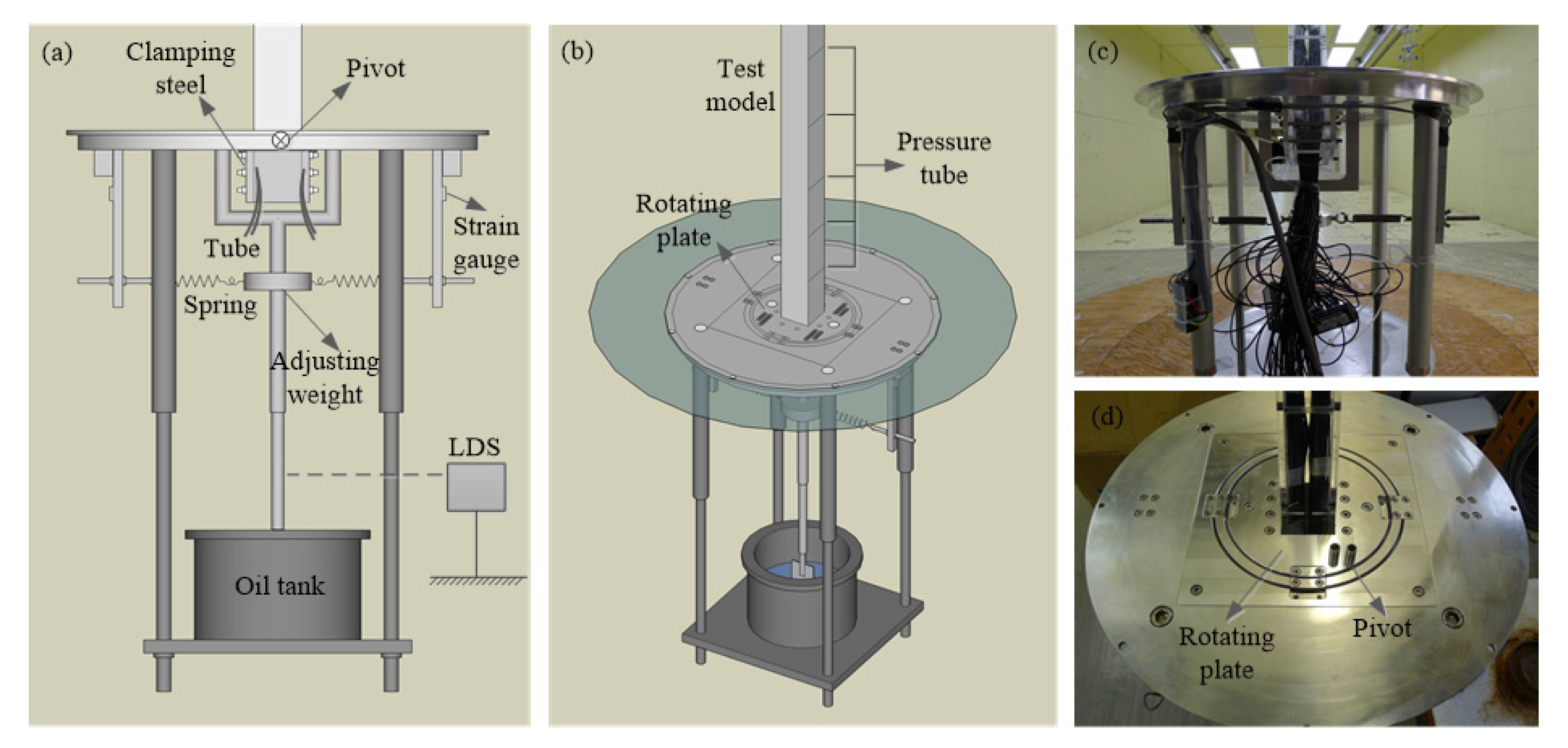
2.3. Aeroelastic Test
3. Advanced Wind Tunnel Test Techniques
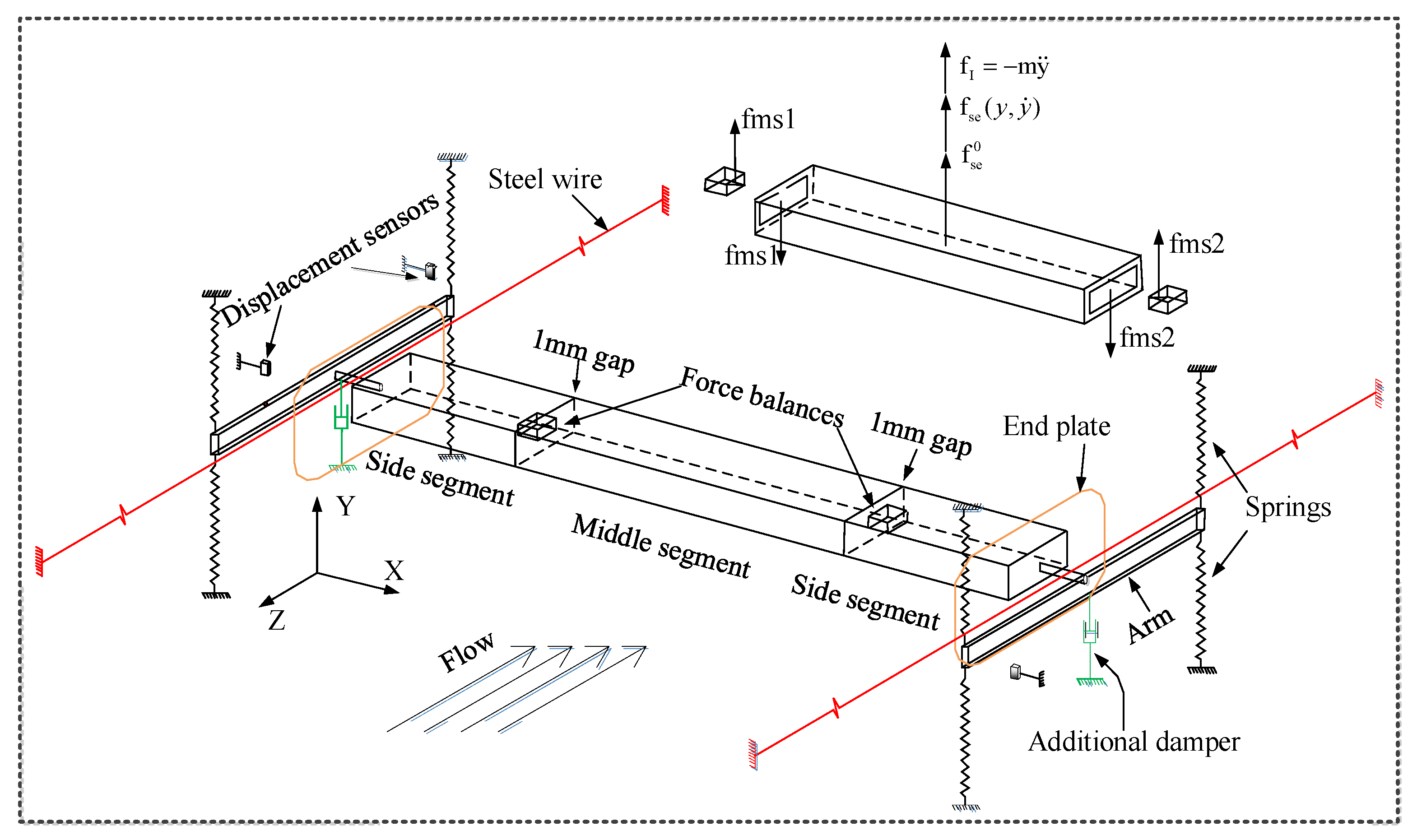
3.1. Forced Vibration Test Technique
3.2. Hybrid Aeroelastic-Force Balance Test Technique
4. Unsteady Aerodynamic Forces Measured from Advanced Wind Tunnel Test Techniques
4.1. Characteristics of Unsteady Wind Force
4.2. Aerodynamic Damping Force
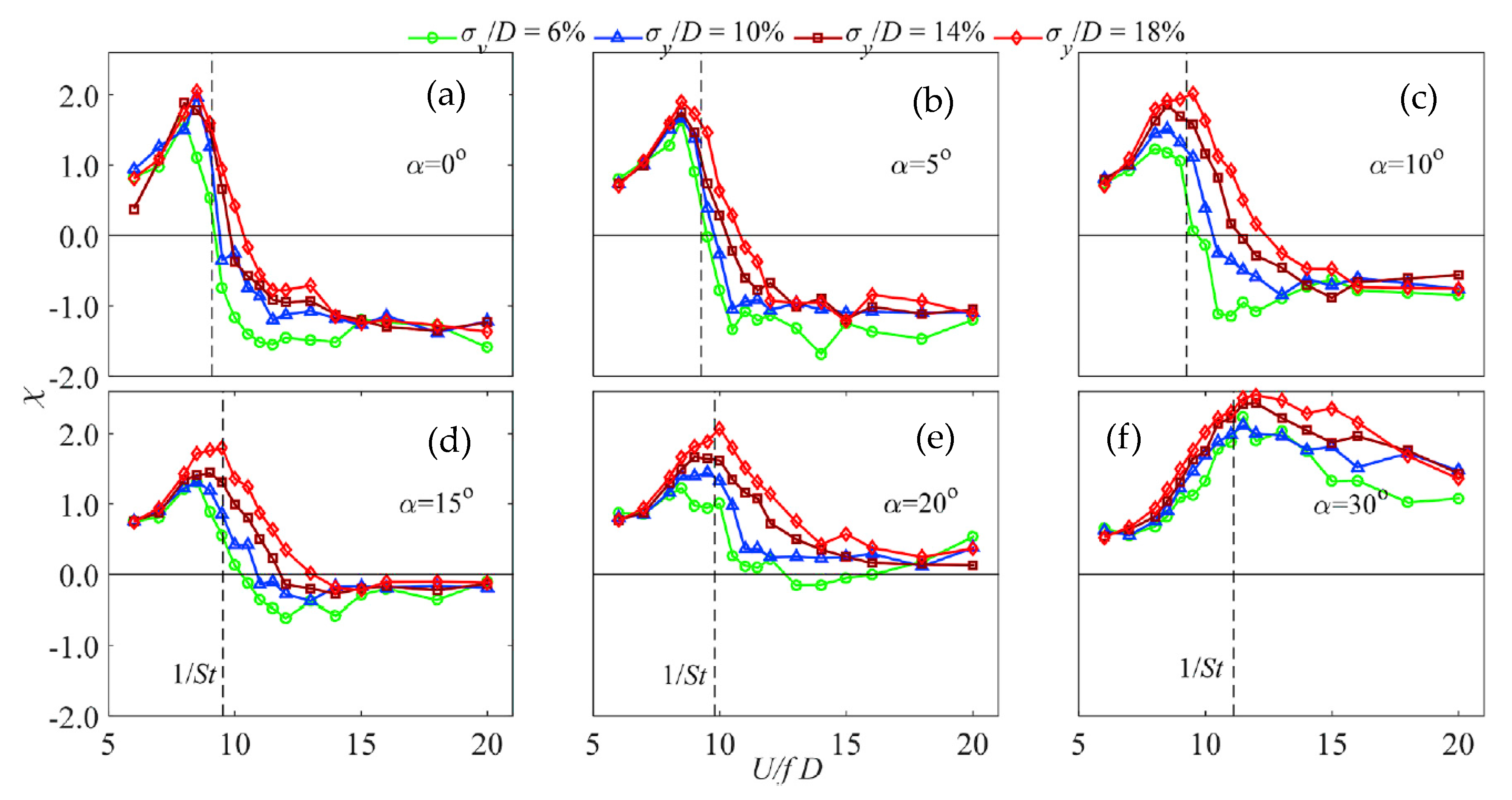
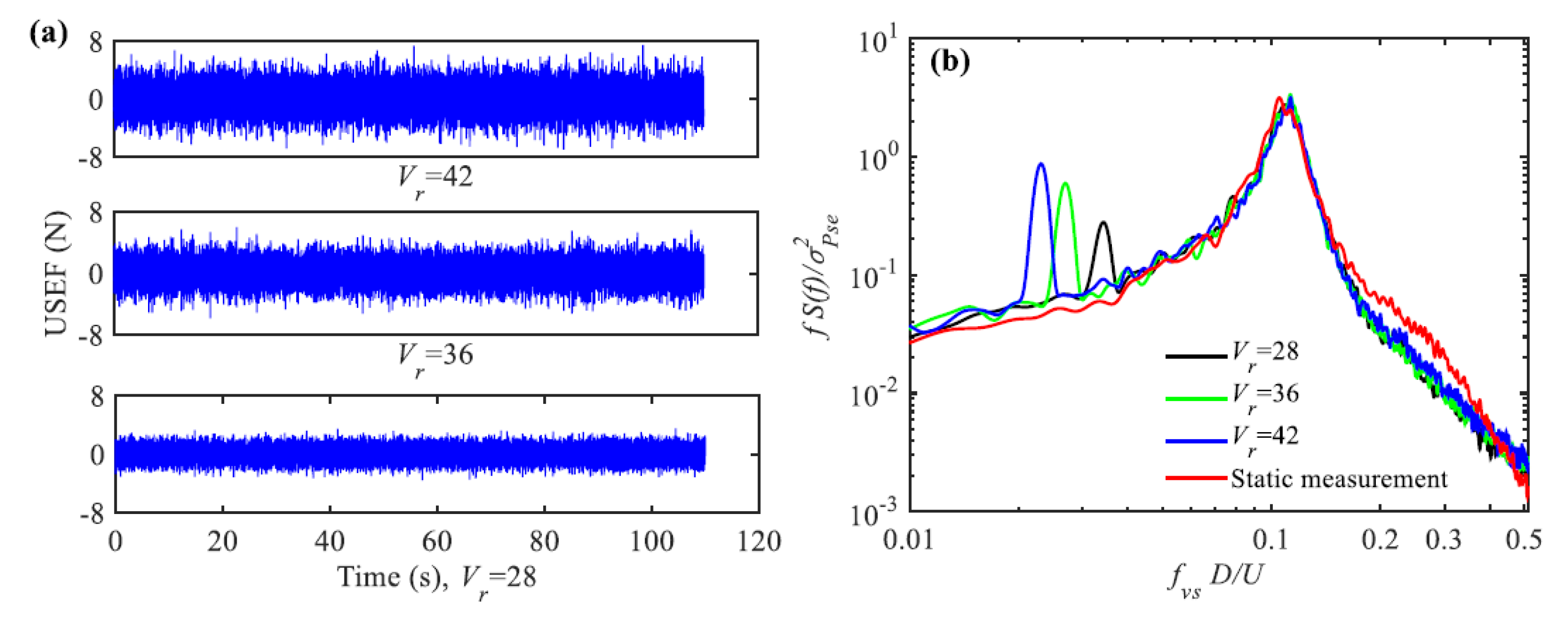
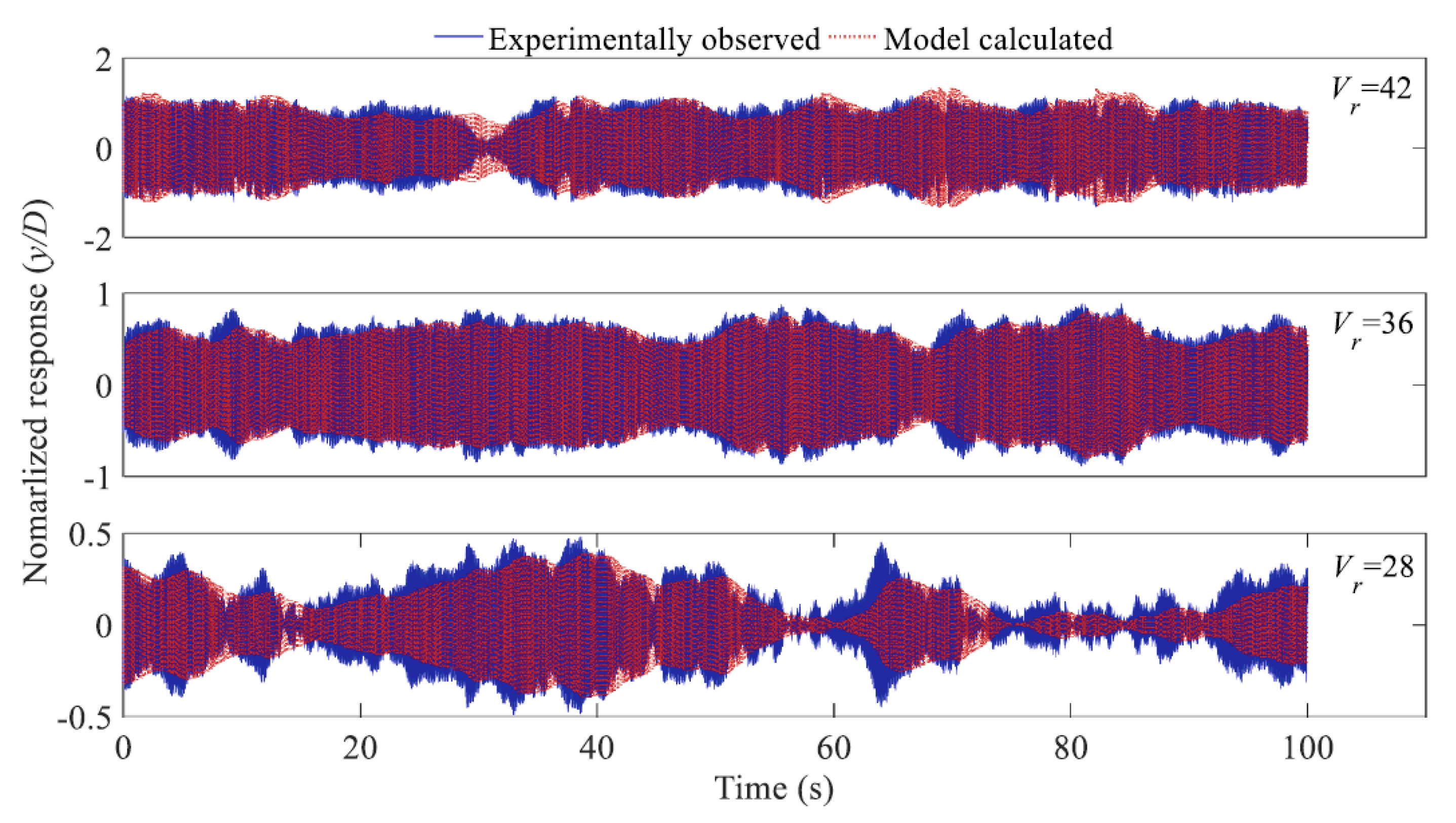
4.3. Unsteady Self-Excited Force
5. Comparison and Perspective
5.1. Comparison of Wind Tunnel Test Techniques
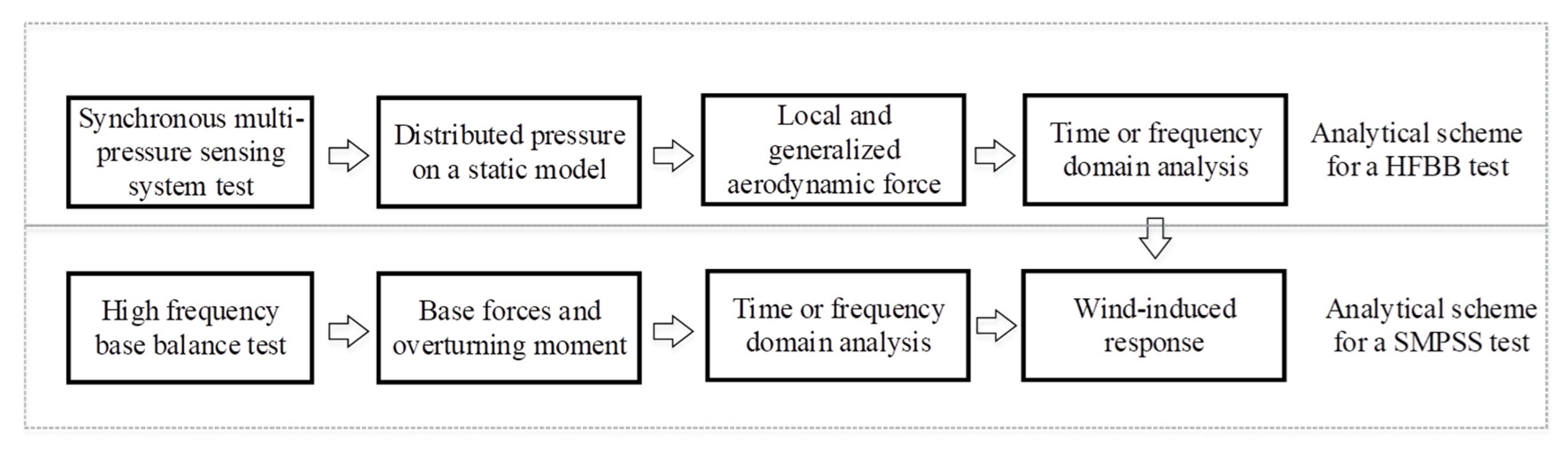
5.2. Analytical Scheme of Conventional and Advanced Wind Tunnel Test Techniques
6. Concluding Remarks and Recommendations
- (1)
- The HFBB and SMPSS techniques neglect the unsteady effect, which has been proved to have a significant influence on the predicted wind-induced response. The response of the bluff bodies cannot be obtained directly from these two techniques.
- (2)
- The aeroelastic test can only obtain the wind-induced response of a bluff body, while the wind force acting on the model cannot be obtained.
- (3)
- Unsteady aerodynamic forces obtained from a forced vibration wind tunnel test takes part of the unsteady effect into consideration, because a test model is forced to oscillate and it only considers the effect from an oscillating model to its surrounding flow and cannot consider the feedback. As a result, unsteady aerodynamic forces on a forced oscillation model may have considerable differences with those on an aeroelastic model or a structure in the real world.
- (4)
- The hybrid aeroelastic-pressure/force balance test techniques are effective in measuring unsteady aerodynamic forces on bluff bodies during aeroelastic oscillations. The obtained forces can well include the ‘unsteady’ effect and can be used to address the shortcomings of classical theories (e.g., the classical quasi-steady theory) in predicting wind-induced responses of bluff bodies.
- (5)
- The HAPB/HAFB test techniques are highly recommended to investigate the unsteady aerodynamics and aeroelasticity of bluff bodies.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, Z.; Tse, K.T.; Kwok, K.C.S. Unsteady Pressure Measurements on an Oscillating Slender Prism Using a Forced Vibration Technique. J. Wind Eng. Ind. Aerodyn. 2017, 170, 81–93. [Google Scholar] [CrossRef]
- Lin, S.; Wang, Q.; Nikitas, N.; Liao, H. Effects of Oscillation Amplitude on Motion-induced forces for 5:1 rectangular cylinders. J. Wind Eng. Ind. Aerodyn. 2019, 186, 68–83. [Google Scholar] [CrossRef]
- Estimation and Modeling of Damping and Engineering Auxiliary Damping Systems in Civil Engineering Structures: An Overview. Available online: https://nathaz.nd.edu/confs/(2000)Estimation_and_Modeling_of_Damping_and_Engineering_Auxiliary_Damping_Systems_in_Civil_Engineering_Structures.pdf (accessed on 4 August 2020).
- Tschanz, T.; Davenport, A. The Base Balance Technique for the Determination of Dynamic Wind Loads. J. Wind Eng. Ind. Aerodyn. 1983, 13, 429–439. [Google Scholar] [CrossRef]
- Tse, K.T.; Hitchcock, P.; Kwok, K.C.S. A Time Domain Analysis Technique for Aerodynamic Wind Tunnel Model Studies. J. Wind Eng. Ind. Aerodyn. 2008, 5, 1–16. [Google Scholar]
- Holmes, J.; Rofail, A.; Aurelius, L. High frequency base balance methodologies for tall buildings with torsional and coupled resonant modes. In Proceedings of the 11th International Conference on Wind Engineering, Lubbock, TX, USA, 2–5 June 2003. [Google Scholar]
- Rofail, A.; Holmes, J. High frequency base balance methodology for linked tall buildings. In Proceedings of the 12th International Conference on Wind Engineering, Cairns, Australia, 1–6 July 2007. [Google Scholar]
- Spence, S.; Bernardini, E.; Gioffrè, M. Influence of the Wind Load Correlation on the Estimation of the Generalized Forces for 3D Coupled Tall Buildings. J. Wind Eng. Ind. Aerodyn. 2011, 99, 757–766. [Google Scholar] [CrossRef]
- Cluni, F.; Gusella, V.; Spence, S.; Bartoli, G. Wind Action on Regular and Irregular Tall Buildings: Higher Order Moment Statistical Analysis by HFFB and SMPSS Measurements. J. Wind Eng. Ind. Aerodyn. 2011, 99, 682–690. [Google Scholar] [CrossRef]
- Steckley, A. Motion-Induced Wind Forces on Chimneys and Tall Buildings. Ph.D. Dissertation, University of Western Ontario, London, ON, Canada, 1989. [Google Scholar]
- Kareem, A. Wind-Excited Response of Buildings in Higher Modes. J. Struct. Div. 1981, 107, 701–706. [Google Scholar]
- Tse, K.T.; Hitchcock, P.; Kwok, K.C.S. Mode Shape Linearization for HFBB Analysis of Wind-Excited Complex Tall Buildings. Eng. Struct. 2009, 31, 675–685. [Google Scholar] [CrossRef]
- Zou, L.; Shi, T.; Song, J.; Cai, C.S. Application of the High-Frequency Base Balance Technique to Tall Slender Structures Considering the Effects of Higher Modes. Eng. Struct. 2017, 151, 1–10. [Google Scholar] [CrossRef]
- Kim, Y.M.; You, K.P. Dynamic Responses of a Tapered Tall Building to Wind Loads. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1771–1782. [Google Scholar] [CrossRef]
- Boggs, D.W. The Past, Present and Future of High-Frequency Balance Testing. J. Wind Struct. 2014, 18, 323–345. [Google Scholar] [CrossRef]
- Kim, W.; Yoshida, A.; Tamura, Y.; Yi, J. Experimental Study of Aerodynamic Damping of a Twisted Supertall Building. J. Wind Eng. Ind. Aerodyn. 2018, 176, 1–12. [Google Scholar] [CrossRef]
- Zou, L.; Li, F.; Song, J.; Shi, T.; Mercan, O. Investigation of Torsional Aeroelastic Effects on High-Rise Buildings Using Forced Vibration Wind Tunnel Tests. J. Wind Eng. Ind. Aerodyn. 2020, 200, 104158. [Google Scholar] [CrossRef]
- Zhang, Z.; Quan, Y.; Gu, M.; Xiong, Y. Aerodynamic Characteristics of Tapered Tall Buildings with Square Section. J. Southwest. Jiaotong. Univ. 2014, 49, 772–778. [Google Scholar]
- Aly, A.M. Pressure Integration Technique for Predicting Wind-Induced Response in High-Rise Buildings. Alex. Eng. J. 2013, 52, 717–731. [Google Scholar] [CrossRef]
- Irwin, P.A.; Kochanski, W.W. Measurement of structural wind loads using the high frequency pressure integration method. In Proceedings of the Structures Congress XIII, Boston, MA, USA, 2–5 April 1995. [Google Scholar]
- Rosa, L.; Tomasini, G.; Zasso, A.; Aly, A. Wind-Induced Dynamics and Loads in a Prismatic Slender Building: A Modal Approach Based on Unsteady Pressure Measurements. J. Wind Eng. Ind. Aerodyn 2012, 107–108, 118–130. [Google Scholar] [CrossRef]
- Song, J. Structural and Aerodynamic Couplings of Wind-Excited Linked Tall Buildings. Ph.D. Thesis, Hong Kong University of Science and Technology, Hong Kong, China, August 2015. [Google Scholar]
- Steckley, A.; Accardo, M.; Gamble, S.; Irwin, P. The Use of Integrated Pressures to Determine Overall Wind-Induced Response. J. Wind Eng. Ind. Aerodyn. 1992, 42, 1023–1034. [Google Scholar] [CrossRef]
- Cermak, J.E. Wind-Tunnel Development and Trends in Applications to Civil Engineering. J. Wind Eng. Ind. Aerodyn. 2003, 91, 355–370. [Google Scholar] [CrossRef]
- Chen, Z.; Tse, K.T.; Kwok, K.C.S.; Kim, B.; Kareem, A. Modelling Unsteady Self-Excited Wind Force on Slender Prisms in a Turbulent Flow. Eng. Struct. 2020, 202, 109855. [Google Scholar] [CrossRef]
- Isyumov, N. The aeroelastic modeling of tall buildings. In Proceedings of the International Workshop on Wind Tunnel Modeling for Civil Engineering Applications, Gaithersburg, MD, USA, April 1982. [Google Scholar]
- Vickery, B.; Steckley, A. Aerodynamic Damping and Vortex Excitation on an Oscillating Prism in Turbulent Shear Flow. J. Wind Eng. Ind. Aerodyn. 1993, 49, 121–140. [Google Scholar] [CrossRef]
- Bearman, P.; Currie, I. Pressure-Fluctuation Measurements on an Oscillating Circular Cylinder. J. Fluid Mech. 1979, 91, 661–677. [Google Scholar] [CrossRef]
- Bearman, P.; Obasaju, E. An Experimental Study of Pressure Fluctuations on Fixed and Oscillating Square-Section Cylinders. J. Fluid Mech. 1982, 119, 297–321. [Google Scholar] [CrossRef]
- Cooper, K.; Nakayama, M.; Sasaki, Y.; Fediw, A.; Resende-Ide, S.; Zan, S. Unsteady Aerodynamic Force Measurements on a Super-Tall Building with a Tapered Cross Section. J. Wind Eng. Ind. Aerodyn. 1997, 72, 199–212. [Google Scholar] [CrossRef]
- Banfi, L.; Carassale, L. Uncertainty in the motion-excited forces on a square prism and probabilistic assessment of galloping instability. In Proceedings of the 1st International Conference on Uncertainty Quantification in Computational Sciences and Engineering, Crete Island, Greece, 25–27 May 2015. [Google Scholar]
- Li, M.; Li, S.; Liao, H.; Zeng, J.; Wang, Q. Spanwise Correlation of Aerodynamic Forces on Oscillating Rectangular Cylinder. J. Wind Eng. Ind. Aerodyn. 2016, 154, 47–57. [Google Scholar] [CrossRef]
- Chen, Z.; Tse, K.T.; Kwok, K.C.S.; Kareem, A. Aerodynamic Damping of Inclined Slender Prisms. J. Wind Eng. Ind. Aerodyn. 2018, 177, 79–91. [Google Scholar] [CrossRef]
- Gu, M.; Zhang, R.; Xiang, H. Identification of Flutter Derivatives of Bridge Decks. J. Wind Eng. Ind. Aerodyn. 2000, 84, 151–162. [Google Scholar] [CrossRef]
- Sarkar, P.P.; Caracoglia, L.; Haan, F.L.; Sato, H.; Murakoshi, J. Comparative and Sensitivity Study of Flutter Derivatives of Selected Bridge Deck Sections, Part 1: Analysis of Inter-Laboratory Experimental Data. Eng. Struct. 2009, 31, 158–169. [Google Scholar] [CrossRef]
- Ehsan, F.; Scanlan, R.H.; Bosch, H.R. Modeling Spanwise Correlation Effects in the Vortex-Induced Response of Flexible Bridges. J. Wind Eng. Ind. Aerodyn. 1990, 36, 1105–1114. [Google Scholar] [CrossRef]
- Pozzuoli, C. Aeroelastic Effects on Tall Buildings: Performance-Based Comfort Analysis. Ph.D. Thesis, University of Florence, Florence, Italy, November 2012. [Google Scholar]
- Ke, S.; Ge, Y. Extreme Wind Pressures and Non-Gaussian Characteristics for Super-Large Hyperbolic Cooling Towers Considering Aeroelastic Effect. J. Eng. Mech. 2015, 04015010. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, X.; Ge, Y. Investigations of Adverse Wind Loads on a Large Cooling Tower for the Six-Tower Combination. Appl. Therm. Eng. 2016, 105, 988–999. [Google Scholar] [CrossRef]
- Ke, S.; Ge, Y.; Zhao, L.; Tamura, Y. Stability and Reinforcement Analysis of Superlarge Exhaust Cooling Towers Based on a Wind Tunnel Test. J. Struct. Eng. 2015, 141, 04015066. [Google Scholar] [CrossRef]
- Gao, G.; Zhu, L. Measurement and Verification of Unsteady Galloping Force on a Rectangular 2: 1 Cylinder. J. Wind Eng. Ind. Aerodyn. 2016, 157, 76–94. [Google Scholar] [CrossRef]
- Gao, G.; Zhu, L. Nonlinearity of Mechanical Damping and Stiffness of a Spring-Suspended Sectional Model System for Wind Tunnel Tests. J. Sound Vib. 2015, 355, 369–391. [Google Scholar] [CrossRef]
- Chen, Z.; Tse, K.T. Identification of Physical Nonlinearities of a Hybrid Aeroelastic-Pressure Balance. Nonlinear Dyn. 2019, 98, 95–111. [Google Scholar] [CrossRef]
- Wu, Y.; Li, D.; Xiang, J.; Da Ronch, A. Piezoaeroelastic Energy Harvesting Based on an Airfoil with Double Plunge Degrees of Freedom: Modeling and Numerical Analysis. J. Fluids Struct. 2017, 74, 111–129. [Google Scholar] [CrossRef]
- Lin, N.; Letchford, C.; Tamura, Y.; Liang, B.; Nakamura, O. Characteristics of Wind Forces Acting on Tall Buildings. J. Wind Eng. Ind. Aerodyn. 2005, 93, 217–242. [Google Scholar] [CrossRef]
- Kareem, A. Measurements of Pressure and Force Fields on Building Models in Simulated Atmospheric Flows. J. Wind Eng. Ind. Aerodyn. 1990, 36, 589–599. [Google Scholar] [CrossRef]
- Hu, G.; Tse, K.T.; Kwok, K.C.S.; Chen, Z. Pressure Measurements on Inclined Square prisms. Wind Struct. 2015, 21, 383–405. [Google Scholar] [CrossRef]
- Li, D.; Wu, Y.; Da Ronch, A.; Xiang, J. Energy Harvesting by Means of Flow-Induced Vibrations on Aerospace Vehicles. Prog. Aerosp. Sci. 2016, 86, 28–62. [Google Scholar] [CrossRef]
- Bearman, P.W. Vortex Shedding from Oscillating Bluff Bodies. Annu. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- Bearman, P.W.; OWen, J.C. Reduction of Bluff-Body Drag and Suppression of Vortex Shedding by the Introduction of Wavy Separation Lines. J. Fluids Struct. 1998, 12, 123–130. [Google Scholar] [CrossRef]
- Khalak, A.; Williamson, C.H.K. Investigation of relative effects of mass and damping in vortex-induced vibration of a circular cylinder. J. Wind Eng. Ind. Aerodyn. 1997, 69–71, 341–350. [Google Scholar] [CrossRef]
- Griffin, O.M.; Hall, M. Review-Vortex Shedding Lock-On and Flow Control in Bluff Body Wakes. J. Fluids Eng. 1991, 113, 526–537. [Google Scholar] [CrossRef]
- Matsumoto, M. Vortex Shedding of Bluff Bodies: A review. J. Fluids Struct. 1999, 13, 791–811. [Google Scholar] [CrossRef]
- Blevins, R.D. Flow-Induced Vibration, 2nd ed.; Krieger Publishing Company: Malabar, FL, USA, 1990. [Google Scholar]
- Pastò, S. Vortex-Induced Vibrations of a Circular Cylinder in Laminar and Turbulent Flows. J. Fluids Struct. 2008, 24, 977–993. [Google Scholar] [CrossRef]
- Katagiri, J.; Ohkuma, T.; Marikawa, H. Motion-Induced Wind Forces Acting on Rectangular High-Rise Buildings with Side Ratio of 2. J. Wind Eng. Ind. Aerodyn. 2001, 89, 1421–1432. [Google Scholar] [CrossRef]
- Katagiri, J.; Ohkuma, T.; Marukawa, H. Analytical Method for Coupled Across-Wind and Torsional Wind Responses with Motion-Induced Wind Forces. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1795–1805. [Google Scholar] [CrossRef]
- Ehsan, F.; Scanlan, R.H. Vortex-Induced Vibrations of Flexible Bridges. J. Eng. Mech. 1990, 116, 1392–1411. [Google Scholar] [CrossRef]
- Chen, X. Estimation of Stochastic Crosswind Response of Wind-Excited Tall Buildings with Nonlinear Aerodynamic Damping. Eng. Struct. 2013, 56, 766–778. [Google Scholar] [CrossRef]
- Fediw, A.; Nakayama, M.; Cooper, K.; Sasaki, Y.; Resende-Ide, S.; Zan, S. Wind Tunnel Study of an Oscillating Tall Building. J. Wind Eng. Ind. Aerodyn. 1995, 57, 249–260. [Google Scholar] [CrossRef]
- Watanabe, Y.; Isyumov, N.; Davenport, A. Empirical Aerodynamic Damping Function for Tall Buildings. J. Wind Eng. Ind. Aerodyn. 1997, 72, 313–321. [Google Scholar] [CrossRef]
- Marukawa, H.; Kato, N.; Fujii, K.; Tamura, Y. Experimental Evaluation of Aerodynamic Damping of Tall Buildings. J. Wind Eng. Ind. Aerodyn. 1996, 59, 177–190. [Google Scholar] [CrossRef]
- Quan, Y.; Gu, M.; Tamura, Y. Experimental Evaluation of Aerodynamic Damping of Square Super High-Rise Buildings. Wind Struct. 2005, 8, 309–324. [Google Scholar] [CrossRef]
- Gu, M.; Cao, H.; Quan, Y. Experimental Study of Across-Wind Aerodynamic Damping of Super High-Rise Buildings with Aerodynamically Modified Square Cross-Sections. Struct. Des. Tall Spec. Build. 2014, 23, 1225–1245. [Google Scholar] [CrossRef]
- Tamura, Y.; Suganuma, S. Evaluation of Amplitude-Dependent Damping and Natural Frequency of Buildings During Strong Winds. J. Wind Eng. Ind. Aerodyn. 1996, 59, 115–130. [Google Scholar] [CrossRef]
- Chen, X.; Kareem, A. Advances in Modeling of Aerodynamic Forces on Bridge Decks. J. Eng. Mech. 2002, 128, 1193–1205. [Google Scholar] [CrossRef]
- Scanlan, R.H.; Tomo, J. Air Foil and Bridge Deck Flutter Derivatives. J. Soil Mech. Found. Div. 1971, 97, 1717–1737. [Google Scholar]
- Falco, M.; Curami, A.; Zasso, A. Nonlinear Effects in Sectional Model Aeroelastic Parameters Identification. J. Wind Eng. Ind. Aerodyn. 1992, 42, 1321–1332. [Google Scholar] [CrossRef]
- Jensen, A.G. Fluid Dynamic Derivatives: Marine and Wind Engineering Approaches. J. Wind Eng. Ind. Aerodyn. 1997, 69, 777–793. [Google Scholar] [CrossRef]
- Noda, M.; Utsunomiya, H.; Nagao, F.; Kanda, M.; Shiraishi, N. Effects of Oscillation Amplitude on Aerodynamic Derivatives. J. Wind Eng. Ind. Aerodyn. 2003, 91, 101–111. [Google Scholar] [CrossRef]
- Diana, G.; Resta, F.; Rocchi, D. A New Numerical Approach to Reproduce Bridge Aerodynamic Non-Linearities in Time Domain. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1871–1884. [Google Scholar] [CrossRef]
- Diana, G.; Rocchi, D.; Argentini, T.; Muggiasca, S. Aerodynamic Instability of a Bridge Deck Section Model: Linear and Nonlinear Approach to Force Modeling. J. Wind Eng. Ind. Aerodyn. 2010, 98, 363–374. [Google Scholar] [CrossRef]
- Diana, G.; Resta, F.; Zasso, A.; Belloli, M.; Rocchi, D. Forced motion and free motion aeroelastic tests on a new concept dynamometric section model of the Messina suspension bridge. J. Wind Eng. Ind. Aerodyn. 2004, 92, 441–462. [Google Scholar] [CrossRef]
- Daito, Y.; Matsumoto, M.; Araki, K. Torsional Flutter Mechanism of Two-Edge Girders for Long-Span Cable-Stayed Bridge. J. Wind Eng. Ind. Aerodyn. 2002, 90, 2127–2141. [Google Scholar] [CrossRef]
- Bokaian, A.; Geoola, F. Hydroelastic Instabilities of Square Cylinders. J. Sound Vib. 1984, 92, 117–141. [Google Scholar] [CrossRef]
- Corless, R.M.; Parkinson, G. A Model of the Combined Effects of Vortex-Induced Oscillation and Galloping. J. Fluids Struct. 1988, 2, 203–220. [Google Scholar] [CrossRef]
- Corless, R.M.; Parkinson, G. Mathematical Modelling of the Combined Effects of Vortex-Induced Vibration and Galloping. Part II. J. Fluids Struct. 1993, 7, 825–848. [Google Scholar] [CrossRef]
- Tamura, Y. A Mathematical Model for the Transverse Oscillations of Square Cylinder; Faculty of Engineering, Tokyo Institute of Polytechnic: Tokyo, Japan, 1987; pp. 56–62. [Google Scholar]
- Birkhoff, G. Formation of Vortex Streets. J. Appl. Phys. 1953, 24, 98–103. [Google Scholar] [CrossRef]
- Mannini, C.; Massai, T.; Marra, A.M.; Bartoli, G. Modelling the interaction of VIV and galloping for rectangular cylinders. In Proceedings of the 14th International Conference on Wind Engineering, Porto Alegre, Brazil, 21–26 May 2015. [Google Scholar]
- Gao, G.; Zhu, L. Nonlinear Mathematical Model of Unsteady Galloping Force on a Rectangular 2: 1 Cylinder. J. Fluids Struct. 2017, 70, 47–71. [Google Scholar] [CrossRef]
- Davenport, A. The treatment of wind loading on tall buildings. In Proceedings of the Symposium on Tall Buildings with Particular Reference to Shear Wall Structures, Southampton, Hampshire, UK, April 1966. [Google Scholar]

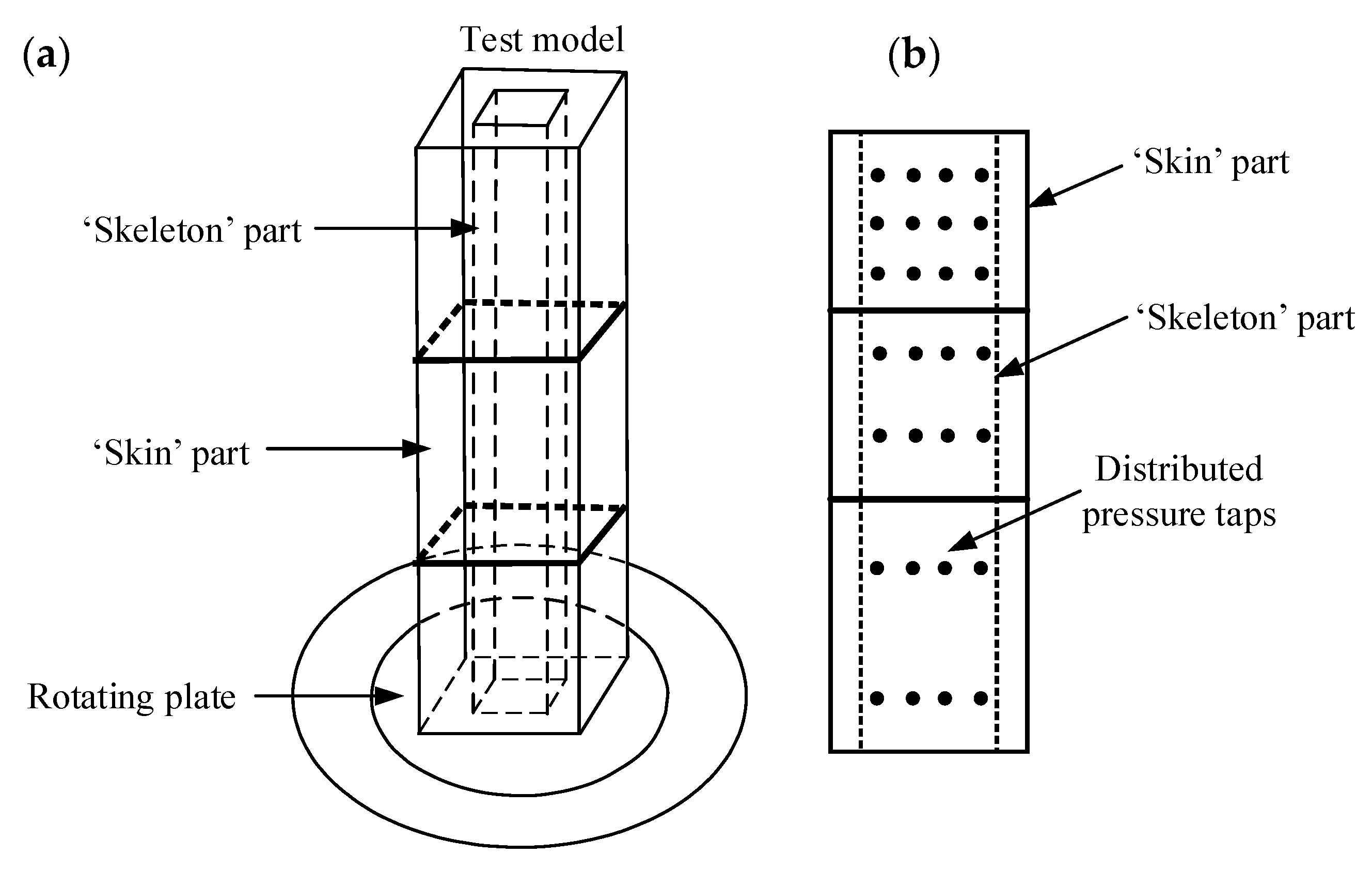
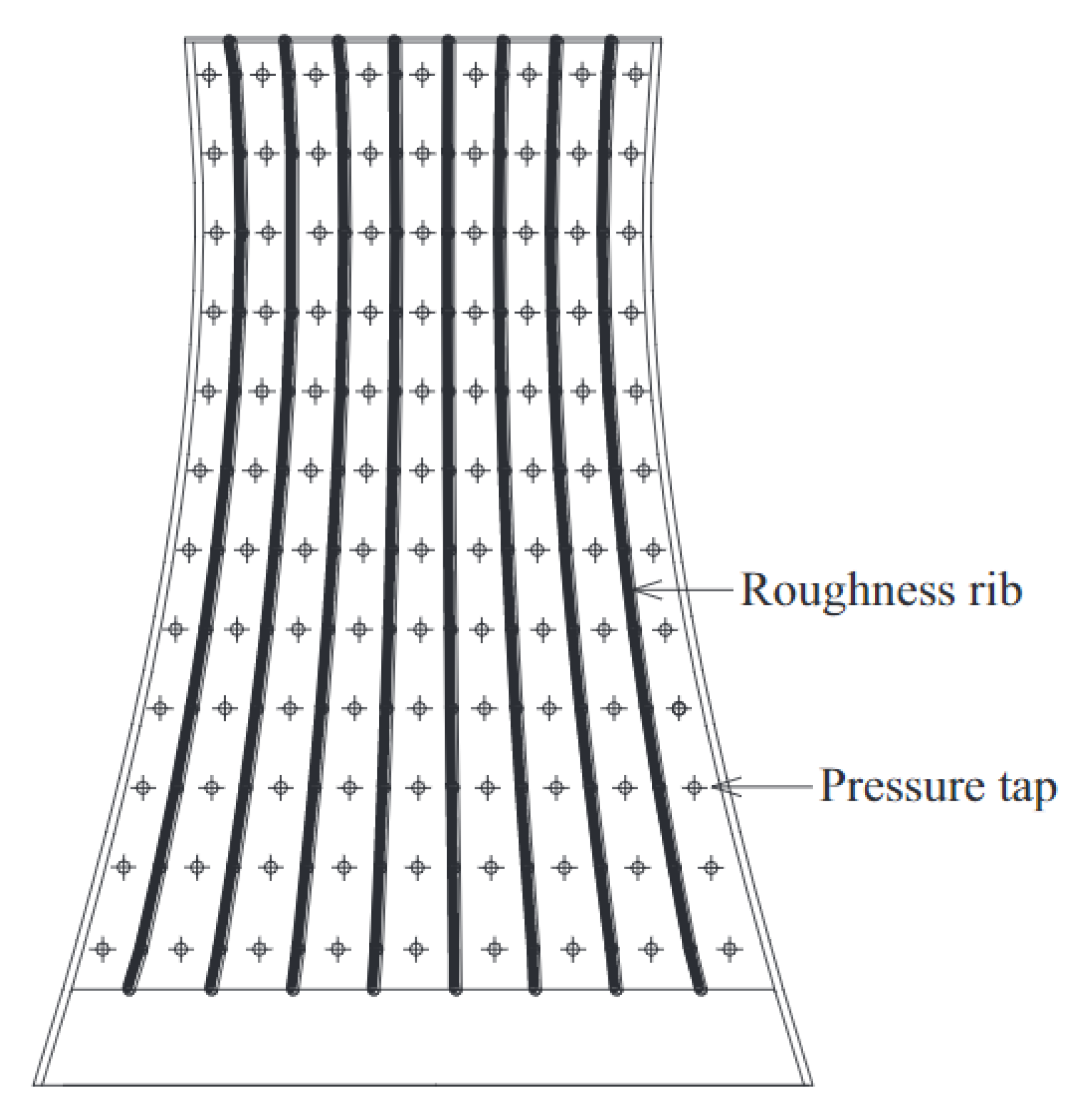

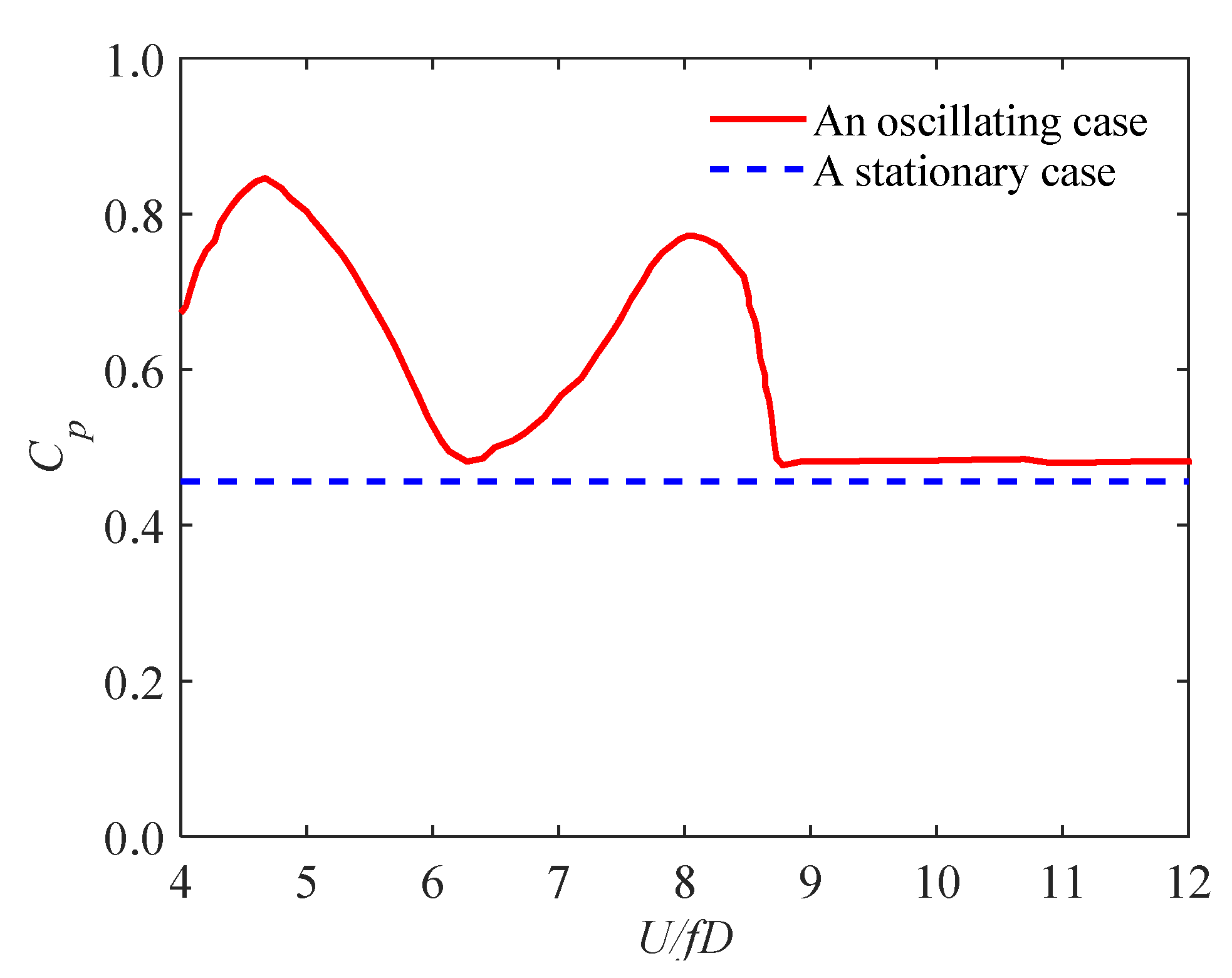
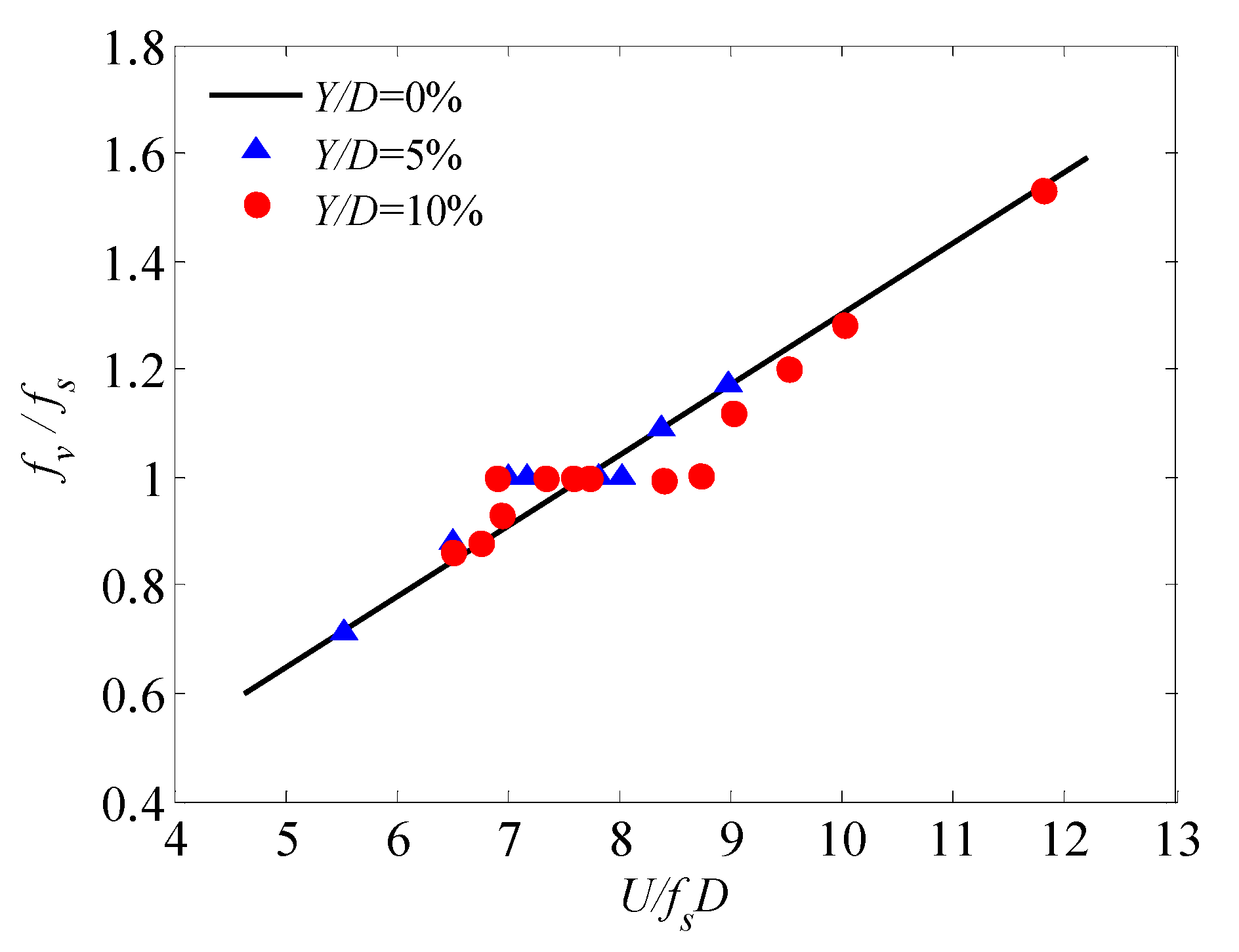
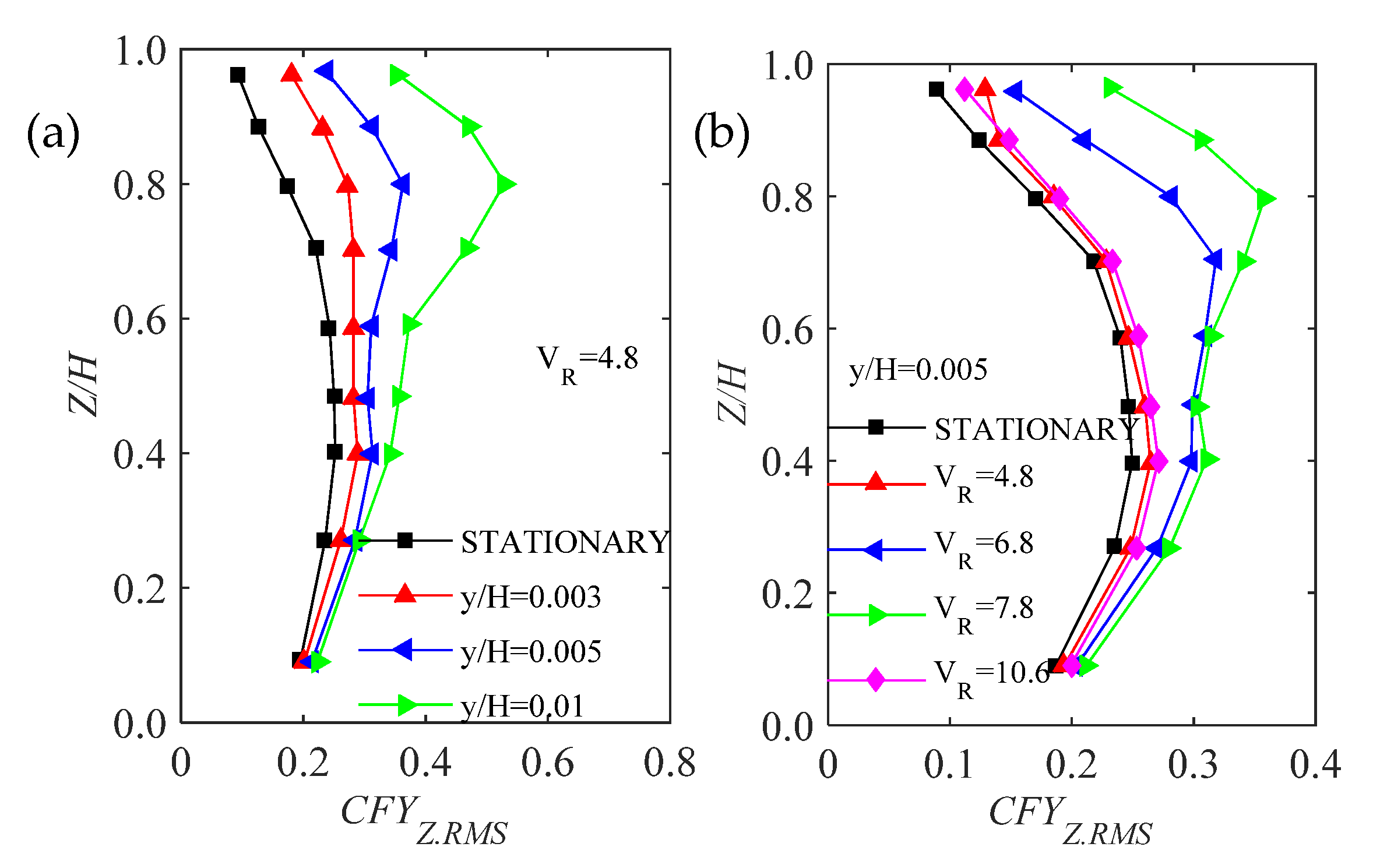
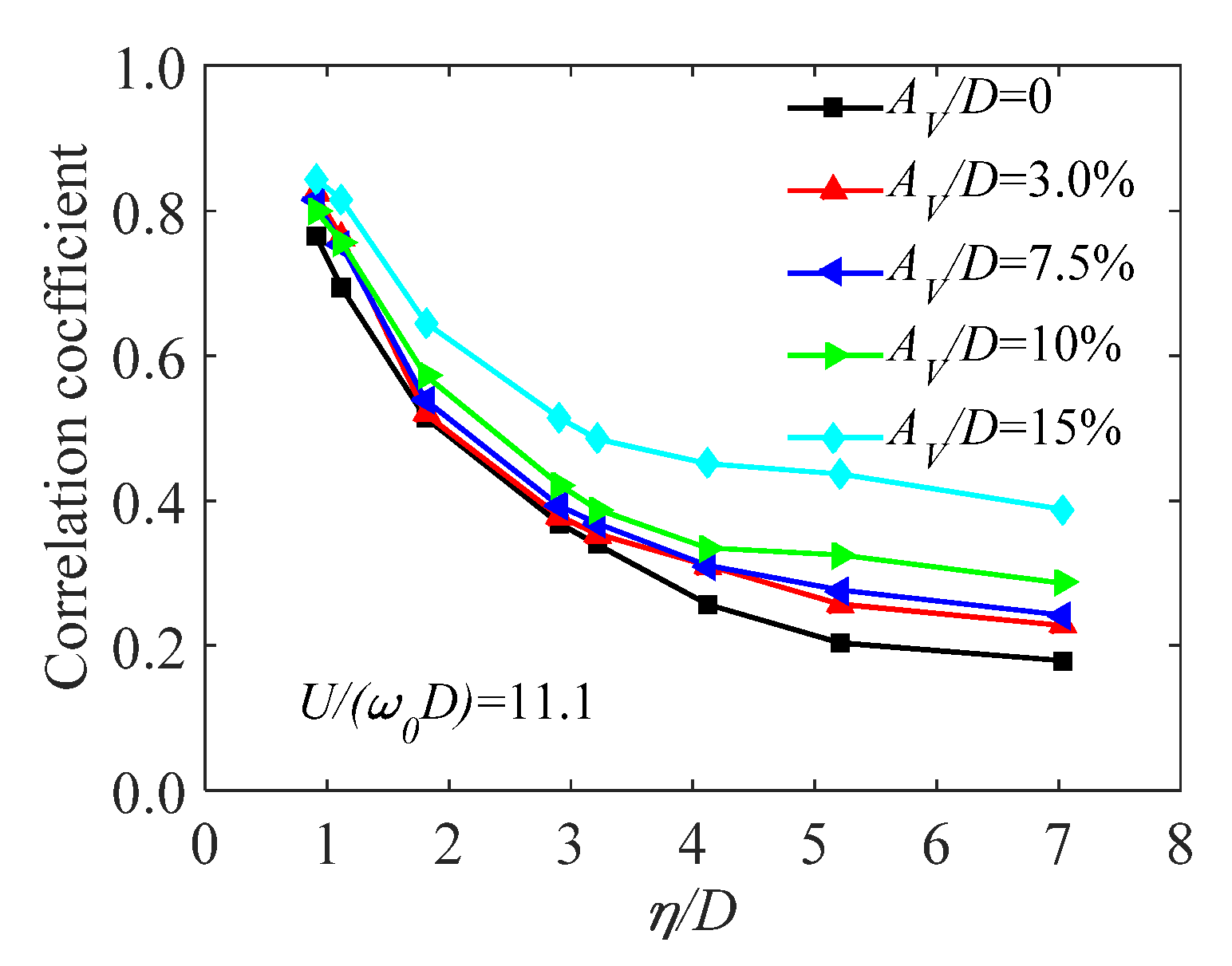
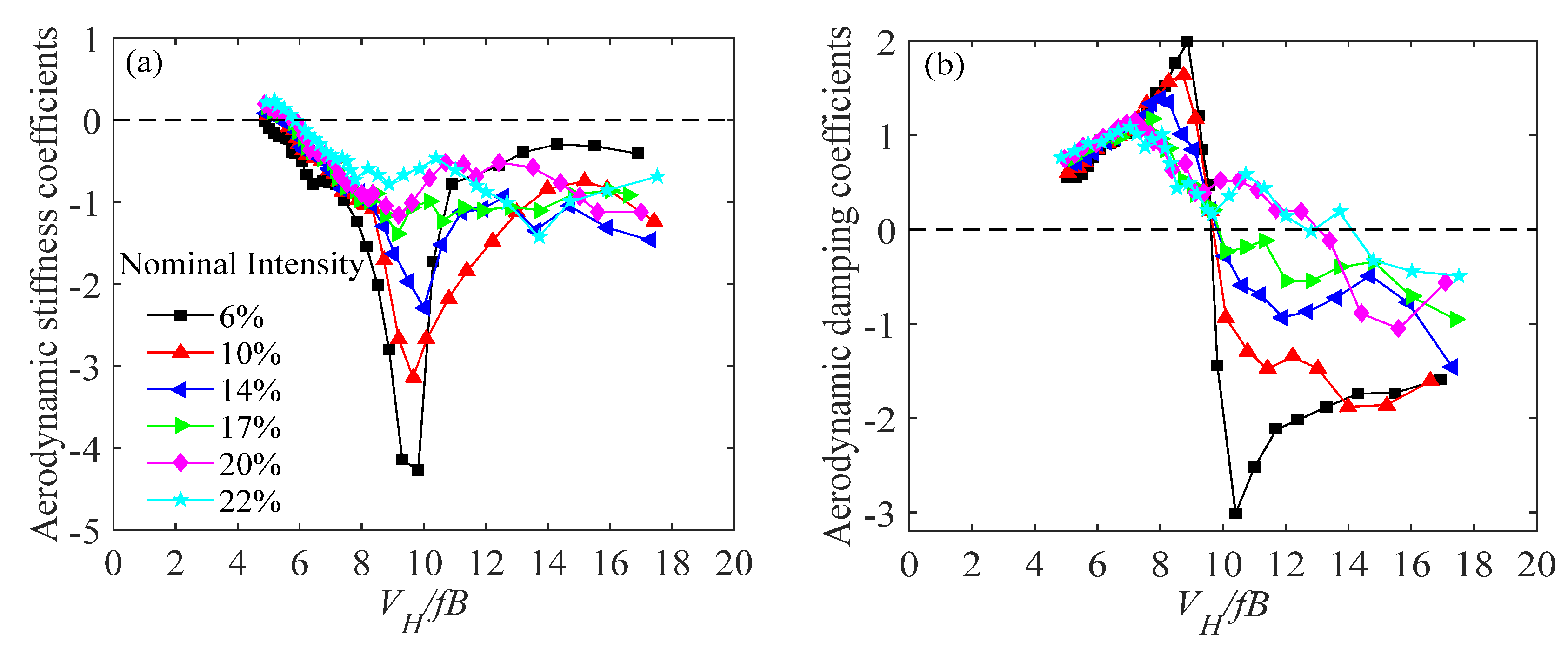
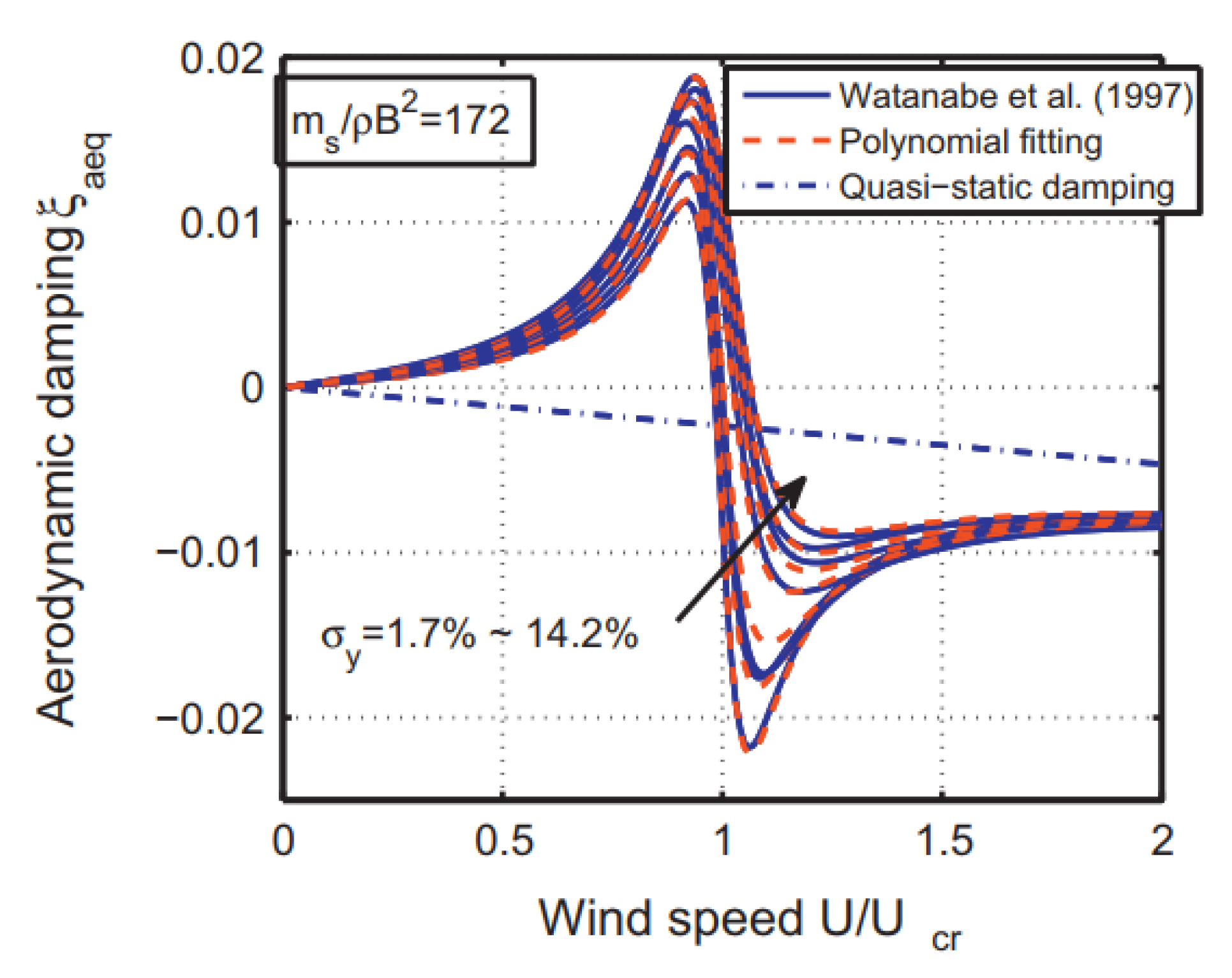


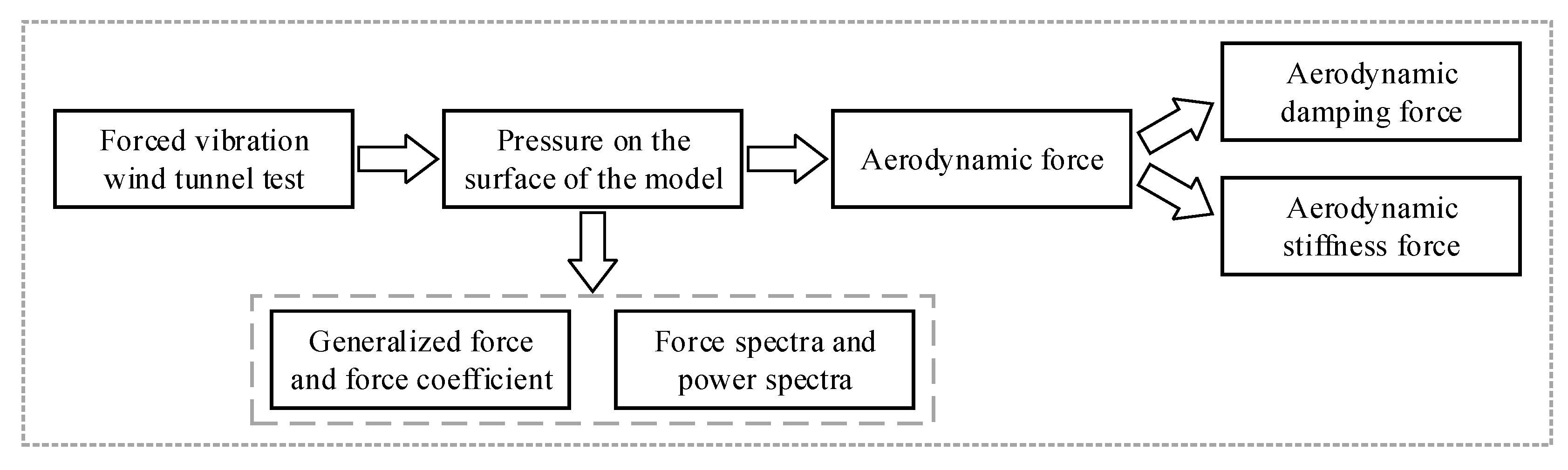
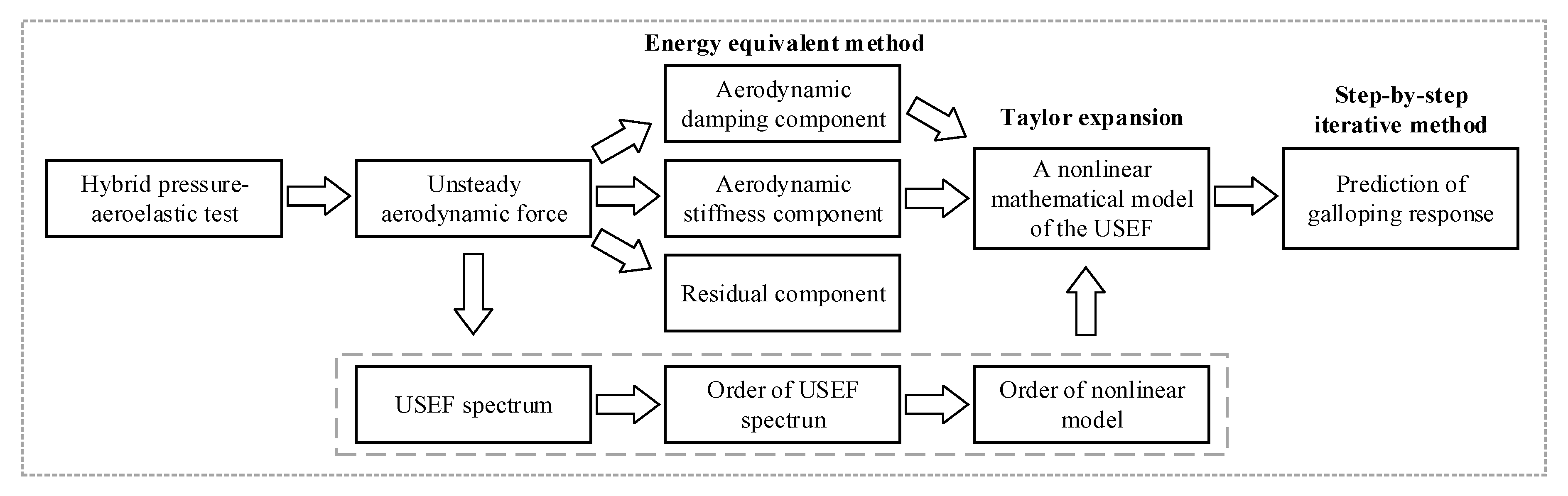
| Test Techniques | Characteristics of Test Model | Measured Content | Disadvantages |
|---|---|---|---|
| High frequency base balance test | Static | Base shear force and base overturning moment | No distributed pressure and unsteady effect |
| Static synchronous multi-pressure sensing system test | Static | Local pressure | No unsteady effect |
| Aeroelastic test | Free vibration | Response | No distributed pressure |
| Forced vibration test | Forced vibration | Local pressure and response | No two-way coupling effect |
| Hybrid aeroelastic-force balance test | Free vibration | Local pressure and response | − |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Xu, Y.; Huang, H.; Tse, K.T. Wind Tunnel Measurement Systems for Unsteady Aerodynamic Forces on Bluff Bodies: Review and New Perspective. Sensors 2020, 20, 4633. https://doi.org/10.3390/s20164633
Chen Z, Xu Y, Huang H, Tse KT. Wind Tunnel Measurement Systems for Unsteady Aerodynamic Forces on Bluff Bodies: Review and New Perspective. Sensors. 2020; 20(16):4633. https://doi.org/10.3390/s20164633
Chicago/Turabian StyleChen, Zengshun, Yemeng Xu, Hailin Huang, and Kam Tim Tse. 2020. "Wind Tunnel Measurement Systems for Unsteady Aerodynamic Forces on Bluff Bodies: Review and New Perspective" Sensors 20, no. 16: 4633. https://doi.org/10.3390/s20164633
APA StyleChen, Z., Xu, Y., Huang, H., & Tse, K. T. (2020). Wind Tunnel Measurement Systems for Unsteady Aerodynamic Forces on Bluff Bodies: Review and New Perspective. Sensors, 20(16), 4633. https://doi.org/10.3390/s20164633