Evaluation of Hyperparameter Optimization in Machine and Deep Learning Methods for Decoding Imagined Speech EEG
Abstract
1. Introduction
2. Methods
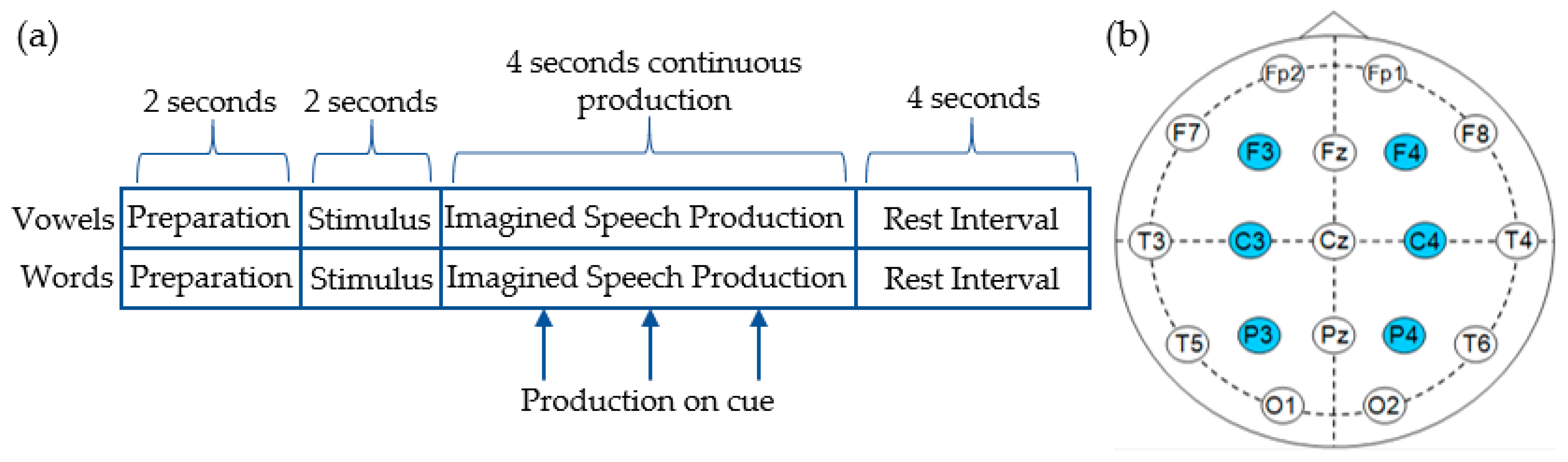
2.1. Dataset and Preprocessing Methods
2.2. Classification Techniques
2.2.1. Benchmark Machine Learning Classifiers
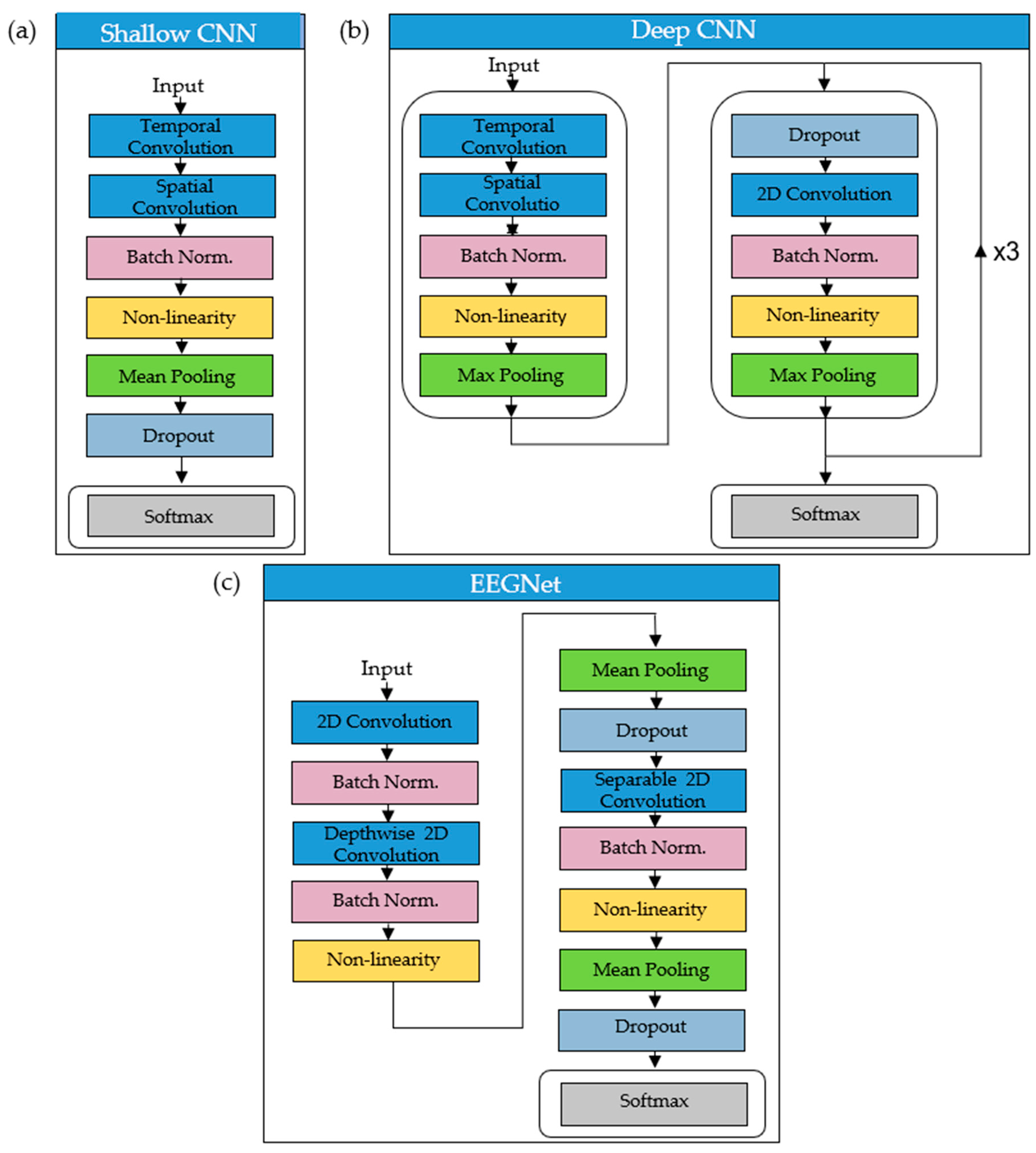
2.2.2. CNN Architectures
2.3. Method for Optimizing Hyperparameters
| Algorithm 1. Nested cross-validation (nCV) |
| Input: Dataset D = (, ), …,(, ) Set of hyperparameters ϴ Classifier C Integer k Outer fold: for each partition D into D1, D2,…,Dk Inner fold: Inner-fold data iD = concatenate iD1,…,iDk−1 partition iD into iD1, iD2,…,iDk for θ in ϴ for i = 1….k = C(iDi, θ;) Acc(θ) = // mean accuracy for HP set totalAcc(θ) = // mean HP accuracy for all inner folds θ* = argmaxθ[totalAcc(θ)] // optimal set of hyper parameters across all folds for i = 1….k = C(Di, θ*) Acc(θ*) = , // mean test accuracy with a single set of HPs |
2.4. CNN Training
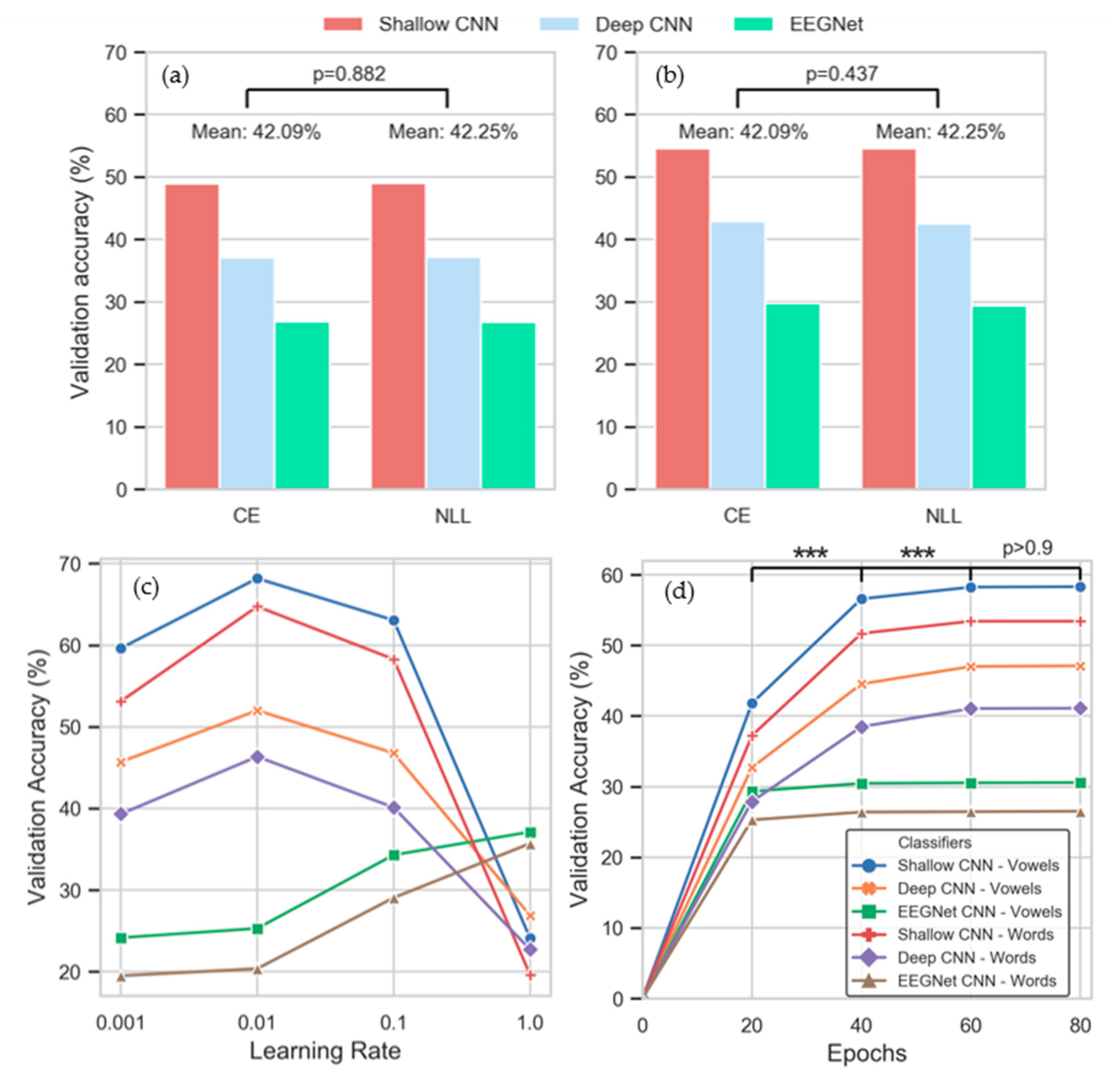
2.5. Statistical Analysis
3. Results
3.1. Hyperparameters and Kernels Selected for Benchmark Classifiers
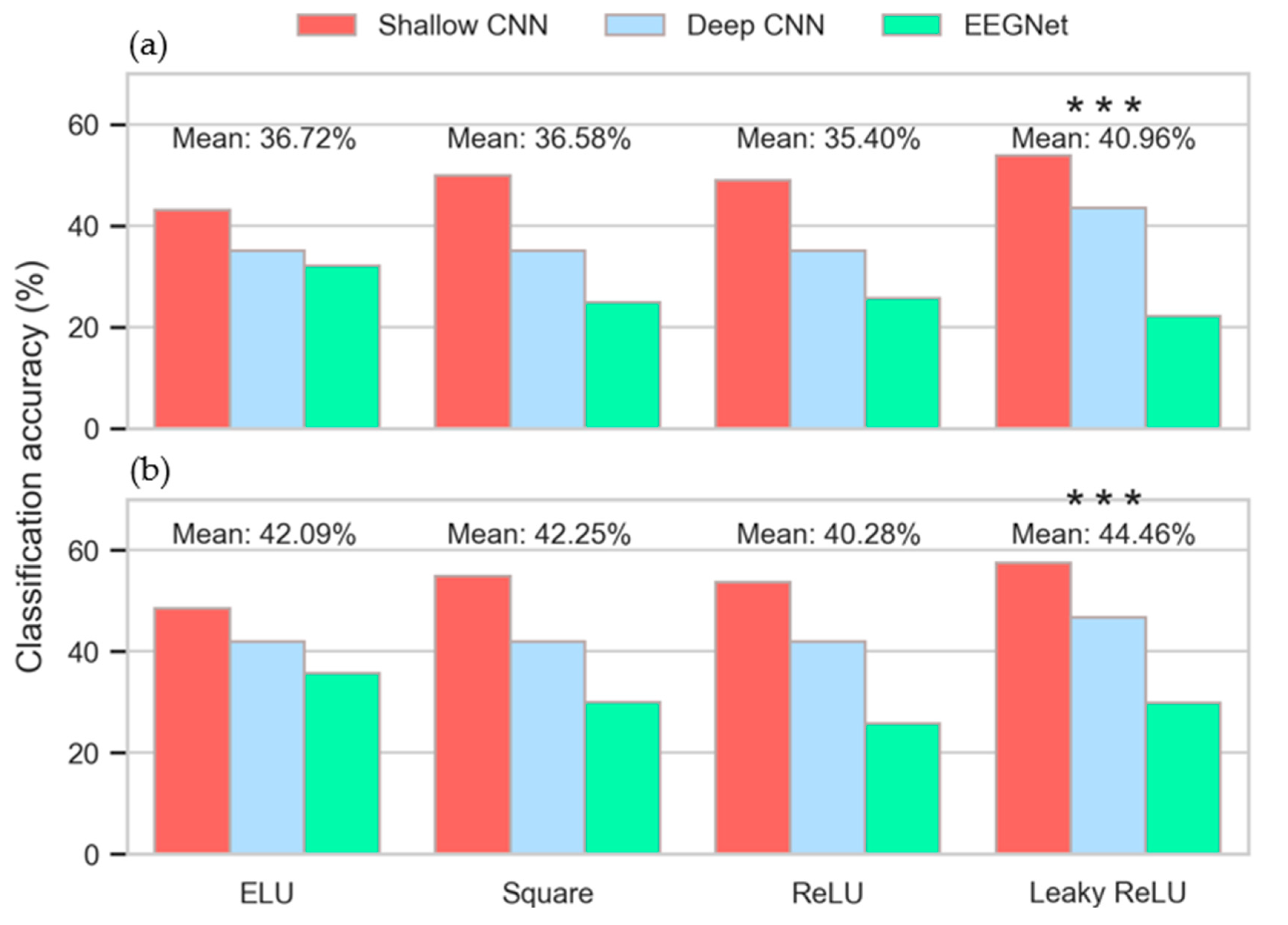
3.2. Hyperparameters Selected for CNNs
3.3. Intra-Subject Selection of Hyperparameters
3.4. Inter-Subject Selection of Hyperparameters
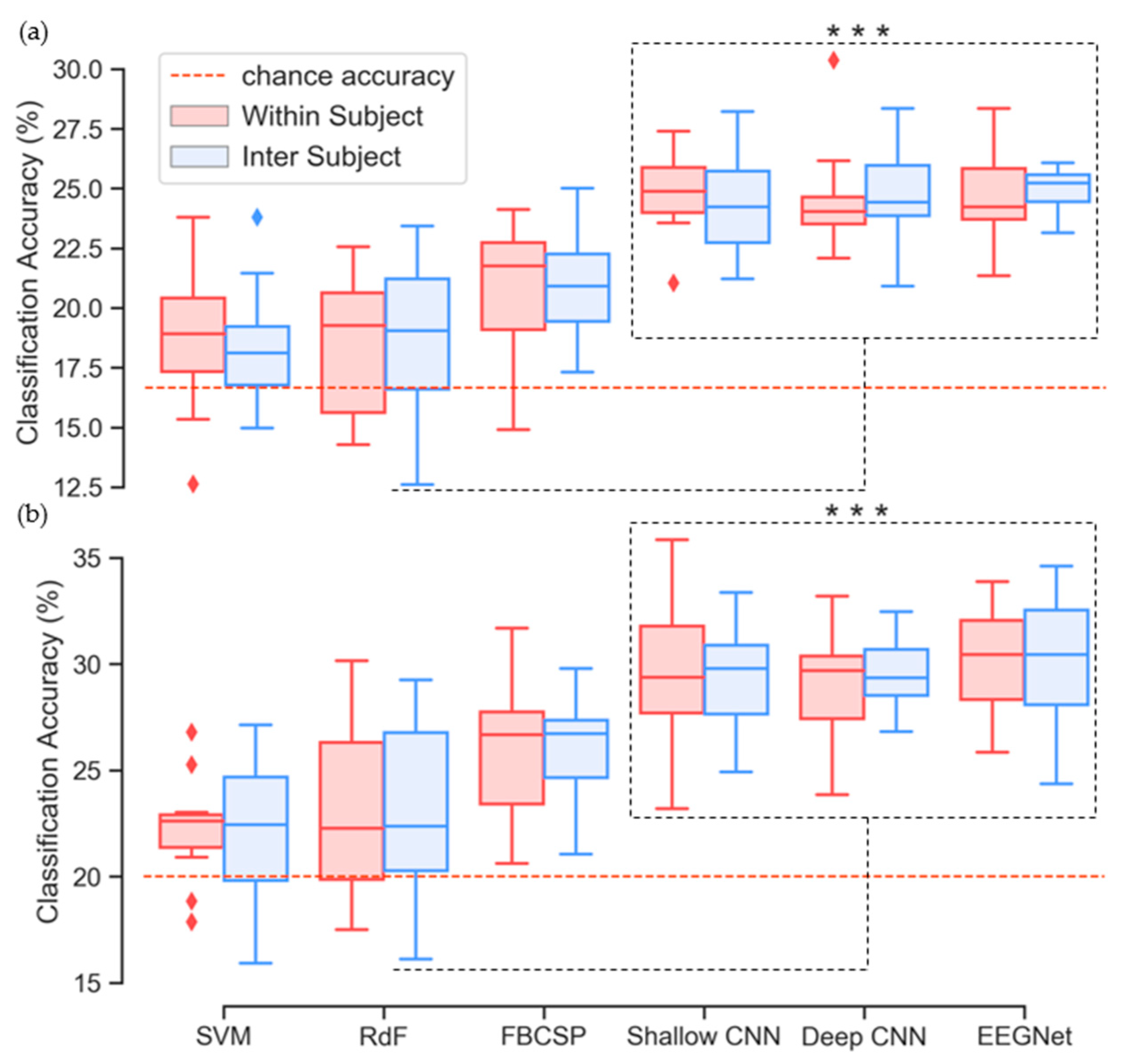
3.5. Classification Performance
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McFarland, D.J.; Lefkowicz, A.T.; Wolpaw, J.R. Design and operation of an EEG-based brain-computer interface with digital signal processing technology. Behav. Res. Methods Instrum. Comput. 1997, 29, 337–345. [Google Scholar] [CrossRef]
- Edelman, B.J.; Baxter, B.; He, B. EEG source imaging enhances the decoding of complex right-hand motor imagery tasks. IEEE Trans. Biomed. Eng. 2016, 63, 4–14. [Google Scholar] [CrossRef]
- Bakardjian, H.; Tanaka, T.; Cichocki, A. Optimization of SSVEP brain responses with application to eight-command Brain–Computer Interface. Neurosci. Lett. 2010, 469, 34–38. [Google Scholar] [CrossRef]
- Marshall, D.; Coyle, D.; Wilson, S.; Callaghan, M. Games, gameplay, and BCI: The state of the art. IEEE Trans. Comput. Intell. AI Games 2013, 5, 82–99. [Google Scholar] [CrossRef]
- Prasad, G.; Herman, P.; Coyle, D.; Mcdonough, S.; Crosbie, J. Using Motor Imagery Based Brain-Computer Interface for Post-stroke Rehabilitation. In Proceedings of the 2009 4th International IEEE/EMBS Conference on Neural Engineering, Antalya, Turkey, 29 April–2 May 2009; pp. 258–262. [Google Scholar]
- Iljina, O.; Derix, J.; Schirrmeister, R.T.; Schulze-Bonhage, A.; Auer, P.; Aertsen, A.; Ball, T. Neurolinguistic and machine-learning perspectives on direct speech BCIs for restoration of naturalistic communication. Brain-Comput. Interfaces 2017, 4, 186–199. [Google Scholar] [CrossRef]
- Cooney, C.; Folli, R.; Coyle, D. Neurolinguistics Research Advancing Development of a Direct-Speech Brain-Computer Interface. IScience 2018, 8, 103–125. [Google Scholar] [CrossRef] [PubMed]
- Ramadan, R.A.; Vasilakos, A.V. Brain computer interface: Control signals review. Neurocomputing 2017, 223, 26–44. [Google Scholar] [CrossRef]
- Moses, D.A.; Leonard, M.K.; Chang, E.F. Real-time classification of auditory sentences using evoked cortical activity in humans. J. Neural Eng. 2018, 15, 036005. [Google Scholar] [CrossRef]
- Moses, D.A.; Leonard, M.K.; Makin, J.G.; Chang, E.F. Real-time decoding of question-and-answer speech dialogue using human cortical activity. Nat. Commun. 2019, 10, 3096. [Google Scholar] [CrossRef]
- Makin, J.G.; Moses, D.A.; Chang, E.F. Machine translation of cortical activity to text with an encoder–decoder framework. Nat. Neurosci. 2020, 23, 575–582. [Google Scholar] [CrossRef]
- D’albis, T.; Blatt, R.; Tedesco, R.; Sbattella, L.; Matteucci, M. A predictive speller controlled by a brain-computer interface based on motor imagery. ACM Trans. Comput. Interact. 2012, 19, 1–25. [Google Scholar] [CrossRef]
- Combaz, A.; Chatelle, C.; Robben, A.; Vanhoof, G.; Goeleven, A.; Thijs, V.; Van Hulle, M.M.; Laureys, S. A Comparison of two spelling brain-computer interfaces based on visual P3 and SSVEP in locked-in syndrome. PLoS ONE 2013, 8, e73691. [Google Scholar] [CrossRef] [PubMed]
- Anumanchipalli, G.K.; Chartier, J.; Chang, E.F. Speech synthesis from neural decoding of spoken sentences. Nature 2019, 568, 493–498. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Wang, Y.; Flinker, A. Reconstructing Speech Stimuli from Human Auditory Cortex Activity Using a WaveNet-like Network. In Proceedings of the 2018 IEEE Signal Processing in Medicine and Biology Symposium (SPMB), Philadelphia, PA, USA, 1 December 2018; pp. 1–6. [Google Scholar]
- Dash, D.; Ferrari, P.; Wang, J. Decoding imagined and spoken phrases from non-invasive neural (MEG) signals. Front. Neurosci. 2020, 14, 290. [Google Scholar] [CrossRef]
- Nguyen, C.H.; Karavas, G.; Artemiadis, P. Inferring imagined speech using EEG signals: A new approach using Riemannian Manifold features. J. Neural Eng. 2017, 15, 016002. [Google Scholar] [CrossRef]
- Hashim, N.; Ali, A.; Mohd-Isa, W.-N. Word-Based Classification of Imagined Speech Using EEG. In Proceedings of the International Conference on Computational Science and Technology, Kuala Lumpur, Malaysia, 29–30 November 2017; pp. 195–204. [Google Scholar]
- Iqbal, S.; Shanir, P.P.M.; Khan, Y.U.K.; Farooq, O. Time Domain Analysis of EEG to Classify Imagined Speech. In Proceedings of the Second International Conference on Computer and Communication Technologies, Hyderabad, India, 24–26 July 2015; pp. 793–800. [Google Scholar]
- Kim, T.; Lee, J.; Choi, H.; Lee, H.; Kim, I.Y.; Jang, D.P. Meaning based covert speech classification for brain-computer interface based on electroencephalography. In Proceedings of the International IEEE/EMBS Conference on Neural Engineering (NER), San Diego, CA, USA, 6–8 November 2013; pp. 53–56. [Google Scholar]
- Sereshkeh, A.R.; Trott, R.; Bricout, A.; Chau, T. EEG Classification of covert speech using regularized neural networks. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 2292–2300. [Google Scholar] [CrossRef]
- Yoshimura, N.; Nishimoto, A.; Belkacem, A.N.; Shin, D.; Kambara, H.; Hanakawa, T.; Koike, Y. Decoding of covert vowel articulation using electroencephalography cortical currents. Front. Neurosci. 2016, 10. [Google Scholar] [CrossRef]
- Zhao, S.; Rudzicz, F. Classifying phonological categories in imagined and articulated speech. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Queensland, Australia, 19–24 April 2015; pp. 992–996. [Google Scholar]
- Acharya, U.R.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adeli, H. Deep convolutional neural network for the automated detection and diagnosis of seizure using EEG signals. Comput. Biol. Med. 2017, 270–278. [Google Scholar] [CrossRef]
- DaSalla, C.S.; Kambara, H.; Sato, M.; Koike, Y. Single-trial classification of vowel speech imagery using common spatial patterns. Neural Netw. 2009, 22, 1334–1339. [Google Scholar] [CrossRef]
- Brigham, K.; Kumar, B.V.K.V. Subject identification from Electroencephalogram (EEG) signals during imagined speech. In Proceedings of the IEEE 4th International Conference on Biometrics: Theory, Applications and Systems (BTAS) 2010, Washington, DC, USA, 27–29 September 2010. [Google Scholar]
- Song, Y.; Sepulveda, F. Classifying speech related vs. idle state towards onset detection in brain-computer interfaces overt, inhibited overt, and covert speech sound production vs. idle state. In Proceedings of the IEEE 2014 Biomedical Circuits and Systems Conference (BioCAS), Tokyo, Japan, 22–24 October 2014; pp. 568–571. [Google Scholar]
- Cooney, C.; Folli, R.; Coyle, D. Mel Frequency Cepstral coefficients enhance imagined speech decoding accuracy from EEG. In Proceedings of the 2018 29th Irish Signals and Systems Conference (ISSC), Belfast, UK, 21–22 June 2018. [Google Scholar]
- Iqbal, S.; Khan, Y.U.; Farooq, O. EEG based classification of imagined vowel sounds. In Proceedings of the 2015 2nd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 11–13 March 2015; pp. 1591–1594. [Google Scholar]
- González-Castañeda, E.F.; Torres-García, A.A.; Reyes-García, C.A.; Villaseñor-Pineda, L. Sonification and textification: Proposing methods for classifying unspoken words from EEG signals. Biomed. Signal Process. Control 2017, 37, 82–91. [Google Scholar] [CrossRef]
- Chi, X.; Hagedorn, J.B.; Schoonover, D.; Zmura, M.D. EEG-Based discrimination of imagined speech phonemes. Int. J. Bioelectromagn. 2011, 13, 201–206. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems25; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Neural Information Processing Systems Foundation Inc.: La Jolla, CA, USA, 2012; pp. 1097–1105. [Google Scholar]
- Graves, A.; Mohamed, A.R.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–30 May 2013; pp. 6645–6649. [Google Scholar]
- Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Hum. Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef] [PubMed]
- Tabar, Y.R.; Halici, U. A novel deep learning approach for classification of EEG motor imagery signals. J. Neural Eng. 2017, 14, 016003. [Google Scholar] [CrossRef] [PubMed]
- Roy, Y.; Banville, H.; Albuquerque, I.; Gramfort, A.; Falk, T.H.; Faubert, J. Deep learning-based electroencephalography analysis: A systematic review. J. Neural Eng. 2019, 16, 051001. [Google Scholar] [CrossRef] [PubMed]
- Kwak, N.S.; Müller, K.R.; Lee, S.W. A convolutional neural network for steady state visual evoked potential classification under ambulatory environment. PLoS ONE 2017, 12, e0172578. [Google Scholar] [CrossRef] [PubMed]
- Cecotti, H.; Graser, A. Convolutional neural networks for P300 Detection with Application to Brain-Computer Interfaces. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 433–445. [Google Scholar] [CrossRef]
- Bashivan, P.; Rish, I.; Yeasin, M.; Codella, N. Learning Representations from EEG with Deep Recurrent-Convolutional Neural Networks. arXiv 2016, arXiv:1511.06448. [Google Scholar]
- Völker, M.; Schirrmeister, R.T.; Fiederer, L.D.J.; Burgard, W.; Ball, T. Deep Transfer Learning for Error Decoding from Non-Invasive EEG. In Proceedings of the 2018 6th International Conference on Brain-Computer Interface (BCI), Gangwon, Korea, 15–17 January 2018; pp. 1–6. [Google Scholar]
- Cooney, C.; Folli, R.; Coyle, D. Optimizing Layers Improves CNN Generalization and Transfer Learning for Imagined Speech Decoding from EEG. In Proceedings of the 2019 IEEE International Conference on Systems, Man, and Cybernetics, SMC 2019, Bari, Italy, 6–9 October 2019. [Google Scholar]
- Heilmeyer, F.A.; Schirrmeister, R.T.; Fiederer, L.D.J.; Völker, M.; Behncke, J.; Ball, T. A Large-Scale Evaluation Framework for EEG Deep Learning Architectures. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics, SMC 2018, Miyazaki, Japan, 7–10 October 2018; pp. 1039–1045. [Google Scholar]
- Cooney, C.; Folli, R.; Coyle, D. Classification of imagined spoken word-pairs using convolutional neural networks. In The 8th Graz BCI Conference, 2019; Verlag der Technischen Universitat Graz: Graz, Austria, 2019; pp. 338–343. [Google Scholar]
- Craik, A.; He, Y.; Contreras-Vidal, Jose, L. Deep Learning for electroencephalogram (EEG) Classification Tasks: A Review. J. Neural Eng. 2019, 16, 031001. [Google Scholar] [CrossRef]
- Reddy, T.K.; Arora, V.; Kumar, S.; Behera, L.; Wang, Y.K.; Lin, C.T. Electroencephalogram based reaction time prediction with differential phase synchrony representations using co-operative multi-task deep neural networks. IEEE Trans. Emerg. Top. Comput. Intell. 2019, 3, 369–379. [Google Scholar] [CrossRef]
- Reddy, T.K.; Arora, V.; Behera, L. HJB-Equation-Based optimal learning scheme for neural networks with applications in brain-computer interface. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 4, 159–170. [Google Scholar] [CrossRef]
- Aznan, N.K.N.; Bonner, S.; Connolly, J.; al Moubayed, N.; Breckon, T. On the classification of SSVEP-Based Dry-EEG signals via convolutional neural networks. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics, SMC 2018, Miyazaki, Japan, 7–10 October 2018; pp. 3726–3731. [Google Scholar]
- Drouin-Picaro, A.; Falk, T.H. Using deep neural networks for natural saccade classification from electroencephalograms. In Proceedings of the 2016 IEEE EMBS International Student Conference Expand. Boundaries Biomedical Engineering Healthy ISC 2016, Ottawa, ON, Canada, 29–31 May 2016; pp. 1–4. [Google Scholar]
- Schwabedal, J.T.C.; Snyder, J.C.; Cakmak, A.; Nemati, S.; Clifford, G.D. Addressing Class Imbalance in Classification Problems of Noisy Signals by using Fourier Transform Surrogates. arXiv 2018, arXiv:1806.08675v2. [Google Scholar]
- Stober, S.; Cameron, D.J.; Grahn, J.A. Using convolutional neural networks to recognize rhythm stimuli from electroencephalography recordings. Adv. Neural Inf. Process. Syst. 2014, 2, 1449–1457. [Google Scholar]
- Stober, S.; Sternin, A.; Owen, A.M.; Grahn, J.A. Deep Feature Learning for EEG Recordings. arXiv 2015, arXiv:1511.04306. [Google Scholar]
- Patnaik, S.; Moharkar, L.; Chaudhari, A. Deep RNN learning for EEG based functional brain state inference. In Proceedings of the 2017 International Conference Advances in Computing, Communication and Control, ICAC3 2017, Mumbai, India, 1–2 December 2017; pp. 1–6. [Google Scholar]
- Abbas, W.; Khan, N.A. DeepMI: Deep Learning for Multiclass Motor Imagery Classification. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering Medical Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 219–222. [Google Scholar]
- Wang, Z.; Cao, L.; Zhang, Z.; Gong, X.; Sun, Y.; Wang, H. Short time Fourier transformation and deep neural networks for motor imagery brain computer interface recognition. Concurr. Comput. 2018, 30, e4413. [Google Scholar] [CrossRef]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A Compact Convolutional Network for EEG-based Brain-Computer Interfaces. J. Neural Eng. 2018, 15, 056013. [Google Scholar] [CrossRef]
- Coretto, G.A.P.; Gareis, I.E.; Rufiner, H.L. Open access database of EEG signals recorded during imagined speech. In Proceedings of the 12th International Symposium on Medical Information Processing and Analysis, Catania, Italy, 11–15 September 2017; p. 1016002. [Google Scholar]
- Neto, E.; Biessmann, F.; Aurlien, H.; Nordby, H.; Eichele, T. Regularized linear discriminant analysis of EEG features in dementia patients. Front. Aging Neurosci. 2016, 8, 273. [Google Scholar] [CrossRef]
- Ang, K.K.; Chin, Z.Y.; Zhang, H.; Guan, C. Filter Bank Common Spatial Pattern (FBCSP) in brain-computer interface. In Proceedings of the International Jt. Conference Neural Networks (IEEE World Congress on Computational Intelligence) 2008, Hong Kong, China, 1–8 June 2008; pp. 2390–2397. [Google Scholar]
- Tangermann, M.; Müller, K.R.; Aertsen, A.; Birbaumer, N.; Braun, C.; Brunner, C.; Leeb, R.; Mehring, C.; Miller, K.J.; Mueller-Putz, G.; et al. Review of the BCI competition IV. Front. Neurosci. 2012, 6, 55. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Hartmann, K.G.; Schirrmeister, R.T.; Ball, T. Hierarchical internal representation of spectral features in deep convolutional networks trained for EEG decoding. In Proceedings of the 2018 6th International Conference on Brain-Computer Interface, BCI 2018, Gangwon, Korea, 15–17 January 2018; pp. 1–6. [Google Scholar]
- Schirrmeister, R.; Gemein, L.; Eggensperger, K.; Hutter, F.; Ball, T. Deep Learning with Convolutional Neural Networks for Decoding and Visualization of EEG Pathology. In Proceedings of the 2017 IEEE Signal Processing in Medicine and Biology Symposium (SPMB), Philadelphia, PA, USA, 2 December 2017; pp. 1–7. [Google Scholar]
- Wang, X.; Gkogkidis, C.A.; Schirrmeister, R.T.; Heilmeyer, F.A.; Gierthmuehlen, M.; Kohler, F.; Schuettler, M.; Stieglitz, T.; Ball, T. Deep learning for micro-electrocorticographic (µECoG) data. In Proceedings of the 2018 IEEE EMBS Conference on Biomedical Engineering Science IECBES 2018, Kuching Sarawak, Malaysia, 3–6 December 2018; pp. 63–68. [Google Scholar]
- Clevert, D.-A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (ELUs). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Korik, A.; Sosnik, R.; Siddique, N.; Coyle, D. Decoding imagined 3D hand movement trajectories from EEG: Evidence to support the use of mu, beta, and low gamma oscillations. Front. Neurosci. 2018, 12, 130. [Google Scholar] [CrossRef] [PubMed]
- Oh, K.; Chung, Y.C.; Kim, K.W.; Kim, W.S.; Oh, I.S. Classification and visualization of Alzheimer’s disease using volumetric convolutional neural network and transfer learning. Sci. Rep. 2019, 9, 18150. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT press Cambridge: Cambridge, MA, USA, 2016; Volume 1. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Tukey, J.W. Comparing Individual Means in the Analysis of Variance. Biometrics 1949, 5, 99–114. [Google Scholar] [CrossRef] [PubMed]
- Varoquaux, G. Cross-validation failure: Small sample sizes lead to large error bars. Neuroimage 2018, 180, 68–77. [Google Scholar] [CrossRef]
- Jeunet, C.; Lotte, F.; Batail, J.; Franchi, J.M. Using recent BCI literature to deepen our understanding of clinical neurofeedback: A short review. Neuroscience 2018, 378, 225–233. [Google Scholar] [CrossRef]
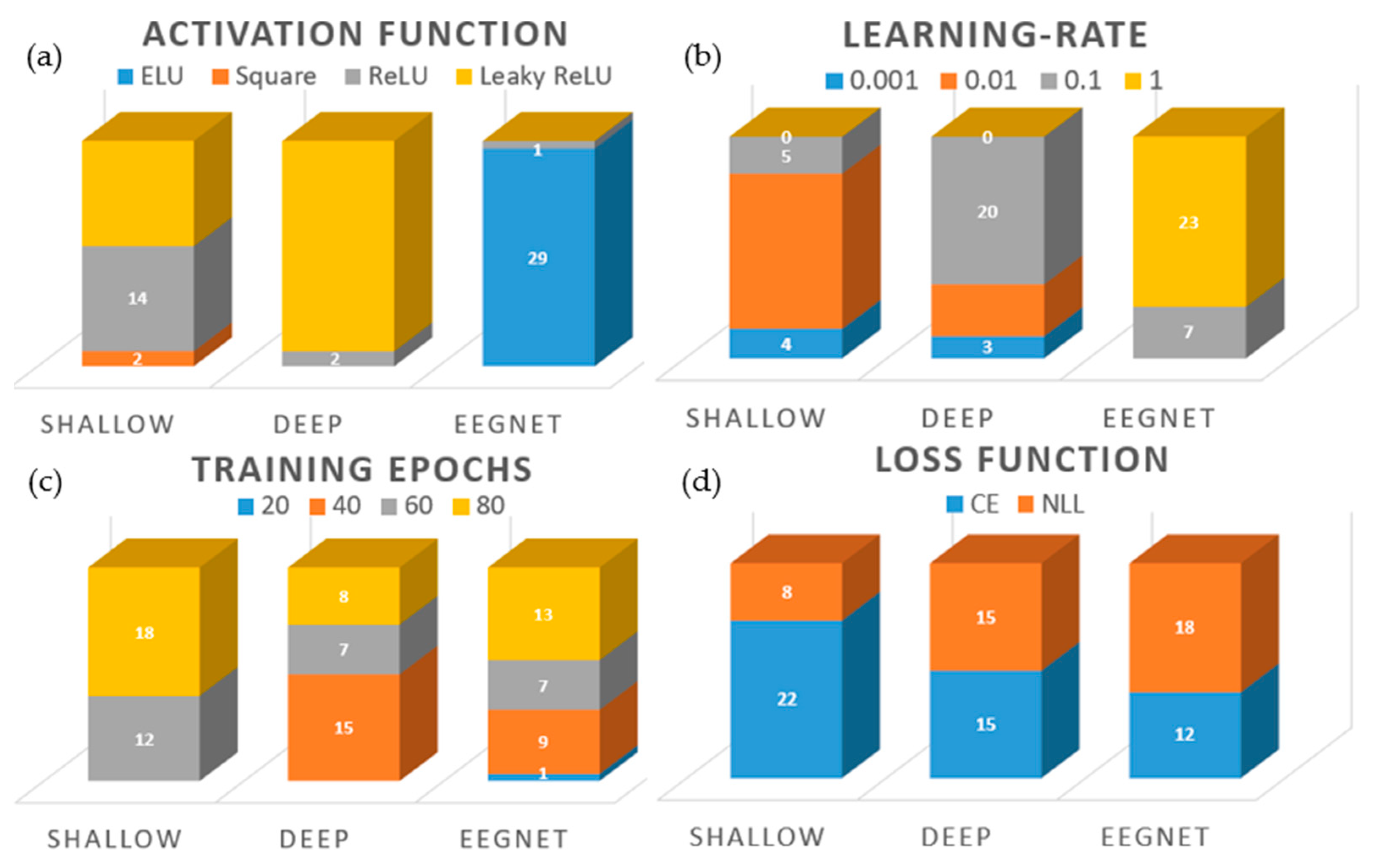
| SVM | RdF | FBCSP | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Kernel | C | g | NoF | Trees | MSL | nSF | MIQL | NoF | |
| Words | poly | 10 | 10 | 7 | 50 | 2 | 2 | 8 | 10 |
| Vowels | poly | 1 | 10 | 5 | 50 | 2 | 4 | 4 | 10 |
| Shallow CNN | Deep CNN | EEGNet | ||||
|---|---|---|---|---|---|---|
| Words | Vowels | Words | Vowels | Words | Vowels | |
| Activation Function | leaky ReLU | leaky ReLU | leaky ReLU | leaky ReLU | ELU | ELU |
| Learning Rate | 0.1 | 0.1 | 0.1 | 0.1 | 1 | 1 |
| Epochs | 60 | 60 | 60 | 60 | 80 | 80 |
| Loss | CE | NLL | CE | CE | NLL | NLL |
| Benchmark Methods | CNN Methods | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM | RdF | rLDA | Shallow | Deep | EEGNet | |||||||
| Intra | Inter | Intra | Inter | Intra | Inter | Intra | Inter | Intra | Inter | Intra | Inter | |
| Accuracy | 18.71 | 18.36 | 18.37 | 18.72 | 20.77 | 21.03 | 24.88 | 24.35 | 24.42 | 24.78 | 24.46 | 24.90 |
| Std. | 2.90 | 2.46 | 2.83 | 3.16 | 2.66 | 2.18 | 1.59 | 1.95 | 1.91 | 1.78 | 1.75 | 0.93 |
| Max. | 23.79 | 23.79 | 22.56 | 23.42 | 24.13 | 25.00 | 27.38 | 28.22 | 30.36 | 28.36 | 28.35 | 26.54 |
| Benchmark Methods | CNN Methods | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM | RdF | rLDA | Shallow | Deep | EEGNet | |||||||
| Intra | Inter | Intra | Inter | Intra | Inter | Intra | Inter | Intra | Inter | Intra | Inter | |
| Accuracy | 22.23 | 22.25 | 23.08 | 23.23 | 25.82 | 26.22 | 29.62 | 29.39 | 29.06 | 29.58 | 30.08 | 30.25 |
| Std. | 2.968 | 3.33 | 3.88 | 4.13 | 3.13 | 2.32 | 3.45 | 2.51 | 2.58 | 1.75 | 2.67 | 2.73 |
| Max. | 26.78 | 27.12 | 30.16 | 29.25 | 31.68 | 29.77 | 35.83 | 33.36 | 33.20 | 32.46 | 32.38 | 35.18 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cooney, C.; Korik, A.; Folli, R.; Coyle, D. Evaluation of Hyperparameter Optimization in Machine and Deep Learning Methods for Decoding Imagined Speech EEG. Sensors 2020, 20, 4629. https://doi.org/10.3390/s20164629
Cooney C, Korik A, Folli R, Coyle D. Evaluation of Hyperparameter Optimization in Machine and Deep Learning Methods for Decoding Imagined Speech EEG. Sensors. 2020; 20(16):4629. https://doi.org/10.3390/s20164629
Chicago/Turabian StyleCooney, Ciaran, Attila Korik, Raffaella Folli, and Damien Coyle. 2020. "Evaluation of Hyperparameter Optimization in Machine and Deep Learning Methods for Decoding Imagined Speech EEG" Sensors 20, no. 16: 4629. https://doi.org/10.3390/s20164629
APA StyleCooney, C., Korik, A., Folli, R., & Coyle, D. (2020). Evaluation of Hyperparameter Optimization in Machine and Deep Learning Methods for Decoding Imagined Speech EEG. Sensors, 20(16), 4629. https://doi.org/10.3390/s20164629





