An Online Classification Method for Fault Diagnosis of Railway Turnouts
Abstract
1. Introduction
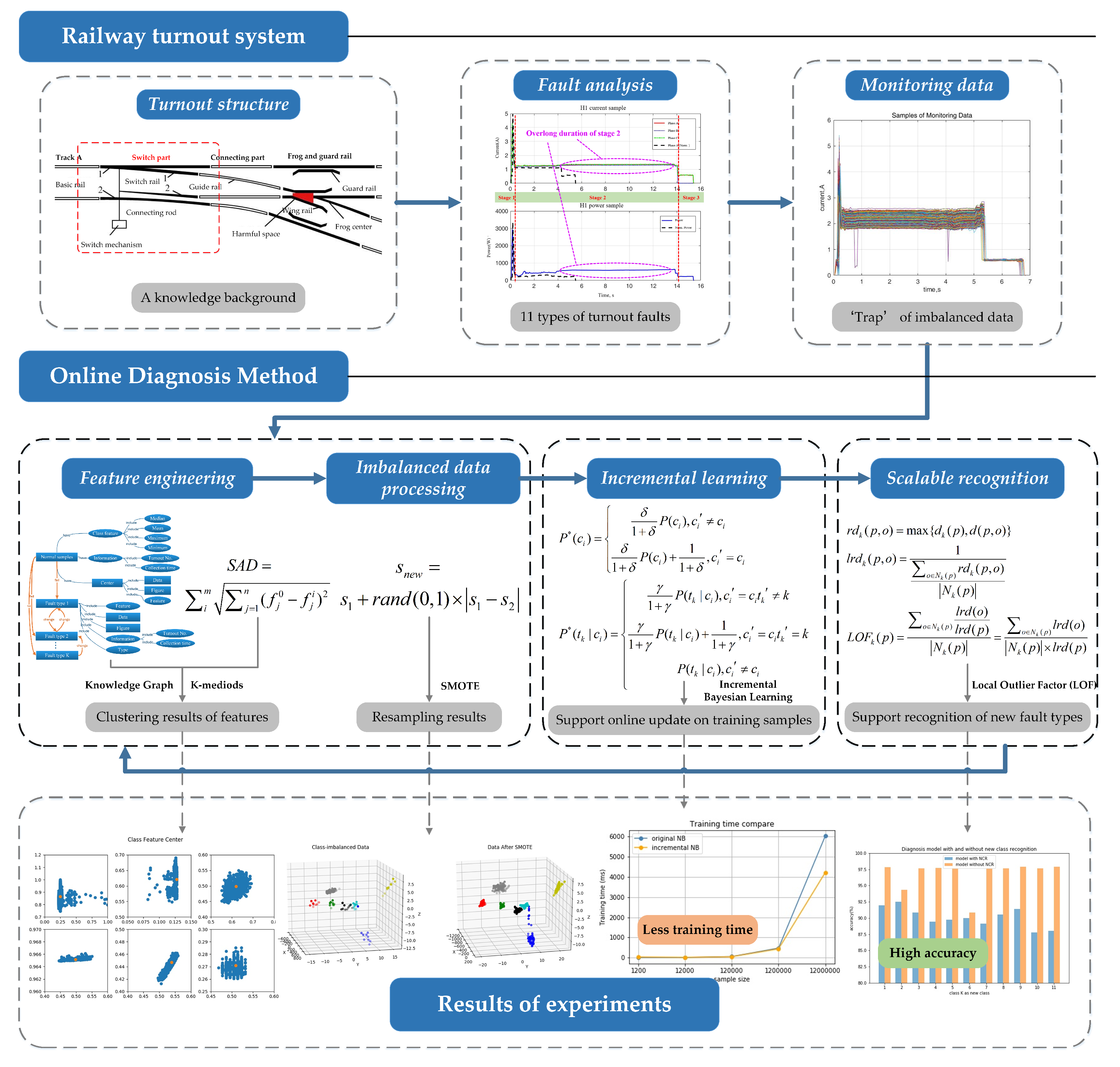
2. Railway Turnout System
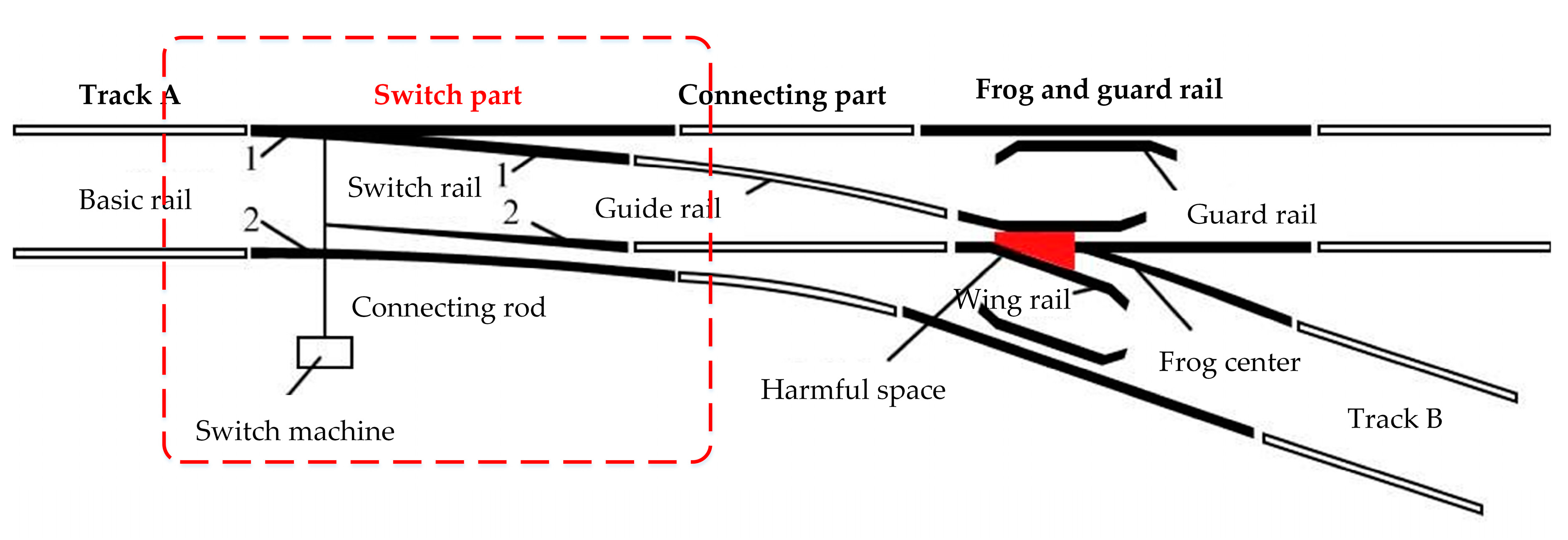
2.1. Turnout System
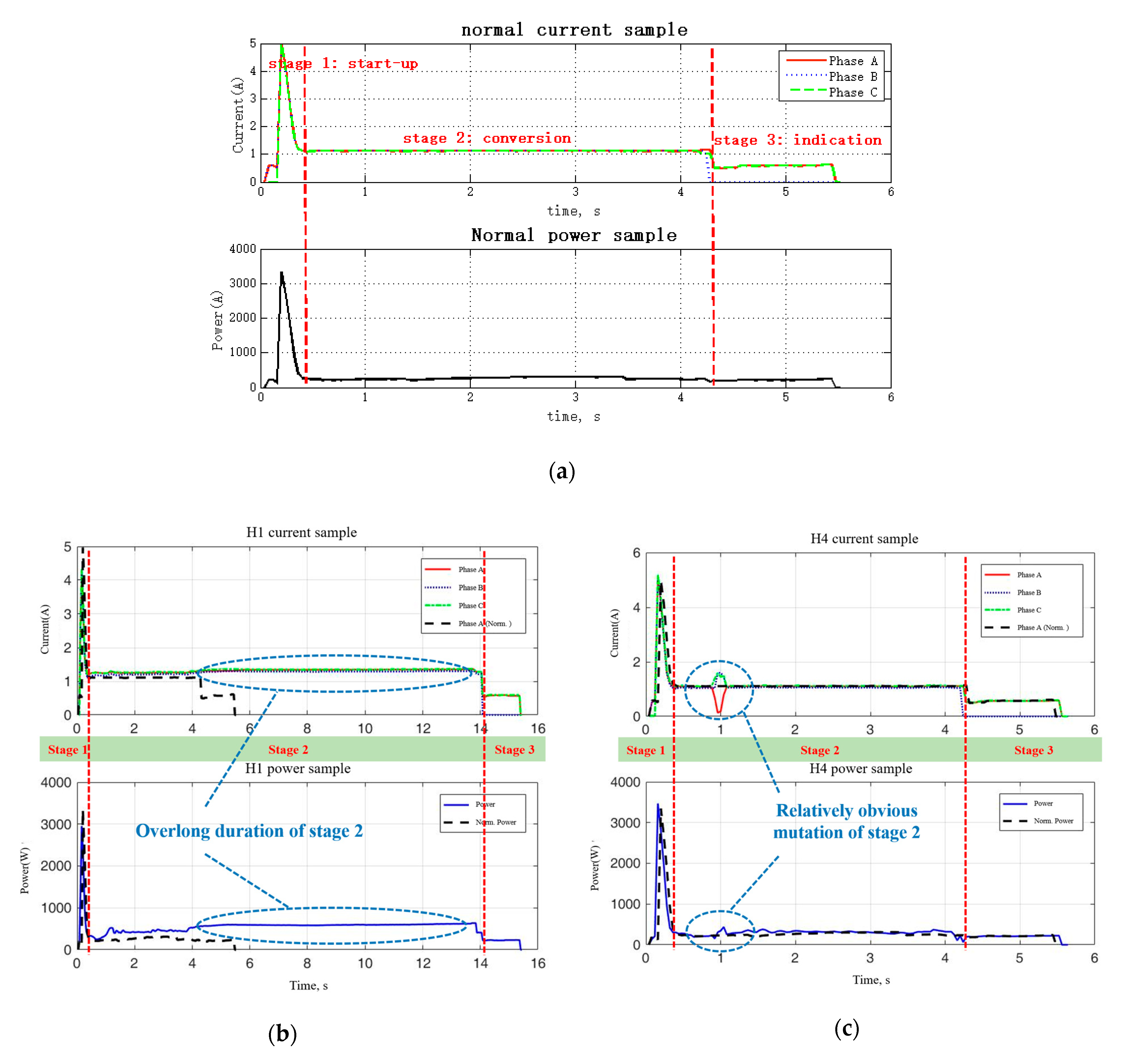
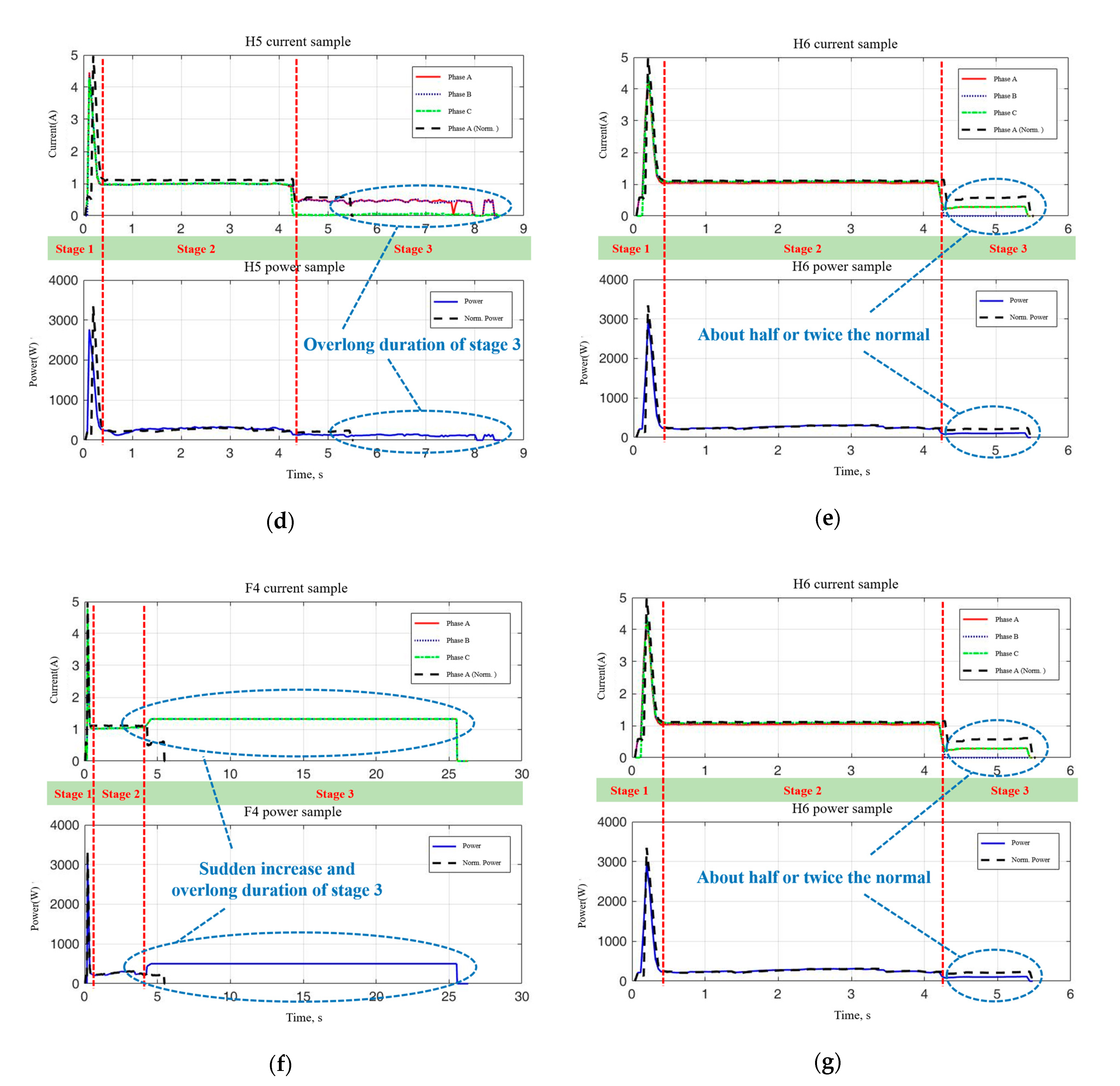
2.2. Fault Type Analysis
- Stage 1 is the starting of the switch machine and unlocking of the turnout, which needs to overcome much resistance;
- Stage 2 is the process of the movement of the switch rail to the other basic rail, as well as the locking of the turnout;
- Stage 3 is responsible for indicating the result of the conversion using a low-power indicating circuit.
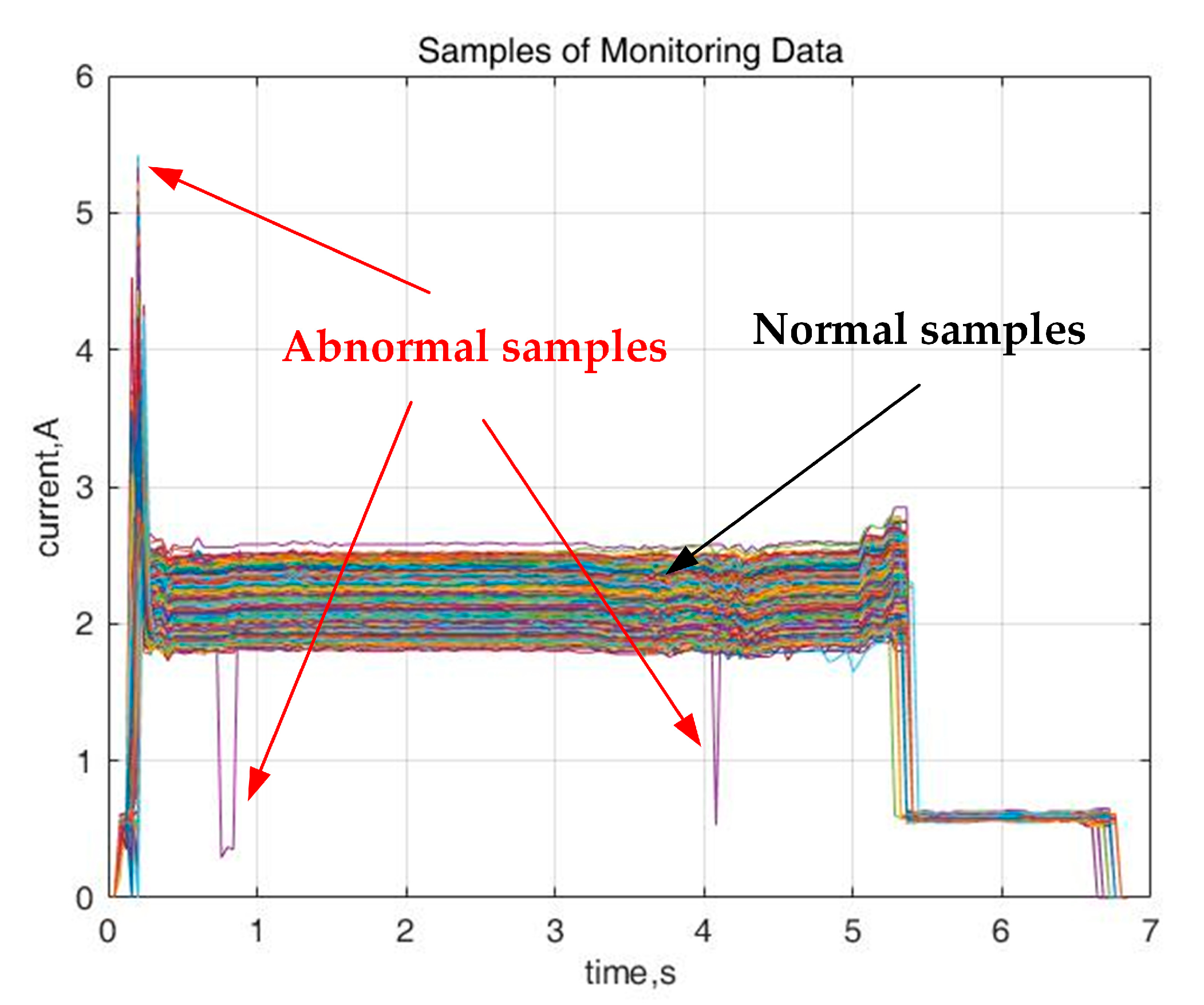
2.3. Imbalanced Monitoring Data
3. Online Learning and Diagnosis Method
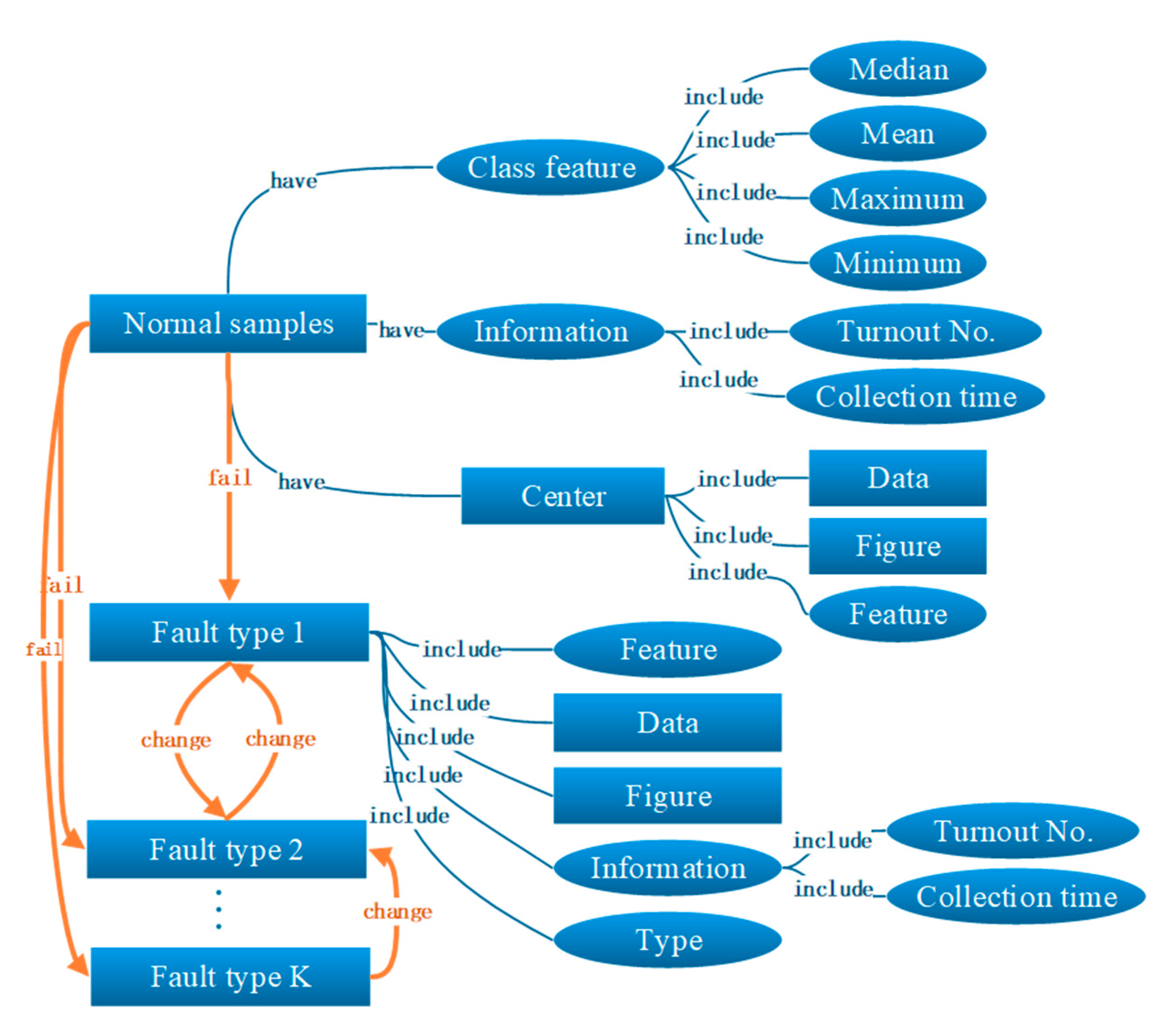
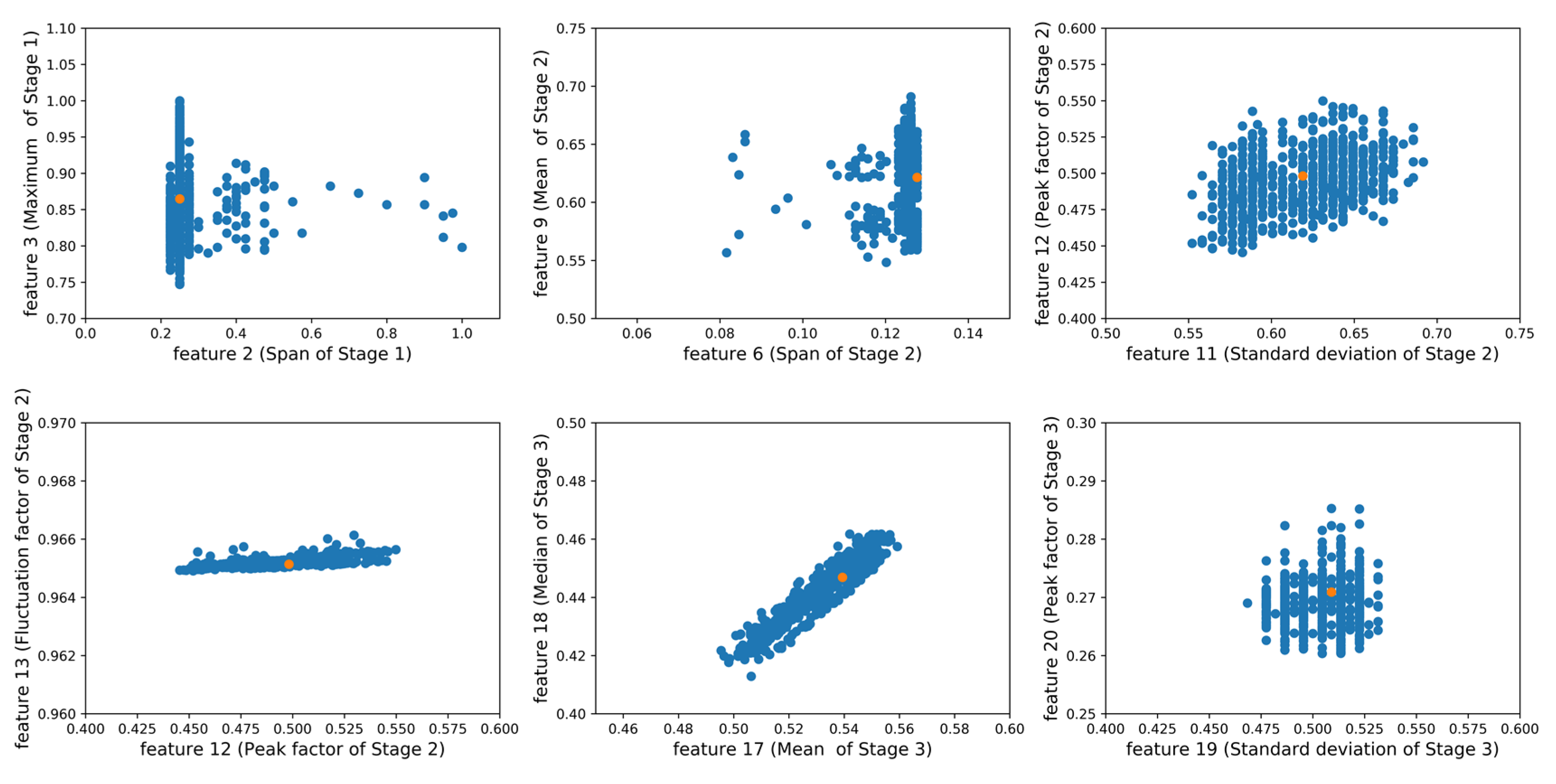
3.1. Knowledge Graph-Based Feature Engineering
- The input feature set is (n is the feature dimension) and choose any row as the original center;
- Define the cluster evaluation variable sum of absolute differences (SAD):
- Choose any sample except as and calculate the corresponding SAD;
- If the SAD of is smaller than the SAD of , update the to be the new center;
- When all the samples have been searched, the SAD of the current center will reach the minimum and the iteration is finished. Otherwise, return to the third step).
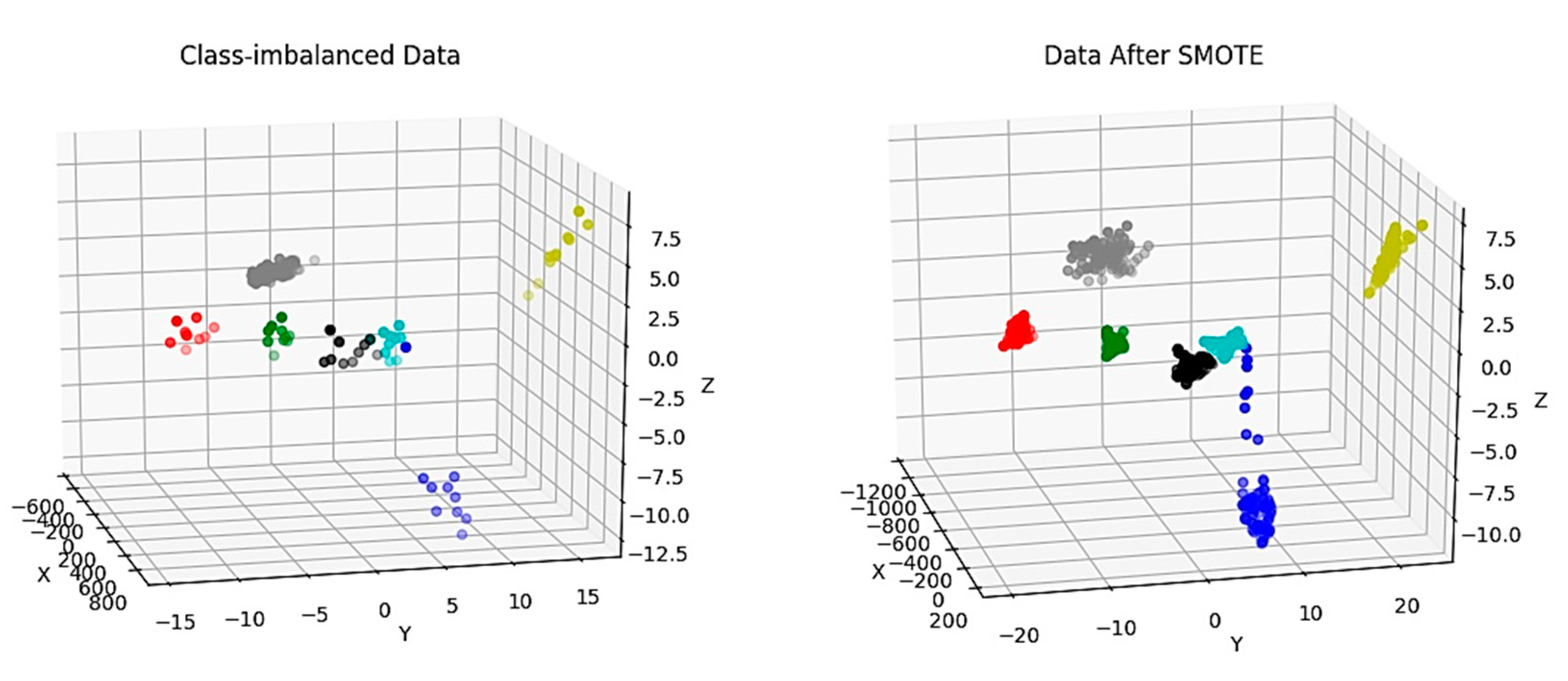
3.2. Imbalanced Data Preprocessing
- For each sample in the minority class, the Euclidean distance is taken as the standard to calculate its distance to all samples in the class so as to find its k-nearest neighbor;
- A sampling ratio is set according to the sample imbalance ratio; For each minority sample , several samples are randomly selected from its k-nearest neighbors, assuming that the chosen nearest neighbor is ;
- For each chosen neighbor , a new sample is constructed according to the following formula with the original sample :
3.3. Bayesian Incremental Learning
3.4. Scalable Fault Recognition
4. Experiment Result
4.1. Clustering and Resampling
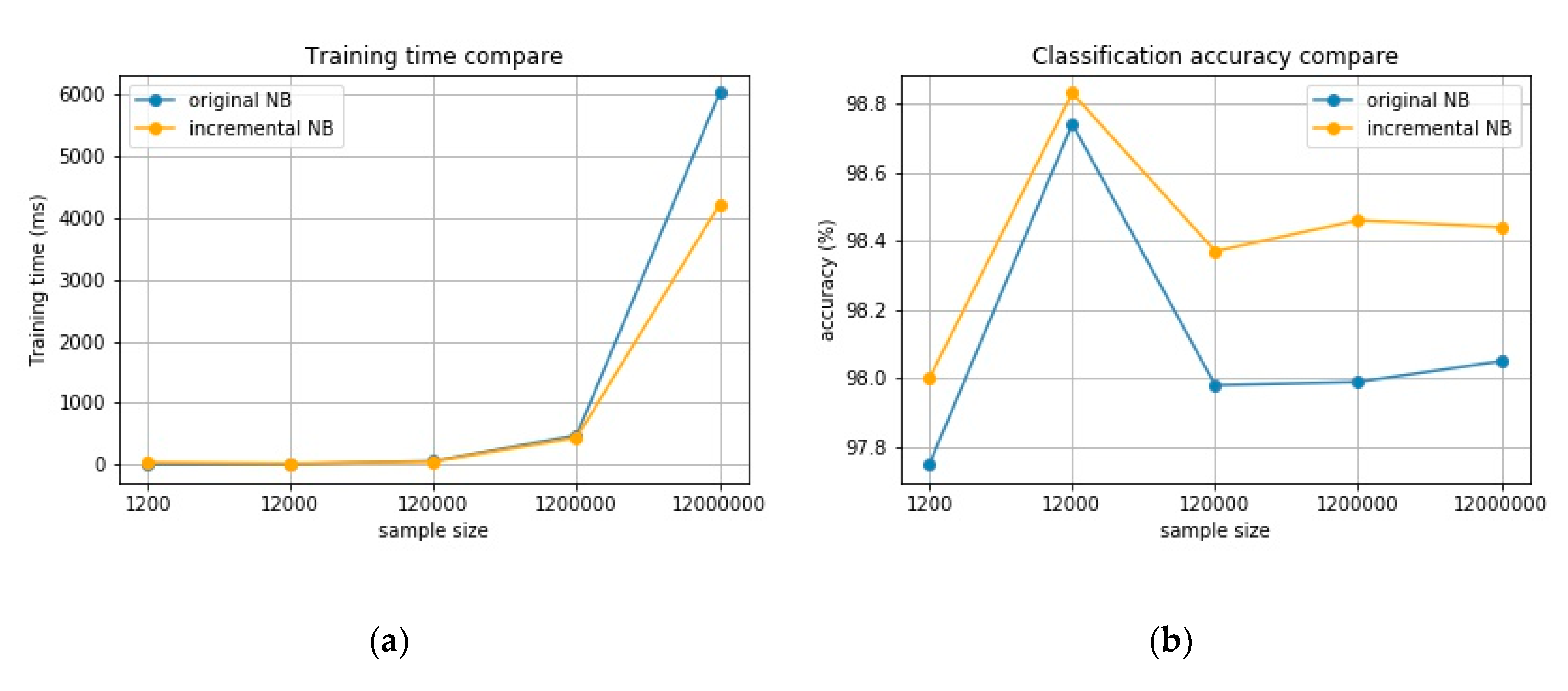
4.2. Incremental and Scalable Fault Diagnosis Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- 2019 Railway Statistical Bulletin; Ministry of Transport of the People’s Republic of China: Beijing, China, 2020; pp. 1–8.
- Atamuradov, V.; Camci, F.; Baskan, S.; Sevkli, M. Failure Diagnostics for Railway Point Machines Using Expert Systems. In Proceedings of the 2009 IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics And Drives, Cargese, France, 31 August–3 September 2009; pp. 1–5. [Google Scholar]
- Yang, Y. Station Signal Control System, 1st ed.; Southwest Jiaotong University Press: Chengdu, China, 2012. [Google Scholar]
- Marquez, F.P.G.; Tercero, D.J.P.; Schmid, F. Unobserved component models applied to the assessment of wear in railway points: A case study. Eur. J. Oper. Res. 2007, 176, 1703–1712. [Google Scholar] [CrossRef]
- Márquez, F.P.G.a.; Schmid, F.; Collado, J.C. A reliability centered approach to remote condition monitoring. A railway points case study. Reliab. Eng. Syst. Saf. 2003, 80, 33–40. [Google Scholar]
- 2017 Annual Report; China Railway Jinan Group Co Ltd.: Jinan, China, 2018.
- 2018 Annual Report; China Railway Guangzhou Group Co Ltd.: Guangzhou, China, 2019.
- Inspection of Switches and Crossings State of the Art Report Preliminary Report; International Union of Railways (UIC): Paris, France, 2011.
- Marquez, F.P.G.; Weston, P.; Roberts, C. Failure analysis and diagnostics for railway trackside equipment. Eng. Fail. Anal. 2007, 14, 1411–1426. [Google Scholar] [CrossRef]
- Yanqing, X. Research on Realization Method of Turnout Equipment Fault Diagnosis Expert System. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2012. [Google Scholar]
- Min, S. Research on Fault Diagnosis Expert System of Railway Signal Equipment. Master’s Thesis, Qingdao University, Qingdao, China, 2009. [Google Scholar]
- Yang, Y. Research on A pplication of Neural Network and Expert System in Rail Switch Fault Diagnosis. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2013. [Google Scholar]
- Cao, H.; Yue, L.; Yang, F. Application of Expert System and Neural Network in Fault Diagnosis of Switch Control Circuit. Heilongjiang Sci. Technol. Inf. 2010, 62. (In Chinese) [Google Scholar] [CrossRef]
- Youmin, H. Research on Fault Diagnosis Method of High-Speed Railway Turnouts. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2014. [Google Scholar]
- Eker, O.F.; Camci, F.; Guclu, A.; Yilboga, H.; Baskan, S. A Simple State-Based Prognostic Model for Railway Turnout Systems. IEEE Trans. Ind. Electron. 2012, 58, 1718–1726. [Google Scholar] [CrossRef]
- Yilboga, H.; Eker, Ö.F.; Güçlü, A.; Camci, F. Failure prediction on railway turnouts using time delay neural networks. In Proceedings of the 2010 IEEE International Conference on Computational Intelligence for Measurement Systems and Applications, Taranto, Italy, 6–8 September 2010; pp. 134–137. [Google Scholar]
- Witczak, M.; Korbicz, J.; Mrugalski, M.; Patton, R.J. A GMDH neural network-based approach to robust fault diagnosis: Application to the DAMADICS benchmark problem. Control Eng. Pract. 2006, 14, 671–683. [Google Scholar] [CrossRef]
- Silmon, J.A.; Roberts, C. Improving railway switch system reliability with innovative condition monitoring algorithms. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit 2010, 224, 293–302. [Google Scholar] [CrossRef]
- Diehl, C.P.; Cauwenberghs, G. SVM Incremental Learning, Adaptation and Optimization. In Proceedings of the International Joint Conference on Neural Networks, Portland, OR, USA, 20–24 July 2003; pp. 2685–2690. [Google Scholar]
- Ye, N.; Li, X. A scalable, incremental learning algorithm for classification problems. Comput. Ind. Eng. 2002, 43, 677–692. [Google Scholar] [CrossRef]
- Wu, J.; Hua, X.-S.; Zhang, H.-J.; Zhang, B. An online-optimized incremental learning framework for video semantic classification. In Proceedings of the 12th annual ACM international conference on Multimedia, New York, NY, USA, 10–16 October 2004; pp. 320–323. [Google Scholar] [CrossRef]
- Kochurov, M.; Garipov, T.; Podoprikhin, D.; Molchanov, D.; Ashukha, A.; Vetrov, D. Bayesian incremental learning for deep neural networks. arXiv 2018, arXiv:1802.07329. [Google Scholar]
- Ross, D.A.; Lim, J.; Lin, R.-S.; Yang, M.-H. Incremental learning for robust visual tracking. Int. J. Comput. Vision 2008, 77, 125–141. [Google Scholar] [CrossRef]
- Ristin, M.; Guillaumin, M.; Gall, J.; Van Gool, L. Incremental learning of random forests for large-scale image classification. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 490–503. [Google Scholar] [CrossRef] [PubMed]
- Ruping, S. Incremental learning with support vector machines. In Proceedings of the 2001 IEEE International Conference on Data Mining, San Jose, CA, USA, 29 November–2 December 2001; pp. 641–642. [Google Scholar]
- Pratama, M.; Anavatti, S.G.; Angelov, P.P.; Lughofer, E. PANFIS: A novel incremental learning machine. IEEE Trans. Neural Netw. Learn. Syst. 2013, 25, 55–68. [Google Scholar] [CrossRef] [PubMed]
- Xiao, T.; Zhang, J.; Yang, K.; Peng, Y.; Zhang, Z. Error-driven Incremental Learning in Deep Convolutional Neural Network for Large-scale Image Classification. In Proceedings of the 22nd ACM international conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 177–186. [Google Scholar] [CrossRef]
- Kotsiantis, S. Increasing the accuracy of incremental naive Bayes classifier using instance based learning. Int. J. Control Autom. Syst. 2013, 11, 159–166. [Google Scholar] [CrossRef]
- Gu, B.; Quan, X.; Gu, Y.; Sheng, V.S.; Zheng, G. Chunk incremental learning for cost-sensitive hinge loss support vector machine. Pattern Recognit. 2018, 83, 196–208. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, F.; Zhao, J. An incremental learning vector quantization algorithm for pattern classification. Neural Comput. Appl. 2012, 21, 1205–1215. [Google Scholar] [CrossRef]
- Ou, D.; Xue, R. Railway Turnout Fault Analysis Based on Monitoring Data of Point Machines. In Proceedings of the 2018 Prognostics and System Health Management Conference (PHM-Chongqing), Chongqing, China, 26–28 October 2018; pp. 546–552. [Google Scholar]
- Cui, K.; Tang, M.; Ou, D. Simulation Data Generating Algorithm for Railway Turnout Fault Diagnosis in Big Data Maintenance Management System. In International Symposium for Intelligent Transportation and Smart City; Springer: Singapore, 2019; pp. 155–166. [Google Scholar] [CrossRef]
- Ou, D.; Xue, R.; Cui, K. A data-driven fault diagnosis method for railway turnouts. Transp. Res. Rec. 2019, 2673, 448–457. [Google Scholar] [CrossRef]
- Ou, D.; TAng, M.; Xue, R.; Yao, H. Hybrid fault diagnosis of railway switches based on the segmentation of monitoring curves. Ekspolatacja i Niezawodn–Maint. Reliab. 2018, 20, 514–522. [Google Scholar] [CrossRef]
- Ou, D.; Tang, M.; Xue, R.; Yao, H. A Segmented Similarity-Based Diagnostic Model for Railway Turnout System. Available online: https://trid.trb.org/view/1572323 (accessed on 14 July 2020).
- Jining Iron Machinery Equipment Co., Ltd. Turnout System. Available online: http://www.juguiji.com/news/Data/354.html (accessed on 14 July 2020).
- Jin, G.; Yan, W.; Lifang, L. Railway Signal Infrastructure; Southwest Jiaotong University Press: Chengdu, China, 2008. [Google Scholar]
- Ding, Z.; Guoning, L. Fault diagnosis of S700K switch machine based on improved WNN analyses power curve. J. Railway Sci. Eng. 2018, 15, 229–236. (In Chinese) [Google Scholar]
- Ruifeng, W.; Wangbin, C. Research on Fault Diagnosis Method for S700K Switch Machine Based on Grey Neural Network. J. Chin. Railway Soc. 2016, 38, 68–72. (In Chinese) [Google Scholar]
- Qingyang, X.; Zhongtian, L.; Huibing, Z. Method of Turnout Fault Diagnosis Based on Hidden Markov Model. J. Chin. Railway Soc. 2018, 40, 98–106. (In Chinese) [Google Scholar]
- Post, C.; Rietz, C.; Büscher, W.; Müller, U. Using Sensor Data to Detect Lameness and Mastitis Treatment Events in Dairy Cows: A Comparison of Classification Models. Sensors 2020, 20, 3863. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Li, W.; Cao, J. A user-adaptive algorithm for activity recognition based on k-means clustering, local outlier factor, and multivariate gaussian distribution. Sensors 2018, 18, 1850. [Google Scholar] [CrossRef] [PubMed]

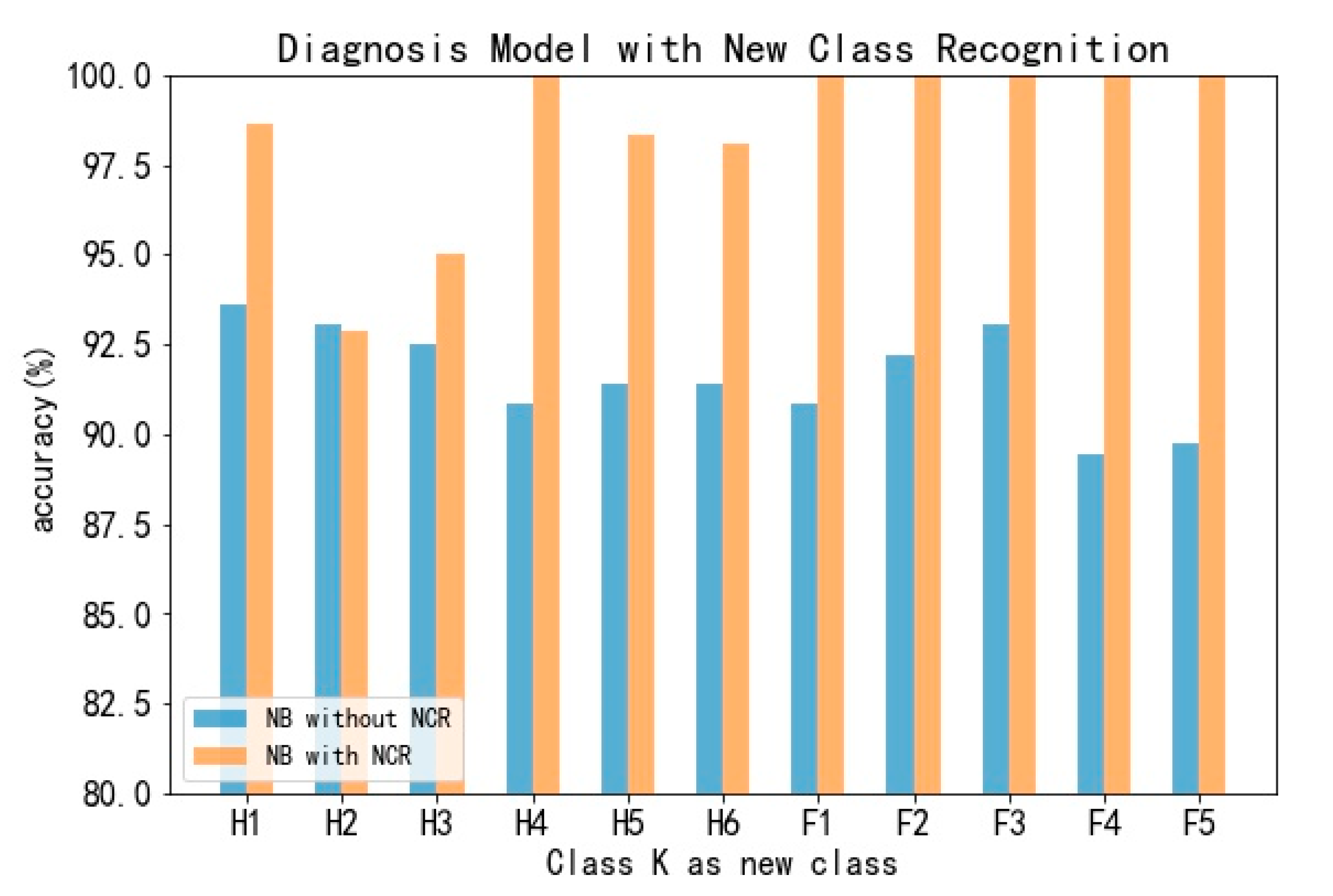
| Fault Label | Fault Type |
|---|---|
| H1 1 | Mechanical jam |
| H2 | Improper position of the slide chair |
| H3 | Abnormal impedance in the switch circuit |
| H4 | Bad contact in the switch circuit |
| H5 | Abnormal open-phase protection device in the indicating circuit |
| H6 | Abnormal impedance in the indicating circuit |
| F1 2 | The electric relay in the start circuit fails to switch |
| F2 | Supply interruption |
| F3 | Open-phase protection device fault |
| F4 | Fail to lock |
| F5 | Indicating rod block in the gap |
| n | 25 | 30 | 35 | 40 | |
| c | |||||
| 0.0001 | 95.35 | 95.35 | 93.76 | 98.13 | |
| 0.001 | 95.35 | 95.35 | 93.76 | 98.13 | |
| 0.01 | 95.38 | 95.83 | 96.01 | 99.11 | |
| Sample size | 1200 | 12,000 | 120,000 | 1,200,000 |
| NB | 6.62 | 10.27 | 59.84 | 476.52 |
| Incremental NB | 38.48 | 19.53 | 51.32 | 436.72 |
| Sample size | 1200 | 12,000 | 120,000 | 1,200,000 |
| NB | 97.75 | 98.74 | 97.98 | 97.99 |
| Incremental NB | 98.00 | 98.83 | 98.37 | 98.46 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, D.; Ji, Y.; Zhang, L.; Liu, H. An Online Classification Method for Fault Diagnosis of Railway Turnouts. Sensors 2020, 20, 4627. https://doi.org/10.3390/s20164627
Ou D, Ji Y, Zhang L, Liu H. An Online Classification Method for Fault Diagnosis of Railway Turnouts. Sensors. 2020; 20(16):4627. https://doi.org/10.3390/s20164627
Chicago/Turabian StyleOu, Dongxiu, Yuqing Ji, Lei Zhang, and Hu Liu. 2020. "An Online Classification Method for Fault Diagnosis of Railway Turnouts" Sensors 20, no. 16: 4627. https://doi.org/10.3390/s20164627
APA StyleOu, D., Ji, Y., Zhang, L., & Liu, H. (2020). An Online Classification Method for Fault Diagnosis of Railway Turnouts. Sensors, 20(16), 4627. https://doi.org/10.3390/s20164627







