A Flow-Measuring Algorithm of Arc-Bottomed Open Channels through Multiple Characteristic Sensing Points of the Flow-Velocity Sensor in Agricultural Irrigation Areas
Abstract
:1. Introduction
2. Methodology
2.1. The Location of Characteristic Sensing Point of the Flow-Velocity Sensor in Arc-Bottom Channel
2.2. Derivation of Estimating Discharge through Multiple Characteristic Sensing Points of the Flow-Velocity Sensor
3. Experimental Setup
4. Results and Discussion
4.1. Analysis along Normal Line Direction
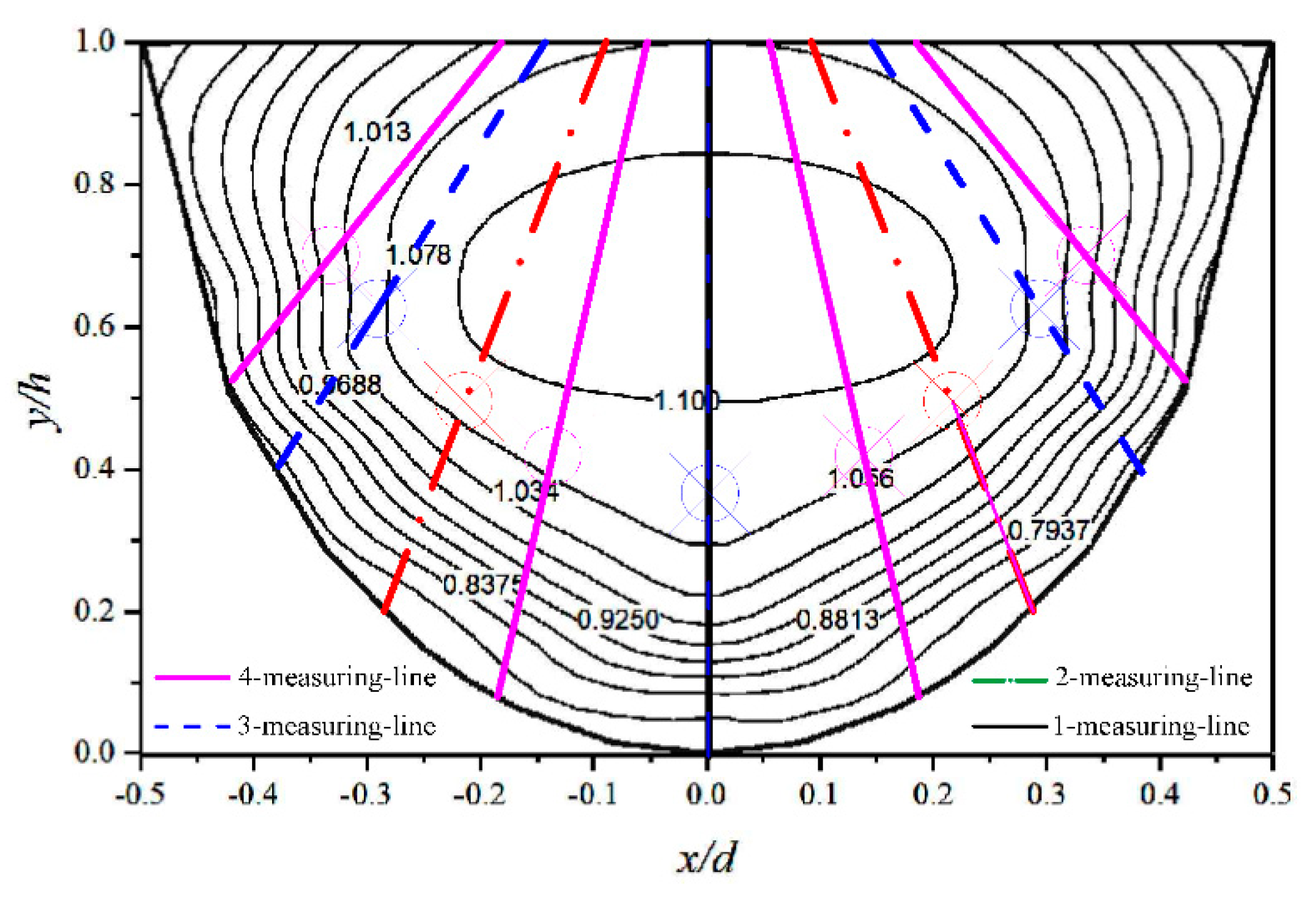
4.2. Multiple Characteristic Sensing Points of the Flow-Velocity Sensor in Arc-Bottom Channel
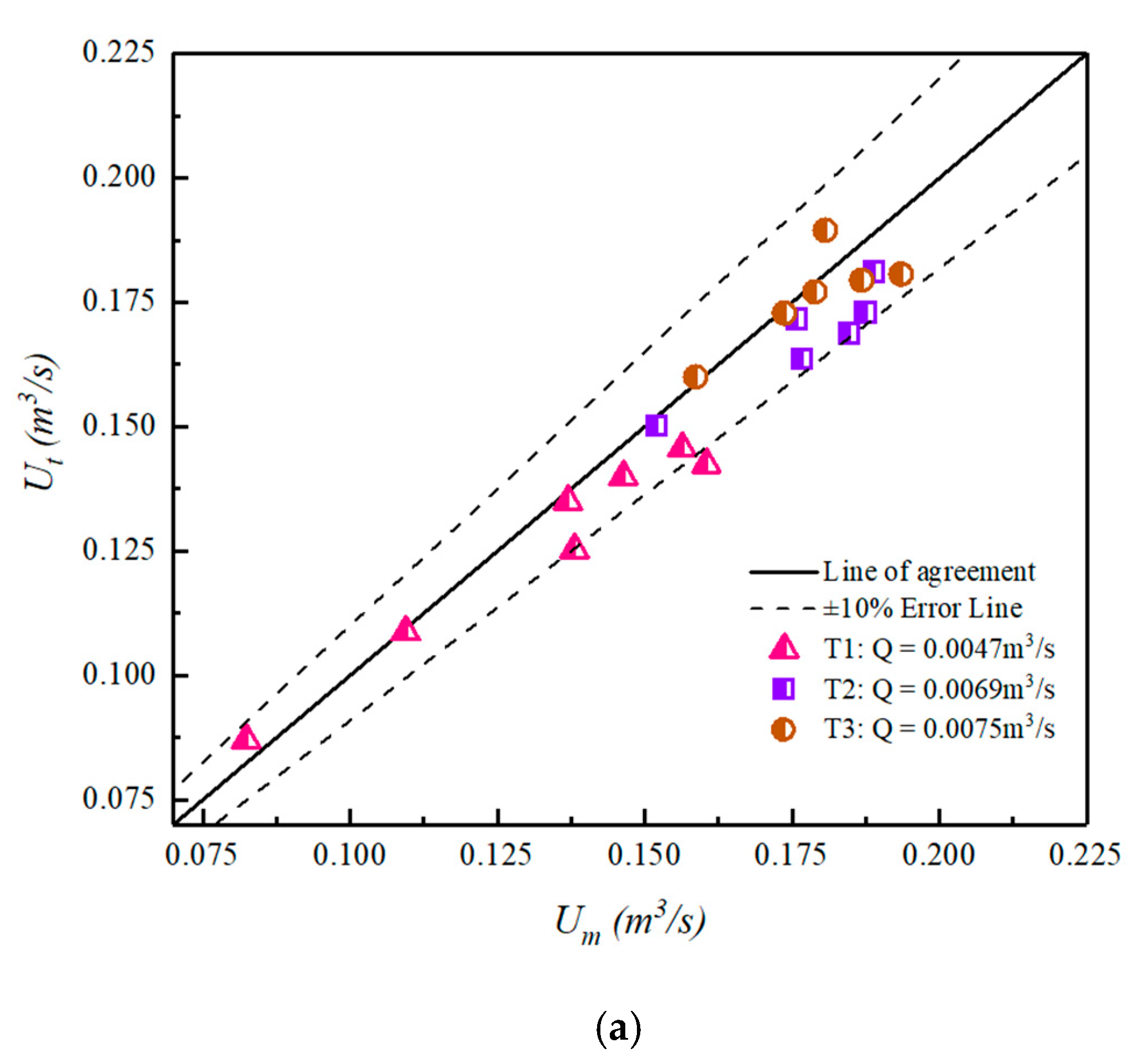
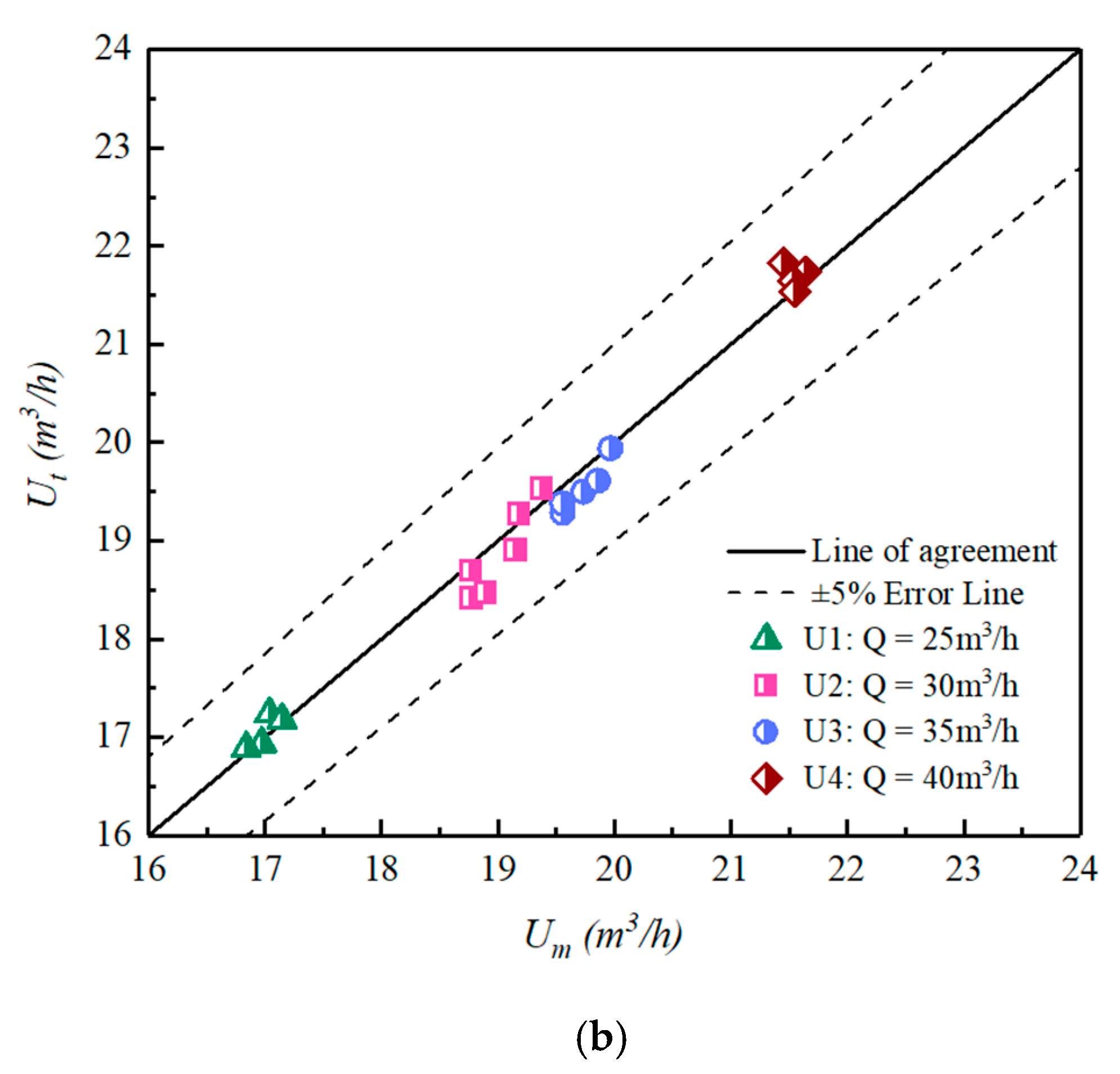
4.3. Estimating Discharge through Multiple Characteristic Sensing Points of the Flow-Velocity Sensor
5. Conclusions
- (1)
- We compared the log-law along the normal direction and along the vertical direction. The results show the accuracy with the normal direction. We thought that the analysis should be carried out along the normal direction in the arc-bottomed channel rather than vertical direction,
- (2)
- Based on the log-law, the theoretical expression for calculating the locations of multiple characteristic sensing points in arc-bottom open channel is derived through the formula transformation. Then, we give the mathematical formula to calculate the discharge of the arc-bottomed channels. We can use sensors to measure the velocity of these characteristic sensing points and obtain the discharge. The correctness of the formula for multiple characteristic sensing points in arc-bottom channels is proved by numerous experimental data;
- (3)
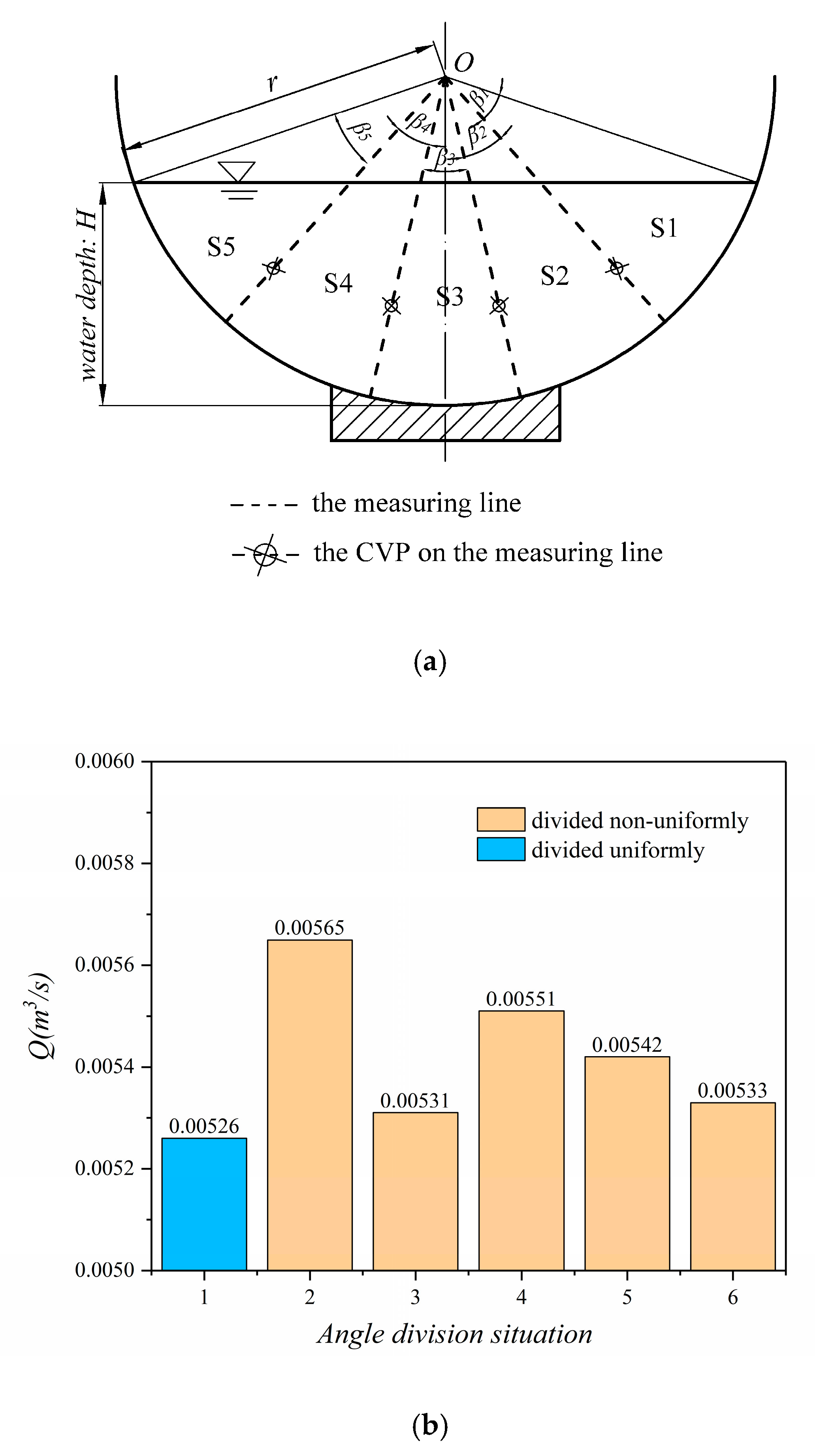
- To prove the validity of the flow calculation formula, we estimate the discharge by setting different measuring lines. Compared with the measuring discharge, the calculating discharge can match well. Moreover, the number of measuring lines is positively correlated with the accuracy of flow measurement. When the angles between lines are the same, the number of measuring lines is positively correlated with the accuracy of flow measurement. When the number of measuring lines is fixed, the accuracy of angle uniformity is higher than that of nonuniformity.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, S.Q.; Han, Y.; Dharmasiri, N. Flow resistance over fixed roughness elements. J. Hydraul. Res. 2011, 49, 257–262. [Google Scholar] [CrossRef]
- An, P.; Xing, Y.C.; Zhang, A.J.; Zhao, L.; Cheng, D.W. Optimal analysis of anti-frost heaping canal with cross section of trapezoidal slopes and curved bed. J. Irrig. Drain. 2017, 36, 56–62. [Google Scholar]
- Han, Y.; Yang, S.Q.; Sivakumar, M.; Qiu, L.C. Investigation of velocity distribution in open channel flows based on conditional average of turbulent structures. Math. Probl. Eng. 2017, 2017, 9. [Google Scholar] [CrossRef]
- Von Kármán, T. Turbulence and skin friction. J. Aeronaut. Sci. 1934, 1–20. [Google Scholar]
- Keulegan, G.H. Laws of turbulent flow in open channels. J. Res. Natl. Bur. Stand. 1938, 21, 707–741. [Google Scholar] [CrossRef]
- Liu, C.J.; Li, D.X.; Wang, X.K. Experimental study on friction velocity and velocity profile of open channel flow. J. Hydraul. Eng. 2005, 36, 950–955. [Google Scholar]
- Nikuradse, J. Laws of Flow in Rough Pipes. 1950. Available online: https://ntrs.nasa.gov/search.jsp?R=19930093938 (accessed on 21 May 2020).
- Cardoso, A.H.; Graf, W.H.; Gust, G. Uniform-flow in a smooth open channel. J. Hydraul. Res. 1989, 27, 606–616. [Google Scholar] [CrossRef]
- Steffler, P.M.; Rajaratnam, N.; Peterson, A.W. LDA measurements in open channel. J. Hydraul. Div. Am. Soc. Civ. Eng. 1985, 111, 119–130. [Google Scholar] [CrossRef]
- Nezu, I.; Rodi, W. Open-channel flow measurements with a Laser Doppler Anemometer. J. Hydraul. Eng. 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Dey, S. Free overall in circular channels with flat base: A method of open channel flow measurement. Flow Meas. Instrum. 2002, 13, 209–221. [Google Scholar] [CrossRef]
- Yang, S.H.; Han, J.X.; Peng, S.Z.; Han, D. Analysis and experiment of distribution properties and its application of velocity in U-shaped open channel. Trans. Chin. Soc. Agric. Mach. 2012, 43, 92–96. [Google Scholar]
- Hu, H.; Huang, J.S.; Qian, Z.D.; Huai, W.X.; Yu, G.J. Hydraulic analysis of parabolic fume for flow measurement. Flow Meas. Instrum. 2014, 37, 54–64. [Google Scholar] [CrossRef]
- Samani, Z. Three simple flumes for flow measurement in open channels. J. Irrig. Drain. Div. Am. 2017, 143, 04017010. [Google Scholar] [CrossRef]
- Mohammadzadeh-Habili, J.; Heidarpour, M.; Afzalimehr, H. Hydraulic characteristics of a new weir entitled of quarter-circular crested weir. Flow Meas. Instrum. 2013, 33, 168–178. [Google Scholar] [CrossRef]
- Vatankhah, A.R.; Ghaderinia, H. Semi-circular flap gate as a flow metering structure in circular channel. Flow Meas. Instrum. 2018, 64, 28–38. [Google Scholar] [CrossRef]
- Yang, S.Q.; Lim, S.Y. Mechanism of energy transportation and turbulent flow in a 3D channel. J. Hydraul. Div. Am. Soc. Civ. Eng. 1997, 123, 684–692. [Google Scholar] [CrossRef]
- Knight, D.W.; Sterling, M. Boundary shear in circular pipes running partially full. J. Hydraul. Div. Am. Soc. Civ. Eng. 2000, 126, 263–275. [Google Scholar] [CrossRef]
- Demetriou, J.D.; Nanou-Giannarou, A.I. Water conveyance in channels with semi-circular cross sections. Agric. Water Manag. 1988, 13, 273–283. [Google Scholar] [CrossRef]
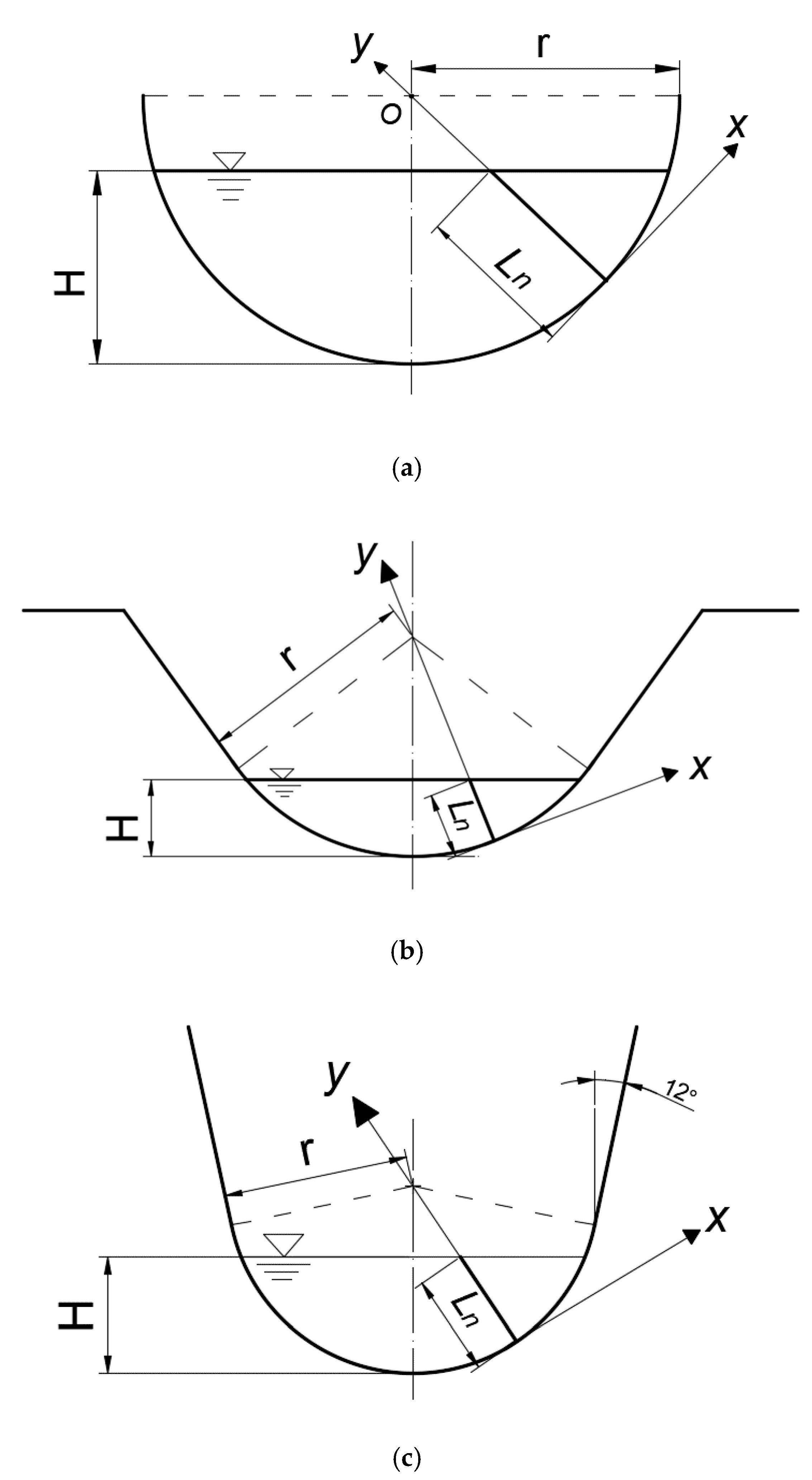
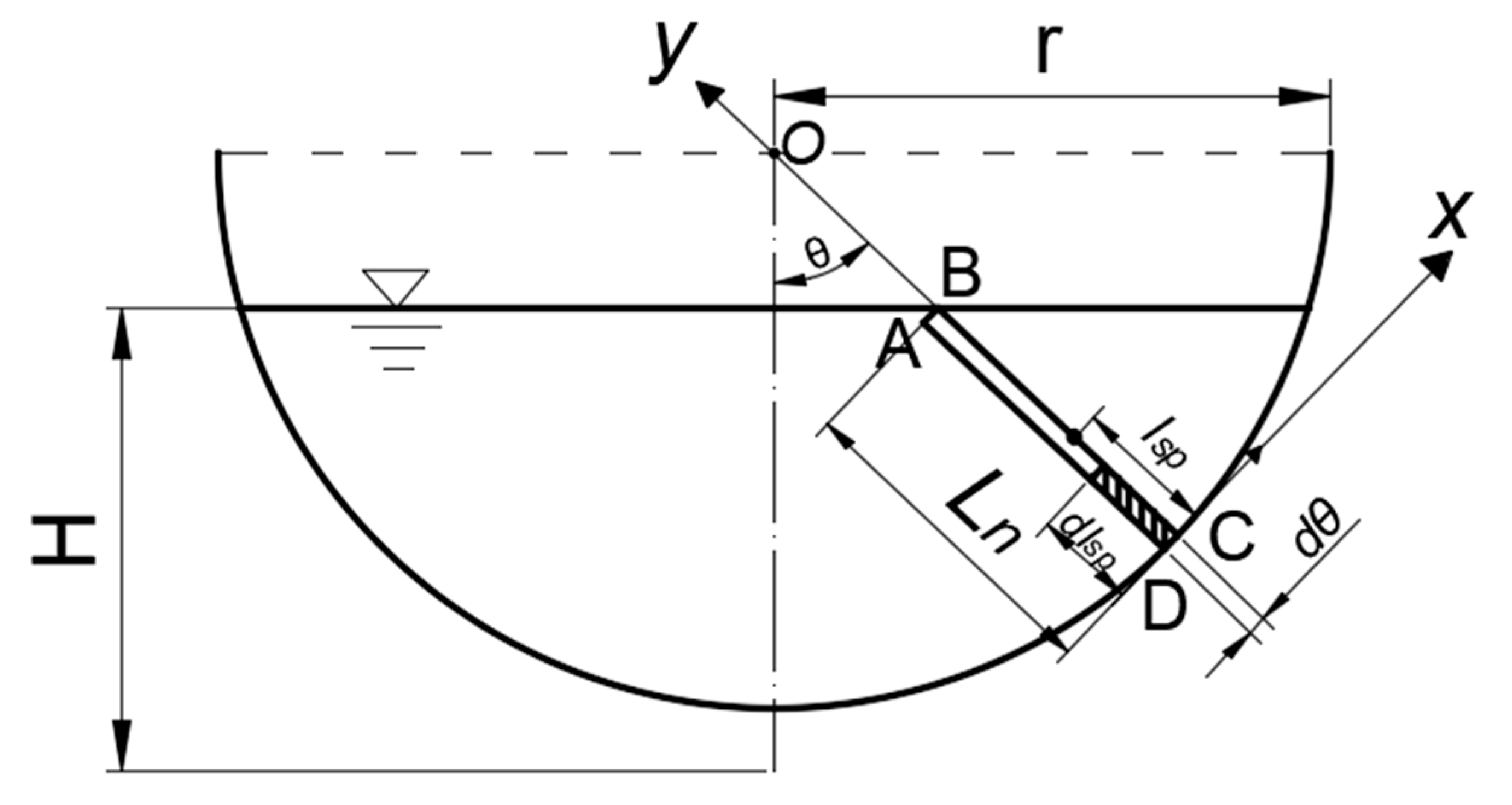

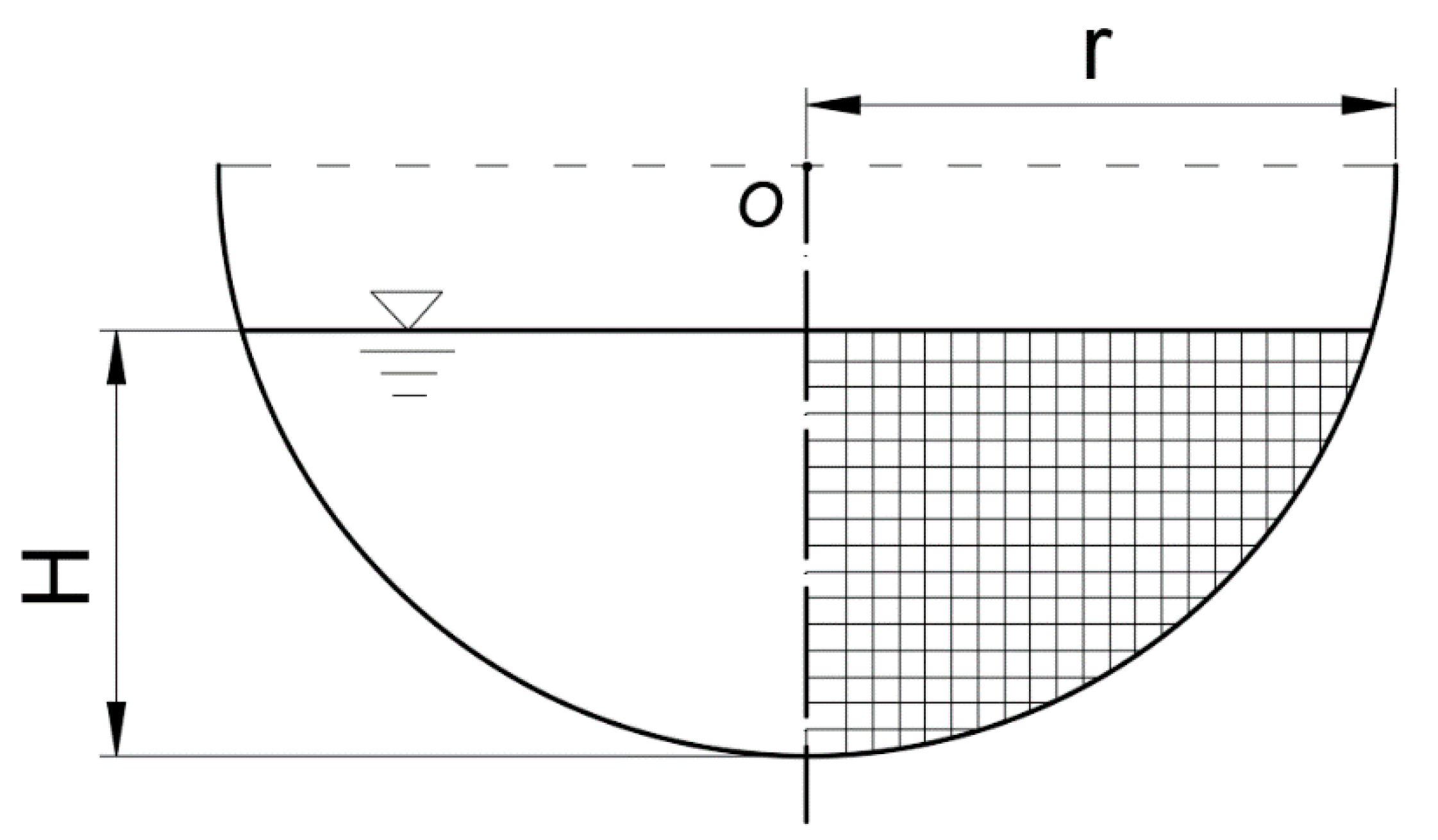
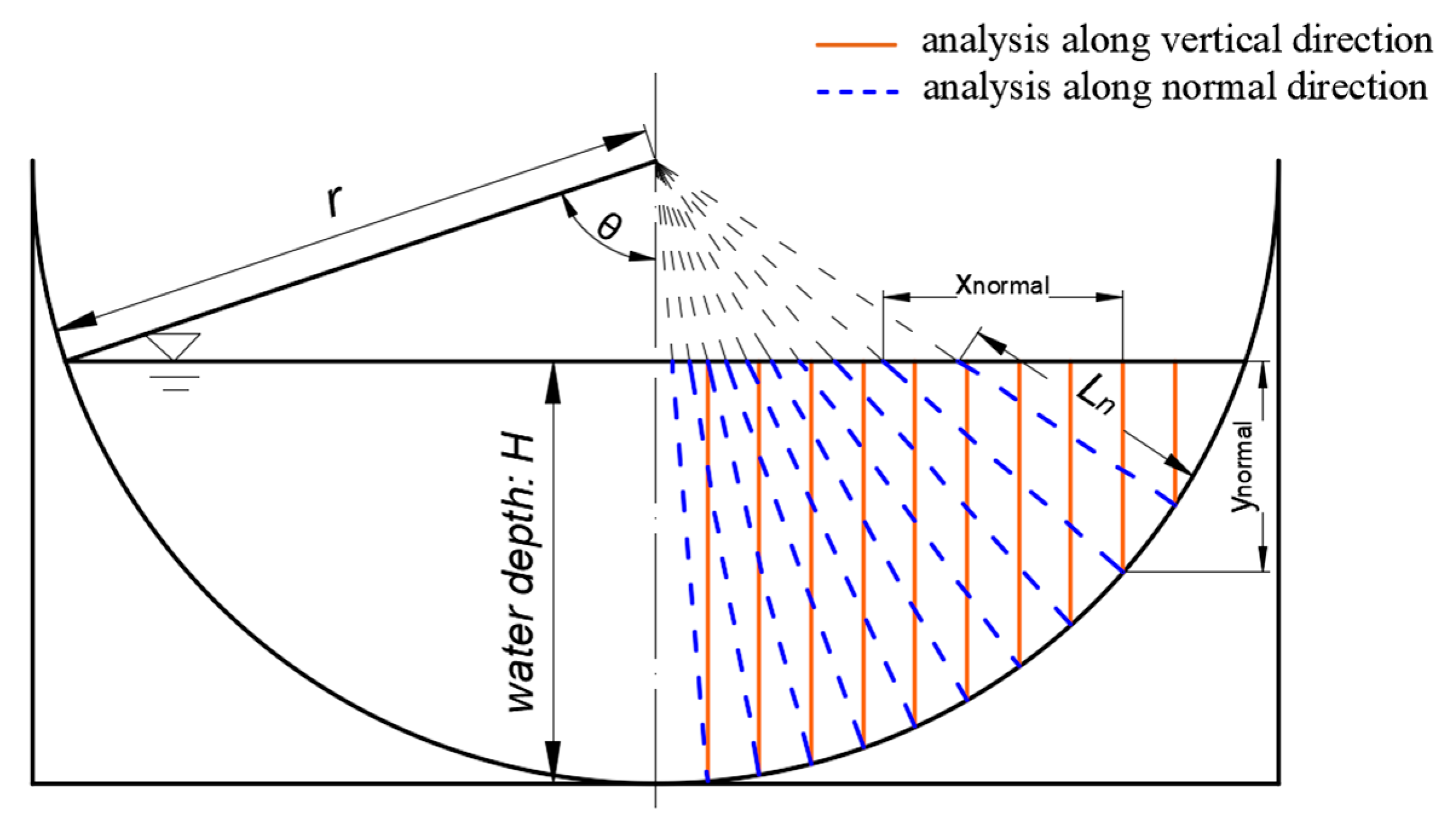
| Cross-Sectional Shape | Arc Radius (m) | Bottom Slope | Q (m3/h) | H (m) |
|---|---|---|---|---|
| Semicircle (C1–C2) | 0.120 a | 0.001 | 19 | 0.0813 |
| 0.240 c | – | 0.2152 | ||
| U-shaped (U1–U4) | 0.250 b | 0.000667 | 25 | 0.123 |
| 30 | 0.138 | |||
| 35 | 0.149 | |||
| 40 | 0.162 | |||
| Arc-bottom trapezium (T1–T3) | 0.190 b | 0.000667 | 17 | 0.0124 |
| 25 | 0.0149 | |||
| 27 | 0.0155 |
| Average Error Value along Normal Direction | Average Error Value along Vertical Direction | ||
|---|---|---|---|
| Normal Slope knormal | Average Error Value E (%) | The Distance from Vertical Line to Central Line Z/R | Average Error Value E (%) |
| 11.96 | 3.35 | 0.08 | 6.63 |
| 5.92 | 3.12 | 0.17 | 5.92 |
| 3.87 | 3.28 | 0.25 | 5.04 |
| 2.83 | 3.15 | 0.33 | 4.17 |
| 2.18 | 1.63 | 0.42 | 3.64 |
| 1.73 | 2.24 | 0.50 | 4.02 |
| 1.39 | 1.07 | 0.58 | 3.92 |
| 1.12 | 1.07 | 0.67 | 4.88 |
| 0.88 | 2.49 | 0.75 | 8.35 |
| 0.66 | 6.53 | 0.83 | 14.42 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Li, T.; Wang, S.; Chen, J. A Flow-Measuring Algorithm of Arc-Bottomed Open Channels through Multiple Characteristic Sensing Points of the Flow-Velocity Sensor in Agricultural Irrigation Areas. Sensors 2020, 20, 4504. https://doi.org/10.3390/s20164504
Han Y, Li T, Wang S, Chen J. A Flow-Measuring Algorithm of Arc-Bottomed Open Channels through Multiple Characteristic Sensing Points of the Flow-Velocity Sensor in Agricultural Irrigation Areas. Sensors. 2020; 20(16):4504. https://doi.org/10.3390/s20164504
Chicago/Turabian StyleHan, Yu, Tongshu Li, Shiyu Wang, and Jian Chen. 2020. "A Flow-Measuring Algorithm of Arc-Bottomed Open Channels through Multiple Characteristic Sensing Points of the Flow-Velocity Sensor in Agricultural Irrigation Areas" Sensors 20, no. 16: 4504. https://doi.org/10.3390/s20164504
APA StyleHan, Y., Li, T., Wang, S., & Chen, J. (2020). A Flow-Measuring Algorithm of Arc-Bottomed Open Channels through Multiple Characteristic Sensing Points of the Flow-Velocity Sensor in Agricultural Irrigation Areas. Sensors, 20(16), 4504. https://doi.org/10.3390/s20164504






