Data-Driven Analysis of Bicycle Sharing Systems as Public Transport Systems Based on a Trip Index Classification
Abstract
1. Introduction
- The creation a quantitative framework to classify BSS trips as transport or leisure.
- The definition of a distance-based index that builds the basis for this classification of trips.
- The mathematical characterization of the shortest path distance in a BSS, considering the set of shortcuts that bikers can use in their routes.
- The application of this framework to classify trips in a real BSS.
- Statistical and operational analysis to confirm the validity of the obtained results.
- The extraction the underlying BSS public transportation network.
2. Data-driven Classification of Trips
2.1. Starting Premise
2.2. Trip Index
2.3. Spaces, Trajectories and Shortcuts in a BSS
- The linear trajectory, with length , i.e., the direct Euclidean distance between origin and destination, which only depends on the real physical space.
- The retrievable shortest path between origin and destination given the underlying graph, which we will refer to as the orthodox trajectory, with length .
- The shortest path between origin and destination using the set of available shortcuts, namely the heterodox trajectory, with length .
- The actual path of the trip traveled by the user, with length .
2.4. Characterizing the Shortest Path in a BSS Trip
3. Application to a Real BSS
3.1. Dataset
- Time stamp: pick up time with 1 hour definition, for privacy and anonymity issues.
- User’s identifier: unique encrypted identifier of user, refreshed daily.
- Type of user: annual, eventual, staff.
- User’s range of age: 6 intervals [0,16], [17,18], [19–26], [27–40], [41–65], [66,∞), and unknown.
- Identifier of the origin docking station.
- Identifier of the destination docking station.
- Travel time: time from pick up to drop off.
- Track: collection of geographical coordinates ordered in time recorded on a 1-minute basis during the trip.
3.2. Applying the Mathematical Framework to the Dataset
3.2.1. Preprocessing
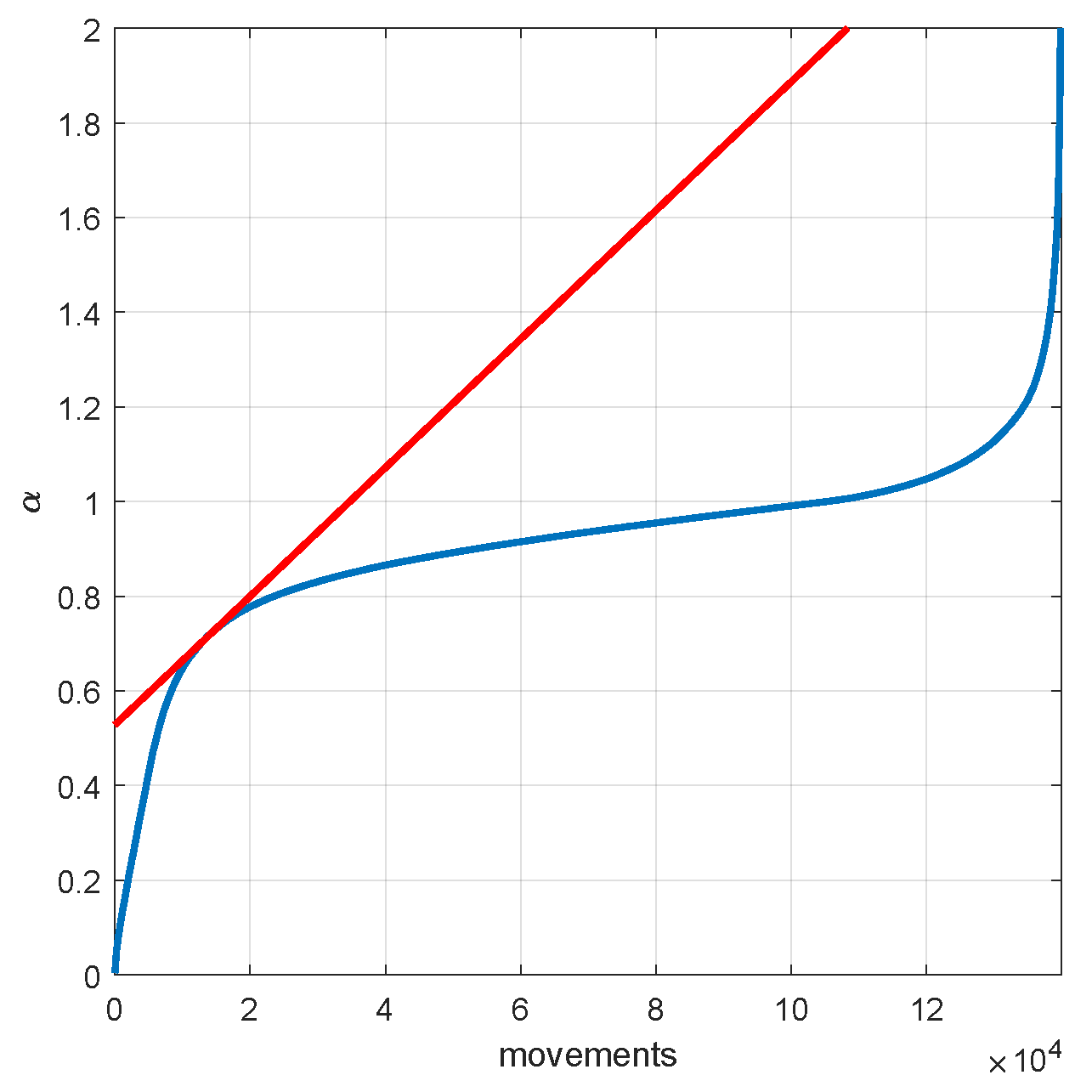
3.2.2. Calculation of the Trip Index
3.3. Results of the Classification of BSS Trips
3.4. Validation of the Results
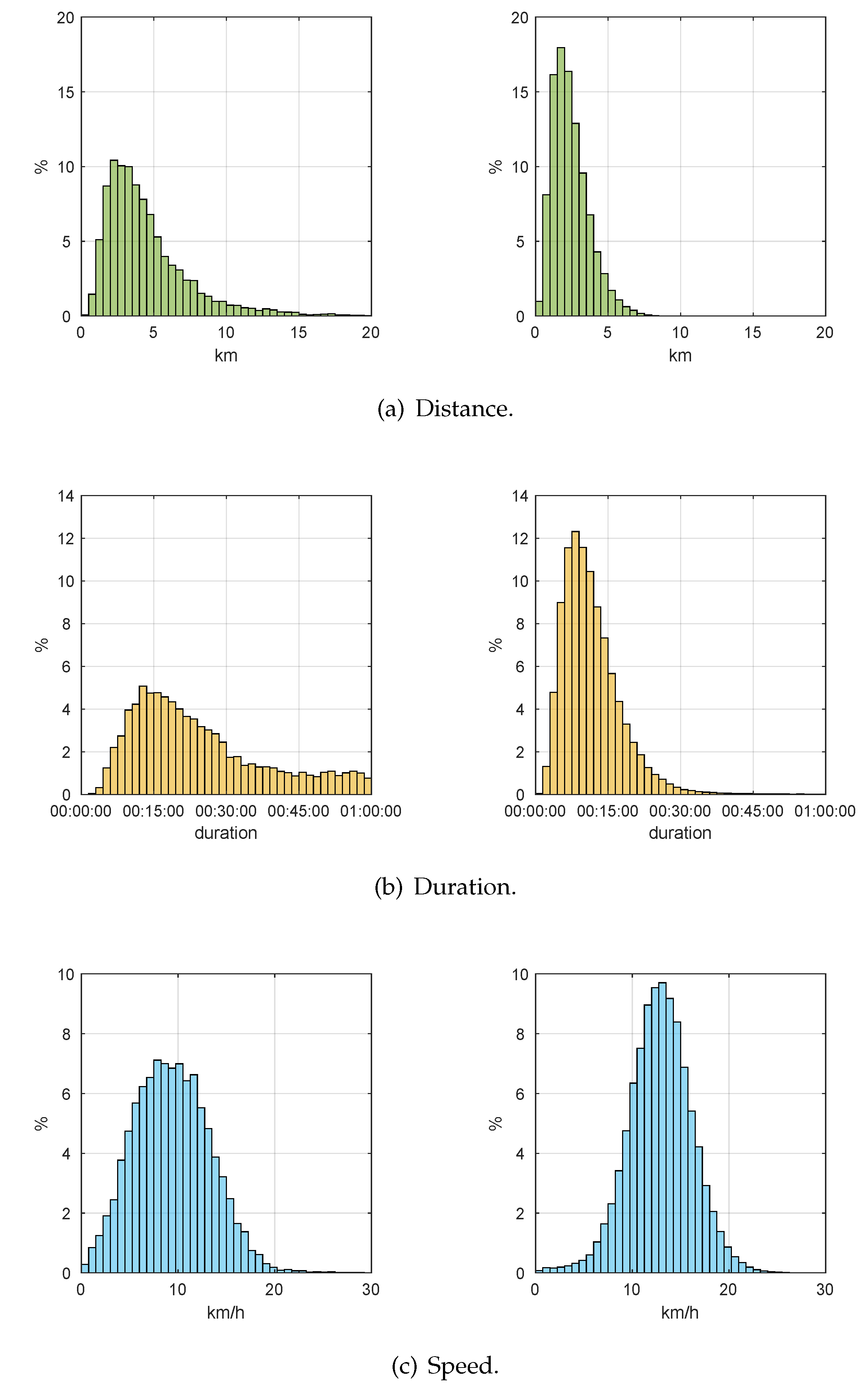
3.4.1. Statistical Analysis
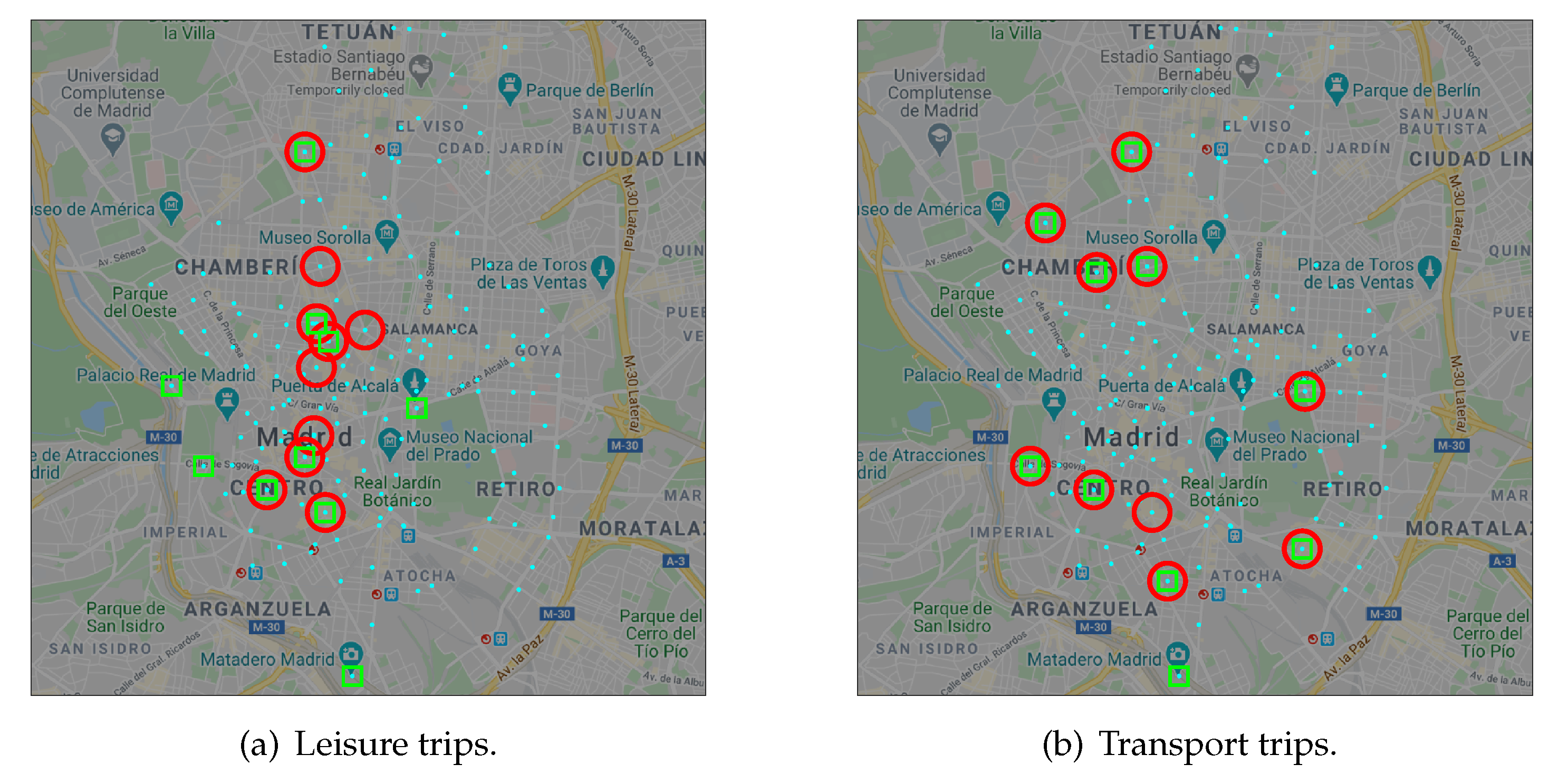
3.4.2. Operational Analysis
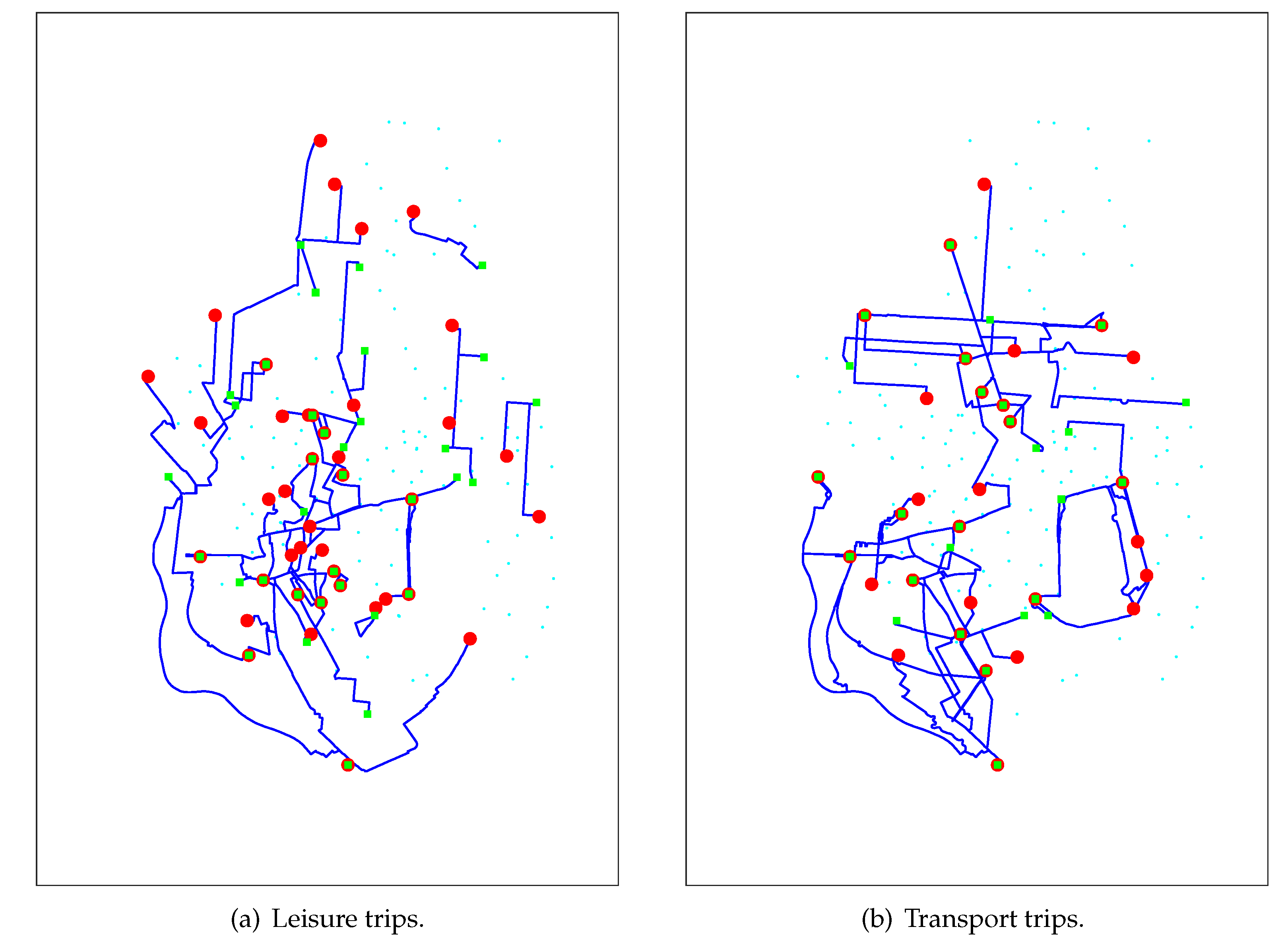
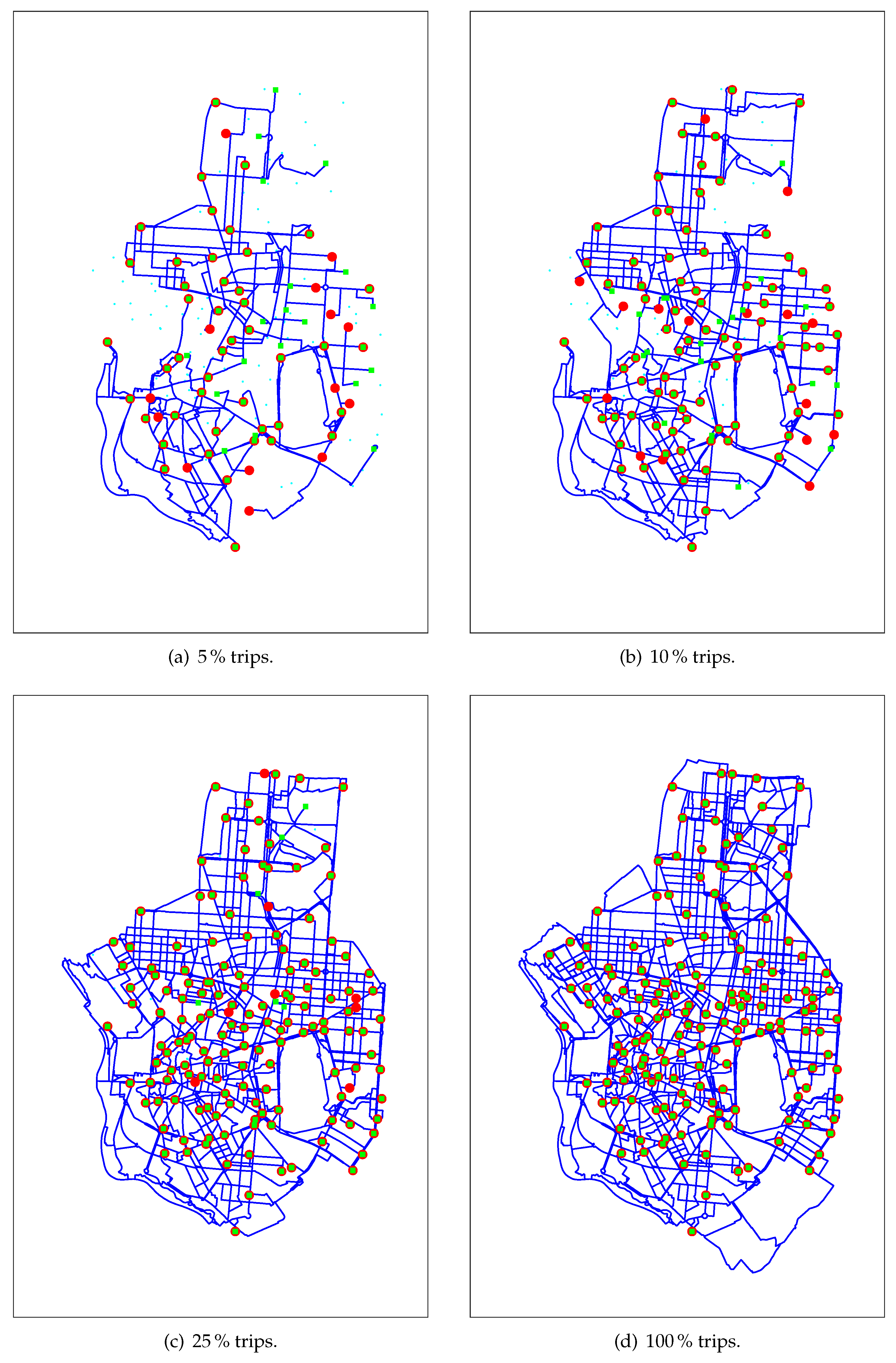
4. Underlying BSS Public Transport Network
5. Conclusions and Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chiariotti, F.; Pielli, C.; Zanella, A.; Zorzi, M. A Dynamic Approach to Rebalancing Bike-Sharing Systems. Sensors 2018, 18, 512. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.H.; Cheng, Z.; Chen, G.; Wang, L.; Ruan, Z.Y.; Zheng, Y.J. The impact of a public bicycle-sharing system on urban public transport networks. Transp. Res. Part Policy Pract. 2018, 107, 246–256. [Google Scholar] [CrossRef]
- Fishman, E.; Washington, S.; Haworth, N. Bike share’s impact on car use: Evidence from the United States, Great Britain, and Australia. Transp. Res. Part Transp. Environ. 2014, 31, 13–20. [Google Scholar] [CrossRef]
- Rydin, Y.; Bleahu, A.; Davies, M.; Dávila, J.D.; Friel, S.; De Grandis, G.; Groce, N.; Hallal, P.C.; Hamilton, I.; Howden-Chapman, P.; et al. Shaping cities for health: Complexity and the planning of urban environments in the 21st century. The Lancet 2012, 379, 2079–2108. [Google Scholar] [CrossRef]
- O’Brien, O.; Cheshire, J.; Batty, M. Mining bicycle sharing data for generating insights into sustainable transport systems. J. Transp. Geogr. 2014, 34, 262–273. [Google Scholar] [CrossRef]
- Song, C.; Koren, T.; Wang, P.; Barabási, A.L. Modelling the scaling properties of human mobility. Nature Phys. 2010, 6, 818–823. [Google Scholar] [CrossRef]
- González, M.C.; Hidalgo, C.; Barabási, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef]
- Koppelman, F.S.; Wen, C.H. Alternative nested logit models: Structure, properties and estimation. Transp. Res. Part Methodol. 1998, 32, 289–298. [Google Scholar] [CrossRef]
- Chen, J.; Li, S. Mode Choice Model for Public Transport with Categorized Latent Variables. Math. Probl. Eng. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- González, F.; Melo-Riquelme, C.; de Grange, L. A combined destination and route choice model for a bicycle sharing system. Transportation 2016, 43, 407–423. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, Y. Citywide Bike Usage Prediction in a Bike-Sharing System. IEEE Trans. Knowl. Data Eng. 2020, 32, 1079–1091. [Google Scholar] [CrossRef]
- Sarkar, A.; Lathia, N.; Mascolo, C. Comparing cities’ cycling patterns using online shared bicycle maps. Transportation 2015, 42, 541–559. [Google Scholar] [CrossRef]
- Shen, S.; Wei, Z.Q.; Sun, L.J.; Su, Y.Q.; Wang, R.C.; Jiang, H.M. The Shared Bicycle and Its Network—Internet of Shared Bicycle (IoSB): A Review and Survey. Sensors 2018, 18, 2581. [Google Scholar] [CrossRef] [PubMed]
- Olmos, L.E.; Tadeo, M.S.; Vlachogiannis, D.; Alhasoun, F.; Espinet Alegre, X.; Ochoa, C.; Targa, F.; González, M.C. A data science framework for planning the growth of bicycle infrastructures. Transp. Res. Part C Emerg. Technol. 2020, 115, 102640. [Google Scholar] [CrossRef]
- Calabrese, F.; Diao, M.; Di Lorenzo, G.; Ferreira, J.; Ratti, C. Understanding individual mobility patterns from urban sensing data: A mobile phone trace example. Transp. Res. Part C Emerg. Technol. 2013, 26, 301–313. [Google Scholar] [CrossRef]
- Curzel, J.; Lüders, R.; Fonseca, K.; Rosa, M. Temporal Performance Analysis of Bus Transportation Using Link Streams. Math. Probl. Eng. 2019, 2019, 1–18. [Google Scholar] [CrossRef]
- Aleta, A.; Meloni, S.; Moreno, Y. A Multilayer perspective for the analysis of urban transportation systems. Sci. Rep. 2017, 7, 44359. [Google Scholar] [CrossRef]
- Domencich, T.; McFadden, D. Statistical estimation of choice probability function. In Urban Travel Demand —A Behavioral Analysis; North-Holland Publishing Company Limited: Oxford, UK, 1975; pp. 101–125. [Google Scholar]
- De Dios Ortúzar, J.; Willumsen, L. Modelling Transport; John Wiley & Sons, Ltd.: New York, NY, USA, 2011. [Google Scholar]
- Bovet, P.; Benhamou, S. Spatial analysis of animals’ movements using a correlated random walk model. J. Theor. Biol. 1988, 131, 419–433. [Google Scholar] [CrossRef]
- Mueller, J.E. An Introduction to the Hydraulic and Topographic Sinuosity Indexes. Ann. Assoc. Am. Geogr. 1968, 58, 371–385. [Google Scholar] [CrossRef]
- Pearl, J. Heuristics: Intelligent Search Strategies for Computer Problem Solving; Addison-Wesley Longman Publishing Co., Inc.: Reading, MA, USA, 1984. [Google Scholar]
- Quddus, M.; Washington, S. Shortest path and vehicle trajectory aided map-matching for low frequency GPS data. Transp. Res. Part Emerg. Technol. 2015, 55, 328–339. [Google Scholar] [CrossRef]
- Zhang, J.; Pan, X.; Li, M.; Yu, P.S. Bicycle-Sharing System Analysis and Trip Prediction. In Proceedings of the 2016 17th IEEE International Conference on Mobile Data Management (MDM), Porto, Portugal, 13–16 June 2016; Volume 1, pp. 174–179. [Google Scholar]
- Jiang, Z.; Evans, M.; Oliver, D.; Shekhar, S. Identifying K Primary Corridors from urban bicycle GPS trajectories on a road network. Inf. Syst. 2016, 57, 142–159. [Google Scholar] [CrossRef]
- Guo, N.; Ma, M.; Xiong, W.; Chen, L.; Jing, N. An Efficient Query Algorithm for Trajectory Similarity Based on Fréchet Distance Threshold. ISPRS Int. J. Geo-Inf. 2017, 6, 326. [Google Scholar] [CrossRef]
- Fréchet, M. Sur quelques points du calcul fonctionnel. Rend. Circ. Matem. Palermo. 1906, 22, 1–72. [Google Scholar] [CrossRef]
- Alt, H.; Godau, M. Measuring the Resemblance of Polygonal Curves. In Proceedings of the Eighth Annual Symposium on Computational Geometry (SoCG ’92), Berlin, Germany, 10–12 June 1992; pp. 102–109. [Google Scholar]
- Eiter, T.; Mannila, H. Computing discrete Fréchet distance; Technical Report CD-TR 94/64; Technische Universität Wien: Wien, Austria, 1994. [Google Scholar]
- Scherrer, L.; Tomko, M.; Ranacher, P.; Weibel, R. Travelers or locals? Identifying meaningful sub-populations from human movement data in the absence of ground truth. EPJ Data Sci. 2018, 7, 19. [Google Scholar] [CrossRef]
- Faghih-Imani, A.; Eluru, N. Analysing bicycle-sharing system user destination choice preferences: Chicago’s Divvy system. J. Transp. Geogr. 2015, 44, 53–64. [Google Scholar] [CrossRef]
- Broach, J.; Dill, J.; Gliebe, J. Where do cyclists ride? A route choice model developed with revealed preference GPS data. Transp. Res. Part A Policy Pract. 2012, 46, 1730–1740. [Google Scholar] [CrossRef]
- Gallotti, R.; Bazzani, A.; Rambaldi, S. Understanding the variability of daily travel-time expenditures using GPS trajectory data. EPJ Data Sci. 2015, 4, 18. [Google Scholar] [CrossRef]
- Vinagre Díaz, J.J.; Fernández Pozo, R.; Rodríguez González, A.B.; Wilby, M.R.; Sánchez Ávila, C. Hierarchical Agglomerative Clustering ob Bicycle Sharing Stations Based on Ultra-Light Edge Computing. Sensors 2020, 20, 3550. [Google Scholar] [CrossRef]
- Domènech, A.; Gutiérrez, A. A GIS-Based Evaluation of the Effectiveness and Spatial Coverage of Public Transport Networks in Tourist Destinations. Int. J. Geo-Inf. 2017, 6, 83. [Google Scholar] [CrossRef]
- Hamilton, T.L.; Wichman, C.J. Bicycle infrastructure and traffic congestion: Evidence from DC’s Capital Bikeshare. J. Environ. Econ. Manag. 2018, 87, 72–93. [Google Scholar]

| Min. | Max. | Mean | Std. Dev. | |
|---|---|---|---|---|
| Leisure () | ||||
| Transport |
| Min. | Max. | Mean | Std. Dev. | |
|---|---|---|---|---|
| Leisure | 00:02:22 | 05:57:57 | 00:37:20 | 00:38:22 |
| Transport | 00:00:58 | 05:59:26 | 00:11:56 | 00:09:52 |
| Min. | Max. | Mean | Std. Dev. | |
|---|---|---|---|---|
| Leisure | ||||
| Transport |
| Total | Leisure | Transport | |
|---|---|---|---|
| trips | |||
| order | 169 | 169 | 169 |
| size | |||
| DENSITY |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilby, M.R.; Vinagre Díaz, J.J.; Fernández Pozo, R.; Rodríguez González, A.B.; Vassallo, J.M.; Sánchez Ávila, C. Data-Driven Analysis of Bicycle Sharing Systems as Public Transport Systems Based on a Trip Index Classification. Sensors 2020, 20, 4315. https://doi.org/10.3390/s20154315
Wilby MR, Vinagre Díaz JJ, Fernández Pozo R, Rodríguez González AB, Vassallo JM, Sánchez Ávila C. Data-Driven Analysis of Bicycle Sharing Systems as Public Transport Systems Based on a Trip Index Classification. Sensors. 2020; 20(15):4315. https://doi.org/10.3390/s20154315
Chicago/Turabian StyleWilby, Mark Richard, Juan José Vinagre Díaz, Rubén Fernández Pozo, Ana Belén Rodríguez González, José Manuel Vassallo, and Carmen Sánchez Ávila. 2020. "Data-Driven Analysis of Bicycle Sharing Systems as Public Transport Systems Based on a Trip Index Classification" Sensors 20, no. 15: 4315. https://doi.org/10.3390/s20154315
APA StyleWilby, M. R., Vinagre Díaz, J. J., Fernández Pozo, R., Rodríguez González, A. B., Vassallo, J. M., & Sánchez Ávila, C. (2020). Data-Driven Analysis of Bicycle Sharing Systems as Public Transport Systems Based on a Trip Index Classification. Sensors, 20(15), 4315. https://doi.org/10.3390/s20154315







