Control Plane Optimisation for an SDN-Based WBAN Framework to Support Healthcare Applications
Abstract
1. Introduction
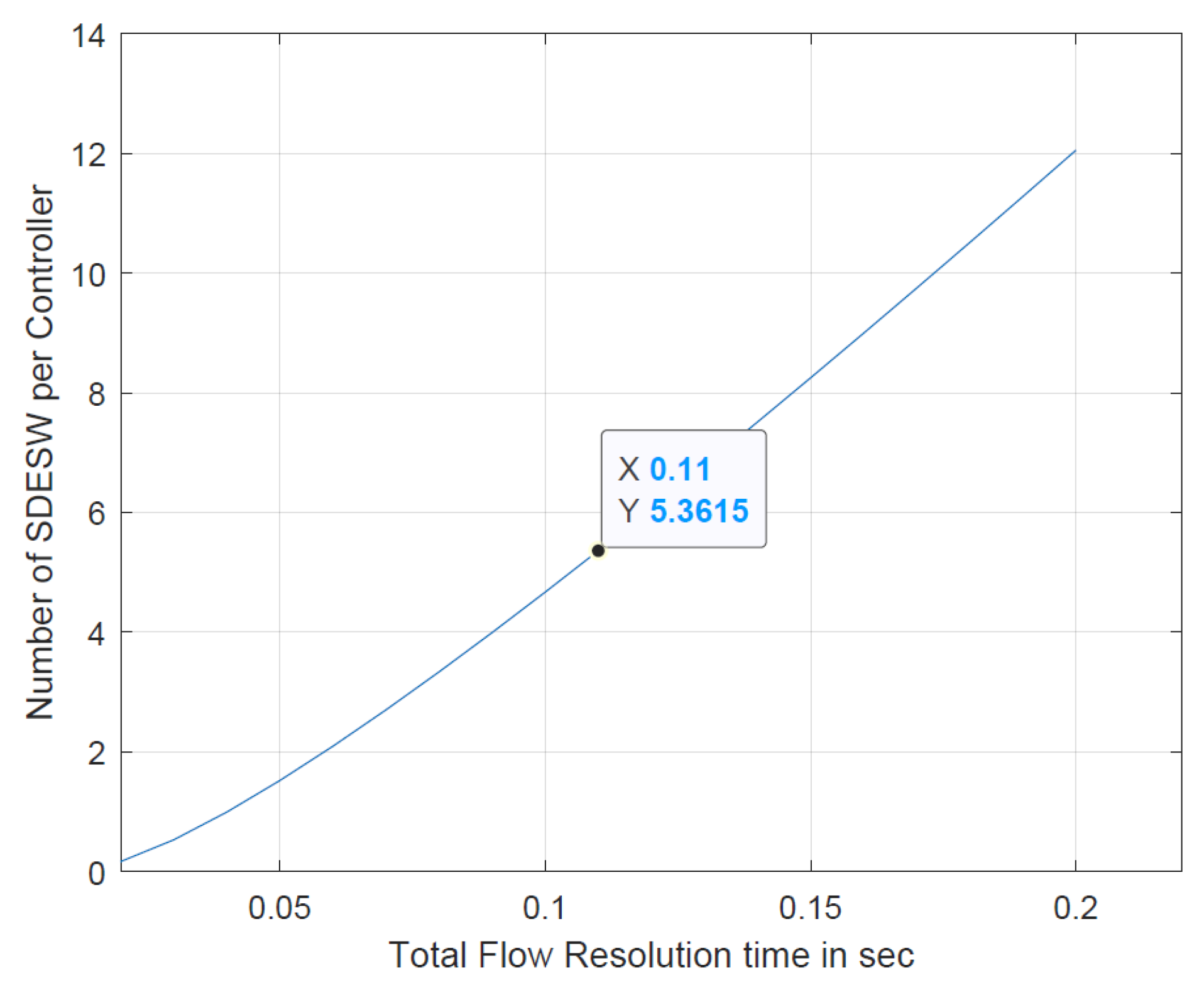
- Development of a mathematical model that determines the optimal number of controllers for an SDWBAN framework. In addition, the mathematical model also establishes a relationship between the number of controllers and SDESWs.
- Implementation and validation of the proposed mathematical model through the Castalia simulator.
2. Related Works
3. Influential Factors of Optimization
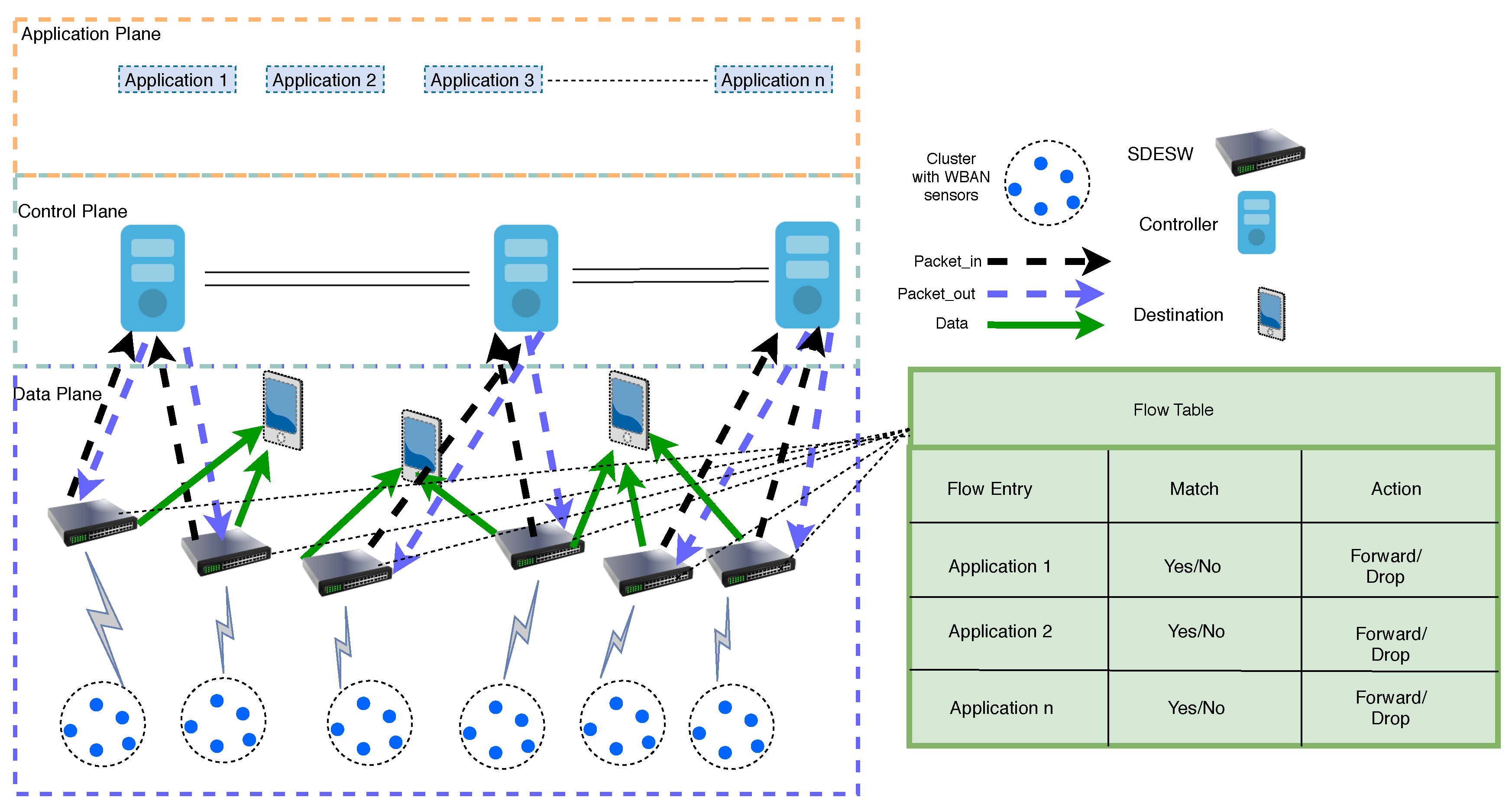
- Number of Controllers: The number of controllers plays a crucial role in the design and implementation of an optimal SDWBAN framework. The installation of a large number of controllers increases the complexity and cost of network management. The processing capacity of commercially available controllers typically varies, for instance, the processing speed of an industrial controller is usually very high and capable of maintaining millions of client devices simultaneously [27,28]. In such a case, the use of industrial controllers for SDWBAN deployment in an elderly home would be redundant. Since responding to the packet_in request initiated by the SDESW mostly depends on its processing speed, it is desirable to have an optimum number of controllers in SDWBAN deployment. The objective is to ensure a well-maintained communication between the controller and the SDESW and thus, patient monitoring activities are not compromised at all.
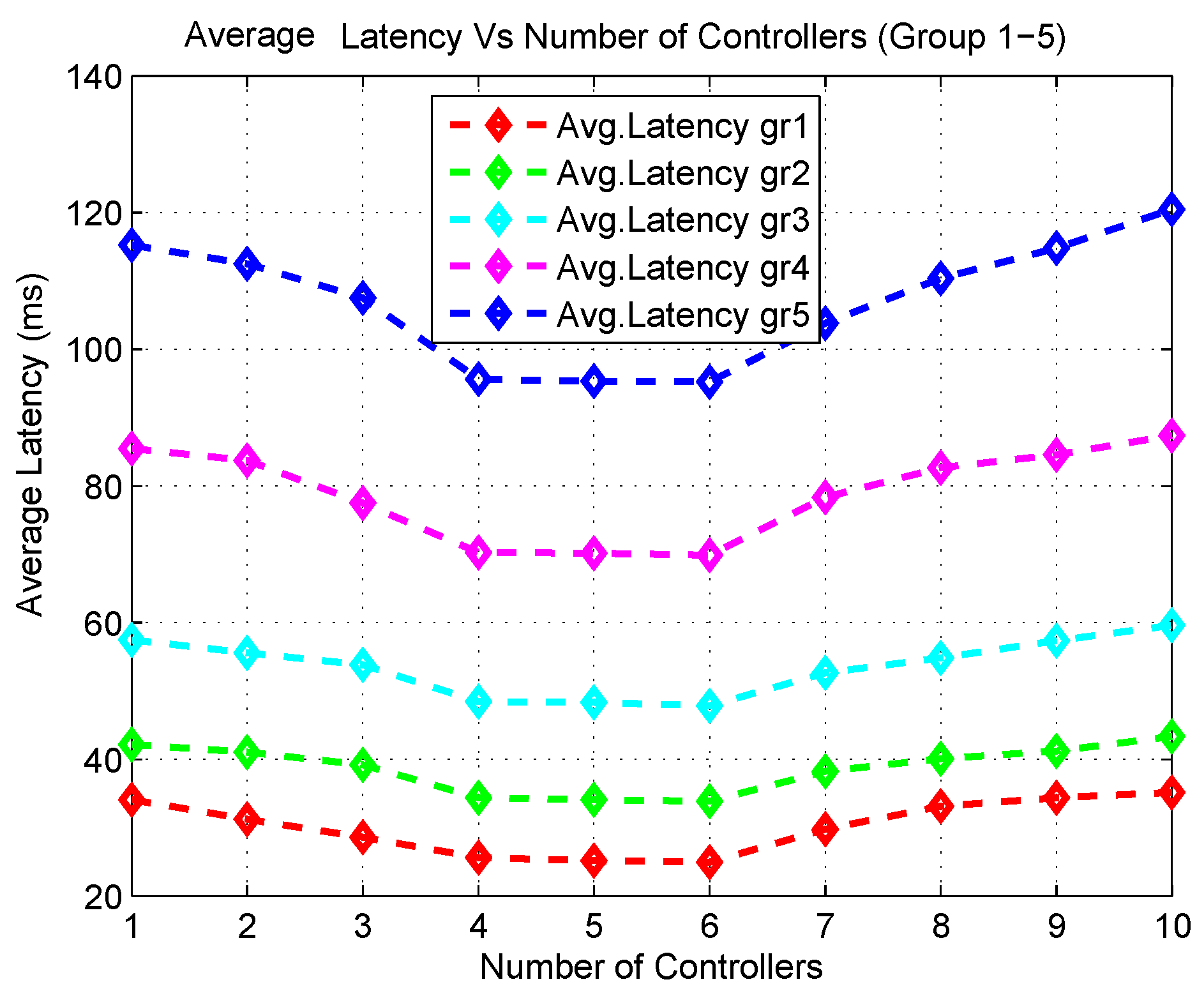
- Latency: Latency is related to several factors such as flow request processing time, propagation delay, service rate etc. In SDWBAN deployment, if an inadequate number of controllers is deployed, the controllers might undergo a considerable amount of delay in route setup. Consequently, sending out the data forwarding instructions to the SDESW will be affected in terms of flow requesting resolving time. In addition, there could be an increased amount of traffic load in the control channel communication between SDESW and the controller as new applications are introduced in the system. Ultimately, the latency incurred by this will affect the overall network performance in terms of packet delivery which will hamper patient monitoring activities.
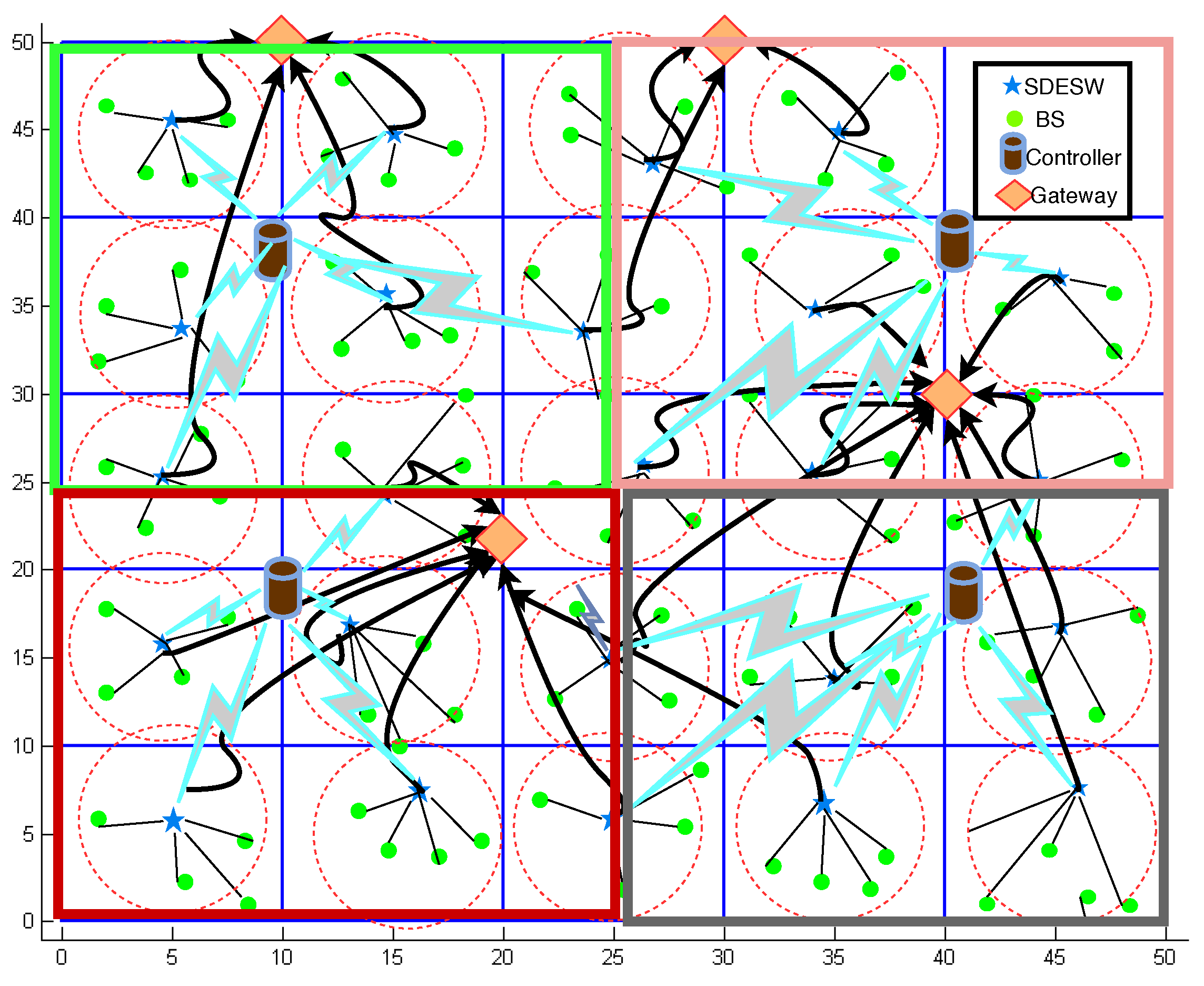
- Geographical Location: The geographical location of controllers and SDESWs is another important factor in designing the control plane. The issue of line of sight (LOS) and non-line of sight (NLOS) exists in wireless network deployment between the transmitter and the receiver. The NLOS scenario could be due to the fact that the patients in SDWBAN are at liberty to roam around, and in addition, the placement of a particular application sensor might block the direct propagation from body sensors to the SDESW. Similarly, other objects such as the walls of buildings, deflections at sharp edges, and multipath propagation may affect the signal strength in an SDWBAN environment. Considering these factors, it is important to design a system that maintains a standard receiver sensitivity level. Furthermore, an arbitrary placement of network elements (controllers, SDESWs, gateway) would cause additional propagation delay between the network elements and ultimately increase overall latency.
- Traffic Load distribution: The number of SDESWs residing under a controller is an important issue in determining traffic load. If the number of SDESWs is high under a controller, the probability of receiving a packet_in request also increases. Consequently, the number of packet_out responses to the SDESW also increases. As a result, traffic load increases between the communication channel of the controller and the SDESW. Considering the processing capacity of a particular type of controller, SDN controllers can be programmed in such a way that the excess load can be distributed to the neighboring controllers.
- Flow Setup Time: The flow setup time is the amount of time a SDESW needs to send a query to the controller to install data forwarding rules in its flow table. If the number of flow requests originating from the underlying SDESW is larger than the processing capacity of the controller, the average flow setup time can increase significantly which will degrade the service performance [29,30].
- Statistics Collection Time and Synchronization Cost: In the case of multiple controllers residing in the control plane, inter-controller communication takes place to maintain an abstract view of the network and this assists the controllers to provide data forwarding decisions to the switches [11]. The controllers deployed in the network can be inter-connected so that upon failure of one controller, the next available controller can serve the orphaned SDESWs. Moreover, to maintain a consistent view of the network, it is important to keep the synchronization between the controllers [12]. The controllers can have an overall view of the network by collecting various statistics such as port information, flows, flow table level etc. from the switches. This requires several messages to be exchanged between the controllers and switches. Consequently, a trade-off is necessary between the flow setup time and statistics collection time in order to avoid delay in flow resolution.
- Number of SDESW: The number of SDESWs in the deployed area could be a crucial point and may create a bottleneck in the network. With a higher number of SDESWs residing in the network, a higher number of flow requests are initiated to the controllers upon realizing an unknown flow. This will ultimately affect the PDR and latency of the network.
4. Development of Optimization Model
4.1. Optimization in SDWBAN Scenario
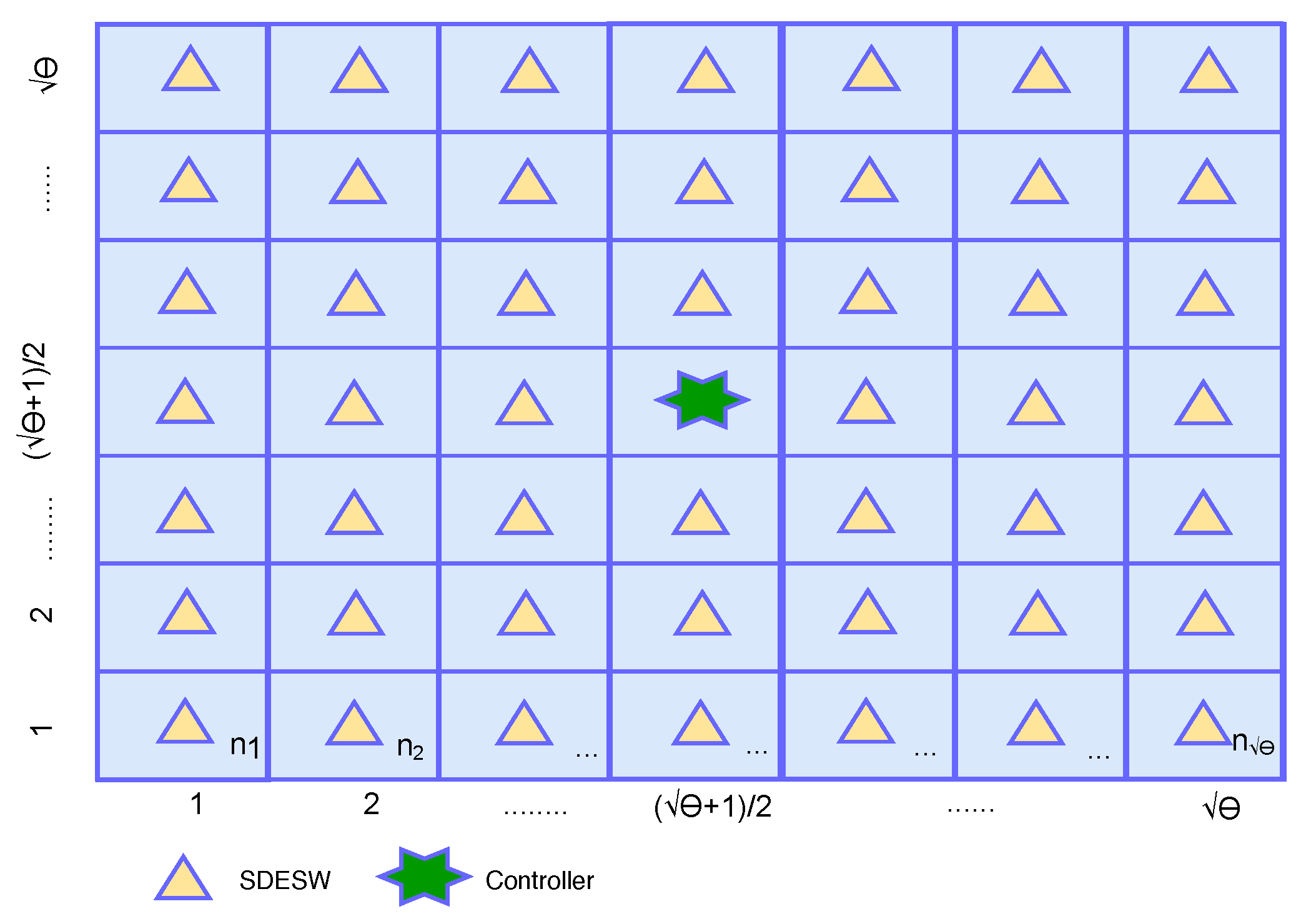
4.2. Proposed Mathematical Model
5. Results and Analysis
5.1. Analytical Output
- The optimal number of controllers required in an implementation scenario largely depends on the processing capacity of the controller. For instance, it is assumed that the service of the controller is 100 pkt/sec, which is based on simulation output. It is found from the simulation that the processing rate of a light-weight controller is 100 pkt/s. However, industrially available controllers have higher processing capacity [35]. The controllers with higher processing capacity or service will result in a faster response to the incoming packet_in request from a SDESW. The consequence will be low queuing delay due to the variable packet arrival rate from the underlying body sensors.
- The flow request delay is another important factor since it depends on the matching probability in the flow table and the speed of the look-up process.
- The packet arrival rate from the heterogeneous sensors affects the performance of the SDESW and the controller. Since the heterogeneous nature of WBAN sensors generates data packets at various intervals, this could imbalance the traffic load in the communication channel between the SDESW and the controller.
- The number of controllers and the number of SDESWs affect the overall performance. If there are fewer controllers in the deployed area, this limited number of controllers might have to cater for all the SDESWs under the assigned controller. In such a case, packet forwarding might route in a multi-hop fashion to the controller if the distance between the SDESW and the controller is out of transmission range. Consequently, it degrades the performance in terms of success rate and latency. In practice, various WBAN applications require to maintain various delay constraints. From the literature, based on the general WBAN guideline, a strict delay of 110 ms–120 ms is required to maintain.
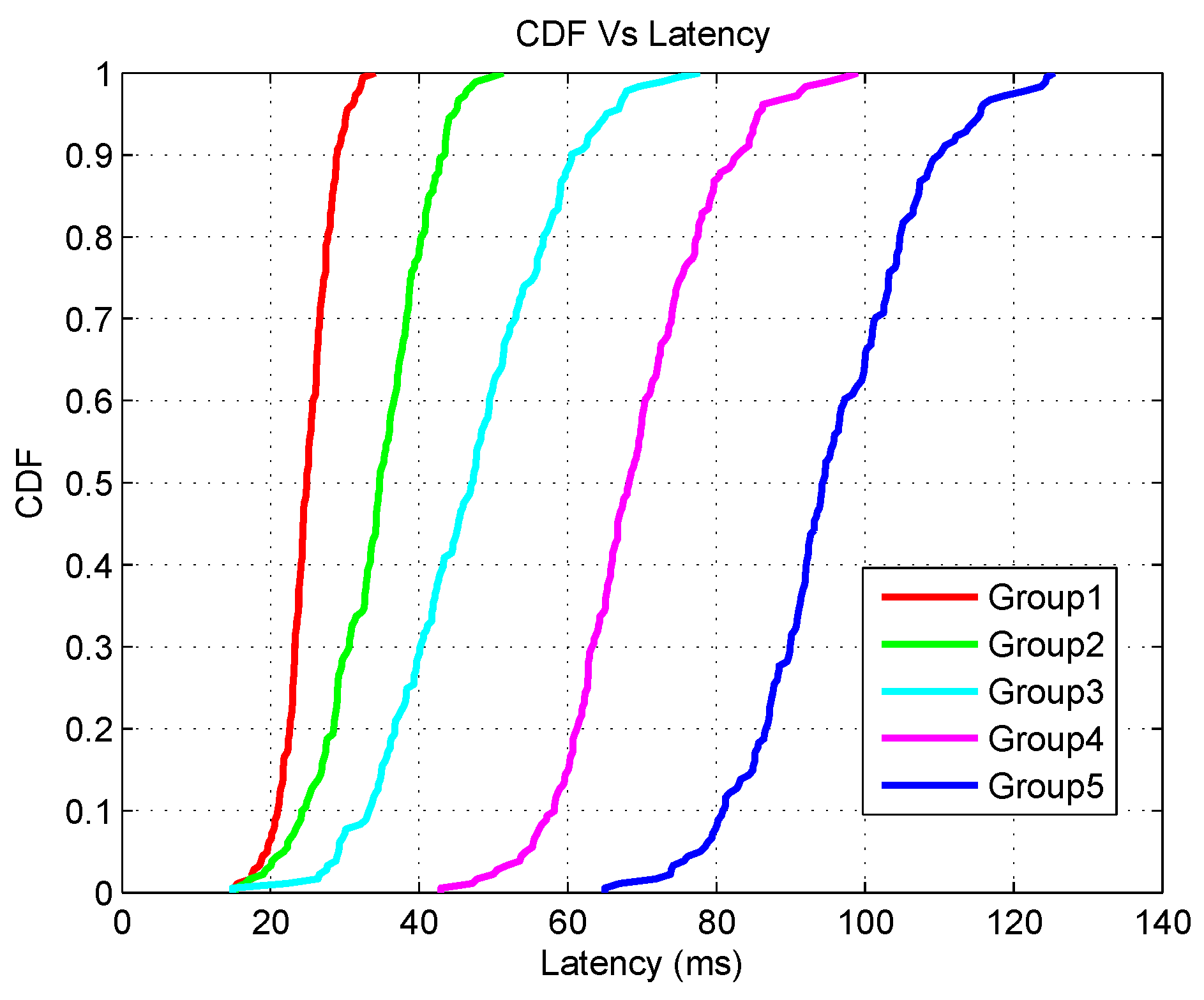
5.2. Simulation Output
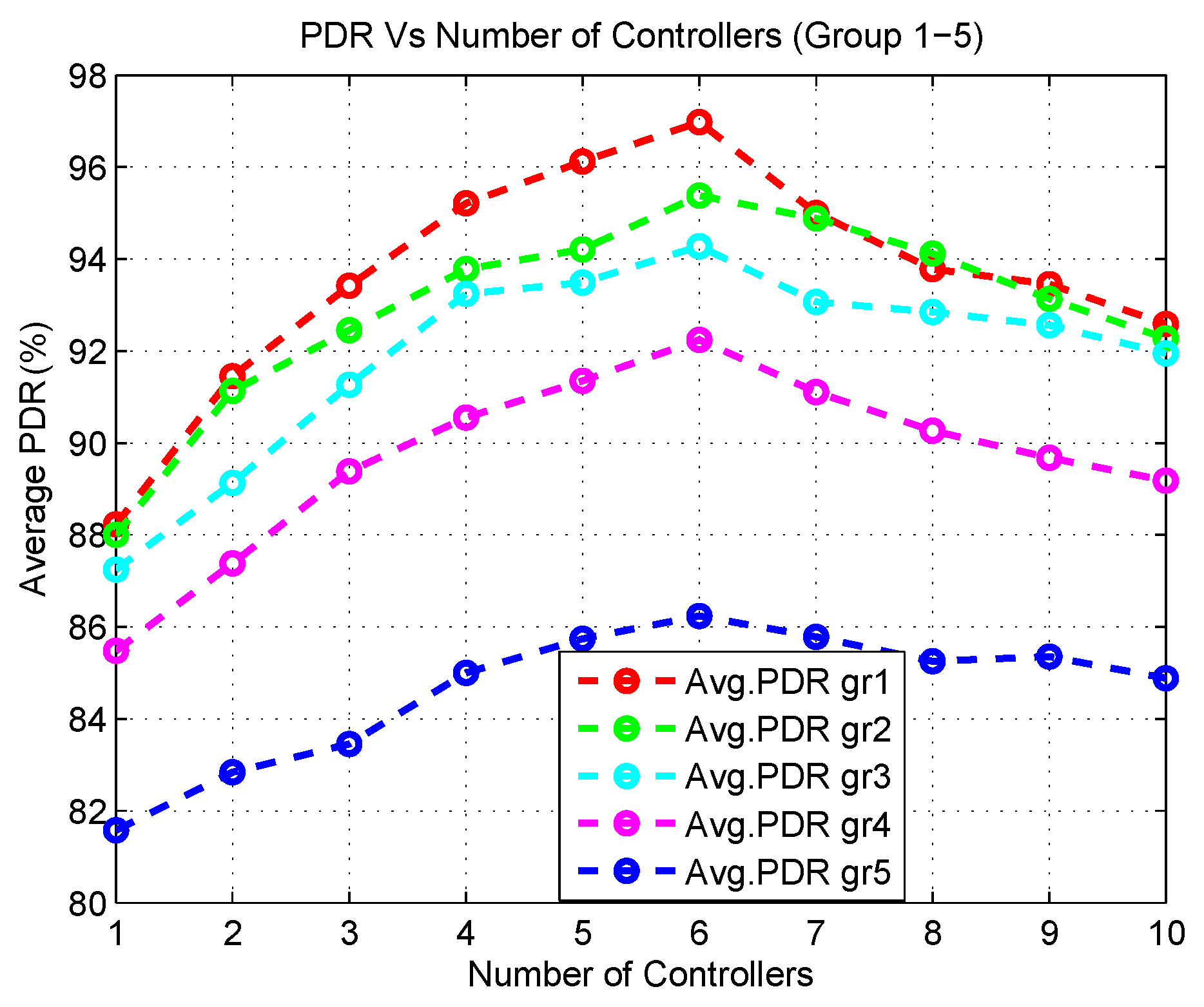
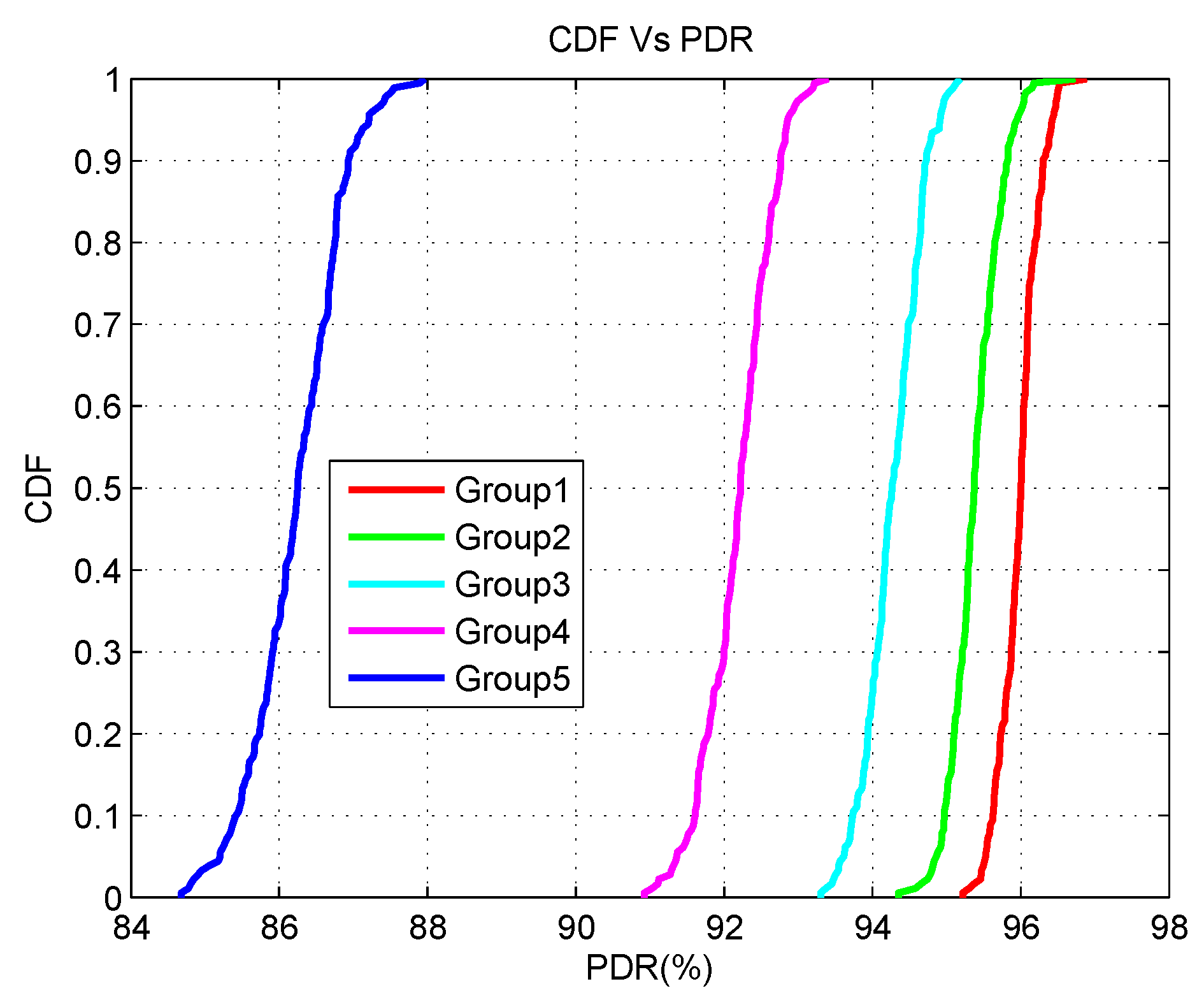
- When the number of controllers is low (1, 2, or 3), less controllers are used to cater for a lot of flow resolve requests from a various number of application groups. This creates a bottleneck to respond to the incoming packet_in requests coming from the SDESWs. Furthermore, a lot of multi-hop communication takes place since the destination controller is beyond the transmission range of SDESWs. This results in a delay in accessing the channel. In addition, the traffic load increases between the communication channel of SDESWs and the controllers. Thus, the PDR of all application groups decreases.
- When the controller number is between 4 to 6, the average PDR shows little variation in the output which actually shows the optimal range of controllers that are required for the SDWBAN framework.
- When the number of controllers is between 7 to 10, the PDR decreases due to the fact that a lot of controllers reside nearby and use in-band frequency. This also causes congestion and interference with the neighbouring nodes in the communication channel.
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Islam, S.R.; Kwak, D.; Kabir, M.H.; Hossain, M.; Kwak, K.S. The internet of things for health care: A comprehensive survey. IEEE Access 2015, 3, 678–708. [Google Scholar] [CrossRef]
- Pramanik, P.K.D.; Solanki, A.; Debnath, A.; Nayyar, A.; El-Sappagh, S.; Kwak, K.S. Advancing Modern Healthcare With Nanotechnology, Nanobiosensors, and Internet of Nano Things: Taxonomies, Applications, Architecture, and Challenges. IEEE Access 2020, 8, 65230–65266. [Google Scholar] [CrossRef]
- Darwish, A.; Hassanien, A.E. Wearable and implantable wireless sensor network solutions for healthcare monitoring. Sensors 2011, 11, 5561–5595. [Google Scholar] [CrossRef]
- Bouazizi, A.; Zaibi, G.; Samet, M.; Kachouri, A. Wireless body area network for e-health applications: Overview. In Proceedings of the 2017 International Conference on Smart, Monitored and Controlled Cities (SM2C), Sfax, Tunisia, 17–19 February 2017; pp. 64–68. [Google Scholar]
- Hasan, K.; Biswas, K.; Ahmed, K.; Nafi, N.S.; Islam, M.S. A comprehensive review of wireless body area network. J. Netw. Comput. Appl. 2019, 143, 178–198. [Google Scholar] [CrossRef]
- Kreutz, D.; Ramos, F.M.V.; Veríssimo, P.J.E.; Rothenberg, C.E.; Azodolmolky, S.; Uhlig, S. Software-Defined Networking: A Comprehensive Survey. Proc. IEEE 2015, 103, 14–76. [Google Scholar] [CrossRef]
- Ahmad, I.; Namal, S.; Ylianttila, M.; Gurtov, A.V. Security in Software Defined Networks: A Survey. IEEE Commun. Surv. Tutor. 2015, 17, 2317–2346. [Google Scholar] [CrossRef]
- Cox, J.H.; Chung, J.; Donovan, S.; Ivey, J.; Clark, R.J.; Riley, G.; Owen, H.L. Advancing software-defined networks: A survey. IEEE Access 2017, 5, 25487–25526. [Google Scholar] [CrossRef]
- Nkenyereye, L.; Nkenyereye, L.; Islam, S.M.R.; Choi, Y.; Bilal, M.; Jang, J. Software-Defined Network-Based Vehicular Networks: A Position Paper on Their Modeling and Implementation. Sensors 2019, 19, 3788. [Google Scholar] [CrossRef]
- Hasan, K.; Wu, X.; Biswas, K.; Ahmed, K. A Novel Framework for Software Defined Wireless Body Area Network. In Proceedings of the International Conference on Intelligent Systems, Modelling and Simulation, Girona, Spain, 28–29 June 2018; pp. 114–119. [Google Scholar] [CrossRef]
- Bari, M.F.; Roy, A.R.; Chowdhury, S.R.; Zhang, Q.; Zhani, M.F.; Ahmed, R.; Boutaba, R. Dynamic Controller Provisioning in Software Defined Networks. In Proceedings of the International Conference on Network and Service Management, Ghent, Belgium, 27–31 May 2013; pp. 18–25. [Google Scholar] [CrossRef]
- Levin, D.; Wundsam, A.; Heller, B.; Handigol, N.; Feldmann, A. Logically Centralized?: State Distribution Trade-offs in Software Defined Networks. In Workshop on Hot Topics in Software Defined Networks; ACM: New York, NY, USA, 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Heller, B.; Sherwood, R.; McKeown, N. The Controller Placement Problem. In Workshop on Hot Topics in Software Defined Networks; ACM: New York, NY, USA, 2012; pp. 7–12. [Google Scholar] [CrossRef]
- Hu, T.; Guo, Z.; Yi, P.; Baker, T.; Lan, J. Multi-controller Based Software-Defined Networking: A Survey. IEEE Access 2018, 6, 15980–15996. [Google Scholar] [CrossRef]
- Singh, A.K.; Srivastava, S. A survey and classification of controller placement problem in SDN. Int. J. Netw. Manag. 2018, 28, e2018. [Google Scholar] [CrossRef]
- Xie, J.; Guo, D.; Hu, Z.; Qu, T.; Lv, P. Control plane of software defined networks: A survey. Comput. Commun. 2015, 67, 1–10. [Google Scholar] [CrossRef]
- Sallahi, A.; St-Hilaire, M. Optimal Model for the Controller Placement Problem in Software Defined Networks. IEEE Commun. Lett. 2015, 19, 30–33. [Google Scholar] [CrossRef]
- Hock, D.; Hartmann, M.; Gebert, S.; Jarschel, M.; Zinner, T.; Tran-Gia, P. Pareto-optimal resilient controller placement in SDN-based core networks. In Proceedings of the International Teletraffic Congress, Shanghai, China, 10–12 September 2013; pp. 1–9. [Google Scholar] [CrossRef]
- Yao, G.; Bi, J.; Li, Y.; Guo, L. On the Capacitated Controller Placement Problem in Software Defined Networks. IEEE Commun. Lett. 2014, 18, 1339–1342. [Google Scholar] [CrossRef]
- Jiménez, Y.; Cervelló-Pastor, C.; García, A.J. On the controller placement for designing a distributed SDN control layer. In Proceedings of the 2014 IFIP Networking Conference, Trondheim, Norway, 2–4 June 2014; pp. 1–9. [Google Scholar] [CrossRef]
- Faragardi, H.R.; Vahabi, M.; Fotouhi, H.; Nolte, T.; Fahringer, T. An efficient placement of sinks and SDN controller nodes for optimizing the design cost of industrial IoT systems. Softw. Pract. Exp. 2018, 48, 1893–1919. [Google Scholar] [CrossRef]
- Ren, W.; Sun, Y.; Luo, H.; Guizani, M. A Novel Control Plane Optimization Strategy for Important Nodes in SDN-IoT Networks. IEEE Internet Things J. 2019, 6, 3558–3571. [Google Scholar] [CrossRef]
- Liyanage, K.S.K.; Ma, M.; Chong, P.H.J. Controller placement optimization in hierarchical distributed software defined vehicular networks. Comput. Netw. 2018, 135, 226–239. [Google Scholar] [CrossRef]
- Bagaa, M.; Taleb, T.; Laghrissi, A.; Ksentini, A.; Flinck, H. Coalitional Game for the Creation of Efficient Virtual Core Network Slices in 5G Mobile Systems. IEEE J. Sel. Areas Commun. 2018, 36, 469–484. [Google Scholar] [CrossRef]
- Zhao, Z.; Wu, B. Scalable SDN architecture with distributed placement of controllers for WAN. Concurr. Comput. 2017, 29, e4030. [Google Scholar] [CrossRef]
- Gorkemli, B.; Tatlicioglu, S.; Tekalp, A.M.; Civanlar, S.; Lokman, E. Dynamic Control Plane for SDN at Scale. IEEE J. Sel. Areas Commun. 2018, 36, 2688–2701. [Google Scholar] [CrossRef]
- The Cisco Application Policy Infrastructure Controller. Available online: https://www.cisco.com/c/en_au/products/cloud-systems-management/application-policy-infrastructure-controller-apic/index.html (accessed on 20 July 2020).
- Yao, L.; Hong, P.; Zhou, W. Evaluating the controller capacity in software defined networking. In Proceedings of the 2014 23rd International Conference on Computer Communication and Networks (ICCCN), Shanghai, China, 4–7 August 2014; pp. 1–6. [Google Scholar]
- Tootoonchian, A.; Gorbunov, S.; Ganjali, Y.; Casado, M.; Sherwood, R. On Controller Performance in Software-defined Networks. In Proceedings of the USENIX Conference on Hot Topics in Management of Internet, Cloud, and Enterprise Networks and Services, San Jose, CA, USA, 24 April 2012; USENIX Association: Berkeley, CA, USA, 2012; p. 10. [Google Scholar]
- AlGhadhban, A.; Shihada, B. Delay analysis of new-flow setup time in software defined networks. In Proceedings of the NOMS 2018—2018 IEEE/IFIP Network Operations and Management Symposium, Taipei, Taiwan, 23–27 April 2018; pp. 1–7. [Google Scholar]
- Sufiev, H.; Haddad, Y.; Barenboim, L.; Soler, J. Dynamic SDN Controller Load Balancing. Future Internet 2019, 11, 75. [Google Scholar] [CrossRef]
- Hasan, K.; Ahmed, K.; Biswas, K.; Islam, M.S.; Sianaki, O.A. Software-defined application-specific traffic management for wireless body area networks. Future Gener. Comput. Syst. 2020. [Google Scholar] [CrossRef]
- Nafi, N.S.; Ahmed, K.; Gregory, M.A.; Datta, M. Software defined neighborhood area network for smart grid applications. Future Gener. Comput. Syst. 2018, 79, 500–513. [Google Scholar] [CrossRef]
- Holmberg, K.; Adgar, A.; Arnaiz, A.; Jantunen, E.; Mascolo, J.; Mekid, S. E-Maintenance; Springer Science & Business Media: London, UK, 2010. [Google Scholar]
- Zhu, L.; Karim, M.M.; Sharif, K.; Li, F.; Du, X.; Guizani, M. SDN Controllers: Benchmarking & Performance Evaluation. arXiv 2019, arXiv:1902.04491. [Google Scholar]
- Boulis, A. Castalia 3.2, User’S Manual; National ICT Australia Ltd.: Eveleigh, Australia, 2011. [Google Scholar]
| Abbreviation | Elaboration |
|---|---|
| WBAN | Wireless Body Area Network |
| SDN | Software-Defined Networking |
| SDWBAN | SDN-based WBAN |
| PDR | Packet Delivery Ratio |
| SDESW | SDN-enabled Switch |
| QoS | Quality of Service |
| Notations | Meaning |
|---|---|
| Flow Request Delay | |
| Queuing Delay | |
| Processing Delay | |
| Propagation Delay—SDESW to Controller | |
| Propagation Delay—Controller to SDESW | |
| Relaying Delay |
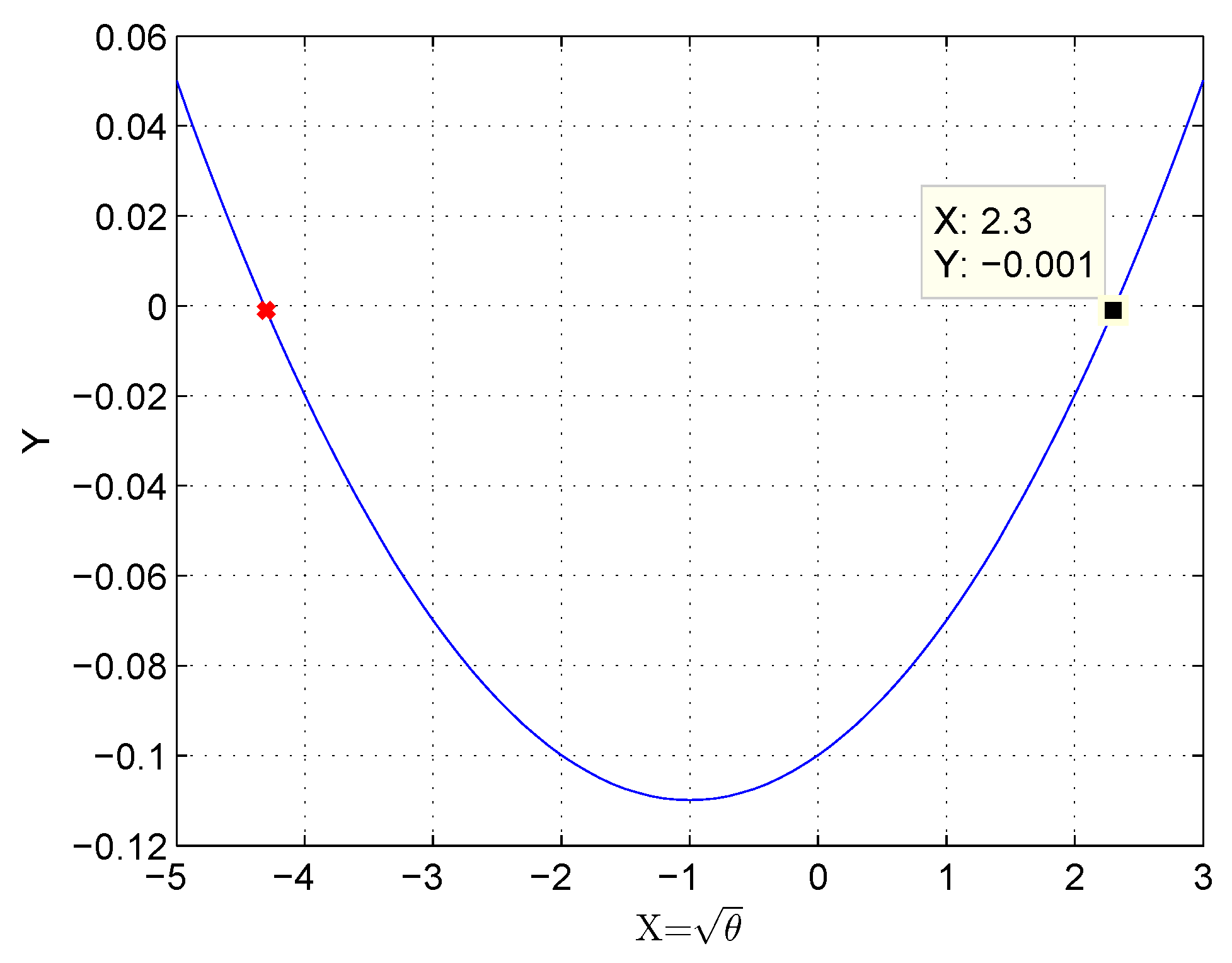
| Flow Resolution Time (T ms) | Numerical Coefficient (c) | Root () |
|---|---|---|
| 20 | −0.0099 | (0.4107, −2.4117) |
| 30 | −0.0199 | (0.7292, −2.7302) |
| 40 | −0.0299 | (0.9976, −2.9986) |
| 50 | −0.0399 | (1.2340, −3.2349) |
| 60 | −0.0499 | (1.4476, −3.4486) |
| 70 | −0.0599 | (1.6441, −3.6451) |
| 80 | −0.0699 | (1.8269, −3.8279) |
| 90 | −0.0799 | (1.9986, −3.9996) |
| 100 | −0.0899 | (2.1610, −4.1620) |
| 110 | −0.0999 | (2.3155, −4.3165) |
| 120 | −0.1099 | (2.4631, −4.4640) |
| 130 | −0.1199 | (2.6046, −4.6056) |
| 140 | −0.1299 | (2.7408, −4.7417) |
| 150 | −0.1399 | (2.8722, −4.8731) |
| 160 | −0.1499 | (2.9993, −5.002) |
| Number of Body Sensors (S) | Optimal Controllers |
|---|---|
| 100 | 5 |
| 200 | 10 |
| 300 | 14 |
| 400 | 19 |
| 500 | 24 |
| Parameters | Values |
|---|---|
| Flow Request Delay, | 100 s [34] |
| Free space propagation speed, C | m/s |
| Average length of a hop from SDESW to Controller, | 32.30 m |
| Propagation Delay in one hop, | |
| Storing and Forwarding delay, | 20 ms |
| Packet Arrival Rate, | 50 pkt/s [23] |
| Service Rate, | 100 pkt/s |
| Maximum Queue Size, K | 15 |
| Groups | Number of Applications |
|---|---|
| Group 1 | 1 |
| Group 2 | 5 |
| Group 3 | 10 |
| Group 4 | 15 |
| Group 5 | 20 |
| Parameter | Value(s) |
|---|---|
| Simulation Area | 75 × 75 m |
| Radio range (BS, SDESW, Controller) | ∼8 m, ∼20 m, ∼20 m |
| Reference Distance () | 1 m |
| Transmission Power (SDESW, BS) | 0 dBm, −10 dBm |
| Data Rate, Modulation Type, Bits Per Symbol, Bandwidth | 250 Kbps, PSK, 4, 20 MHz |
| Number of BS, Gateway | 100, 4 |
| Noise Bandwidth, Noise Floor, Sensitivity | 194 MHz, −100 dBm, −95 dBm |
| BS density | 4 nodes/225 m |
| Free Space Path Loss exponent | 2.4 |
| Total SDESW | 25 (1 node per sector) |
| Initial Average Path Loss () | 55 dB |
| Total Controller | 4 (2 × 2 grid) |
| Gaussian Zero-Mean Random Variable (X) | 4.0 |
| Number of Clusters | 25 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, K.; Ahmed, K.; Biswas, K.; Islam, M.S.; Kayes, A.S.M.; Islam, S.M.R. Control Plane Optimisation for an SDN-Based WBAN Framework to Support Healthcare Applications. Sensors 2020, 20, 4200. https://doi.org/10.3390/s20154200
Hasan K, Ahmed K, Biswas K, Islam MS, Kayes ASM, Islam SMR. Control Plane Optimisation for an SDN-Based WBAN Framework to Support Healthcare Applications. Sensors. 2020; 20(15):4200. https://doi.org/10.3390/s20154200
Chicago/Turabian StyleHasan, Khalid, Khandakar Ahmed, Kamanashis Biswas, Md. Saiful Islam, A. S. M. Kayes, and S. M. Riazul Islam. 2020. "Control Plane Optimisation for an SDN-Based WBAN Framework to Support Healthcare Applications" Sensors 20, no. 15: 4200. https://doi.org/10.3390/s20154200
APA StyleHasan, K., Ahmed, K., Biswas, K., Islam, M. S., Kayes, A. S. M., & Islam, S. M. R. (2020). Control Plane Optimisation for an SDN-Based WBAN Framework to Support Healthcare Applications. Sensors, 20(15), 4200. https://doi.org/10.3390/s20154200










