A 1 V 92 dB SNDR 10 kHz Bandwidth Second-Order Asynchronous Delta-Sigma Modulator for Biomedical Signal Processing
Abstract
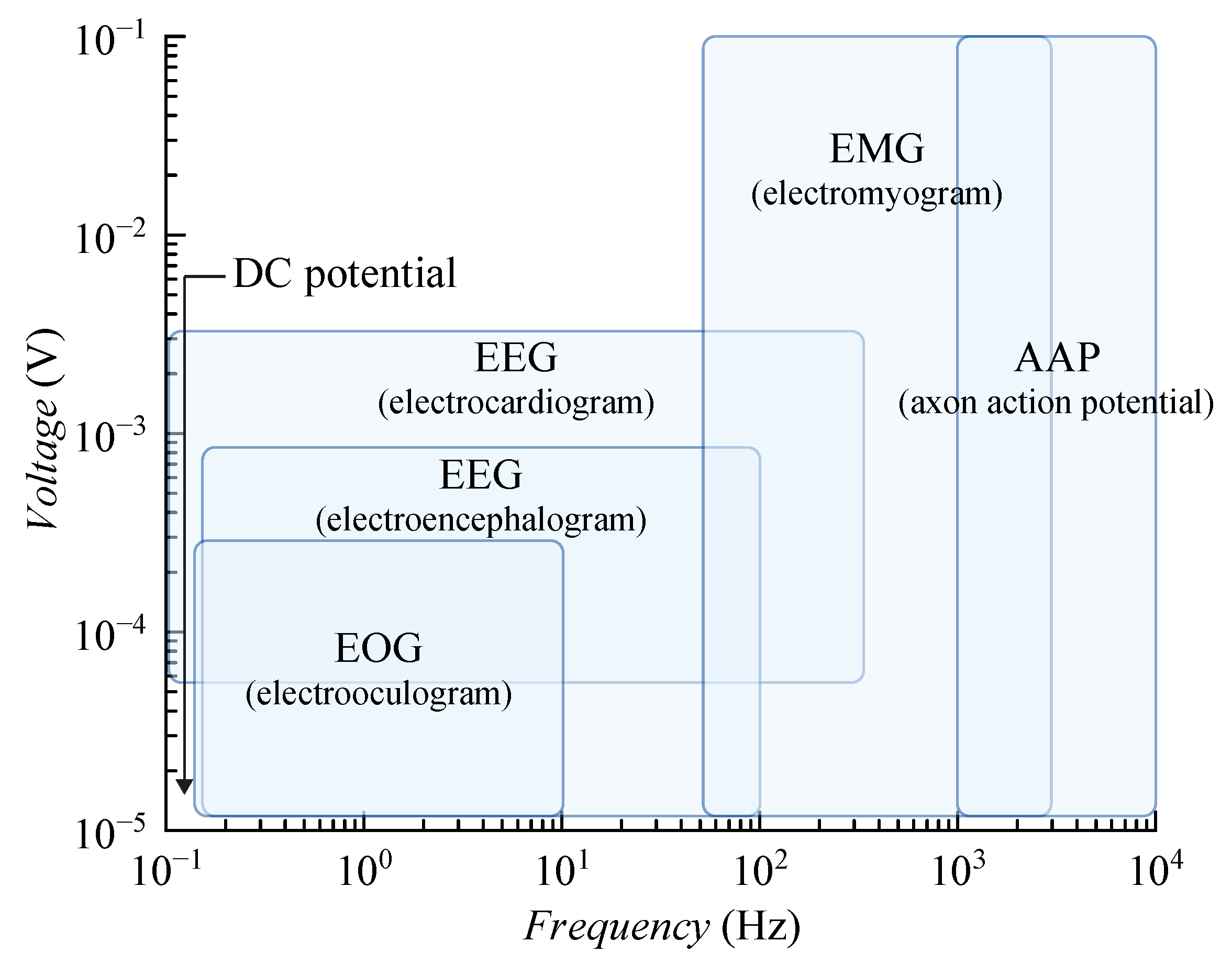
1. Introduction
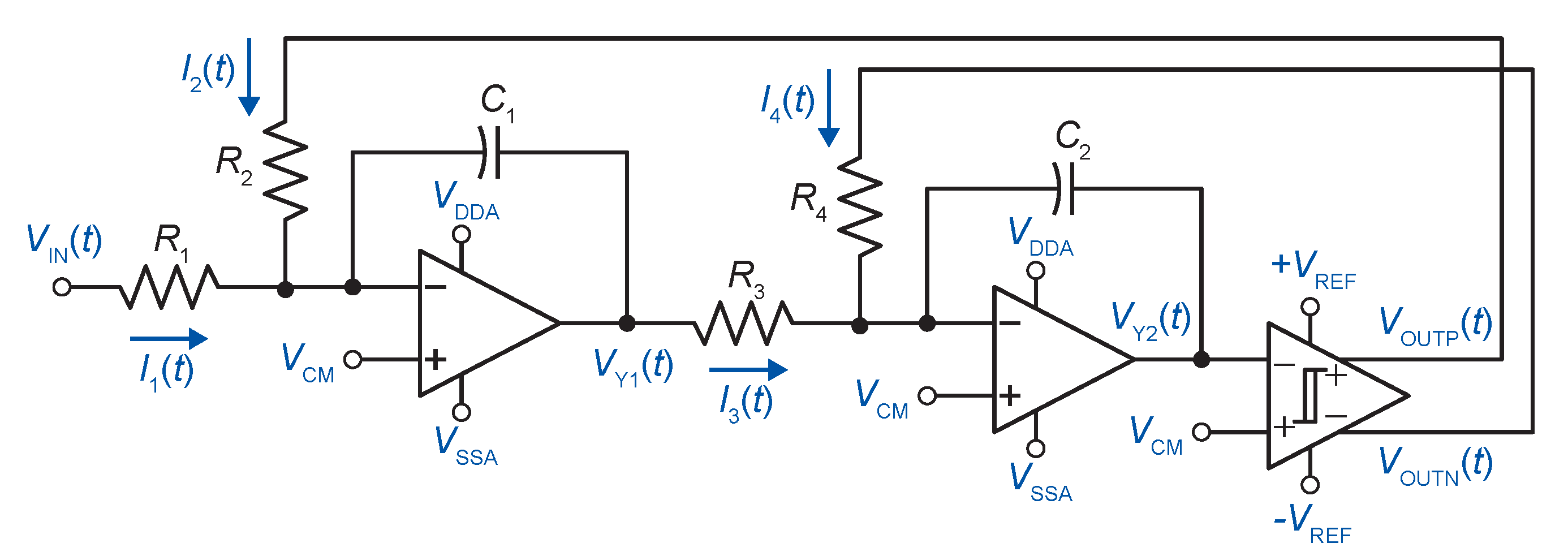
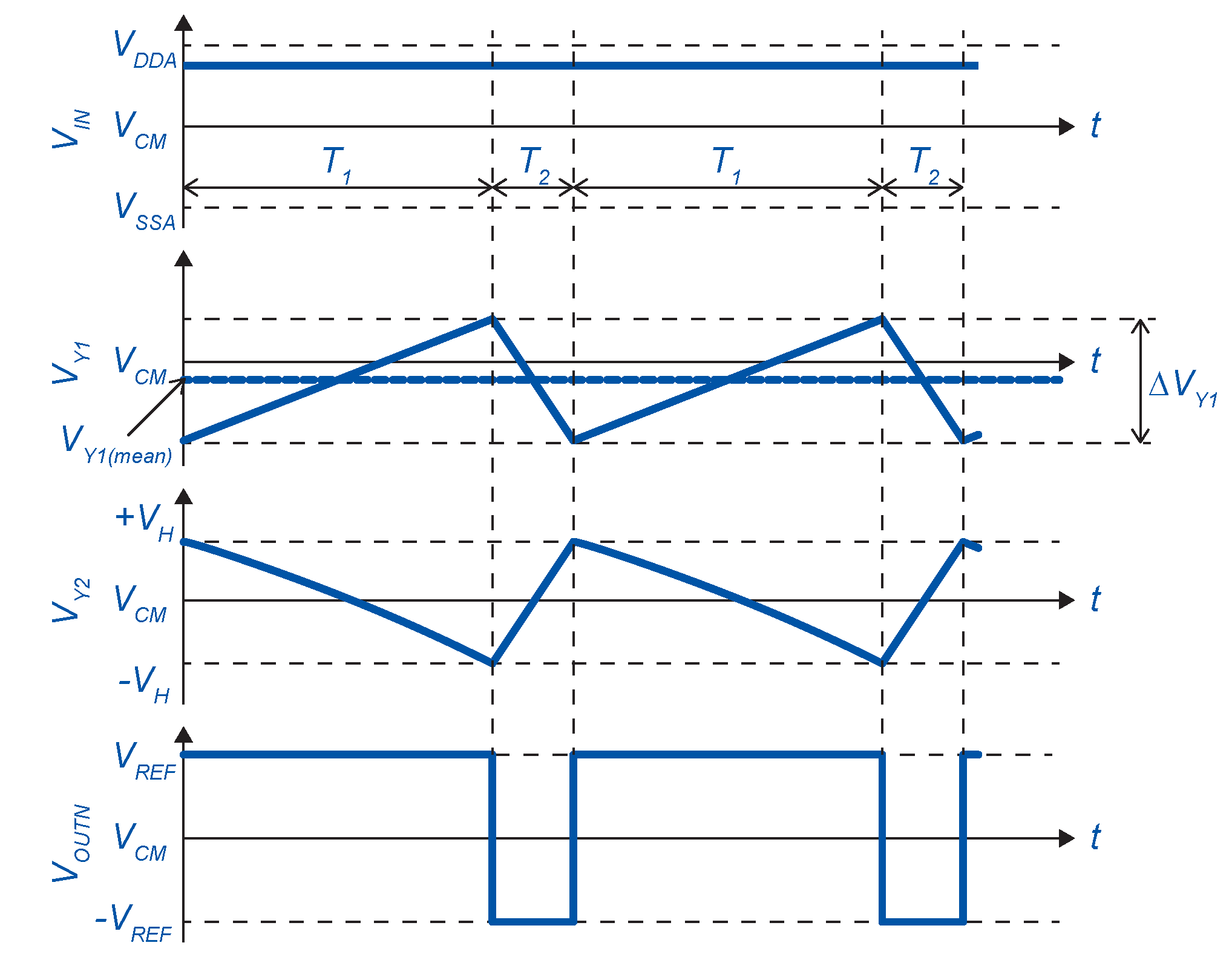
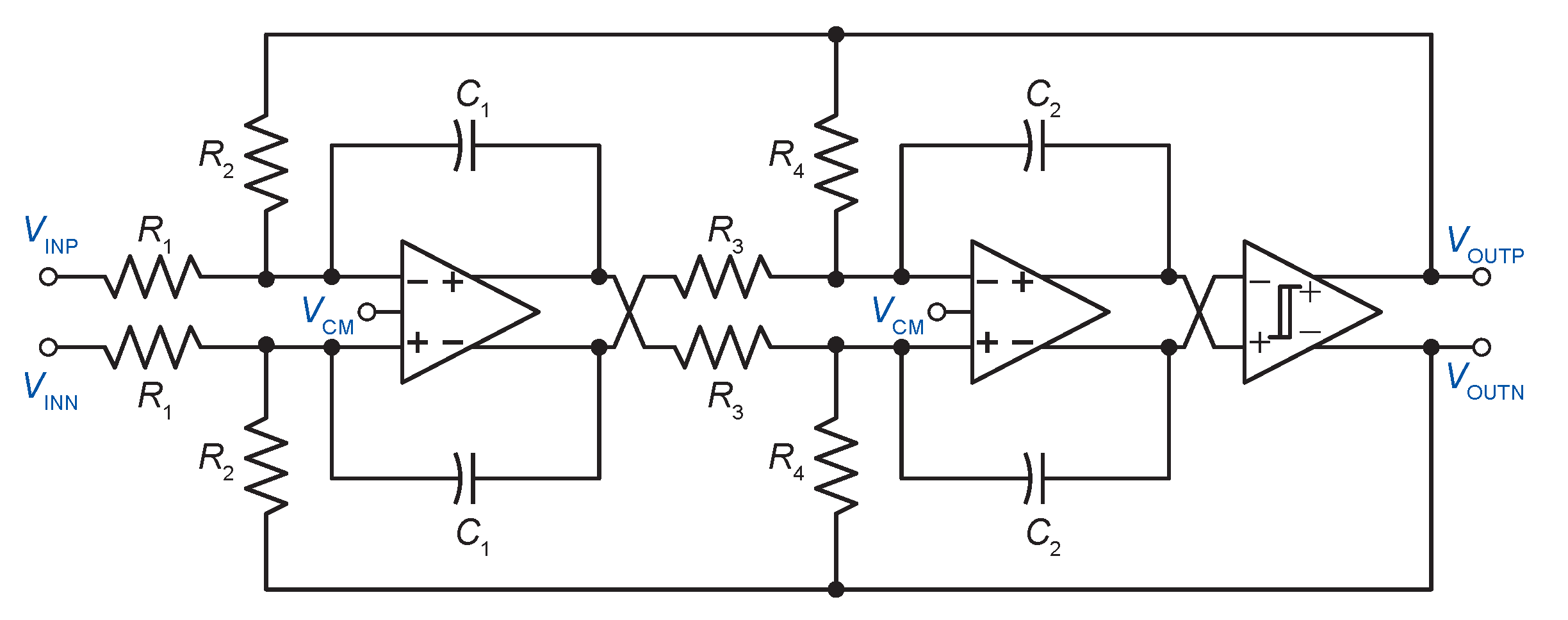
2. Asynchronous Delta-Sigma Modulator
3. Transistor Level Realization
3.1. Active-RC Integrator
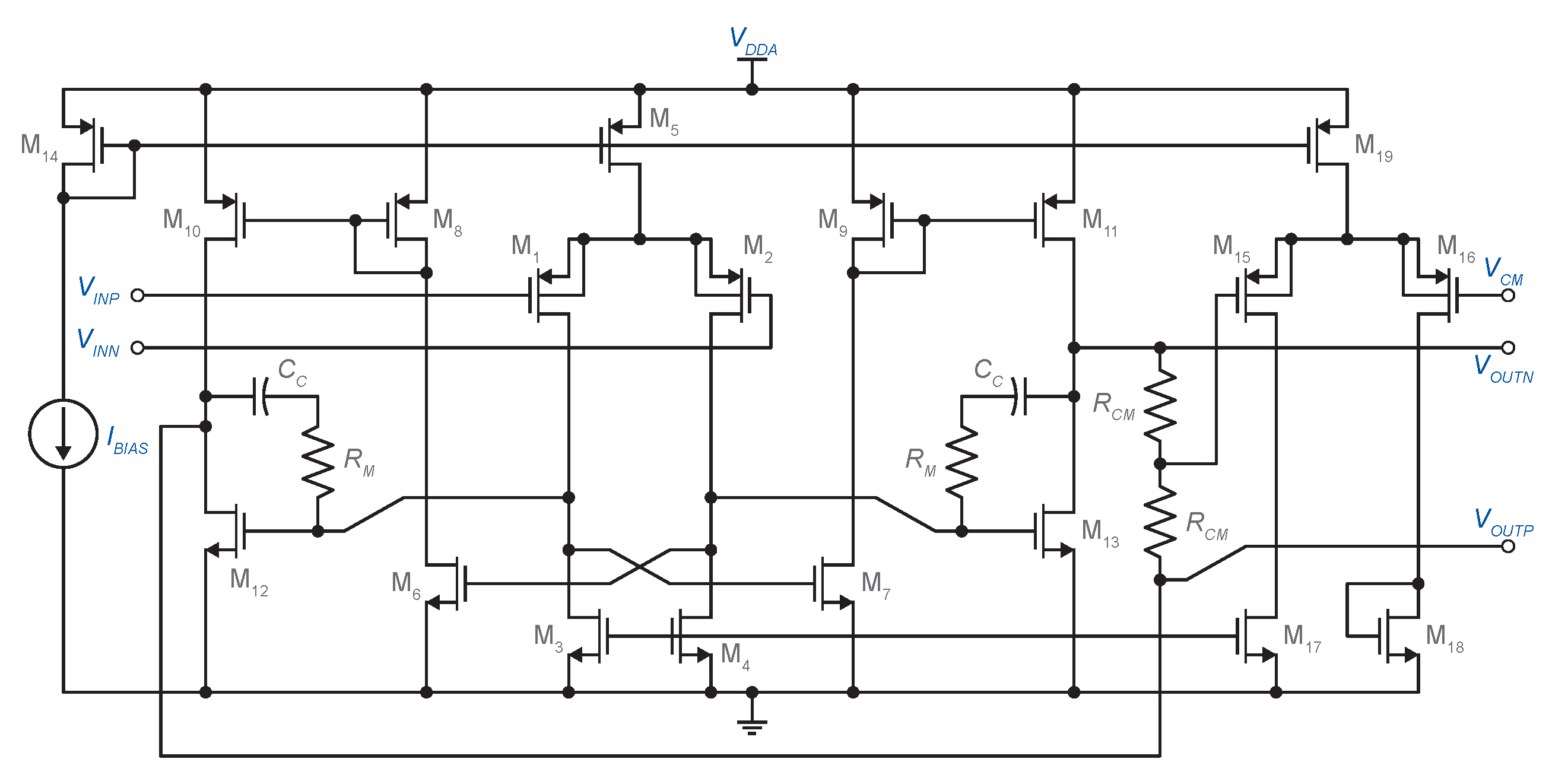
3.2. Class AB Fully Differential Operational Amplifier
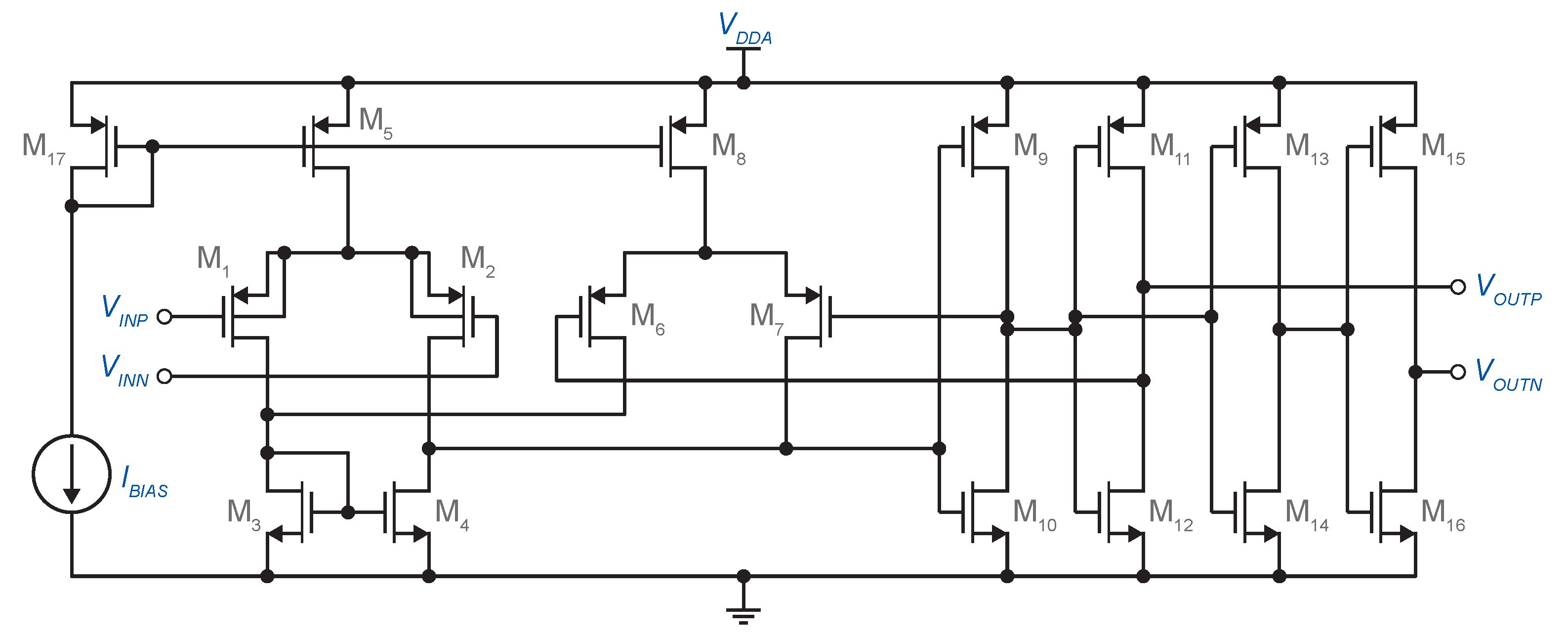
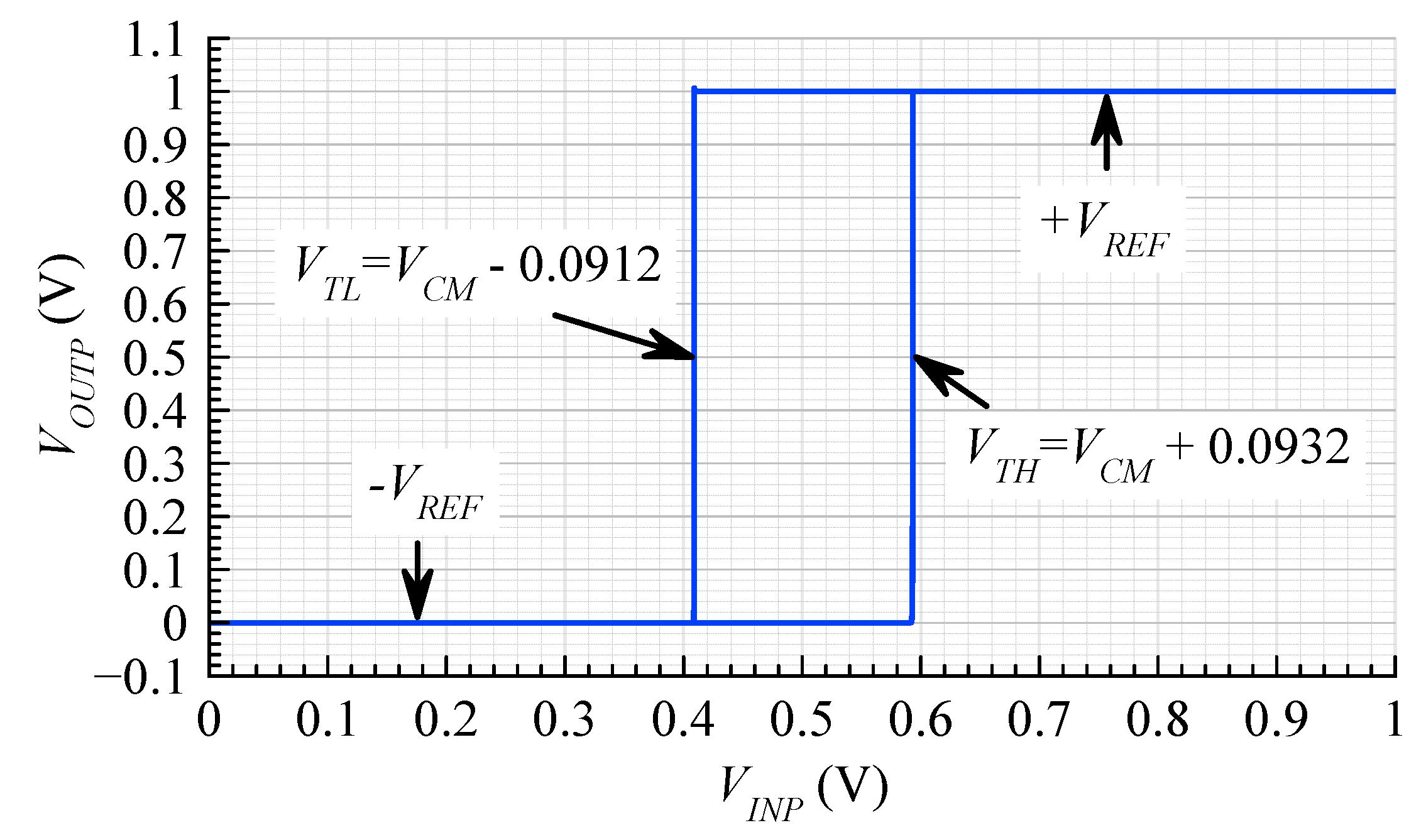
3.3. Comparator with Hysteresis
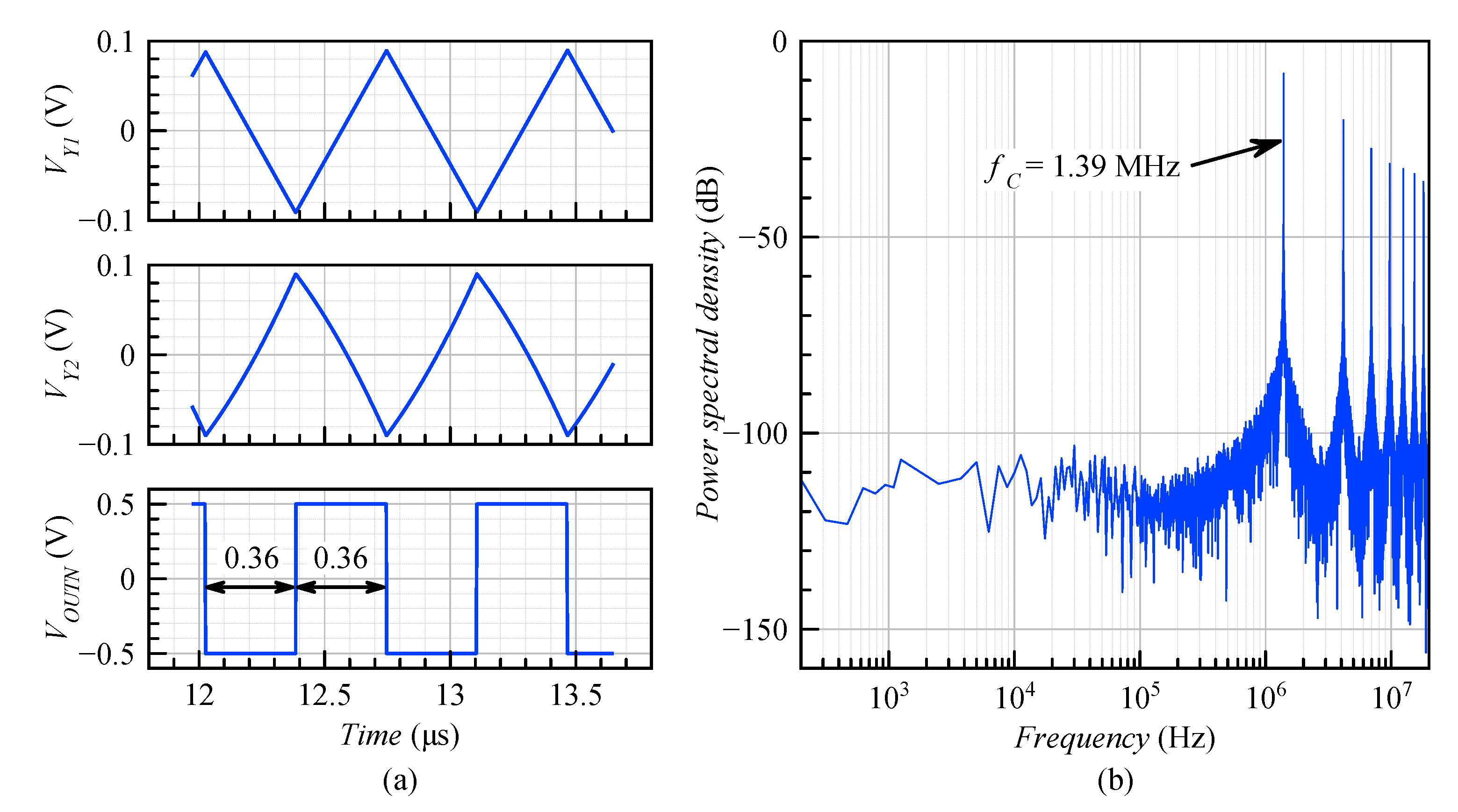
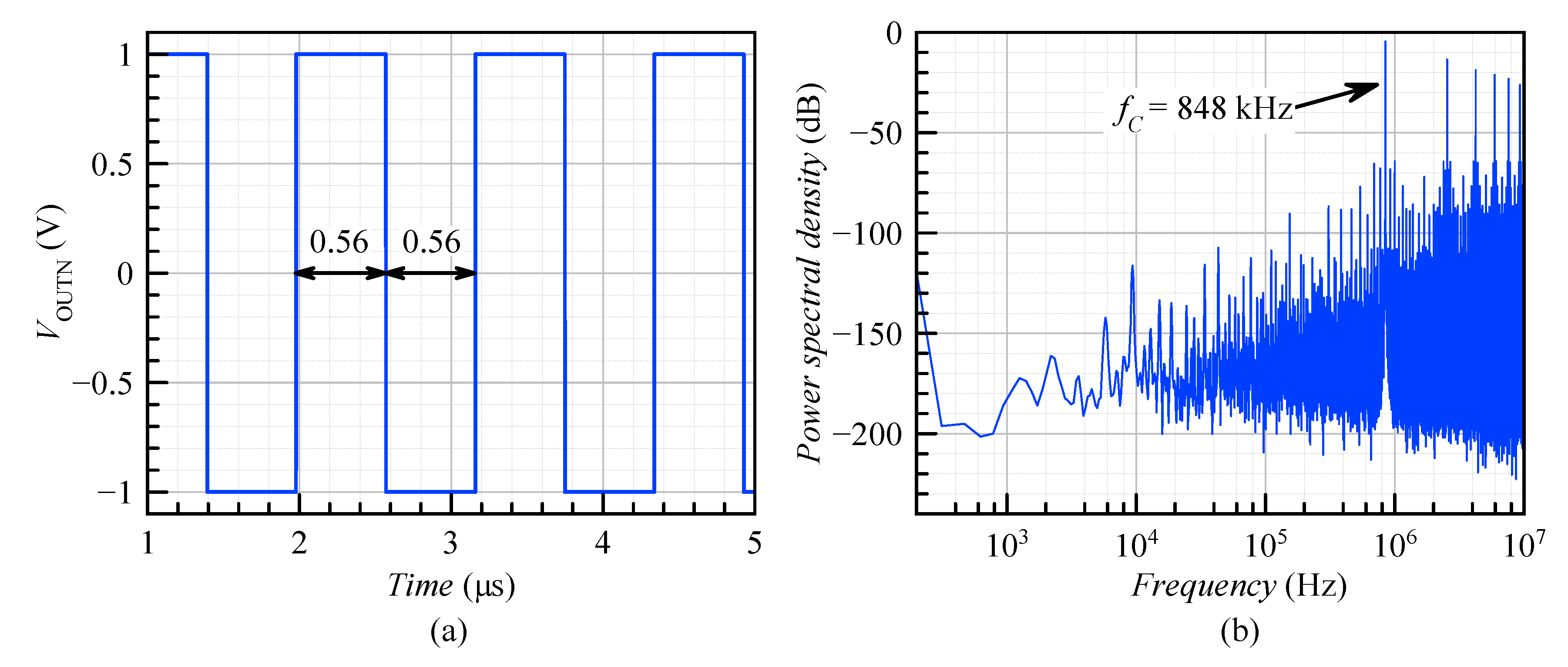
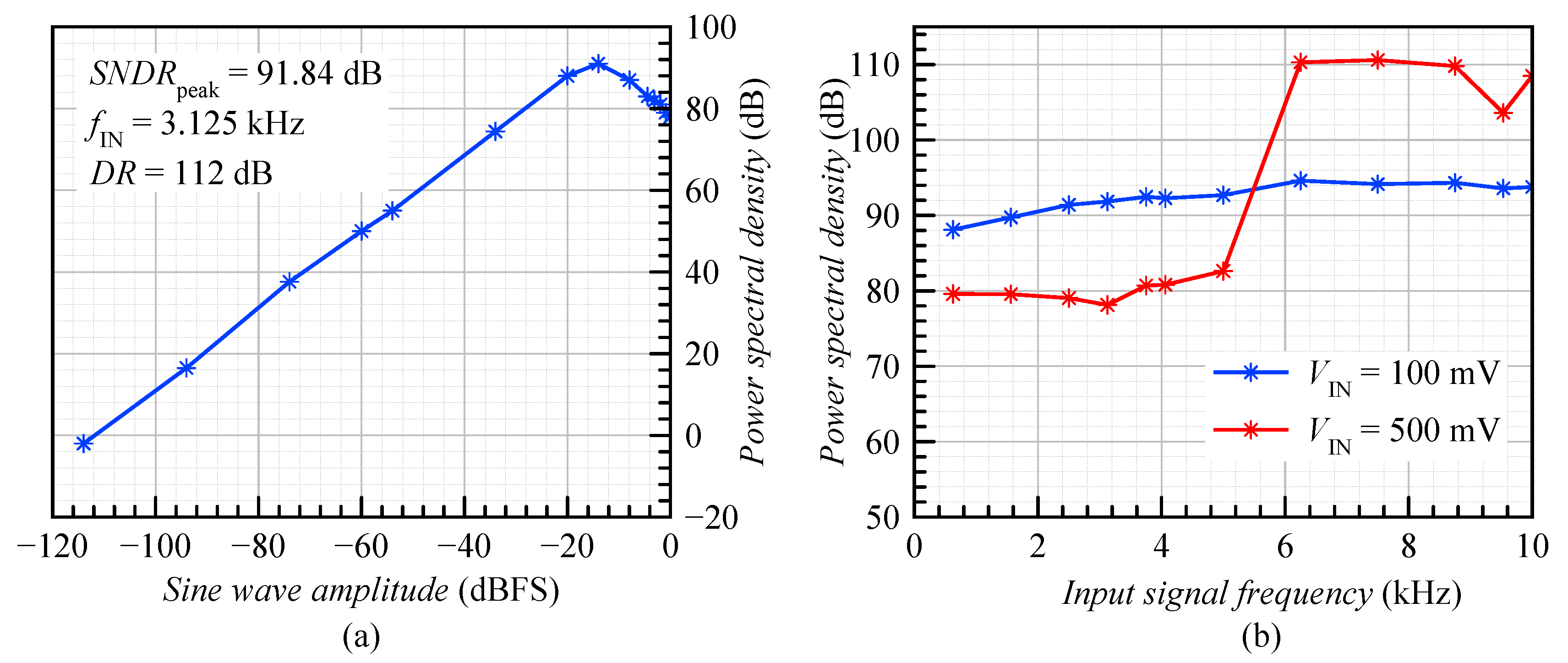
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADC | Analog-to-digital converter |
| ADSM | Asynchronous delta-sigma modulator |
| Carrier-to-bandwidth ratio | |
| CIFB | Cascade of integrators with distributed feedback |
| CTDSM | Continuous-time delta-sigma modulator |
| Dynamic Range | |
| DTDSM | Discrete-time delta-sigma modulator |
| Figure-of-merit | |
| MASH | Multi-stage noise shaping |
| Signal-to-noise and distortion ratio |
References
- Kledrowetz, V.; Prokop, R.; Fujcik, L.; Pavlik, M.; Háze, J. Low-power ASIC suitable for miniaturized wireless EMG systems. J. Electr. Eng. 2019, 70, 393–399. [Google Scholar] [CrossRef]
- Magno, M.; Benini, L.; Spagnol, C.; Popovici, E. Wearable low power dry surface wireless sensor node for healthcare monitoring application. In Proceedings of the 2013 IEEE 9th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Lyon, France, 7–9 October 2013; pp. 189–195. [Google Scholar]
- Vinod, A.P.; Da, C.Y. An integrated surface EMG data acquisition system for sports medicine applications. In Proceedings of the 2013 7th International Symposium on Medical Information and Communication Technology (ISMICT), Tokyo, Japan, 6–8 March 2013; pp. 98–102. [Google Scholar]
- Northrop, R.B. Analysis and Application of Analog Electronic Circuits to Biomedical Instrumentation (Biomedical Engineering); CRC Press, Inc.: Boca Raton, FL, USA, 2004. [Google Scholar]
- Webster, J. Medical Instrumentation: Application and Design; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Prutchi, D.; Norris, M. Design and Development of Medical Electronic Instrumentation; Wiley Online Library: Hoboken, NJ, USA, 2005. [Google Scholar]
- Delgado, J.M. Electrodes for extracellular recording and stimulation. In Electrophysiological Methods; Elsevier: Amsterdam, The Netherlands, 1964; pp. 88–143. [Google Scholar]
- Rodríguez-Pérez, A.; Delgado-Restituto, M.; Medeiro, F. Power Efficient ADCs for Biomedical Signal Acquisition. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.936.432&rep=rep1&type=pdf (accessed on 25 July 2020).
- Zou, X.; Xu, X.; Yao, L.; Lian, Y. A 1-V 450-nW Fully Integrated Programmable Biomedical Sensor Interface Chip. IEEE J. Solid-State Circuits 2009, 44, 1067–1077. [Google Scholar] [CrossRef]
- Sundarasaradula, Y.; Constandinou, T.G.; Thanachayanont, A. A 6-bit, two-step, successive approximation logarithmic ADC for biomedical applications. In Proceedings of the 2016 IEEE International Conference on Electronics, Circuits and Systems (ICECS), Monte Carlo, Monaco, 11–14 December 2016; pp. 25–28. [Google Scholar]
- Mesgarani, A.; Ay, S.U. A low voltage, energy efficient supply boosted SAR ADC for biomedical applications. In Proceedings of the 2011 IEEE Biomedical Circuits and Systems Conference (BioCAS), San Diego, CA, USA, 10–12 November 2011; pp. 401–404. [Google Scholar]
- De la Rosa, J.M.; Schreier, R.; Pun, K.; Pavan, S. Next-Generation Delta-Sigma Converters: Trends and Perspectives. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 484–499. [Google Scholar] [CrossRef]
- Ouzounov, S.; Engel, R.; Hegt, J.A.; van der Weide, G.; van Roermund, A.H.M. Analysis and design of high-performance asynchronous sigma-delta Modulators with a binary quantizer. IEEE J. Solid-State Circuits 2006, 41, 588–596. [Google Scholar] [CrossRef]
- Dazhi, W.; Vaibhav, G.; Harris, J.G. An asynchronous delta-sigma converter implementation. In Proceedings of the 2006 IEEE International Symposium on Circuits and Systems, Island of Kos, Greece, 21–24 May 2006; p. 4. [Google Scholar]
- Daniels, J.; Dehaene, W.; Steyaert, M.S.; Wiesbauer, A. A/D conversion using asynchronous delta-sigma modulation and time-to-digital conversion. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 2404–2412. [Google Scholar] [CrossRef]
- Lee, J.; Song, S.; Roh, J. A 103 dB DR Fourth-Order Delta-Sigma Modulator for Sensor Applications. Electronics 2019, 8, 1093. [Google Scholar] [CrossRef]
- Sohel, A.; al Khadir, A.; Naaz, M.; Najeeb, A. A 1.8V 204.8-μW 12-Bit Fourth Order Active Passive ΣΔ Modulator for Biomedical Applications. In Proceedings of the 2019 Devices for Integrated Circuit (DevIC), Kalyani, India, 23–24 March 2019; pp. 124–127. [Google Scholar]
- Ferreira, L.H.C.; Sonkusale, S.R. A 0.25-V 28-nW 58-dB Dynamic Range Asynchronous Delta Sigma Modulator in 130-nm Digital CMOS Process. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2015, 23, 926–934. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F.; Ferreira, L.H.C. A 0.3-V 37-nW 53-dB SNDR Asynchronous Delta–Sigma Modulator in 0.18-μm CMOS. IEEE Trans. Large Scale Integr. (VLSI) Syst. 2019, 27, 316–325. [Google Scholar] [CrossRef]
- Akbari, M.; Hashemipour, O.; Moradi, F. Design and analysis of an ultra-low-power second-order asynchronous delta–sigma modulator. Circuits Syst. Signal Process. 2017, 36, 4919–4936. [Google Scholar] [CrossRef]
- Roza, E. Analog-to-digital conversion via duty-cycle modulation. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1997, 44, 907–914. [Google Scholar] [CrossRef]
- Rabii, S.; Wooley, B.A. A 1.8-V digital-audio sigma-delta modulator in 0.8-/spl mu/m CMOS. IEEE J. Solid-State Circuits 1997, 32, 783–796. [Google Scholar] [CrossRef]
- Furth, P.M.; Tsen, Y.C.; Kulkarni, V.B.; Raju, T.K.P.H. On the design of low-power CMOS comparators with programmable hysteresis. In Proceedings of the 2010 53rd IEEE International Midwest Symposium on Circuits and Systems, Seattle, WA, USA, 1–4 August 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1077–1080. [Google Scholar]
- Yoon, Y.; Choi, D.; Roh, J. A 0.4 V 63 μW 76.1 dB SNDR 20 kHz Bandwidth Delta-Sigma Modulator Using a Hybrid Switching Integrator. IEEE J. Solid-State Circuits 2015, 50, 2342–2352. [Google Scholar] [CrossRef]
- Leow, Y.H.; Tang, H.; Sun, Z.C.; Siek, L. A 1 V 103 dB 3rd-Order Audio Continuous-Time ΔΣ ADC with Enhanced Noise Shaping in 65 nm CMOS. IEEE J. Solid-State Circuits 2016, 51, 2625–2638. [Google Scholar] [CrossRef]
- Liao, S.; Wu, J. A 1 V 175 μW 94.6 dB SNDR 25 kHz bandwidth delta-sigma modulator using segmented integration techniques. In Proceedings of the 2018 IEEE Custom Integrated Circuits Conference (CICC), San Diego, CA, USA, 8–11 April 2018; pp. 1–4. [Google Scholar]
- Michel, F.; Steyaert, M.S.J. A 250 mV 7.5 μW 61 dB SNDR SC ΔΣ Modulator Using Near-Threshold-Voltage-Biased Inverter Amplifiers in 130 nm CMOS. IEEE J. Solid-State Circuits 2012, 47, 709–721. [Google Scholar] [CrossRef]


| DTDSM | CTDSM | ADSM |
|---|---|---|
| + Synchronous system | + Synchronous system | + Immunity to clock jitter |
| + High resolution | + Implicit antialiasing filter | + Implicit antialiasing filter |
| + Highly linear SC integrator | + Higher sampling frequency | + Simple circuit |
| + Accurately defined integrator | + Relaxed operational amplifier | + Relaxed OpAmp |
| gains and transfer function | speed requirements | speed requirements |
| + Low sensitivity to clock jitter | + Higher conversion speed | + Higher conversion speed |
| and excess loop delay | + Low power | + Low power |
| + Low sensitivity to DAC settling time | + Do not require a clock | |
| - Low conversion speed | - Sensitivity to clock jitter | - Complex decoding scheme |
| - Required pre-antialiasing filter | - Excess loop delay | - Lack of noise shaping |
| - Required non-overlapping | - Lower resolution | - Lower resolution |
| clock generator |
| Parameter | Condition | Value |
|---|---|---|
| Hysteresis | 90 mV | |
| Time delay | 50 ns | |
| Slew-rate | 42 V/s | |
| Power consumption | duty cycle = 50% | 5 W |
| Input capacitance | 0.4 pF | |
| 2.5 A |
| Parameter | Condition | Value |
|---|---|---|
| Hysteresis | 90 mV | |
| Time delay | 50 ns | |
| Slew-rate | 42 V/s | |
| Power consumption | duty cycle = 50% | 5 W |
| Input capacitance | 0.4 pF | |
| 2.5 A |
| Parameter | This Work | [24] 2015 | [25] 2016 | [26] 2018 | [27] 2012 |
|---|---|---|---|---|---|
| Technology | 180 nm | 130 nm | 65 nm | 65 nm | 130 nm |
| Topology | ADSM | DTDSM | CTDSM | DTDSM | DTDSM |
| Order | 2 | 3 | 3 | 3 (2-1 MASH) | 3 |
| Quantizer | 1 bit | 1 bit | 5 bit | 1 bit | 1 bit |
| Supply voltage | 1 V | 0.4 V | 1 V | 1 V | 0.25 V |
| Modulator frequency | 848 kHz | 3.2 MHz | 6.4 MHz | 5 MHz | 1.4 MHz |
| Bandwidth | 10 kHz | 20 kHz | 25 kHz | 25 kHz | 10 kHz |
| Peak | 92 dB | 76.1 dB | 95.2 dB | 94.6 dB | 61 dB |
| Dynamic range | 112 dB | 82 dB | 103 dB | 98.5 dB | ≅ 58 dB |
| Power consumption | 290 W | 63 W | 800 W | 175 W | 7.5 W |
| Area | 0.54 mm | 0.33 mm | 0.256 mm | 0.384 mm | 0.3375 mm |
| 0.45 pJ/step | 0.31 pJ/step | 0.34 pJ/step | 0.079 pJ/step | 0.41 pJ/step | |
| 187 dB | 167 dB | 177.9 dB | 176.2 dB | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kledrowetz, V.; Fujcik, L.; Prokop, R.; Háze, J. A 1 V 92 dB SNDR 10 kHz Bandwidth Second-Order Asynchronous Delta-Sigma Modulator for Biomedical Signal Processing. Sensors 2020, 20, 4137. https://doi.org/10.3390/s20154137
Kledrowetz V, Fujcik L, Prokop R, Háze J. A 1 V 92 dB SNDR 10 kHz Bandwidth Second-Order Asynchronous Delta-Sigma Modulator for Biomedical Signal Processing. Sensors. 2020; 20(15):4137. https://doi.org/10.3390/s20154137
Chicago/Turabian StyleKledrowetz, Vilém, Lukáš Fujcik, Roman Prokop, and Jiří Háze. 2020. "A 1 V 92 dB SNDR 10 kHz Bandwidth Second-Order Asynchronous Delta-Sigma Modulator for Biomedical Signal Processing" Sensors 20, no. 15: 4137. https://doi.org/10.3390/s20154137
APA StyleKledrowetz, V., Fujcik, L., Prokop, R., & Háze, J. (2020). A 1 V 92 dB SNDR 10 kHz Bandwidth Second-Order Asynchronous Delta-Sigma Modulator for Biomedical Signal Processing. Sensors, 20(15), 4137. https://doi.org/10.3390/s20154137






