Ultimately Bounded Filtering for Time-Delayed Nonlinear Stochastic Systems with Uniform Quantizations under Random Access Protocol
Abstract
1. Introduction
2. Problem Formulation and Preliminaries
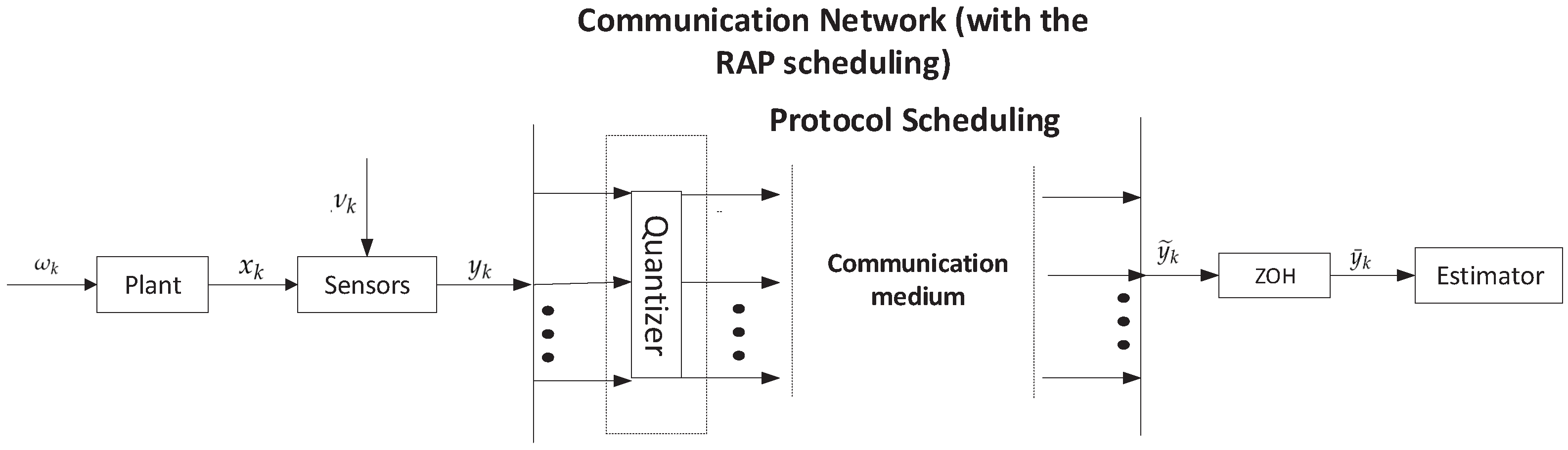
2.1. System Model and Communication Channel
2.2. Structure of the Filter
3. Main Results
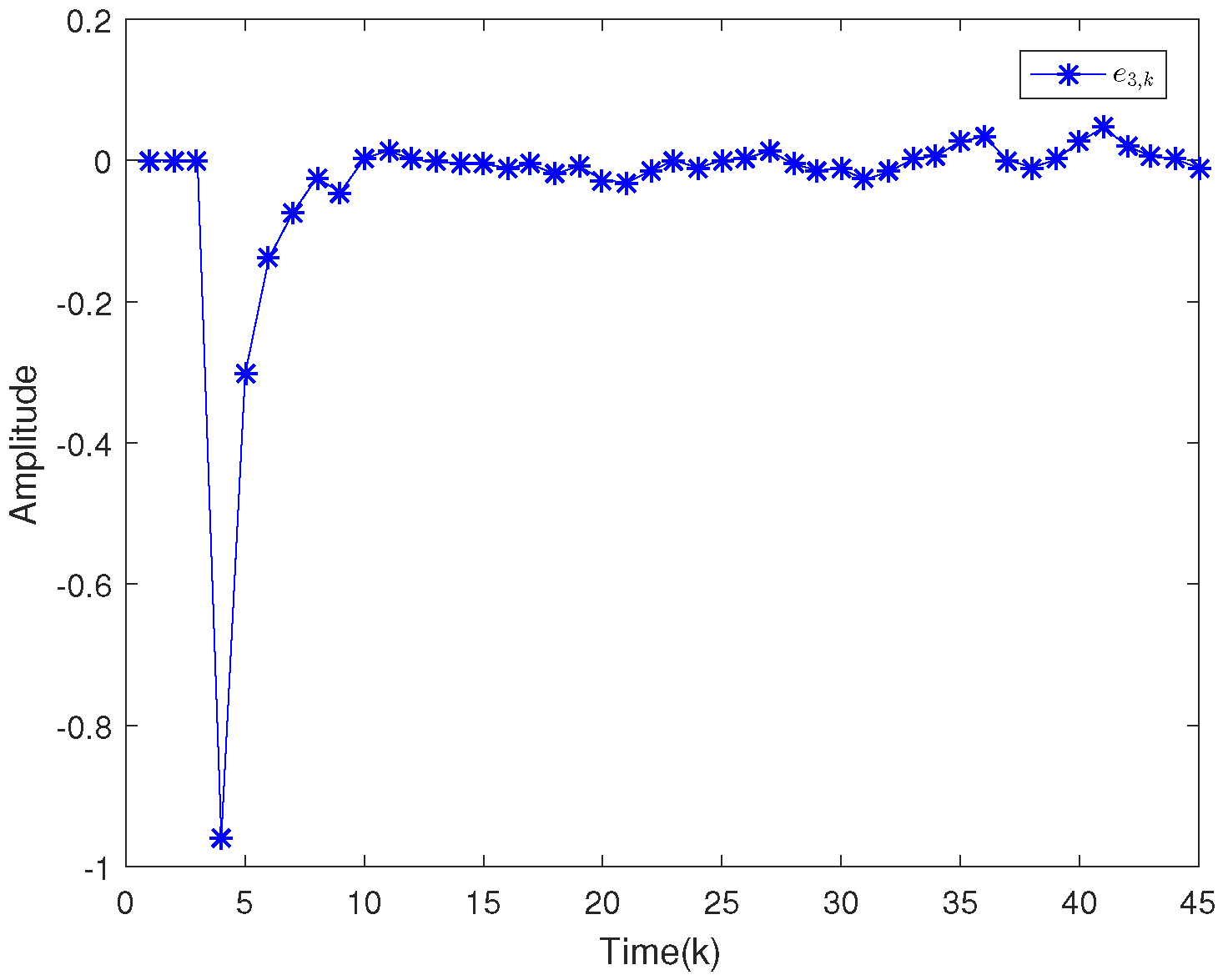
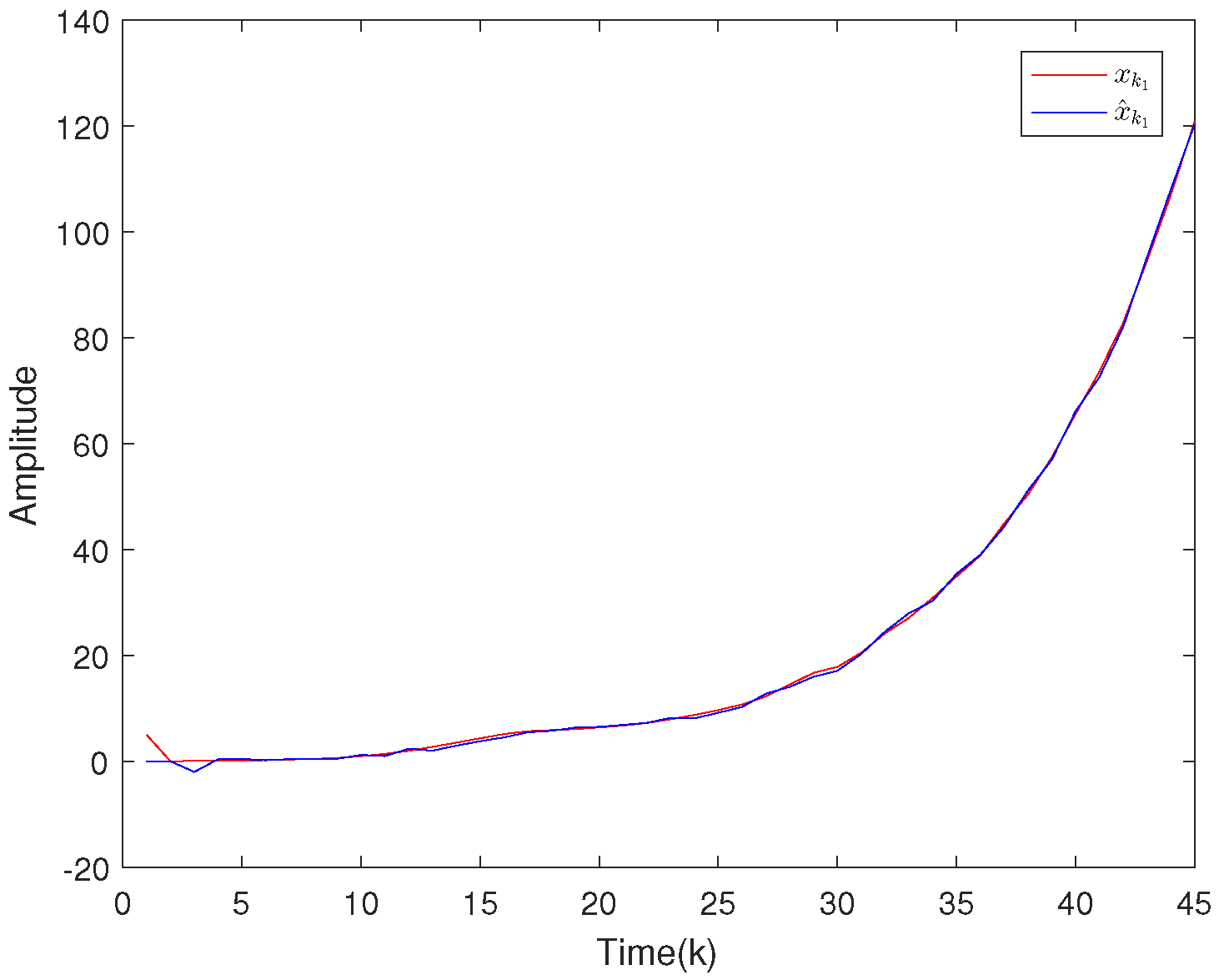
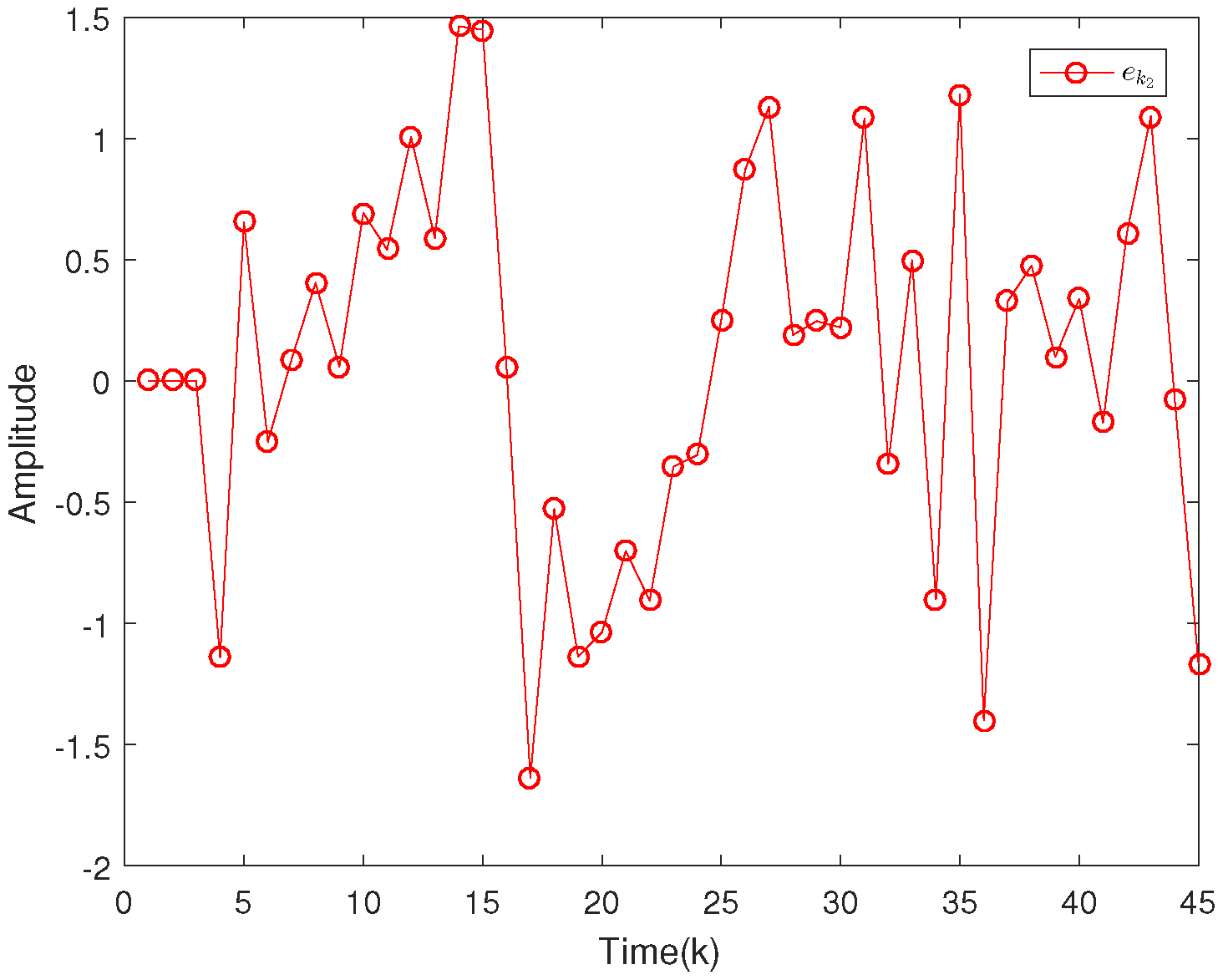
4. Illustrative Examples
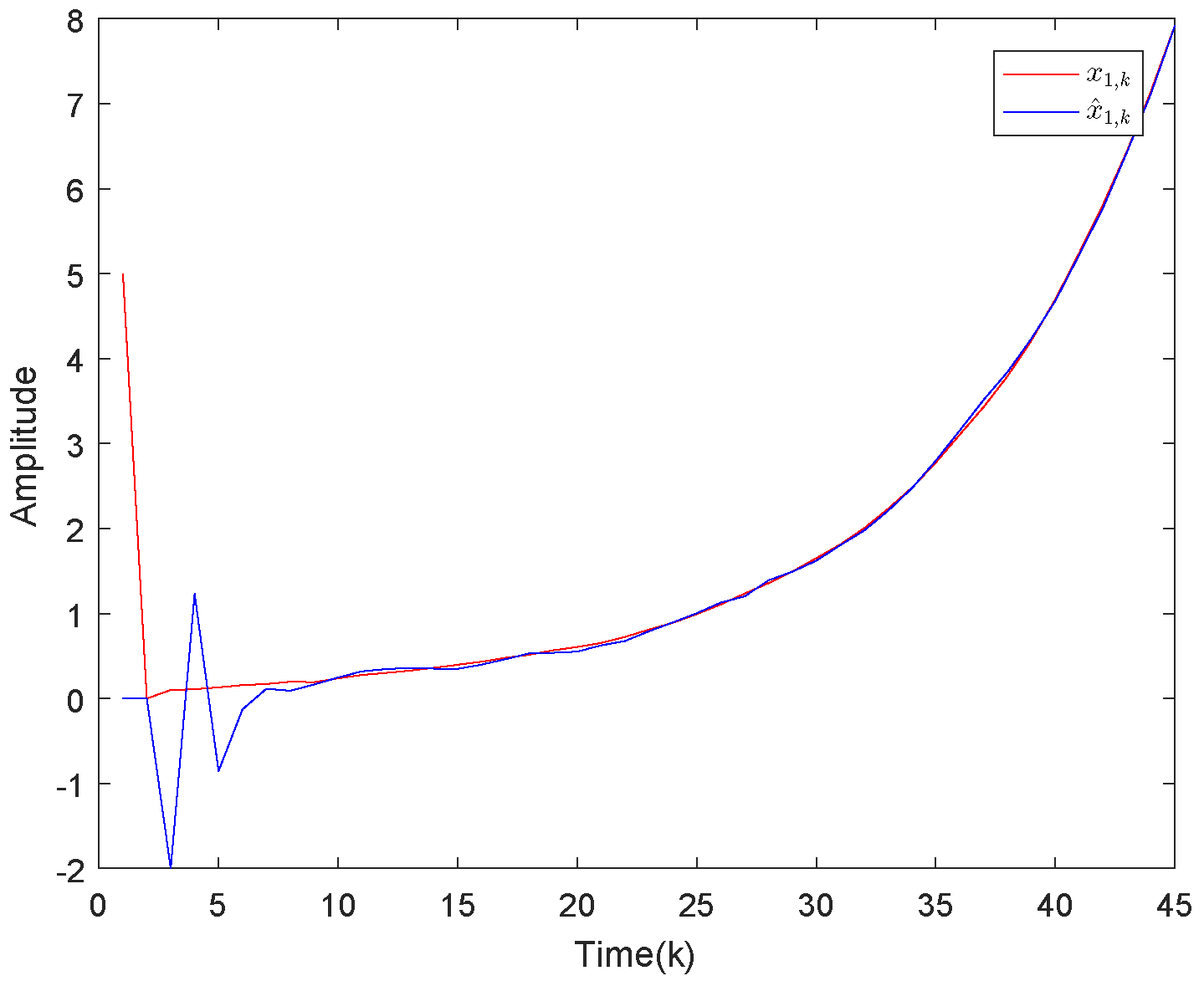
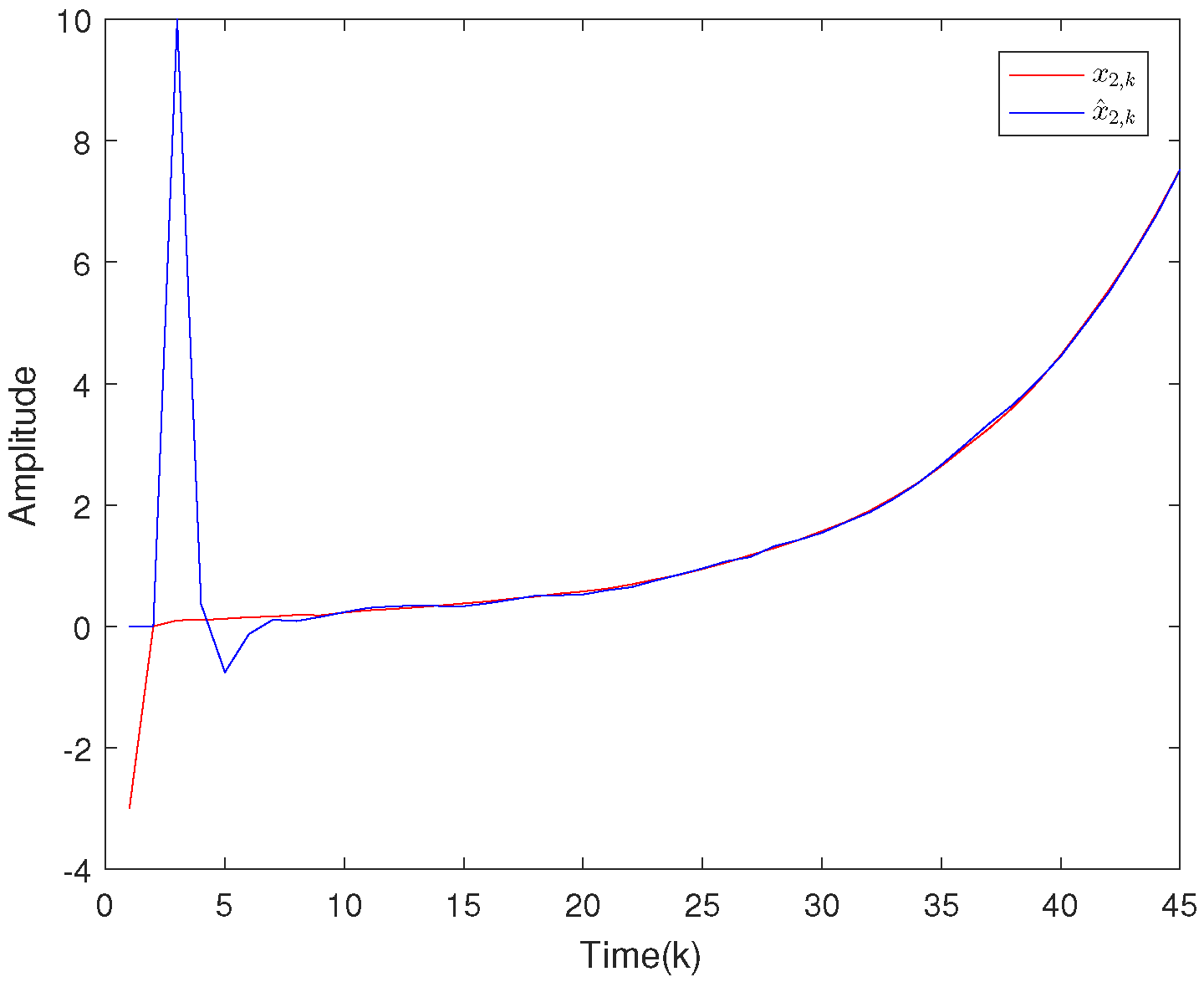
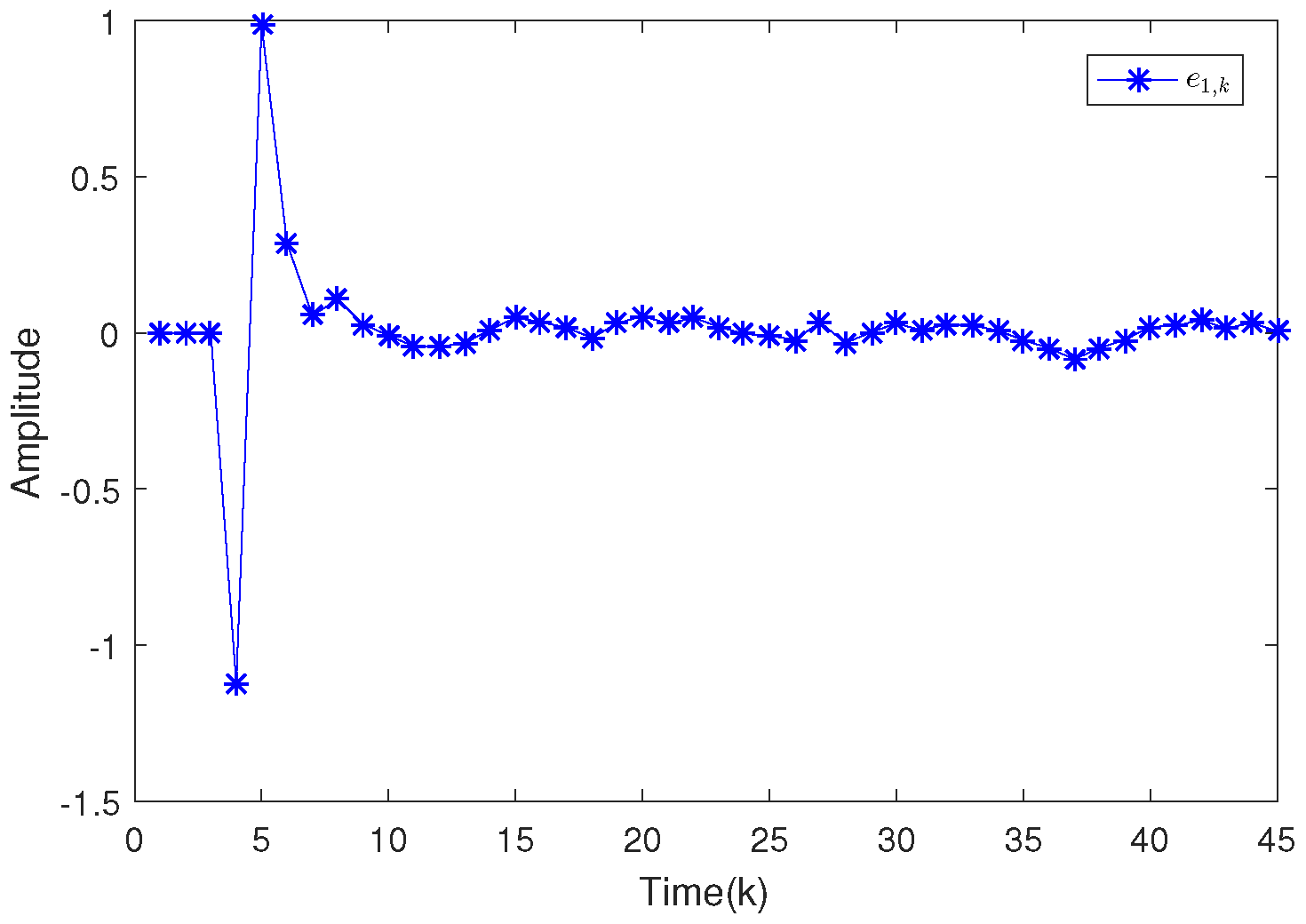
4.1. Example 1
4.2. Example 2
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RAP | random access protocol |
| UQEs | uniform quantization effcets |
| EUBMS | exponentially ultimately bounded in mean square |
| LMIs | linear matrix inequalities |
| EUB | exponential ultimate boundedness |
| ZOH | zero-order holder |
References
- Basin, M.V.; Loukianov, A.G.; Hernandez-Gonzalez, M. Joint state and parameter estimation for uncertain stochastic nonlinear polynomial systems. Int. J. Syst. Sci. 2013, 44, 1200–1208. [Google Scholar] [CrossRef]
- Caballero-Águila, R.; García-Garrido, I.; Linares-Pérez, J. Information fusion algorithms for state estimation in multi-sensor systems with correlated missing measurements. Appl. Math. Comput. 2014, 226, 548–563. [Google Scholar] [CrossRef]
- Donkers, M.C.F.; Heemels, W.P.M.H.; Bernardini, D.; Bemporad, A.; Shneer, V. Stability analysis of stochastic Networked Control Systems. Automatica 2012, 48, 917–925. [Google Scholar] [CrossRef]
- Han, F.; Wei, G.; Ding, D.; Song, Y. Local condition based consensus filtering with stochastic nonlinearities and multiple missing measurements. IEEE Trans. Autom. Control 2017, 62, 4784–4790. [Google Scholar] [CrossRef]
- Liu, M.; Ho, D.W.C.; Niu, Y. Robust filtering design for stochastic system with mode-dependent output quantization. IEEE Trans. Signal Process. 2016, 58, 6410–6416. [Google Scholar] [CrossRef]
- Mao, J.; Ding, D.; Wei, G.; Liu, H. Networked recursive filtering for time-delayed nonlinear stochastic systems with uniform quantisation under Round-Robin protocol. Int. J. Syst. Sci. 2019, 50, 871–884. [Google Scholar] [CrossRef]
- Tabbara, M.; Nesic, D. Input-output stability of Networked Control Systems with stochastic protocols and channels. IEEE Trans. Autom. Control 2008, 53, 1160–1175. [Google Scholar] [CrossRef]
- Wan, X.; Wang, Z.; Han, Q.L.; Wu, M. A recursive approach to quantized H∞ state estimation for genetic regulatory networks under stochastic communication protocols. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2840–2852. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Song, H.; Yu, L. Robust fuzzy-model-based filtering for nonlinear cyber-physical systems with multiple stochastic incomplete measurements. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1826–1838. [Google Scholar] [CrossRef]
- Zhang, D.; Yu, L.; Zhang, W.A. Energy efficient distributed filtering for a class of nonlinear systems in sensor networks. IEEE Sens. J. 2015, 15, 3026–3036. [Google Scholar] [CrossRef]
- Hung, Y.; Yang, F. Robust H∞ filtering with error variance constraints for discrete time-varying systems with uncertainty. Automatica 2003, 39, 1185–1194. [Google Scholar] [CrossRef]
- Xu, L.; Dai, Z.; He, D. Exponential ultimate boundedness of impulsive stochastic delay differential equations. Appl. Math. Lett. 2018, 85, 70–76. [Google Scholar] [CrossRef]
- Xu, L.; Ge, S.S. Exponential ultimate boundedness of nonlinear stochastic difference systems with time-varying delays. Int. J. Control 2015, 88, 1–7. [Google Scholar] [CrossRef]
- Xu, L.; Hu, H.; Qin, F. Ultimate boundedness of impulsive fractional differential equations. Appl. Math. Lett. 2016, 62, 110–117. [Google Scholar] [CrossRef]
- Hoecht, L.; Bierling, T.; Holzapfel, F. Ultimate boundedness theorem for model reference adaptive control systems. J. Guid. Control Dyn. 2014, 37, 1595–1603. [Google Scholar] [CrossRef]
- Arbel, A. Sensor placement in optimal filtering and smoothing problems. IEEE Trans. Autom. Control 1982, 27, 94–98. [Google Scholar] [CrossRef]
- Hou, M.; Patton, R.J. Optimal filtering for systems with unknown inputs. IEEE Trans. Autom. Control 1998, 43, 445–449. [Google Scholar] [CrossRef]
- Kwakernaak, H. Optimal filtering in linear systems with time delays. IEEE Trans. Autom. Control 1967, 12, 169–173. [Google Scholar] [CrossRef]
- Lu, X.; Xie, L.; Zhang, H.; Wang, W. Robust Kalman filtering for discrete-time systems with measurement delay. IEEE Trans. Circuits Syst. II 2007, 54, 522–526. [Google Scholar] [CrossRef]
- Xie, L.; Soh, Y.C.; De Souza, C.E. Robust Kalman filtering for uncertain discrete-time systems. IEEE Trans. Autom. Control 1994, 39, 1310–1314. [Google Scholar]
- Jia, C.; Hu, J.; Chen, D.; Liu, Y.; Alsaadi, F.E. Event-triggered resilient filtering with stochastic uncertainties and successive packet dropouts via variance-constrained approach. Int. J. Gen. Syst. 2018, 47, 438–453. [Google Scholar] [CrossRef]
- Chen, S.; Guo, J.; Ma, L. Sliding mode observer design for discrete nonlinear time-delay systems with stochastic communication protocol. Int. J. Control Autom. Syst. 2019, 17, 1666–1676. [Google Scholar] [CrossRef]
- Mao, J.; Ding, D.; Song, Y.; Liu, Y.; Alsaadi, F.E. Event-based recursive filtering for time-delayed stochastic nonlinear systems with missing measurements. Signal Process. 2017, 134, 158–165. [Google Scholar] [CrossRef]
- Wang, Z.; Ho, D.W.C. Filtering on nonlinear time-delay stochastic systems. Automatica 2003, 39, 101–109. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, H.; Kaynak, O. Network-induced constraints in Networked Control Systems—A survey. IEEE Trans. Ind. Inform. 2013, 9, 403–416. [Google Scholar] [CrossRef]
- Han, F.; Wei, G.; Song, Y.; Li, W. Distributed H∞ filtering for piecewise discrete-time linear systems. J. Frankl. Inst. Eng. Appl. Math. 2015, 352, 2029–2046. [Google Scholar] [CrossRef]
- Caballero-Águila, R.; Hermoso-Carazo, A.; Linares-Pérez, J. Distributed fusion filters from uncertain measured outputs in sensor networks with random packet losses. Inf. Fusion 2017, 34, 70–79. [Google Scholar] [CrossRef]
- Liu, Y.; Shen, B.; Li, Q. State estimation for neural networks with Markov-based nonuniform sampling: The partly unknown transition probability case. Neurocomputing 2019, 357, 261–270. [Google Scholar] [CrossRef]
- Tian, E.; Yue, D.; Wei, G. Robust H∞ filter for discrete-time linear system with uncertain missing measurements and non-linearity. IET Signal Process. 2013, 7, 239–248. [Google Scholar] [CrossRef]
- Wei, G.; Liu, S.; Song, Y.; Liu, Y. Probability-guaranteed set-membership filtering for systems with incomplete measurements. Automatica 2015, 60, 12–16. [Google Scholar] [CrossRef]
- Wang, F.; Liang, J. Constrained H∞ estimation for time-varying networks with hybrid incomplete information. Int. J. Robust Nonlinear Control 2018, 28, 699–715. [Google Scholar] [CrossRef]
- Huo, X.; Ma, L.; Zhao, X.; Zong, G. Observer-based fuzzy adaptive stabilization of uncertain switched stochastic nonlinear systems with input quantization. J. Frankl. Inst. 2019, 356, 1789–1809. [Google Scholar] [CrossRef]
- Liu, S.; Wei, G.; Song, Y.; Ding, D. Set-membership state estimation subject to uniform quantization effects and communication constraints. J. Frankl. Inst. 2017, 354, 7012–7027. [Google Scholar] [CrossRef]
- Wang, Y.; Bian, T.; Xiao, J.; Wen, C. Global synchronization of complex dynamical networks through digital communication with limited data rate. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2487–2499. [Google Scholar] [CrossRef] [PubMed]
- Yun, S.W.; Choi, Y.J.; Park, P. Dynamic output-feedback guaranteed cost control for linear systems with uniform input quantization. Nonlinear Dyn. 2010, 62, 95–104. [Google Scholar] [CrossRef]
- Gaid, M.E.M.B.; Çela, A. Trading quantization precision for update rates for systems with limited communication in the uplink channel. Automatica 2016, 46, 1210–1214. [Google Scholar] [CrossRef]
- Zou, L.; Wang, Z.; Han, Q.-L.; Zhou, D.H. Moving horizon estimation of networked nonlinear systems with random access protocol. IEEE Trans. Syst. Man Cybern. Syst. 2019. [Google Scholar] [CrossRef]
- Liu, K.; Fridman, E.; Hetel, L. Stability and L2-gain analysis of Networked Control Systems under Round-Robin scheduling: A time-delay approach. Syst. Control Lett. 2012, 61, 666–675. [Google Scholar] [CrossRef]
- Ugrinovskii, V.; Fridman, E. A Round-Robin type protocol for distributed estimation with H∞ consensus. Syst. Control Lett. 2014, 69, 103–110. [Google Scholar] [CrossRef]
- Xu, Y.; Lu, R.; Shi, P.; Li, H.; Xie, S. Finite-time distributed state estimation over sensor networks with Round-Robin protocol and fading channels. IEEE Trans. Cybern. 2016, 48, 336–345. [Google Scholar] [CrossRef]
- Zou, L.; Wang, Z.; Han, Q.-L.; Zhou, D.H. Moving horizon estimation for networked time-delay systems under Round-Robin protocol. IEEE Trans. Autom. Control 2019, 64, 5191–5198. [Google Scholar] [CrossRef]
- Cao, Z.; Niu, Y.; Karimi, H.R. Sliding mode control of automotive electronic valve system under weighted Try-Once-Discard protocol. Inf. Sci. 2020, 515, 324–340. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Z.; Shen, B.; Alsaadi, F.E.; Alsaadi, F.E. Fusion estimation for multi-rate linear repetitive processes under weighted Try-Once-Discard protocol. Inf. Fusion 2020, 55, 281–291. [Google Scholar] [CrossRef]
- Zou, L.; Wang, Z.; Han, Q.-L.; Zhou, D.H. Recursive filtering for time-varying systems with random access protocol. IEEE Trans. Autom. Control 2019, 64, 720–727. [Google Scholar] [CrossRef]
- Liu, A.; Yu, L.; Zhang, W. H∞ control for network-based systems with time-varying delay and packet disordering. J. Frankl. Inst. Eng. Appl. Math. 2011, 348, 917–932. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, S.; Zhang, L.; Ren, L. Robust sliding mode predictive control of uncertain Networked Control System with random time delay. Discret. Dyn. Nat. Soc. 2018, 85, 1218–1234. [Google Scholar] [CrossRef]
- Åkesson, B.M.; Jørgensen, J.B.; Poulsen, N.K.; Jørgensen, S.B. A generalized autocovariance least-squares method for Kalman filter tuning. J. Process Control 2008, 18, 769–779. [Google Scholar] [CrossRef]
- Dunik, J.; Straka, O.; Simandl, M. On autocovariance least-squares method for noise covariance matrices estimation. IEEE Trans. Autom. Control 2016, 62, 967–972. [Google Scholar] [CrossRef]
- Yuen, K.V.; Liang, P.F.; Kuok, S.C. Online estimation of noise parameters for Kalman filter. Struct. Eng. Mech. 2013, 47, 361–381. [Google Scholar] [CrossRef]
- Boyd, S.; Ghaoul, L.E.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in Systems and Control Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]






| 0.64 | 0.16 | 0.0064 | |
| 0.81 | 0.225 | 0.0081 | |
| Ultimate bound | 163.9338 | 43.5281 | 1.6394 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Wang, Z.; Zou, L.; Zhao, Z. Ultimately Bounded Filtering for Time-Delayed Nonlinear Stochastic Systems with Uniform Quantizations under Random Access Protocol. Sensors 2020, 20, 4134. https://doi.org/10.3390/s20154134
Guo J, Wang Z, Zou L, Zhao Z. Ultimately Bounded Filtering for Time-Delayed Nonlinear Stochastic Systems with Uniform Quantizations under Random Access Protocol. Sensors. 2020; 20(15):4134. https://doi.org/10.3390/s20154134
Chicago/Turabian StyleGuo, Jiyue, Zidong Wang, Lei Zou, and Zhongyi Zhao. 2020. "Ultimately Bounded Filtering for Time-Delayed Nonlinear Stochastic Systems with Uniform Quantizations under Random Access Protocol" Sensors 20, no. 15: 4134. https://doi.org/10.3390/s20154134
APA StyleGuo, J., Wang, Z., Zou, L., & Zhao, Z. (2020). Ultimately Bounded Filtering for Time-Delayed Nonlinear Stochastic Systems with Uniform Quantizations under Random Access Protocol. Sensors, 20(15), 4134. https://doi.org/10.3390/s20154134





