Deep Vibro-Tactile Perception for Simultaneous Texture Identification, Slip Detection, and Speed Estimation
Abstract
1. Introduction
2. Slip And Texture Detection
2.1. Image-Based Methods
2.2. Force Vector Measuring Methods
2.3. Vibration Detection Methods
3. Experiments
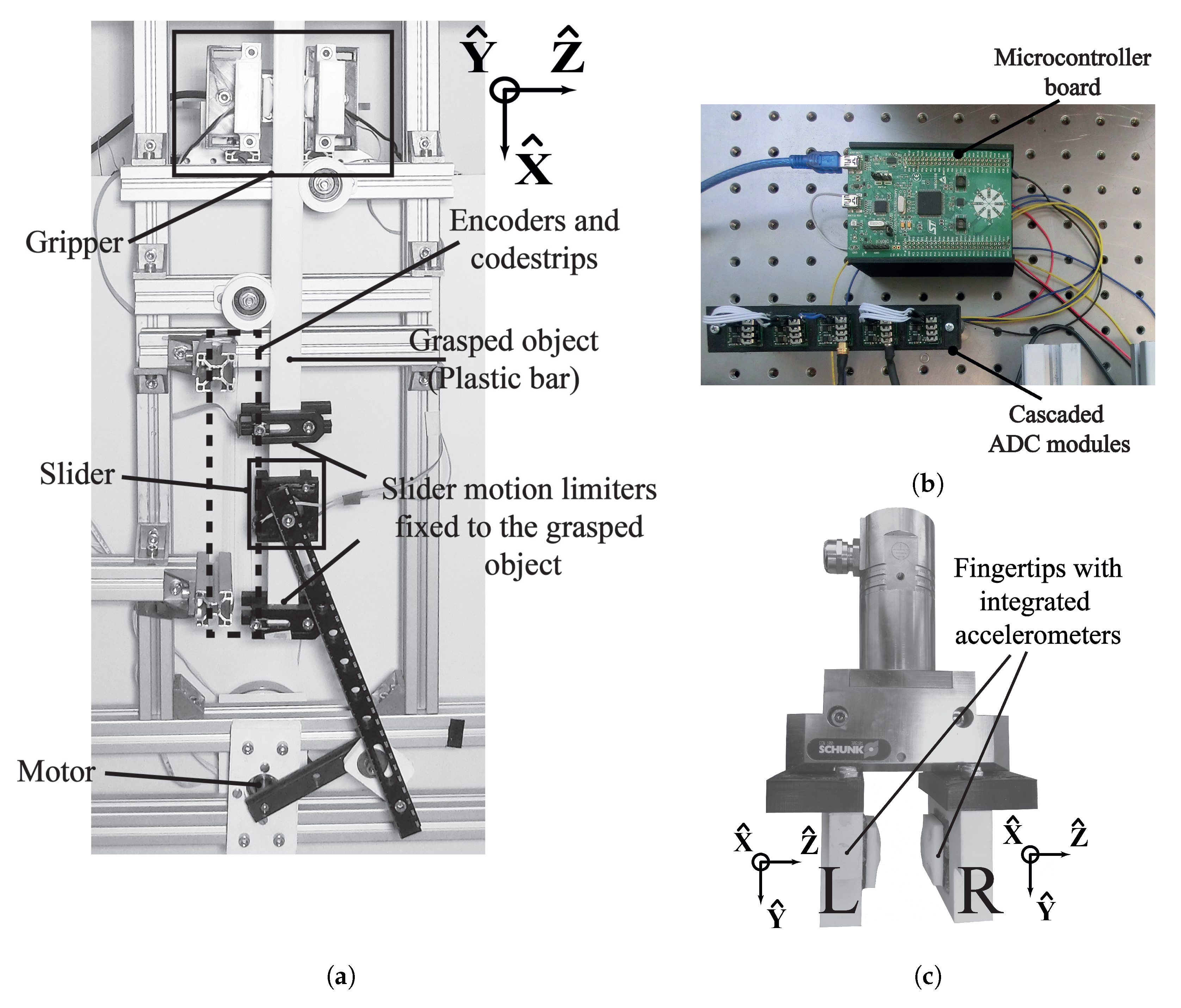
3.1. Experimental Setup
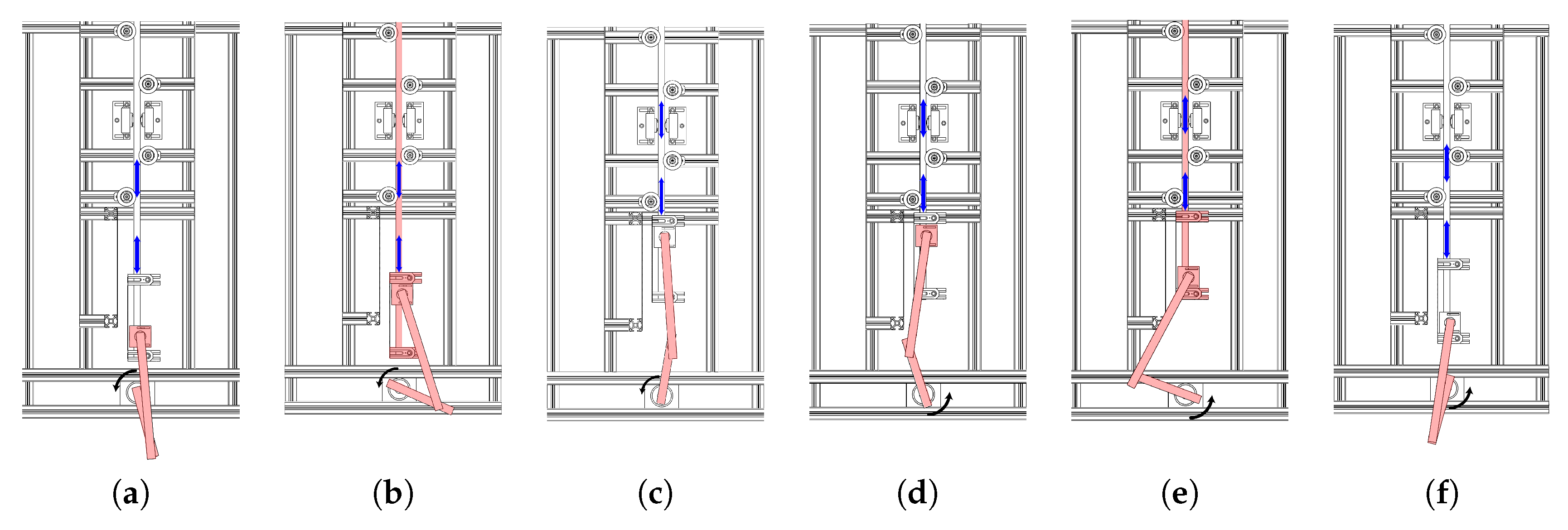
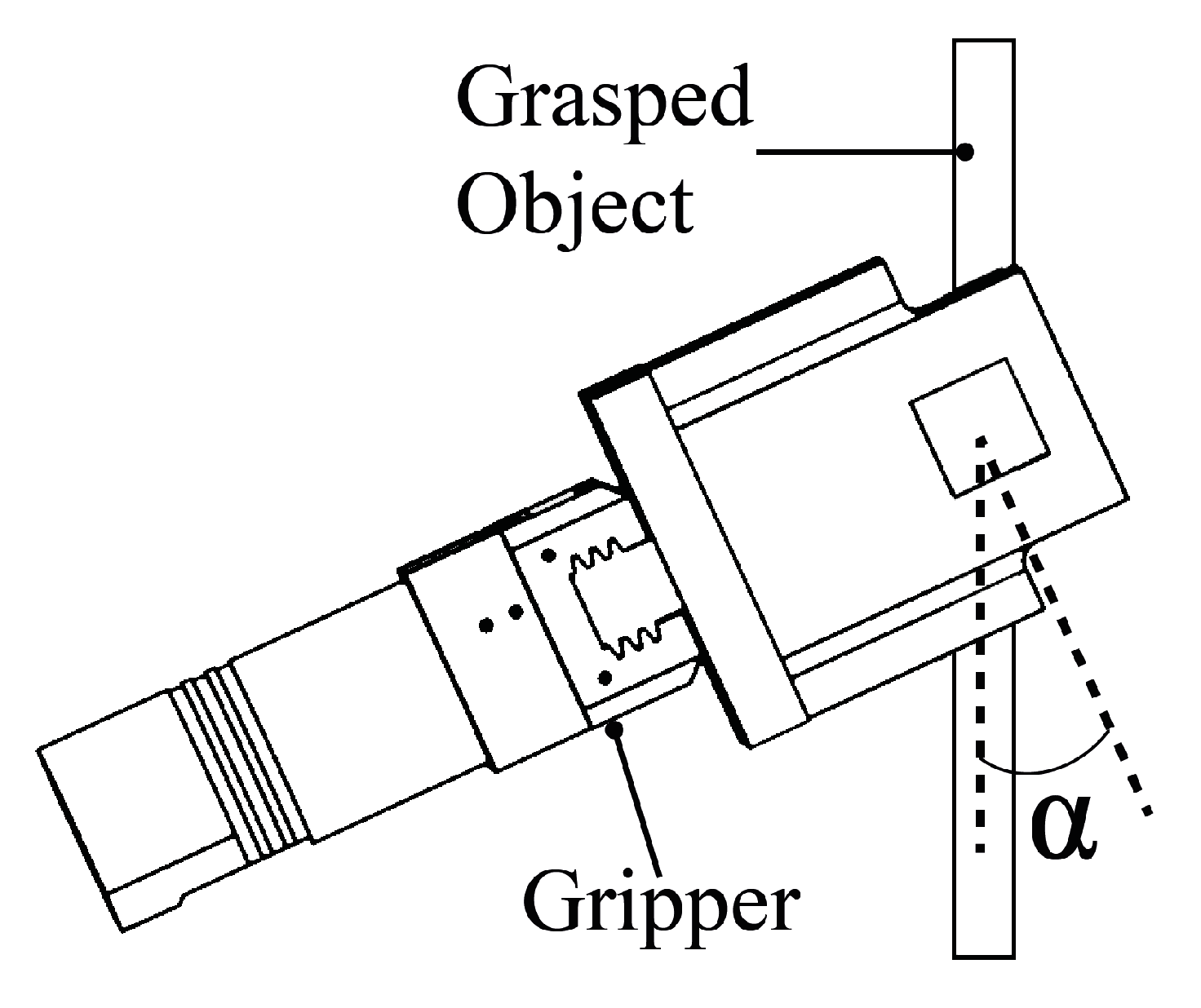
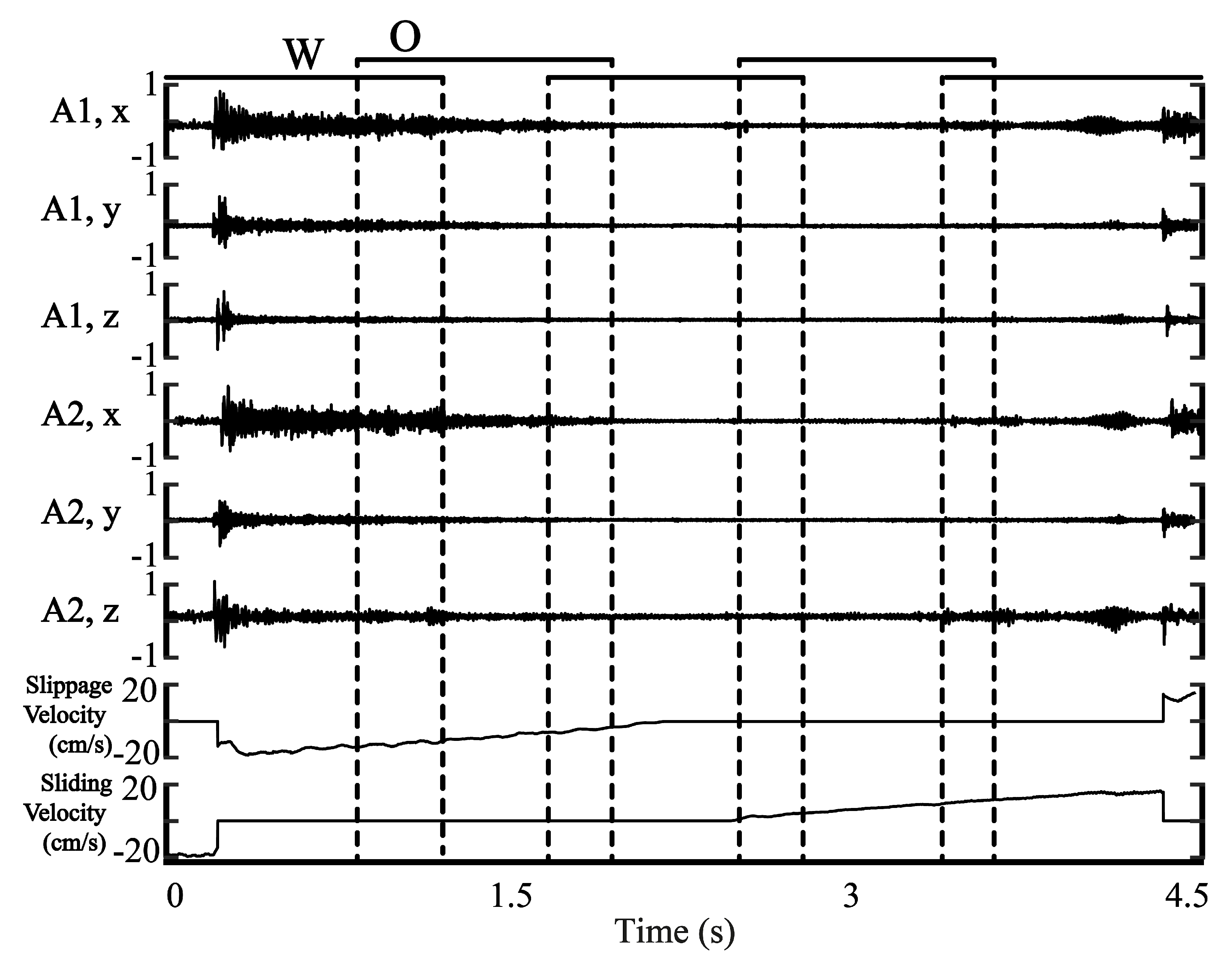
3.2. Experimental Procedure
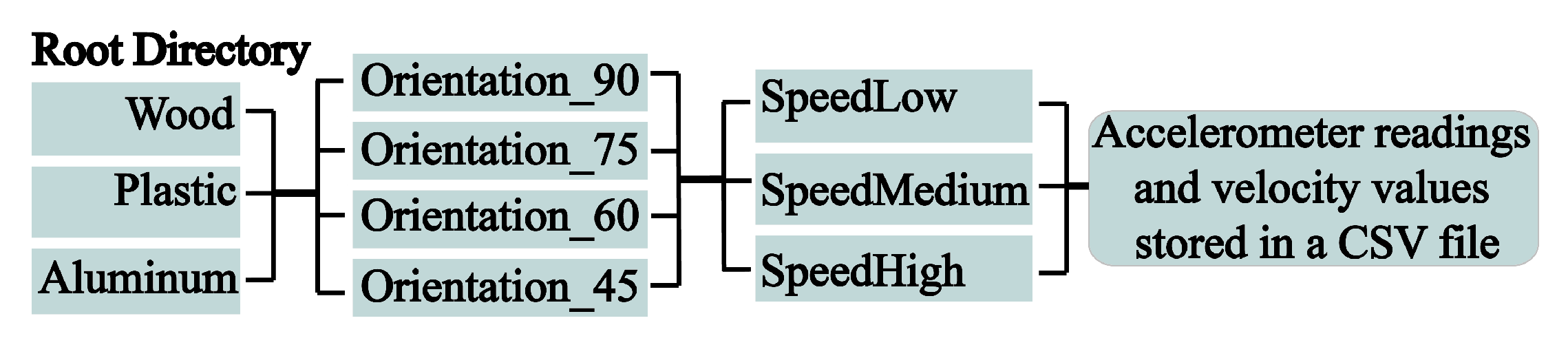
4. Dataset Structure
5. Deep Learning to Decipher Vibro-Tactile Signals
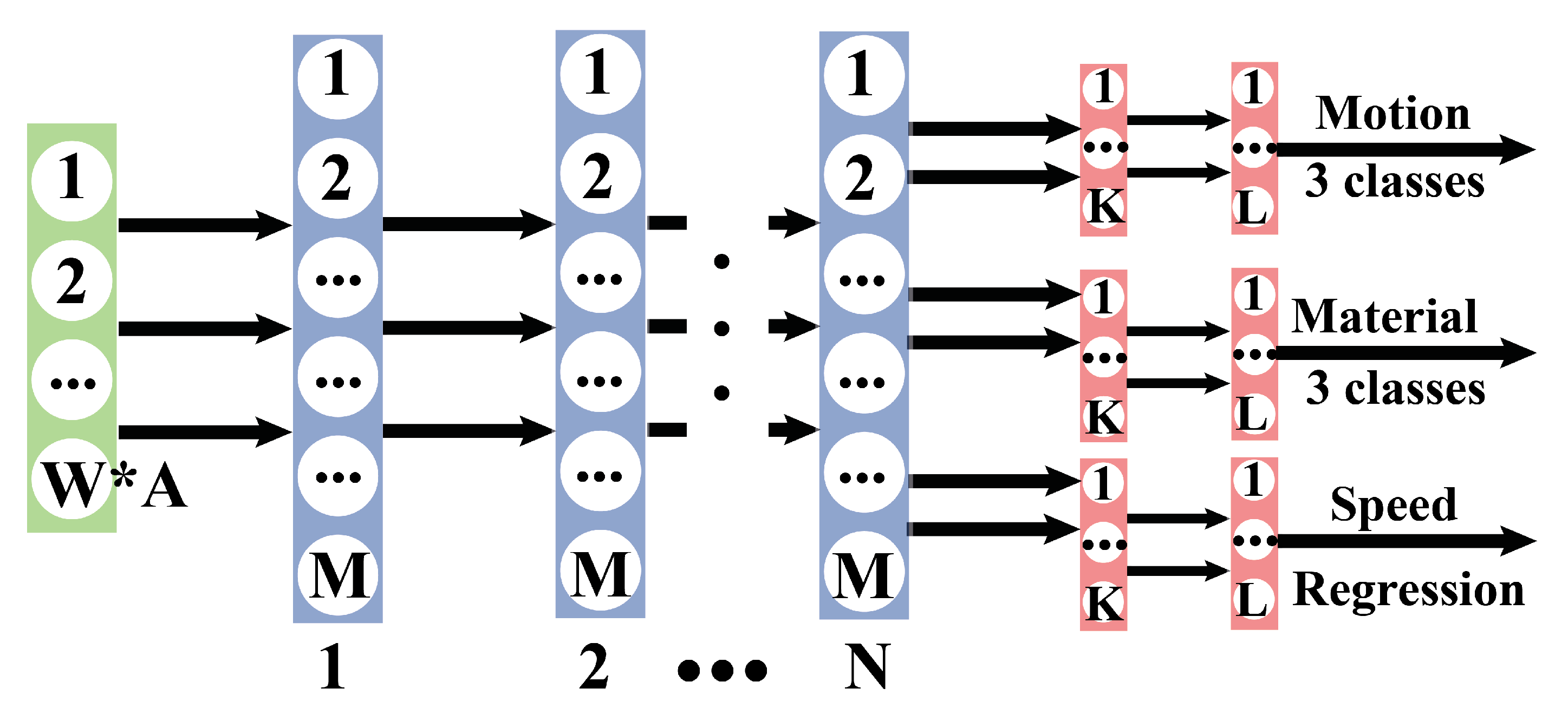
5.1. FNN
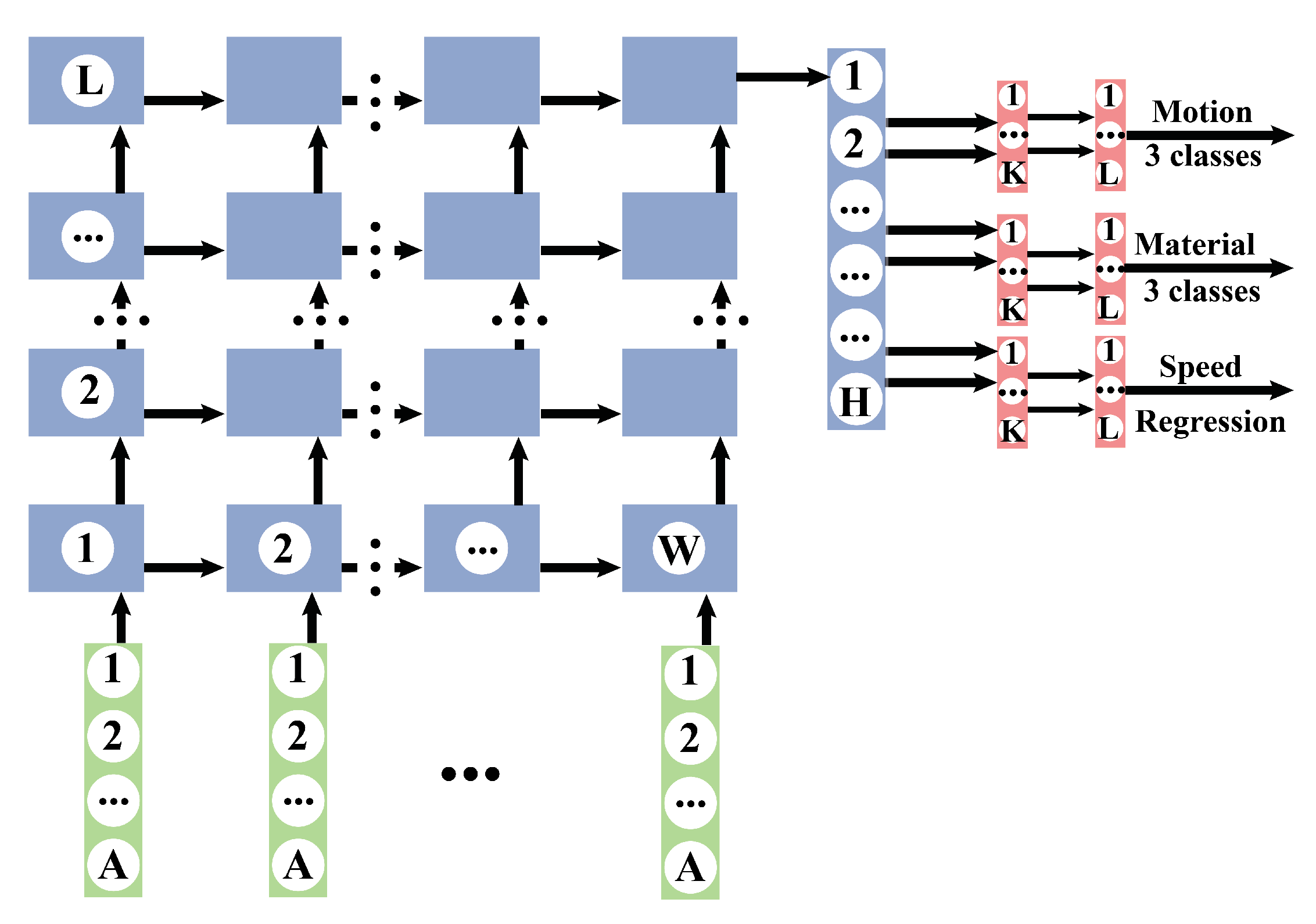
5.2. RNN
5.3. CNN
6. Results and Discussion
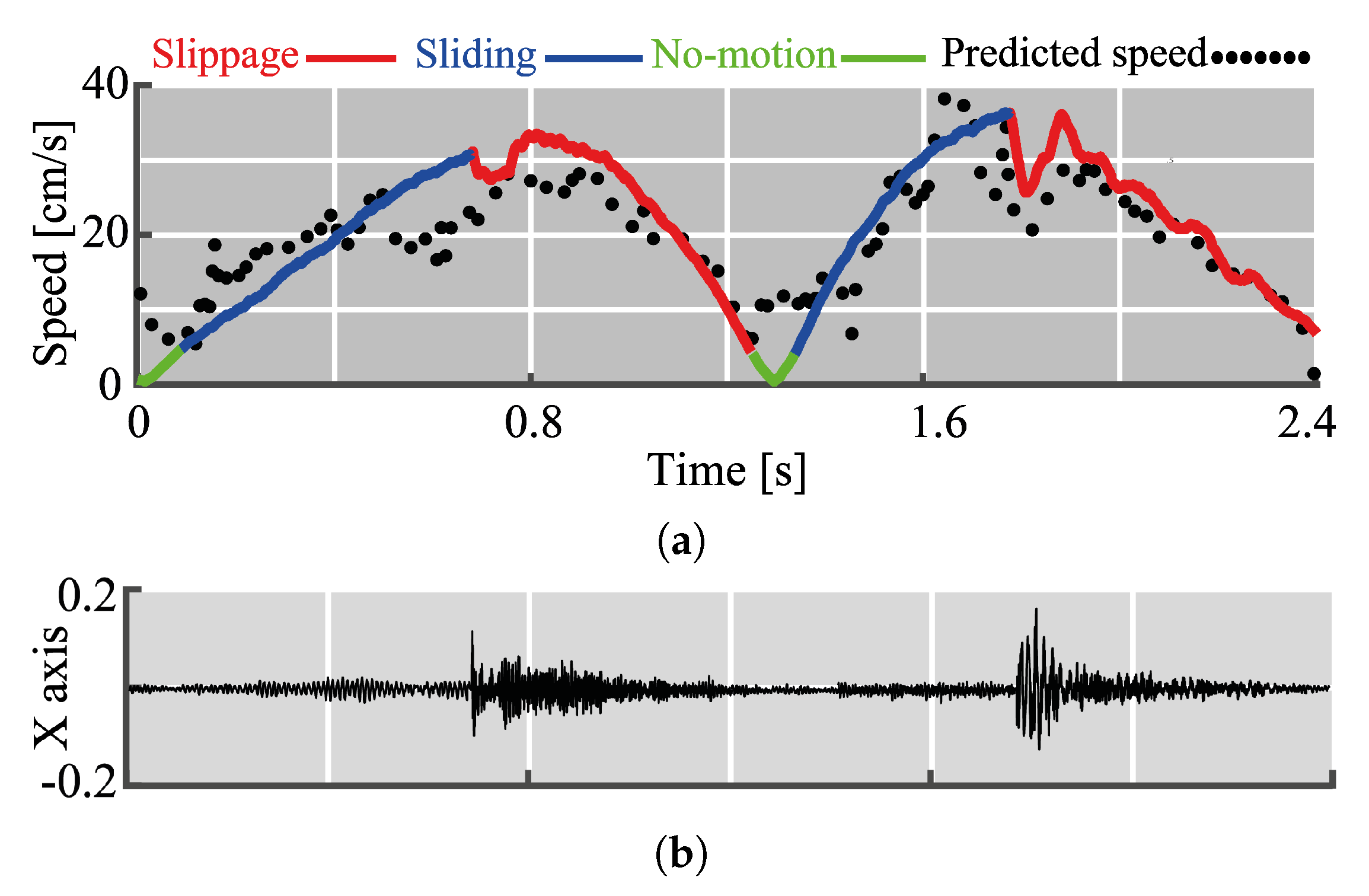
6.1. Motion Classification
6.2. Texture Identification
6.3. Speed Estimation
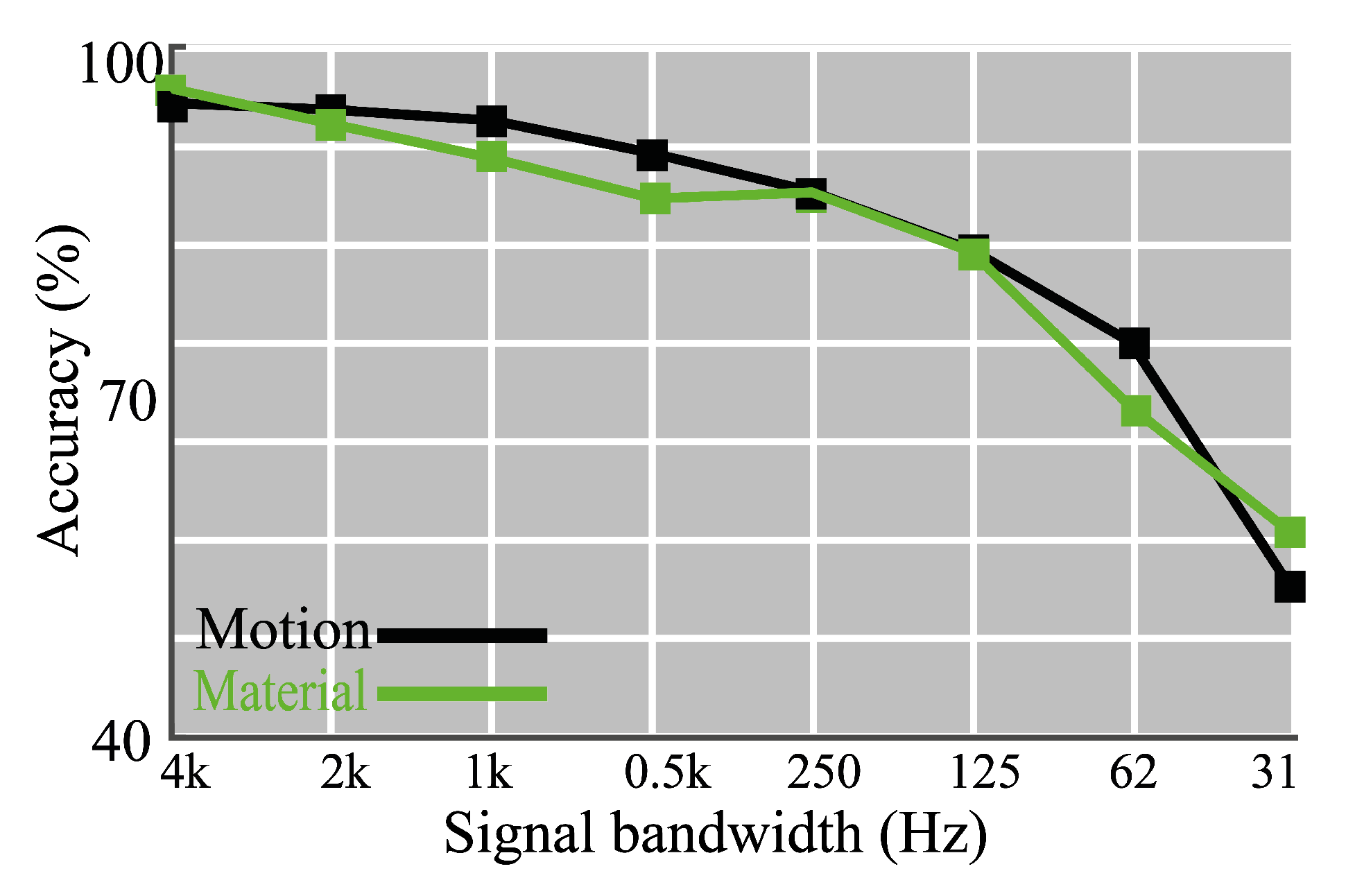
6.4. Effects of the Signal Bandwidth
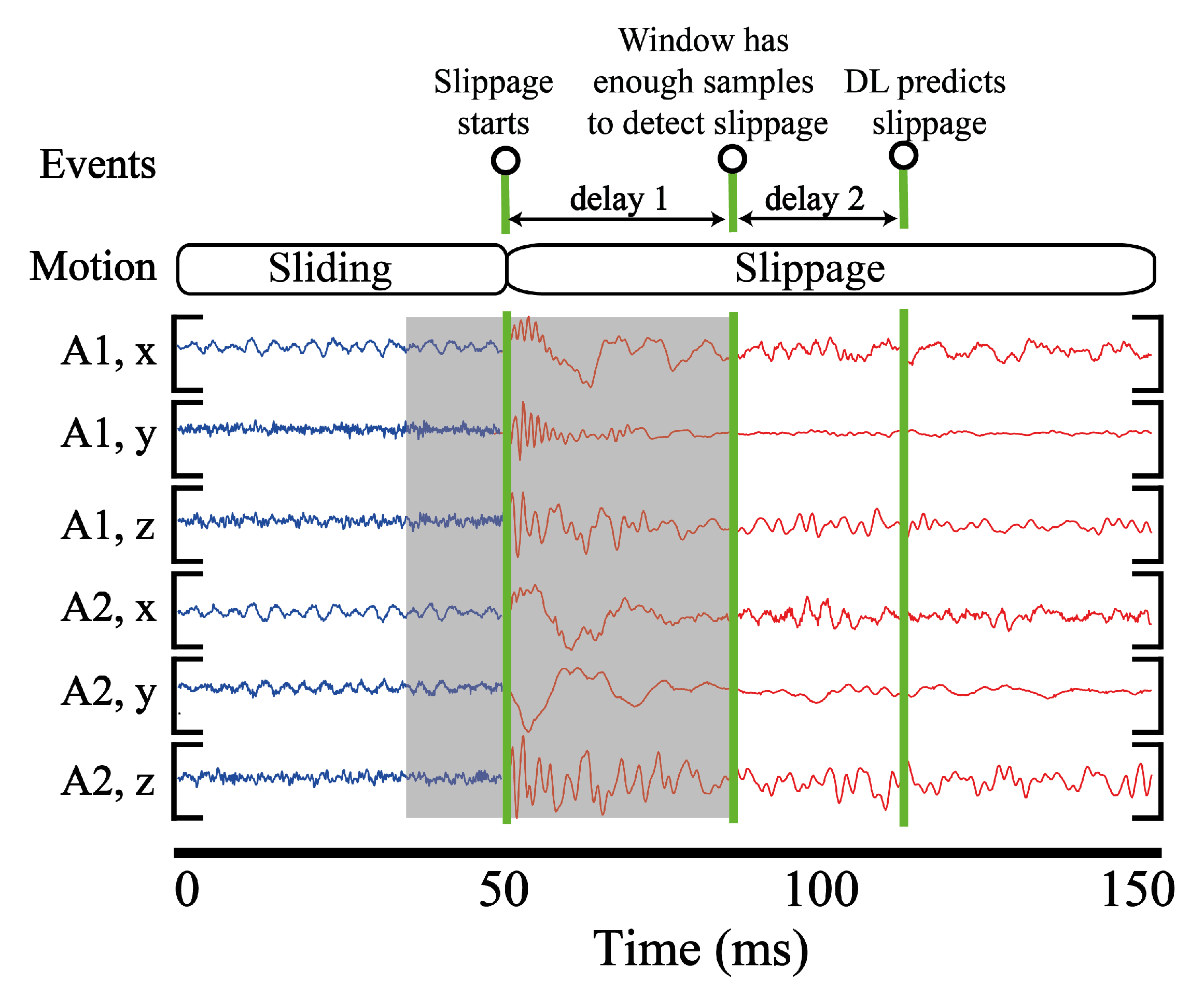
6.5. Computational Aspects: Latency and Memory
7. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Hutchings, I.M. Leonardo da Vinci’s studies of friction. Wear 2016, 360–361, 51–66. [Google Scholar] [CrossRef]
- Salisbury, J.K.; Craig, J.J. Articulated Hands: Force Control and Kinematic Issues. Int. J. Robot. Res. 1982, 1, 4–17. [Google Scholar] [CrossRef]
- Bicchi, A. On the form-closure property of robotic grasping. IFAC Proc. Vol. 1994, 27, 219–224. [Google Scholar] [CrossRef]
- Montana, D.J. The kinematics of contact and grasp. Int. J. Robot. Res. 1988, 7, 17–32. [Google Scholar] [CrossRef]
- Eberman, B.; Salisbury, J.K. Application of Change Detection to Dynamic Contact Sensing. Int. J. Robot. Res. 1994, 13, 369–394. [Google Scholar] [CrossRef]
- Robles-De-La-Torre, G.; Hayward, V. Force can overcome object geometry in the perception of shape through active touch. Nature 2001, 412, 445. [Google Scholar] [CrossRef] [PubMed]
- Lederman, S.J.; Klatzky, R.L. Hand movements: A window into haptic object recognition. Cogn. Psychol. 1987, 19, 342–368. [Google Scholar] [CrossRef]
- Roudaut, Y.; Lonigro, A.; Coste, B.; Hao, J.; Delmas, P.; Crest, M. Touch sense. Channels 2012, 6, 234–245. [Google Scholar] [CrossRef]
- Johansson, R.S.; Flanagan, J.R. Coding and use of tactile signals from the fingertips in object manipulation tasks. Nat. Rev. Neurosci. 2009, 10, 345. [Google Scholar] [CrossRef]
- Kappassov, Z.; Corrales, J.A.; Perdereau, V. Tactile sensing in dexterous robot hands. Robot. Auton. Syst. 2015, 195–220. [Google Scholar] [CrossRef]
- Edin, B.B.; Westling, G.; Johansson, R.S. Independent control of human finger-tip forces at individual digits during precision lifting. J. Physiol. 1992, 450, 547–564. [Google Scholar] [CrossRef] [PubMed]
- Johansson, R.S.; Flanagan, J.R. The Senses: A Comprehensive Reference; Chapter Tactile Sensory Control of Object Manipulation in Humans; Academic Press: New York, NY, USA, 2008; pp. 67–86. [Google Scholar] [CrossRef]
- Wiertlewski, M.; Endo, S.; Wing, A.M.; Hayward, V. Slip-induced vibration influences the grip reflex: A pilot study. In Proceedings of the World Haptics Conference (WHC), Daejeon, Korea, 14–17 April 2013; pp. 627–632. [Google Scholar]
- Li, M.; Bekiroglu, Y.; Kragic, D.; Billard, A. Learning of grasp adaptation through experience and tactile sensing. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 3339–3346. [Google Scholar]
- Romano, J.; Hsiao, K.; Niemeyer, G.; Chitta, S.; Kuchenbecker, K. Human-Inspired Robotic Grasp Control With Tactile Sensing. IEEE Trans. Robot. 2011, 1067–1079. [Google Scholar] [CrossRef]
- Falco, J.A.; Marvel, J.A.; Messina, E.R. A Roadmap to Advance Measurement Science in Robot Dexterity and Manipulation; Technical Report; NIST: Gaithersburg, MD, USA, 2014. [Google Scholar]
- Howe, R.D.; Cutkosky, M.R. Sensing skin acceleration for slip and texture perception. In Proceedings of the International Conference on Robotics and Automation (ICRA), Scottsdale, AZ, USA, 14–19 May 1989; Volume 1, pp. 145–150. [Google Scholar] [CrossRef]
- Massalim, Y.; Kappassov, Z. Array of Accelerometers as a Dynamic Vibro-Tactile Sensing for Assessing the Slipping Noise. In Proceedings of the IEEE/SICE International Symposium on System Integration (SII), Paris, France, 14–16 January 2019; pp. 438–443. [Google Scholar] [CrossRef]
- Kyberd, P.J.; Evans, M.; te Winkel, S. An Intelligent Anthropomorphic Hand, with Automatic Grasp. Robotica 1998, 16, 531–536. [Google Scholar] [CrossRef]
- Kappassov, Z.; Baimukashev, D.; Kuanyshuly, Z.; Massalin, Y.; Urazbayev, A.; Varol, H.A. Color-Coded Fiber-Optic Tactile Sensor for an Elastomeric Robot Skin. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 2146–2152. [Google Scholar] [CrossRef]
- Chen, W.; Khamis, H.; Birznieks, I.; Lepora, N.F.; Redmond, S.J. Tactile Sensors for Friction Estimation and Incipient Slip Detection—Toward Dexterous Robotic Manipulation: A Review. IEEE Sens. J. 2018, 18, 9049–9064. [Google Scholar] [CrossRef]
- Adams, M.J.; Johnson, S.A.; Lefèvre, P.; Lévesque, V.; Hayward, V.; André, T.; Thonnard, J.L. Finger pad friction and its role in grip and touch. J. R. Soc. Interface 2013, 10, 20120467. [Google Scholar] [CrossRef]
- Ho, V.A.; Nagatani, T.; Noda, A.; Hirai, S. What can be inferred from a tactile arrayed sensor in autonomous in-hand manipulation? In Proceedings of the International Conference on Automation Science and Engineering (CASE), Seoul, Korea, 20–24 August 2012; pp. 461–468. [Google Scholar] [CrossRef]
- James, J.W.; Pestell, N.; Lepora, N.F. Slip Detection With a Biomimetic Tactile Sensor. IEEE Robot. Autom. Lett. 2018, 3, 3340–3346. [Google Scholar] [CrossRef]
- Luo, S.; Bimbo, J.; Dahiya, R.; Liu, H. Robotic tactile perception of object properties: A review. Mechatronics 2017, 48, 54–67. [Google Scholar] [CrossRef]
- Gandarias, J.M.; García-Cerezo, A.J.; de Gabriel, J.M.G. CNN-Based Methods for Object Recognition With High-Resolution Tactile Sensors. IEEE Sens. J. 2019, 19, 6872–6882. [Google Scholar] [CrossRef]
- Pezzementi, Z.; Hager, G.D. Tactile Object Recognition and Localization Using Spatially-Varying Appearance. In Robotics Research: The 15th International Symposium ISRR; Christensen, H.I., Khatib, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 201–217. [Google Scholar] [CrossRef]
- Luo, S.; Mou, W.; Althoefer, K.; Liu, H. iCLAP: Shape recognition by combining proprioception and touch sensing. Auton. Robot. 2018, 1–12. [Google Scholar] [CrossRef]
- Shimonomura, K. Tactile Image Sensors Employing Camera: A Review. Sensors 2019, 19, 3933. [Google Scholar] [CrossRef]
- Maekawa, H.; Tanie, K.; Komoriya, K.; Kaneko, M.; Horiguchi, C.; Sugawara, T. Development of a finger-shaped tactile sensor and its evaluation by active touch. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Nice, France, 12–14 May 1992; pp. 1327–1334. [Google Scholar] [CrossRef]
- Begej, S. Planar and finger-shaped optical tactile sensors for robotic applications. IEEE J. Robot. Autom. 1988, 4, 472–484. [Google Scholar] [CrossRef]
- Li, R.; Adelson, E.H. Sensing and Recognizing Surface Textures Using a GelSight Sensor. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Goger, D.; Gorges, N.; Worn, H. Tactile sensing for an anthropomorphic robotic hand: Hardware and signal processing. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Kobe, Japan, 12–17 May 2009; pp. 895–901. [Google Scholar]
- Yuan, W.; Dong, S.; Adelson, E.H. GelSight: High-Resolution Robot Tactile Sensors for Estimating Geometry and Force. Sensors 2017, 17, 2762. [Google Scholar] [CrossRef]
- Ward-Cherrier, B.; Pestell, N.; Cramphorn, L.; Winstone, B.; Giannaccini, M.E.; Rossiter, J.; Lepora, N.F. The TacTip Family: Soft Optical Tactile Sensors with 3D-Printed Biomimetic Morphologies. Soft Robot. 2018, 5, 216–227. [Google Scholar] [CrossRef] [PubMed]
- Wettels, N.; Parnandi, A.; Moon, J.H.; Loeb, G.; Sukhatme, G. Grip Control Using Biomimetic Tactile Sensing Systems. IEEE/ASME Trans. Mechatron. 2009, 14, 718–723. [Google Scholar] [CrossRef]
- Song, X.; Liu, H.; Althoefer, K.; Nanayakkara, T.; Seneviratne, L. Efficient Break-Away Friction Ratio and Slip Prediction Based on Haptic Surface Exploration. IEEE Trans. Robot. 2014, 30, 203–219. [Google Scholar] [CrossRef]
- Melchiorri, C. Slip detection and control using tactile and force sensors. IEEE/ASME Trans. Mechatron. 2000, 5, 235–243. [Google Scholar] [CrossRef]
- Kappassov, Z.; Corrales, J.A.; Perdereau, V. Touch driven controller and tactile features for physical interactions. Robot. Auton. Syst. 2020, 123, 103332. [Google Scholar] [CrossRef]
- Sun, T.; Back, J.; Liu, H. Combining Contact Forces and Geometry to Recognize Objects During Surface Haptic Exploration. IEEE Robot. Autom. Lett. 2018, 3, 2509–2514. [Google Scholar] [CrossRef]
- Fishel, J.A.; Loeb, G.E. Bayesian Exploration for Intelligent Identification of Textures. Front. Neurorobot. 2012, 6. [Google Scholar] [CrossRef]
- Meier, M.; Walck, G.; Haschke, R.; Ritter, H.J. Distinguishing sliding from slipping during object pushing. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Seoul, Korea, 8–9 October 2016; pp. 5579–5584. [Google Scholar] [CrossRef]
- Heyneman, B.; Cutkosky, M.R. Slip classification for dynamic tactile array sensors. Int. J. Robot. Res. 2015, 35, 404–421. [Google Scholar] [CrossRef]
- Naeini, F.B.; Alali, A.; Al-Husari, R.; Rigi, A.; AlSharman, M.K.; Makris, D.; Zweiri, Y. A Novel Dynamic- Vision-Based Approach for Tactile Sensing Applications. IEee Trans. Instrum. Meas. 2019, 1. [Google Scholar] [CrossRef]
- Roberge, J.; Rispal, S.; Wong, T.; Duchaine, V. Unsupervised feature learning for classifying dynamic tactile events using sparse coding. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 2675–2681. [Google Scholar]
- Taunyazov, T.; Koh, H.F.; Wu, Y.; Cai, C.; Soh, H. Towards Effective Tactile Identification of Textures using a Hybrid Touch Approach. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4269–4275. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]

| Window size | 400 | 200 | 100 | 50 | 25 | 10 |
| Overlap | 200 | 100 | 50 | 25 | 15 | 0 |
| Number of samples | 115 k | 234 k | 463 k | 927 k | 1546 k | 2319 k |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massalim, Y.; Kappassov, Z.; Varol, H.A. Deep Vibro-Tactile Perception for Simultaneous Texture Identification, Slip Detection, and Speed Estimation. Sensors 2020, 20, 4121. https://doi.org/10.3390/s20154121
Massalim Y, Kappassov Z, Varol HA. Deep Vibro-Tactile Perception for Simultaneous Texture Identification, Slip Detection, and Speed Estimation. Sensors. 2020; 20(15):4121. https://doi.org/10.3390/s20154121
Chicago/Turabian StyleMassalim, Yerkebulan, Zhanat Kappassov, and Huseyin Atakan Varol. 2020. "Deep Vibro-Tactile Perception for Simultaneous Texture Identification, Slip Detection, and Speed Estimation" Sensors 20, no. 15: 4121. https://doi.org/10.3390/s20154121
APA StyleMassalim, Y., Kappassov, Z., & Varol, H. A. (2020). Deep Vibro-Tactile Perception for Simultaneous Texture Identification, Slip Detection, and Speed Estimation. Sensors, 20(15), 4121. https://doi.org/10.3390/s20154121







