A Kalman Filter-Based Method for Diagnosing the Structural Condition of Medium- and Small-Span Beam Bridges during Brief Traffic Interruptions
Abstract
1. Introduction
2. A Kalman Filter-Based Method for Diagnosing the Structural Condition of Medium- and Small-Span Beam Bridges
2.1. Condition Diagnosis Feature Based on the Innovation Obtained by the Kalman Filter
2.2. Condition Diagnosis Index Based on the Energy Ratio between the Innovation and the Measured Response
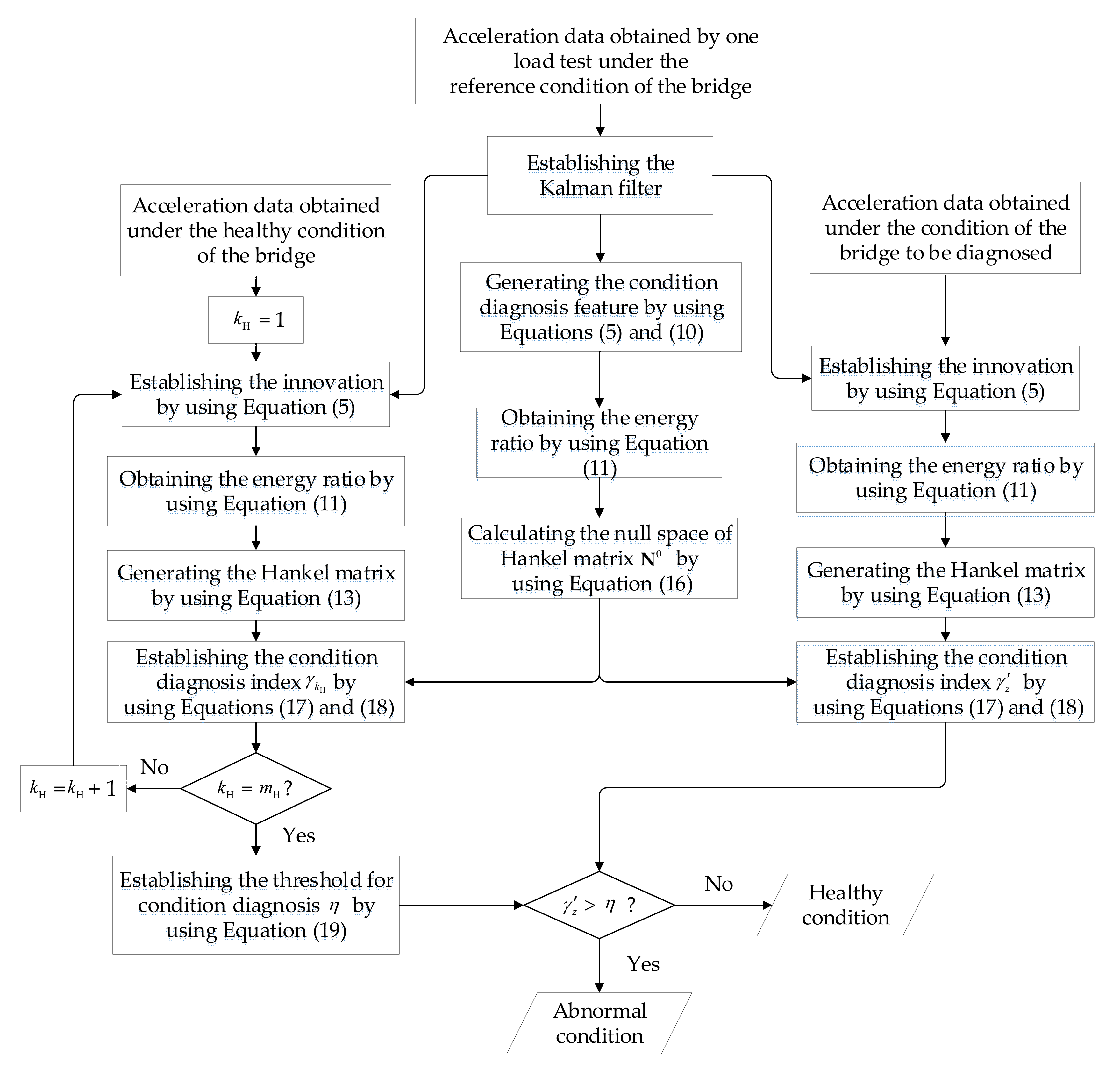
2.3. Procedure of the Proposed Method
3. Example of an Experimental Model Bridge
3.1. Description of the Model Bridge Experiment
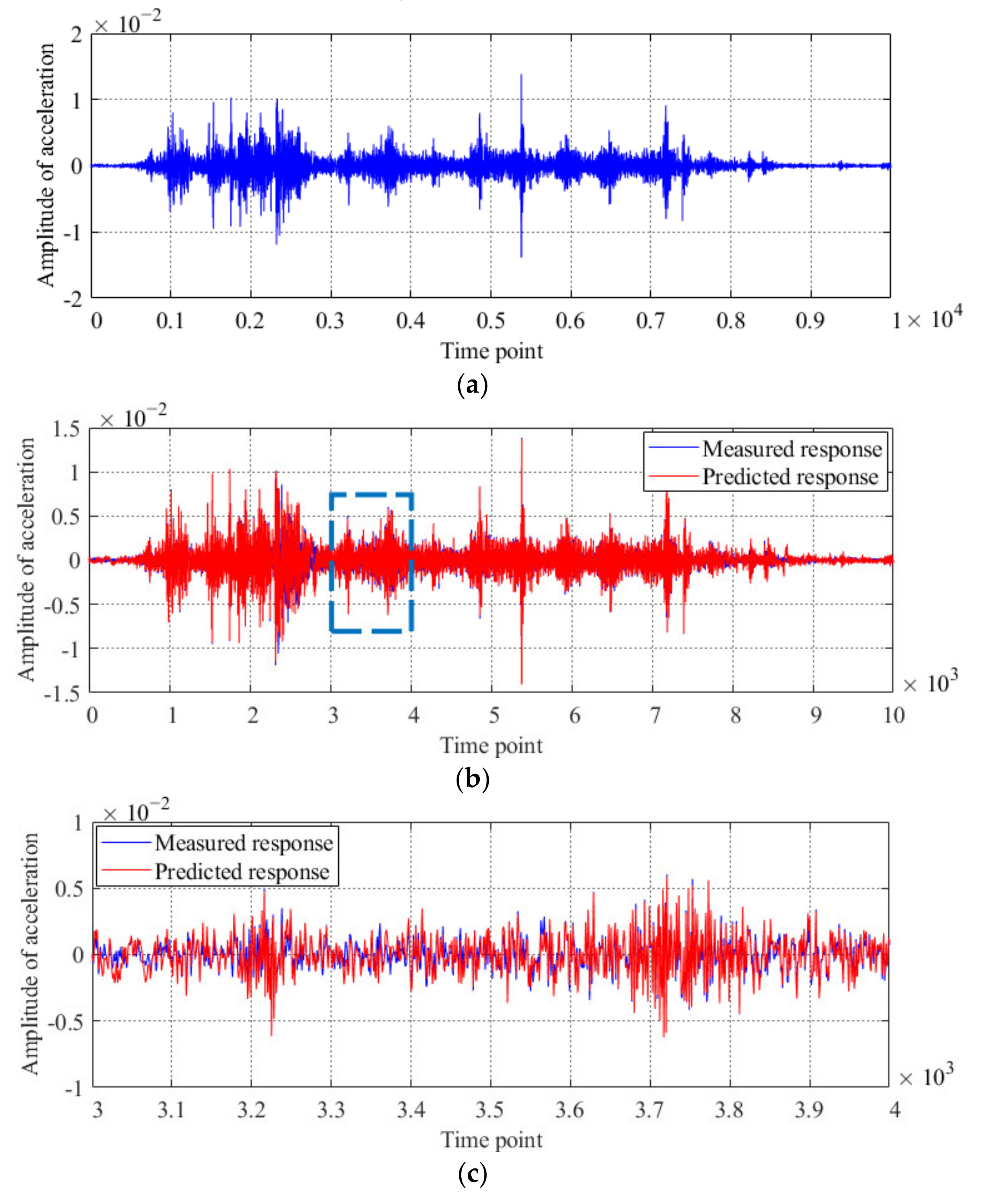
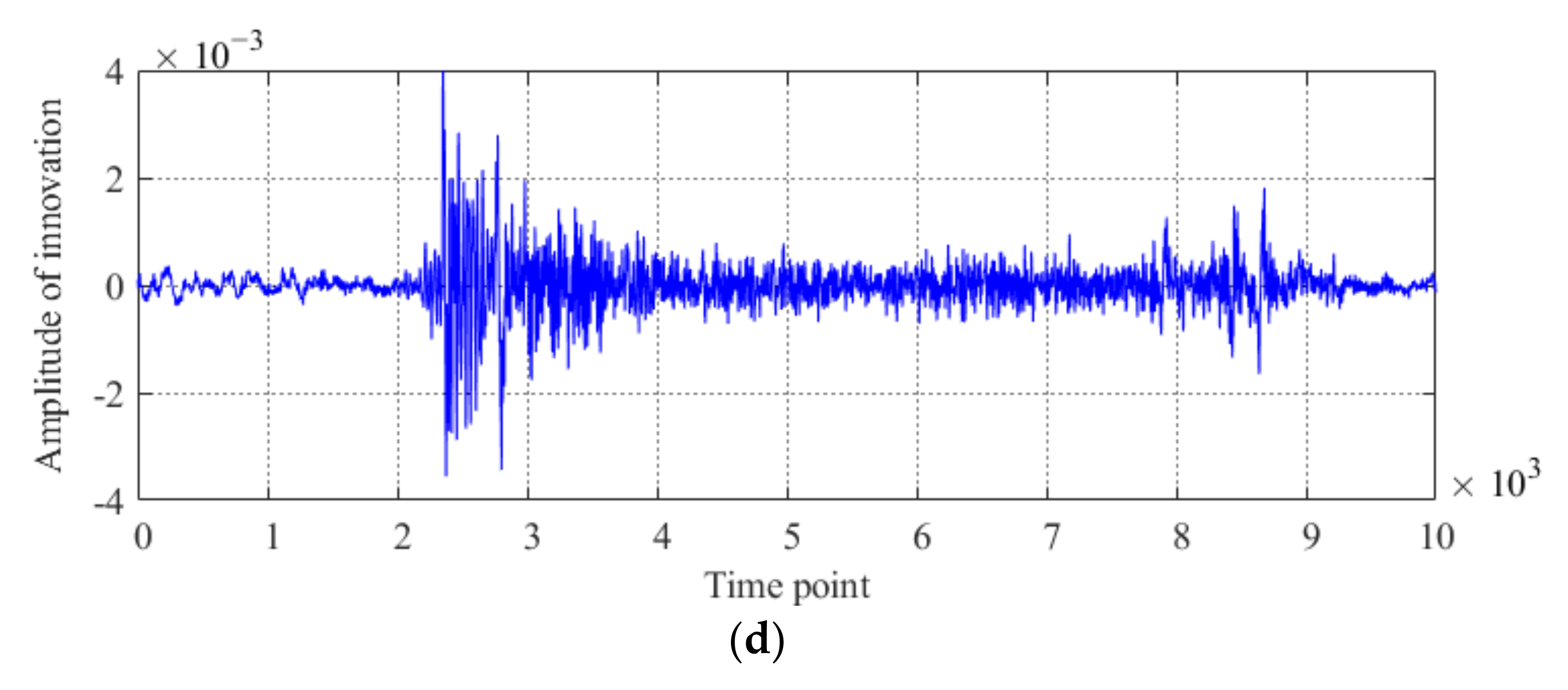
3.2. Results of Condition Diagnosis of the Model Bridge Obtained by the Proposed Method
3.3. Comparison of the Performance between the Proposed Method and the Method Based on Modal Parameters
3.4. Influence of Different Moving Loads on the Results of Condition Diagnosis of the Model Bridge
4. Example of an Actual Bridge
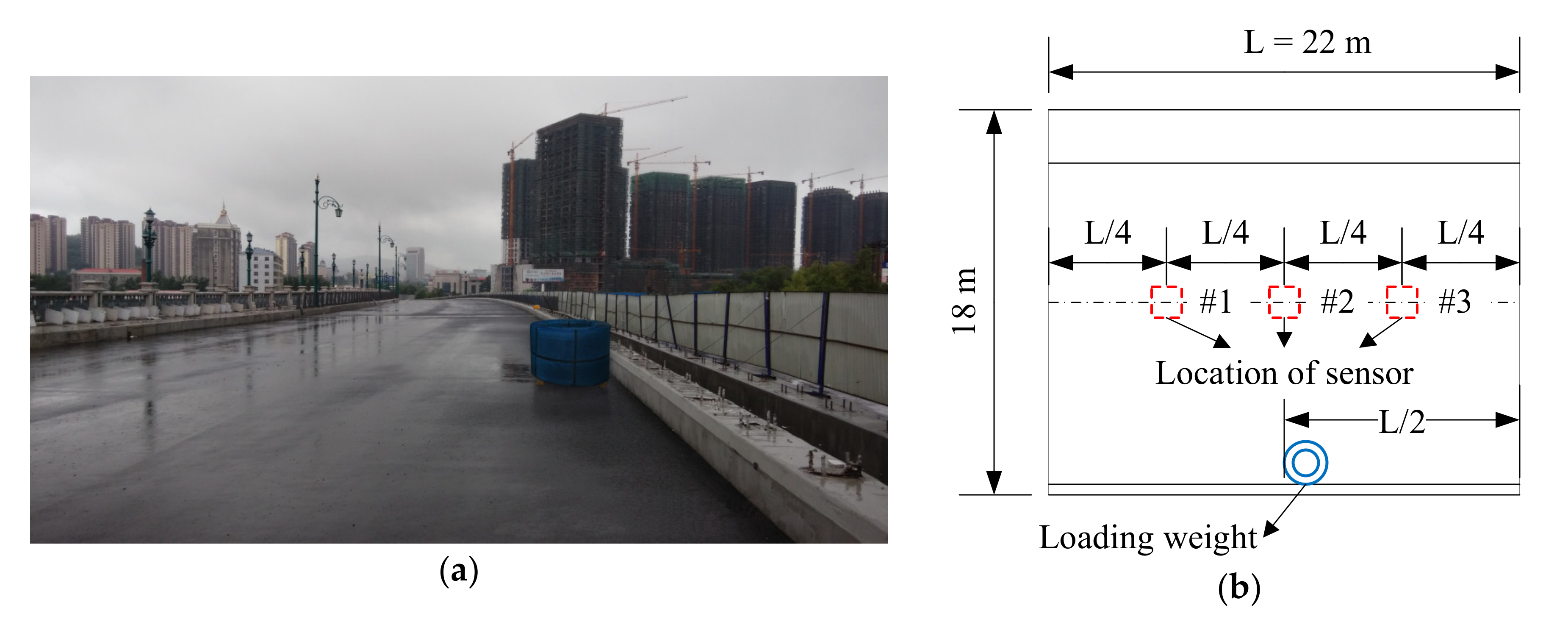
4.1. Description of the Selected Bridge and Corresponding Load Test
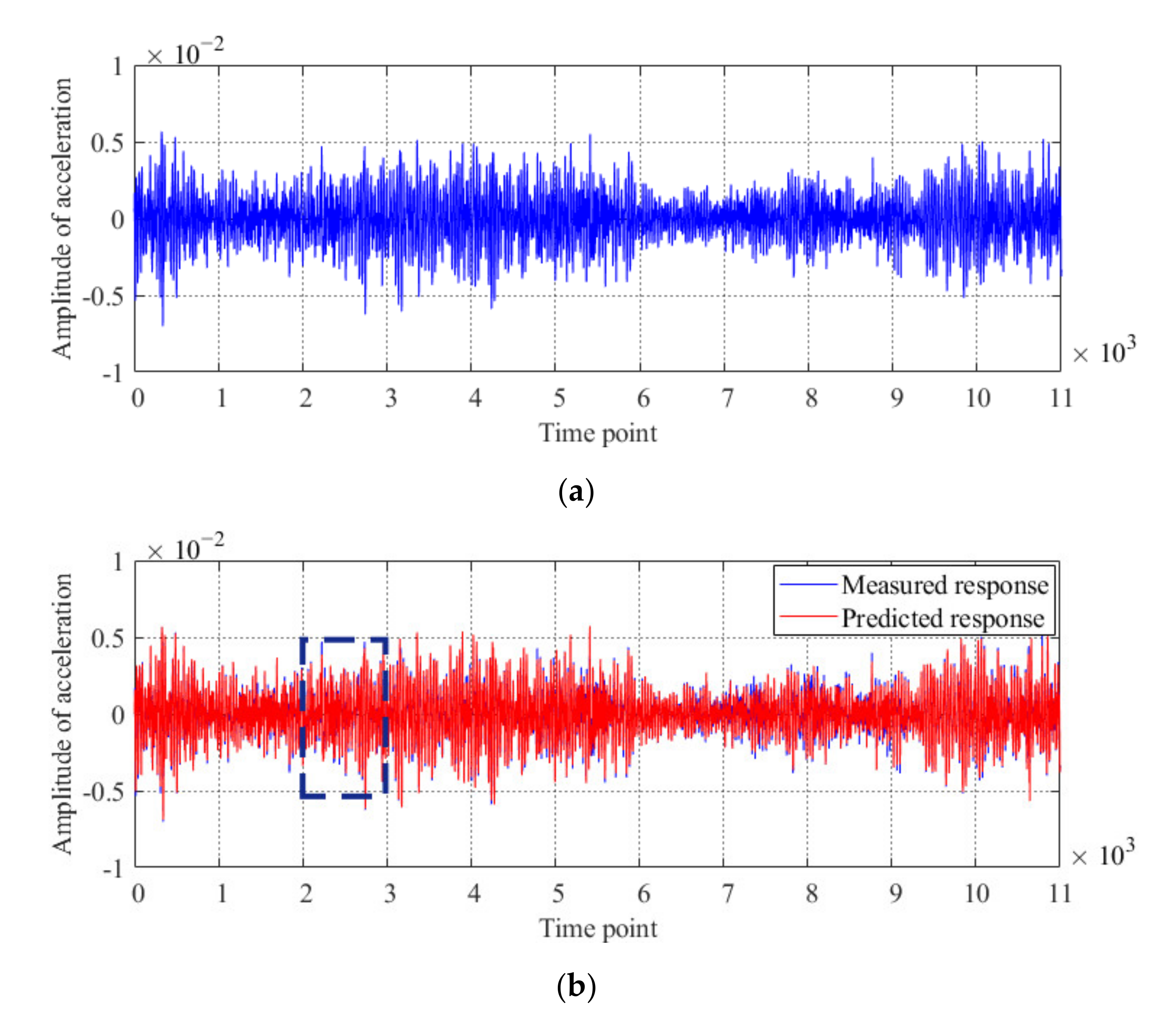
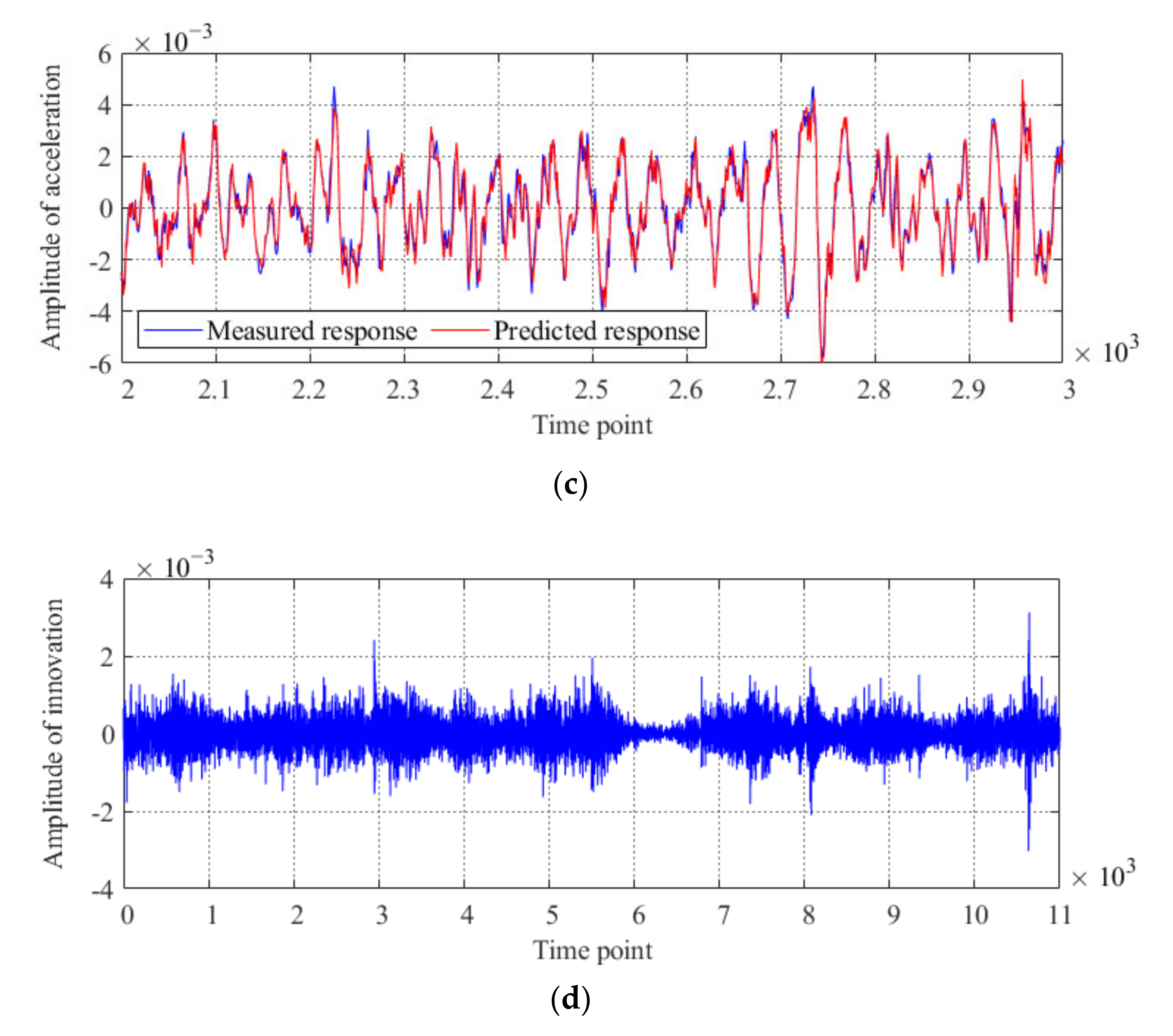
4.2. Results of Condition Diagnosis for the Actual Beam Bridge
5. Conclusions
- (1)
- The proposed Kalman filter-based method is suitable to diagnose the structural condition of bridges without any long-duration interruption of the traffic flow, and this method is convenient for practical application since its does not need to establish the FEM of the bridge.
- (2)
- There is good agreement between the predicted and measured acceleration responses, which shows that the performance of Kalman filter is sufficient to predict the dynamic response of actual bridges excited by a moving load.
- (3)
- A condition diagnosis index based on the energy ratio between the innovation obtained by the Kalman filter and the measured acceleration is proposed. The results of condition diagnosis using data from experiments and field tests show that this index is sensitive to changes in the structural condition of the bridge superstructure, thereby illustrating that the proposed index is suitable for evaluating the condition of actual medium- and small-span beam bridges.
- (4)
- The results obtained from a model bridge and an actual bridge demonstrate that, in comparison with the traditional method based on modal parameters, the proposed method is more sensitive to the changes in the structural condition of bridges.
- (5)
- The limitation of the proposed method in application is keeping the load consistent for each load test, and the difference in the weight difference of the moving vehicle between each test should be less than 10%.
Author Contributions
Funding
Conflicts of Interest
References
- Dilena, M.; Morassi, A. Dynamic testing of a damaged bridge. Mech. Syst. Signal Process. 2011, 25, 1485–1507. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Law, S.S. Wavelet-based crack identification of bridge beam from operational deflection time history. Int. J. Solids Struct. 2006, 43, 2299–2317. [Google Scholar] [CrossRef]
- Alsharqawi, M.; Zayed, T.; Abu Dabous, S. Integrated condition rating and forecasting method for bridge decks using Visual Inspection and Ground Penetrating Radar. Automat. Constr. 2018, 89, 135–145. [Google Scholar] [CrossRef]
- An, Y.H.; Chatzi, E.; Sim, S.H.; Laflamme, S.; Blachowski, B.; Ou, J.P. Recent progress and future trends on damage identification methods for bridge structures. Struct. Control. Health Monit. 2019, 26, e2416. [Google Scholar] [CrossRef]
- Reiff, A.J.; Sanayei, M.; Vogel, R.M. Statistical bridge damage detection using girder distribution factors. Eng. Struct. 2016, 109, 139–151. [Google Scholar] [CrossRef]
- Seventekidis, P.; Giagopoulos, D.; Arailopoulos, A.; Markogiannaki, O. Structural Health Monitoring using deep learning with optimal finite element model generated data. Mech. Syst. Signal Process. 2020, 145, 106972. [Google Scholar] [CrossRef]
- Annamdas, V.G.M.; Bhalla, S.; Soh, C.K. Applications of structural health monitoring technology in Asia. Struct. Health Monit. 2017, 16, 324–346. [Google Scholar] [CrossRef]
- Vagnoli, M.; Remenyte-Prescott, R.; Andrews, J. Railway bridge structural health monitoring and fault detection: State-of-the-art methods and future challenges. Struct. Health Monit. 2018, 17, 971–1007. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Y. Damage detection of bridges monitored within one cluster based on the residual between the cumulative distribution functions of strain monitoring data. Struct. Health Monit. 2020. (In press) [CrossRef]
- Ngeljaratan, L.; Moustafa, M.A. Structural health monitoring and seismic response assessment of bridge structures using target-tracking digital image correlation. Eng. Struct. 2020, 213, 110551. [Google Scholar] [CrossRef]
- Cross, E.J.; Koo, K.Y.; Brownjohn, J.M.W.; Worden, K. Long-term monitoring and data analysis of the Tamar Bridge. Mech. Syst. Signal Process. 2013, 35, 16–34. [Google Scholar] [CrossRef]
- Zhu, X.; Cao, M.S.; Ostachowicz, W.; Xu, W. Structural Damage Identification of Bridges from Passing Test Vehicles. Sensors 2019, 19, 4035. [Google Scholar]
- Yang, Y.; Zhu, Y.H.; Wang, L.L.; Jia, B.Y.L.; Jin, R.Y. Damage Identification in Bridges by Processing Dynamic Responses to Moving Loads: Features and Evaluation. Sensors 2018, 18, 463. [Google Scholar]
- Bertola, N.J.; Smith, I.F.C. A methodology for measurement-system design combining information from static and dynamic excitations for bridge load testing. J. Sound Vib. 2019, 463, 114953. [Google Scholar] [CrossRef]
- Bakht, B.; Jaeger, L. Bridge testing—A surprise every time. J. Struct. Eng. 1990, 116, 1370–1383. [Google Scholar] [CrossRef]
- Lu, P.Z.; Xu, Z.J.; Chen, Y.R.; Zhou, Y.T. Prediction method of bridge static load test results based on Kriging model. Eng. Struct. 2020, 214, 110641. [Google Scholar] [CrossRef]
- Cao, W.J.; Koh, C.G.; Smith, I.F.C. Enhancing static-load-test identification of bridges using dynamic data. Eng. Struct. 2019, 186, 410–420. [Google Scholar] [CrossRef]
- Huseynov, F.; Brownjohn, J.M.W.; O’Brien, E.J.; Hester, D. Analysis of load test on composite I-girder bridge. J. Civ. Struct. Health Monit. 2017, 7, 163–173. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; Technical Report TR 95-041; Department of Computer Science, University of North Carolina: Chapel Hill, NC, USA, 1995. [Google Scholar]
- Xia, D.Z.; Hu, Y.W.; Kong, L. Adaptive Kalman filtering based on higher-order statistical analysis for digitalized silicon microgyroscope. Measurement 2015, 75, 244–254. [Google Scholar] [CrossRef]
- Heffes, H. The effect of erroneous models on the Kalman filter response. IEEE Trans. Autom. Control 2003, 11, 541–543. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Zhang, F.Q. Review of the Ensemble Kalman Filter for Atmospheric Data Assimilation. Mon. Weather Rev. 2016, 144, 4489–4532. [Google Scholar] [CrossRef]
- Zhao, J.B.; Mili, L. Robust Unscented Kalman Filter for Power System Dynamic State Estimation With Unknown Noise Statistics. IEEE Trans. Smart Grid 2019, 10, 1215–1224. [Google Scholar] [CrossRef]
- Gao, F.; Lu, Y. A Kalman-filter based time-domain analysis for structural damage diagnosis with noisy signals. J. Sound Vib. 2006, 297, 916–930. [Google Scholar] [CrossRef]
- Zhou, L.; Wu, S.Y.; Yang, J.N. Experimental study of an adaptive extended Kalman filter for structural damage identification. J. Infrastruct. Syst. 2008, 14, 42–51. [Google Scholar] [CrossRef][Green Version]
- Sarwar, M.Z.; Park, J.W. Bridge Displacement Estimation Using a Co-Located Acceleration and Strain. Sensors 2020, 20, 1109. [Google Scholar] [CrossRef]
- Liu, X.; Escamilla-Ambrosio, P.J.; Lieven, N.A.J. Extended Kalman filtering for the detection of damage in linear mechanical structures. J. Sound Vib. 2009, 325, 1023–1046. [Google Scholar] [CrossRef]
- Lai, Z.L.; Lei, Y.; Zhu, S.Y.; Xu, Y.L.; Krishnaswamy, S. Moving-window extended Kalman filter for structural damage detection with unknown process and measurement noises. Measurement 2016, 88, 428–440. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, J.Z.; Song, G.Q.; Chen, L. Structural damage identification by extended Kalman filter with l1-norm regularization scheme. Struct. Control. Health Monit. 2017, 24, e1999. [Google Scholar] [CrossRef]
- Wu, M.L.; Smyth, A.W. Application of the unscented Kalman filter for real-time nonlinear structural system identification. Struct. Control. Health Monit. 2007, 14, 971–990. [Google Scholar] [CrossRef]
- Cha, Y.J.; Chen, J.G.; Büyüköztürk, O. Output-only computer vision based damage detection using phase-based optical flow and unscented Kalman filters. Eng. Struct. 2017, 132, 300–313. [Google Scholar] [CrossRef]
- Sen, S.; Bhattacharya, B. Progressive damage identification using dual extended Kalman filter. Acta Mech. 2016, 227, 2099–2109. [Google Scholar] [CrossRef]
- Azam, S.E.; Chatzi, E.; Papadimitriou, C. A dual Kalman filter approach for state estimation via output-only acceleration measurements. Mech. Syst. Signal Process. 2015, 60, 866–886. [Google Scholar] [CrossRef]
- Huang, X.H.; Xu, Z.D. An in-time damage identification approach based on the Kalman filter and energy equilibrium theory. J. Zhejiang Univ. Sci. A 2015, 16, 105–116. [Google Scholar] [CrossRef]
- Jin, C.H.; Jang, S.A.; Sun, X.R.; Li, J.C.; Christenson, R. Damage detection of a highway bridge under severe temperature changes using extended Kalman filter trained neural network. J. Civ. Struct. Health Monit. 2016, 6, 545–560. [Google Scholar] [CrossRef]
- Bernal, D. Kalman filter damage detection in the presence of changing process and measurement noise. Mech. Syst. Signal Process. 2013, 39, 361–371. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.Y. Damage localization of beam bridges using quasi-static strain influence lines based on the BOTDA technique. Sensors 2018, 18, 4446. [Google Scholar] [CrossRef]

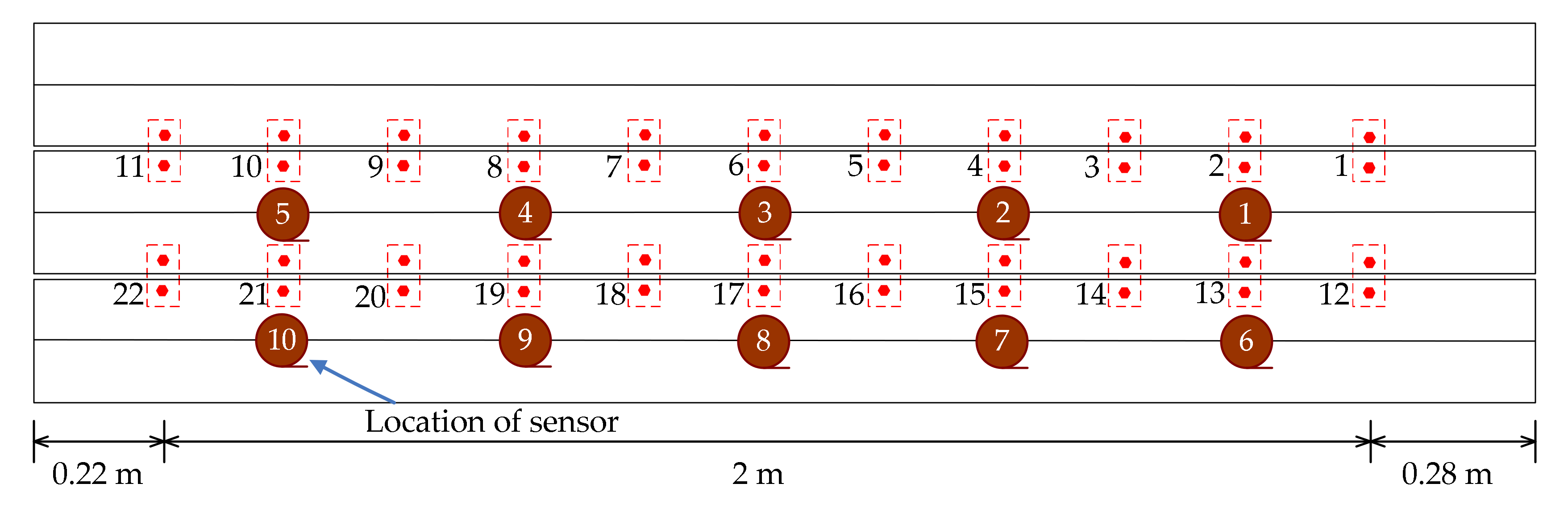

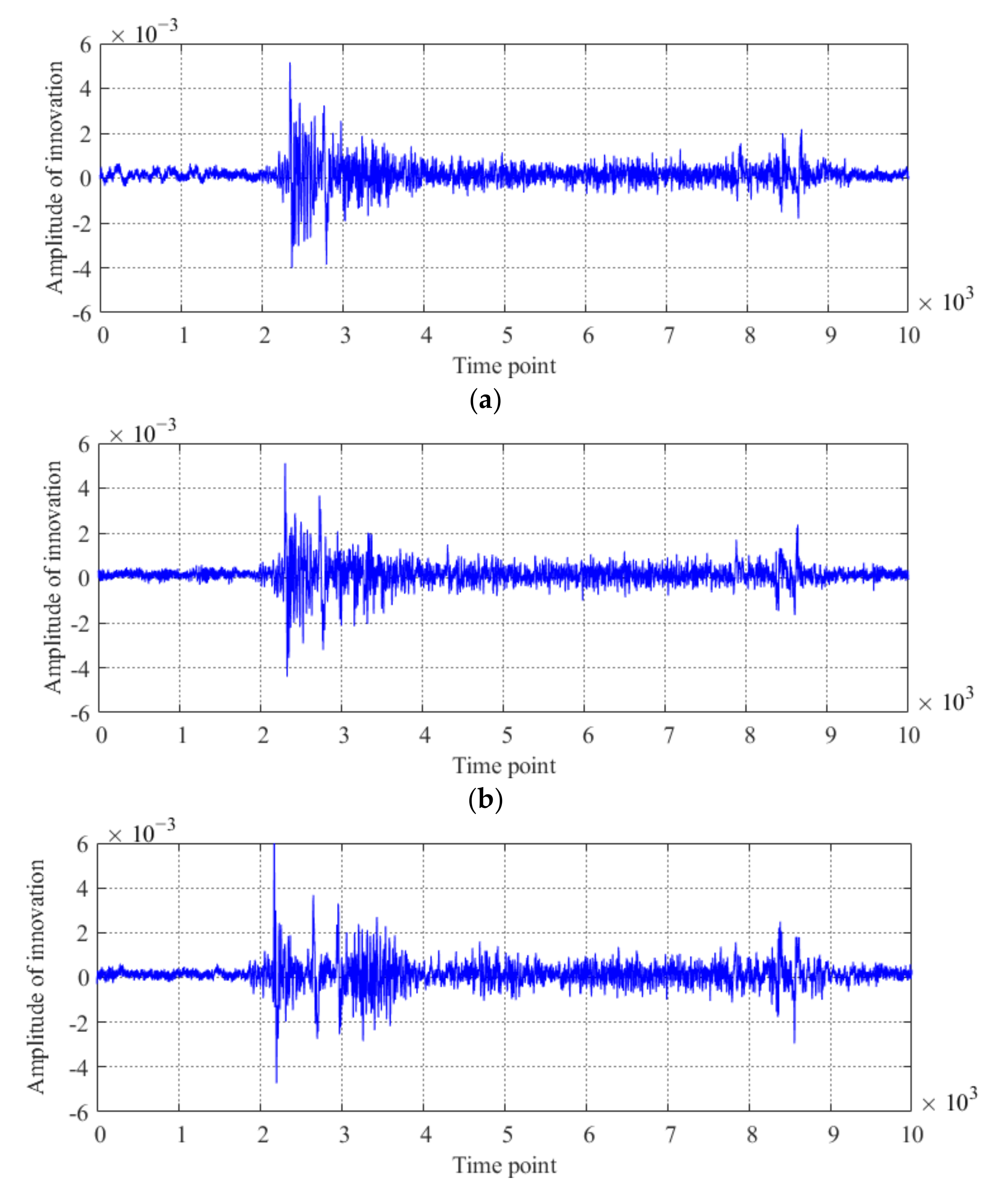
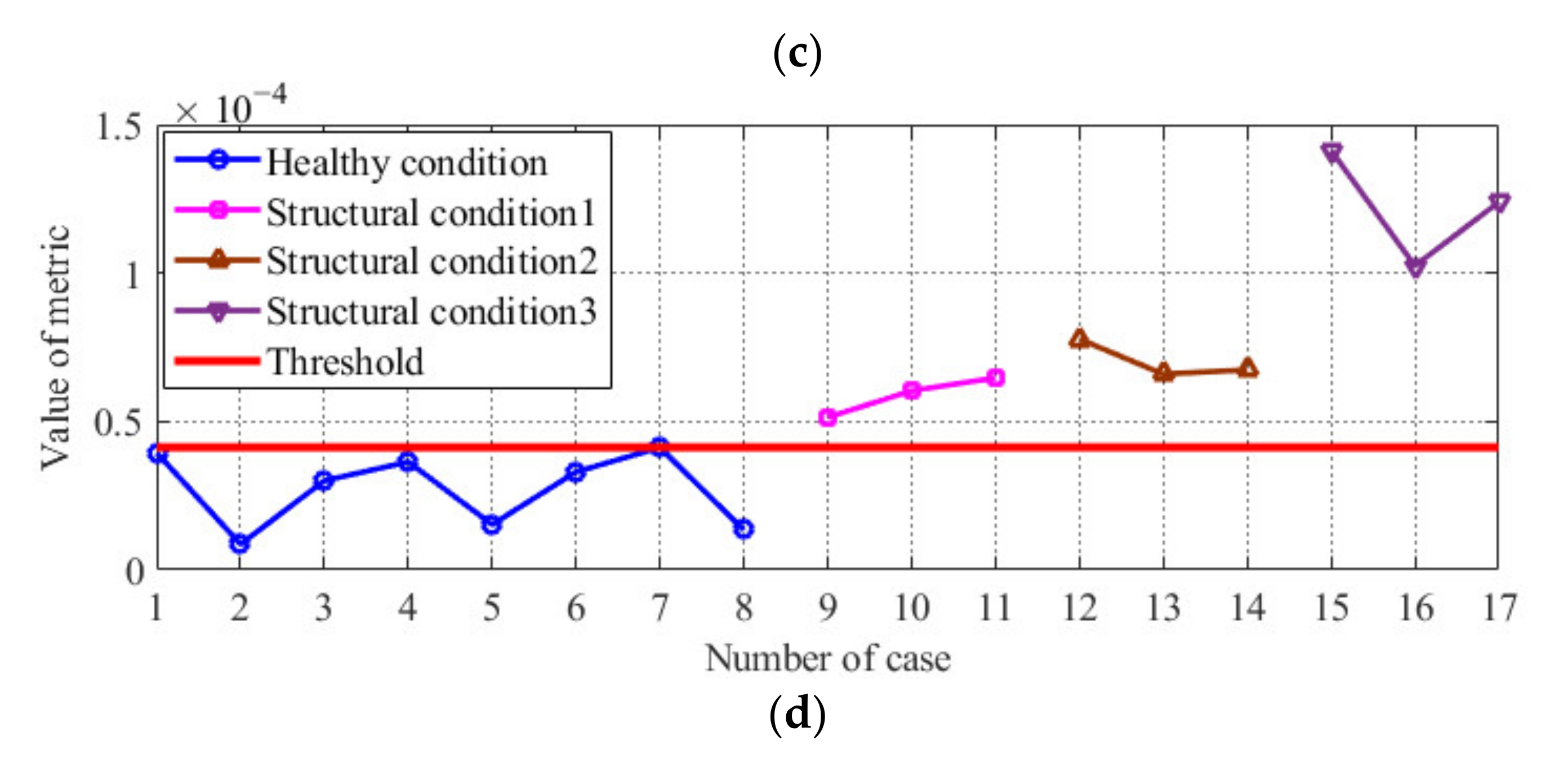
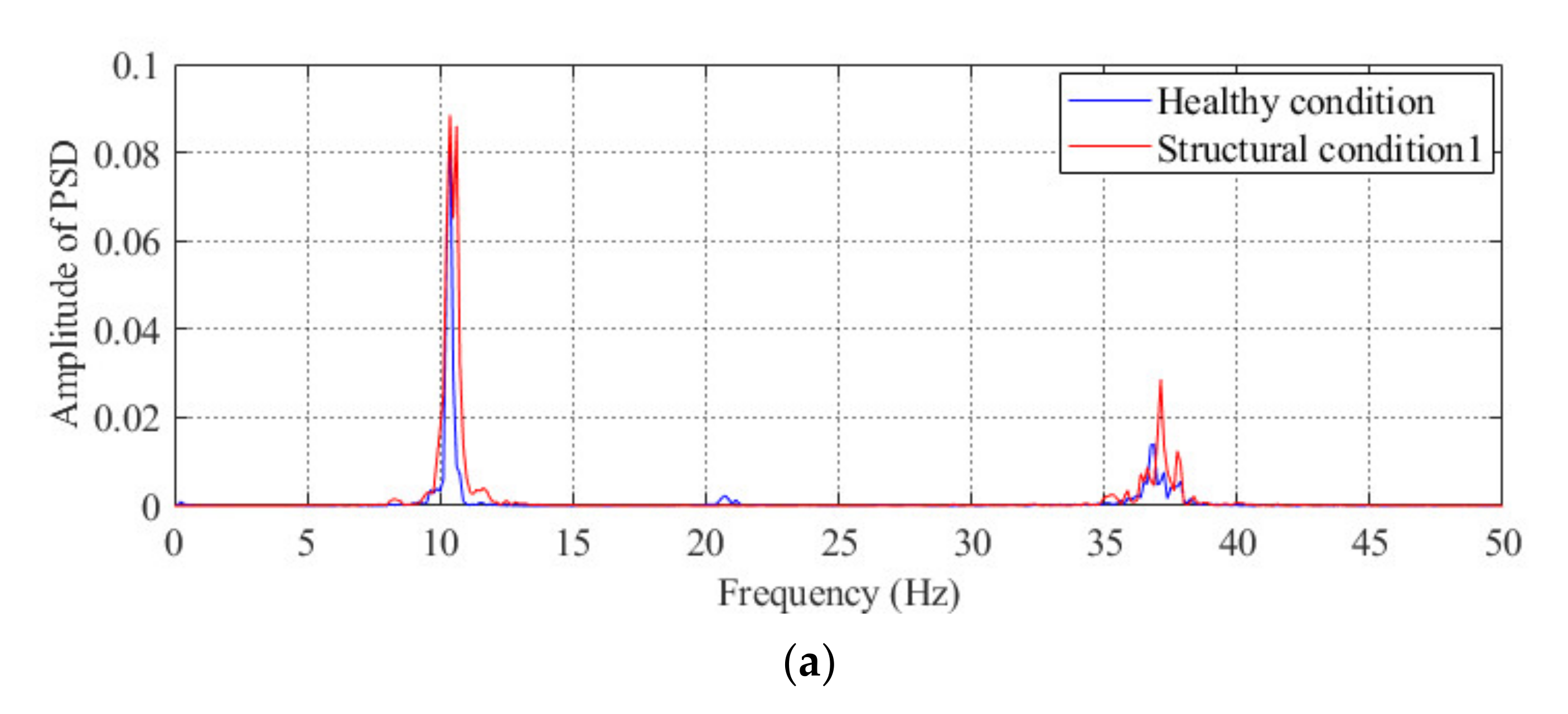

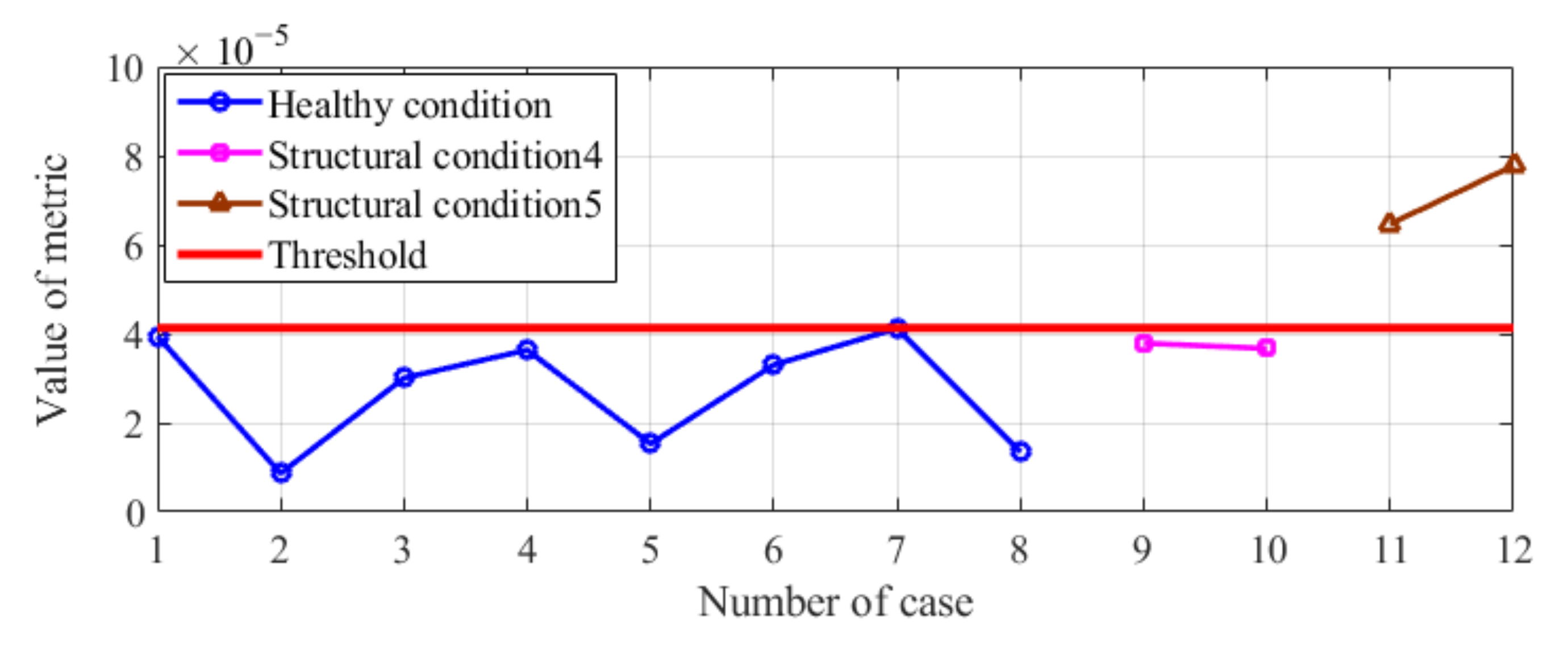

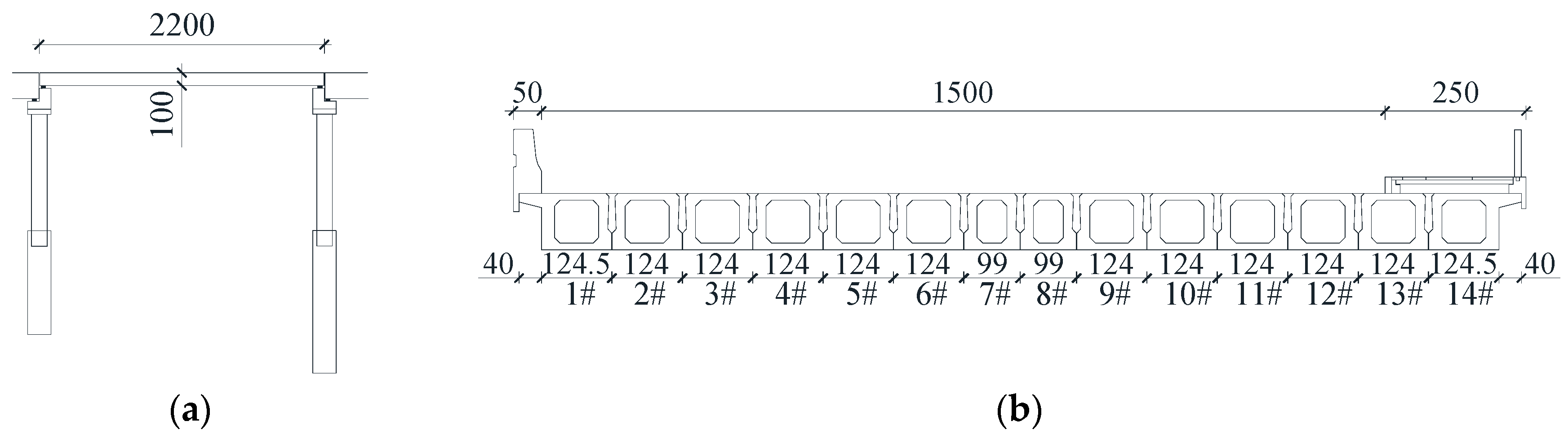


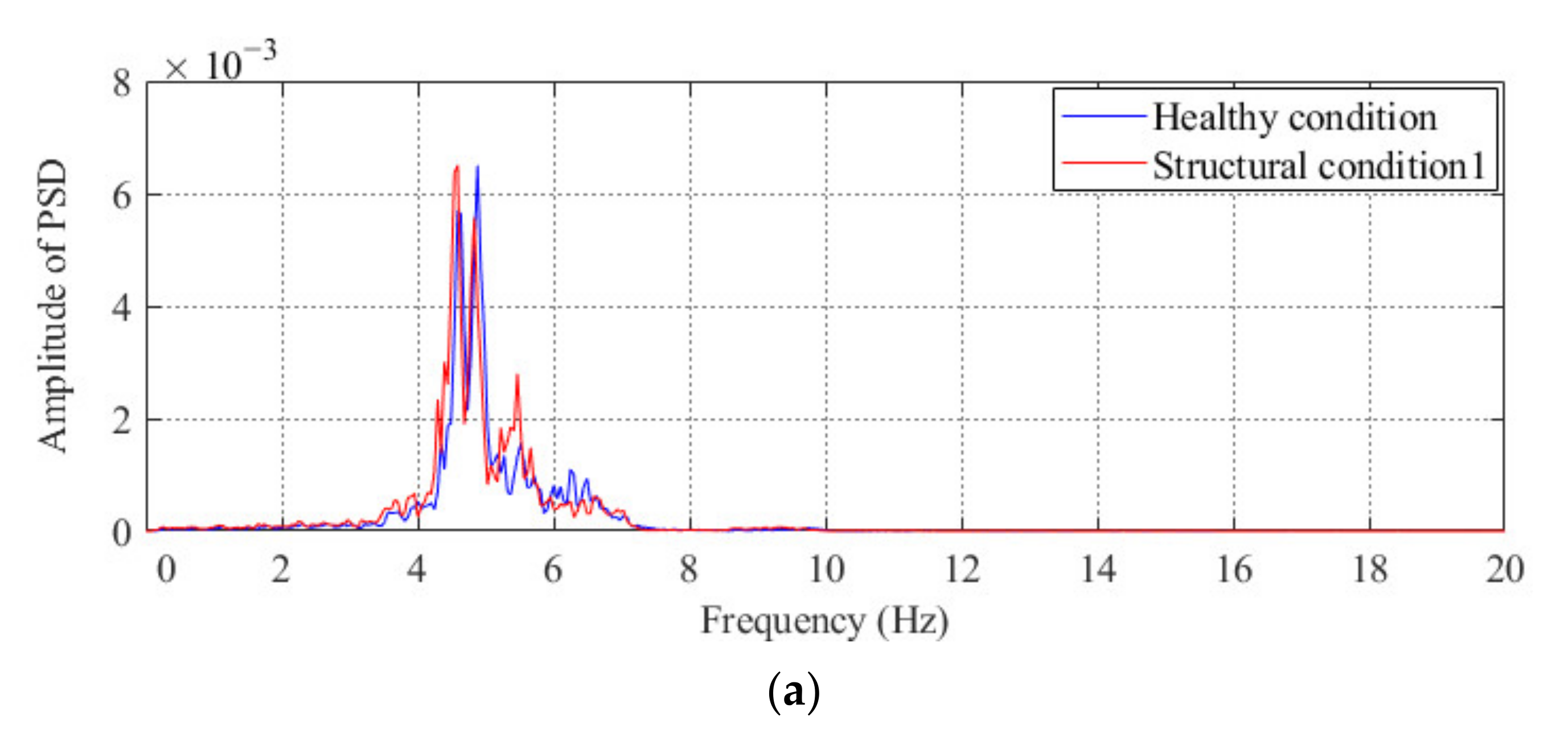
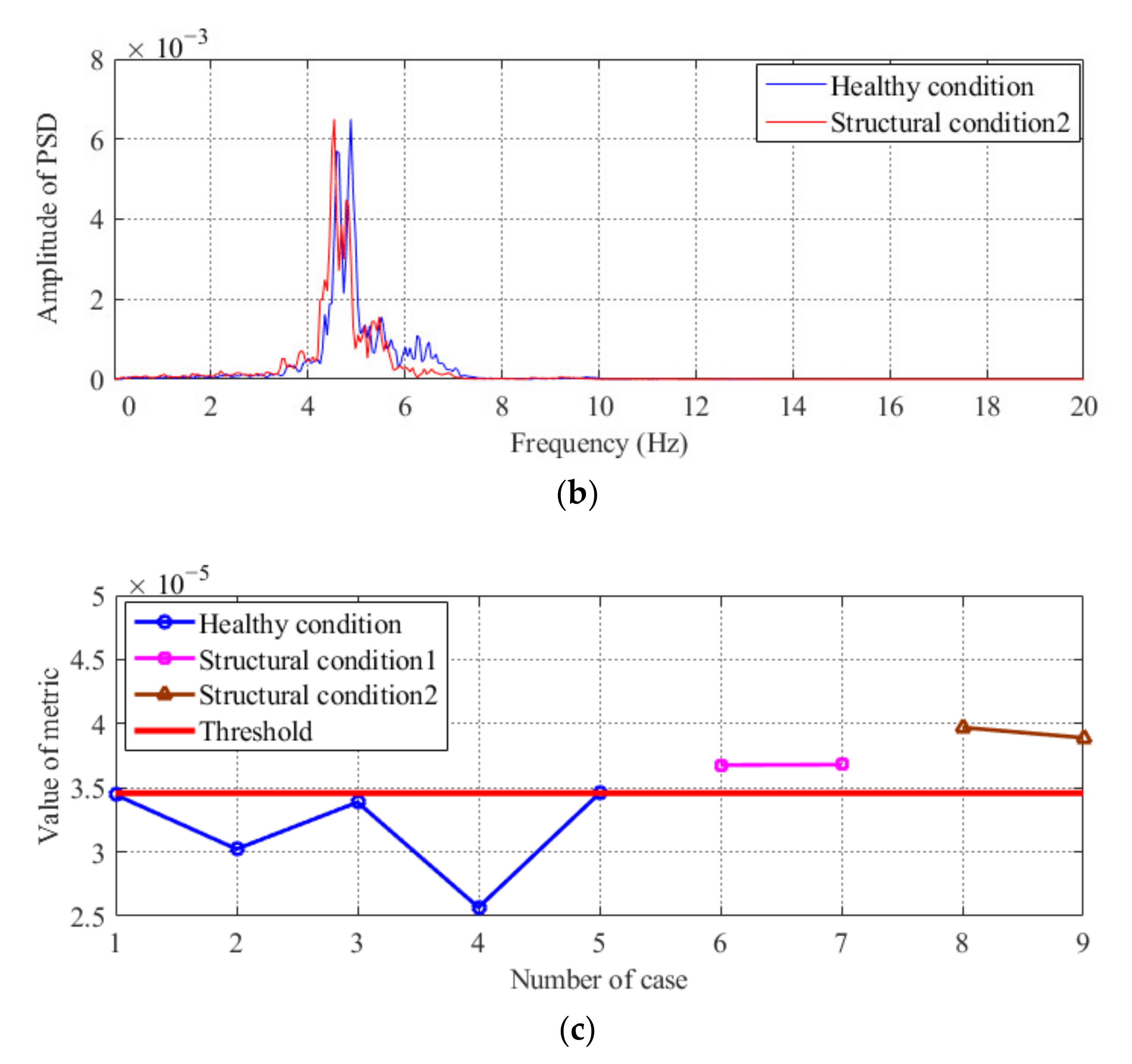
| Case Number | Description of Case |
|---|---|
| 1–9 | Healthy condition: bridge without any damage excited by a 120 kg moving load |
| 10–12 | Structural condition 1: damaged bridge (removing the #17 transverse connection) excited by a 120 kg moving load |
| 13–15 | Structural condition 2: damaged bridge (removing the #17 and #6 transverse connections) excited by a 120 kg moving load |
| 16–18 | Structural condition 3: damaged bridge (removing the #17, #6, #5, and #16 transverse connections) excited by a 120 kg moving load |
| 19–20 | Structural condition 4: bridge without any damage excited by a 130 kg moving load |
| 21–22 | Structural condition 5: bridge without any damage excited by a 140 kg moving load |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Q.; Wang, X.; Liu, Y. A Kalman Filter-Based Method for Diagnosing the Structural Condition of Medium- and Small-Span Beam Bridges during Brief Traffic Interruptions. Sensors 2020, 20, 4130. https://doi.org/10.3390/s20154130
Gao Q, Wang X, Liu Y. A Kalman Filter-Based Method for Diagnosing the Structural Condition of Medium- and Small-Span Beam Bridges during Brief Traffic Interruptions. Sensors. 2020; 20(15):4130. https://doi.org/10.3390/s20154130
Chicago/Turabian StyleGao, Qingfei, Xiang Wang, and Yang Liu. 2020. "A Kalman Filter-Based Method for Diagnosing the Structural Condition of Medium- and Small-Span Beam Bridges during Brief Traffic Interruptions" Sensors 20, no. 15: 4130. https://doi.org/10.3390/s20154130
APA StyleGao, Q., Wang, X., & Liu, Y. (2020). A Kalman Filter-Based Method for Diagnosing the Structural Condition of Medium- and Small-Span Beam Bridges during Brief Traffic Interruptions. Sensors, 20(15), 4130. https://doi.org/10.3390/s20154130







