Solar Blue Light Radiation Enhancement during Mid to Low Solar Elevation Periods under Cloud Affected Skies
Abstract
1. Introduction
2. Materials and Methods
2.1. Instrumentation
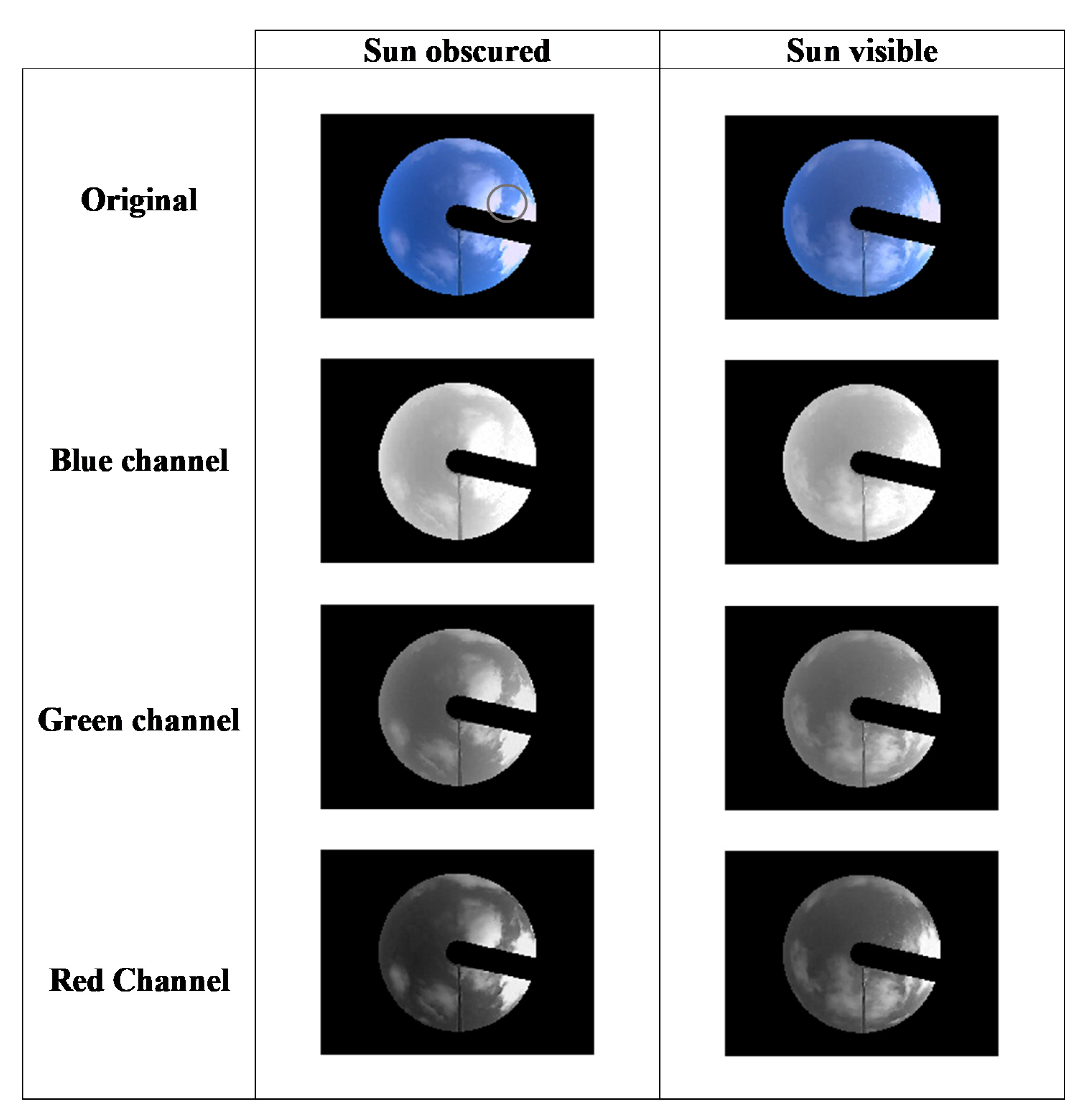
2.2. Data Analysis
2.3. CMF Calculations
3. Results
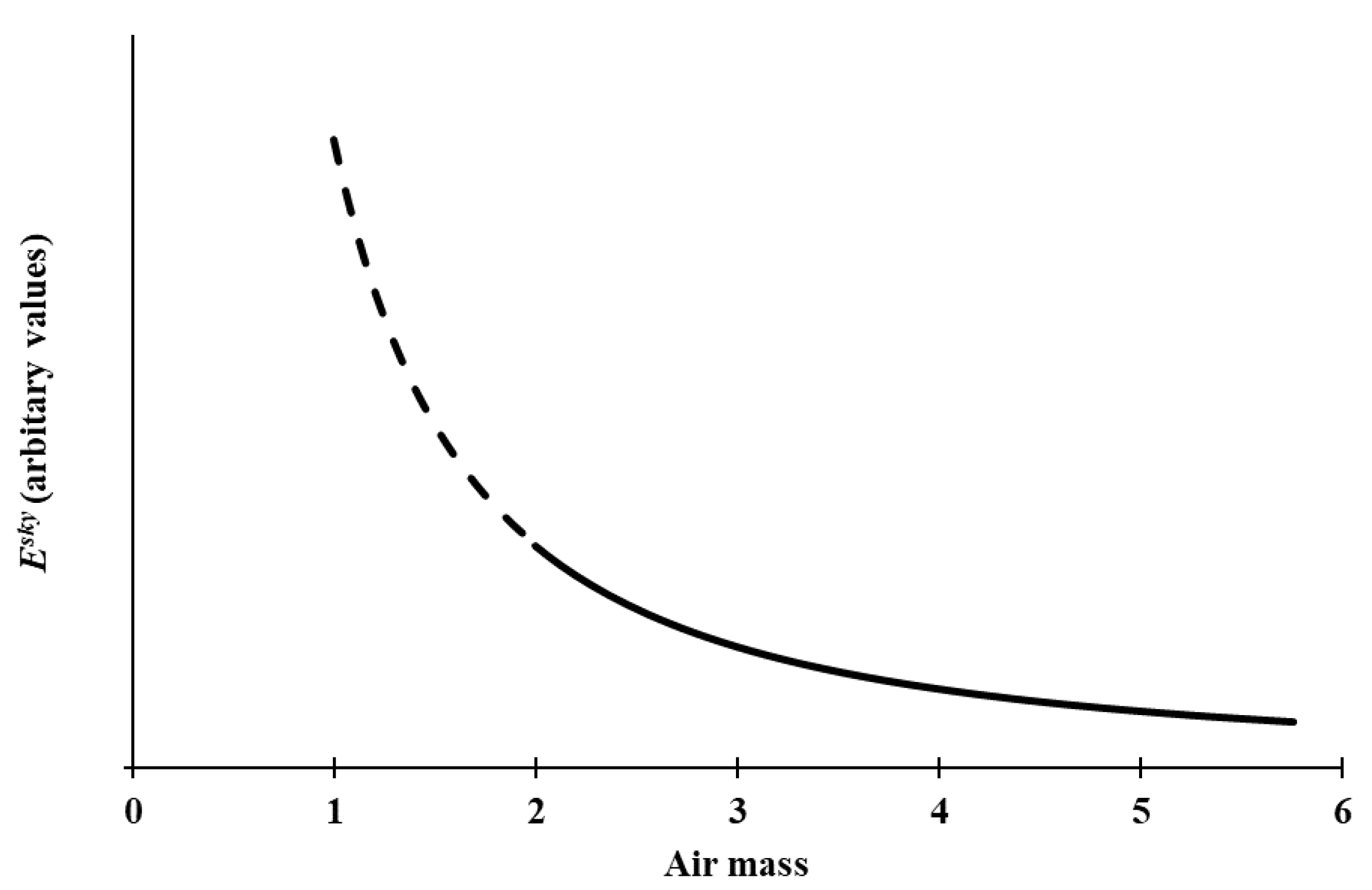
3.1. Cloud-Free Irradiance
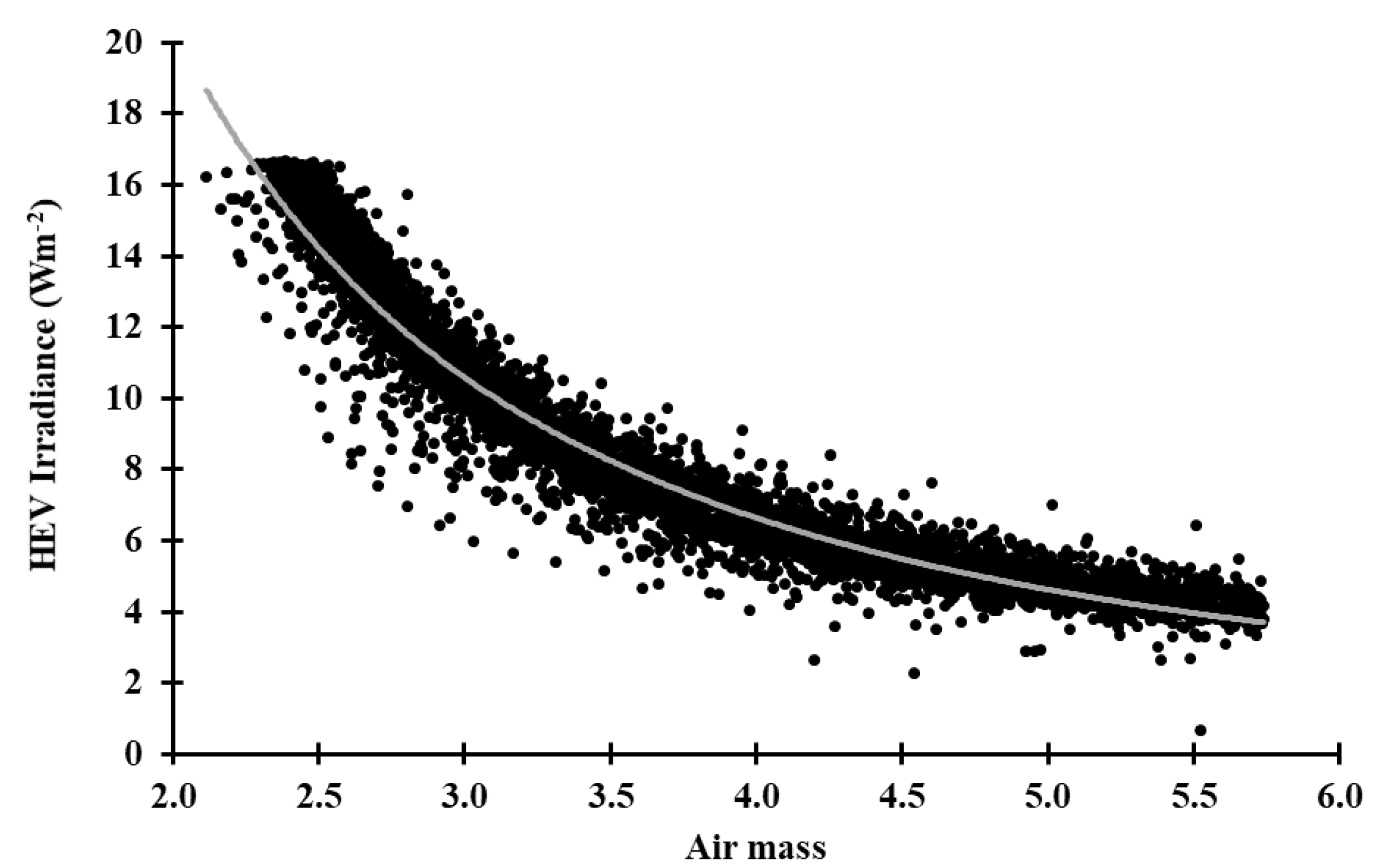
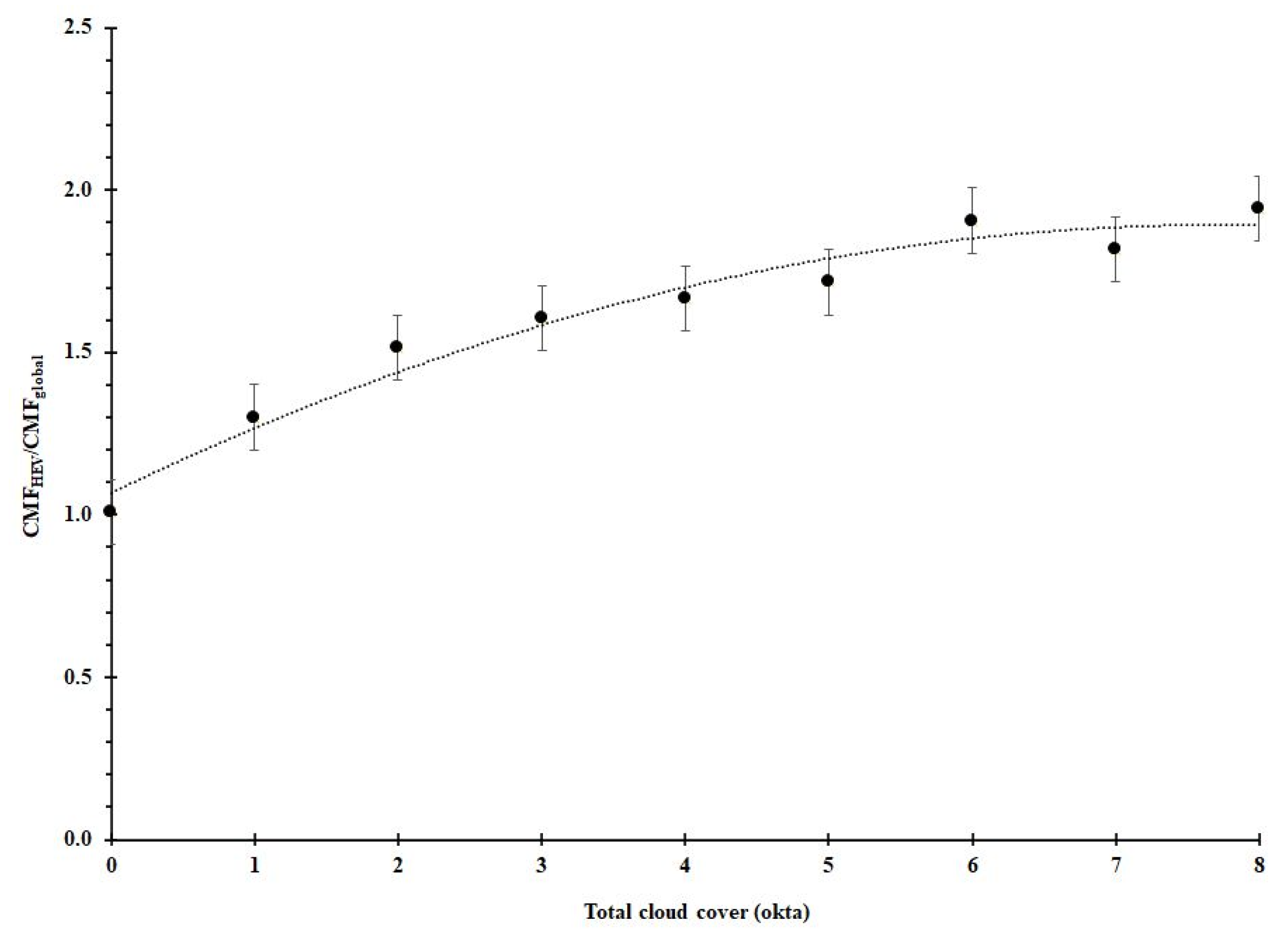
3.2. Modelling HEV Data
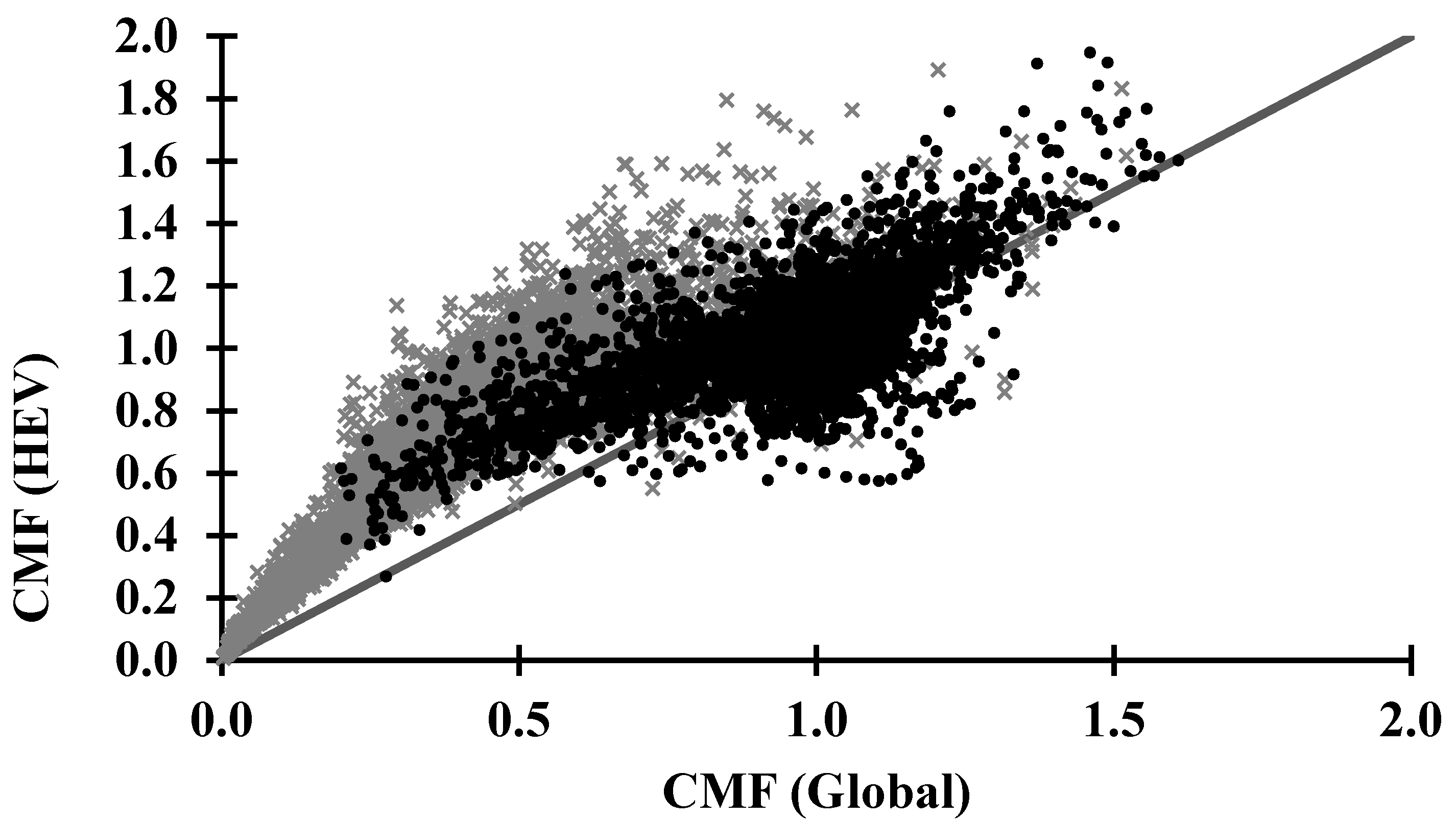
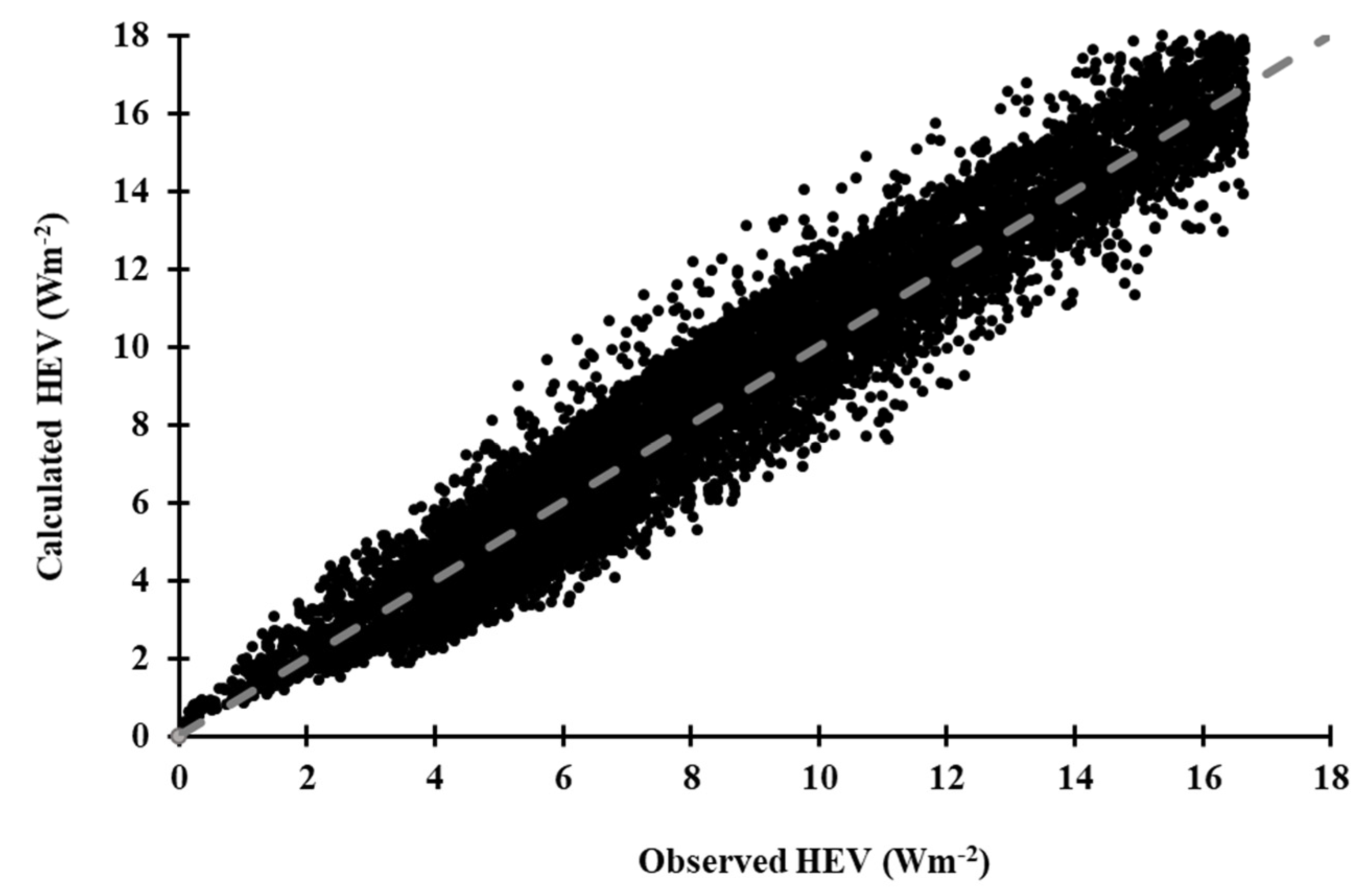
3.3. Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Melton, R. Ultraviolet and blue light. Rev. Optom. 2014, 151, S1. [Google Scholar]
- Pardhan, S.; Sapkota, R.J. Eye Complications of Exposure to Ultraviolet and Blue-Violet Light. 2016. Available online: https://www.pointsdevue.com/article/eye-complications-exposure-ultraviolet-and-blue-violet-light (accessed on 22 May 2020).
- International Commission on Non-Ionizing Radiation Protection (ICNIRP). Guidelines on incoherent visible and infrared radiation. Health Phys. 2013, 105, 74–96. [Google Scholar]
- Chen, D.C.; Huang, K.L.; Lee, S.L.; Wang, J.T. Blue light blocking lenses measuring device. Procedia Eng. 2016, 140, 17–29. [Google Scholar] [CrossRef]
- International Commission of Illumination (CIE). CIE Position Statement on the Blue Light Hazard. 2019. Available online: http://cie.co.at/publications/position-statement-blue-light-hazard-april-23-2019 (accessed on 22 May 2020).
- Kitchell, E. The effects of blue light on ocular health. J. Vis. Impair. Blind. 2000, 94, 399–403. [Google Scholar] [CrossRef]
- Sliney, D.H. Photoprotection of the eye—UV radiation and sunglasses. J. Photochem. Photobiol. B Biol. 2001, 64, 166–175. [Google Scholar] [CrossRef]
- Fletcher, A.E.; Bentham, G.C.; Agnew, M.; Young, I.S.; Augood, C.; Chakravarthy, U.; de Jong, P.T.V.M.; Rahu, M.; Seland, J.; Soubrane, G.; et al. Sunlight exposure, antioxidants, and age-related macular degeneration. Arch. Ophthalmol. 2008, 126, 1396–1403. [Google Scholar] [CrossRef] [PubMed]
- Bullough, J.D.; Bierman, A.; Rea, M.S. Evaluating the blue-light hazard from solid state lighting. Int. J. Occup. Saf. Ergon. 2019, 25, 311–320. [Google Scholar] [CrossRef]
- Pautler, E.L.; Morita, M.; Beezley, D. Hemoprotein(s) mediate blue light damage in the retinal pigment epithelium. Photochem. Photobiol. 1990, 51, 599–605. [Google Scholar] [CrossRef]
- Okuno, T. Hazards of Solar Blue Light. Available online: https://www.pointsdevue.com/article/hazards-solar-blue-light (accessed on 22 May 2020).
- Turnbull, D.J.; Parisi, A.V. Potential dosemeter for quantifying biologically effective blue light exposures. Rad. Prot. Dos. 2012, 149, 245–250. [Google Scholar] [CrossRef]
- Zuber, R.; Ribnitzky, M.; Tobar, M.; Lange, K.; Kutscher, D.; Schrempf, M.; Niedzwiedz, A.; Seckmeyer, G. Global spectral irradiance array spectroradiometer validation according to WMO. Meas. Sci. Technol. 2018, 29, 105801. [Google Scholar] [CrossRef]
- Sliney, D.H. Exposure geometry and spectral environment determine photobiological effects on the human eye. Photochem. Photobiol. 2005, 81, 483–489. [Google Scholar] [CrossRef] [PubMed]
- Algvere, P.V.; Marshall, J.; Seregard, S. Age-related maculopathy and the impact of blue light hazard. Acta Ophthamol. Scand. 2006, 84, 4–15. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Sregard, S.; Algvere, P.V. Photochemical damage of the retina. Surv. Ophthal. 2006, 51, 461–481. [Google Scholar] [CrossRef] [PubMed]
- O’Hagan, J.B.; Khazova, M.; Price, L.L.A. Low-energy light bulbs, computers, tablets, and the blue light hazard. Eye 2016, 30, 230–233. [Google Scholar] [CrossRef] [PubMed]
- Chorley, A.C.; Evans, B.J.W.; Benwell, M.J. Civilian pilot exposure to ultraviolet and blue light, and pilot use of sunglasses. Aviat. Space Environ. Med. 2011, 82, 895–900. [Google Scholar] [CrossRef] [PubMed]
- Chorley, A.C.; Higlett, M.; Baczynska, K.; Hunter, R.; Khazova, M. Measurements of pilots’ occupational solar UV exposure. Photochem. Photobiol. 2014, 90, 935–940. [Google Scholar] [CrossRef]
- Legierski, M.; Michaek, P. Assessment of photobiological safety of passing beam and driving beam headlamps with different light sources. IOP Conf. Ser. Mater. Sci. Eng. 2018, 421, 032016. [Google Scholar] [CrossRef]
- Dye, D.G. Spectral composition and quanta-to-energy ratio of diffuse photosynthetically active radiation under diverse cloud conditions. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Wallace, J.M.; Hobbs, P.V. Atmospheric Science: An Introductory Survey, 2nd ed.; Elsevier Academic Press: Amsterdam, Netherlands, 2006. [Google Scholar]
- Juzeniene, A.; Brekke, P.; Dahlback, A.; Andersson-Engels, S.; Reichrath, J.; Moan, K.; Holick, M.P.; Grant, W.B.; Moan, J. Solar radiation and human health. Rep. Prog. Phys. 2011, 74, 066701. [Google Scholar] [CrossRef]
- Iishi, T.; Otani, K.; Takashima, T.; Xue, Y. Solar spectral influence on the performance of photovoltaic (PV) modules under fine weather and cloudy weather conditions. Prog. Photovolt.: Res. Appl. 2013, 21, 481–489. [Google Scholar] [CrossRef]
- Pierce, R.M.; Ramaprasad, J.; Eisenberg, E.C. Optical attenuation of fog and clouds. Proc. SPIE Opt. Wirel. Commun. IV 2001, 4350, 58–71. [Google Scholar]
- Hietanen, M. Ocular exposure to solar ultraviolet and visible radiation at high latitudes. Scand. J. Work Environ. Health 1991, 17, 398–403. [Google Scholar] [CrossRef] [PubMed]
- Bortoli, D.; Silva, A.M.; Costa, M.J.; Domingues, A.F.; Giovanelli, G. Measurements of stratospheric ozone and nitrogen dioxide at Evora, Portugal. Int. J. Remote Sens. 2009, 30, 4209–4266. [Google Scholar] [CrossRef]
- Horvath, H. Atmospheric light absorption—A review. Atmos. Environ. Part A Gen. Top. 1993, 27, 293–317. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A. Aerosol Optics: Light Absorption and Scattering by Particles in the Atmosphere; Praxis Publishing: Chichester, UK, 2008. [Google Scholar]
- Igoe, D.P. Analysing Urban Aerosols using a Digital Camera. MSc Thesis, University of Southern Queensland, Toowoomba, Australia, 2014. [Google Scholar]
- Diémoz, H.; Eleftheraton, K.; Kazadzis, S.; Amiridis, V.; Zerefos, C.S. Retrieved of aerosol optical depth in the visible range with a Brewer spectrophotometer in Athens. Atmos. Meas. Tech. 2016, 9, 1871–1888. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, Q.; Xu, J.; Wang, T. Analysis of optical properties of different types of aerosols. In Proceedings of the International Symposium on Optoelectronic Technology and Application, Beijing, China, 12 December 2018. [Google Scholar]
- Sun, D.; El-Basyouny, K.; Kwon, T.J. Sun glare: Network characterisation and safety effects. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 79–92. [Google Scholar] [CrossRef]
- Yordanov, G.H.; Saetre, T.O.; Midtgård, O.M. Extreme overirradiance events in Norway: 1.6 suns measured close to 60°N. Sol. Energy 2015, 115, 68–73. [Google Scholar] [CrossRef]
- Chase, O.A.; Teles, M.B.; de Jesus dos Santos Rodrigues, M.; De Almeida, J.F.S.; Macêdo, W.N.; Da Costa Junior, C.T. A low cost stand-alone sensory platform for monitoring extreme solar overirradiance events. Sensors 2018, 18, 2685. [Google Scholar] [CrossRef]
- do Nascimento, L.R.; de Souza Viana, T.; Camos, R.A.; Rüther, R. Extreme dollar overirradiance events: Occurrence and impacts on utility-scale photovoltaic power plants in Brazil. Sol. Energy 2019, 186, 370–381. [Google Scholar] [CrossRef]
- Zehner, M.; Hartmann, M.; Weizenbeck, J.; Gratzl, T.; Weigl, T.; Mayer, B.; Wirth, G.; Krawczynski, M.; Betts, T.; Gottschalg, R.; et al. Systematic analysis of meteorological irradiation effects. In Proceedings of the 25th Photovoltaic Solar Energy Conference, Valencia, Spain, 6–10 September 2010. [Google Scholar]
- Bodecker, G.E.; McKenzie, R.L. An algorithm for inferring surface UV irradiance including cloud effects. J. Appl. Climatol. 1996, 35, 1860–1877. [Google Scholar] [CrossRef]
- Foyo-Moreno, I.; Alados, T.; Olmo, F.J.; Vida, J.; Alados-Arboledas, L. On the use of cloud modification factor for solar UV (290-385 nm) spectral range. Theor. Appl. Climatol. 2001, 68, 41–50. [Google Scholar] [CrossRef]
- Schwander, H.; Koepke, P.; Kaifel, A.; Seckmeyer, G. Modification of spectral UV irradiance by clouds. J. Geophys. Res.: Atmos. 2002, 107, AAC-7. [Google Scholar] [CrossRef]
- Foyo-Moreno, I.; Alados, T.; Olmo, F.J.; Alados-Arboledas, L. The influence of cloudiness on UV global irradiance (295–385 nm). Agric. For. Meteorol. 2003, 120, 101–111. [Google Scholar] [CrossRef]
- Badosa, J.; Calbó, J.; McKenzie, R.; Liley, B.; González, J.A.; Forgan, B.; Long, C.N. Two methods for retrieving UV index for all cloud conditions from sky imager products or total SW radiation measurements. Photochem. Photobiol. 2014, 90, 941–951. [Google Scholar] [CrossRef] [PubMed]
- Feister, U.; Cabrol, N.; Häder, D. UV irradiance enhancements by scattering of solar radiation from clouds. Atmosphere 2015, 6, 1211–1228. [Google Scholar] [CrossRef]
- Park, S.S.; Kim, M.; Lee, H.; Lee, H.; Kim, S.M.; Lee, Y.G. Estimating cloud and aerosol UV modification factors based on spectral measurement from the Brewer Spectrophotometer. Atmosphere 2017, 8, 109. [Google Scholar] [CrossRef]
- Parisi, A.V.; Sabburg, J.; Turner, J.; Dunn, P.K. Cloud observation for the statistical evaluation of the UV index at Toowoomba, Australia. Int. J. Biometeor. 2008, 52, 159–166. [Google Scholar] [CrossRef]
- Villán, D.M.; Castrillo, A.M.; Santos, J.B. Empirical models of UV total radiation and cloud effect study. Int. J. Climatol. 2010, 30, 1407–1415. [Google Scholar]
- Staiger, H.; de Outer, P.N.; Bais, A.F.; Feister, U.; Johnsen, B.; Vuilleumier, L. Hourly resolved cloud modification factors in the ultraviolet. Atmos. Chem. Phys. 2008, 8, 2493–2508. [Google Scholar] [CrossRef]
- Bais, A.F.; Lucas, R.M.; Bornman, J.F.; Williamson, C.E.; Sulzberger, B.; Austin, A.T.; Wilson, S.R.; Andrady, A.L.; Bernhard, G.; McKenzie, R.L.; et al. Environmental effects of ozone depletion, UV radiation and interaction with climate change: UNEP Environmental Effects Assessment Panel, update 2017. Photochem. Photobiol. Sci. 2018, 17, 127–179. [Google Scholar] [CrossRef]
- Pfister, G.; McKenzie, R.L.; Liley, J.B.; Thomas, A.; Forgan, B.W.; Long, C.N. Cloud coverage based on all-sky imaging and its impact on surface solar irradiance. J. App. Meteorol. 2003, 42, 1421–1434. [Google Scholar] [CrossRef]
- Parisi, A.V.; Turnbull, D.J.; Turner, J. Calculation of cloud modification factors for the horizontal plane eye damaging ultraviolet radiation. Atmos. Res. 2007, 86, 278–285. [Google Scholar] [CrossRef]
- Turnbull, D.J.; Parisi, A.V.; Schouten, P.W. Empirical evaluation of global vitamin D effective ultraviolet irradiance under cloudy conditions for a subtropical southern hemisphere site. Rad. Res. 2010, 173, 703–708. [Google Scholar] [CrossRef] [PubMed]
- Solar Light. Model PMA1121 Analog Blue Light Safety Sensor. Available online: https://solarlight.com/product/blue-light-safety-sensor-pma1121/ (accessed on 3 July 2019).
- Parisi, A.V.; Sabburg, J.; Kimlin, M.G. Scattered and Filtered Solar UV Measurements; Springer Science and Business Media: Dordrecht, The Netherlands, 2004. [Google Scholar]
- CIMO. Guide to Meteorological Instruments and Methods of Observation; WMO: Geneva, Switzerland, 2014. [Google Scholar]
- Igoe, D.P.; Parisi, A.V.; Downs, N.J. Cloud segmentation property extraction from total sky image repositories using Python. Inst. Sci. Tech. 2019, 47, 522–534. [Google Scholar] [CrossRef]
- Wang, L.; Gong, W.; Li, J.; Ma, Y.; Hu, B. Empirical studies of cloud effects on ultraviolet radiation in Central China. Int. J. Climatol. 2014, 34, 2218–2228. [Google Scholar] [CrossRef]
- Long, C.N.; Ackerman, T.P. Identification of clear skies from broadband pyranometer measurements and calculation of downwelling shortwave cloud effects. J. Geophys. Res. 2000, 105, 15609–15626. [Google Scholar] [CrossRef]
- Kasten, F.; Young, A.T. Revised optical air mass tables and approximation formula. Appl. Opt. 1989, 28, 4735–4738. [Google Scholar] [CrossRef] [PubMed]
| Okta | WMO Cloud Fraction | This Research Cloud Fraction |
|---|---|---|
| 0 | 0 | <0.02 |
| 1 | Up to 1/10, but not 0 | 0.02 to < 0.15 |
| 2 | 2/10–3/10 | 0.15 to < 0.35 |
| 3 | 4/10 | 0.35 to < 0.45 |
| 4 | 5/10 | 0.45 to < 0.55 |
| 5 | 6/10 | 0.55 to < 0.65 |
| 6 | 7/10–8/10 | 0.65 to < 0.85 |
| 7 | Greater than 9/10 but not 10/10 | 0.85 to 0.98 |
| 8 | 10/10 | >0.98 |
| HEV Irradiance Model | UV Model 1 Villán et al. [46] | UV Model 2 Wang et al. [56] | |
|---|---|---|---|
| MBE | −1.62% | −2.71% to 1.86% | −0.91% to 1.52% |
| MABE | 10.3% | 6.77% to 7.82% | 8.76% to 9.18% |
| RMSE | 14.6% | 9.83% to 10.46% | 11.13% to 12.32% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parisi, A.V.; Igoe, D.P.; Amar, A.; Downs, N.J. Solar Blue Light Radiation Enhancement during Mid to Low Solar Elevation Periods under Cloud Affected Skies. Sensors 2020, 20, 4105. https://doi.org/10.3390/s20154105
Parisi AV, Igoe DP, Amar A, Downs NJ. Solar Blue Light Radiation Enhancement during Mid to Low Solar Elevation Periods under Cloud Affected Skies. Sensors. 2020; 20(15):4105. https://doi.org/10.3390/s20154105
Chicago/Turabian StyleParisi, Alfio V., Damien P. Igoe, Abdurazaq Amar, and Nathan J. Downs. 2020. "Solar Blue Light Radiation Enhancement during Mid to Low Solar Elevation Periods under Cloud Affected Skies" Sensors 20, no. 15: 4105. https://doi.org/10.3390/s20154105
APA StyleParisi, A. V., Igoe, D. P., Amar, A., & Downs, N. J. (2020). Solar Blue Light Radiation Enhancement during Mid to Low Solar Elevation Periods under Cloud Affected Skies. Sensors, 20(15), 4105. https://doi.org/10.3390/s20154105





