1. Introduction
Wearable inertial measurement units (IMUs) have become a key technology for a range of applications, from performance assessment and optimization in sports [
1], to objective measurements and progress monitoring in health care [
2], as well as real-time motion tracking for feedback-controlled robotic or neuroprosthetic systems [
3]. In all these application domains, IMUs are used to track or capture the motion of mechatronic or biological joint systems such as robotic or human limbs. In this work we consider such systems where the joint is a hinge joint with one degree of freedom. Examples of hinge joints include the knee and finger joints, which are essential in applications targeting lower limb [
4] and hand [
5] kinematics.
In contrast to stationary optical motion tracking systems, miniature IMU networks can be used in ambulatory settings and facilitate motion tracking outside lab environments. While this is an important step towards ubiquitous sensing, one major limitation of the technology is that the IMUs’ local coordinate systems must be aligned with the anatomical axes of the joints and body segments to which they are attached. This sensor-to-segment calibration is a crucial step that establishes the connection between the motion of the IMUs and the motion of the joint system to which they are attached.
Several different approaches have been proposed for sensor-to-segment calibration of inertial sensor networks, from trying to align the sensor axes with body axes by precise attachment to predefined calibration poses and motions; see, e.g., [
6,
7,
8,
9]. However, in all of these cases, the calibration crucially depends on the knowledge and skills of the person who attaches the sensors or the person who performs the calibration procedure. This might be acceptable in supervised settings with trained and able-bodied users, but it represents a major limitation of IMU-based motion tracking and capture in clinical applications and in motion assessment of elderly and children. Finding solutions for these application domains and enabling ubiquitous sensing in daily life requires the development of less restrictive methods for sensor-to-segment calibration.
Ideally, wearable IMU networks should be plug-and-play, and the sensor-to-segment calibration should be performed by the network autonomously, which means without additional effort or requirements on the user’s knowledge or on the performed motion. An important step towards this goal was the development of methods that exploit the kinematic constraints of the joints to identify sensor-to-segment calibration parameters from almost arbitrary motions [
10,
11]. For joints with one degree of freedom (DOF), the feasibility of this approach has been demonstrated [
12,
13,
14,
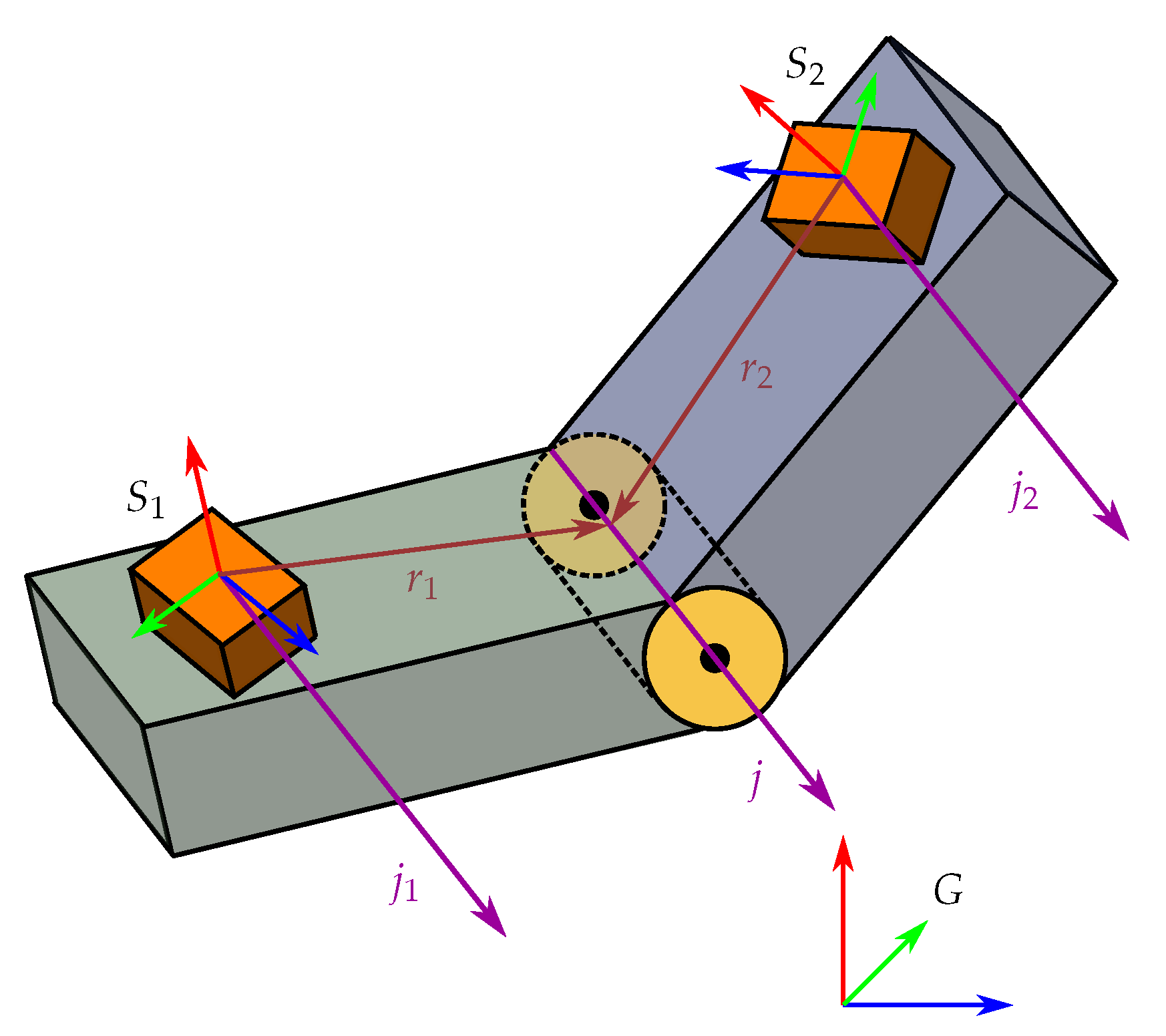
15]. Methods have been proposed that require the user to perform a sufficiently informative but otherwise arbitrary motion during an initial calibration time window and determine the functional joint axis in intrinsic coordinates of both IMUs, cf.
Figure 1. It was recently shown that almost every motion, including purely sequential motions and simultaneous planar motions, is informative enough to render the joint axis identifiable unless the joint remains stiff throughout the motion [
16].
Several methods targeting different types of joints or sensor-to-segment calibration parameters have been developed. In [
17], a method for identifying the joint axes of a joint with two DOF was proposed. Methods for identifying the position of the joint center relative to sensors attached to adjacent segments have been proposed in [
12,
18,
19]. A method enabling automatic pairing of sensors to lower limb segments have been proposed in [
20].
The published kinematic-constraint-based methods constitute an important step forward but still impose undesirable and unnecessary limitations. If the user does not move during the initial calibration time window or if the motion is not sufficiently informative, the calibration will be wrong and all subsequently derived motion parameters will be subject to unpredictable errors. For a truly plug-and-play system, it is therefore crucial that the IMU network is able to
Recognize how informative motions are and whether they render the joint axis identifiable;
Wait for sufficiently informative data to be generated and combine useful data even if it is spread and intermitted by useless data;
Determine how accurate the current estimate of the joint axis is and provide only sufficiently reliable estimates.
An IMU network with such properties can be used without the aforementioned limitations. Once it is installed, it will autonomously gather all available useful information and provide reliable calibration parameters as soon as possible, which immediately enable calculation of accurate motion parameters from the incoming raw data as well as from already recorded data. To explain the practical value of the proposed concept of plug-and-play calibration, we briefly compare this concept to the aforementioned existing calibration concepts that use predefined motions [
6,
7,
8,
9] or arbitrary motions [
10,
11,
12,
13,
14,
15]:
Predefined-Motions: The calibration is based on the assumption that the user performs a sequence of predefined motions and poses with sufficient precision within a predefined initial time interval. The approach fails and provides inaccurate calibration without warning if
- (a)
The user performs the sequence of predefined motions and poses without sufficient precision;
- (b)
The user performs the sequence with sufficient precision but not within the predefined initial time interval;
- (c)
The user performs sufficiently informative but otherwise arbitrary motions;
- (d)
The user performs no sufficiently informative motion at all, e.g., he/she moves with a stiff joint.
Arbitrary-Motions: The calibration is based on the assumption that the user performs sufficiently informative but otherwise arbitrary motions within a predefined initial time interval. The motion does not need to be precise, and it has been shown that sufficient excitation is provided by almost every motion for which the joint does not remain stiff [
16]. However, the approach fails and provides inaccurate calibration without warning if
- (a)
The user performs a sequence of predefined motions but not within the predefined initial time interval;
- (b)
The user performs sufficiently informative arbitrary motions but not within the predefined initial time interval;
- (c)
The user performs no sufficiently informative motion at all, e.g., he/she moves with a stiff joint.
Plug-and-Play: The proposed sensor-to-segment calibration approach. It works well for all mentioned cases and exceptions in the sense that it always provides accurate calibration parameters as soon as the user’s motions are sufficiently informative, and it clearly indicates at all times whether the desired calibration accuracy has yet been reached.
It is important to note that the cases without warning are very dangerous, because inaccurate information is provided and claimed as accurate. In many applications, this leads to unacceptable risks. This and the other listed differences between the two existing approaches and the proposed new method have large implications for the way wearable IMU networks can be used in offline and online applications.
Offline Applications include motion capture for ergonomic workplace assessment [
21], for monitoring of movement disorders [
2] and for sport performance analysis [
1]. In state-of-the-art solutions, the user performs an initial calibration procedure before (or after) recording data from the motions to be analyzed. The user can only hope that the calibration was accurate enough. If the calibration was inaccurate, then all recorded data is corrupted and might lead to false interpretation and conclusions. In contrast, when the calibration is plug-and-play, the user starts recording data from motions that should be analyzed immediately after attaching the sensors. Calibration automatically takes place as soon as sufficiently informative data has been gathered. The system indicates that calibration has been successful, and the user can be sure that all obtained measurements are valid and accurate. The identified calibration parameters are used to evaluate the data that was recorded before and after the moment at which accurate calibration was achieved.
Online Applications include real-time motion tracking for wearable biofeedback systems [
22] as well as robotic and neuroprosthetic motion support systems [
23]. In state-of-the-art solutions, the user first performs an initial calibration procedure before the sensor system is connected to an assistive device that uses the measurements to provide e.g., biofeedback or motion support. The user can only hope that the calibration was accurate enough. If the calibration was inaccurate, then the provided biofeedback or motion support might be wrong and dangerous. In contrast, when the calibration is plug-and-play, the user instead attaches the sensors and starts moving. As soon as the desired calibration accuracy has been achieved, the sensor system automatically provides measurements to the assistive device. The user can be sure that all provided biofeedback and motion support is based on valid and accurate measurements.
In the present contribution we propose the first joint axis identification method for one-dimensional joints that is plug-and-play in the aforementioned sense. The main contributions of the present work are the following:
We leverage recent results on joint axis identifiability [
16] to develop a sample selection method that overcomes the limitation of a dedicated initial calibration time window.
To assure that the motion needs to fulfill only the minimum required conditions, we combine accelerometer-based and gyroscope-based joint constraints and weight them according to the information contained in both signals.
We propose an uncertainty quantification method that assures validity of the estimated joint axis parameters and thereby eradicates the risk of false calibration.
We provide an experimental validation in a mechanical joint performing a large range of different motions with different identifiability properties.
In the proposed system, successful calibration no longer depends on performing certain motions in a predefined manner or time window but only on fulfilling the minimum required conditions at some point. Moreover, the system knows when these conditions are fulfilled and provides only reliable calibration parameters.
2. Inertial Measurement Models
Inertial sensors collectively refers to accelerometers and gyroscopes, which are sensors used to measure linear acceleration and angular velocity, respectively. When the sensors have three sensitive axes which are orthogonal to each other, the inertial sensors can measure these quantities in three dimensions. Such sensors are referred to as triaxial. An IMU is a single sensor that contains one triaxial accelerometer and one triaxial gyroscope. The measurements from the IMU are obtained with respect to (w.r.t.) a reference frame, referred to as the sensor frame (S), its axes and origin corresponding to those of the accelerometer triad. The axes of the gyroscope is assumed to be aligned with the axes of the accelerometer. The measured quantities describe the motion of the sensor frame w.r.t. a global frame (G) that is fixed w.r.t. the environment.
The accelerometer measurements at time
, where the integer
k is used as a sample index, can be modeled as
where
is the acceleration of the sensor w.r.t. the global frame and
is the gravitational acceleration, which is assumed to be constant in the environment. The measurements are corrupted by a constant additive bias
and noise
, which is assumed to be Gaussian
, with zero mean and covariance matrix
. The superscript
S and
G are used to denote in which reference frame a quantity is expressed in, and the rotation matrix
describes the rotation from the global frame to the sensor frame, i.e., we have that
The multiplication between a rotation matrix and a vector is equivalent to a change of orthonormal basis.
The gyroscope measurements are modeled as
where
is the angular velocity of the sensor frame in the global frame. Similar to the accelerometer, the measurements are corrupted by constant additive bias
and noise
, which is assumed to be zero-mean Gaussian
. Note that the same rotation matrix
as in (
1) is used to rotate quantities from the global frame to the sensor frame because the accelerometer and the gyroscope are contained in the same IMU and their axes are assumed to be aligned. The gyroscope bias term
can be compensated for through pre-calibration of the gyroscopes [
24]. In
Section 7.5, we will evaluate the effect of uncompensated biases on the proposed method.
Biases and Gaussian measurement noise have been shown to be the dominating error sources, even for low-cost IMUs [
25]. However, for longer experiments or for low-quality IMUs, there are other types of errors that may need to be considered. These errors can still be well compensated for by pre-calibration or by online auto-calibration methods. Therefore, we only consider biases in our models, as these are the dominating systematic errors. The bias terms
and
are not constant, but drift slowly over time [
26]. Sensor manufacturers typically provide a bias stability metric for their sensors, which tells the user the expected rate of the bias drift. Bias instability in inertial sensors is primarily caused by low-frequency flicker noise in the electronics and temperature fluctuations [
27]. If the bias drift is significant enough that it needs to be compensated for, there are methods that model the biases as time or temperature dependent, enabling continuous estimation of drifting biases (see, e.g., [
28,
29]). Such methods can be used in combination with the method proposed in this paper. Low-quality IMUs may be affected by other systematic errors such as non-unit scale factors and misalignments/non-orthogonalities in the sensor axes. If the effect from these types of errors are non-negligible, it is advised to perform a more sophisticated pre-calibration of the sensors to compensate for these errors. Methods for in-field pre-calibration of such errors exist; see, e.g., [
30,
31,
32,
33].
4. Joint Axis Estimation
We assume that we have two IMUs, one attached to each segment of a hinge joint system. Measurements from a completely unspecified motion has been collected. We will use
to refer to the gyroscope measurements (
3) and
to refer to the accelerometer measurements (
1) from Sensor
. We will use the non-indexed
and
to refer to measurements from both sensors as
and similarly for
. We let
denote our data, which consists of
N samples of recorded motion. Each sample in the data set is assigned a sample index
, such that
refers to the sampling time of the
kth measurement relative to the beginning of the recorded motion.
Given the data from the two IMUs, the variables we want to estimate are the unit vectors which corresponds to the directions of the joint axis j in the two sensor frames. We let denote the estimate of . Note that the joint axis in one sensor frame can be described by either since a clockwise rotation w.r.t. the positive axis is equivalent to a counter-clockwise rotation w.r.t. the negative axis. However, we require both and to have the same sign (direction) to correspond to either in the global frame, otherwise a clockwise rotation for one sensor might be considered a counter-clockwise rotation for the other sensor and vice versa. That is, the sign pairing of the joint axes in the sensor coordinate frames is important. Consequently, is the correct sign pairing and is the wrong sign pairing.
4.1. Formulating the Optimization Problem
We parametrize
using spherical coordinates to enforce the unit vector constraint
which then become the unknown parameters to estimate. The estimation problem for the joint axis is formulated as
where
and
are scalar residual terms, based on the angular velocity constraint (
14) and acceleration constraints (
18) of the hinge joint system
Two scalars and are used to change the relative weighting of the residuals.
4.2. Identifiability and Local Minima
For the gyroscope measurements to contain information about the joint axis, they have to be recorded from motions where the joint angle is excited, i.e., when the two segments rotate independently. These motions should contain either simultaneous planar rotations, where the segments rotate simultaneously in the plane perpendicular to the joint axis, or sequential rotations of the segments. However, stiff joint motions, which can have a significant angular rate but no independent rotation of the segments, do not facilitate identifiability of the joint axis [
16]. For the non-informative stiff joint motions, the relative rotation of the two sensors can be described by a time-invariant rotation matrix
R and we have that
where we see that for any choice of
, the vector
will minimize the gyroscope residual (
24). Therefore, we want motions where
, which implies that the segments are rotating independently and we require motions where
for at least some time, since
.
If only acceleration information is considered, we get the following over-determined system of linear equations
which has a unique solution if
, in which case
lies in the null-space of
A. This holds when the acceleration constraint holds exactly for all
, the accelerations measured are exact and the angular rate and angular accelerations of the sensors are parallel with
j [
16]. Therefore, for the accelerometer, we want measurements that increase the separation between the column-space and the null-space of
A.
The proposed method uses both gyroscope and accelerometer information, and their relative contribution to the cost function is controlled by the weight parameters
and
.
Figure 2 shows how the weights affect the cost function in the case that
and
is allowed to vary. For small
, the local minima corresponds to the correct sign pairing
, whereas the local maxima corresponds to the wrong sign pairing
. Note that each local minimum is equally valid for small
because of the periodicity of the spherical coordinates. The acceleration residuals are relatively large whereas the gyroscope residuals are relatively small at the locations corresponding to the wrong sign pairing. Therefore, as
increases the gyroscope residuals will contribute more to the cost function. The peaks associated with the wrong sign pairing are flattened and new local minima will eventually appear at these locations. Therefore, for large
an optimization method (solver) can end up in the wrong local minimum. However, regardless of which sign pairing the solver finds, the opposite sign pairing can always be obtained at
. Therefore, if our solver finds the estimate
we can reinitialize at
and obtain a new estimate
. Then we select the local minimum with the smallest value of the cost function as our estimate
Therefore, it is possible to find the correct sign pairing as long as
is numerically distinguishable from
. As discussed in this section and shown in
Figure 2, the relative weighting of the residuals determines how easy it is to distinguish a correct local minimum from a wrong one. If
is set to be significantly larger than
, we expect the acceleration residuals to eventually become so small relative to the gyroscope residuals, that the solver is no longer sensitive enough to detect the difference between correct and wrong local minima.
4.3. Solving the Optimization Problem
The optimization problem (
22) is a nonlinear least-squares problem. An efficient solver for such problems is the Gauss–Newton method [
34]. Given an initial estimate
the Gauss–Newton method iteratively updates the estimate according to
where
k is only used here as an integer index denoting the iterations of the method and is not to be confused with the sample index. The method uses the Jacobian matrix
, which contains all first-order partial derivatives of
and
and
is the residual vector
The term
is an approximation of the Hessian of
, which is given by
where the higher-order terms are ignored, yielding
The partial derivatives of the residuals (
24) and (
25) in the Jacobian (
31) are computed in the following way using the chain rule
The term
in (
30) defines the search direction, and
is a descent direction, meaning that moving our estimate in that direction will decrease the value of the cost function. The scalar
is known as the step length, which controls how far our estimates move in the descent direction. By using a method known as backtracking line search [
35], we find a value for
that is guaranteed to lower the value of the cost function. If no such
is found or the change in the value of
is too small, below a set tolerance level
, the Gauss–Newton method terminates and returns the estimate corresponding to the current iteration
.
The complete joint axis estimation method, including the steps of the Gauss–Newton method and the re-initialization step (
28) required to identify the minimum corresponding to the correct sign pairing, is described in Algorithm 1.
| Algorithm 1 Joint axis estimation |
Require: Data , initial estimate , tolerance , residual weights and .
- 1:
for do - 2:
. ▹ Begin Gauss–Newton. - 3:
. - 4:
. ▹ defined by ( 23). - 5:
while do - 6:
Compute the Jacobian and the residuals according to ( 31) and ( 32). - 7:
. - 8:
Obtain step length using backtracking line search. - 9:
. - 10:
. - 11:
. - 12:
. - 13:
end while - 14:
. ▹ End Gauss–Newton. - 15:
. - 16:
. ▹ Initialize at . - 17:
end for - 18:
. ▹Correct sign pairing. - 19:
return .
|
5. Sample Selection
A key feature of plug-and-play estimation is that it should not require specific calibration data, recorded from predetermined motions. Rather, such plug-and-play methods should be able to use data recorded from arbitrary motions. Such data sets could be very large, and using all available data for identification is often unnecessary and resource-demanding. It is also possible that very few samples in the data set contain information about the joint axis. In a sense, too much bad information might ruin the good information. To handle this, we propose a method for selecting samples to use for estimation.
In the following sections we assume that we want a maximum of gyroscope and accelerometer measurements can be used to identify the joint axis, but that we have measurements available to us to choose from.
5.1. Gyroscope
To distinguish between informative and non-informative motions, we use the difference in angular velocity magnitude measured by the two gyroscopes
which is a sufficient metric for detecting independent rotations of the sensors, and hence the two segments. For stationary segments
. One thing to note is that
cannot differentiate between informative motions where
and non-informative stiff joint rotations. For example, the two segments can undergo simultaneous planar rotations, where the two segments rotate in different directions but with approximately the same magnitude. However, for realistic motions, especially for motions performed by humans, it is unlikely that independent rotations will have the same magnitude, even for short moments.
Each gyroscope measurement is given a score
that is equal to the
with smallest magnitude in a window of
samples. This is to avoid selecting large outliers of
. For example, if the system is not completely rigid or the sensors are not rigidly attached, the kinematic constraints are violated, and some samples of stiff joint motion can obtain a large
value. However, if the outliers are relatively few, there should be
with smaller magnitude among neighboring samples. In some sense,
assumes a conservative score for each sample.
When the score
has been computed for all measurements, the list of measurements is sorted in descending order such that
, where
is a new index variable used to denote the sorted order. The first and last
of the sorted gyroscope measurements are selected, or, equivalently, the measurements corresponding to the middle of the list, i.e., with index
are removed from the set of measurements. By doing this, the algorithm will make sure that measurements with excitation in both sensors are selected, since
means that Sensor 1 has larger angular rate than Sensor 2 and vice versa for
. The gyroscope sample selection method is described in Algorithm 2. In essence, the algorithm picks half the required points from either end of the sorted list.
| Algorithm 2 Gyroscope sample selection |
Require: Gyroscope data , number of allowed measurements, , window size n.
- 1:
if then - 2:
Compute according to ( 43). - 3:
Obtain the sorted order such that . - 4:
Remove the samples from . - 5:
end if - 6:
return
|
5.2. Accelerometer
The acceleration constraint is accurate when the angular rate and angular accelerations are small, since that makes the right hand side of (
17) vanish. Note that linear acceleration terms in (
17), which are collected in
, always cancel out. Therefore, we do not use the energy of the accelerometer measurements to determine if the acceleration constraint is valid. Instead, we give each acceleration measurement a penalty based on the average angular rate energy
where the average is calculated from a window of size
, centered around each sample. This angular rate energy statistic has been shown to be an effective detector of stationarity in foot-mounted inertial navigation [
36], so-called zero-velocity detection.
Small
indicate that Sensor
i is stationary. For the hinge joint system, it is sufficient for one sensor to be stationary since the acceleration components in the plane normal to the joint axis does not change the r.h.s of (
17). If one sensor is stationary, then the other sensor can only have accelerations that are induced by independent rotation, which has to be in the plane. For this reason, the penalty given to each pair of acceleration measurements is chosen as
As a first step of the accelerometer sample selection, measurements with are removed, where is a scalar threshold parameter, which should be chosen to remove measurements for which it is likely that the motion violates the acceleration constraint.
We also need to consider the conditions for identifiability of the joint axis. That is, we want our measurements to increase the separation between the column-space and the null-space of the matrix
A in (
27). In practice,
A will have full rank regardless of the motion, since the measurements are corrupted by noise and bias and the acceleration constraint does not hold for arbitrary motions. However, if
A has one singular value that is relatively small compared to the other singular values, it can be considered to be approximately rank 5. Consider the singular value decomposition (SVD) of
A
where the diagonal elements
to
of
are the singular values and the columns of
U and
W represents orthonormal bases in
and
, respectively. The columns of
W are known as the right-singular vectors of
A, and each is associated with a corresponding singular value, i.e., if
the right-singular vector
is associated with
. The singular values are ordered
. We have that
is the direction in
where the rows of
A are most coherent, meaning that
which has the interpretation that
is the direction that is most separated from the null-space of
A. The information about
j that is contained in
A is directly linked to the separation between the null-space and the column space of
A. The intuition behind this can be seen by comparing the system of linear equations in (
27) to the definition of
in (
50), where it appears most unlikely that
j should be parallel with
. In fact, the least-squares estimator for
j given by
has solutions on the line in
, which is spanned by
, the right-singular vector associated with the smallest singular value. If we add the constraints
the two solutions with correct sign pairing, corresponding to
and
can be obtained through normalization. A problem arises when multiple singular values are close to zero, in which case the value of
will be small in more than one direction, and the uncertainty in the estimate increases. If
A is only allowed to have
rows, we should therefore only remove measurements whose rows in
A are most coherent with
, the direction with most information. This way, we make sure that space is always allocated for measurements with rows that do not align with
, which over time should increase the discrepancy between the two smallest singular values and increase the certainty of the least-squares estimator.
The coherence between a row in
A and the right-singular vector
is computed as the vector
, with the elements
where
is the
row vector in
A, and
has a value of 1 if
is parallel to
and 0 if they are orthogonal. A
means that
has most of its magnitude in the direction of
. Therefore, we choose to remove measurements with the largest
where
. This ensures that we also keep good measurements in the
direction, while allocating space for measurements with new information about
j. The algorithm for selecting accelerometer samples is described in Algorithm 3.
| Algorithm 3 Accelerometer sample selection |
Require: Data , number of allowed measurements , window size n, threshold .
- 1:
if then - 2:
Compute according to ( 46) using window size n. - 3:
Remove measurements where from a. - 4:
. - 5:
while do - 6:
Compute the SVD , with A given by ( 27). - 7:
Compute the coherence c according to ( 52). - 8:
Remove the measurement with largest where from a. - 9:
. ▹ A changes in subsequent iterations. - 10:
end while - 11:
end if - 12:
return .
|
5.3. Online Implementation
The two proposed sample selection algorithms can be implemented for an online application. For Algorithm 2, simply save the scores and re-use them when a new batch of data is available, new only needs to be computed for the previously unseen measurements. The same principle holds for Algorithm 3 and .
6. Uncertainty Quantification
When identifying an unknown quantity, it is useful for the user of the method to know if they can expect their estimate to be accurate given the data that is available, or if more informative data needs to be collected. Here we propose a method for quantifying both local and global uncertainty of an estimate .
The local uncertainty is obtained through estimating the covariance matrix of the estimation errors using the Jacobian of the cost function. Global uncertainty is obtained through solving multiple parallel or sequential optimization problems with different random initializations, then comparing the resulting estimates to see if they correspond to the same joint axis.
The local and global uncertainty metrics are combined into an algorithm that can be used to determine if a current estimate is of acceptable accuracy or if more informative data needs to be collected.
6.1. Local Uncertainty
We approximate the cost function
(
23) as a quadratic function near the estimate
where
is the approximate Hessian of
evaluated at
according to (
34).
We make the assumption that the uncertainty can be captured by a Gaussian distribution. Given the estimate
and the covariance matrix
, the probability that
x is the true parameter vector is given by the probability density function (PDF)
This is the same as assuming the estimation errors
to be zero-mean Gaussian with covariance
. We are interested in finding
to quantify the uncertainty of estimates. We now consider the negative log-likelihood of this PDF
Note the similarities to
in (
54). If (
54) is a good local approximation of the cost function and our estimator is unbiased, the distribution of the estimation errors
will be asymptotically (
) zero-mean Gaussian with covariance matrix [
37]
where
is Jacobian from (
31) where the partial derivatives of the gyroscope and acceleration residuals have been scaled by
and
, respectively. Here,
denotes the sample standard deviation of the residuals
We want to measure the uncertainty in terms of angular deviation
where
and
are vectors of the same dimension,
returns the positive angle between the two vectors. Let
then we want to find the probability distribution of
or its first two moments (mean
and covariance matrix
).
We use a Monte Carlo method to estimate the mean
and covariance
[
38]
where we let
,
is obtained as in (
57) and
is given by (
60). The covariance matrix
is estimated by the unbiased sample covariance estimator, hence the division by
.
The metric we will be using to determine local uncertainty is the mean plus two standard deviations, , where .
6.2. Global Uncertainty
The cost function may have multiple local minima. In the case that the local minima correspond to either the correct or the wrong sign pairing of and , we can find the correct one by comparing minima located near the opposite sign of either or . If these minima are not distinctly different in terms of the values of , we expect the estimates to have the correct sign half of the times our method finds a solution given that the initial estimates are uniformly spread over the parameter space. Furthermore, in the case where our data has little information about j, there may be other local minima that corresponds to wrong solutions. Wrong local minima can still have low local uncertainty, meaning that if our estimates are initialized near them, it is likely that wrong solutions are found. Therefore, to be confident that the method has found the global minimum, we need to solve the optimization problem multiple times with different initial estimates and compare the angular deviations of the sequential estimates.
We compute estimates
for
as
where
is chosen as either
, such that one of the two estimated joint axes
always has the sign that is most consistent with its previous estimate. Note that this only forces either
or
to be consistent with the previous estimate, whereas the other one may still be inconsistent. We then consider the maximum sequential angular deviation as our metric for whether the estimate at time
t corresponds to the same minimum as the estimate at time
The metric corresponds to the angular deviation of the joint axis estimate that is most inconsistent with its previous estimate. Consecutive estimates will differ when there is no clear and consistent global minimum. Therefore, if we observe that as t increases, we can be more certain that the local minimum found by our solver corresponds to a global minimum.
6.3. Identifying Estimates with Acceptable Uncertainty
Suppose that we receive data sequentially, i.e., we obtain
, the sets of
gyroscope and
accelerometer measurements that have been recorded from time
to
t. If we use sample selection according to Algorithms 2–3, then
. For each
we obtain an estimate
by solving the optimization problem (
22). Furthermore, we will select the estimate associated with time
t to be
as in (
66), such that either
or
is consistent with the sign of the previous estimate.
We now want to assess if has acceptable uncertainty. Let denote the maximum uncertainty that we accept. We use the following two criteria to determine if the local and global uncertainty is sufficiently small
We require that
, where
and
are obtained from (
64) and (
65) through the procedure described in
Section 6.1.
We require that the sequential angular deviations given by (
67) satisfy
for a minimum of
consecutive estimates, that were randomly initialized uniformly over the parameter space. This is equivalent to
We summarize the method for selecting an estimate
of acceptable uncertainty in Algorithm 4.
| Algorithm 4 Identifying an estimate of acceptable uncertainty |
Require: Data , number of Monte Carlo samples L, maximum acceptable uncertainty , threshold for minimum number of sequential estimates with acceptable deviation .
- 1:
- 2:
for do - 3:
Obtain an estimate by solving the optimization problem ( 22) using the data and Algorithm 1. - 4:
Obtain from ( 66). - 5:
Compute the covariance matrix according to ( 57). - 6:
Compute and according to the Monte Carlo method ( 62)–( 65). - 7:
Compute as in ( 67). - 8:
if AND then - 9:
return . - 10:
end if - 11:
end for
|
9. Discussion
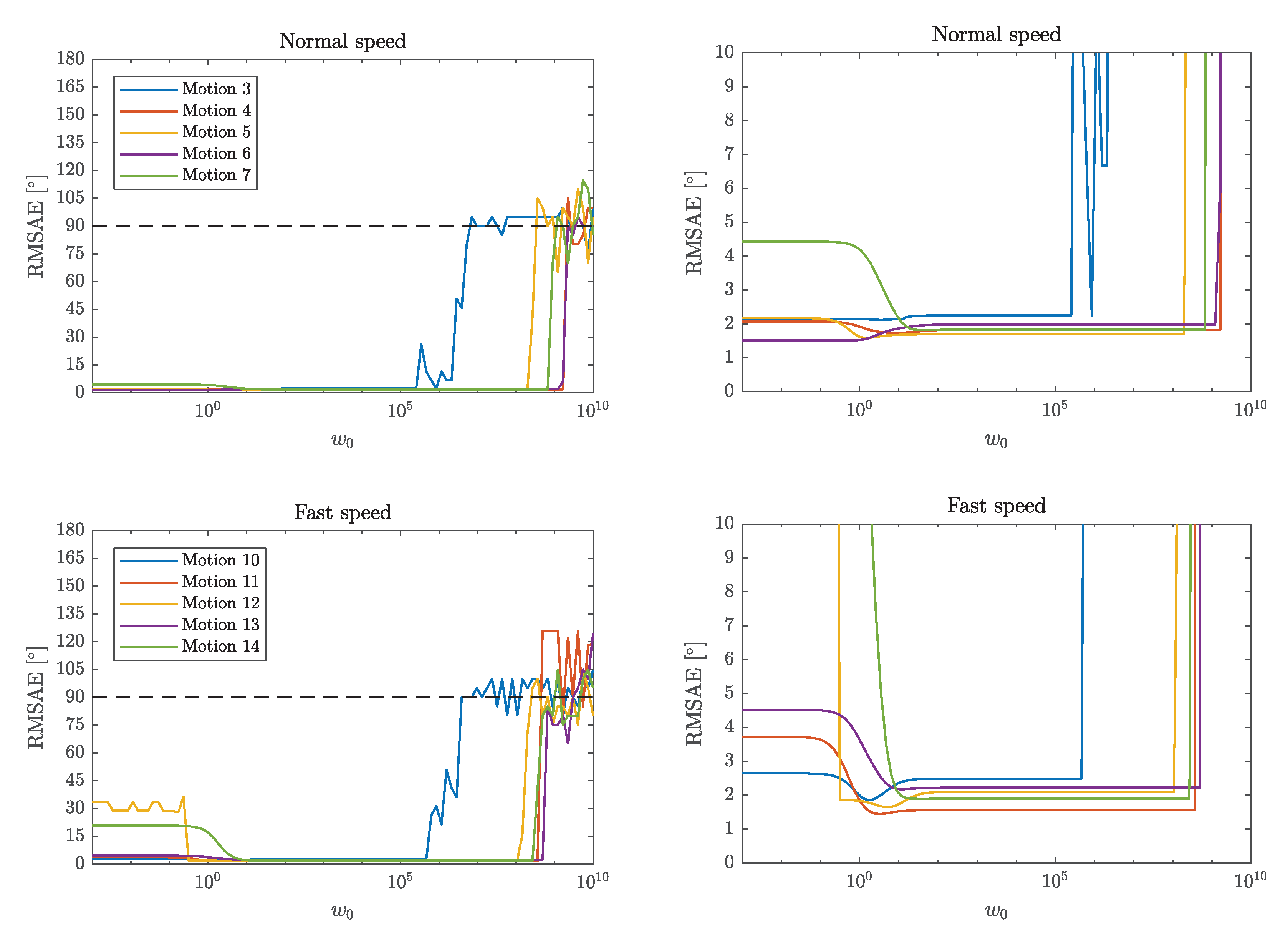
9.1. The Method Is Not Sensitive to the Relative Weighting
The parameter
, which is defined from (
70), controls the relative weighting of the residuals
and
. As
increases, the relative weighting of the gyroscope residual is increased. As we see in
Figure 5, the optimal choice of
for most motions in terms of RMSAE (
71), is somewhere in the large range between 10 and
. The errors are also small (
) for
for the slower planar motions (3–6), which shows that the acceleration information can be reliable for these motions. However, some larger errors can be observed for small
for the faster planar motion 12 and the errors are also significantly larger for the free axis rotations (motions 7 and 14), which can be explained by the fact that these motions violate the acceleration constraint, meaning that the r.h.s. of (
17) is nonzero.
Since we can select any from within such a large interval and still obtain similar performance, our method is not sensitive to the relative weighting of the residuals. It makes sense that , since the angular velocities, measured in rad/s, have smaller magnitudes than the accelerations, that typically fluctuate around m/s2 due to the gravitational acceleration. Furthermore, the angular velocity constraint always holds for a rigid hinge joint system. Hence, we expect the angular velocity information to be more reliable. The method is robust for larger up to where the RMSAE become large for motions 3 and 10. This large increase in RMSAE occurs when the acceleration residual becomes numerically indistinguishable to the tolerance of the optimization algorithm, and it becomes more likely that the method selects an estimate which corresponds to the wrong sign pairing. Therefore, as increases we see the RMSAE approach as the AD for is still small but the probability of selecting is approaching , meaning that approximately half of the estimates will have the wrong sign pairing. This can also depend on the numerical tolerance and stopping criteria of the optimization method, since a global minimum corresponding to the correct sign pairing might not be significantly different from other local minima that correspond to the wrong sign pairing.
9.2. Sample Selection Offers Substantial Benefits
From the results shown in
Figure 6 we see that we can achieve similar, and in some cases even better performance by selecting relatively few measurements to use for estimation out of all
measurements that have been observed up to time
t. For Scenario 1,
have angular errors within
and
have errors within
from the case with
.
In Scenario 2, the errors for drop below at s for the methods using sample selection, but it takes until s for the method where to stay consistently below . However, the method with again shows a slightly larger deviation from the others, with some momentary spikes in error around s and s. Note that Scenario 2 is designed to have no independent rotation of Segment 2 until s. So the only information about until then has to come from the accelerometer. This shows that carefully selecting accelerometer samples according to Algorithm 3 is beneficial, especially if angular velocity information is missing. Comparing the results from Scenarios 1 and 2, the final errors are very similar, indicating that the methods are not sensitive to the sequence of motions.
Scenarios 3 and 4 represent challenging cases where only a small minority of samples contain motion with independent rotation (only 20s of motion 6). In Scenario 3, we note that the final error for is significantly larger than the cases with , and for the final error for is at the same level as . Scenario 4 has a similar performance in terms of final errors. However, Scenario 4 does not have any motions with independent rotations of the segments until around s. The only information about the joint axis until that point comes from the accelerometer, in Motions 1, 8, 2 and 9. The errors start to decrease around s when data from Motion 9 comes in, but do not settle until after Motion 6. The large fluctuations in errors we see for during Motion 9 indicate that there are still at least two local minima corresponding to the wrong joint axis at this point. Errors for are smaller during motion 9, but still vary between and .
Using Algorithms 2–3 is therefore beneficial, not only for reducing the computational complexity of the optimization problem, but it can even improve the performance in situations where gyroscope information is limited. However, judging by Scenario 4 in particular, appears to be the best choice in terms of overall performance. Even then, is only a small fraction of the total number of measurements. With a sample period of s, we have that and .
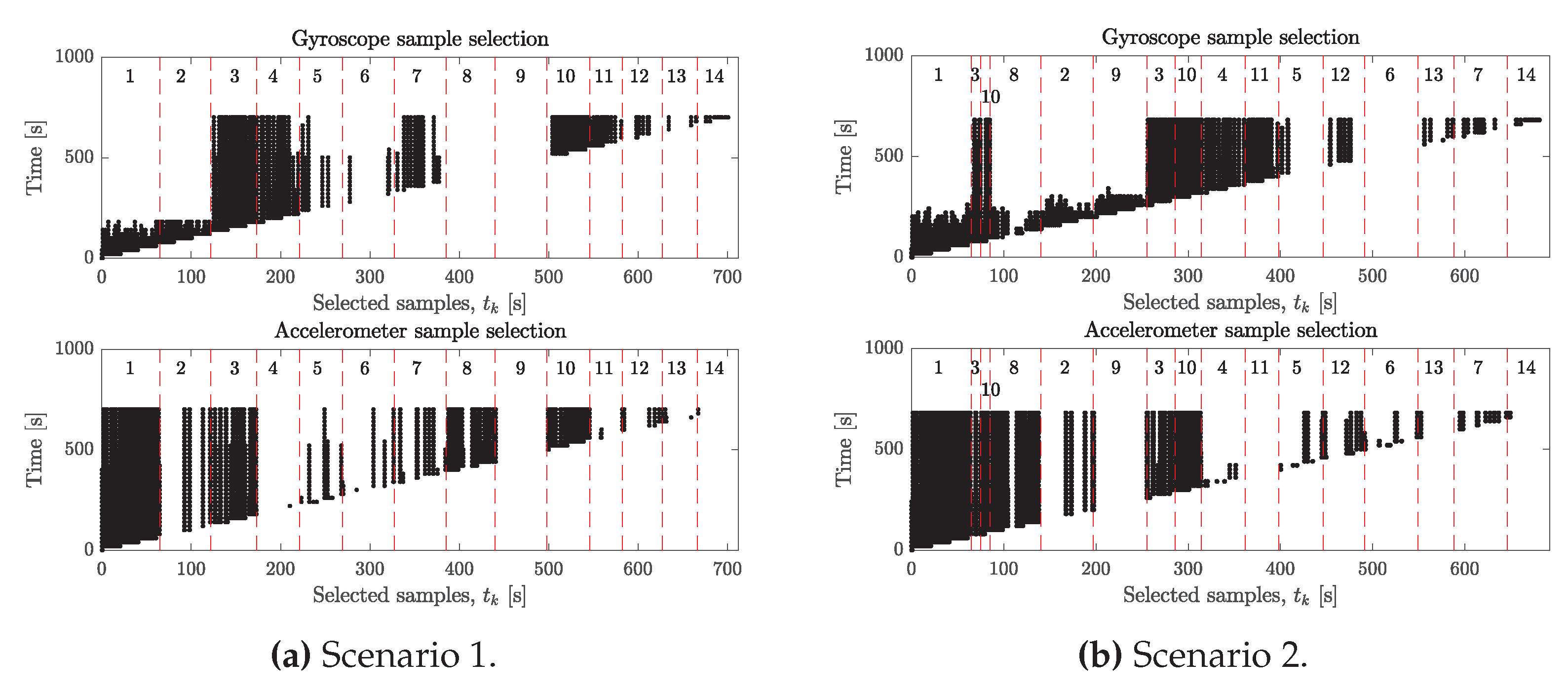
Figure 7 shows the samples that were selected over time from Scenarios 1 and 2 with
and which motions these samples come from. For both scenarios, we see that gyroscope samples from non-informative motions 1,2,8,9 are all deselected by the end. Samples from these motions are only kept until enough samples from informative motions have been parsed by the algorithm. For the accelerometer, we see that samples from stationary sensors are preferred since many samples of motions 1 and 8 are kept, which is in line with the penalty we give samples based on the angular rate energy. It is also important that samples from other motions are selected since the criterion for identifiability requires a strong separation between the nullspace and the column space of the matrix
A given by (
27). Had the selection criterion of the accelerometer only been based on the angular rate energy, we would risk ending up in the situation where all samples are selected from the same stationary position, in which case all rows of
A are linearly dependent. Lines 5–10 in Algorithm 3 prevent this by removing the worst samples that are coherent with the right-singular vector of the largest singular value. This can be thought of as allocating space in the
A matrix for novel information by removing redundant information.
9.3. Reliability of the Proposed Uncertainty Quantification
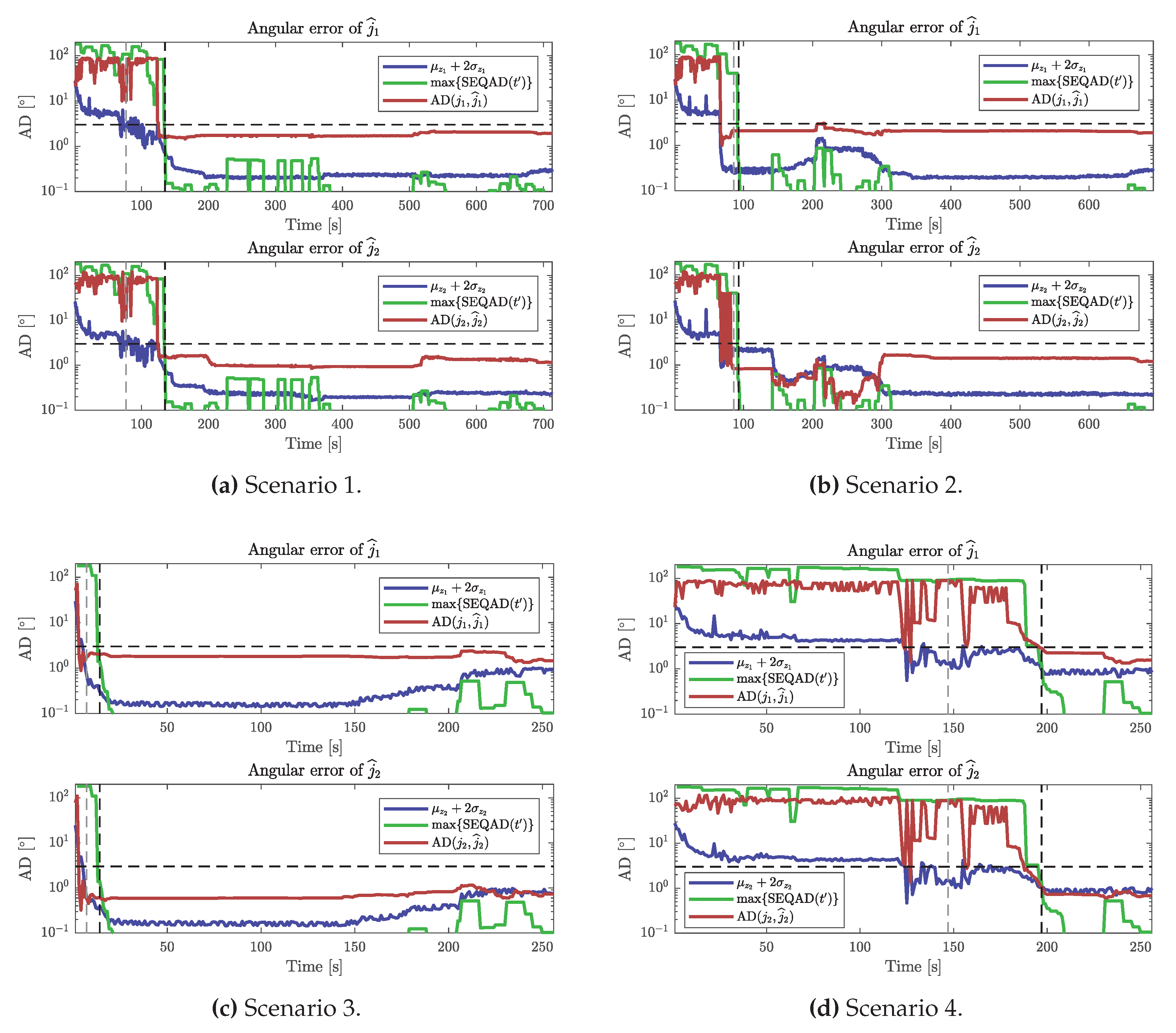
We obtained reliable estimates with errors below that of the maximum acceptable error , of the time when the parameter . However, estimates were not reliable for , where the results were particularly bad for Scenario 1, with of estimates of acceptable error and for Scenario 4 with of estimates of acceptable error. Both of these scenarios contained no informative motions in the beginning, and we found that the estimates that were returned often had not used any batch of informative data for estimation because the criteria for local and global uncertainty were satisfied prematurely by Algorithm 4.
In
Figure 8 it can be seen that local uncertainty metric
can be below
(horizontal dashed lines) while the actual angular error fluctuates between values below and above
. This occurs when there exist multiple other local minima than those corresponding to the true joint axis. Furthermore,
Figure 8 shows how the SEQAD remains large as the angular errors fluctuate in the same way as the angular errors. Interestingly, Scenario 2 appears to fluctuate between one correct and one wrong local minimum between
s and
s. If we assume that the probability of finding the correct local minimum is
, having
that means that the probability of ending up in the wrong local minimum
times in a row is
. This matches well with the results obtained for Scenario 2, where
of the estimates were acceptable for
.
For Scenarios 1 and 4, where the results were significantly worse for , it appears that wrong local minima were dominating. These two scenarios have sequences of stiff-joint motion before any informative motions are observed, which can explain why wrong local minima were found more frequently. Scenario 3, which had informative motion in the beginning did not have this issue, and hence of the estimates were acceptable even for .
We can conclude that setting the parameter sufficiently large is important for fully capturing the global uncertainty. Sequential data dominated by non-informative motions in the beginning are more sensitive to the choice of . The results showed that Algorithm 4 successfully identified all of the estimates that satisfied the accuracy criteria when . Here, this corresponds to 10 consecutive estimates (computed once per second), that differed by at most.
9.4. The Method Is Robust to Realistic and Uncompensated Sensor Bias
As shown in
Table 1, even with added artificial biases of relatively large magnitudes
m/s
2 and
s, the errors were at most
across all
estimation runs for all four scenarios. The average errors in terms of RMSAE were less than
even with the added artificial biases. As a comparison, the IMUs used in our experiments had bias magnitudes in the order of
m/s
2 and
s, so the artificial biases were significantly larger. This shows that the method is robust to sensor biases of at least these magnitudes. However, we had to lower the threshold
from
to
to achieve this. This means that Algorithm 4 will be more conservative in selecting an estimate. With added artificial bias and
, the method would sometimes terminate prematurely, when no informative motion had been observed because a global minimum that satisfied this threshold value was found. Therefore, lowering
was required to achieve robustness to the added artificial biases. It is therefore still highly recommend that pre-calibration of the biases is performed when possible. If bias drift is significant enough to exceed the magnitudes tested here across the duration of the experiment, it is advised to use a method that allows for online compensation of biases alongside the proposed method. Lowering
is only an optional measure one would take in the unusual case where late bias occurs and is not compensated for.
10. Conclusions
We have proposed a method which facilitates plug-and-play sensor-to-segment calibration for two IMUs attached to the segments of a hinge joint system. The method identifies the direction of the joint axis j in the intrinsic reference frames of each sensor, thus providing the user with information about the sensors’ orientation with respect to the joint. Accurate sensor-to-segment calibration is crucial for tracking the motion of the segments.
The method was experimentally validated on data collected from a mechanical joint, which performed a wide range of motions with different identifiability properties. As soon as sufficiently informative data was available, the method achieved a sensor-to-segment calibration accuracy in the order of , assessed as the angular deviation from the ground truth of the joint axis.
The proposed method includes the following features that were evaluated separately using the experimental data:
Gyroscope and accelerometer information are weighted and combined, which makes the joint axis identifiable for a wider range of different motions. Experimental evaluation showed that the method is not sensitive to the weighting parameters, and that it performs comparably well for a wide range of different motions across a large interval of weights.
A method to select a smaller subset of samples to use from a long sequence of recorded motion is proposed. Samples are selected from motions that yield identifiability, and measurements of non-informative motions are automatically discarded. The experimental evaluation showed that using between 125 and 1000 samples can achieve similar and in some cases even better performance than using all available samples collected from a long sequence of motions. Sample selection was shown to be particularly beneficial when data consisted of more non-informative than informative motions. Furthermore, using less samples for estimation reduces the computational complexity of the estimation.
A method to quantify local and global uncertainty properties of sequential estimates, which provides the user with an estimate when criteria for acceptable uncertainty are met. The method successfully identified estimates that satisfied the uncertainty criteria ().
The proposed method is the first truly plug-and-play calibration method that directly enables plug-and-play motion tracking in hinge joints. For the first time, the user can simply start using the sensors instead of performing precise or sufficiently informative motion in a predefined initial time window, and the proposed method provides reliable calibration parameters as soon as possible, which immediately enable calculation of accurate motion parameters from the incoming raw data as well as from already recorded data. Regardless of the performed motion, it provides only parameters that are actually accurate, which is not guaranteed by any state of the art method. This enables the kind of truly non-restrictive and reliable motion tracking that is needed in a range of application domains including ubiquitous motion assessment to wearable biofeedback systems.
In future work, the method could be extended to different joint types and be applied to motion tracking in mechatronic and biomechanical systems. For the latter case in particular, it would be of great interest to study the reliability of the method in non-rigid systems, such as human limbs, where motion of soft tissue is significant.