A Federated Derivative Cubature Kalman Filter for IMU-UWB Indoor Positioning
Abstract
1. Introduction
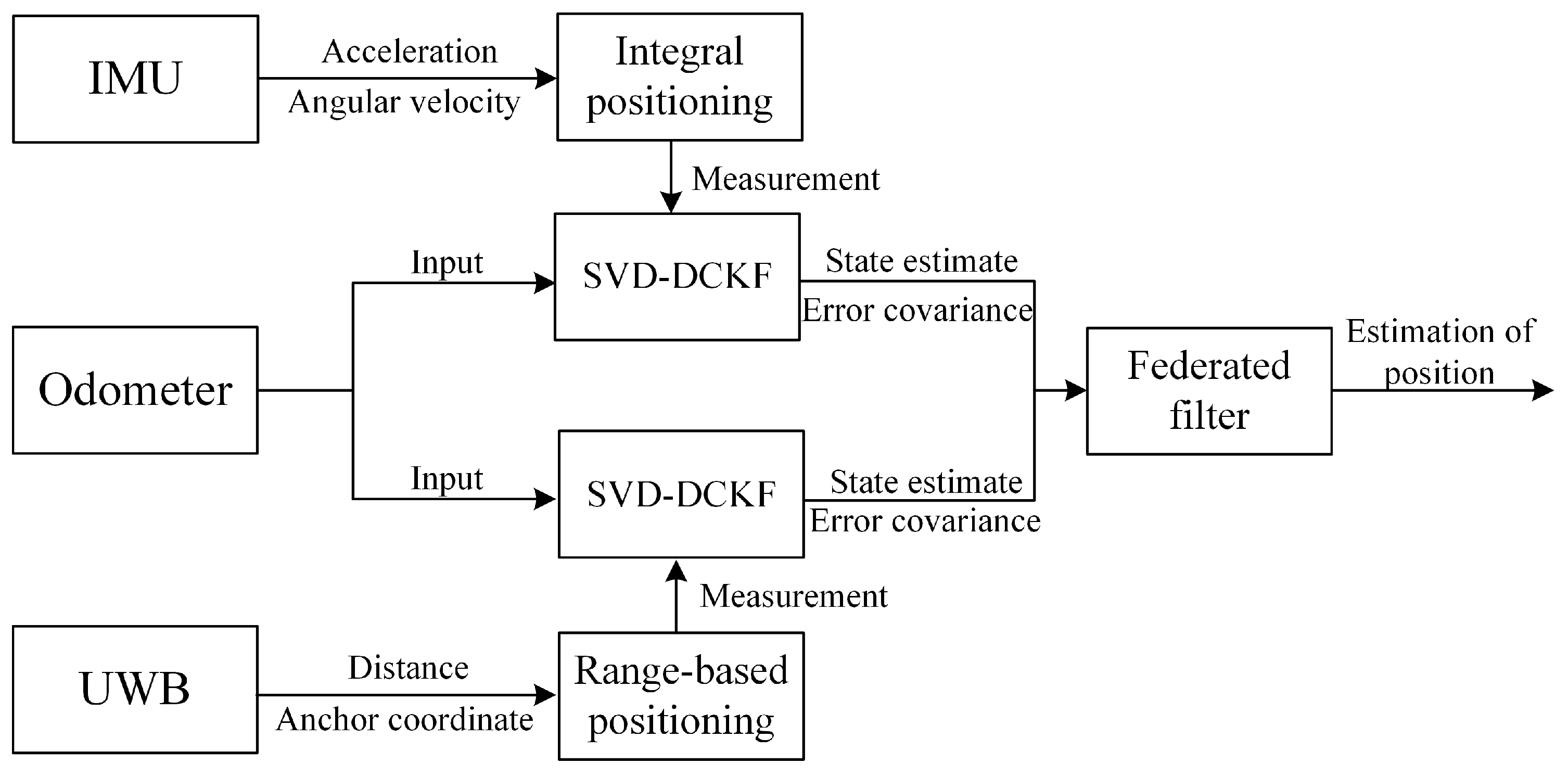
2. IMU-UWB Mobile Robot System Model
2.1. Description of System State Equation
2.2. Description of System Measurement Equations
2.2.1. IMU Measurement Equation
2.2.2. UWB Measurement Equation
3. The Federated Derivative Cubature Kalman Filter
3.1. Problem Statement
| Algorithm 1 A Cycle of SVD-FDCKF Algorithm to Estimate System State. |
| Input:, , , , , |
| Output:, |
| - |
|
| - |
|
3.2. Algorithm Description
- Step 1. Initialize state estimate and the error covariance matrix .
- Step 2. Since the error covariance matrix is a positive definite matrix, the state cubature points are calculated by SVD decomposition, and its weight as follows:where m is the total number of cubature points. According to Spherical–Radial Cubature law, we have where n is the dimension of the state quantity. is a diagonal matrix composed of eigenvalues. is the cubature point which is set to:where represents the jth column of the identity matrix. The cubature points’ weights are set to:
- Step 3. Evaluate the propagated cubature points. The transformed cubature points yielded through the nonlinear state model are given as follows:
- Step 4. Calculate the predicted state and the error covariance as follows:After the time update, the measurement update is then performed.
- Step 5. As the system measurement equation is linear, the KF method is used for the measurement update and the Kalman gain calculation. The predicted measurement can be computed as follows:
- Step 6. The state estimate and the corresponding error covariance matrix can be updated by:where is filtering error. The Kalman gain at time k can be obtained as follows:
- Step 7. Adopt the federated filtering framework to fuse the local estimation information of two local filters to obtain a better estimation:where and in the above formula are used respectively to re-initialize and in Step 1, and then repeat Step 1 to Step 7 for the next sample.
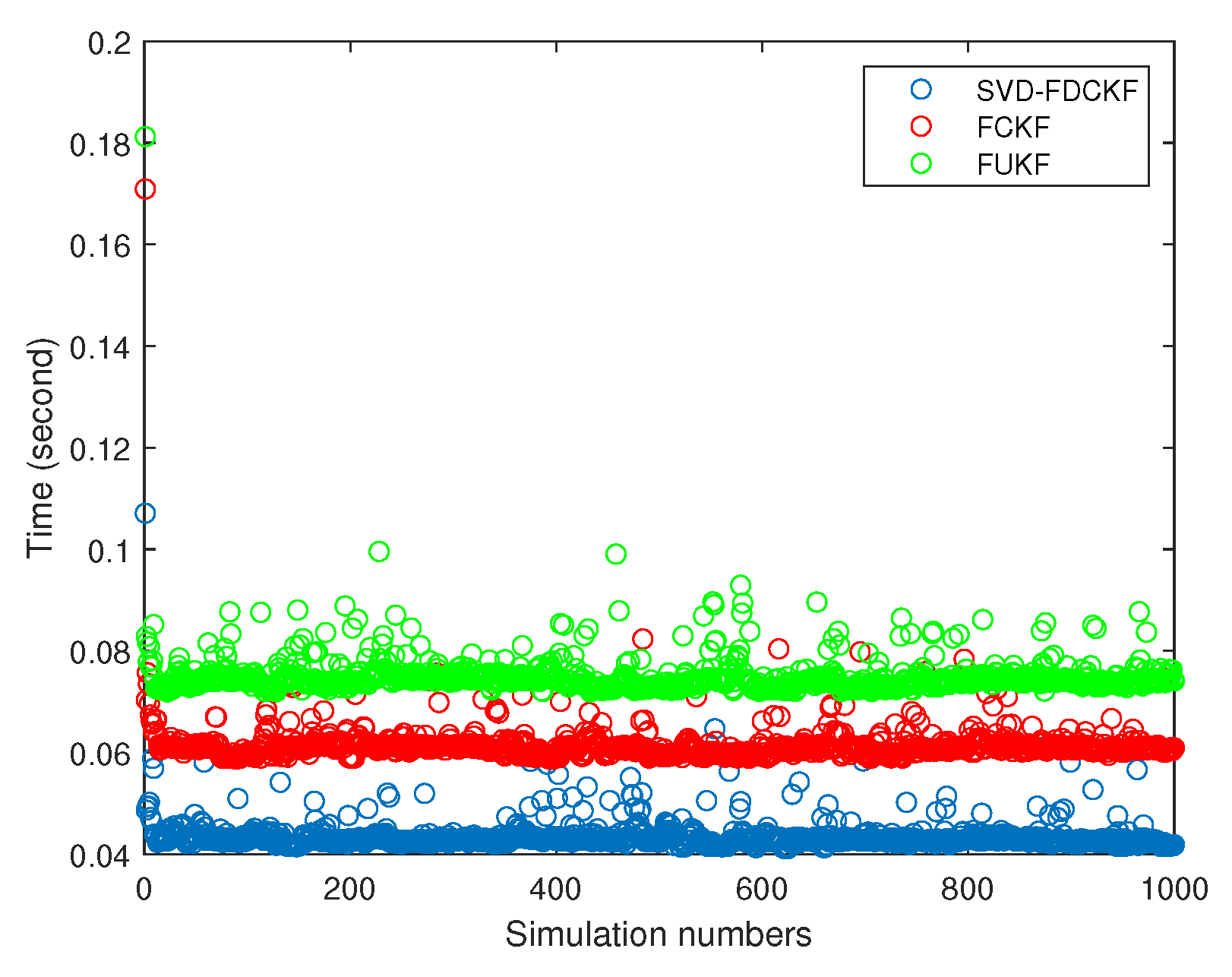
3.3. Computational Burden Analysis
3.4. Improvement of the Stability of the DCKF
4. Simulations
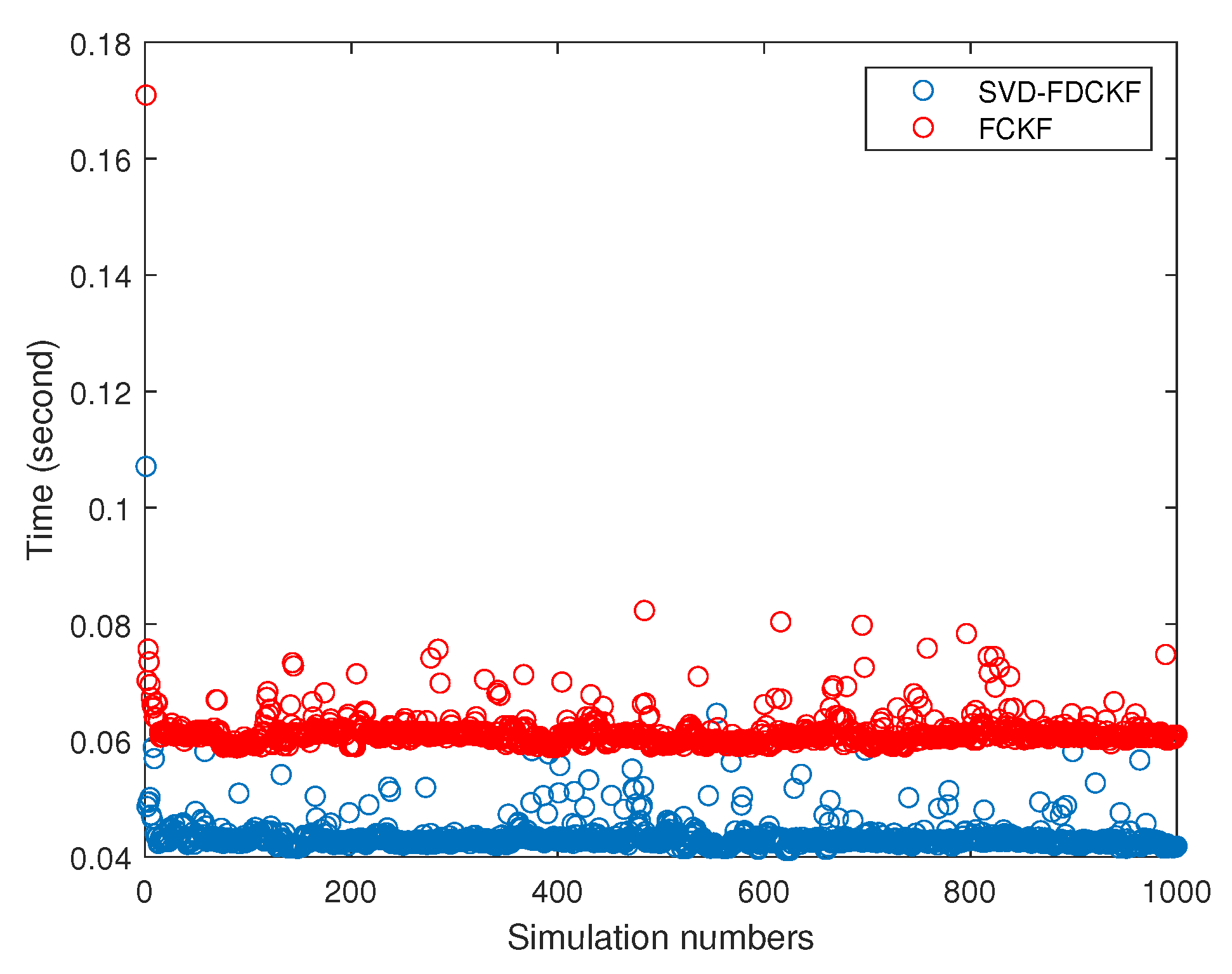
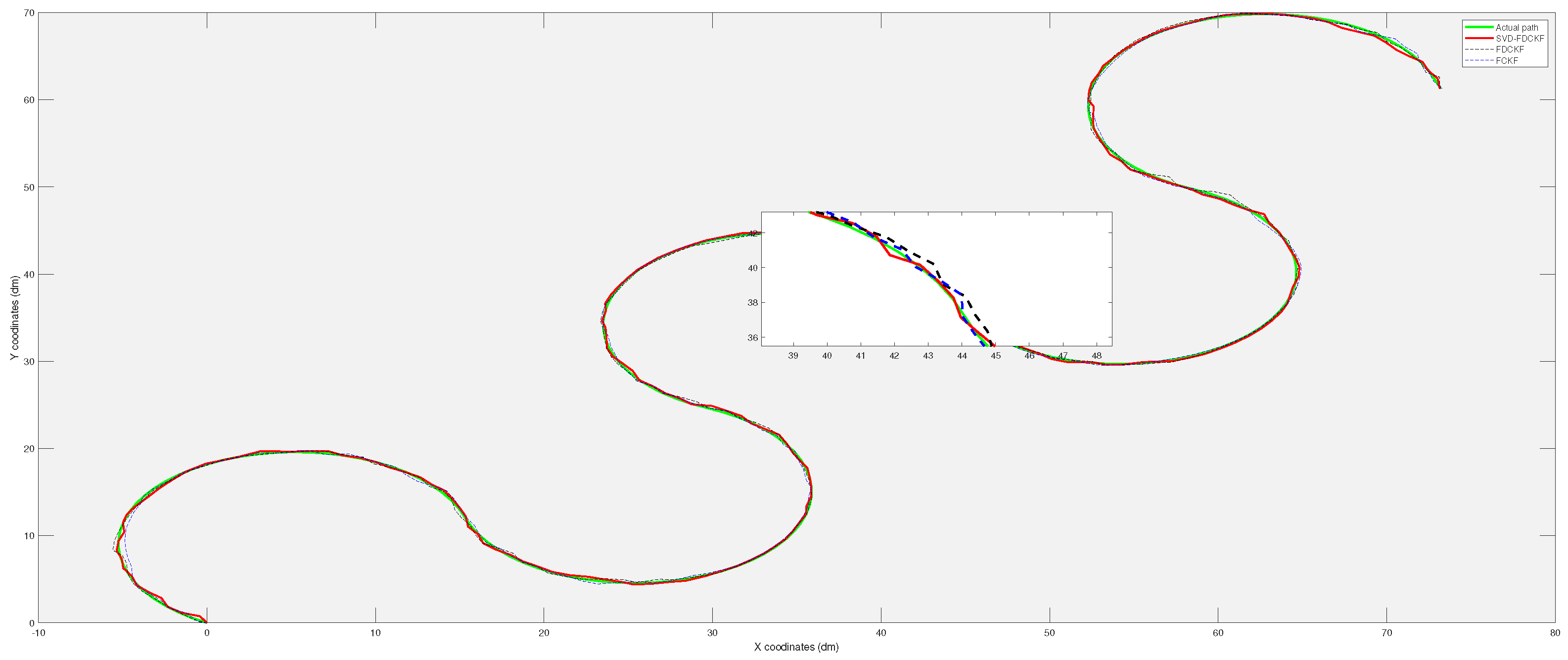
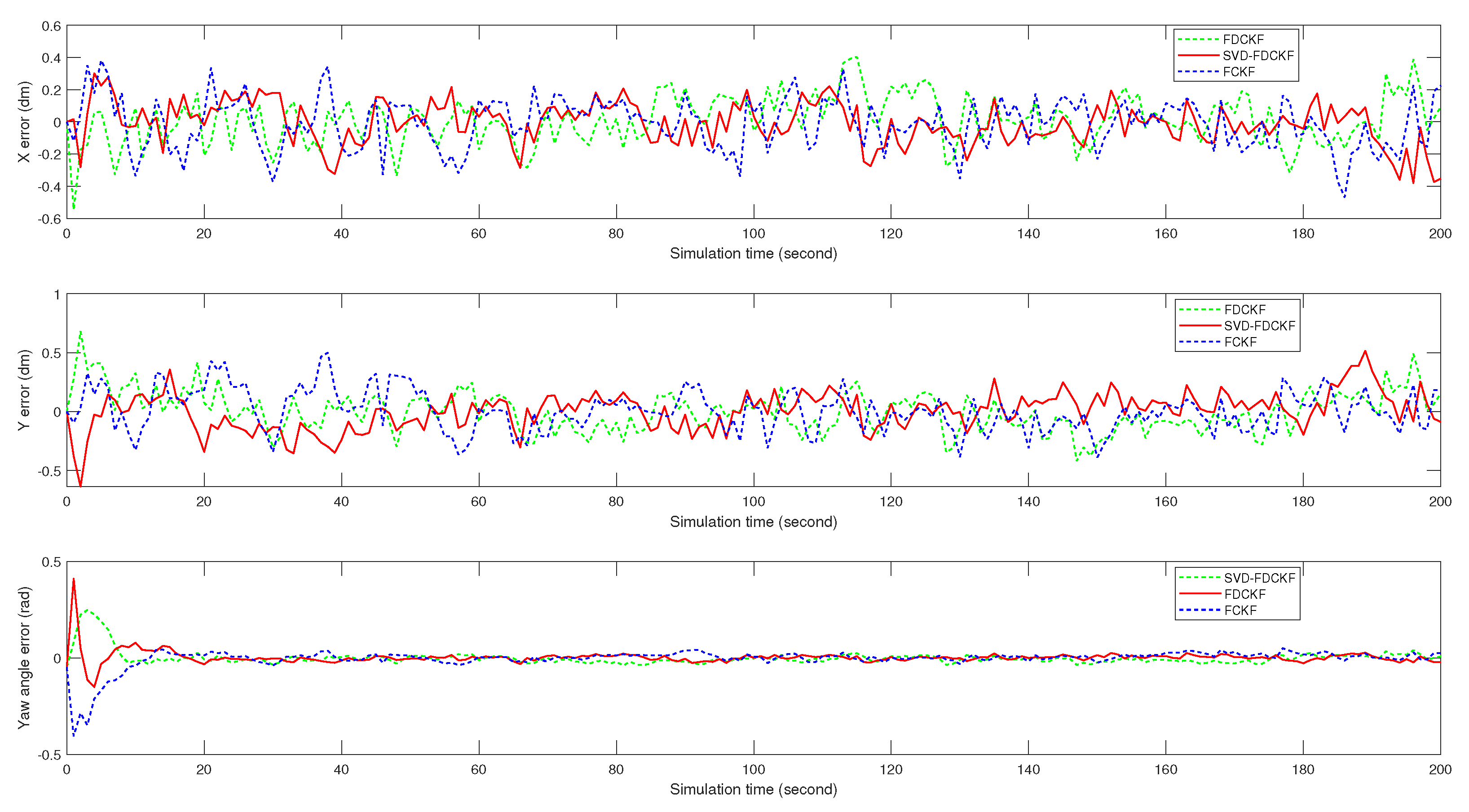
4.1. Comparison Test of SVD-FDCKF and FCKF
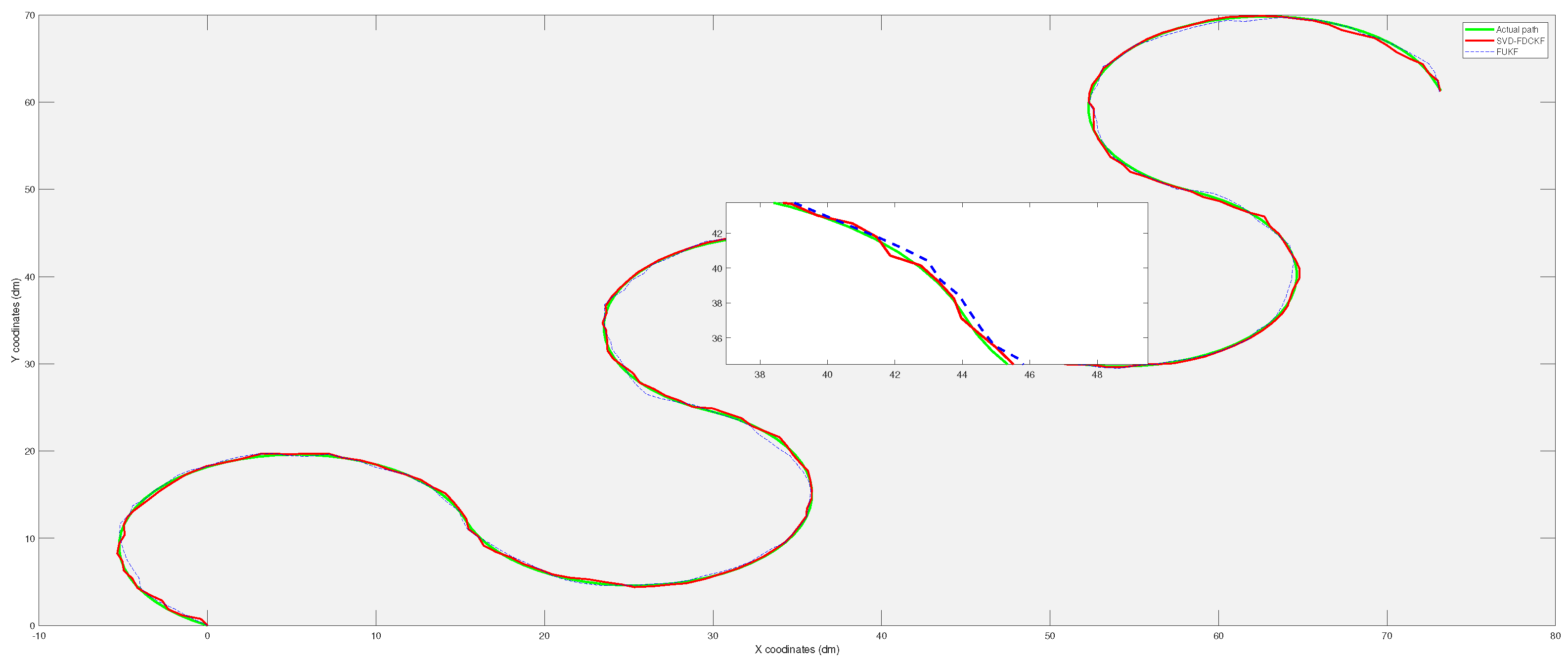
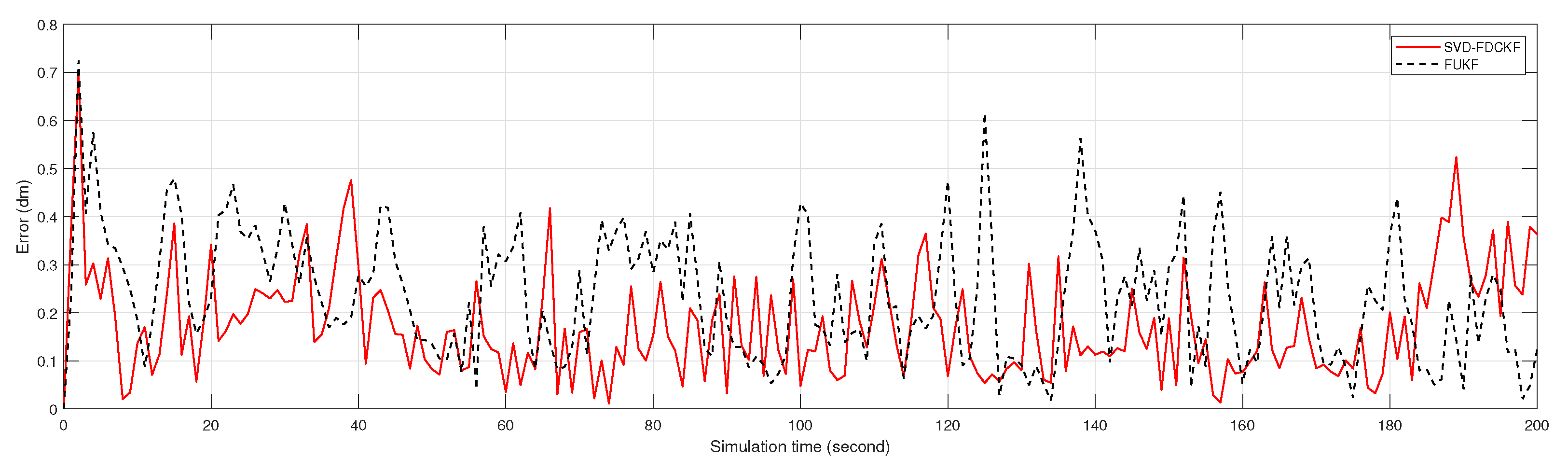
4.2. Comparison Test of SVD-FDCKF and FUKF
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ismail, M.B.; Fathi, A.; Boud, A.; Nurdiana, W.; Ibrahim, W. Implementation of location determination in a wireless local area network (WLAN) environment. In Proceedings of the 10th International Conference on Advanced Communication Technology, Phoenix Park, Korea, 17–20 February 2008; pp. 894–899. [Google Scholar]
- Iglesias, H.J.P.; Barral, V.; Escudero, C.J. Indoor person localization system through RSSI Bluetooth fingerprinting. In Proceedings of the 2012 International Conference on Systems, Signals and Image Processing (IWSSIP), Vienna, Austria, 11–13 April 2012; pp. 40–43. [Google Scholar]
- Li, Z.; Dehaene, W.; Gielen, G. System Design for Ultra-Low-Power UWB-based Indoor Localization. In Proceedings of the 2007 IEEE International Conference on Ultra-Wideband (ICUWB 2007), Singapore, 24–26 September 2007; pp. 159–164. [Google Scholar]
- Denis, B.; Pierrot, J.B.; Abou-Rjeily, C. Joint distributed synchronization and positioning in UWB ad hoc networks using TOA. IEEE Trans. Microw. Theory Tech. 2006, 54, 1896–1911. [Google Scholar] [CrossRef]
- Li, H.B.; Wang, J.; Wang, C.Y. Discussion on affection factors of UWB indoor kinematic positioning. J. Navig. Position. 2018, 6, 45–48. [Google Scholar]
- Hevrdejs, K.; Knoll, J.; Miah, S. A ZigBee-based framework for approximating sensor range and bearing. In Proceedings of the 30th IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April–3 May 2017. [Google Scholar]
- Jwo, D.J.; Weng, T.P. An Adaptive Sensor Fusion Method with Applications in Integrated Navigation. J. Navig. 2008, 61, 705–722. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S. A vehicular positioning with GPS/IMU using adaptive control of filter noise covariance. ICT Express 2016, 2, 41–46. [Google Scholar] [CrossRef][Green Version]
- Shen, F.; Cheong, J.W.; Dempster, A.G. A DSRC Doppler/IMU/GNSS Tightly-coupled Cooperative Positioning Method for Relative Positioning in VANETs. J. Navig. 2017, 70, 120–136. [Google Scholar] [CrossRef]
- Ruotsalainen, L.; Kirkko-Jaakkola, M.; Rantanen, J.; Maija, M. Error Modelling for Multi-Sensor Measurements in Infrastructure-Free Indoor Navigation. Sensors 2018, 18, 590. [Google Scholar] [CrossRef]
- decaWave. Available online: https://www.decawave.com/ (accessed on 15 January 2020).
- Krishnan, S.; Sharma, P.; Guoping, Z.; Woon, O.H. A UWB based Localization System for Indoor Robot Navigation. In Proceedings of the 2007 IEEE International Conference on Ultra-Wideband (ICUWB 2007), Singapore, 24–26 September 2007; pp. 77–82. [Google Scholar]
- Jiao, H.; Shen, C.; Feng, G.; Ling, P. Research on multi-tag anti-collision algorithm based on UWB real-time positioning system. In Proceedings of the IEEE Conference on Wireless Sensors (ICWiSE), Langkawi, Malaysia, 10–12 October 2016; pp. 54–58. [Google Scholar]
- Li, J.; Bi, Y.; Li, K.; Wang, K.; Lin, F.; Chen, B.M. Accurate 3D Localization for MAV Swarms by UWB and IMU Fusion. In Proceedings of the 2018 IEEE 14th International Conference on Control and Automation (ICCA), Anchorage, AK, USA, 12–15 June 2018; pp. 100–105. [Google Scholar]
- Corrales, J.A.; Candelas, F.A.; Torres, F. Hybrid tracking of human operators using IMU/UWB data fusion by a Kalman filter. In Proceedings of the 2008 3rd ACM/IEEE International Conference on Human-Robot Interaction (HRI 2008), Amsterdam, The Netherlands, 12–15 March 2008; pp. 193–200. [Google Scholar]
- Zihajehzadeh, S.; Yoon, P.K.; Park, E.J. A magnetometer-free indoor human localization based on loosely coupled IMU/UWB fusion. In Proceedings of the 37th Annual International Conference of the IEEE-Engineering-in-Medicine-and-Biology-Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 3141–3144. [Google Scholar]
- Wan, Y.; Keviczky, T. Real-time fault-tolerant moving horizon air data estimation for the RECONFIGURE benchmark. IEEE Trans. Control Syst. Technol. 2019, 27, 997–1011. [Google Scholar] [CrossRef]
- Alspach, D.; Sorenson, H. Nonlinear Bayesian estimation using Gaussian sum approximations. IEEE Trans. Autom. Control. 1972, 17, 439–448. [Google Scholar] [CrossRef]
- Djuric, P.M.; Chun, J.H. An MCMC sampling approach to estimation of nonstationary hidden Markov models. IEEE Trans. Signal Process. 2002, 50, 1113–1123. [Google Scholar] [CrossRef]
- Doucet, A.; Logothetis, A.; Krishnamurthy, V. Stochastic sampling algorithms for state estimation of jump Markov linear systems. IEEE Trans. Autom. Control. 2000, 45, 188–202. [Google Scholar] [CrossRef]
- Murphy, R.R. Dempster-Shafer theory for sensor fusion in autonomous mobile robots. IEEE Trans. Robot. Autom. 1998, 14, 197–206. [Google Scholar] [CrossRef]
- Bloch, I. Information combination operators for data fusion: A comparative review with classification. IEEE Trans. Syst. Man Cybern. 1996, 26, 52–67. [Google Scholar] [CrossRef]
- Peers, S.M.C. A blackboard system approach to electromagnetic sensor data interpretation. Expert Syst. 2008, 15, 197–215. [Google Scholar] [CrossRef]
- Ljung, L. Asymptotic behavior of the extended Kalman filter as a parameter estimator for linear systems. IEEE Trans. Autom. Control. 1979, 24, 36–50. [Google Scholar] [CrossRef]
- Sabatini, A.M. Variable-State-Dimension Kalman-Based Filter for Orientation Determination Using Inertial and Magnetic Sensors. Sensors 2012, 12, 8491–8506. [Google Scholar] [CrossRef]
- Julier, S.J. Unscented filtering and nonlinear estimation. IEEE Proc. 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Carlos, S.; de Marina, H.G.; Felipe, E. Adaptive UAV Attitude Estimation Employing Unscented Kalman Filter, FOAM and Low-Cost MEMS Sensors. Sensors 2012, 12, 9566–9585. [Google Scholar]
- Guoliang, C.; Xiaolin, M.; Yunjia, W.; Yanzhe, Z.; Peng, T.; Huachao, Y. Integrated WiFi/PDR/Smartphone Using an Unscented Kalman Filter Algorithm for 3D Indoor Localization. Sensors 2015, 15, 24595–24614. [Google Scholar]
- Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans. Autom. Control. 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman smoothers. Automatica 2011, 47, 2245–2250. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S.; Hurd, T.R. Cubature Kalman Filtering for Continuous-Discrete Systems: Theory and Simulations. IEEE Trans. Signal Process. 2010, 58, 4977–4993. [Google Scholar] [CrossRef]
- Wei, Z.; Wei, W.; Gannan, Y. An Improved Interacting Multiple Model Filtering Algorithm Based on the Cubature Kalman Filter for Maneuvering Target Tracking. Sensors 2016, 16, 805. [Google Scholar]
- Yu, C.; Chen, J.; Verhaegen, M. Subspace Identification of Individual Systems in a Large-Scale Heterogeneous Network. Automatica 2019, 109, 108517. [Google Scholar] [CrossRef]
- Yu, C.; Ljung, L.; Wills, A.; Verhaegen, M. Constrained Subspace Method for the Identification of Structured State-Space Models. IEEE Trans. Autom. Control. 2019. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Gao, Z. Distributed optimal control for multiple high-speed train movement: An alternating direction method of multipliers. Automatica 2020, 112, 108646. [Google Scholar] [CrossRef]
- Carlson, N.A. Information-sharing approach to federated Kalman filtering. In Proceedings of the IEEE 1988 National Aerospace and Electronics Conference: NAECON 1988, Dayton, OH, USA, 23–28 May 1988; p. 1581. [Google Scholar]
- Wang, G.; Li, N.; Zhang, Y. Diffusion distributed Kalman filter over sensor networks without exchanging raw measurements. Signal Process. 2017, 132, 1–7. [Google Scholar] [CrossRef]
- Xu, Z.Z.; Zhuang, Y.B. Comparative study of methods for mobile robot localization. J. Syst. Simul. 2009, 21, 1891–1896. [Google Scholar]
- Hajiyev, C.; Cilden, D.; Somov, Y. Integrated SVD/EKF for Small Satellite Attitude Determination and Rate Gyro Bias Estimation. IFAC Pap. Online 2015, 48, 233–238. [Google Scholar] [CrossRef]
- Sun, L.; Huang, G.; Li, Y. Exploration of improved strong tracking SVD-UKF used in BDS/INS integrated navigation. Comput. Eng. Appl. 2017, 53, 225–229. [Google Scholar]
- Crassidis, J.L.; Markley, F.L. Unscented filtering for spacecraft attitude estimation. J. Guid. Control Dyn. 2003, 26, 536–542. [Google Scholar] [CrossRef]
- Merwe, R.V.D.; Wan, E.A. The square-root unscented Kalman filter for state and parameter-estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001; pp. 3461–3464. [Google Scholar]
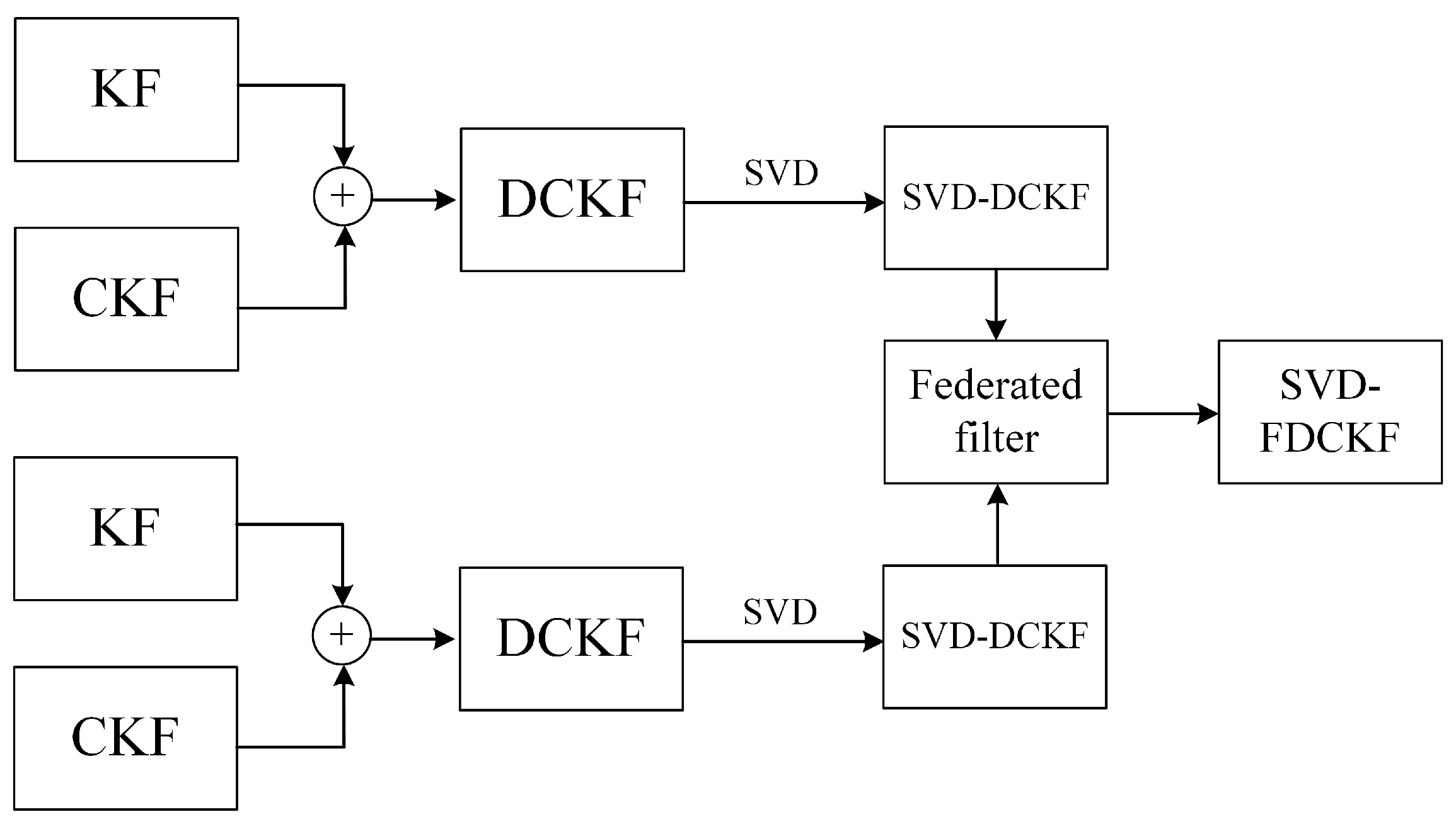



| A method for state estimation of linear systems. | |
| A method for state estimation of nonlinear systems. | |
| Aiming at the system introduced in this article, a derivative algorithm is proposed by combining the KF and CKF algorithms. The KF algorithm is used for the linear part of the system, and the CKF algorithm is used for the nonlinear part of the system. | |
| The Cholesky decomposition for solving cubature points in the DCKF algorithm is replaced with SVD decomposition. | |
| An information fusion framework. | |
| Apply SVD-DCKF as a sub-filter to the federated filter. |
| Step | CKF | DCKF | Flops Difference |
|---|---|---|---|
| Calculate the measurement cubature point | none | ||
| Estimate the predicted measurement | |||
| Calculate Kalman gain | |||
| See (26) and (27) for details | |||
| Update states | × | ||
| Update error covariance | × |
| Method | Average Error/dm | Variance/dm |
|---|---|---|
| SVD-FDCKF | 0.1721 | 0.0119 |
| FDCKF | 0.1919 | 0.0138 |
| FCKF | 0.2006 | 0.0146 |
| Method | Average Error/dm | Variance/dm |
|---|---|---|
| SVD-FDCKF | 0.1721 | 0.0119 |
| FUKF | 0.2344 | 0.0171 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, C.; Tang, C.; Yu, C. A Federated Derivative Cubature Kalman Filter for IMU-UWB Indoor Positioning. Sensors 2020, 20, 3514. https://doi.org/10.3390/s20123514
He C, Tang C, Yu C. A Federated Derivative Cubature Kalman Filter for IMU-UWB Indoor Positioning. Sensors. 2020; 20(12):3514. https://doi.org/10.3390/s20123514
Chicago/Turabian StyleHe, Chengyang, Chao Tang, and Chengpu Yu. 2020. "A Federated Derivative Cubature Kalman Filter for IMU-UWB Indoor Positioning" Sensors 20, no. 12: 3514. https://doi.org/10.3390/s20123514
APA StyleHe, C., Tang, C., & Yu, C. (2020). A Federated Derivative Cubature Kalman Filter for IMU-UWB Indoor Positioning. Sensors, 20(12), 3514. https://doi.org/10.3390/s20123514




