An Application of the Orthogonal Matching Pursuit Algorithm in Space-Time Adaptive Processing
Abstract
1. Introduction
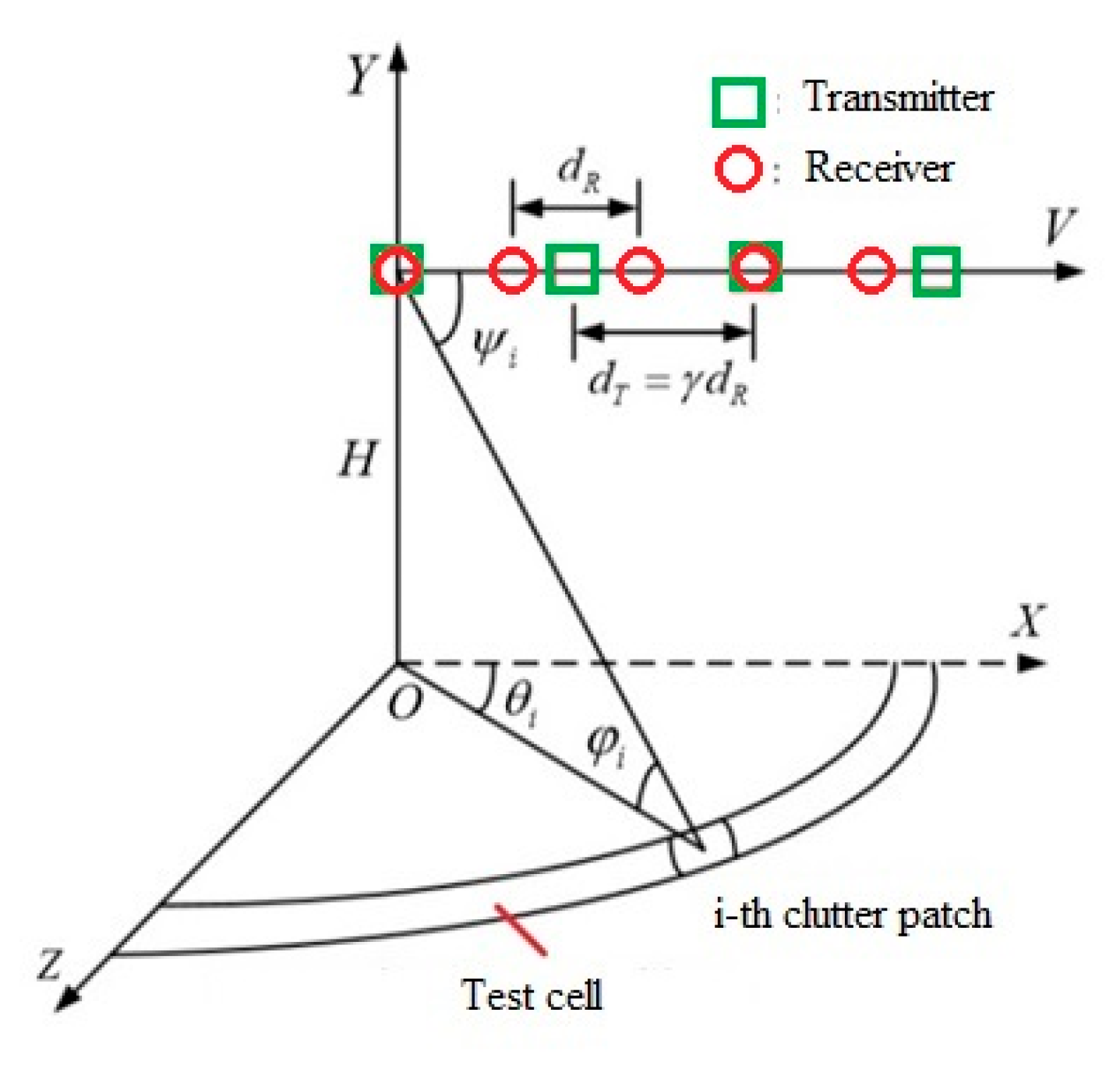
2. Model of System Geometry and Model of Signal
3. Joint Sparse Recovery Model
4. Application of Sparse Recovery Algorithms
5. Definition of Clutter Plus Noise Covariance Matrix and Weight Vector
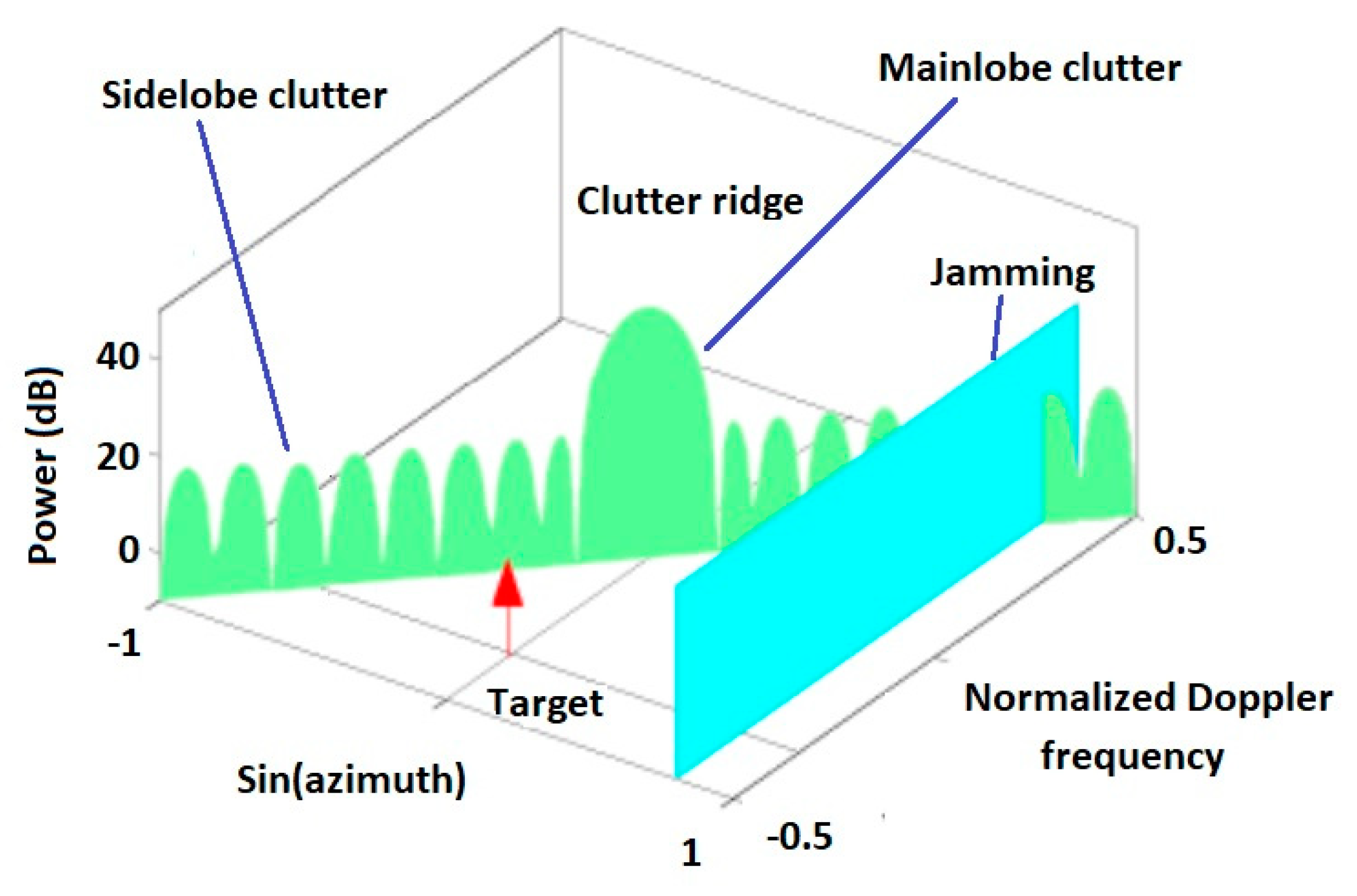
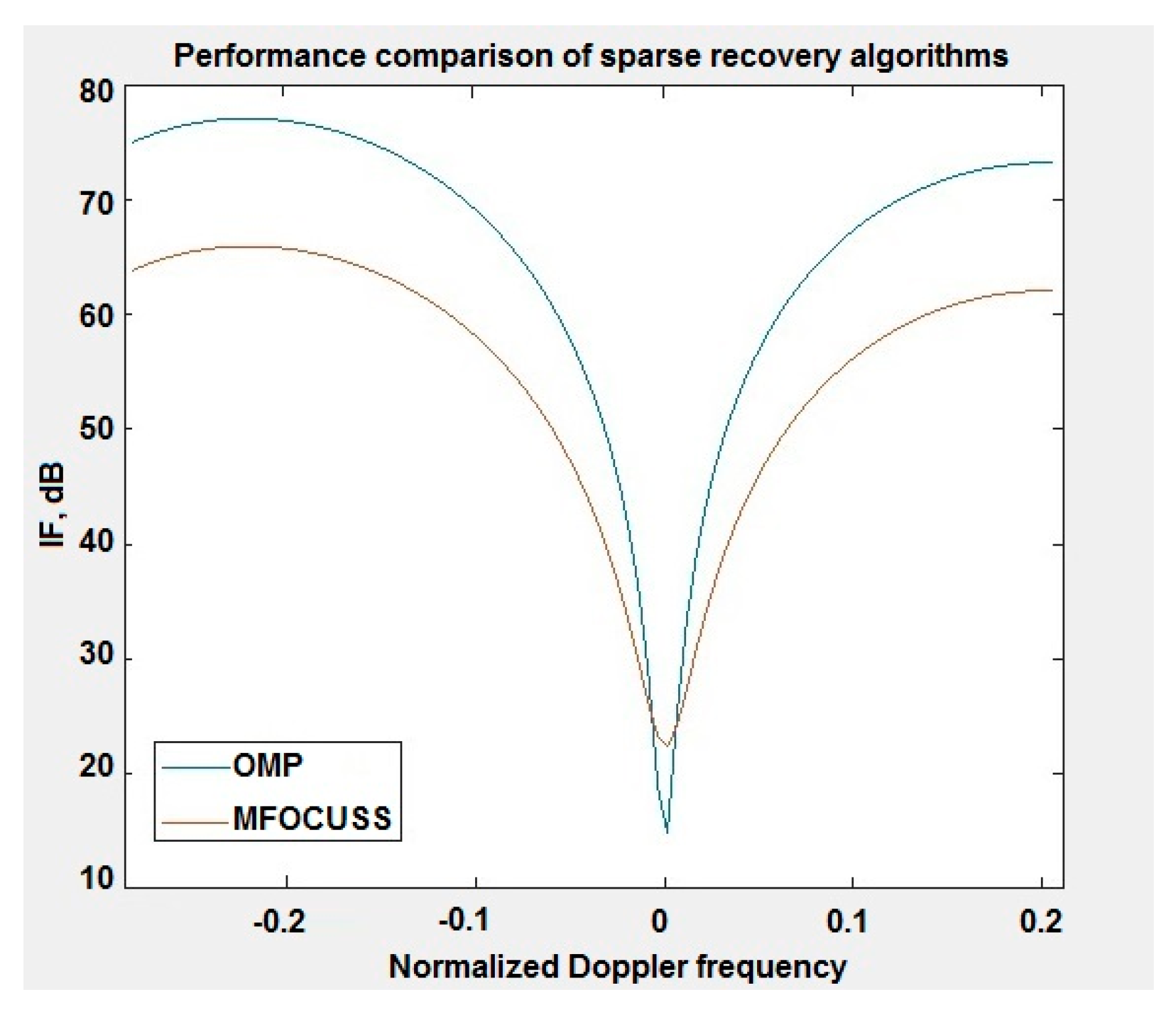
6. Simulation Results
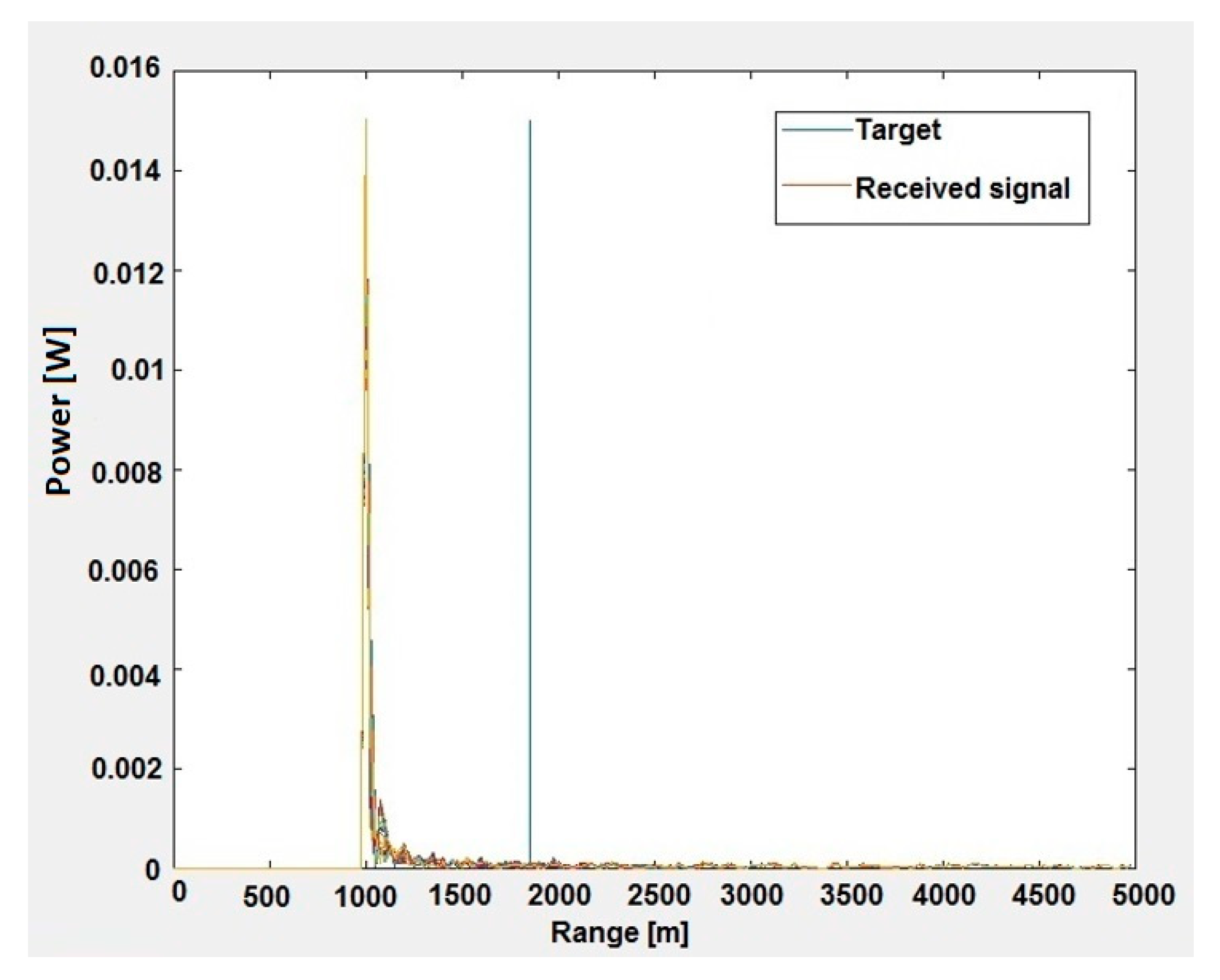
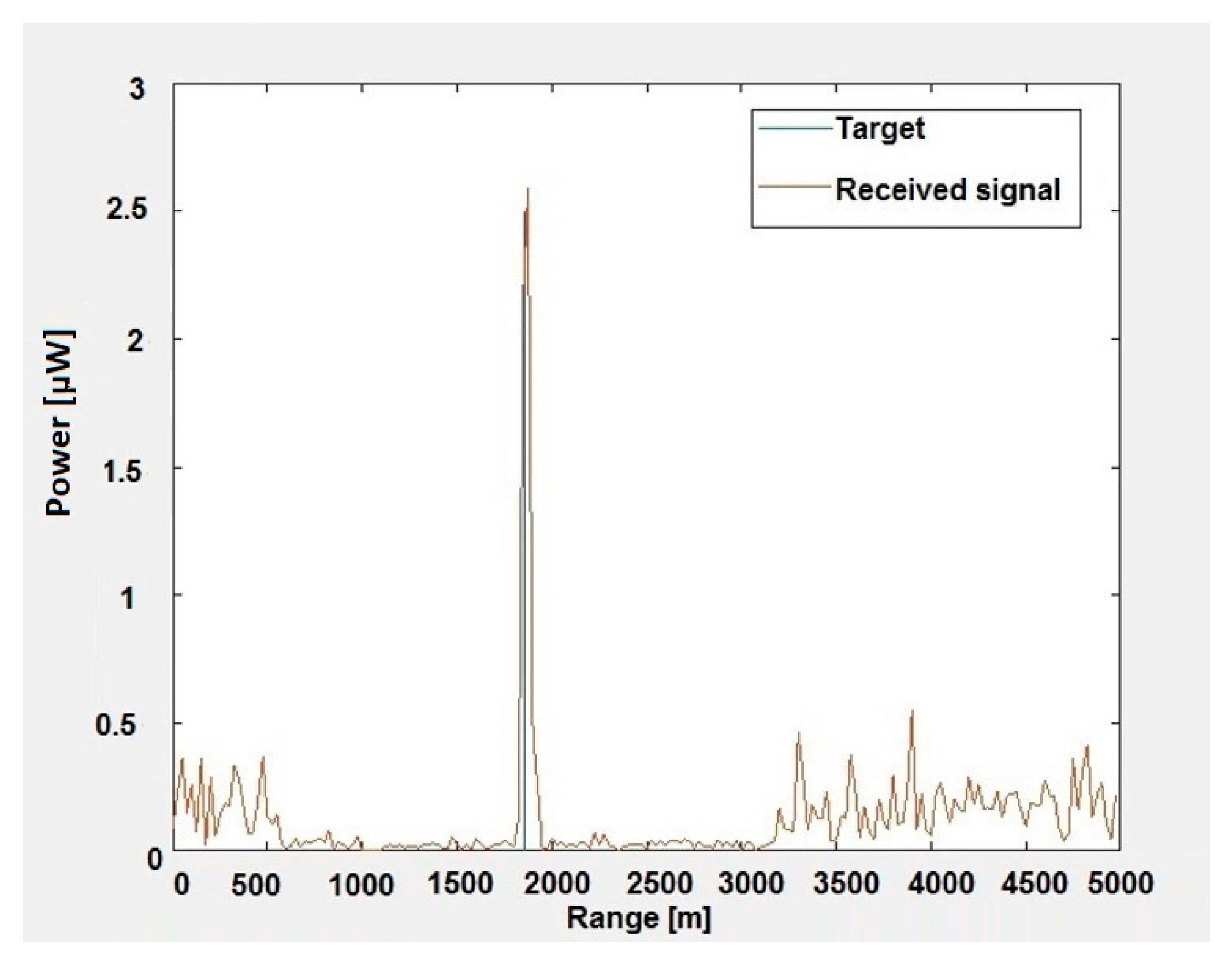
6.1. Performance of Spatio-Temporal Spectrum Estimation and Target Detection
6.2. Performance of Clutter Suppression
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Application of M-FOCCUS Algorithm
- Initialization of the algorithm—setting initial variables. It was assumed that:where Y0,i, i = 1, 2, …, NsKd denotes ith row of Y0, Y0,i(j) denotes jth element of Y0,i, j = 1, 2, …, M.
- Calculation of the weight matrix W:while the other elements of the weight matrix are zeros. Wt denotes the t-th (t = 1, 2, …, tmax) iteration weight matrix W, tmax denotes maximum number of iterations and Ct−1 denotes the (t−1)-th iteration value of C.
- Iteration loop:where Yt and Ct represent t-th iteration value of Y and C respectively, Yt,i, i = 1, 2, …, NsKd is i-th row Yt, Yt,i(j) is jth element of Yt,i and (∙)ϯ denotes the matrix pseudo-inverse.
- Condition to stop iteration:If the convergence condition is met and the maximum number of iterations has been reached, the iteration is stopped, and the calculation result is 𝜰0 = Yt. Otherwise, return to step 2.
Appendix B
Application of OMP Algorithm
- Initialization of the algorithm—setting initial variables. It was assumed that:where r0 indicates an approximation error, 𝛤0 denotes the selected set of dictionary atoms and 𝜰0 is the wanted spectrum.
- Iteration loop consists of eight consecutive steps:where 𝜙T indicates the transposition of a normalized dictionary 𝛹, p𝛤n is a new direction and d𝛤n is the given column vector of the dictionary 𝛹.The OMP algorithm in the first step selects from the dictionary 𝜙T the given atom 𝛤n best matched to the X vector, i.e., giving the largest value of the scalar product with the X vector. In each subsequent step, the atoms are analogously matched to the residue rn−1, remain after subtracting the result of the previous iteration, and the residue rn is determined. The atom is selected from the dictionary in each iteration step; it meets the obvious condition in = arg max | gin |.
- Condition to stop iteration:If the convergence condition is satisfied for the assumed ε, the iteration is stopped and the result of the calculation is 𝜰n𝛤n. Otherwise, return to step 2.
References
- Dong, R.; Zheng, B. Direct data domain STAP algorithm for airborne radar applications. In Proceedings of the 2001 CIE International Conference on Radar, Beijing, China, 15–18 October 2001. [Google Scholar]
- Sarkar, T.; Koh, J.; Adve, R.; Schneible, R.; Wicks, M.; Choi, S.; Salazar-Palma, M. A pragmatic approach to adaptive antennas. IEEE Antennas Propag. Mag. 2000, 42, 39–55. [Google Scholar] [CrossRef]
- Burintramart, S.; Sarkar, T.K.; Zhang, Y.; Wicks, M.C. Performance comparison between statistical-based and direct data domain STAPs. Digit. Signal Process. 2007, 17, 737–755. [Google Scholar] [CrossRef]
- Carlo, J.; Sarkar, T.; Wicks, M. A least squares multiple constraint direct data domain approach for STAP. In Proceedings of the 2003 IEEE Radar Conference, Huntsville, AL, USA, 8 May 2003; pp. 431–438. [Google Scholar] [CrossRef]
- Li, M.; Sun, G.; He, Z. Direct Data Domain STAP Based on Atomic Norm Minimization. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Adve, R.S.; Hale, T.B.; Wicks, M.C. A two stage hybrid space-time adaptive processing algorithm. In Proceedings of the 1999 IEEE Radar Conference. Radar into the Next Millennium, Waltham, MA, USA, 22 April 1999; pp. 279–284. [Google Scholar]
- Choi, W.; Sarkar, T.; Wang, H.; Mokole, E.L. Adaptive processing using real weights based on a direct data domain least squares approach. IEEE Trans. Antennas Propag. 2006, 54, 182–191. [Google Scholar] [CrossRef]
- Sun, K.; Meng, H.; Wang, Y.; Wang, X. Direct data domain STAP using sparse representation of clutter spectrum. Signal Process. 2011, 91, 2222–2236. [Google Scholar] [CrossRef]
- Jeon, H.; Chung, Y.; Chung, W.; Kim, J.; Yang, H. Clutter covariance matrix estimation using weight vectors in knowledge-aided STAP. Electron. Lett. 2017, 53, 560–562. [Google Scholar] [CrossRef]
- Peng, H.; Sun, Y.; Yang, X.; Yang, J. Robust knowledge-aided sparse recovery STAP method for non-homogeneity clutter suppression. J. Eng. 2019, 2019, 6373–6376. [Google Scholar] [CrossRef]
- Sen, S. Low-Rank Matrix Decomposition and Spatio-Temporal Sparse Recovery for STAP Radar. IEEE J. Sel. Top. Signal Process. 2015, 9, 1510–1523. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, Y.; Meng, H.; Wang, X. Jointly sparse recovery of multiple snapshots in STAP. In Proceedings of the 2013 IEEE Radar Conference (RadarCon13), Ottawa, ON, Canada, 29 April–3 May 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Wang, H.; Fa, R. Knowledge-aided STAP with sparse-recovery by exploiting spatio-temporal sparsity. IET Signal Process. 2016, 10, 150–161. [Google Scholar] [CrossRef]
- Duan, K.; Wang, Z.; Xie, W.; Chen, H.; Wang, Y. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar. IET Signal Process. 2017, 11, 544–553. [Google Scholar] [CrossRef]
- Guo, Y.; Liao, G.; Feng, W. Sparse Representation Based Algorithm for Airborne Radar in Beam-Space Post-Doppler Reduced-Dimension Space-Time Adaptive Processing. IEEE Access 2017, 5, 5896–5903. [Google Scholar] [CrossRef]
- Zhang, W.; An, R.; He, N.; He, Z.; Li, H. Reduced Dimension STAP Based on Sparse Recovery in Heterogeneous Clutter Environments. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 785–795. [Google Scholar] [CrossRef]
- Ward, J. Space-time adaptive processing for airborne radar. In Proceedings of the IEE Colloquium on Space-Time Adaptive Processing, London, UK, 6 April 1998. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, Y. MMV-JSR based STAP method using MIMO radar. IEICE Commun. Express 2016, 5, 163–168. [Google Scholar] [CrossRef]
- Chen, J.; Huo, X. Theoretical Results on Sparse Representations of Multiple-Measurement Vectors. IEEE Trans. Signal Process. 2006, 54, 4634–4643. [Google Scholar] [CrossRef]
- Knee, P. Sparse Representations for Radar with MATLAB®Examples. Synth. Lect. Algorithms Softw. Eng. 2012, 4, 1–85. [Google Scholar] [CrossRef]
- Le Caillec, J.-M.; Gorski, T.; Sicot, G.; Kawalec, A. Theoretical Performance of Space-Time Adaptive Processing for Ship Detection by High-Frequency Surface Wave Radars. IEEE J. Ocean. Eng. 2018, 43, 238–257. [Google Scholar] [CrossRef]
- Klemm, R. Principles of Space-Time Adaptive Processing, 3rd ed.; Institution of Engineering and Technology: London, UK, 2006. [Google Scholar]


| Parameter | Value |
|---|---|
| number of transmitters of MIMO radar | 18 |
| number of receivers of MIMO radar | 8 |
| number of pulses | 8 |
| wavelength | 0.23 m |
| distance between transmitters | 0.115 m |
| distance between receivers | 0.115 m |
| distance between elements of the antenna array | 0.115 m |
| flight altitude of the platform | 5 km |
| velocity of the platform | 250 m/s |
| pulse repetition frequency | 4347.8 Hz |
| normalized Doppler frequency of target | 0.2 |
| normalized spatial frequency of target | 0.2 |
| clutter-to-noise ratio | 30 dB |
| signal-to-noise ratio | 10 dB |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ślesicka, A.; Kawalec, A. An Application of the Orthogonal Matching Pursuit Algorithm in Space-Time Adaptive Processing. Sensors 2020, 20, 3468. https://doi.org/10.3390/s20123468
Ślesicka A, Kawalec A. An Application of the Orthogonal Matching Pursuit Algorithm in Space-Time Adaptive Processing. Sensors. 2020; 20(12):3468. https://doi.org/10.3390/s20123468
Chicago/Turabian StyleŚlesicka, Anna, and Adam Kawalec. 2020. "An Application of the Orthogonal Matching Pursuit Algorithm in Space-Time Adaptive Processing" Sensors 20, no. 12: 3468. https://doi.org/10.3390/s20123468
APA StyleŚlesicka, A., & Kawalec, A. (2020). An Application of the Orthogonal Matching Pursuit Algorithm in Space-Time Adaptive Processing. Sensors, 20(12), 3468. https://doi.org/10.3390/s20123468





