Visual Saliency Detection for Over-Temperature Regions in 3D Space via Dual-Source Images
Abstract
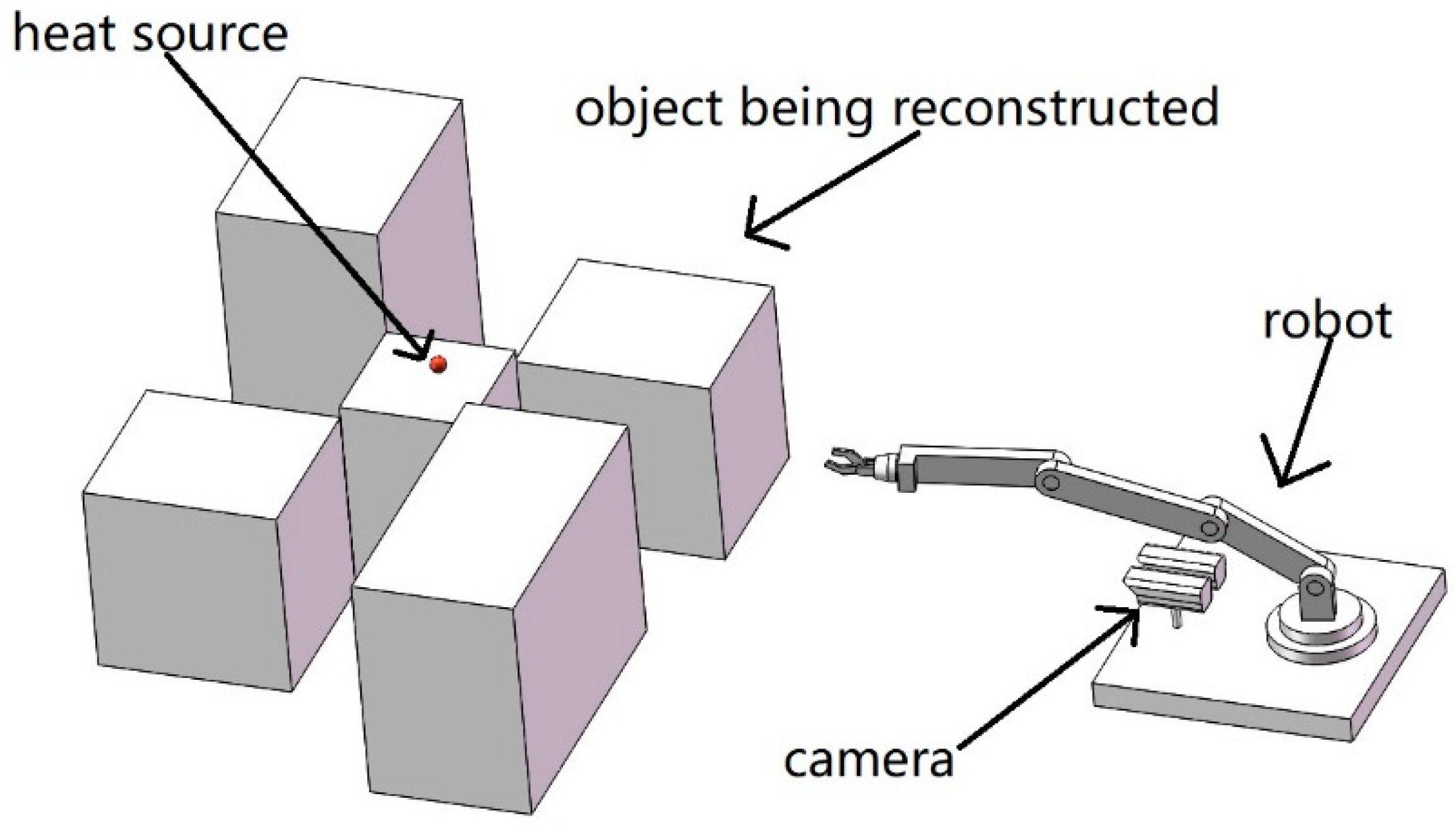
1. Introduction
2. Materials and Methods
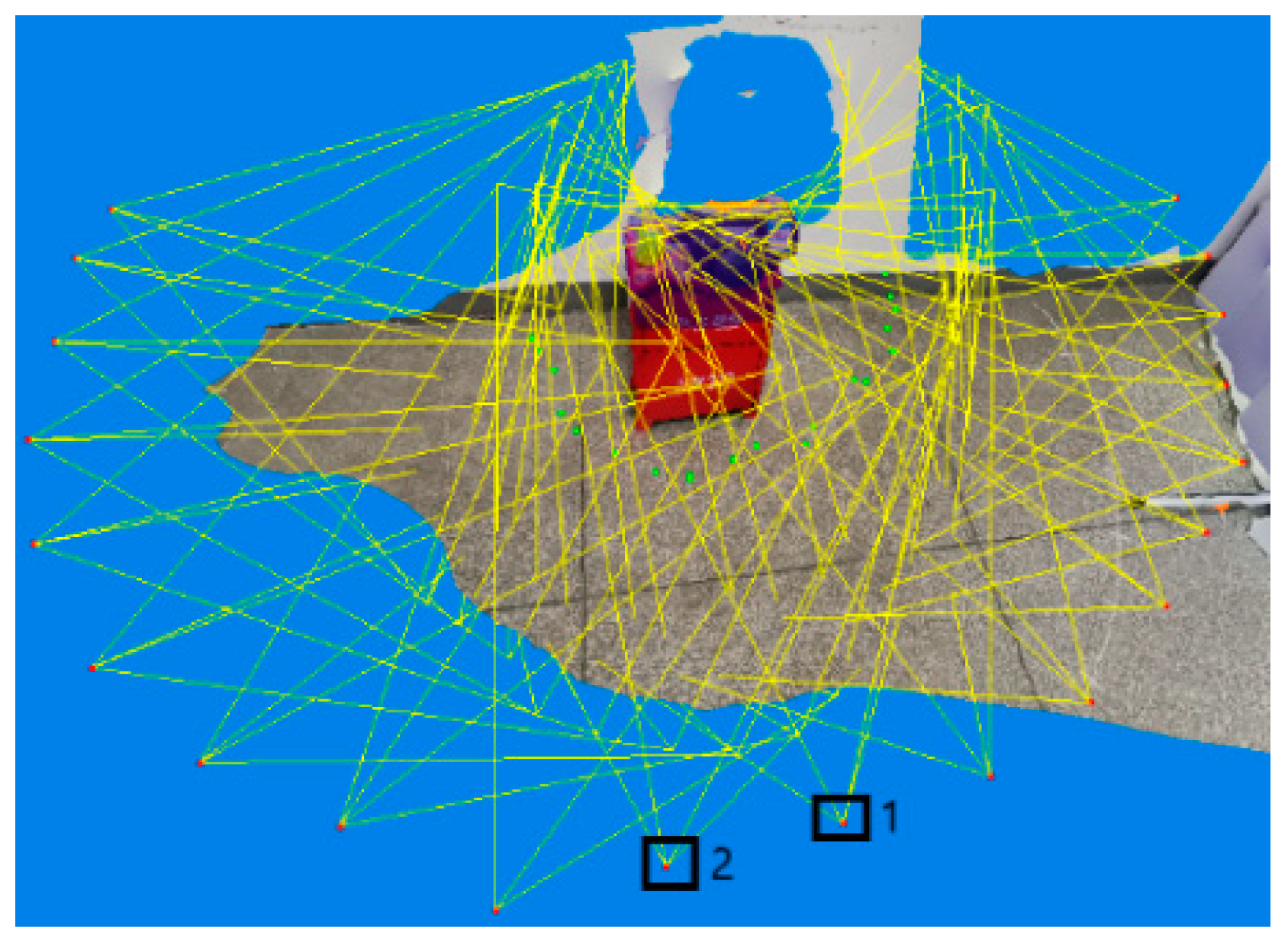
2.1. Reconstruction of the Sparse Point Cloud to Obtain the Camera Attitude
2.1.1. Use of the Scale-Invariant Feature Transform (SIFT) Algorithm to Find Feature Points
- Multi-scale spatial extreme point detection: This searches image locations on all scales and uses Gaussian differential functions to identify potential rotation invariants and scale candidate points.
- Accurate positioning of key points: After determining candidate positions, a high-precision model is fitted to determine the scale and position. The stability of key points is used as the basis for selection.
- Calculation of the main direction of key points: Based on the local gradient direction of the image, each key point obtains one or more directions. In the future, the image processing will be transformed relative to the key-point scale, direction, and position to ensure the invariance of the transformation.
- Descriptor construction: In the field of key points, the direction of local gradients is measured according to the scale selected above, and these gradients are transformed into another representation.
2.1.2. Error Matching Elimination Based on the RANSAC Algorithm
2.1.3. The Position Pose of the Phase Machine Is Solved by the Beam Adjustment Method
2.2. Three-Dimensional Surface Generation
2.2.1. Adaptive Random Sampling
- A pixel point is randomly selected from the obtained point cloud image. is the depth value of the pixel point and is inversely mapped into the three-dimensional space according to Equation (4). The tangent plane is obtained according to the normal direction. is the camera internal parameter, is the rotation matrix, and is the translation vector.
- Expand outwards with as the center, expand the radius r one pixel at a time, and calculate the three-dimensional coordinates of each pixel in the expansion range.
- Calculate the distance of each pixel to the tangent plane within the current expansion range, and set the threshold size as . If , the pixel point can be considered to be in the smooth area, and the point can be removed.
- When the expansion radius r is larger than the maximum expansion radius , or a point cloud of a certain proportion of in the expansion range is removed, the expansion stops. and are tunable parameters. They can be determined according to the point cloud redundancy. During debugging, it is found that there are still many redundant point clouds after culling. can be increased and can be decreased. If the point cloud is over-eliminated, the parameter adjustment method is reversed.
- Then, randomly select a pixel point and repeat the above steps until all the sampling points in the current 3D point cloud image are sampled.
2.2.2. Deep Confidence Removes the Cloud of Error Points
- The point cloud for the current frame k is sorted from high to low according to the estimated value, and the confidence threshold is set, starting from the point where the estimated value is the smallest. If , the point is eliminated, the calculation continues until stops, and the remaining point clouds are stored in the sequence . Then, the same calculation is performed on the next frame point cloud image until the point cloud image is calculated and the sequence set is obtained.
- Starting from the k frame depth map, all three-dimensional points are mapped to on the k + 1 frame. Compare the estimated values of the two points, the s.
- maller three-dimensional coordinates of the larger estimated points of the estimated values, and so on, until all depth maps are completed.
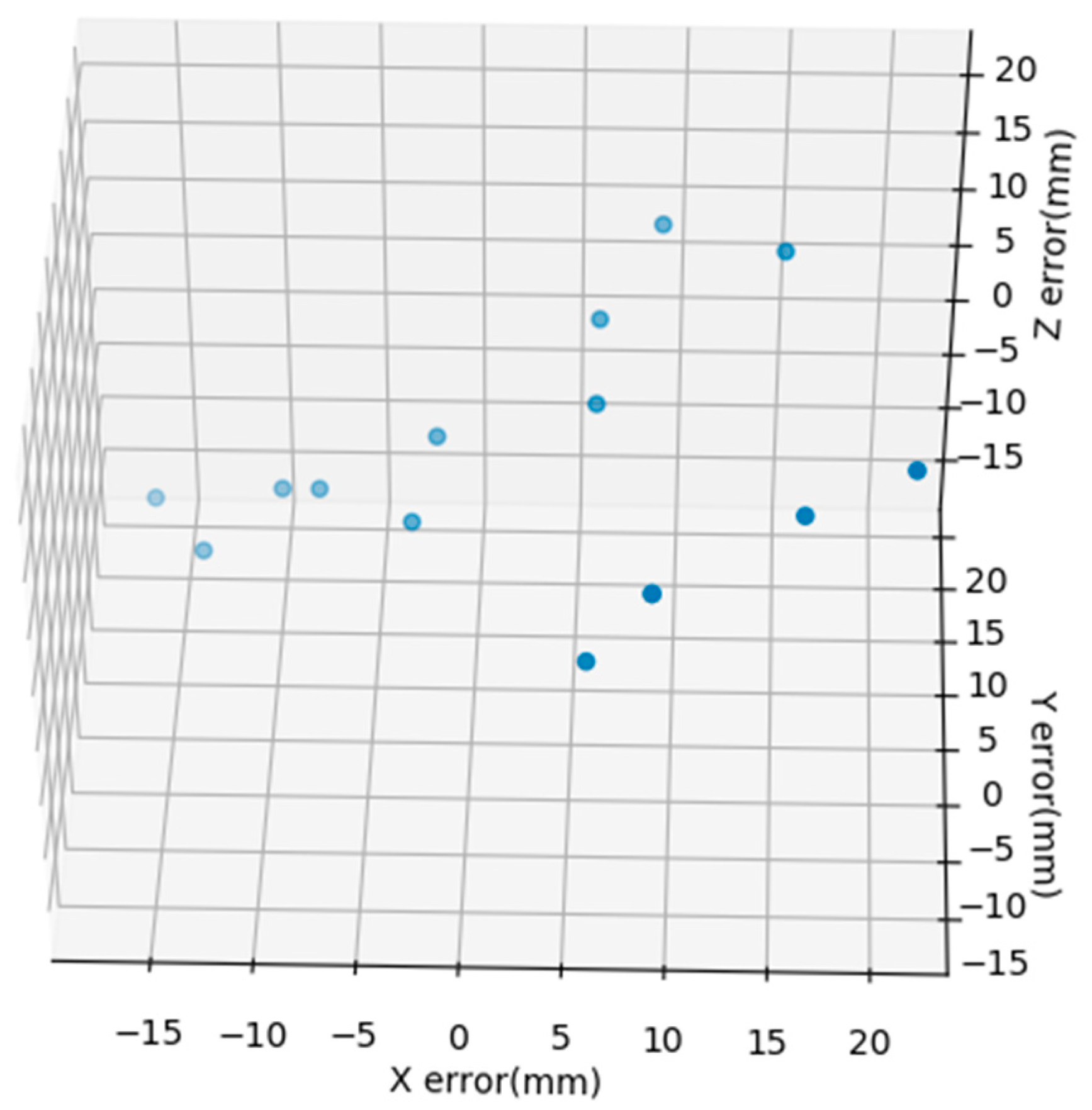
- The three-dimensional sampling points of all depth maps are intersected to obtain the final three-dimensional point cloud image. Then, perform the mesh reconstruction and mesh texture generation on the filtered dense point cloud. The effect before and after filtering is shown in Figure 5.
2.3. Image Fusion
2.3.1. Calculate Scale Factor
2.3.2. Relative Offset of the Image
2.4. 3D Target Detection
2.4.1. Target Detection of the Heat Source
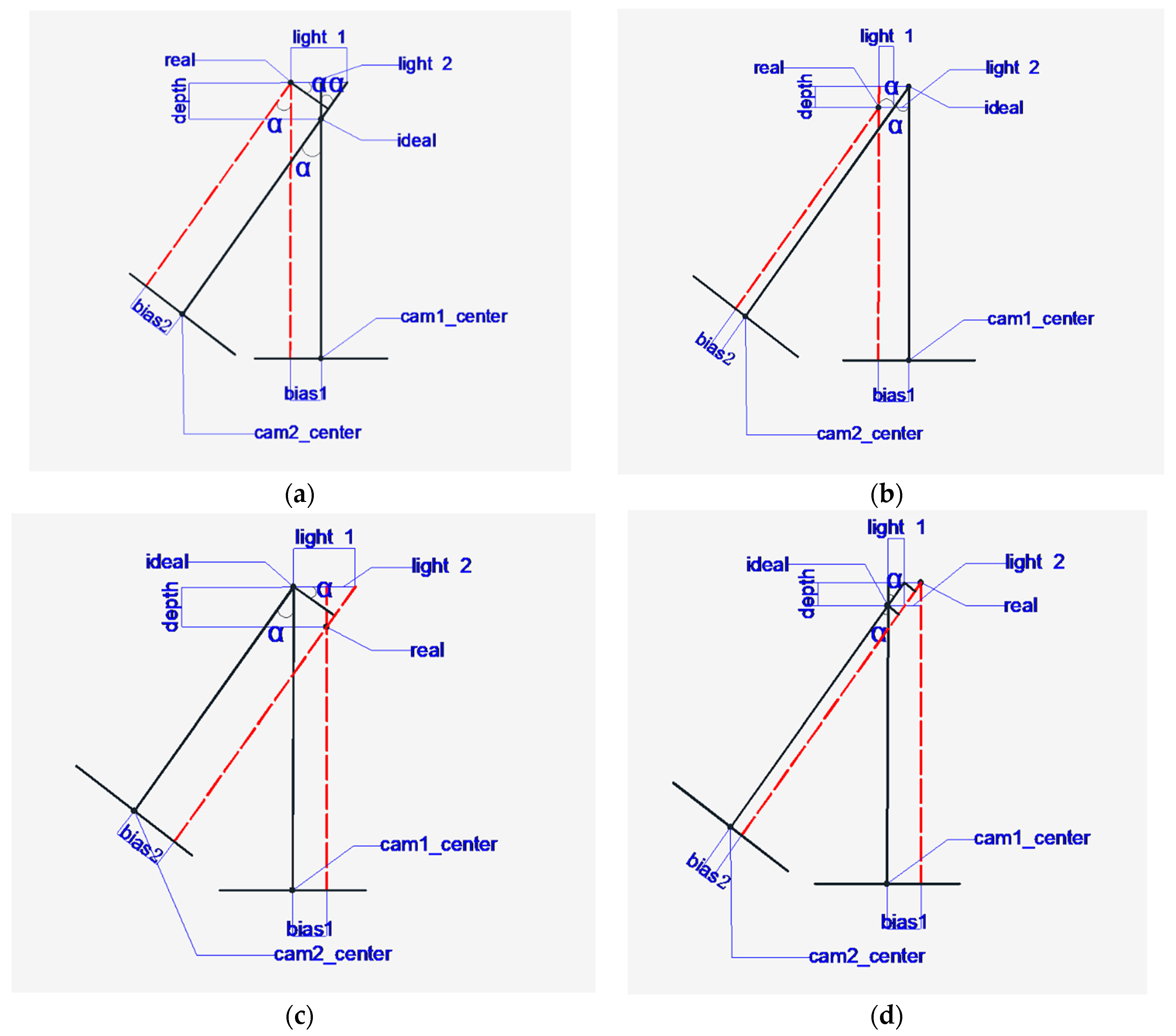
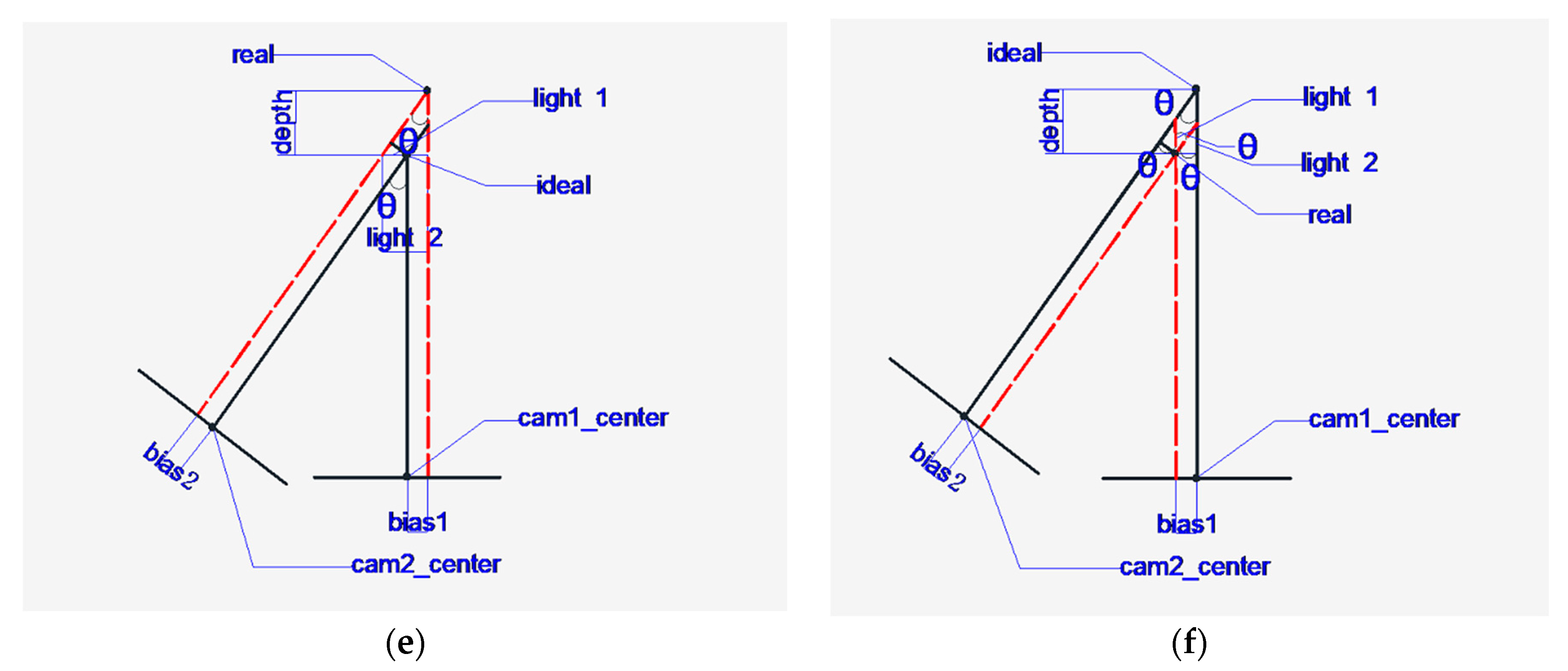
2.4.2. Coordinate Transformation Mapping in 3D Space
3. Conclusions
4. Patents
Author Contributions
Funding
Conflicts of Interest
References
- Fan, Y.; Lv, X.; Lin, J.; Ma, J.; Zhang, G.; Zhang, L.; Correction: Zhang, G. Autonomous Operation Method of Multi-DOF Robotic Arm Based on Binocular Vision. Appl. Sci. 2019, 9, 5294. [Google Scholar] [CrossRef]
- Kassir, M.M.; Palhang, M.; Ahmadzadeh, M.R. Qualitative vision-based navigation based on sloped funnel lane concept. Intell. Serv. Robot. 2018, 13, 235–250. [Google Scholar] [CrossRef]
- Li, C.; Yu, L.; Fei, S. Large-Scale, Real-Time 3D Scene Reconstruction Using Visual and IMU Sensors. IEEE Sens. J. 2020, 20, 5597–5605. [Google Scholar] [CrossRef]
- Yang, C.; Jiang, Y.; He, W.; Na, J.; Li, Z.; Xu, B. Adaptive Parameter Estimation and Control Design for Robot Manipulators with Finite-Time Convergence. IEEE Trans. Ind. Electron. 2018, 65, 8112–8123. [Google Scholar] [CrossRef]
- Yang, C.; Peng, G.; Cheng, L.; Na, J.; Li, Z. Force Sensorless Admittance Control for Teleoperation of Uncertain Robot Manipulator Using Neural Networks. IEEE Trans. Syst. ManCybern. Syst. 2019. [Google Scholar] [CrossRef]
- Peng, G.; Yang, C.; He, W.; Chen, C.P. Force Sensorless Admittance Control with Neural Learning for Robots with Actuator Saturation. IEEE Trans. Ind. Electron. 2020, 67, 3138–3148. [Google Scholar] [CrossRef]
- Mao, C.; Li, S.; Chen, Z.; Zhang, X.; Li, C. Robust kinematic calibration for improving collaboration accuracy of dual-arm manipulators with experimental validation. Measurement 2020, 155, 107524. [Google Scholar] [CrossRef]
- Xu, L.; Feng, C.; Kamat, V.R.; Menassa, C.C. A scene-adaptive descriptor for visual SLAM-based locating applications in built environments. Autom. Constr. 2020, 112, 103067. [Google Scholar] [CrossRef]
- Yang, C.; Wu, H.; Li, Z.; He, W.; Wang, N.; Su, C.Y. Mind Control of a Robotic Arm with Visual Fusion Technology. IEEE Trans. Ind. Inform. 2018, 14, 3822–3830. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, T.; Chen, Z.; Song, H.; Yang, C. Adaptive Fuzzy Gaussian Mixture Models for Shape Approximation in Robot Grasping. Int. J. Fuzzy Syst. 2019, 21, 1026–1037. [Google Scholar] [CrossRef]
- Shen, S. Accurate Multiple View 3D Reconstruction Using Patch-Based Stereo for Large-Scale Scenes. IEEE Trans. Image Process. 2013, 22, 1901–1914. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Li, R.; Sun, J.; Liu, X.; Zhao, L.; Seah, H.S.; Quah, C.K.; Tandianus, B. Multi-View Fusion-Based 3D Object Detection for Robot Indoor Scene Perception. Sensors 2019, 19, 4092. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, T.; Sugimura, D.; Hamamoto, T. Discovering Correspondence Among Image Sets with Projection View Preservation For 3D Object Detection in Point Clouds. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 3111–3115. [Google Scholar]
- Zhou, Y.; Tuzel, O. VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Fu, K.; Zhao, Q.; Gu, I.Y.; Yang, J. Deepside: A general deep framework for salient object detection. Neurocomputing 2019, 356, 69–82. [Google Scholar] [CrossRef]
- Wang, W.; Shen, J. Deep Visual Attention Prediction. IEEE Trans. Image Process. 2018, 27, 2368–2378. [Google Scholar] [CrossRef]
- Tang, Y.; Zou, W.; Hua, Y.; Jin, Z.; Li, X. Video salient object detection via spatiotemporal attention neural networks. Neurocomputing 2020, 377, 27–37. [Google Scholar] [CrossRef]
- Zhao, J.X.; Liu, J.J.; Fan, D.P.; Cao, Y.; Yang, J.; Cheng, M.M. EGNet:Edge Guidance Network for Salient Object Detection. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Ren, Q.; Hu, R. Multi-scale deep encoder-decoder network for salient object detection. Neurocomputing 2018, 316, 95–104. [Google Scholar] [CrossRef]
- Fan, D.P.; Cheng, M.M.; Liu, J.J.; Gao, S.H.; Hou, Q.; Borji, A. Salient Objects in Clutter: Bringing Salient Object Detection to the Foreground. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Zhang, J.; Yu, X.; Li, A.; Song, P.; Liu, B.; Dai, Y. Weakly-Supervised Salient Object Detection via Scribble Annotations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–18 June 2020. [Google Scholar]
- Zhang, J.; Fan, D.P.; Dai, Y.; Anwar, S.; Saleh, F.S.; Zhang, T.; Barnes, N. UC-Net: Uncertainty Inspired RGB-D Saliency Detection via Conditional Variational Autoencoders. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–18 June 2020. [Google Scholar]
- Wang, Z.; Liu, J. Research on flame location based on adaptive window and weight stereo matching algorithm. Multimed. Tools Appl. 2020, 79, 7875–7887. [Google Scholar]
- Fan, D.P.; Ji, G.P.; Sun, G.; Cheng, M.M.; Shen, J.; Shao, L. Rethinking RGB-D Salient Object Detection: Models, Datasets, and Large-Scale Benchmarks. IEEE Trans. Neural Netw. Learn. Syst. 2019. [Google Scholar] [CrossRef]
- Hu, Q.H.; Huang, Q.X.; Mao, Y.; Liu, X.L.; Tan, F.R.; Wang, Y.Y.; Yin, Q.; Wu, X.M.; Wang, H.Q. A near-infrared large Stokes shift probe based enhanced ICT strategy for F- detection in real samples and cell imaging. Tetrahedron 2019, 75, 130762. [Google Scholar] [CrossRef]
- Song, W.T.; Hu, Y.; Kuang, D.B.; Gong, C.L.; Zhang, W.Q.; Huang, S. Detection of ship targets based on CFAR-DCRF in single infrared remote sensing images. J. Infrared Millim. Waves 2019, 38, 520–527. [Google Scholar]
- Zhao, X.; Wang, W.; Ni, X.; Chu, X.; Li, Y.F.; Lu, C. Utilising near-infrared hyperspectral imaging to detect low-level peanut powder contamination of whole wheat flour. Biosyst. Eng. 2019, 184, 55–68. [Google Scholar] [CrossRef]
- Hruda, L.; Dvořák, J.; Váša, L. On evaluating consensus in RANSAC surface registration. Comput. Graph. Forum 2019, 38, 175–186. [Google Scholar] [CrossRef]
- Qu, Y.; Huang, J.; Zhang, X. Rapid 3D Reconstruction for Image Sequence Acquired from UAV Camera. Sensors 2018, 18, 225. [Google Scholar]
- Aldeeb, N.H.; Hellwich, O. 3D Reconstruction Under Weak Illumination Using Visibility-Enhanced LDR Imagery. Adv. Comput. Vis. 2020, 1, 515–534. [Google Scholar]
- Xie, Q.H.; Zhang, X.W.; Cheng, S.Y.; Lv, W.G. 3D Reconstruction Method of Image Based on Digital Microscope. Acta Microsc. 2019, 28, 1289–1300. [Google Scholar]
- Zhang, J.; Zhang, S.X.; Chen, X.X.; Jiang, B.; Wang, L.; Li, Y.Y.; Li, H.A. A Novel Medical 3D Reconstruction Based on 3D Scale-Invariant Feature Transform Descriptor and Quaternion-Iterative Closest Point Algorithm. J. Med. Imaging Health Inf. 2019, 9, 1361–1372. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, M.; Huang, T.; Zheng, J.; Li, Z. 3D reconstruction of complex spatial weld seam for autonomous welding by laser structured light scanning. J. Manuf. Process. 2019, 39, 200–207. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, P.; Hu, Q.; Wang, H.; Ai, M.; Li, J. A 3D Reconstruction Pipeline of Urban Drainage Pipes Based on MultiviewImage Matching Using Low-Cost Panoramic Video Cameras. Water 2019, 11, 2101. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, J.; Liu, Z.; Wang, T.; Ahmad, R. A primitive-based 3D reconstruction method for remanufacturing. Int. J. Adv. Manuf. Technol. 2019, 103, 3667–3681. [Google Scholar] [CrossRef]
- Zhu, C.; Yu, S.; Liu, C.; Jiang, P.; Shao, X.; He, X. Error estimation of 3D reconstruction in 3D digital image correlation. Meas. Sci. Technol. 2019, 30, 10. [Google Scholar] [CrossRef]
- Kiyasu, S.; Hoshino, H.; Yano, K.; Fujimura, S. Measurement of the 3-D shape of specular polyhedrons using an M-array coded light source. IEEE Trans. Instrum. Meas. 1995, 44, 775–778. [Google Scholar] [CrossRef]
- Pollefeys, M.; Nistér, D.; Frahm, J.M.; Akbarzadeh, A.; Mordohai, P.; Clipp, B.; Engels, C.; Gallup, D.; Kim, S.J.; Merrell, P.; et al. Detailed Real-Time Urban 3D Reconstruction from Video. Int. J. Comput. Vis. 2008, 78, 143–167. [Google Scholar] [CrossRef]
- Furukawa, Y.; Ponce, J. Carved Visual Hulls for Image-Based Modeling. Int. J. Comput. Vis. 2009, 81, 53–67. [Google Scholar] [CrossRef]
- Zhan, Y.; Hong, W.; Sun, W.; Liu, J. Flexible Multi-Positional Microsensors for Cryoablation Temperature Monitoring. IEEE Electron Device Lett. 2019, 40, 1674–1677. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, Y.; Zhao, C.; Wang, F.; Liang, Z. Feedback Design of Temperature Control Measures for Concrete Dams based on Real-Time Temperature Monitoring and Construction Process Simulation. KSCE J. Civ. Eng. 2018, 22, 1584–1592. [Google Scholar] [CrossRef]
- Zrelli, A. Simultaneous monitoring of temperature, pressure, and strain through Brillouin sensors and a hybrid BOTDA/FBG for disasters detection systems. IET Commun. 2019, 13, 3012–3019. [Google Scholar] [CrossRef]
- Sun, H.; Meng, Z.H.; Du, X.X.; Ang, M.H. A 3D Convolutional Neural Network towards Real-time Amodal 3D Object Detection. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 8331–8338. [Google Scholar]
- Shen, X.L.; Dou, Y.; Mills, S.; Eyers, D.M.; Feng, H.; Huang, Z. Distributed sparse bundle adjustment algorithm based on three-dimensional point partition and asynchronous communication. Front. Inf. Technol. Electron. Eng. 2018, 19, 889–904. [Google Scholar] [CrossRef]
- Snavely, N.; Seitz, S.; Szeliski, R. Photo tourism: Exploring photo collections in 3D. ACM Trans. Graph. (TOG) 2006, 25, 835–846. [Google Scholar] [CrossRef]
- Bian, J.-W. GMS: Grid-Based Motion Statistics for Fast, Ultra-robust Feature Correspondence. Int. J. Comput. Vis. 2020, 128, 1580–1594. [Google Scholar] [CrossRef]









© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, D.; He, Z.; Ye, X.; Fang, Z. Visual Saliency Detection for Over-Temperature Regions in 3D Space via Dual-Source Images. Sensors 2020, 20, 3414. https://doi.org/10.3390/s20123414
Gong D, He Z, Ye X, Fang Z. Visual Saliency Detection for Over-Temperature Regions in 3D Space via Dual-Source Images. Sensors. 2020; 20(12):3414. https://doi.org/10.3390/s20123414
Chicago/Turabian StyleGong, Dawei, Zhiheng He, Xiaolong Ye, and Ziyun Fang. 2020. "Visual Saliency Detection for Over-Temperature Regions in 3D Space via Dual-Source Images" Sensors 20, no. 12: 3414. https://doi.org/10.3390/s20123414
APA StyleGong, D., He, Z., Ye, X., & Fang, Z. (2020). Visual Saliency Detection for Over-Temperature Regions in 3D Space via Dual-Source Images. Sensors, 20(12), 3414. https://doi.org/10.3390/s20123414





