Multipath Map Method for TDOA Based Indoor Reverse Positioning System with Improved Chan-Taylor Algorithm
Abstract
1. Introduction
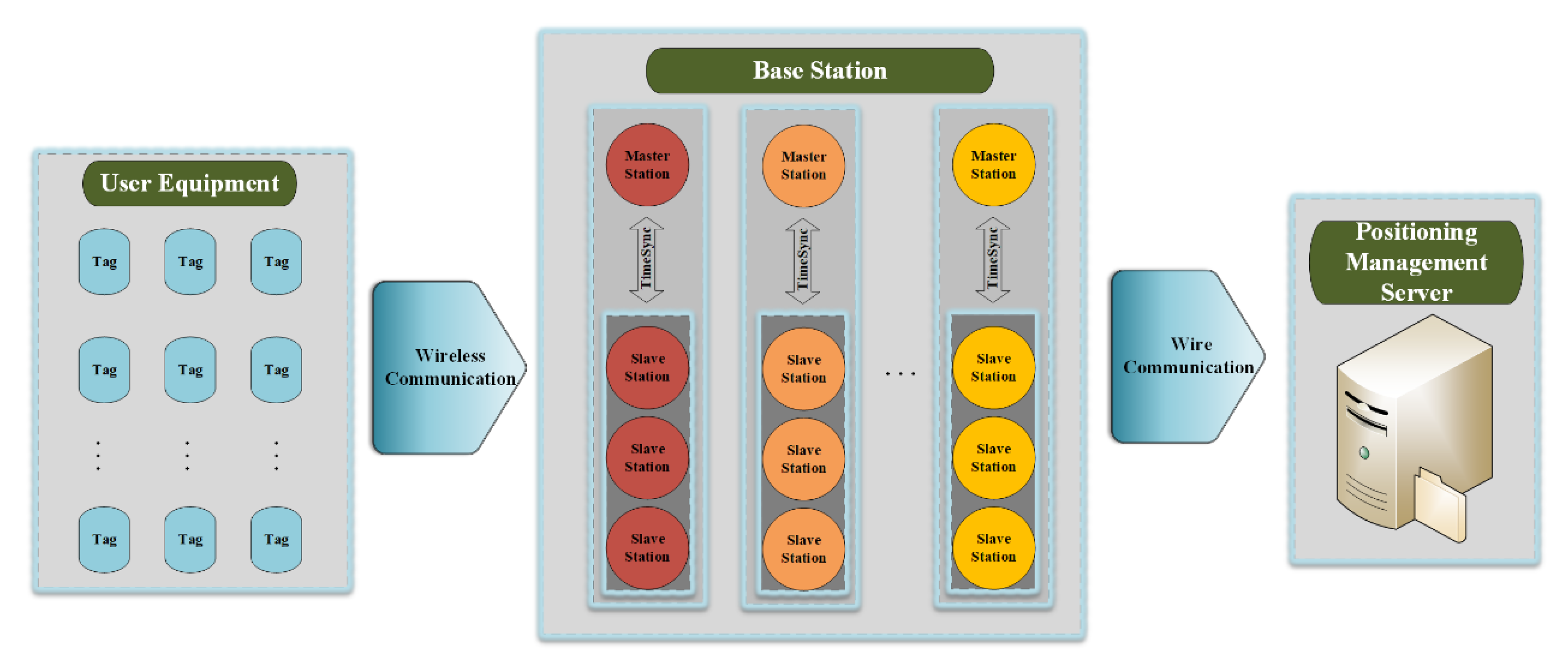
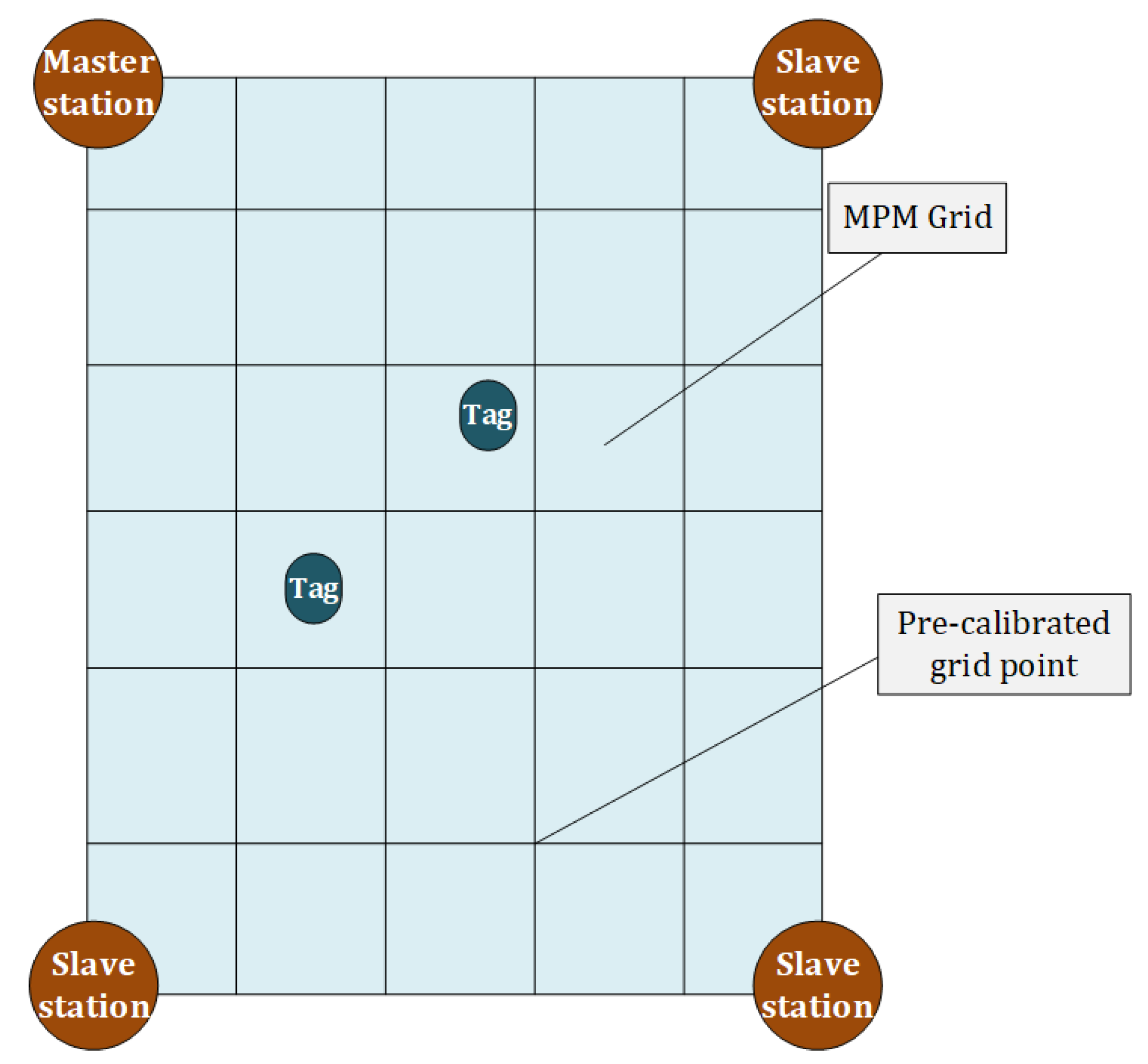
2. System Model of Indoor Reverse Positioning and MPM Method
3. Improved Chan-Taylor Algorithm with MPM
| Algorithm 1 Optimization of TDOA based on MPM. |
| Input: MPM, initial coordinate, , error threshold, ; |
| Output: Final positioning coordinate, ; |
| 1: ; |
| 2: repeat |
| 3: Get multipath error by substituting into MPM; |
| 4: ; |
| 5: Obtain by substituting into improved Chan-Taylor algorithm; |
| 6: until ; |
| 7: ; |
| 8: return T; |
4. Experiment Results
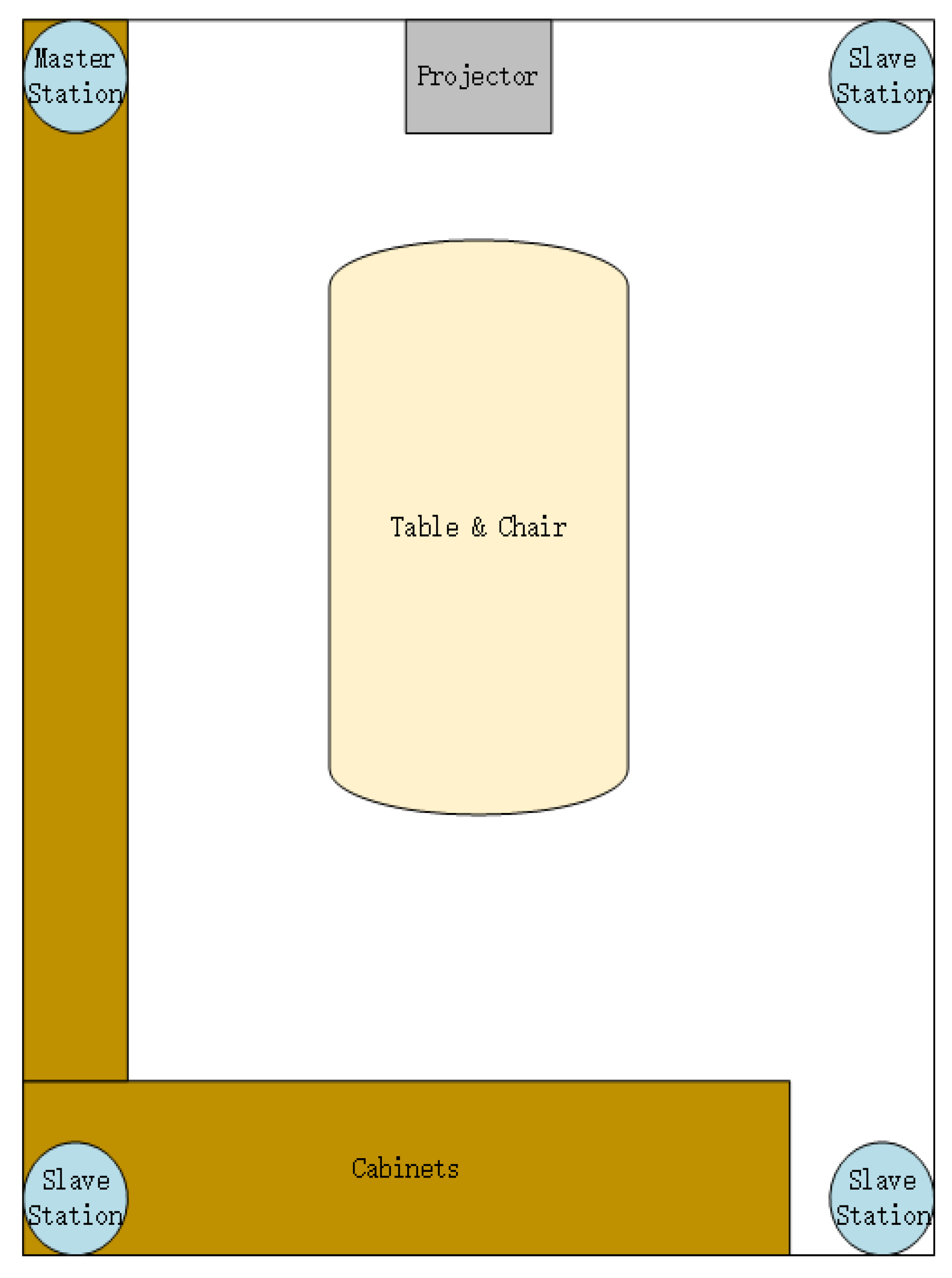
4.1. Introduction to Experimental Environment
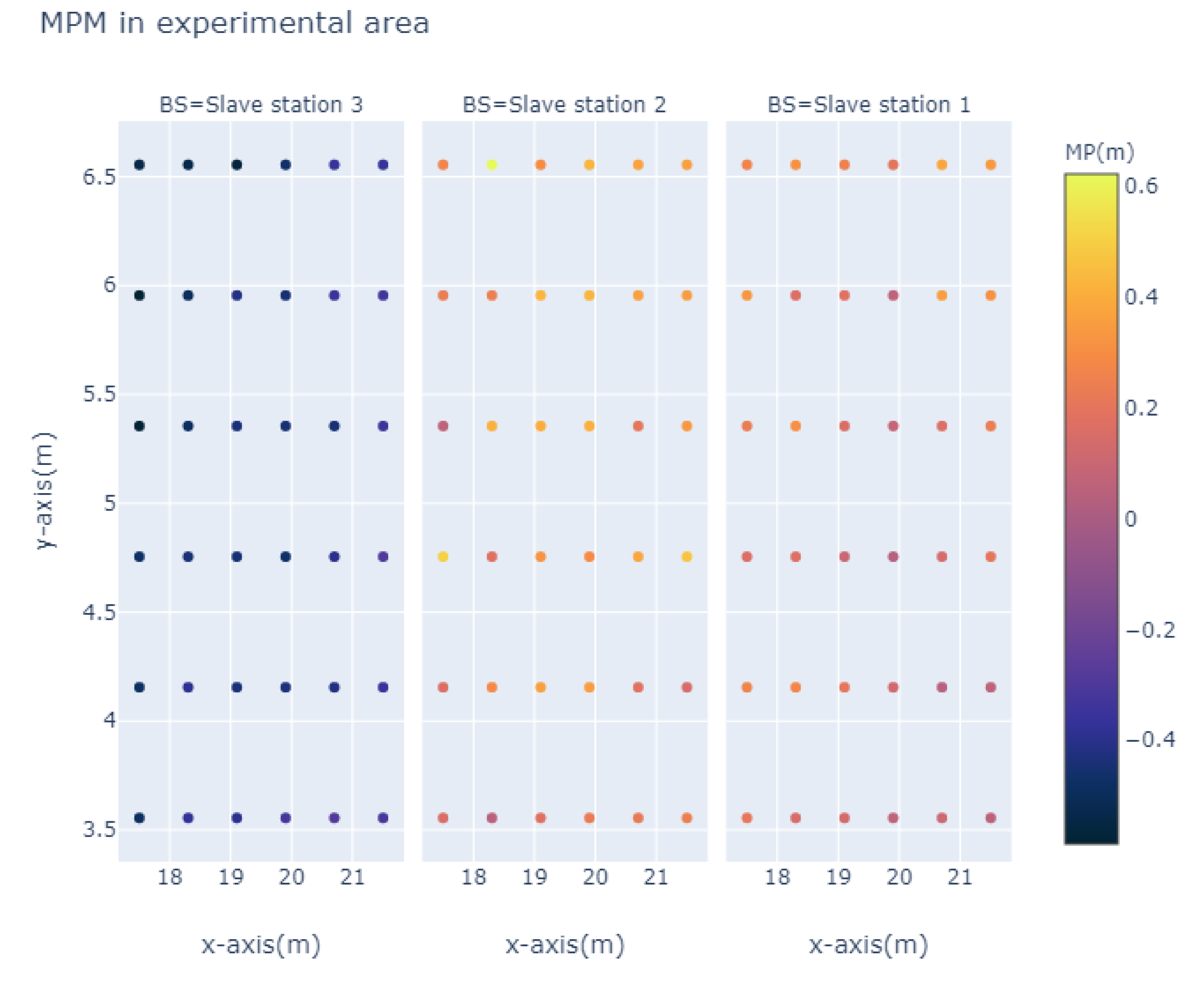
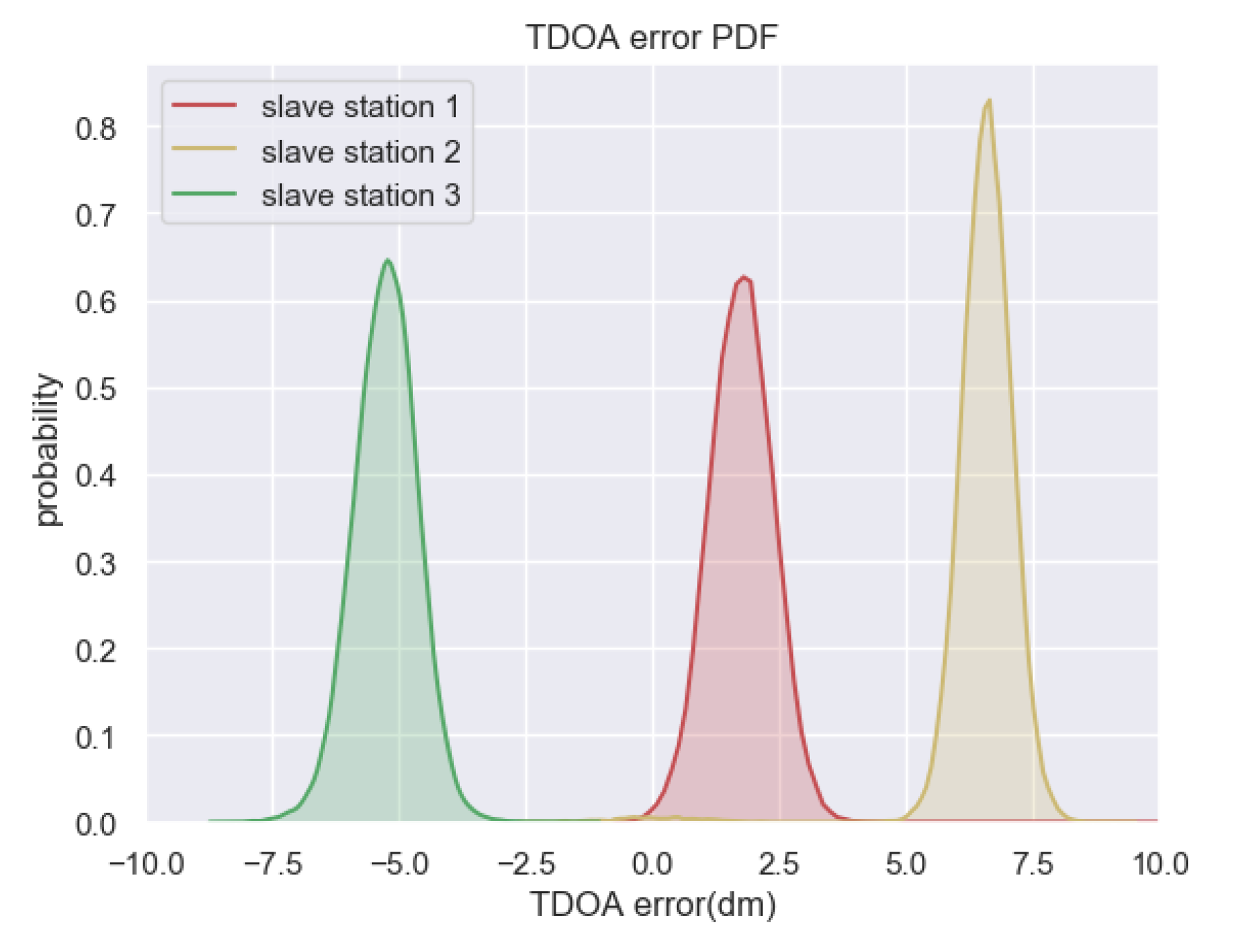
4.2. Robustness of MPM in Non-Disturbed Environment
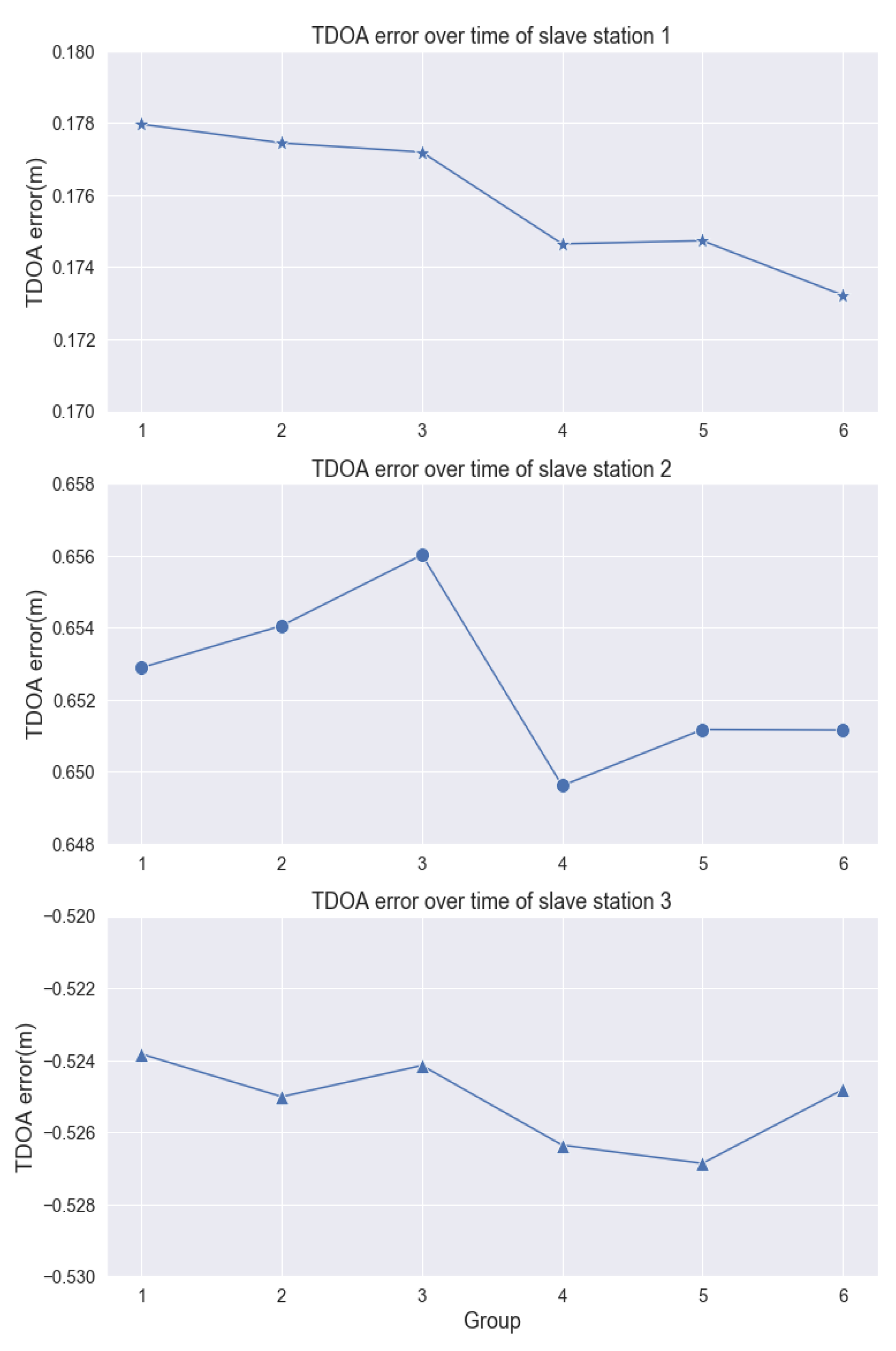
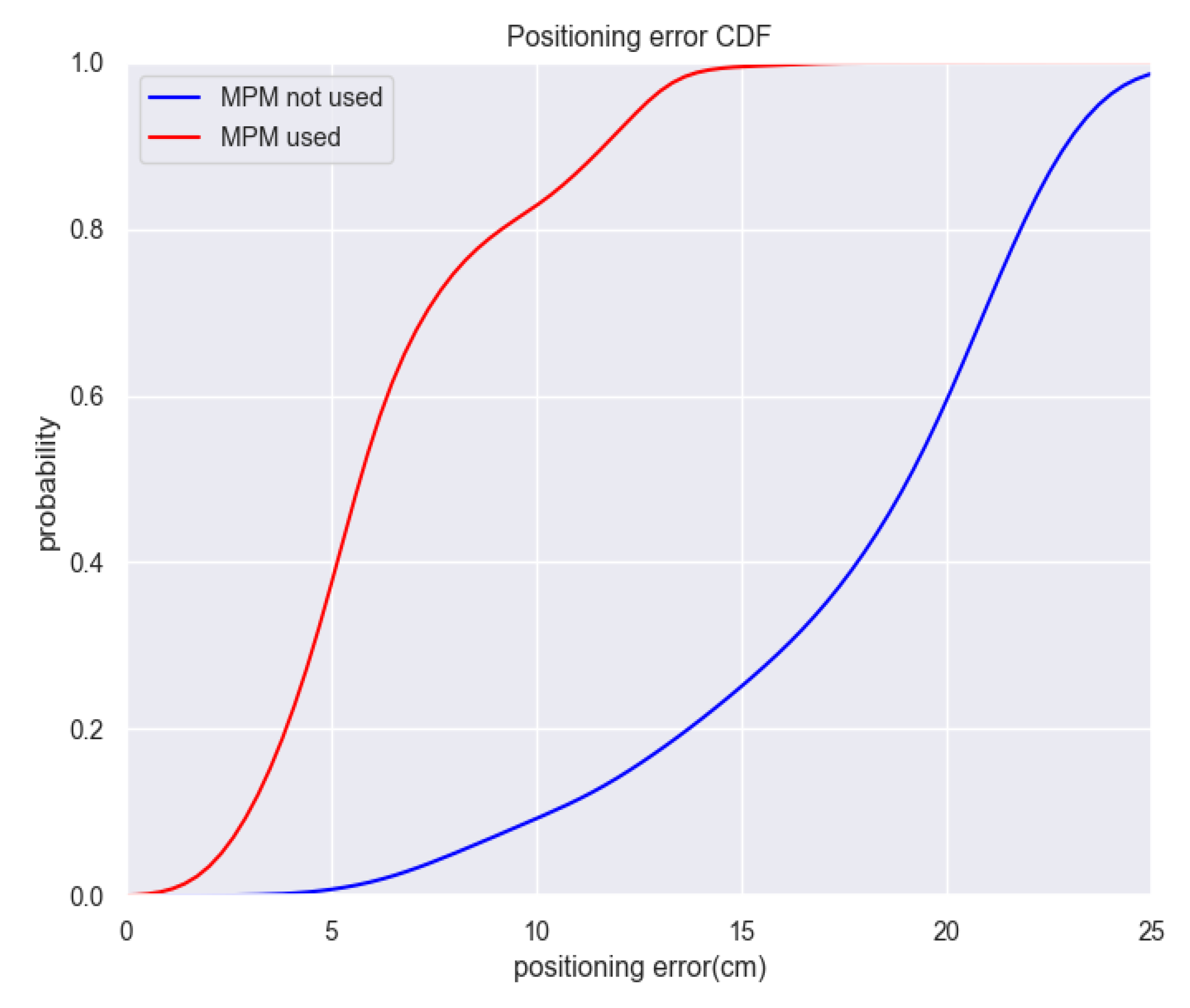
4.3. Robustness of MPM in Disturbed Environment
4.4. Comparison between Improved Chan-Taylor Algorithm and Chan-Taylor Algorithm
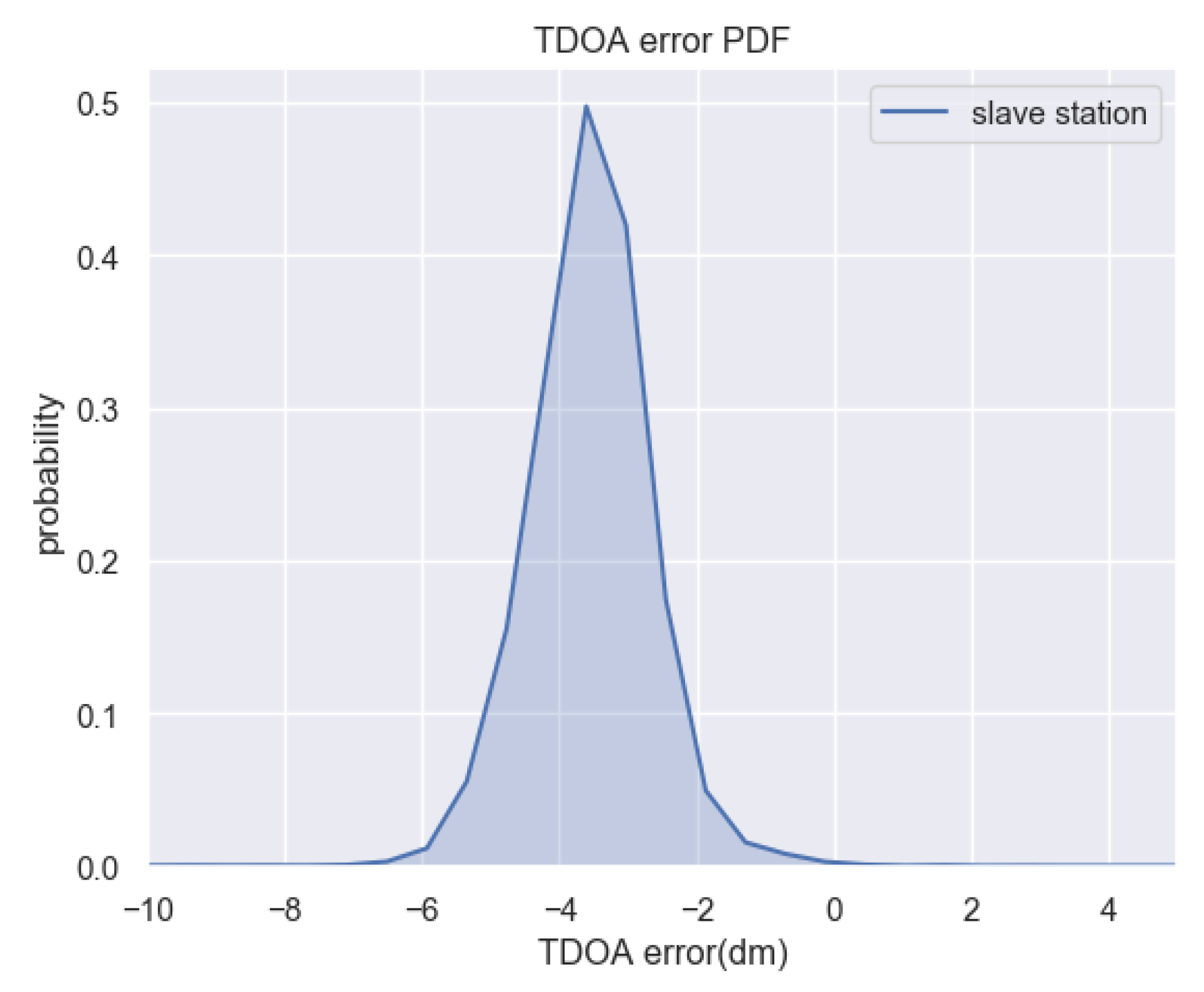
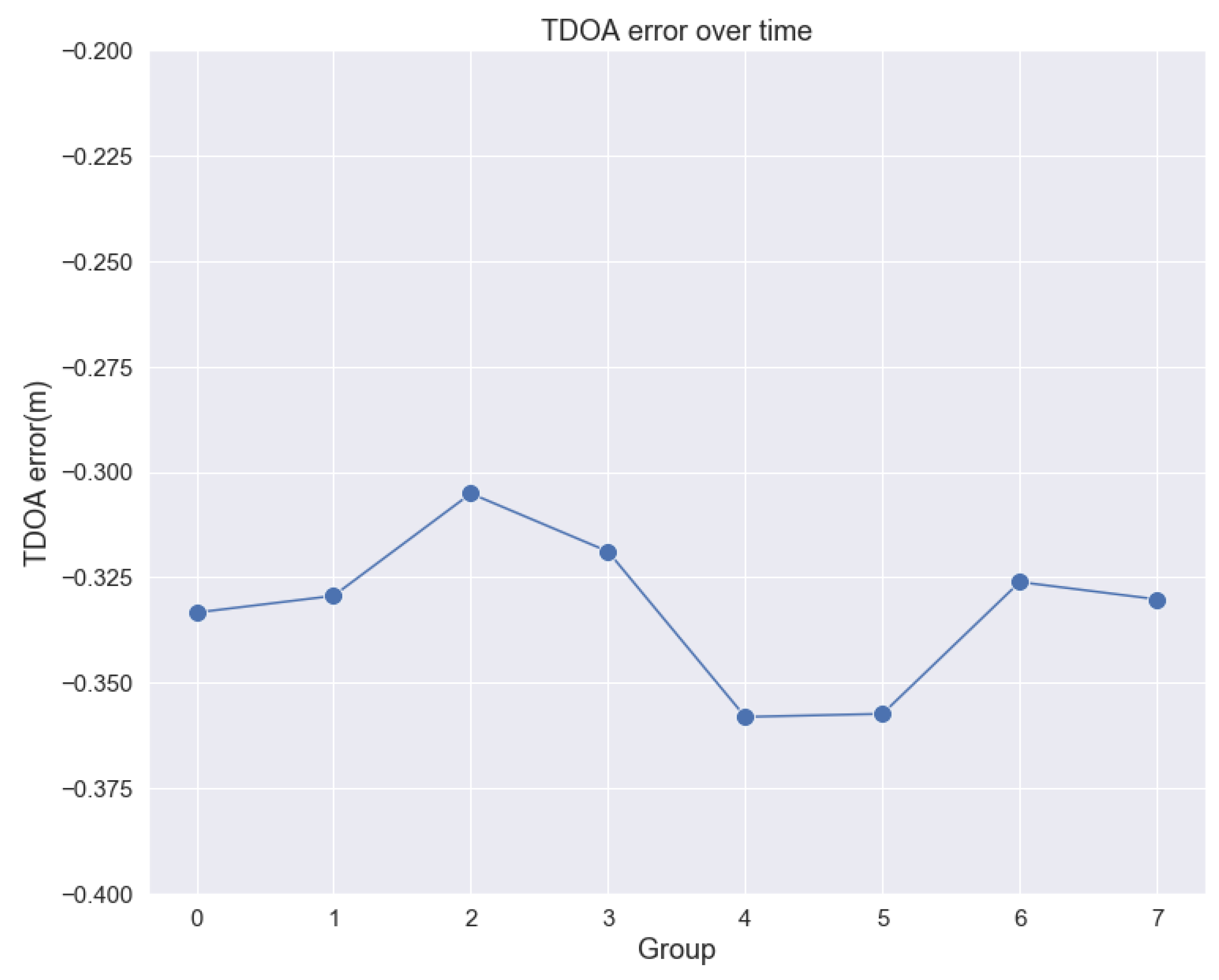
4.5. Application of MPM in Actual Positioning Scene
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Perez-Cruz, F.; Lin, C.K.; Huang, H. Blade: A universal, blind learning algorithm for ToA localization in NLOS channels. In 2016 IEEE Globecom Workshops (GC Wkshps); IEEE: Piscataway, NJ, USA, 2016; pp. 1–7. [Google Scholar]
- Salamah, A.H.; Tamazin, M.; Sharkas, M.A.; Khedr, M. An enhanced WiFi indoor localization system based on machine learning. In Proceedings of the 2016 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Spain, 4–7 October 2016; pp. 1–8. [Google Scholar]
- Zou, H.; Lu, X.; Jiang, H.; Xie, L. A fast and precise indoor localization algorithm based on an online sequential extreme learning machine. Sensors 2015, 15, 1804–1824. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Gao, L.; Mao, S. CSI phase fingerprinting for indoor localization with a deep learning approach. IEEE Internet Things J. 2016, 3, 1113–1123. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L.; Wymeersch, H.; Hoydis, J.; Marzetta, T.L. Massive MIMO is a reality—What is next? Five promising research directions for antenna arrays. Digit. Signal Proc. 2019, 94, 3–20. [Google Scholar] [CrossRef]
- Sadowski, S.; Spachos, P. Rssi-based indoor localization with the internet of things. IEEE Access 2018, 6, 30149–30161. [Google Scholar] [CrossRef]
- Pahlavan, K.; Li, X.; Makela, J.P. Indoor geolocation science and technology. IEEE Commun. Mag. 2002, 40, 112–118. [Google Scholar] [CrossRef]
- Yin, J.; Wan, Q.; Yang, S.; Ho, K. A simple and accurate TDOA-AOA localization method using two stations. IEEE Signal Proc. Lett. 2015, 23, 144–148. [Google Scholar] [CrossRef]
- Li, S.; Rashidzadeh, R. Hybrid indoor location positioning system. IET Wirel. Sens. Syst. 2019, 9, 257–264. [Google Scholar] [CrossRef]
- Bloom, B.; Nicholson, T.; Williams, J.; Campbell, S.; Bishof, M.; Zhang, X.; Zhang, W.; Bromley, S.; Ye, J. An optical lattice clock with accuracy and stability at the 10–18 level. Nature 2014, 506, 71. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.; Wang, G.; Razul, S.G. Comparisons of the super-resolution TOA/TDOA estimation algorithms. In 2017 Progress in Electromagnetics Research Symposium-Fall (PIERS-FALL); IEEE: Piscataway, NJ, USA, 2017; pp. 2752–2758. [Google Scholar]
- Foy, W.H. Position-location solutions by Taylor-series estimation. IEEE Trans. Aerosp. Electr. Syst. 1976, 12, 187–194. [Google Scholar] [CrossRef]
- Chan, Y.T.; Ho, K. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Proc. 1994, 42, 1905–1915. [Google Scholar] [CrossRef]
- Fang, B.T. Simple solutions for hyperbolic and related position fixes. IEEE Trans. Aerosp. Electr. Syst. 1990, 26, 748–753. [Google Scholar] [CrossRef]
- Li, H.; Oussalah, M. Combination of Taylor and Chan method in mobile positioning. In Proceedings of the 2011 IEEE 10th International Conference on Cybernetic Intelligent Systems (CIS), London, UK, 1–2 September 2011; pp. 104–110. [Google Scholar]
- Xu, B.; Yu, R.; Sun, G.; Yang, Z. Whistle: Synchronization-free TDOA for localization. In 2011 31st International Conference on Distributed Computing Systems; IEEE: Piscataway, NJ, USA, 2011; pp. 760–769. [Google Scholar]
- Zhao, T.; Zhao, K.; Yu, C.; Dong, D.; Zheng, Z.; Zhang, Y. Application of Differential Time Synchronization in Indoor Positioning. In Proceedings of the 2019 11th International Conference on Wireless Communications and Signal Processing (WCSP), Xian, China, 23–25 October 2019; pp. 1–6. [Google Scholar]
- Zhang, C.; Bao, X.; Wei, Q.; Ma, Q.; Yang, Y.; Wang, Q. A Kalman filter for UWB positioning in LOS/NLOS scenarios. In 2016 Fourth International Conference on Ubiquitous Positioning, Indoor Navigation and Location Based Services (UPINLBS); IEEE: Piscataway, NJ, USA, 2016; pp. 73–78. [Google Scholar]
- Zandian, R.; Witkowski, U. NLOS Detection and Mitigation in Differential Localization Topologies based on UWB Devices. In 2018 International Conference on Indoor Positioning and Indoor Navigation (IPIN); IEEE: Piscataway, NJ, USA, 2018; pp. 1–8. [Google Scholar]
- Dong, D.; Wang, M.; Chen, W.; Zeng, Z.; Song, L.; Zhang, Q.; Cai, M.; Cheng, Y.; Lv, J. Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map. J. Geod. 2016, 90, 255–262. [Google Scholar] [CrossRef]
- Cai, M.; Chen, W.; Dong, D.; Song, L.; Wang, M.; Wang, Z.; Zhou, F.; Zheng, Z.; Yu, C. Reduction of kinematic short baseline multipath effects based on multipath hemispherical map. Sensors 2016, 16, 1677. [Google Scholar] [CrossRef] [PubMed]

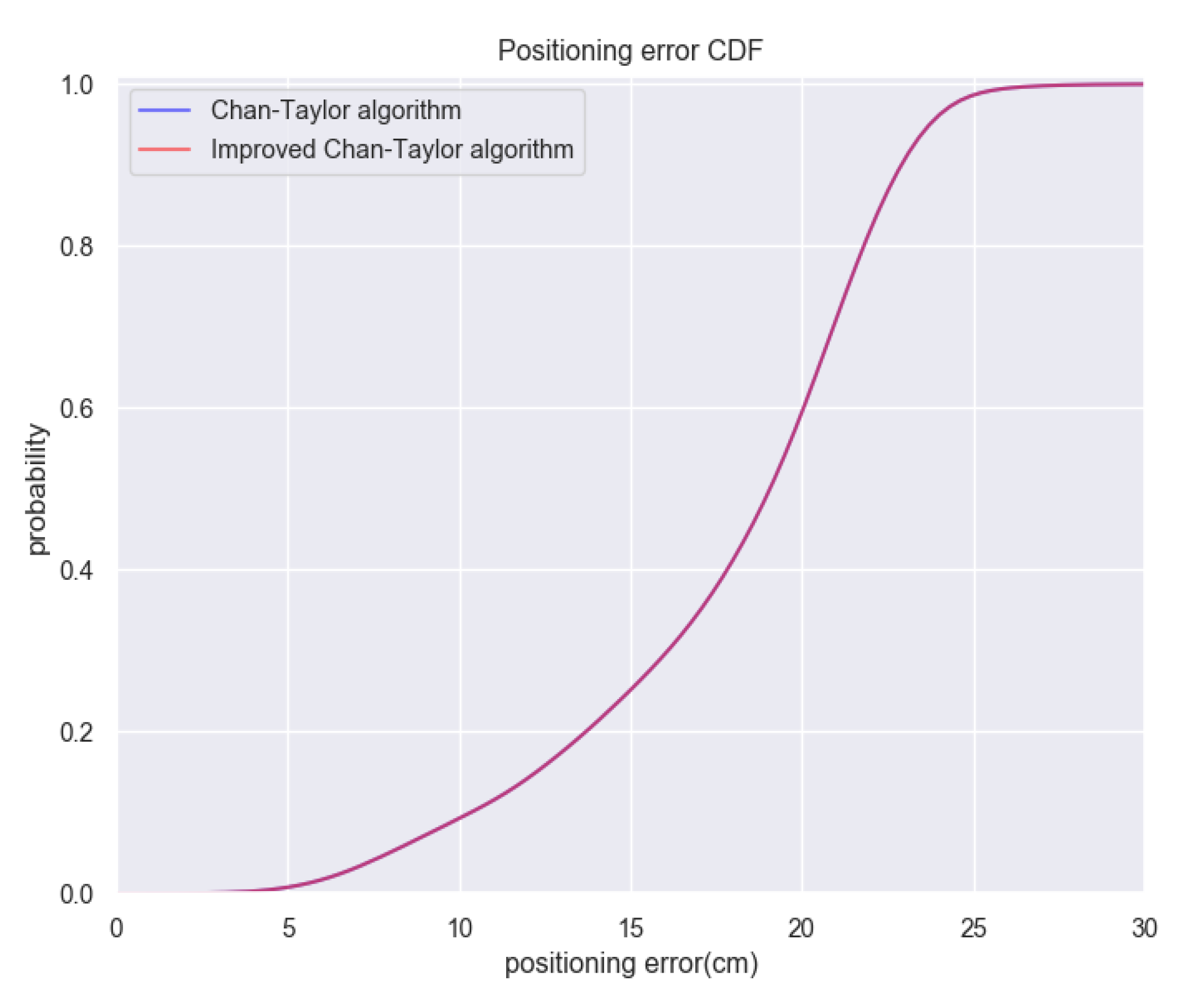
| Improved Chan-Taylor (ms) | Chan-Taylor (ms) | |
|---|---|---|
| Average time | 0.220 | 0.331 |
| MPM Not Used (cm) | MPM Used (cm) | |
|---|---|---|
| R.M.S.E. | 18.42 | 7.16 |
| M.A.E. | 17.81 | 6.45 |
| S.D. | 4.72 | 3.12 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, C.; Zhao, K.; Dong, D.; Zheng, Z.; Yu, C.; Zhang, Y.; Zhao, T. Multipath Map Method for TDOA Based Indoor Reverse Positioning System with Improved Chan-Taylor Algorithm. Sensors 2020, 20, 3223. https://doi.org/10.3390/s20113223
Hua C, Zhao K, Dong D, Zheng Z, Yu C, Zhang Y, Zhao T. Multipath Map Method for TDOA Based Indoor Reverse Positioning System with Improved Chan-Taylor Algorithm. Sensors. 2020; 20(11):3223. https://doi.org/10.3390/s20113223
Chicago/Turabian StyleHua, Cheng, Kun Zhao, Danan Dong, Zhengqi Zheng, Chao Yu, Yu Zhang, and Tiantian Zhao. 2020. "Multipath Map Method for TDOA Based Indoor Reverse Positioning System with Improved Chan-Taylor Algorithm" Sensors 20, no. 11: 3223. https://doi.org/10.3390/s20113223
APA StyleHua, C., Zhao, K., Dong, D., Zheng, Z., Yu, C., Zhang, Y., & Zhao, T. (2020). Multipath Map Method for TDOA Based Indoor Reverse Positioning System with Improved Chan-Taylor Algorithm. Sensors, 20(11), 3223. https://doi.org/10.3390/s20113223






