Probe Sector Matching for Freehand 3D Ultrasound Reconstruction
Abstract
1. Introduction
2. Space Plane Inverse Operation
3. Spatial Position and Attitude of Probe Sector
3.1. Optical Positioning of the Probe
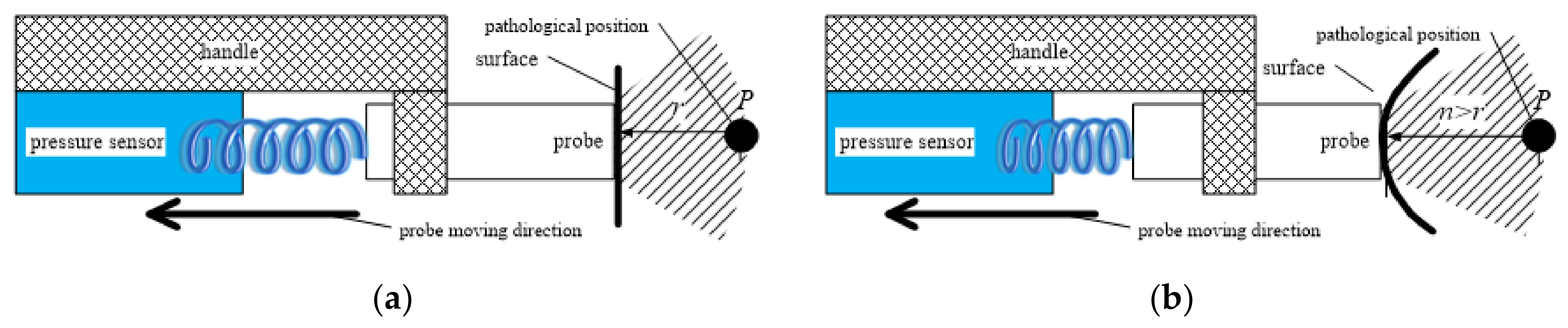
3.2. Pressure Sensor of the Probe
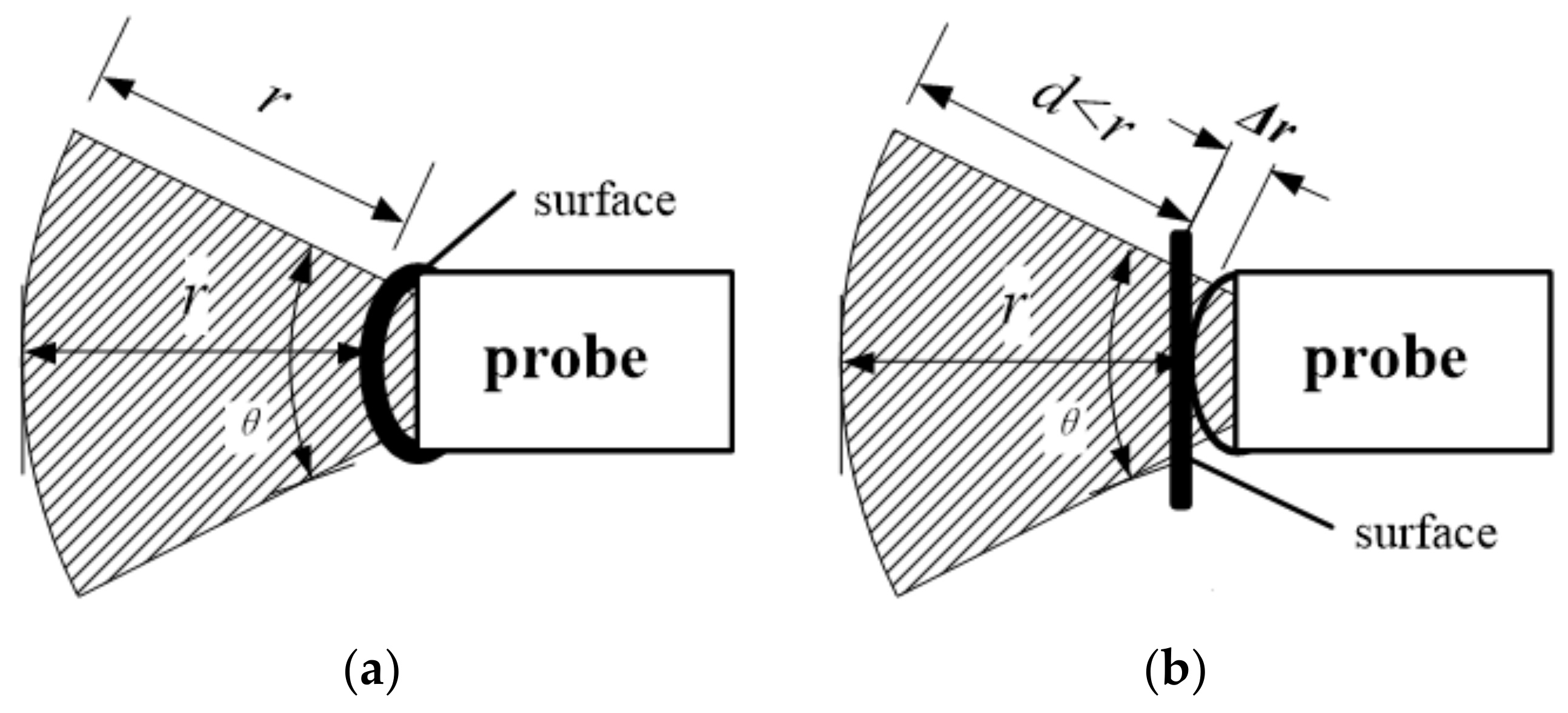
3.3. Error Analysis of the Sector
4. Improved 3D Hough Transform
5. Reconstruction Experiment
5.1. Experiment Preparation
5.2. Numerical Model Reconstruction Result
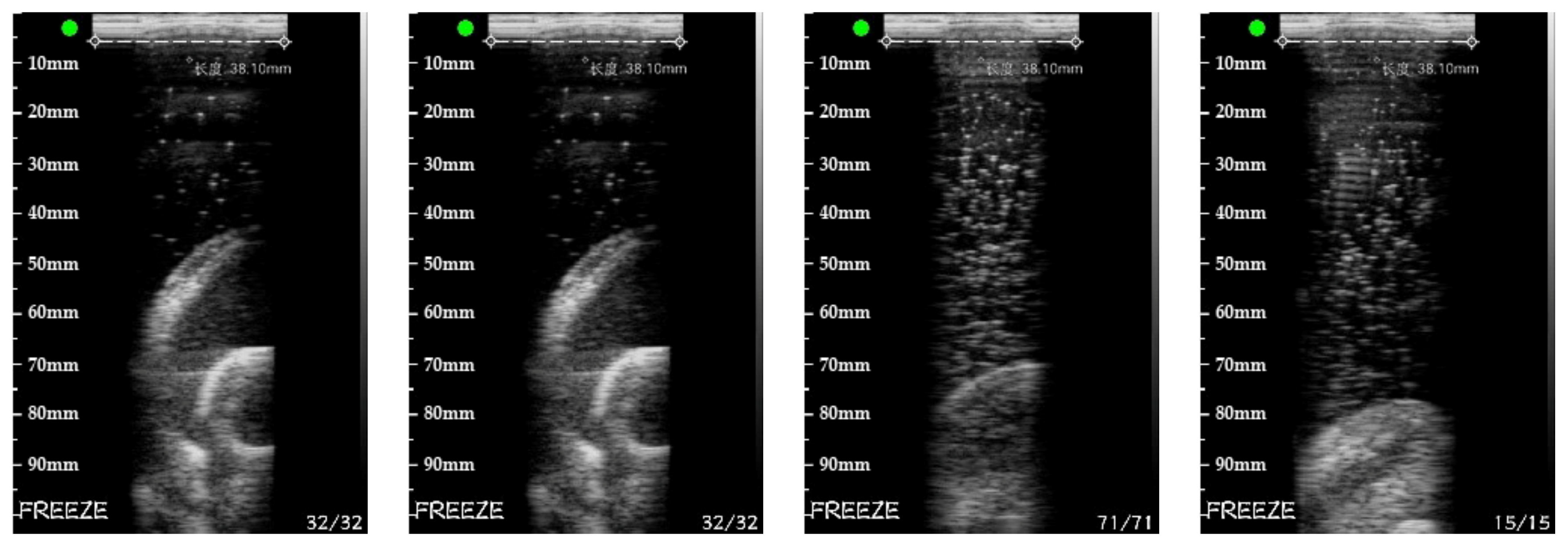
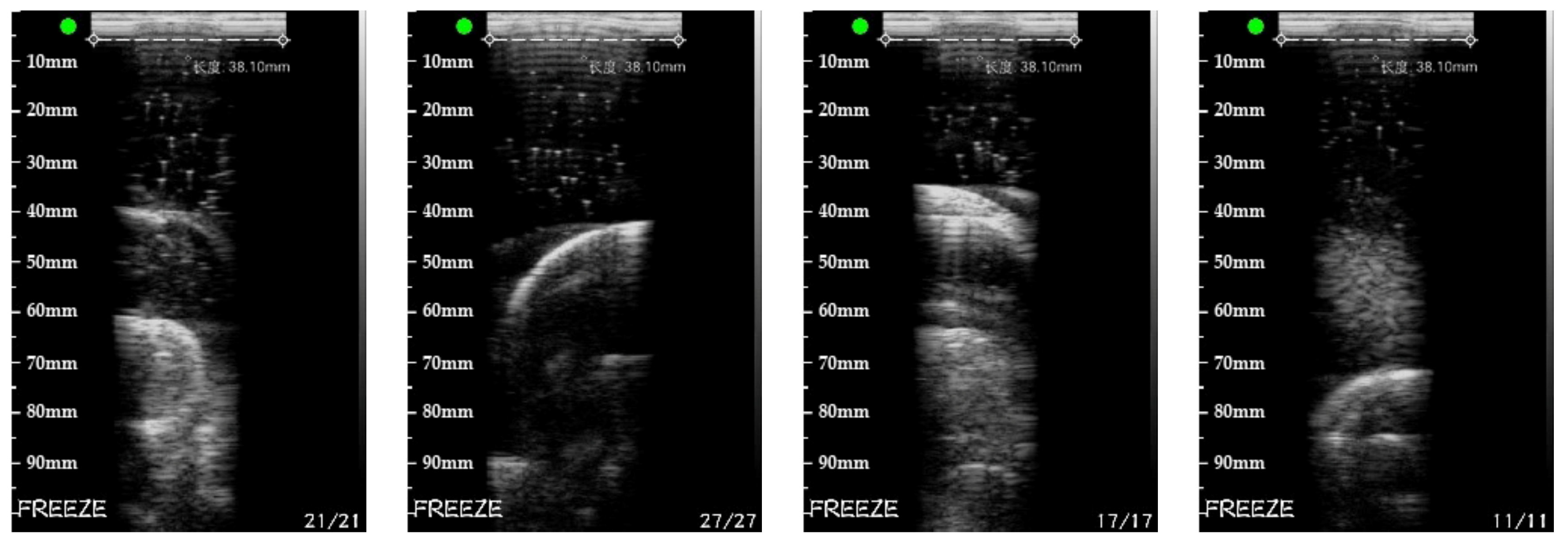
5.3. Real Target Reconstruction Result
6. Conclusions
- More realistic models for the surface and the medium changes.
- A better pressure feedback device to account for multidimensional pressure.
- Animal experiments that may help to further validate the PSM for applications in biological sciences.
Author Contributions
Funding
Conflicts of Interest
References
- Noble, J.A.; Boukerroui, D. Ultrasound image segmentation: A survey. IEEE Trans. Medical Imaging 2006, 25, 987–1010. [Google Scholar] [CrossRef] [PubMed]
- Ritter, F.; Boskamp, T.; Homeyer, A.; Laue, H.; Schwier, M.; Link, F.; Peitgen, H.-O. Medical image analysis. Comput. Phys. Commun. 2013, 2, 60–70. [Google Scholar] [CrossRef] [PubMed]
- Lazebnik, R.; Desser, T.S. Clinical 3D ultrasound imaging: Beyond obstetrical applications. Diagn. Imaging 2007, 1, 1–6. [Google Scholar]
- Sanches, J.; Bioucas-Dias, J.; Marques, J.S. Minimum Total Variation in 3D Ultrasound Reconstruction. In Proceedings of the IEEE International Conference on Image Processing 2005, Genova, Italy, 14–14 September 2005; Volume 3, p. III-597. [Google Scholar]
- Fenster, A.; Downey, D.; Cardinal, H.N. Three-dimensional ultrasound imaging. Phys. Med. Biol. 2001, 46, R67–R99. [Google Scholar] [CrossRef]
- Fenster, A.; Surry, K.; Smith, W.; Gill, J.; Downey, D.B. 3D ultrasound imaging: Applications in image-guided therapy and biopsy. Comput. Graph. 2002, 26, 557–568. [Google Scholar] [CrossRef]
- Chiu, B.; Egger, M.; Spence, D.J.; Parraga, G.; Fenster, A. Area-preserving flattening maps of 3D ultrasound carotid arteries images. Med Image Anal. 2008, 12, 676–688. [Google Scholar] [CrossRef]
- Wen, T.; Yang, F.; Gu, J.; Chen, S.; Wand, L.; Xie, Y. An adaptive kernel regression method for 3D ultrasound reconstruction using speckle prior and parallel GPU implementation. Neurocomputing 2018, 275, 208–223. [Google Scholar] [CrossRef]
- Solberg, O.V.; Lindseth, F.; Torp, H.; Blake, R.E.; Hernes, T.A.N. Freehand 3D Ultrasound Reconstruction Algorithms-A Review. Ultrasound Med. Biol. 2007, 33, 991–1009. [Google Scholar] [CrossRef]
- EJuszczyk, J.; Galinska, M.; Pietka, E. Time Regarded Method of 3D Ultrasound Reconstruction. In Proceedings of the International Conference on Information Technologies in Biomedicine, Kamień Śląski, Poland, 18–20 June 2018; Springer: Cham, Switzerland, 2018; pp. 205–216. [Google Scholar]
- Solberg, O.V.; Lindseth, F.; Bø, L.E.; Muller, S.; Bakeng, J.B.L.; Tangen, G.A.; Hernes, T.A.N. 3D ultrasound reconstruction algorithms from analog and digital data. Ultrasonics 2011, 51, 405–419. [Google Scholar] [CrossRef][Green Version]
- Jayarathne, U.L.; Moore, J.; Chen, E.C.S.; Pautler, S.E.; Peters, T.M. Real-Time 3D Ultrasound Reconstruction and Visualization in the Context of Laparoscopy. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Quebec City, QC, Canada, 11–13 September 2017; Springer: Cham, Switzerland, 2017; pp. 602–609. [Google Scholar]
- Gee, A.; Prager, R.; Treece, G.; Berman, L. Engineering a freehand 3D ultrasound system. Pattern Recognit. Lett. 2003, 24, 757–777. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, Q. Real-time freehand 3D ultrasound imaging. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 74–83. [Google Scholar] [CrossRef]
- Coupé, P.; Hellier, P.; Azzabou, N.; Barillot, C. 3D Freehand Ultrasound Reconstruction based on Probe Trajectory. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Copenhagen, Denmark, 1–6 October 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 597–604. [Google Scholar]
- Chen, X.; Chen, H.; Tao, D.; Xie, J.; Li, X. Ultrasonic Section Locating Method Based on Hough Transform. In Proceedings of the 2019 IEEE International Conference on Consumer Electronics—Taiwan (ICCE-TW), Yilan, Taiwan, 20–22 May 2019. [Google Scholar]
- Gilbertson, M.; Anthony, B.W. Force and Position Control System for Freehand Ultrasound. IEEE Trans. Robot. 2015, 31, 835–849. [Google Scholar] [CrossRef]
- Daoud, M.; Alshalalfah, A.; Al-Najar, M. GPU Accelerated Implementation of Kernel Regression for Freehand 3D Ultrasound Volume Reconstruction. In Proceedings of the 2016 IEEE EMBS Conference on Biomedical Engineering and Sciences (IECBES), Kuala Lumpur, Malaysia, 4–8 December 2016; pp. 586–589. [Google Scholar]
- Vo, Q.; Le, L.; Lou, E. A semi-automatic 3D ultrasound reconstruction method to assess the true severity of adolescent idiopathic scoliosis. Med Biol. Eng. Comput. 2019, 57, 2115–2128. [Google Scholar] [CrossRef] [PubMed]
- Daoud, M.; Alshalalfah, A.; Awwad, F.; Al-Najar, M. A Freehand 3D Ultrasound Imaging System using Open-Source Software Tools with Improved Edge-Preserving Interpolation. Int. J. Open Source Software Process. 2014, 5, 39–57. [Google Scholar] [CrossRef]
- Daoud, M.; Alshalalfah, A.; Awwad, F.; Al-Najar, M. Freehand 3D Ultrasound Imaging System Using Electromagnetic Tracking. In Proceedings of the 2015 International Conference on Open Source Software Computing (OSSCOM), Amman, Jordan, 10–13 September 2015; pp. 1–5. [Google Scholar]
- Huang, Q.; Xie, B.; Ye, P.; Chen, Z. 3-D Ultrasonic Strain Imaging Based on a Linear Scanning System. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 392–400. [Google Scholar] [CrossRef] [PubMed]
- Prevost, R.; Salehi, M.; Sprung, J.; Bauer, R.; Wein, W. Deep Learning for Sensorless 3D Freehand Ultrasound Imaging. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Quebec City, QC, Canada, 11–13 September 2017; Springer: Cham, Switzerland, 2017; pp. 628–636. [Google Scholar]
- Gao, H.; Huang, Q.; Xu, X.; Li, X. Wireless and sensorless 3D ultrasound imaging. Neurocomputing 2016, 195, 159–171. [Google Scholar] [CrossRef]
- Rezajoo, S.; Sharafat, A.R. Robust Estimation of Displacement in Real-Time Freehand Ultrasound Strain Imaging. IEEE Trans. Med Imaging 2018, 37, 1664–1677. [Google Scholar] [CrossRef]
- Schimmoeller, T.; Colbrunn, R.; Nagle, T.; Lobosky, M.; Neumann, E.; Owings, T.; Landis, B.; Jelovsek, J.; Erdemir, A. Instrumentation of off-the-shelf ultrasound system for measurement of probe forces during freehand imaging. J. Biomech. 2019, 83, 117–124. [Google Scholar] [CrossRef]
- Mozaffari, M.; Lee, W.S. Freehand 3-D ultrasound imaging: A systematic review. Ultrasound Med. Biol. 2017, 43, 2099–2124. [Google Scholar] [CrossRef]
- Mohamed, F.; Siang, C.V. A Survey on 3D Ultrasound Reconstruction Techniques. In Artificial Intelligence-Applications in Medicine and Biology; Mohamed, F., Siang, C.V., Eds.; IntechOpen: London, UK, 2019. [Google Scholar]
- Coupé, P.; Hellier, P.; Morandi, X.; Barillot, C. Probe trajectory interpolation for 3D reconstruction of freehand ultrasound. Med. Image Anal. 2007, 11, 604–615. [Google Scholar] [CrossRef]
- De Lorenzo, D.; Vaccarella, A.; Khreis, G.; Moennich, H.; Ferrigno, G.; De Momi, E. Accurate calibration method for 3D freehand ultrasound probe using virtual plane. Med. Phys. 2011, 38, 6710–6720. [Google Scholar] [CrossRef] [PubMed]
- Gemmeke, H.; Hopp, T.; Zapf, M.; Kaiser, C.G.; Ruiter, N. 3D ultrasound computer tomography: Hardware setup, reconstruction methods and first clinical results. Nucl. Instrum. Methods Phys. Res. Sect. A 2017, 873, 59–65. [Google Scholar] [CrossRef]
- Muller, T.; Stotzka, R.; Ruiter, N.; Schlote-Holubek, K.; Gemmeke, H. 3D Ultrasound Computer Tomography: Data Acquisition Hardware. In Proceedings of the IEEE Symposium Conference Record Nuclear Science 2004, Rome, Italy, 16–22 October 2004; Volume 5, pp. 2788–2792. [Google Scholar]
- Huang, Q.; Wu, B.; Lan, J.; Li, X. Fully automatic three-dimensional ultrasound imaging based on conventional B-scan. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 426–436. [Google Scholar] [CrossRef] [PubMed]
- Song, F.; Zhou, Y.; Chang, L.; Zhang, H.K. Modeling space-terrestrial integrated networks with smart collaborative theory. IEEE Network 2019, 33, 51–57. [Google Scholar] [CrossRef]
- Song, F.; Ai, Z.; Zhou, Y.; You, I.; Raymond Choo, K.; Zhang, H.K. Smart collaborative automation for receive buffer control in multipath industrial networks. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef]
- Kiryati, N.; Eldar, Y.; Bruckstein, A.M. A probabilistic Hough transform. Pattern Recognit. 1991, 24, 303–316. [Google Scholar] [CrossRef]
- Song, F.; Zhu, M.; Zhou, Y.; You, I.; Zhang, H.K. Smart collaborative tracking for ubiquitous power IoT in edge-cloud interplay domain. IEEE Internet Things J. 2019. [Google Scholar] [CrossRef]
- Wang, R.Z.; Tao, D. Context-Aware Implicit Authentication of Smartphone Users Based on Multi-Sensor Behavior. IEEE Access. 2019, 7, 119654–119667. [Google Scholar] [CrossRef]
- Hwang, S.; Kim, C.; Beak, J.; Eom, H.; Lee, M. A study on Obstacle Detection Using 3D Hough Transform with corner. In Proceedings of the SICE Annual Conference 2010, Taipei, Taiwan, 18–21 August 2010; pp. 2507–2510. [Google Scholar]
- Qiu, W.; Ding, M.; Yuchi, M. Needle Segmentation Using 3D Quick Randomized Hough Transform. In Proceedings of the 2008 First International Conference on Intelligent Networks and Intelligent Systems, Wuhan, China, 1–3 November 2008; pp. 449–452. [Google Scholar]
- Xu, L.; Oja, E. Randomized Hough transform (RHT): Basic mechanisms, algorithms, and computational complexities. CVGIP: Image Underst. 1993, 57, 131–154. [Google Scholar] [CrossRef]
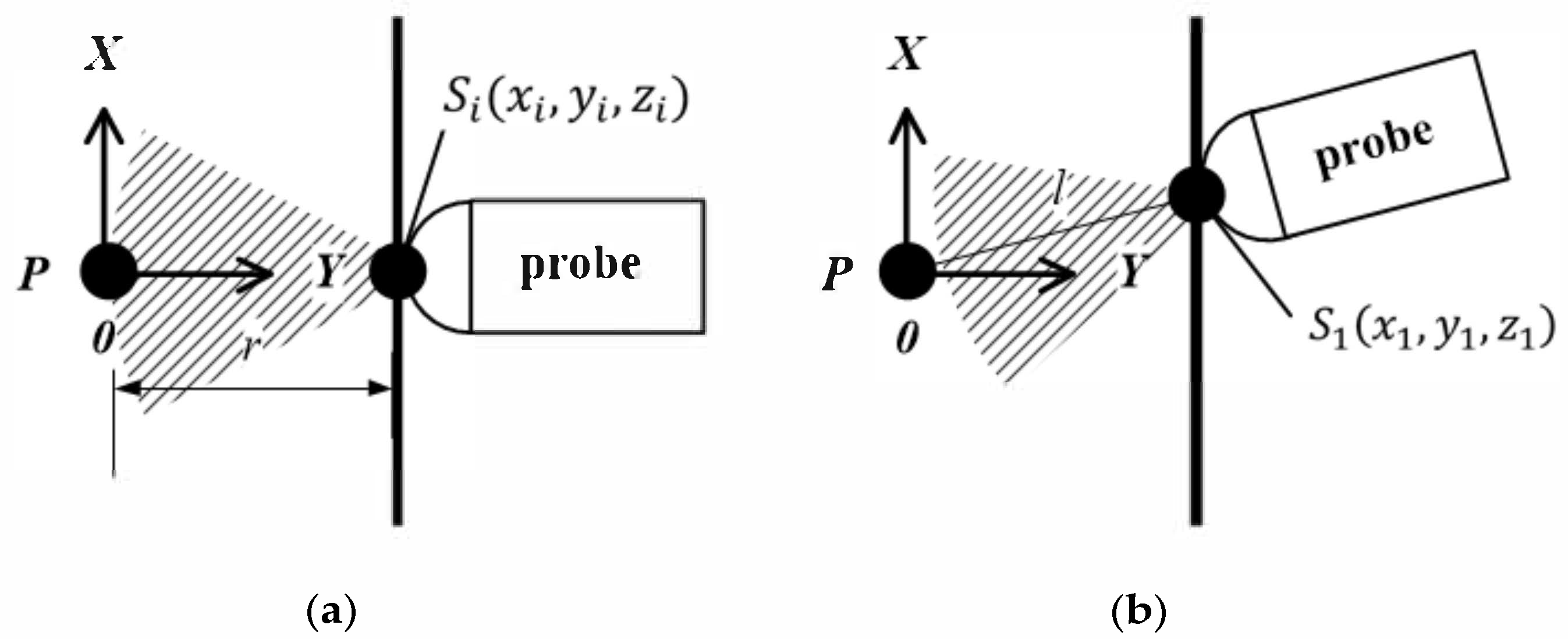
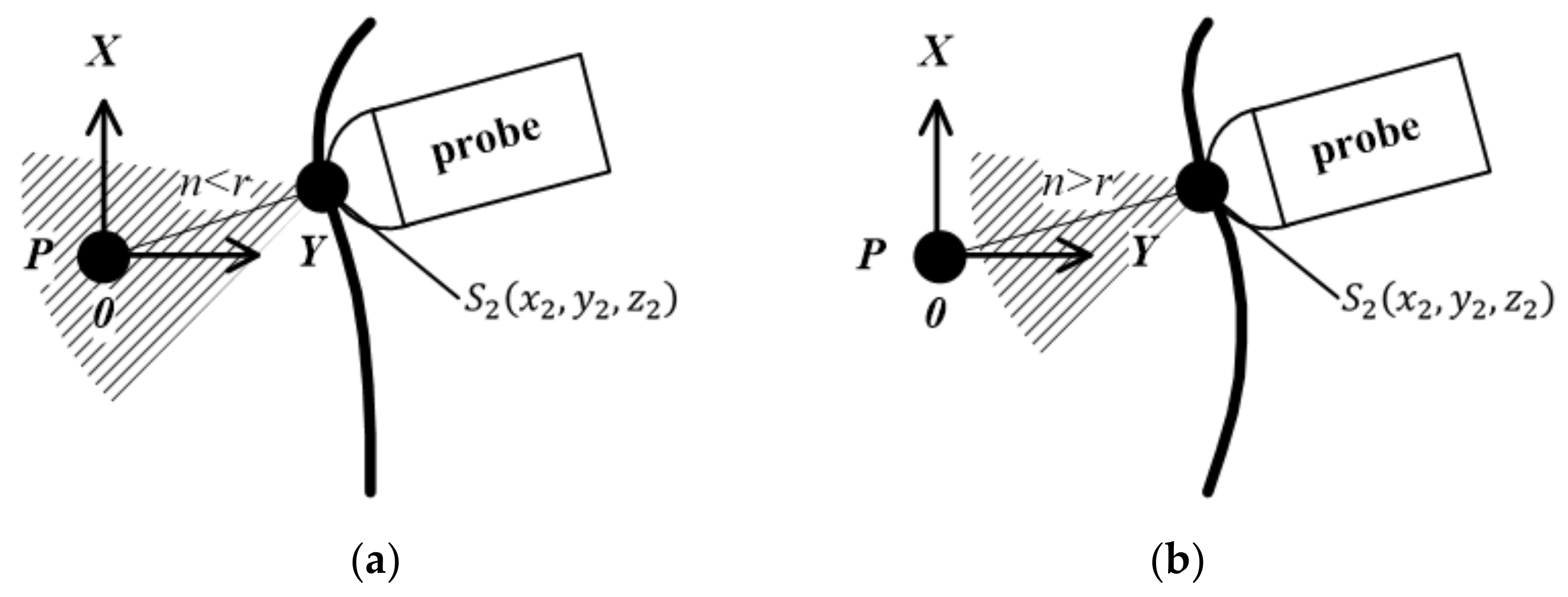

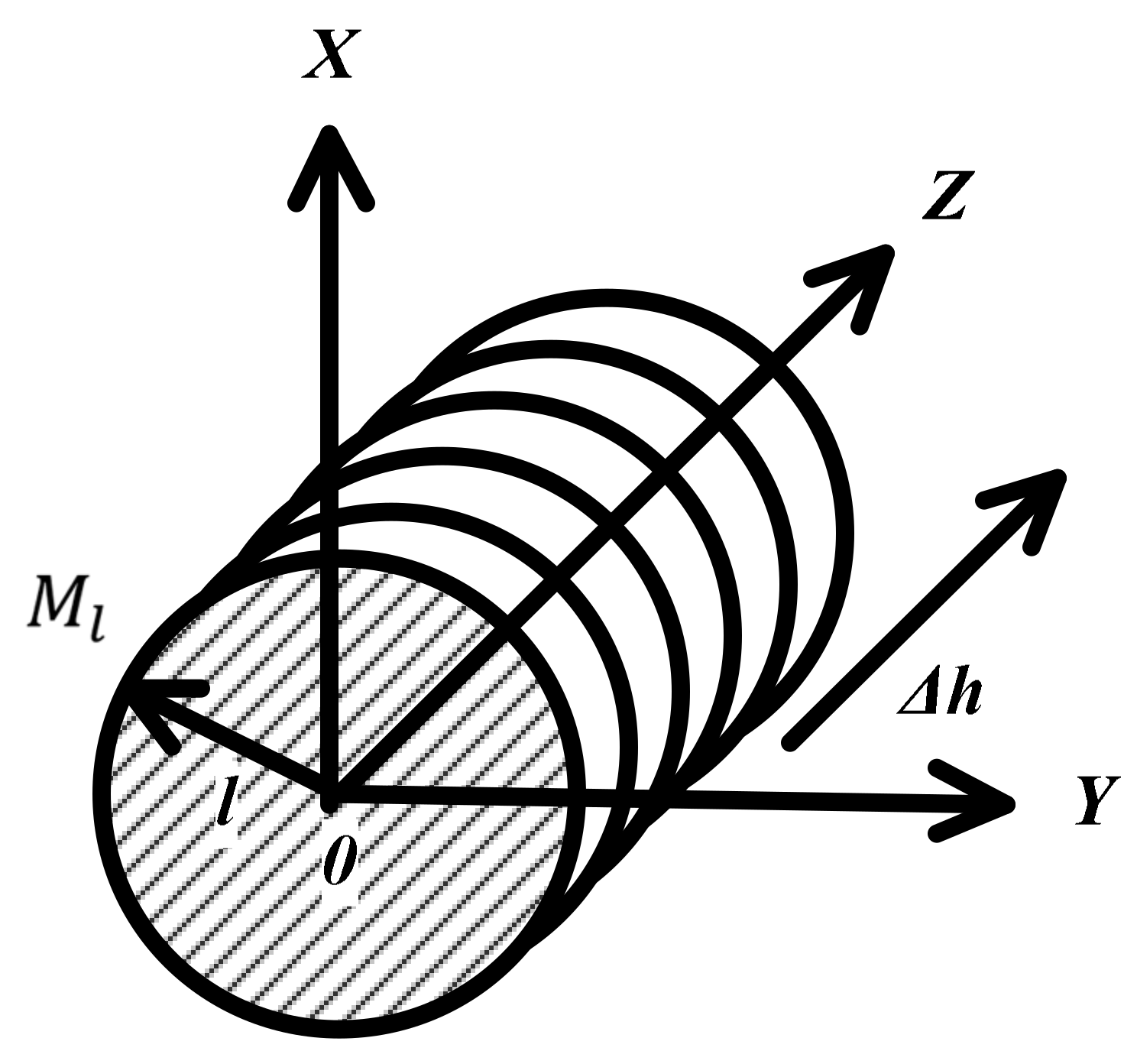



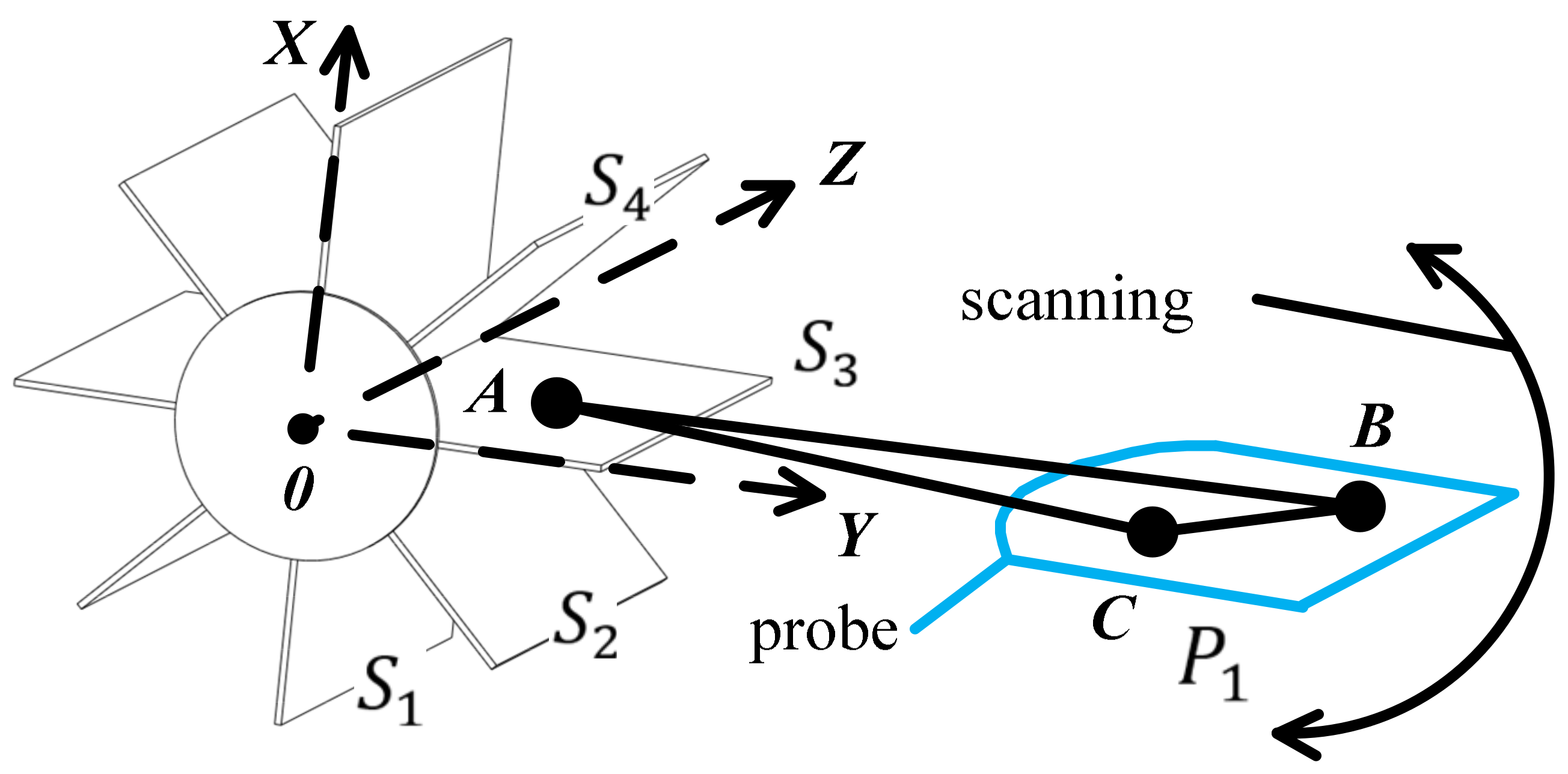






| STEP1 | According to the target position, set the probe detection depth parameter r. Then, set the target point Pi (x, y, z) inside the measured target. The direct distance D between Pi (x, y, z) and the probe may change during the measurement procedure. The actual value of D is obtained by the spatial position of the probe and pressure compensation, which will be analyzed in detail later. The value of D is generally much larger than l which is the radius of the measured target M as shown in Figure 4. |
| STEP2 | Select any straight line L that is passing through Pi (x, y, z) and parallel to the plane of the movement of the freehand probe. |
| STEP3 | According to real-time requirements and the situation regarding data storage space, the value of the vertical resolution Δ𝑣 is determined and the number of sectors is set. A point on each sector is taken to form a set of spatial points S1 (x1, y1, z1),…,Sn (xn, yn, zn ) where n = Δ𝑣. Using Equation (2), the space plane inverse operation can be completed to obtain the sectors S1,…,Sn. The data for these sectors will be used to create the Sector Database (SD), which is used for the quick matching step later on. |
| The Angle Between the Straight Line and the Positive Direction of the Z-Axis | |
| The projection of the line on the plane and the positive angle of the X-axis | |
| The distance from the origin to the target point |
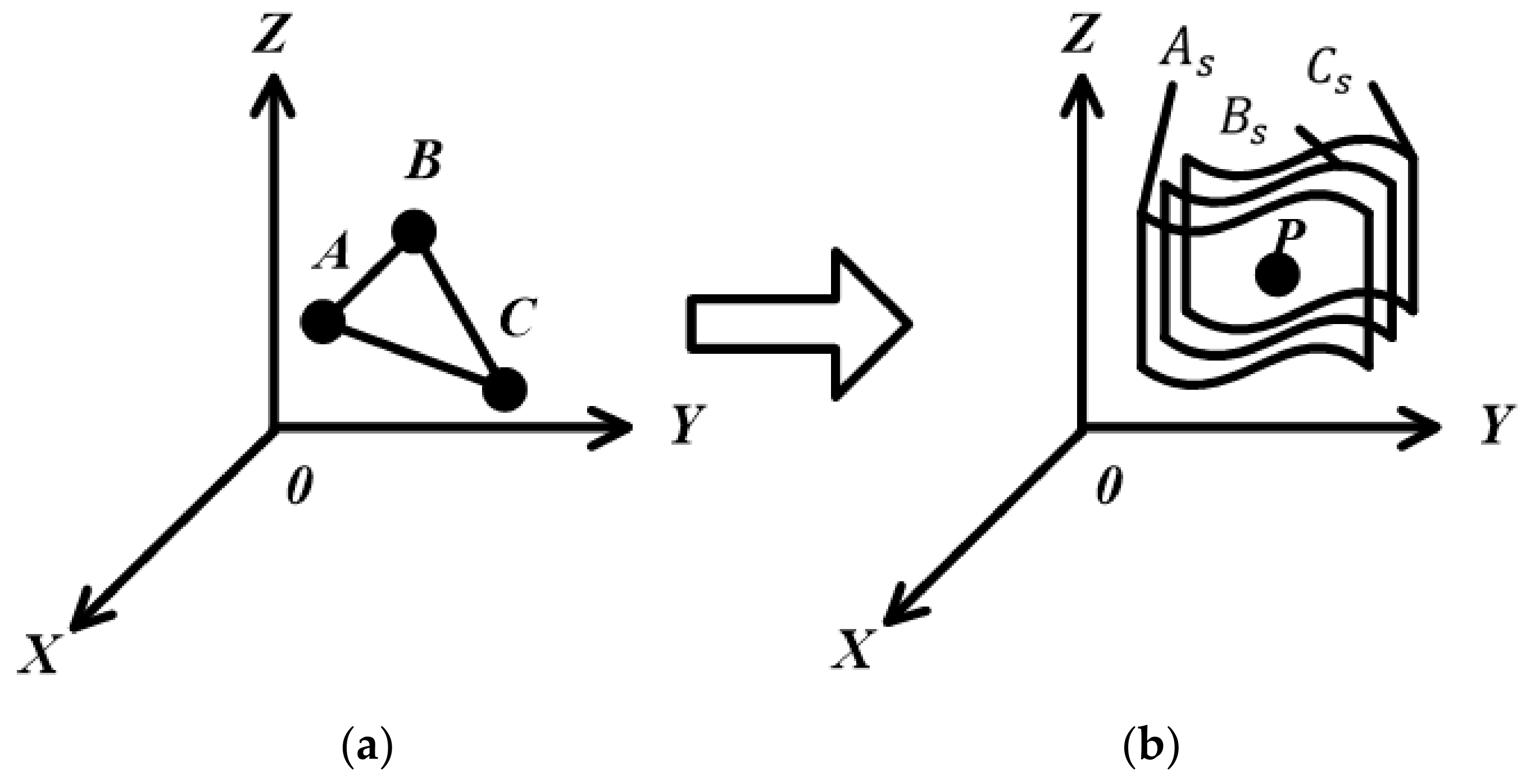
| STEP1 | Take B and C on the current plane of the probe sector. |
| STEP2 | Select a plane and take point A from the Sector Database (SD). |
| STEP3 | The randomly generated points A, B and C are respectively subjected to the 3D Hough transform. If the result is a point in the parameter space, the current sector plane P1 of the probe corresponds to S3 of the database. Conversely, if the result is not a point, then repeat STEP2. If there is no corresponding plane after traversing all the sectors of the database, a re-establishment of the spatial plane model is needed and the vertical resolution Δ𝑣 is improved. |
| Parameter | Value |
|---|---|
| Elements | 128 |
| Dimension | 156 × 60 × 20 mm |
| Image frame rate | 18 frames/s |
| Weight | 220 gs ~ 250 g |
| Δv = 8, Speed of Sound = 1500 m/s Ultrasound Frequency = 1 kHz, n = 4 mm | ||
|---|---|---|
| D/mm | T/us | ∆t/us |
| 1.75 | 1.2 | −1.5 |
| 2.5 | 1.7 | −1 |
| 3.25 | 2.2 | −0.5 |
| 4 | 2.7 | 0 |
| 4.75 | 3.2 | 0.5 |
| 5.5 | 3.7 | 1 |
| 6.25 | 4.2 | 1.5 |
| 7 | 4.7 | 2 |
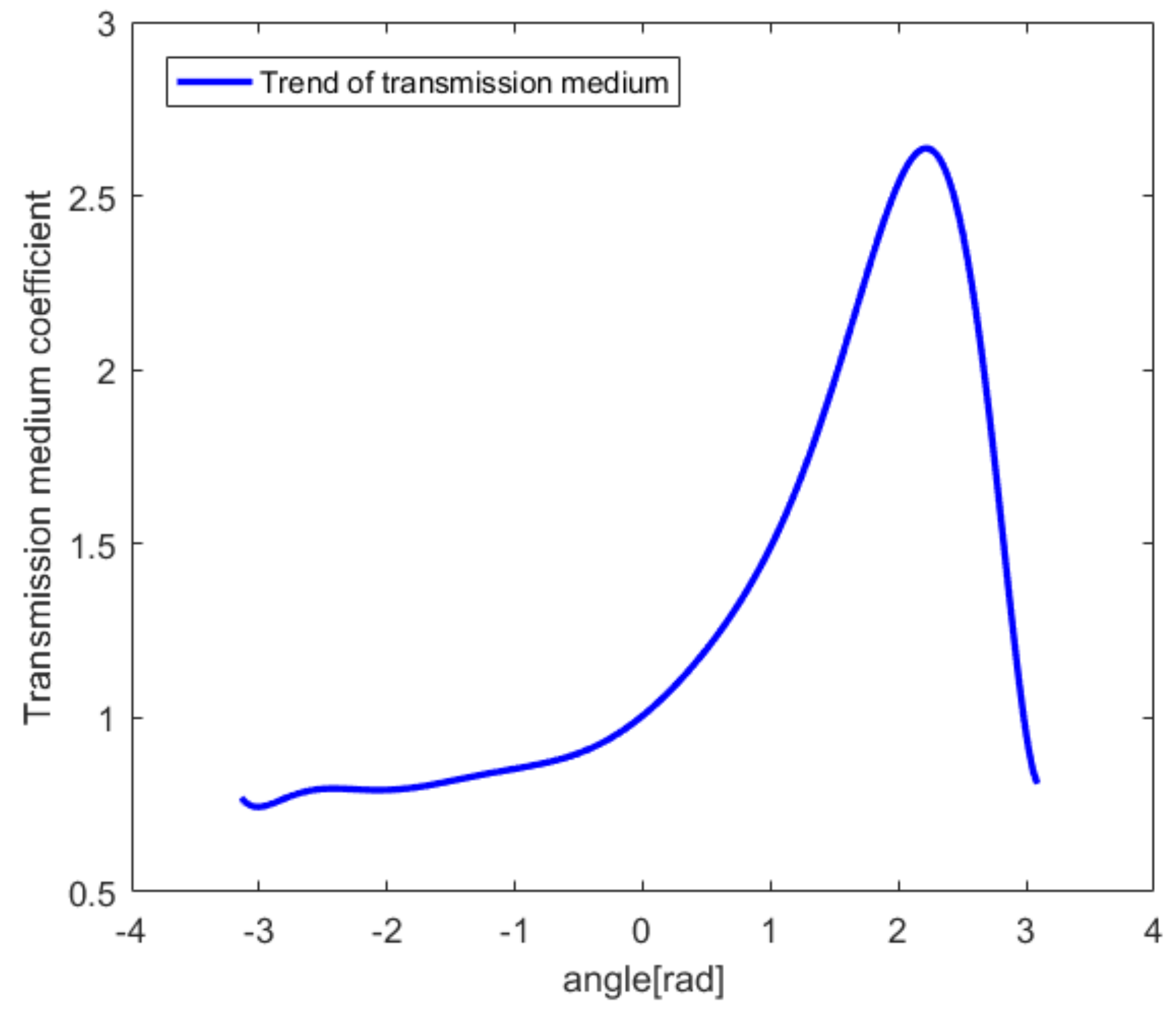
| Δv = 8, Speed of Sound = 1500 m/s Ultrasound Frequency = 1 kHz, n = D = 4 mm | ||
|---|---|---|
| TMC | T/us | ∆t/us |
| 2.77 | 11.2 | 8.5 |
| 2.04 | 7.7 | 5 |
| 1.28 | 4 | 1.3 |
| 1 | 2.7 | 0 |
| 0.85 | 2 | −0.7 |
| 0.82 | 1.8 | −0.9 |
| 0.81 | 1.7 | −1 |
| 0.75 | 1.5 | −1.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Chen, H.; Peng, Y.; Tao, D. Probe Sector Matching for Freehand 3D Ultrasound Reconstruction. Sensors 2020, 20, 3146. https://doi.org/10.3390/s20113146
Chen X, Chen H, Peng Y, Tao D. Probe Sector Matching for Freehand 3D Ultrasound Reconstruction. Sensors. 2020; 20(11):3146. https://doi.org/10.3390/s20113146
Chicago/Turabian StyleChen, Xin, Houjin Chen, Yahui Peng, and Dan Tao. 2020. "Probe Sector Matching for Freehand 3D Ultrasound Reconstruction" Sensors 20, no. 11: 3146. https://doi.org/10.3390/s20113146
APA StyleChen, X., Chen, H., Peng, Y., & Tao, D. (2020). Probe Sector Matching for Freehand 3D Ultrasound Reconstruction. Sensors, 20(11), 3146. https://doi.org/10.3390/s20113146







