A Method for Measuring the Height of Hand Movements Based on a Planar Array of Electrostatic Induction Electrodes
Abstract
1. Introduction
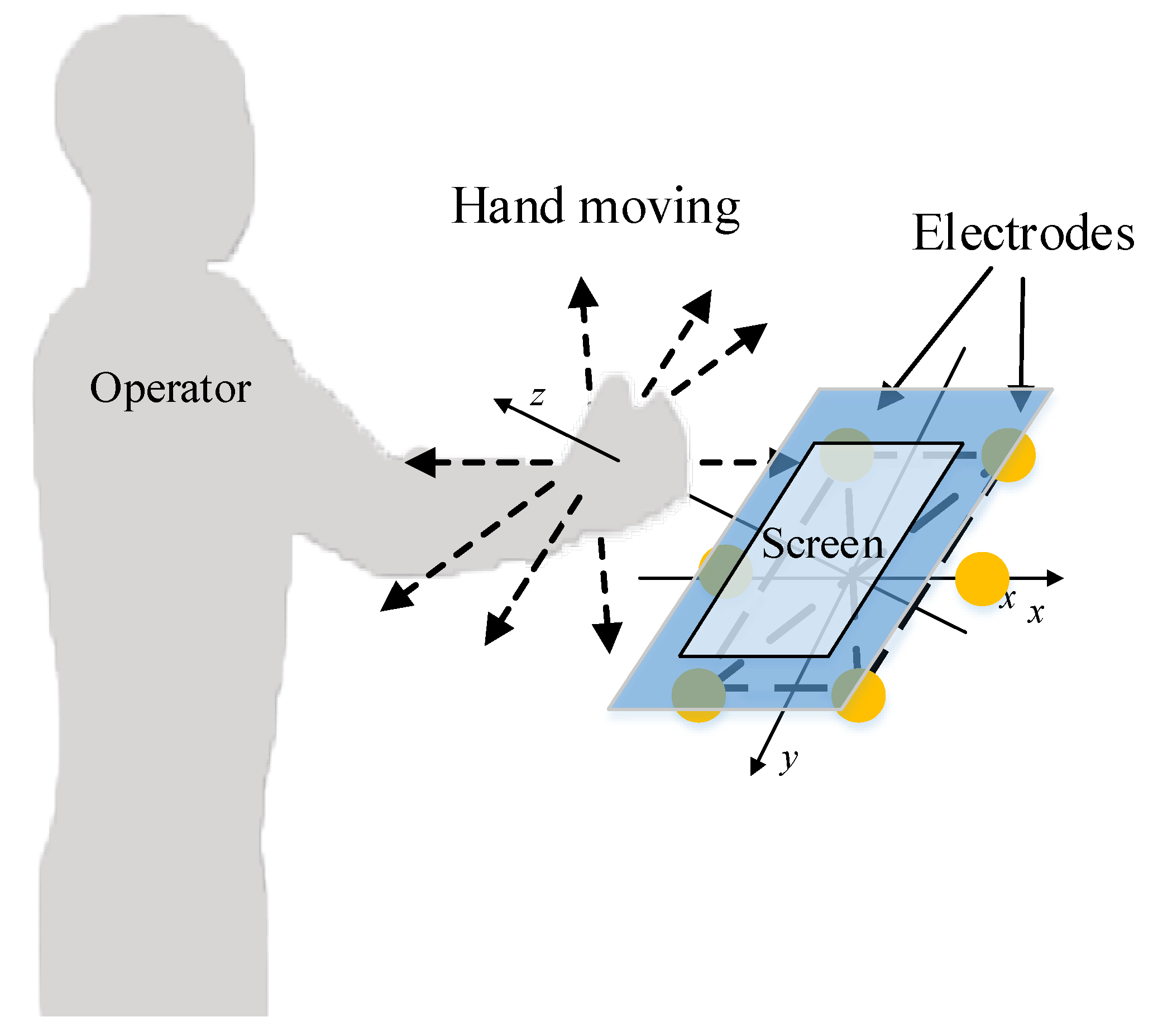
2. Methods
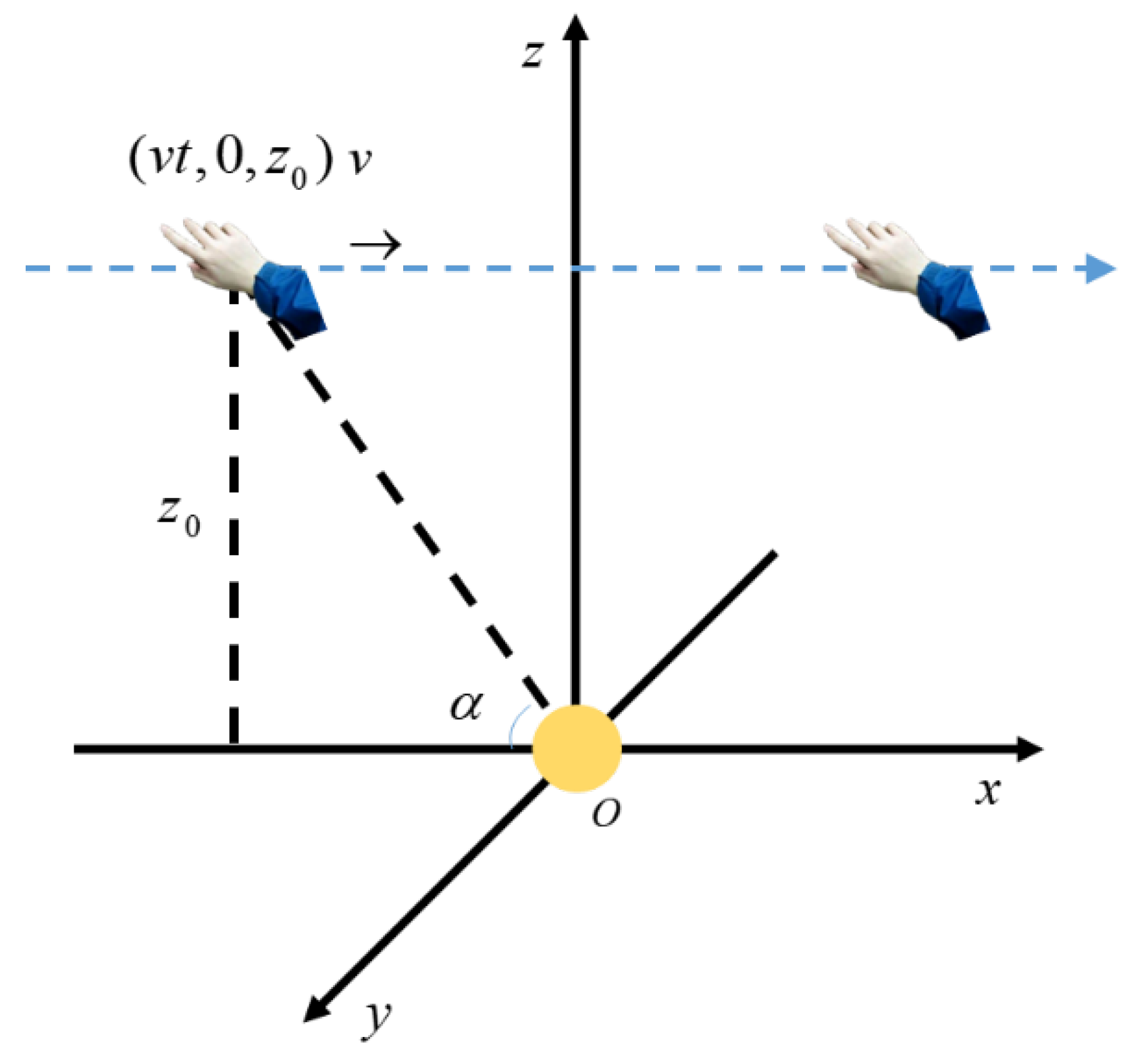
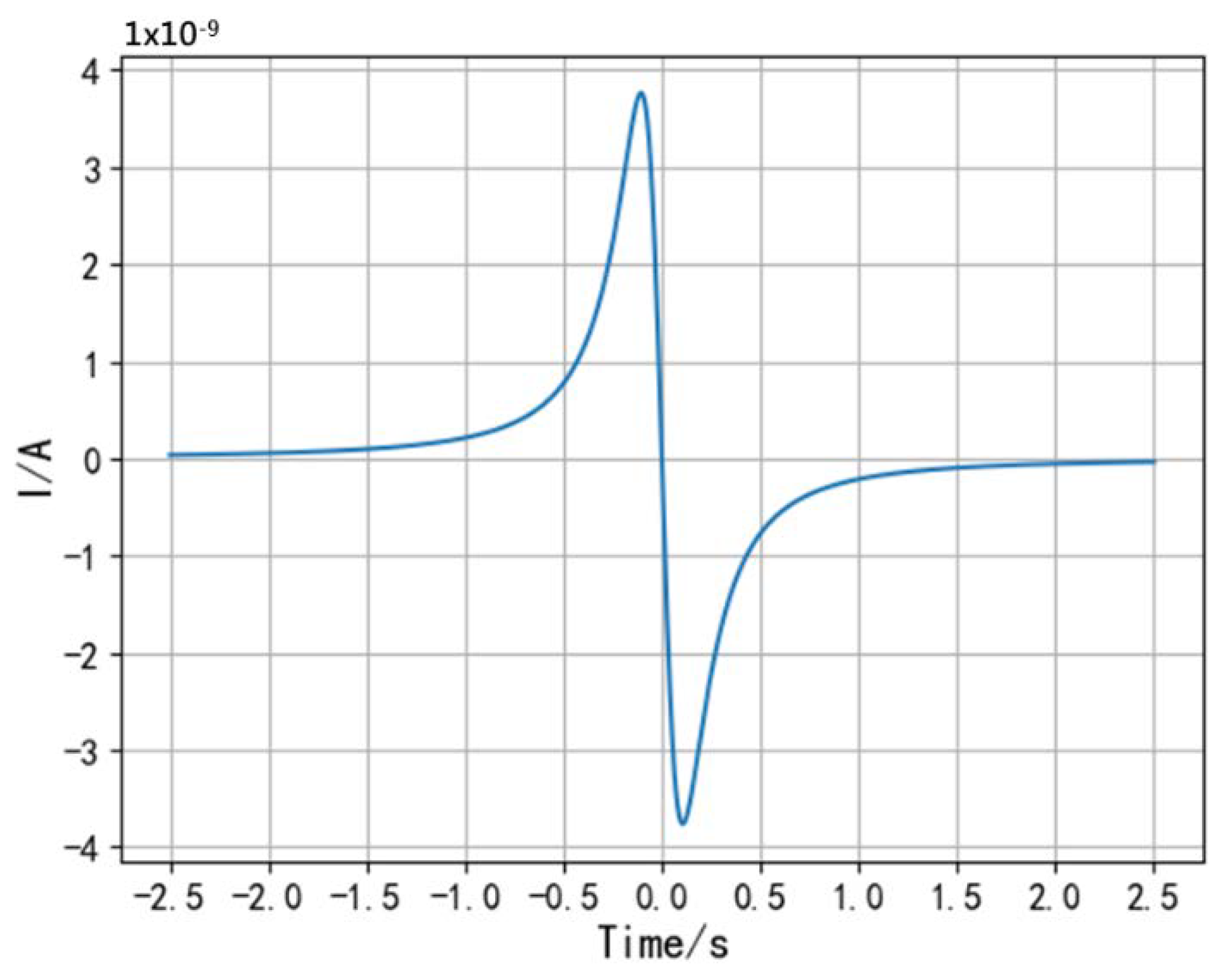
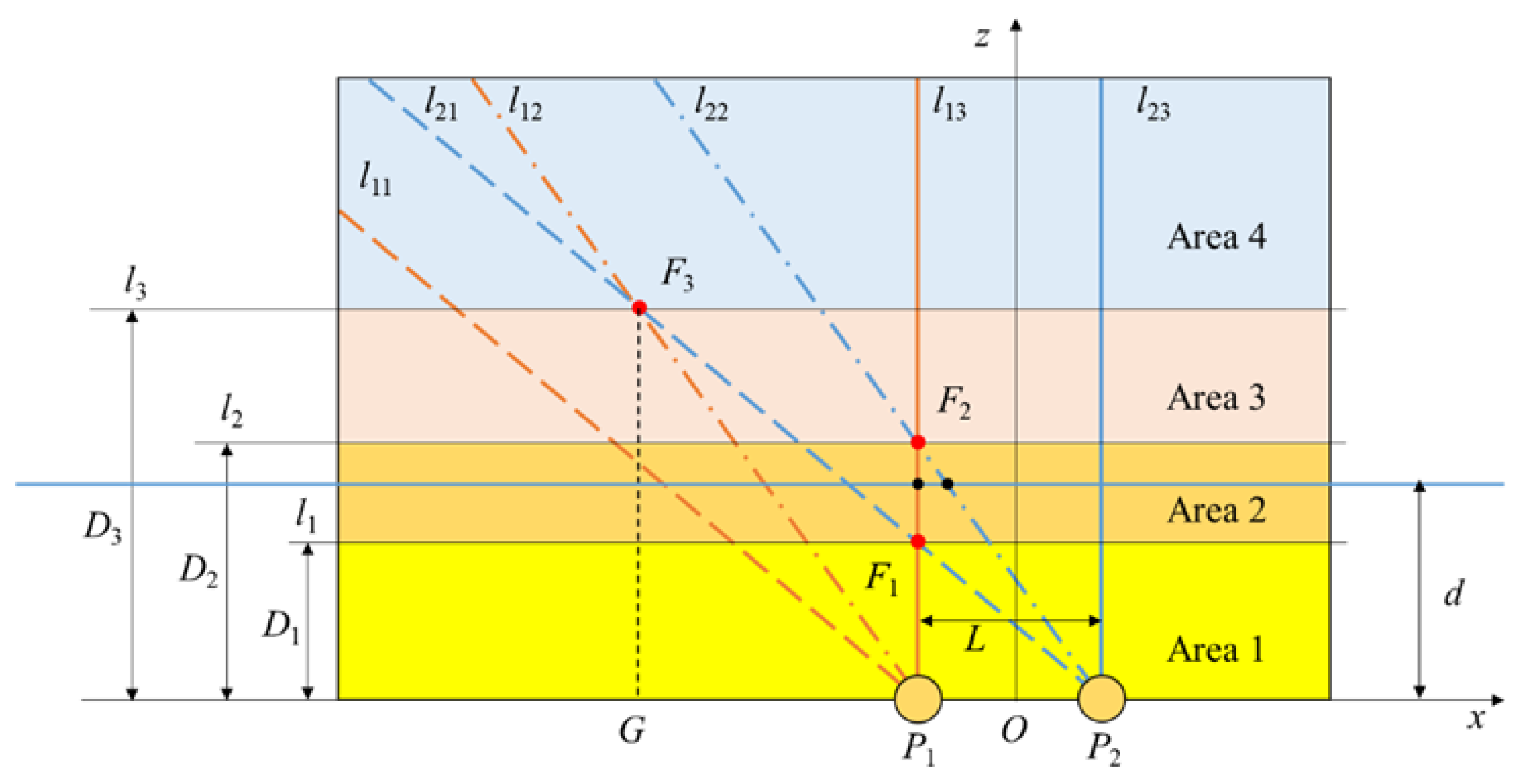
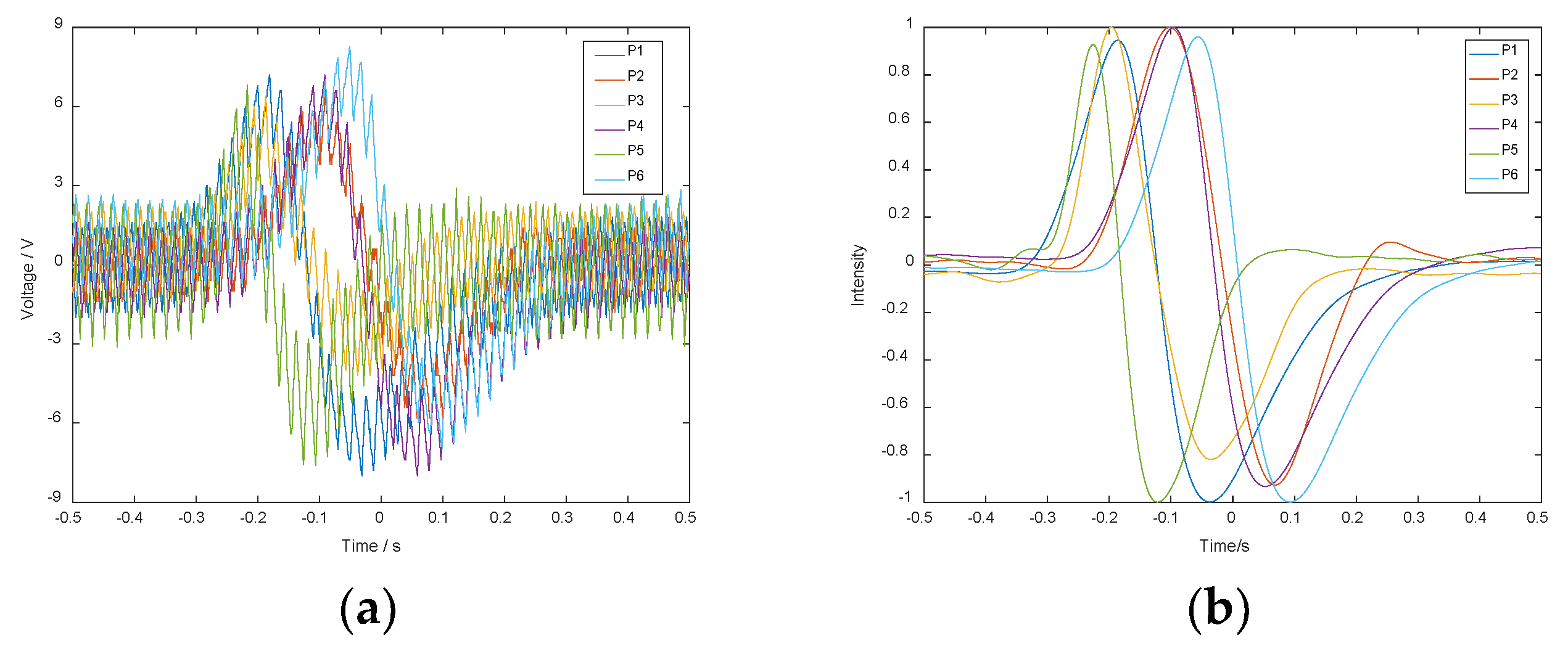
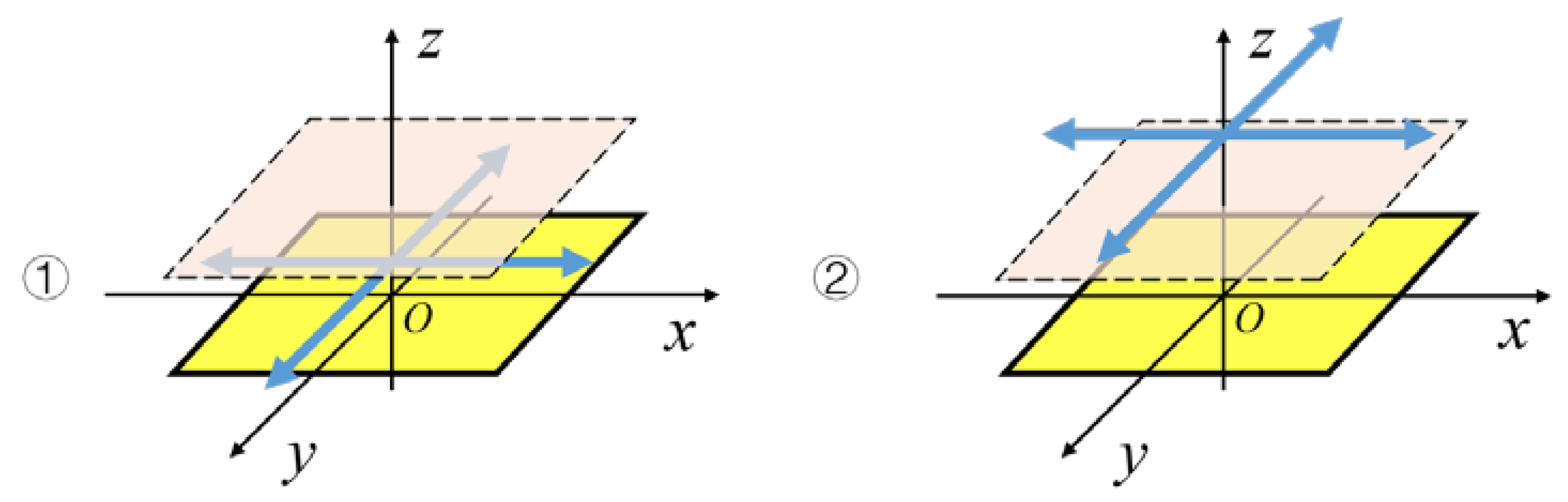
2.1. Regularity of the Occurrence of the Maximum Value of the Induced Current, the Zero-Crossing of the Induced Current, and the Maximum Value of the Change Rate of the Induced Current
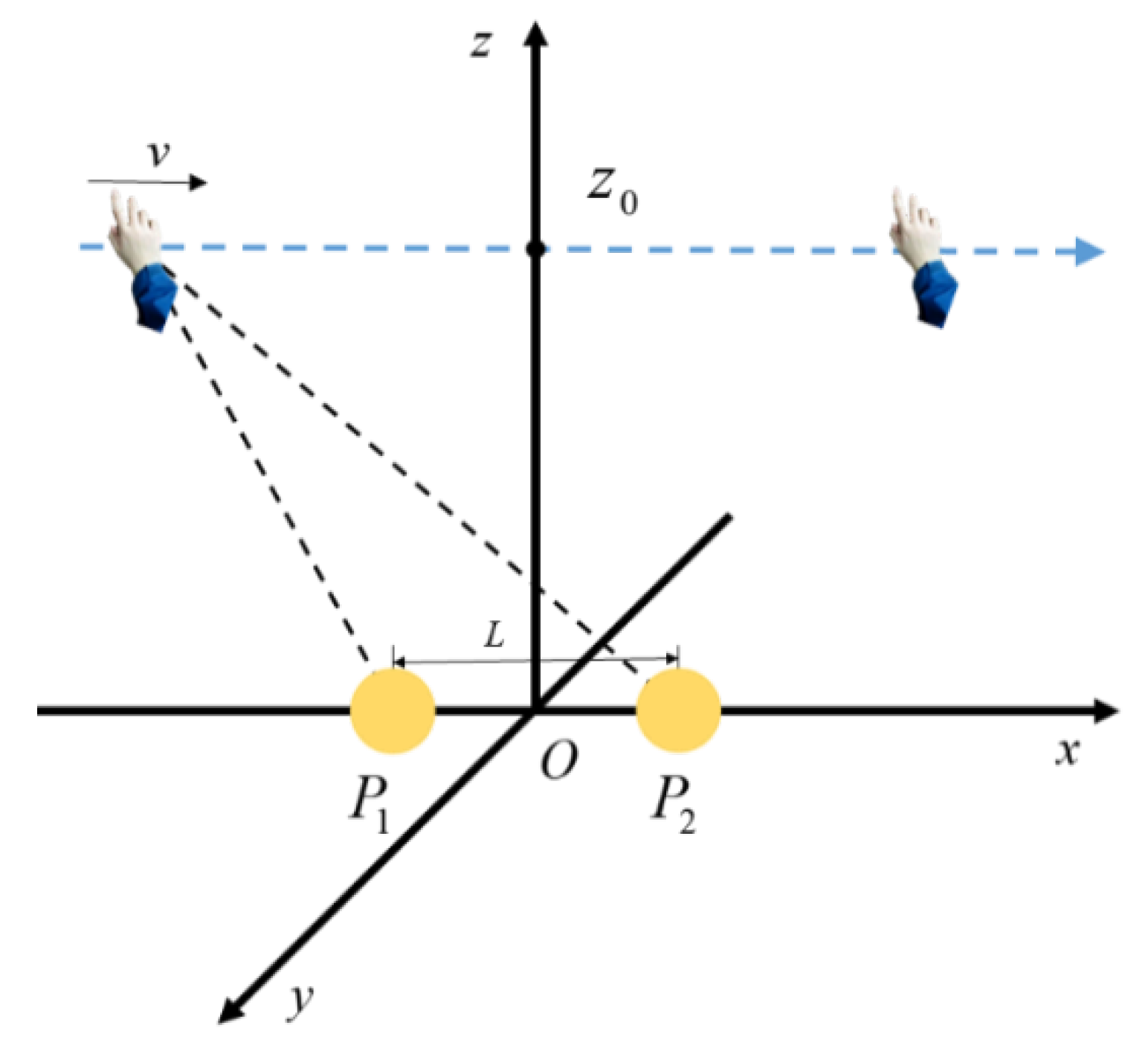
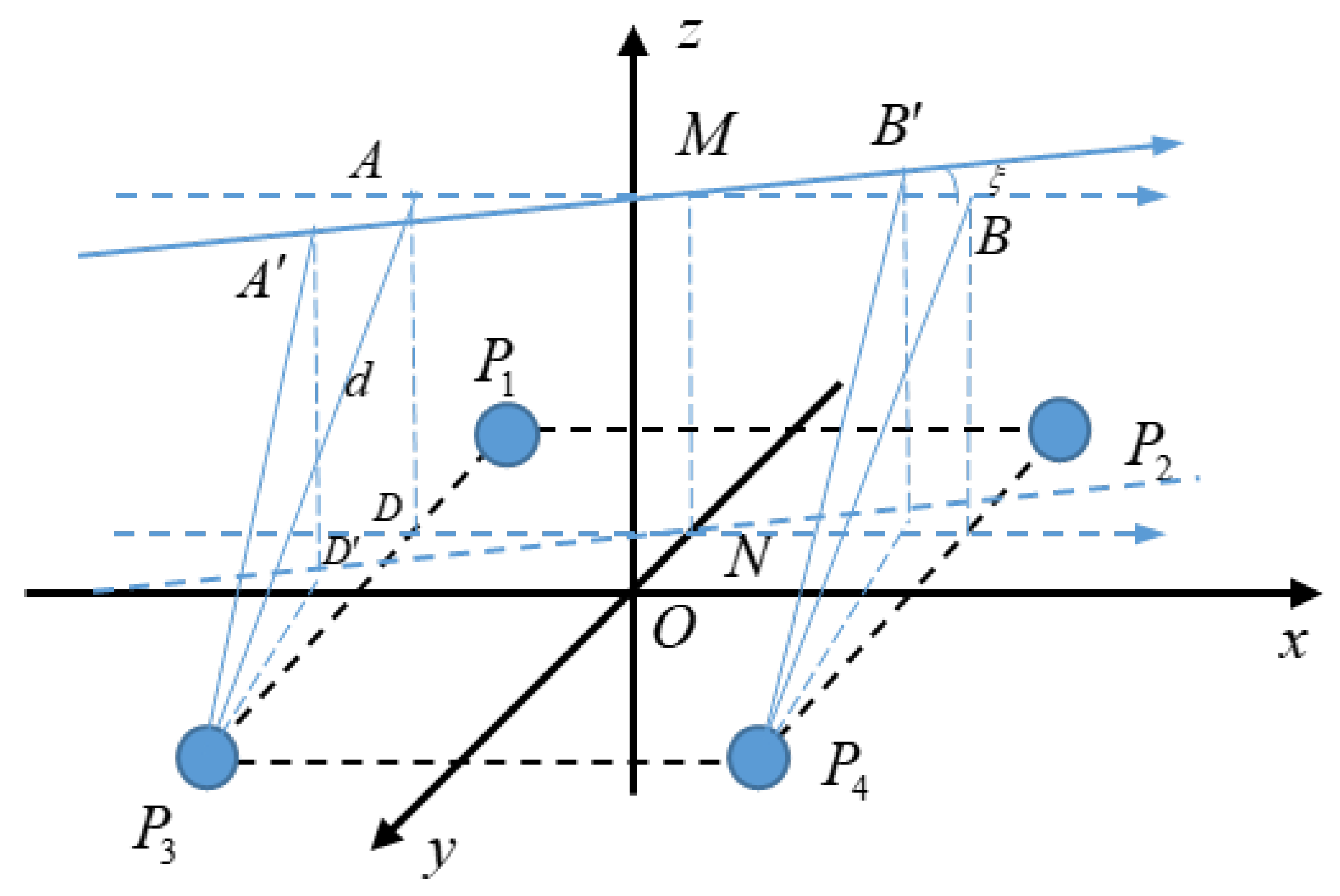
2.2. Algorithm for Measuring the Distance between the Trajectory of a Hand Movement and the Straight Line of Two Electrodes
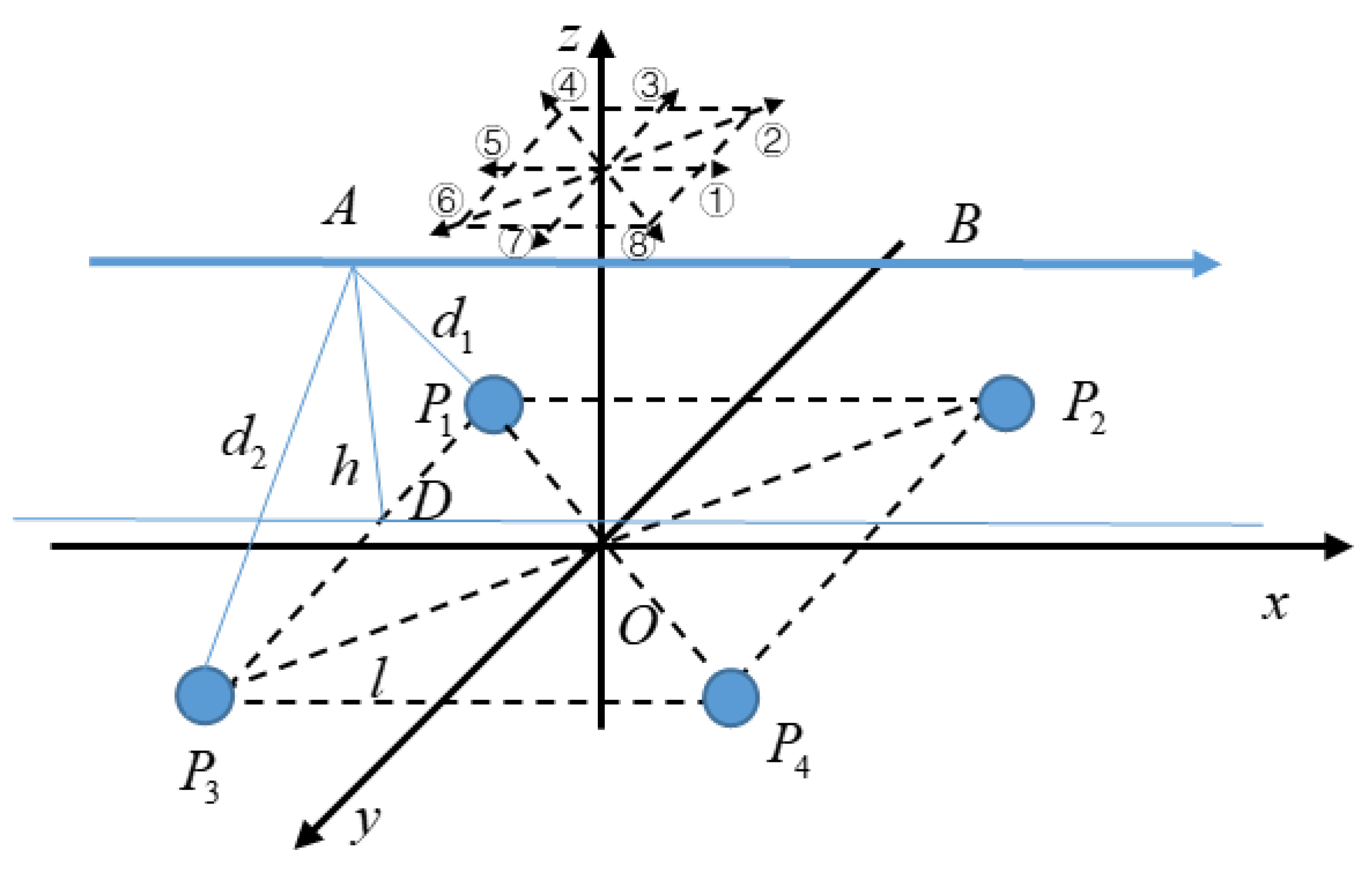
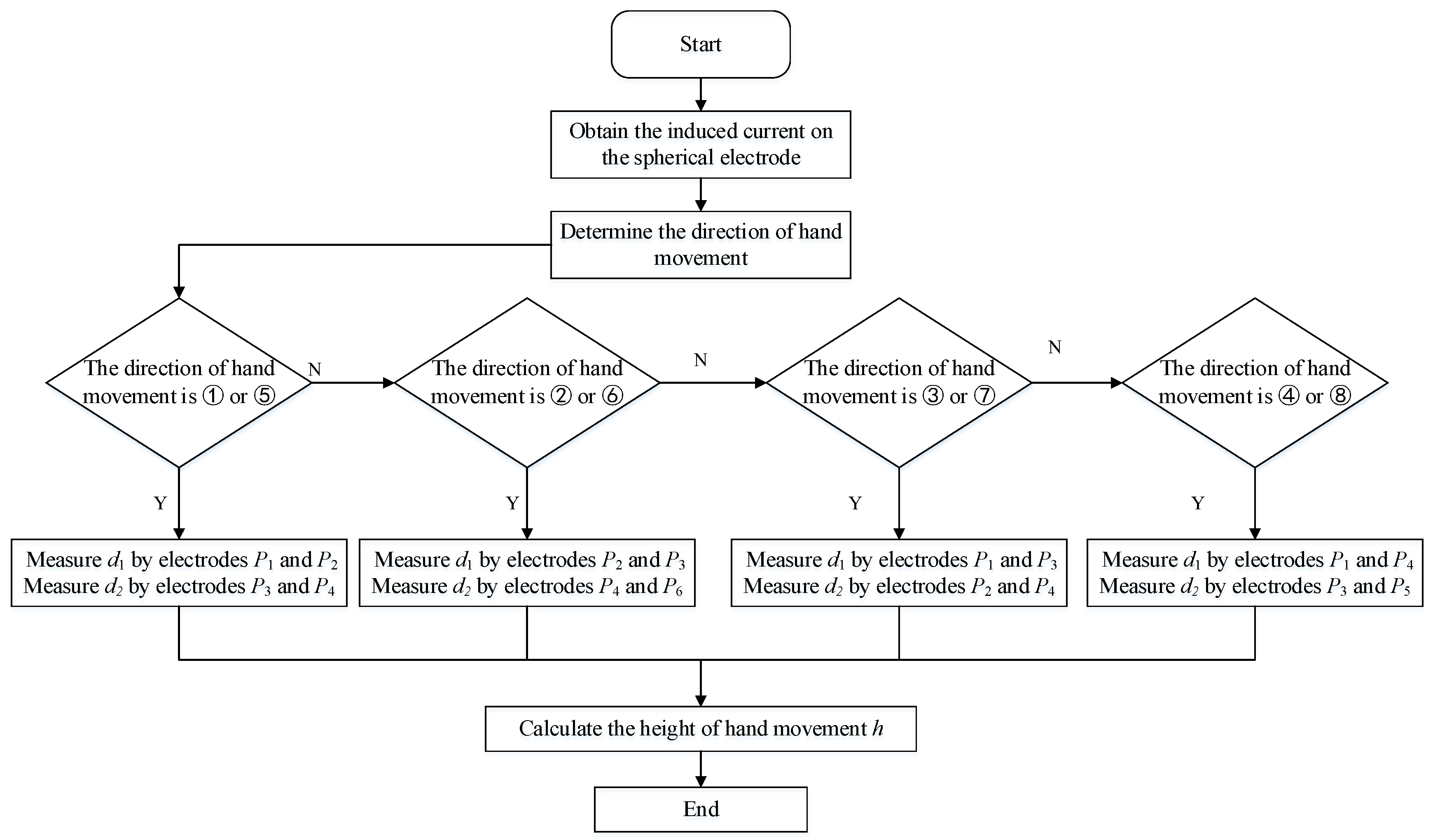
2.3. Measurement Algorithm for the Height of Hand Movements Based on Human Body Electrostatics
2.4. Simulation Noise Test
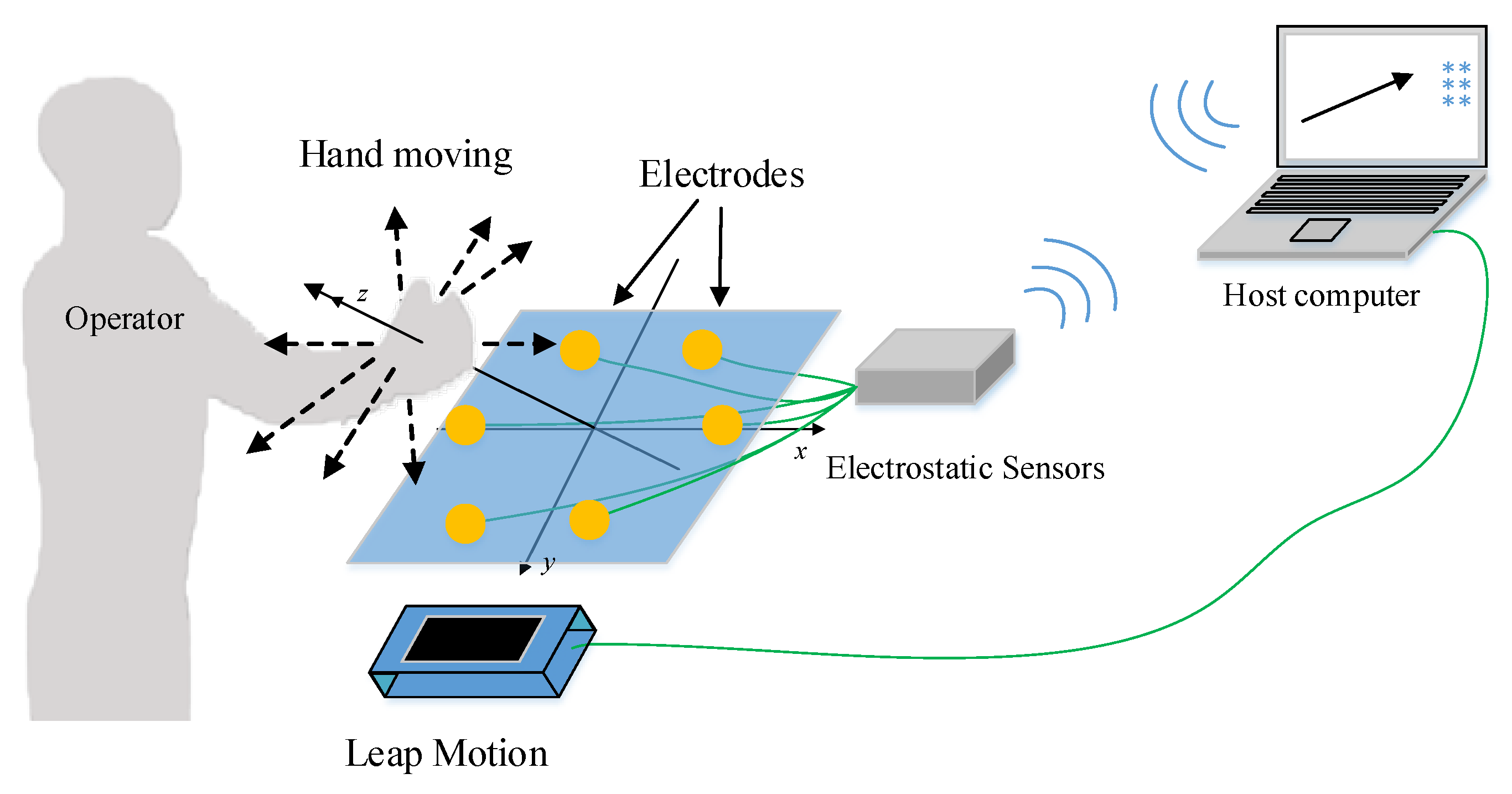
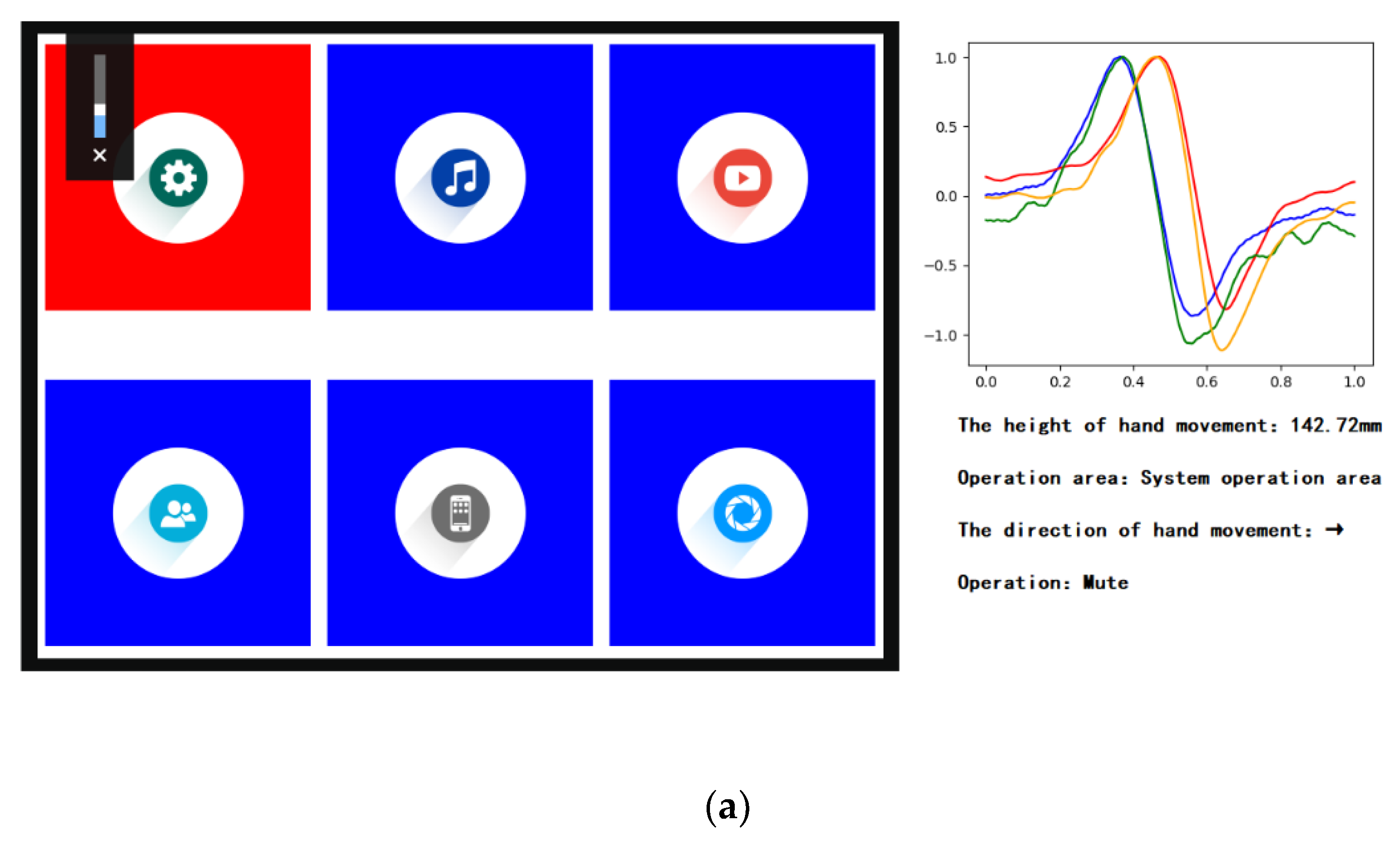
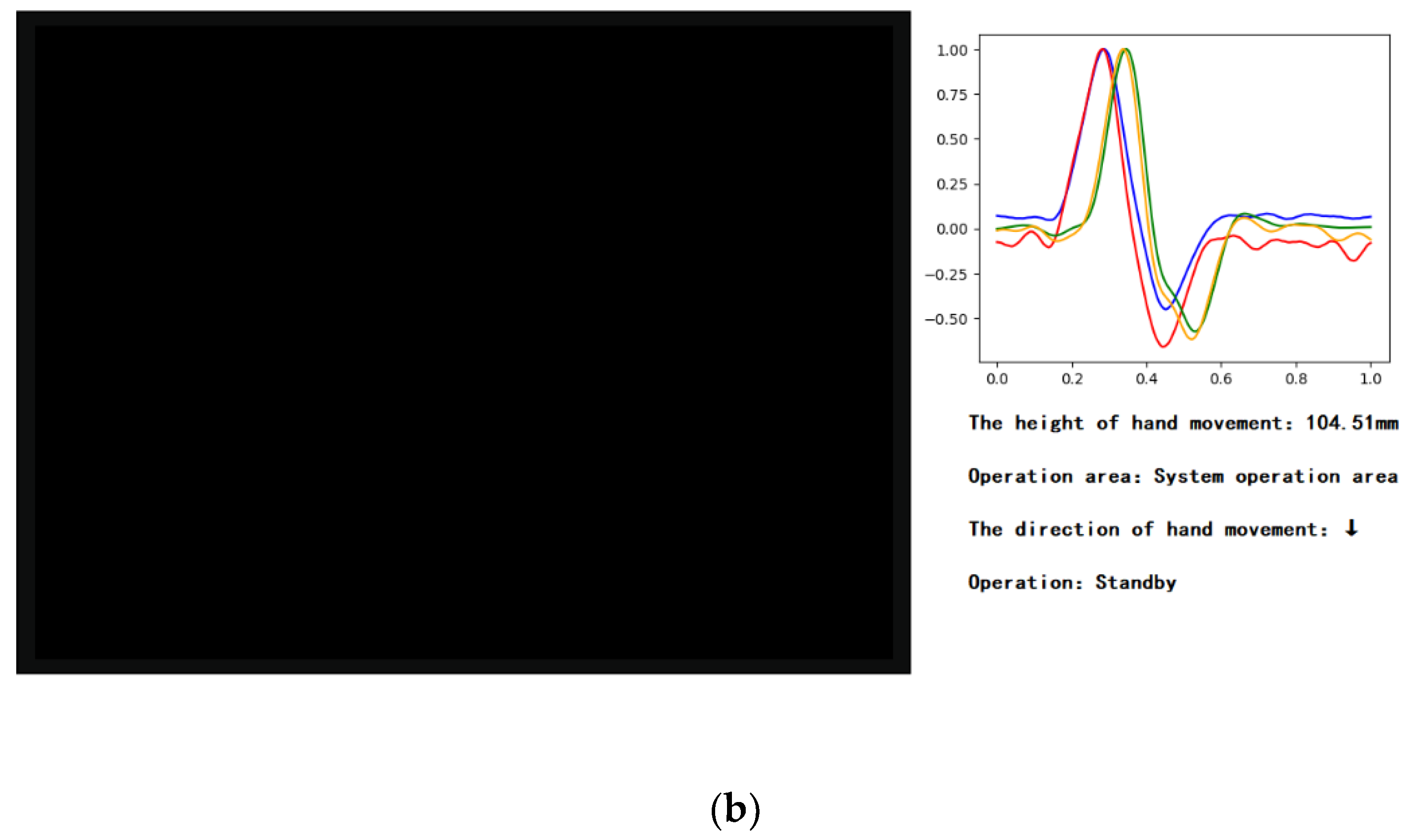
2.5. Design and Experiment
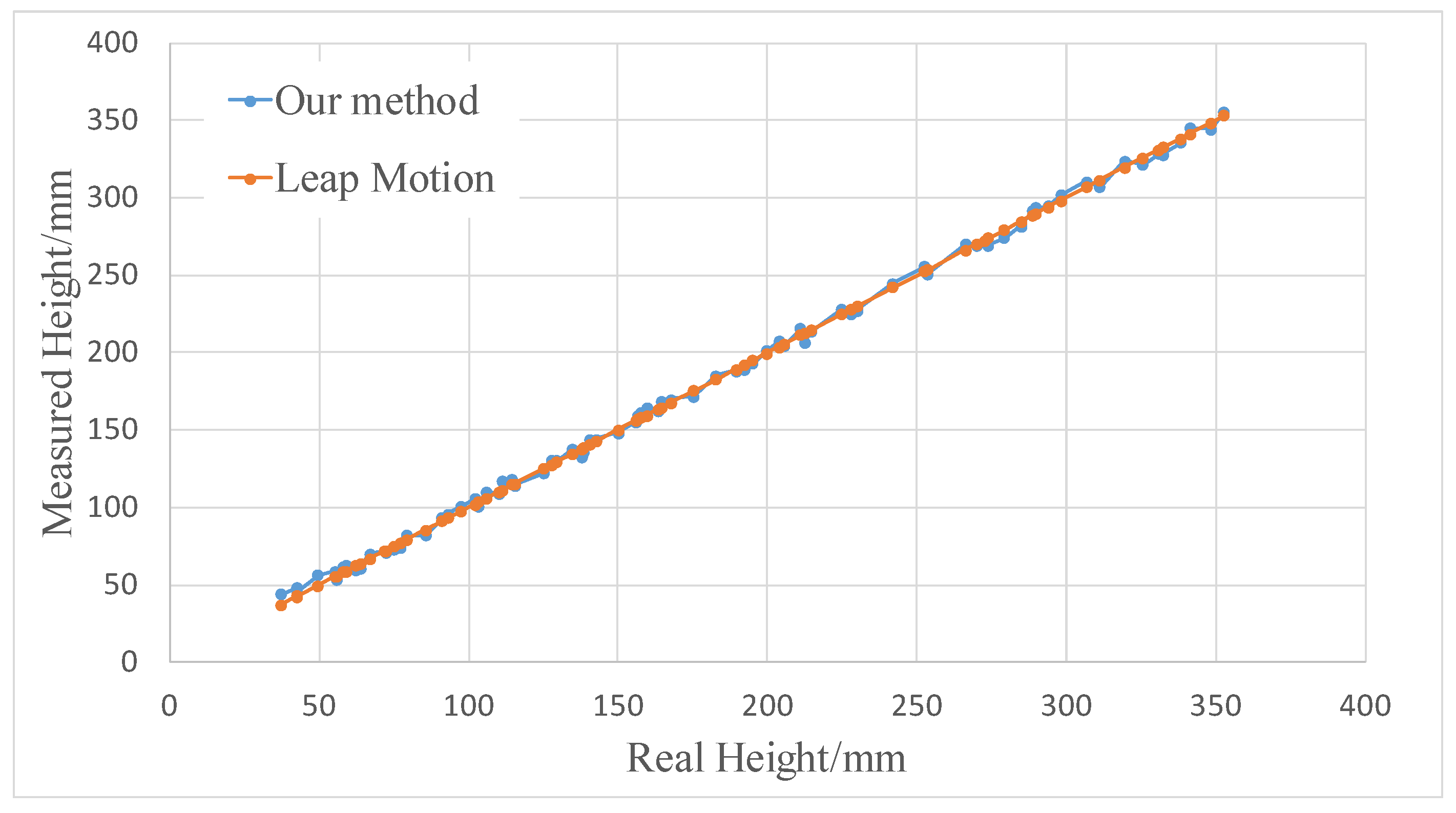
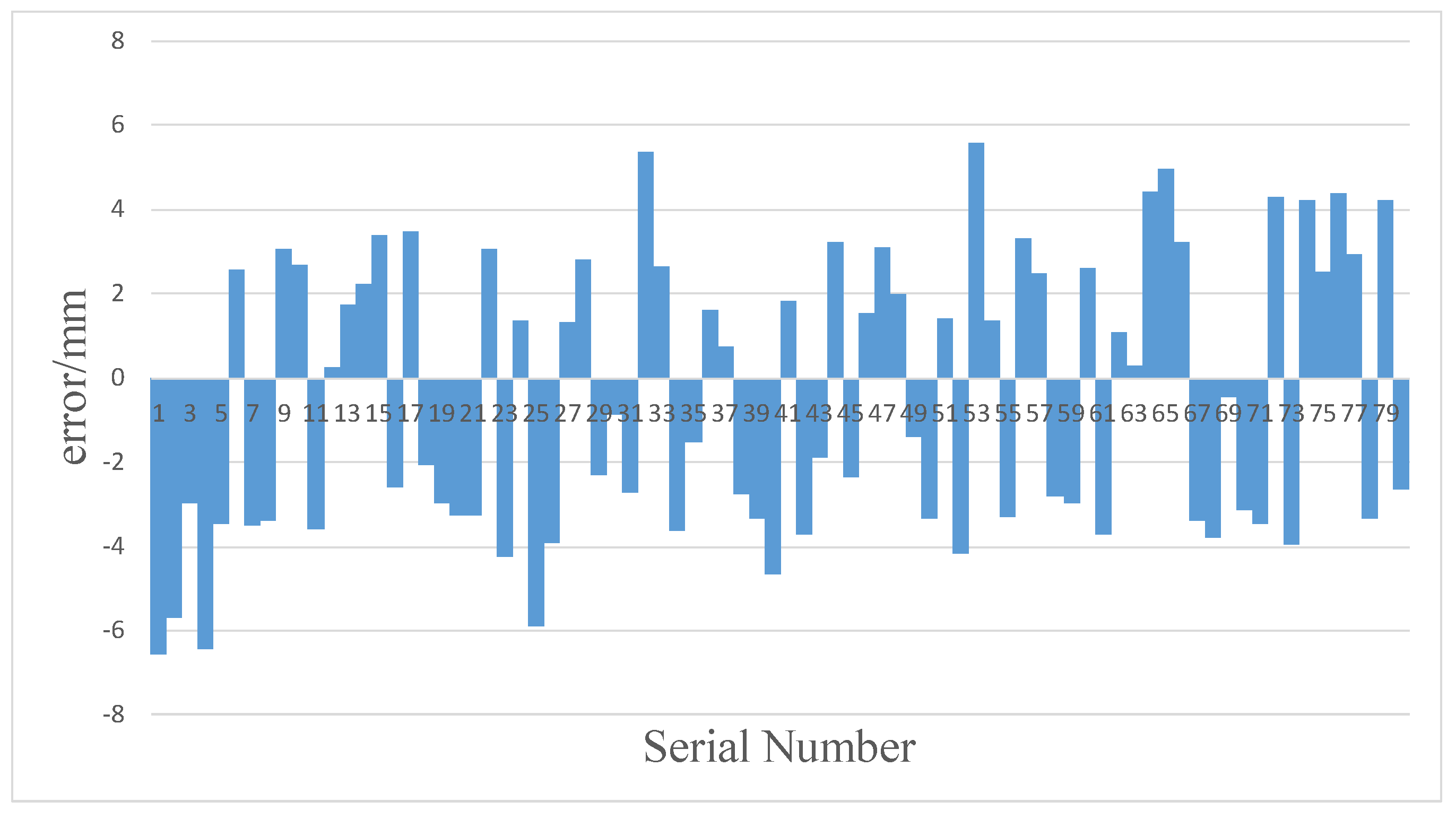
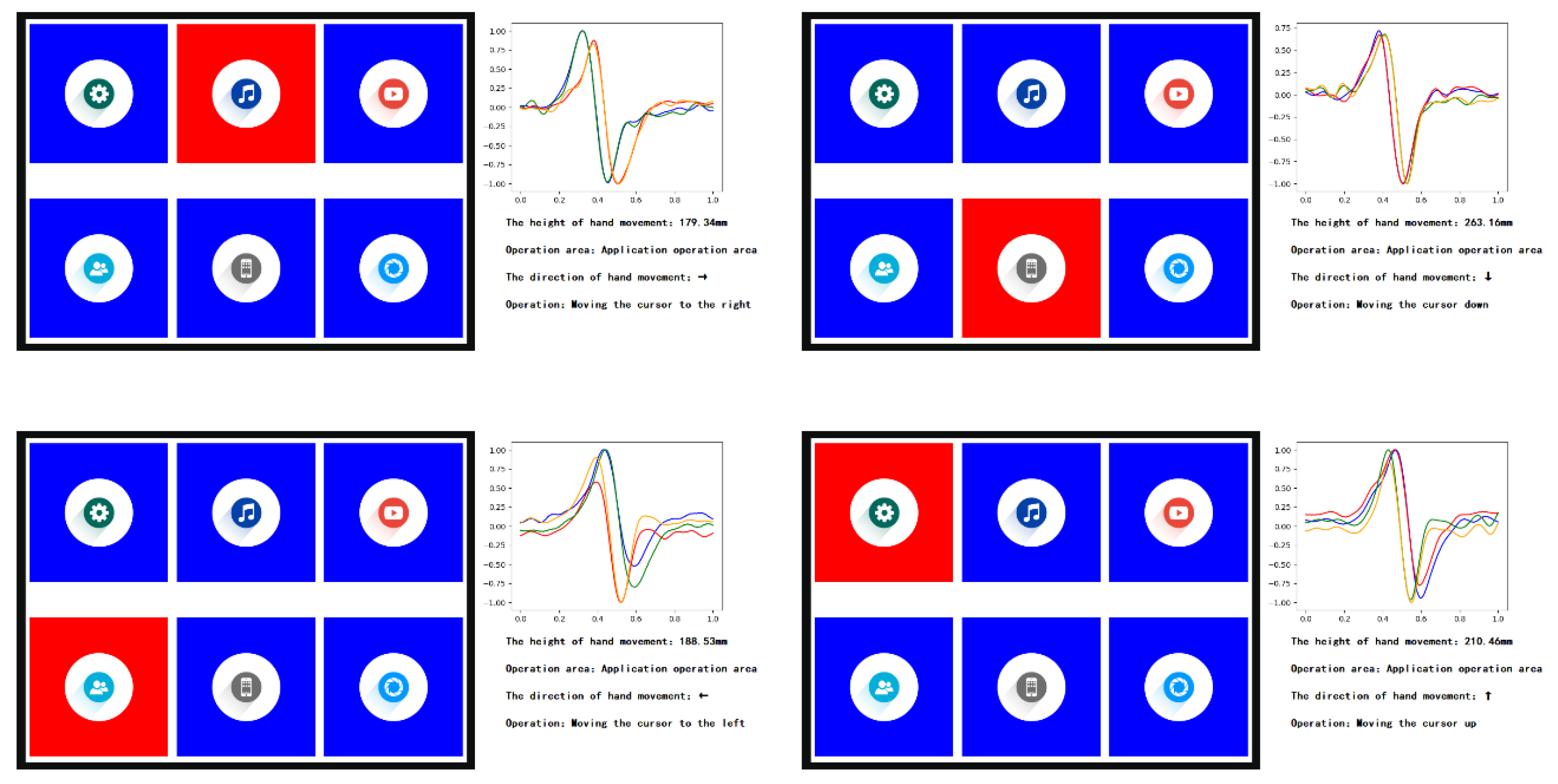
3. Results
4. Discussion
4.1. Operation Error
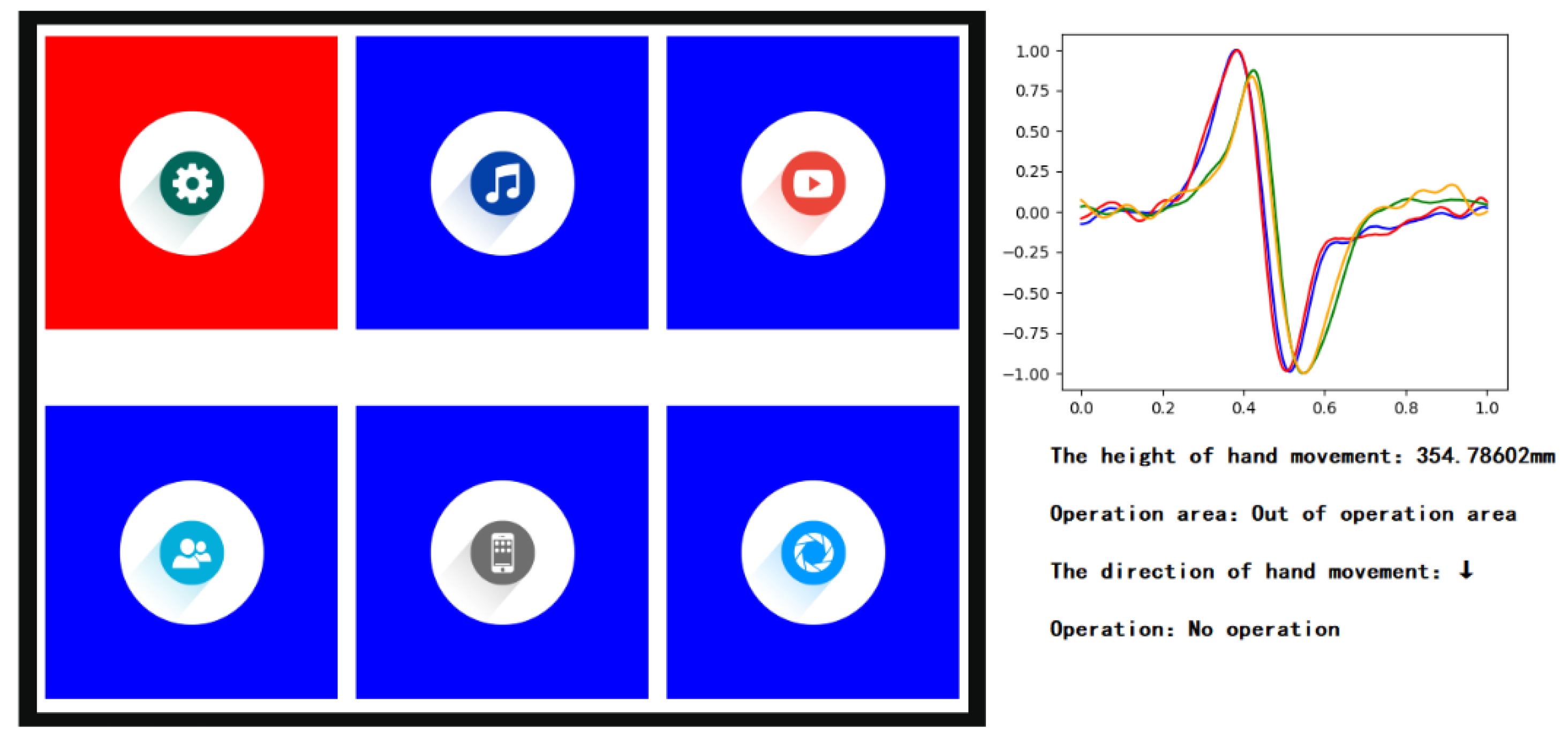
4.2. Application Example
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jennifer, P.; Yvonne, R.; Helen, S. Interaction Design: Beyond Human-Computer Interaction, 4th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2015; pp. 219–221. [Google Scholar]
- Liu, W. Natural user interface- next mainstream product user interface. In Proceedings of the 2010 IEEE 11th International Conference on Computer-Aided Industrial Design & Conceptual Design 1, Yiwu, China, 17–19 November 2010. [Google Scholar]
- Fernandez, R.A.S.; Sanchez-Lopez, J.L.; Sampedro, C. Natural user interfaces for human-drone multi-modal interaction. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 20–24 June 2016; pp. 2372–9198. [Google Scholar]
- Günter, E.; Holzner, C.; Guger, C. A Hybrid Brain-Computer Interface for Smart Home Control. In Human-Computer Interaction. In Proceedings of the Interaction Techniques and Environments-14th International Conference, HCI International 2011, Orlando, FL, USA, 9–14 July 2011. Part II. [Google Scholar]
- Moeslund, T.B.; Granum, E. A Survey of Computer Vision-Based Human Motion Capture. Comput. Vis. Image Underst. 2001, 81, 231–268. [Google Scholar] [CrossRef]
- Nishiyama, M.; Watanabe, K. Wearable Sensing Glove with Embedded Hetero-Core Fiber-Optic Nerves for Unconstrained Hand Motion Capture. IEEE Trans. Instrum. Meas. 2009, 58, 3995–4000. [Google Scholar] [CrossRef]
- Cheng, J.; Xie, C.; Bian, W.; Tao, D. Feature fusion for 3D hand gesture recognition by learning a shared hidden space. Pattern Recognit. Lett. 2012, 33, 476–484. [Google Scholar] [CrossRef]
- Ji, X.; Wang, C.; Ju, Z. A New Framework of Human Interaction Recognition Based on Multiple Stage Probability Fusion. Appl. Sci. 2017, 7, 567. [Google Scholar] [CrossRef]
- Ádám, E.; Thomas, W.; Bernhard, R. Privacy protection vs. utility in visual data-An objective evaluation framework. Multimed. Tools Appl. 2018, 77, 2285–2312. [Google Scholar]
- Liu, J.; Pan, Z.; Li, X. An accelerometer-based gesture recognition algorithm and its application for 3D interaction. Comput. Sci. Inf. Syst. 2010, 7, 177–188. [Google Scholar] [CrossRef]
- Kevin, R.W.; Mindy, H.C.; Kevin, H.K. Gesture based control and EMG decomposition. IEEE Trans. Ind. Appl. 2006, 36, 503–514. [Google Scholar]
- Panagiotis, K.A.; Kostas, J.K. EMG-based control of a robot arm using low-dimensional embeddings. IEEE Trans. 2010, 26, 393–398. [Google Scholar]
- Harland, C.J.; Clark, T.D.; Prance, R.J. Electric Potential Probes-New Directions in the Remote Sensing of the Human Body. Meas. Sci. Technol. 2002, 13, 163–169. [Google Scholar] [CrossRef]
- Beardsmore-Rust, S.T.; Prance, R.J.; Aydin, A.; Prance, H.; Harl, C.J.; Stiffell, P.B. Signal specific electric potential sensors for operation in noisy environments. J. Phys. Conf. Ser. 2009, 178, 12011. [Google Scholar] [CrossRef]
- Han, Q.; Chen, X.; Tang, K.; Li, P. A non-contact human-computer interaction application design based on electrostatic current of human body. Int. J. Comput. Appl. Technol. 2016, 53, 23–31. [Google Scholar] [CrossRef]
- Kurita, K. A novel non-contact hand motion classification technique for application to human machine interfaces. In Proceedings of the SICE Annual Conference 2011, Tokyo, Japan, 13–18 September 2011. [Google Scholar]
- Von, W.J.; Florian, K.; Biying, F. An experimental overview on electric field sensing. J. Ambient Intell. Humaniz. Comput. 2019, 10, 813–824. [Google Scholar]
- Takiguchi, K.; Wada, T.; Toyama, S. Human Body Detection that Uses Electric Field by Walking. Adv. Mech. Des. Syst. Manuf. 2007, 1, 294–305. [Google Scholar] [CrossRef]
- Takiguchi, K.; Wada, T.; Toyama, S. Rhythm Pattern of Sole through Electrification of the Human Body WhenWalking. J. Adv. Mech. Des. Syst. Manuf. 2008, 2, 429–440. [Google Scholar] [CrossRef]
- Tang, K.; Chen, X.; Zheng, W.; Han, Q.; Li, P. A Non-contact Technique Using Electrostatics to SenseThree-dimensional Hand Movement for Human Computer Interaction. J. Electrost. 2015, 77, 101–109. [Google Scholar] [CrossRef]
- Tang, K.; Li, P.; Wang, C.; Wang, Y.; Chen, X. Real-time hand position sensing technology based on human body electrostatics. Sensors 2018, 18, 1677. [Google Scholar] [CrossRef] [PubMed]
- Kurita, K. Novel Non-contact and Non-attached Technique for Detecting Sports Motion. Measurement 2011, 44, 1361–1366. [Google Scholar] [CrossRef]
- Kurita, K.; Nishikubo, K. Development of a Human Motion Measurement System for Application to the Human Machine Interface. In Proceedings of the ICCAS-SICE International Joint Conference, Fukuka, Japan, 18–21 August 2009; IEEE Publisher: Piscataway, NJ, USA, 2009. [Google Scholar]
- Kurita, K. New Estimation Method for the Electric Potential of the Human Body under Perfect Non-contact Conditions. IEEJ T. Electr. Electr. 2009, 4, 309–311. [Google Scholar] [CrossRef]
- Jean, C. Electrostatics: Principles, Problems and Applications; Adam Higher: Bristol, UK, 1987; pp. 16–17. [Google Scholar]
- Chen, X.; Han, H. Research on Human-Computer Interaction Technology Based on Electrical Detection Technology. TechConnect Briefs 2016, 3, 144–147. [Google Scholar]




| SNR | 10 dB | 15 dB | 20 dB | |||
|---|---|---|---|---|---|---|
| Absolute Values of Errors/mm | Mean Error | Max Error | Mean Error | Max Error | Mean Error | Max Error |
| 13.32 | 28.71 | 5.04 | 11.70 | 1.09 | 5.76 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Chen, X.; Li, P.; Wang, C.; Li, M. A Method for Measuring the Height of Hand Movements Based on a Planar Array of Electrostatic Induction Electrodes. Sensors 2020, 20, 2943. https://doi.org/10.3390/s20102943
Zhang L, Chen X, Li P, Wang C, Li M. A Method for Measuring the Height of Hand Movements Based on a Planar Array of Electrostatic Induction Electrodes. Sensors. 2020; 20(10):2943. https://doi.org/10.3390/s20102943
Chicago/Turabian StyleZhang, Linyi, Xi Chen, Pengfei Li, Chuang Wang, and Mengxuan Li. 2020. "A Method for Measuring the Height of Hand Movements Based on a Planar Array of Electrostatic Induction Electrodes" Sensors 20, no. 10: 2943. https://doi.org/10.3390/s20102943
APA StyleZhang, L., Chen, X., Li, P., Wang, C., & Li, M. (2020). A Method for Measuring the Height of Hand Movements Based on a Planar Array of Electrostatic Induction Electrodes. Sensors, 20(10), 2943. https://doi.org/10.3390/s20102943




