Estimating Lower Extremity Running Gait Kinematics with a Single Accelerometer: A Deep Learning Approach
Abstract
1. Introduction
1.1. IMU-Based Gait Kinematic Estimation
1.2. Reducing Number and Degrees of Freedom of IMUs:
1.3. Other Considerations
2. Materials and Methods
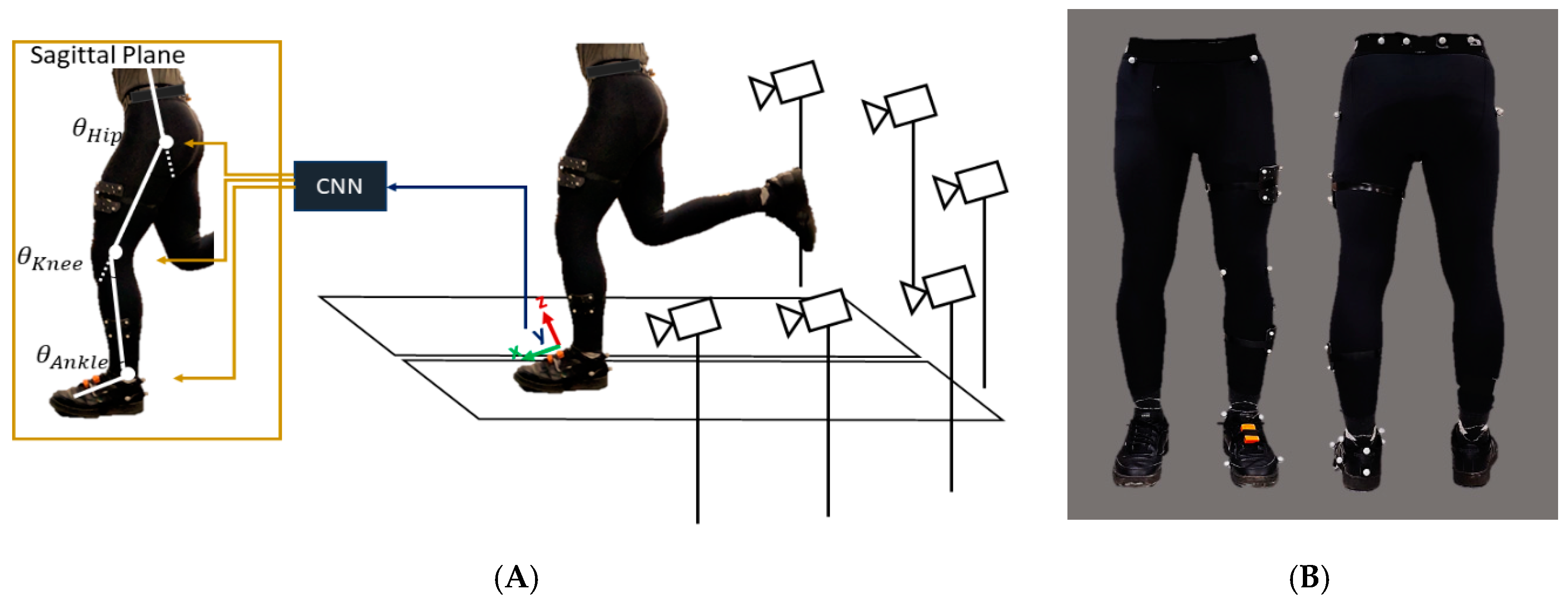
2.1. Experiment Setup
2.2. Data Collection
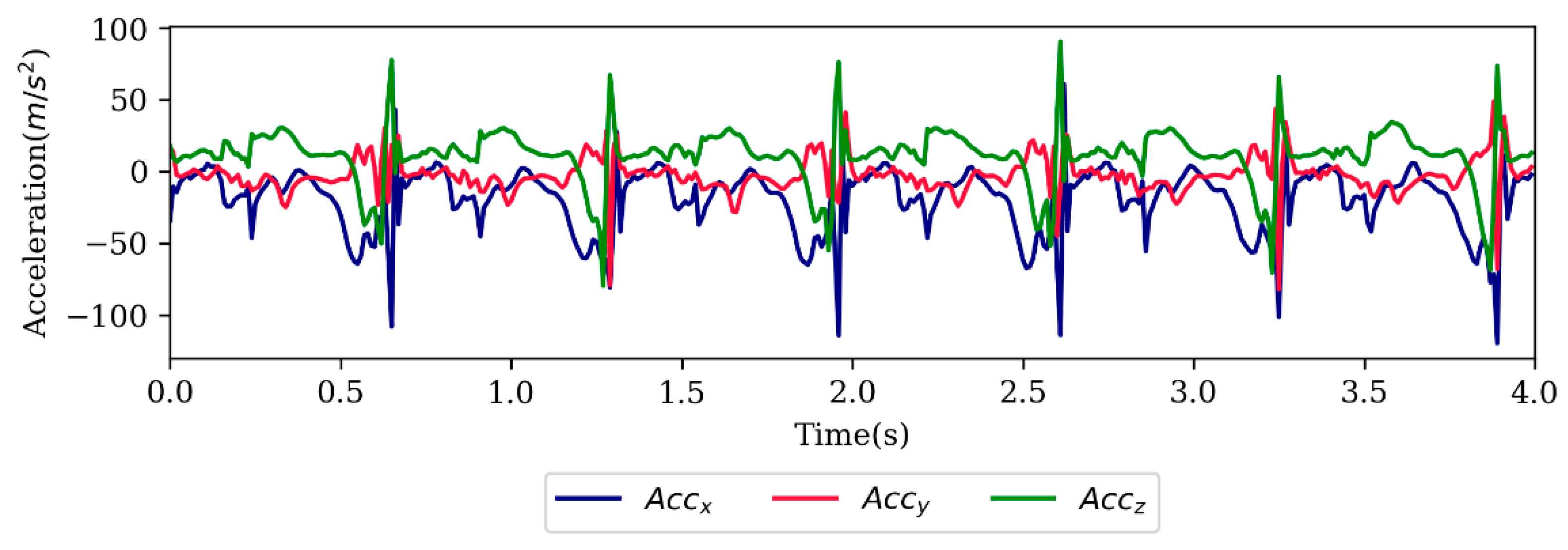
2.3. Data Preprocessing
2.4. Deep Learning Model
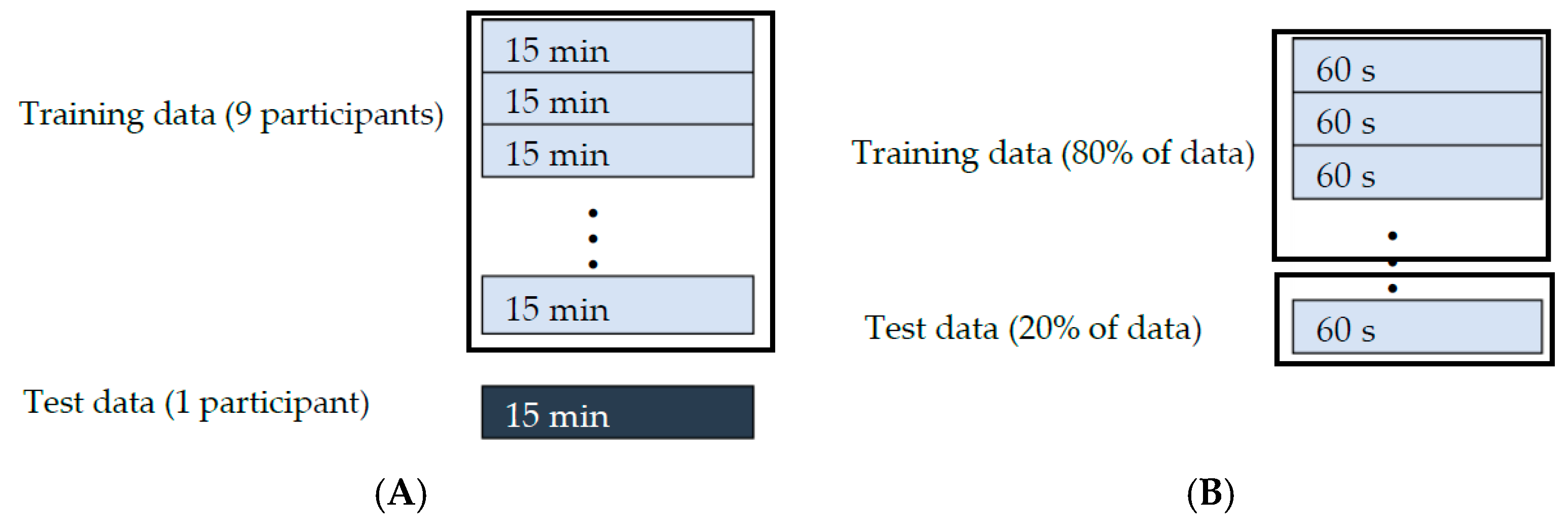
2.5. Evaluation Methods
3. Results
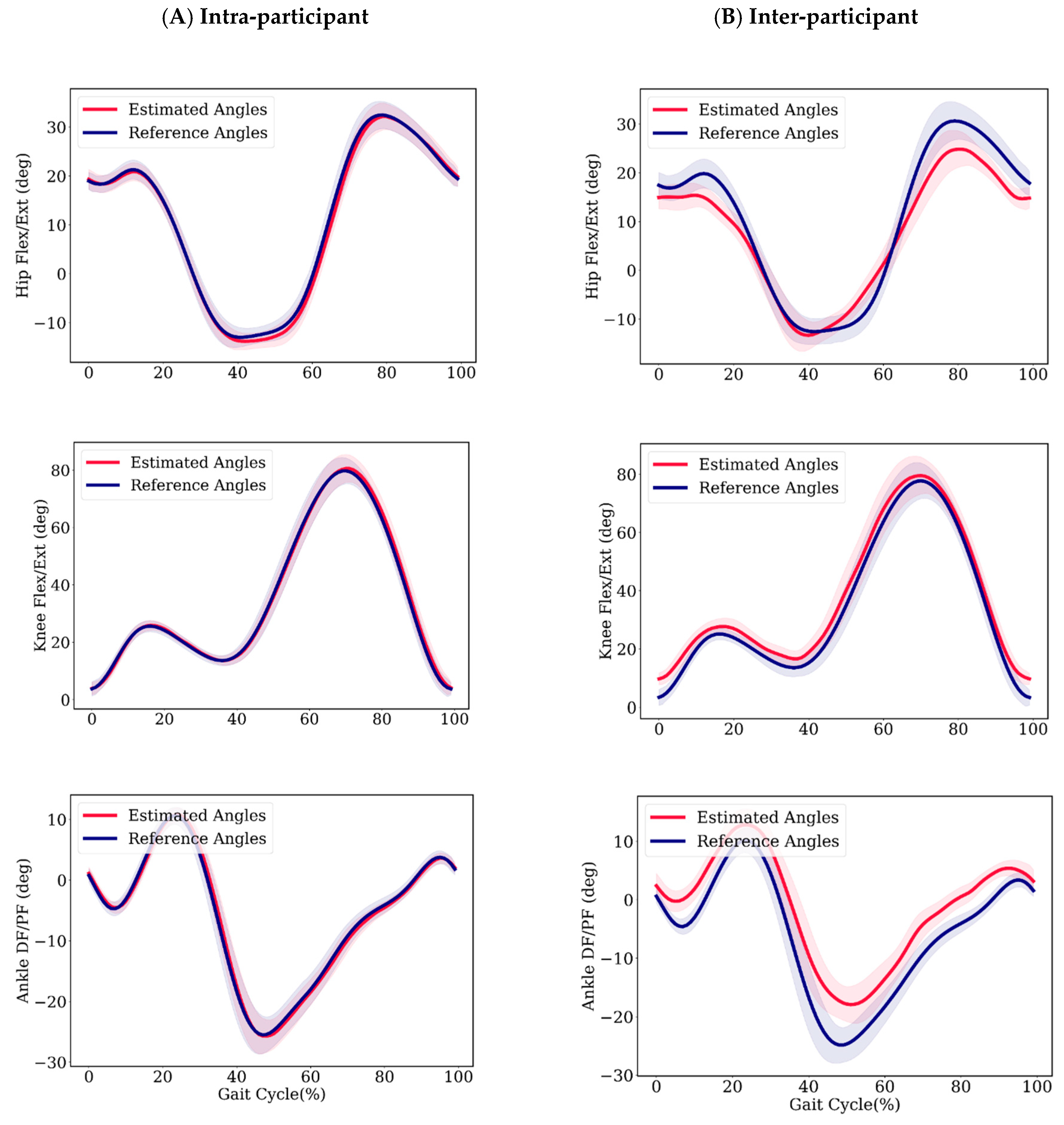
3.1. Intra-Participant Models
3.2. Inter-Participant Models
4. Discussion and Conclusions
5. Limitations and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Neal, B.S.; Barton, C.J.; Birn-Jeffery, A.; Morrissey, D. Increased hip adduction during running is associated with patellofemoral pain and differs between males and females: A case-control study. J. Biomech. 2019, 91, 133–139. [Google Scholar] [CrossRef]
- Bramah, C.; Preece, S.J.; Gill, N.; Herrington, L. Is there a pathological gait associated with common soft tissue running injuries? Am. J. Sports Med. 2018, 46, 3023–3031. [Google Scholar] [CrossRef]
- Bramah, C.; Preece, S.J.; Gill, N.; Herrington, L. A 10% increase in step rate improves running kinematics and clinical outcomes in runners with patellofemoral pain at 4 weeks and 3 months. Am. J. Sports Med. 2019, 47, 3406–3413. [Google Scholar] [CrossRef] [PubMed]
- Chan, Z.Y.S.; Zhang, J.H.; Au, I.P.H.; An, W.W.; Shum, G.L.K.; Ng, G.Y.F.; Cheung, R.T.H. Gait retraining for the reduction of injury occurrence in novice distance runners: 1-year follow-up of a randomized controlled trial. Am. J. Sports Med. 2018, 46, 388–395. [Google Scholar] [CrossRef]
- García-Pinillos, F.; Cartón-Llorente, A.; Jaén-Carrillo, D.; Delgado-Floody, P.; Carrasco-Alarcón, V.; Martínez, C.; Roche-Seruendo, L.E. Does fatigue alter step characteristics and stiffness during running? Gait Posture 2020, 76, 259–263. [Google Scholar] [CrossRef]
- Derrick, T.R.; Dereu, D.; McLean, S.P. Impacts and kinematic adjustments during an exhaustive run. Med. Sci. Sports Exerc. 2002, 34, 998–1002. [Google Scholar] [CrossRef]
- Sanno, M.; Willwacher, S.; Epro, G.; Brüggemann, G.-P. Positive work contribution shifts from distal to proximal joints during a prolonged run. Med. Sci. Sports Exerc. 2018, 50, 2507–2517. [Google Scholar] [CrossRef] [PubMed]
- Clermont, C.A.; Pohl, A.J.; Ferber, R. Fatigue-related changes in running gait patterns persist in the days following a marathon race. J. Sport Rehabil. 2019, 1, 1–8. [Google Scholar] [CrossRef]
- Clansey, A.C.; Hanlon, M.; Wallace, E.S.; Lake, M.J. Effects of fatigue on running mechanics associated with tibial stress fracture risk. Med. Sci. Sports Exerc. 2012, 44, 1917–1923. [Google Scholar] [CrossRef] [PubMed]
- Napier, C.; MacLean, C.L.; Maurer, J.; Taunton, J.E.; Hunt, M.A. Real-time biofeedback of performance to reduce braking forces associated with running-related injury: An exploratory study. J. Orthop. Sports Phys. Ther. 2018, 49, 136–144. [Google Scholar] [CrossRef]
- Willy, R.W.; Buchenic, L.; Rogacki, K.; Ackerman, J.; Schmidt, A.; Willson, J.D. In-field gait retraining and mobile monitoring to address running biomechanics associated with tibial stress fracture. Scand. J. Med. Sci. Sports 2016, 26, 197–205. [Google Scholar] [CrossRef] [PubMed]
- Sheerin, K.R.; Reid, D.; Taylor, D.; Besier, T.F. The effectiveness of real-time haptic feedback gait retraining for reducing resultant tibial acceleration with runners. Phys. Ther. Sport 2020, 43, 173–180. [Google Scholar] [CrossRef] [PubMed]
- Picerno, P. 25 years of lower limb joint kinematics by using inertial and magnetic sensors: A review of methodological approaches. Gait Posture 2017, 51, 239–246. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Gholami, M.; Khoshnam, M.; Eng, J.J.; Menon, C. Estimation of ankle joint power during walking using two inertial sensors. Sensors 2019, 19, 2796. [Google Scholar] [CrossRef]
- Weygers, I.; Kok, M.; Konings, M.; Hallez, H.; De Vroey, H.; Claeys, K. Inertial sensor-based lower limb joint kinematics: A methodological systematic review. Sensors 2020, 20, 673. [Google Scholar] [CrossRef]
- Seel, T.; Raisch, J.; Schauer, T. IMU-based joint angle measurement for gait analysis. Sensors 2014, 14, 6891–6909. [Google Scholar] [CrossRef]
- Kok, M.; Hol, J.D.; Schön, T.B. An optimization-based approach to human body motion capture using inertial sensors. IFAC Proc. Vol. 2014, 47, 79–85. [Google Scholar] [CrossRef]
- Dejnabadi, H.; Jolles, B.M.; Aminian, K. A new approach to accurate measurement of uniaxial joint angles based on a combination of accelerometers and gyroscopes. IEEE Trans. Biomed. Eng. 2005, 52, 1478–1484. [Google Scholar] [CrossRef]
- Tadano, S.; Takeda, R.; Miyagawa, H. Three dimensional gait analysis using wearable acceleration and gyro sensors based on quaternion calculations. Sensors 2013, 13, 9321–9343. [Google Scholar] [CrossRef]
- Cooper, G.; Sheret, I.; McMillian, L.; Siliverdis, K.; Sha, N.; Hodgins, D.; Kenney, L.; Howard, D. Inertial sensor-based knee flexion/extension angle estimation. J. Biomech. 2009, 42, 2678–2685. [Google Scholar] [CrossRef]
- Roetenberg, D.; Luinge, H.J.; Baten, C.T.M.; Veltink, P.H. Compensation of magnetic disturbances improves inertial and magnetic sensing of human body segment orientation. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 395–405. [Google Scholar] [CrossRef] [PubMed]
- Koning, B.H.W.; van der Krogt, M.M.; Baten, C.T.M.; Koopman, B.F.J.M. Driving a musculoskeletal model with inertial and magnetic measurement units. Comput. Methods Biomech. Biomed. Engin. 2015, 18, 1003–1013. [Google Scholar] [CrossRef]
- Dorschky, E.; Nitschke, M.; Seifer, A.-K.; van den Bogert, A.J.; Eskofier, B.M. Estimation of gait kinematics and kinetics from inertial sensor data using optimal control of musculoskeletal models. J. Biomech. 2019, 95, 109278. [Google Scholar] [CrossRef] [PubMed]
- van den Bogert, A.J.; Blana, D.; Heinrich, D. Implicit methods for efficient musculoskeletal simulation and optimal control. Procedia IUTAM 2011, 2, 297–316. [Google Scholar] [CrossRef]
- Goulermas, J.Y.; Findlow, A.H.; Nester, C.J.; Liatsis, P.; Zeng, X.-J.; Kenney, L.P.J.; Tresadern, P.; Thies, S.B.; Howard, D. An instance-based algorithm with auxiliary similarity information for the estimation of gait kinematics from wearable sensors. IEEE Trans. Neural Netw. 2008, 19, 1574–1582. [Google Scholar] [CrossRef] [PubMed]
- Findlow, A.; Goulermas, J.Y.; Nester, C.; Howard, D.; Kenney, L.P.J. Predicting lower limb joint kinematics using wearable motion sensors. Gait Posture 2008, 28, 120–126. [Google Scholar] [CrossRef]
- Wouda, F.J.; Giuberti, M.; Bellusci, G.; Maartens, E.; Reenalda, J.; van Beijnum, B.J.F.; Veltink, P.H. Estimation of vertical ground reaction forces and sagittal knee kinematics during running using three inertial sensors. Front. Physiol. 2018, 9, 218. [Google Scholar] [CrossRef]
- Favre, J.; Jolles, B.M.; Aissaoui, R.; Aminian, K. Ambulatory measurement of 3D knee joint angle. J. Biomech. 2008, 41, 1029–1035. [Google Scholar] [CrossRef]
- Ohtaki, Y.; Sagawa, K.; Inooka, H. A method for gait analysis in a daily living environment by body-mounted instruments. JSME Int. J. C Mech. Syst. 2001, 44, 1125–1132. [Google Scholar] [CrossRef]
- Rouhani, H.; Favre, J.; Crevoisier, X.; Aminian, K. Measurement of multi-segment foot joint angles during gait using a wearable system. J. Biomech. Eng. 2012, 134, 061006. [Google Scholar] [CrossRef]
- Bonnet, V.; Joukov, V.; Kulić, D.; Fraisse, P.; Ramdani, N.; Venture, G. Monitoring of hip and knee joint angles using a single inertial measurement unit during lower limb rehabilitation. IEEE Sens. J. 2016, 16, 1557–1564. [Google Scholar] [CrossRef]
- Hu, X.; Yao, C.; Soh, G.S. Performance evaluation of lower limb ambulatory measurement using reduced inertial measurement units and 3R gait model. In Proceedings of the 2015 IEEE International Conference on Rehabilitation Robotics (ICORR), Singapore, 11–14 August 2015; pp. 549–554. [Google Scholar]
- Riaz, Q.; Tao, G.; Krüger, B.; Weber, A. Motion reconstruction using very few accelerometers and ground contacts. Graph. Models 2015, 79, 23–38. [Google Scholar] [CrossRef]
- Mousas, C. Full-body locomotion reconstruction of virtual characters using a single inertial measurement unit. Sensors 2017, 17, 2589. [Google Scholar] [CrossRef] [PubMed]
- Lim, H.; Kim, B.; Park, S. Prediction of lower limb kinetics and kinematics during walking by a single IMU on the lower back using machine learning. Sensors 2020, 20, 130. [Google Scholar] [CrossRef]
- Liu, Q.; Williamson, J.; Li, K.; Mohrman, W.; Lv, Q.; Dick, R.P.; Shang, L. Gazelle: Energy-efficient wearable analysis for running. IEEE Trans. Mob. Comput. 2017, 16, 2531–2544. [Google Scholar] [CrossRef]
- Napier, C.; Esculier, J.-F.; Hunt, M.A. Gait retraining: Out of the lab and onto the streets with the benefit of wearables. Br. J. Sports Med. 2017, 51, 1642–1643. [Google Scholar] [CrossRef]
- Napier, C.; MacLean, C.L.; Maurer, J.; Taunton, J.E.; Hunt, M.A. Kinetic risk factors of running-related injuries in female recreational runners. Scand. J. Med. Sci. Sports 2018, 28, 2164–2172. [Google Scholar] [CrossRef]
- Bell, A.L.; Brand, R.A.; Pedersen, D.R. Prediction of hip joint centre location from external landmarks. Hum. Mov. Sci. 1989, 8, 3–16. [Google Scholar] [CrossRef]
- Wille, C.M.; Lenhart, R.L.; Wang, S.; Thelen, D.G.; Heiderscheit, B.C. Ability of sagittal kinematic variables to estimate ground reaction forces and joint kinetics in running. J. Orthop. Sports Phys. Ther. 2014, 44, 825–830. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0—Fundamental algorithms for scientific computing in python. Nat. Methods 2019, 17, 261–272. [Google Scholar] [CrossRef]
- Żuk, M.; Pezowicz, C. Kinematic analysis of a six-degrees-of-freedom model based on ISB recommendation: A repeatability analysis and comparison with conventional gait model. Appl. Bionics Biomech. 2015, 2015, 9. [Google Scholar] [CrossRef] [PubMed]
- Gholami, M.; Rezaei, A.; Cuthbert, T.J.; Napier, C.; Menon, C. Lower body kinematics monitoring in running using fabric-based wearable sensors and deep convolutional neural networks. Sensors 2019, 19, 5325. [Google Scholar] [CrossRef] [PubMed]
- Chollet, F. Keras. Available online: https://keras.io/ (accessed on 10 August 2019).
- Edwards, W.B.; Derrick, T.R.; Hamill, J. Musculoskeletal attenuation of impact shock in response to knee angle manipulation. J. Appl. Biomech. 2012, 28, 502–510. [Google Scholar] [CrossRef] [PubMed]
- Chew, D.-K.; Ngoh, K.J.-H.; Gouwanda, D.; Gopalai, A.A. Estimating running spatial and temporal parameters using an inertial sensor. Sports Eng. 2018, 21, 115–122. [Google Scholar] [CrossRef]
- Cheung, R.T.H.; Zhang, J.H.; Chan, Z.Y.S.; An, W.W.; Au, I.P.H.; MacPhail, A.; Davis, I.S. Shoe-mounted accelerometers should be used with caution in gait retraining. Scand. J. Med. Sci. Sports 2019, 29, 835–842. [Google Scholar] [CrossRef]
- Almeida, M.O.; Davis, I.S.; Lopes, A.D. Biomechanical differences of foot-strike patterns during running: A systematic review with meta-analysis. J. Orthop. Sports Phys. Ther. 2015, 45, 738–755. [Google Scholar] [CrossRef]
- Stoneham, R.; Barry, G.; Saxby, L.; Wilkinson, M. Measurement error of 3D kinematic and kinetic measures during overground endurance running in recreational runners between two test sessions separated by 48 h. Physiol. Meas. 2019, 40, 024002. [Google Scholar] [CrossRef]

| Index | Layer | Output Shape | Setting |
|---|---|---|---|
| 0 | Input | (60,4) | |
| 1 | Dropout | 0.1 | |
| 2 | 1D-Conv | (58,50) | ReLU |
| 3 | 1D-Conv | (56,50) | ReLU |
| 4 | MaxPool | (28,50) | |
| 5 | 1D-Conv | (26,100) | ReLU |
| 6 | 1D-Conv | (24,100) | ReLU |
| 7 | Flatten | 2400 | ReLU |
| 8 | Dense | 100 | ReLU |
| 9 | Dense | 3 | Linear |
| Hip | Knee | Ankle | |
|---|---|---|---|
| R2 | 0.97 (0.00) | 0.98 (1.30) | 0.97 (1.59) |
| RMSE (deg) | 2.3 (0.5) | 3.4 (1.2) | 1.8 (0.4) |
| NRMSE (%) | 4.6 (0.1) | 3.5 (0.1) | 4.3 (0.1) |
| Hip | Hip | Knee | Ankle | Ankle | Ankle | |
|---|---|---|---|---|---|---|
| Peak Flexion | Peak Extension | Peak Flexion during Stance | Peak DF | Peak PF | PF/DF at Initial Contact | |
| Reference | 27.6 (7.3) | 15.3 (3.9) | 30.1 (6.4) | 12.8 (3.6) | 21.4 (5.0) | 2.2 (3.1) |
| Estimated | 28.3 (8.0) | 15.5 (4.8) | 30.2 (6.4) | 13.1 (3.9) | 20.9 (5.5) | 2.2 (3.2) |
| MAE | 2.4 (2.5) | 1.5 (0.3) | 1.2 (0.3) | 1.0 (0.6) | 1.0 (0.3) | 1.0 (0.3) |
| Hip | Knee | Ankle | |
|---|---|---|---|
| R2 | 0.84 (0.10) | 0.93 (0.04) | 0.78 (0.10) |
| RMSE (deg) | 5.6 (2.2) | 6.5 (2.1) | 4.7 (1.6) |
| NRMSE (%) | 9.9 (2.2) | 6.5 (1.8) | 11.1 (3.1) |
| Hip | Hip | Knee | Ankle | Ankle | Ankle | |
|---|---|---|---|---|---|---|
| Peak Flexion | Peak Extension | Peak Flexion during Stance | Peak DF | Peak PF | PF/DF at Initial Contact | |
| Reference | 27.6 (5.6) | 15.6 (3.9) | 30.0 (5.7) | 13.1 (3.9) | 21.0 (5.5) | 2.4 (3.1) |
| Estimated | 25.9 (3.0) | 13.9 (1.4) | 26.4 (2.4) | 10.8 (2.0) | 19.8 (4.1) | 0.9 (1.5) |
| MAE | 5.9 (3.3) | 4.0 (1.5) | 6.4 (4.6) | 5.0 (2.3) | 4.0 (2.5) | 2.8 (1.3) |
| Ref. | Number of Sensors | Inter/Intra -Model | Method | Joint | RMSE |
|---|---|---|---|---|---|
| [23] | 7 (Gyro + Acc) | Yes/No | Musculoskeletal modeling | Hip | 8.7 |
| Knee | 5.3 | ||||
| Ankle | 4.6 | ||||
| [27] | 3 (Gyro + Acc + Mag) | Yes/Yes | Data-Driven | Knee | ~4/<13 |
| [20] | 2 (Gyro + Acc) | Yes/No | Model-based | Knee | 3.4 |
| Ours | 1 (Acc) | Yes/Yes | Data-Driven | Hip | 2.3/5.6 |
| Knee | 3.4/6.5 | ||||
| Ankle | 1.8/4.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholami, M.; Napier, C.; Menon, C. Estimating Lower Extremity Running Gait Kinematics with a Single Accelerometer: A Deep Learning Approach. Sensors 2020, 20, 2939. https://doi.org/10.3390/s20102939
Gholami M, Napier C, Menon C. Estimating Lower Extremity Running Gait Kinematics with a Single Accelerometer: A Deep Learning Approach. Sensors. 2020; 20(10):2939. https://doi.org/10.3390/s20102939
Chicago/Turabian StyleGholami, Mohsen, Christopher Napier, and Carlo Menon. 2020. "Estimating Lower Extremity Running Gait Kinematics with a Single Accelerometer: A Deep Learning Approach" Sensors 20, no. 10: 2939. https://doi.org/10.3390/s20102939
APA StyleGholami, M., Napier, C., & Menon, C. (2020). Estimating Lower Extremity Running Gait Kinematics with a Single Accelerometer: A Deep Learning Approach. Sensors, 20(10), 2939. https://doi.org/10.3390/s20102939






