A Safe Charging Algorithm Based on Multiple Mobile Chargers
Abstract
1. Introduction
- The mobile chargers can find and charge the wireless sensor nodes quickly by using the charging time and antenna waveform.
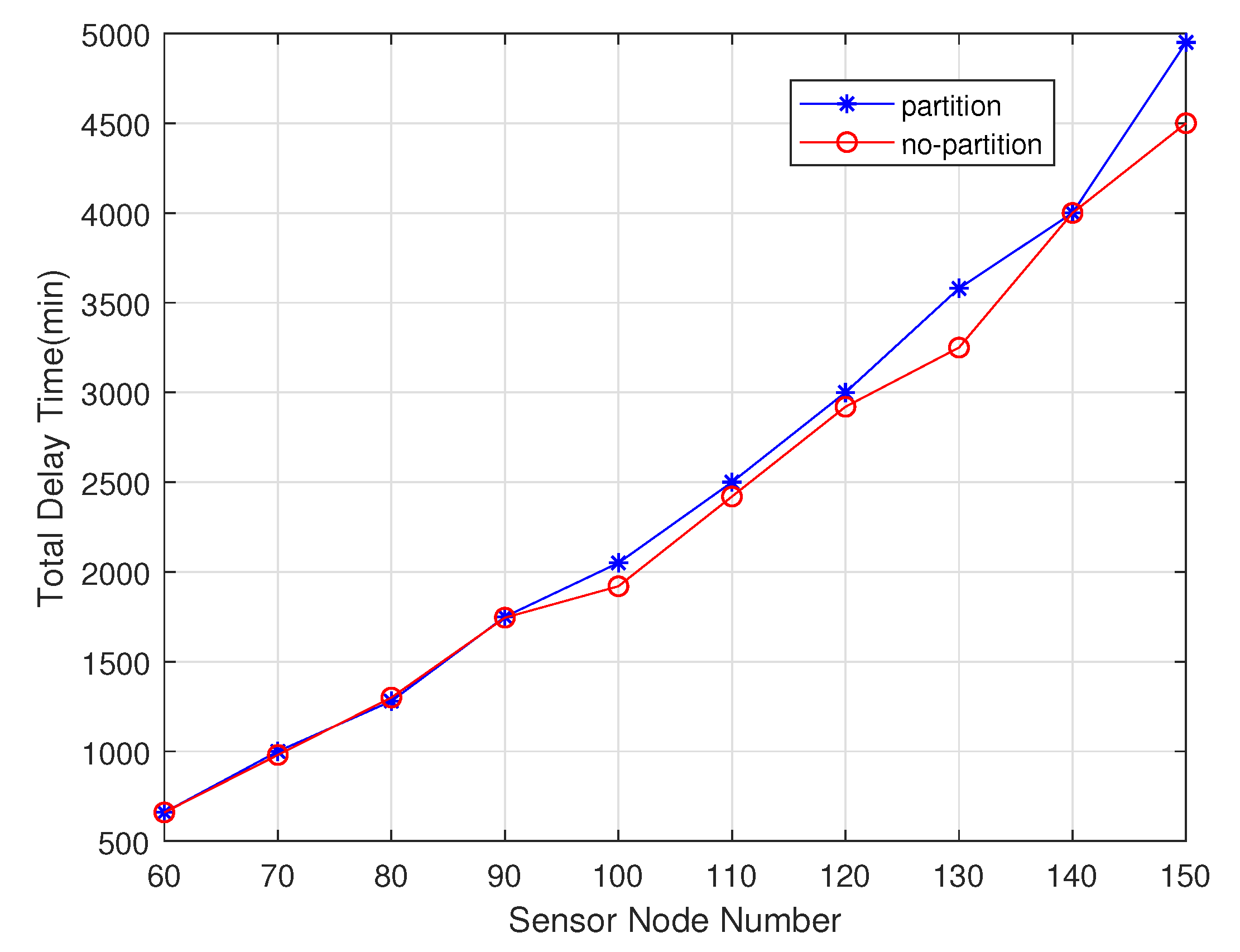
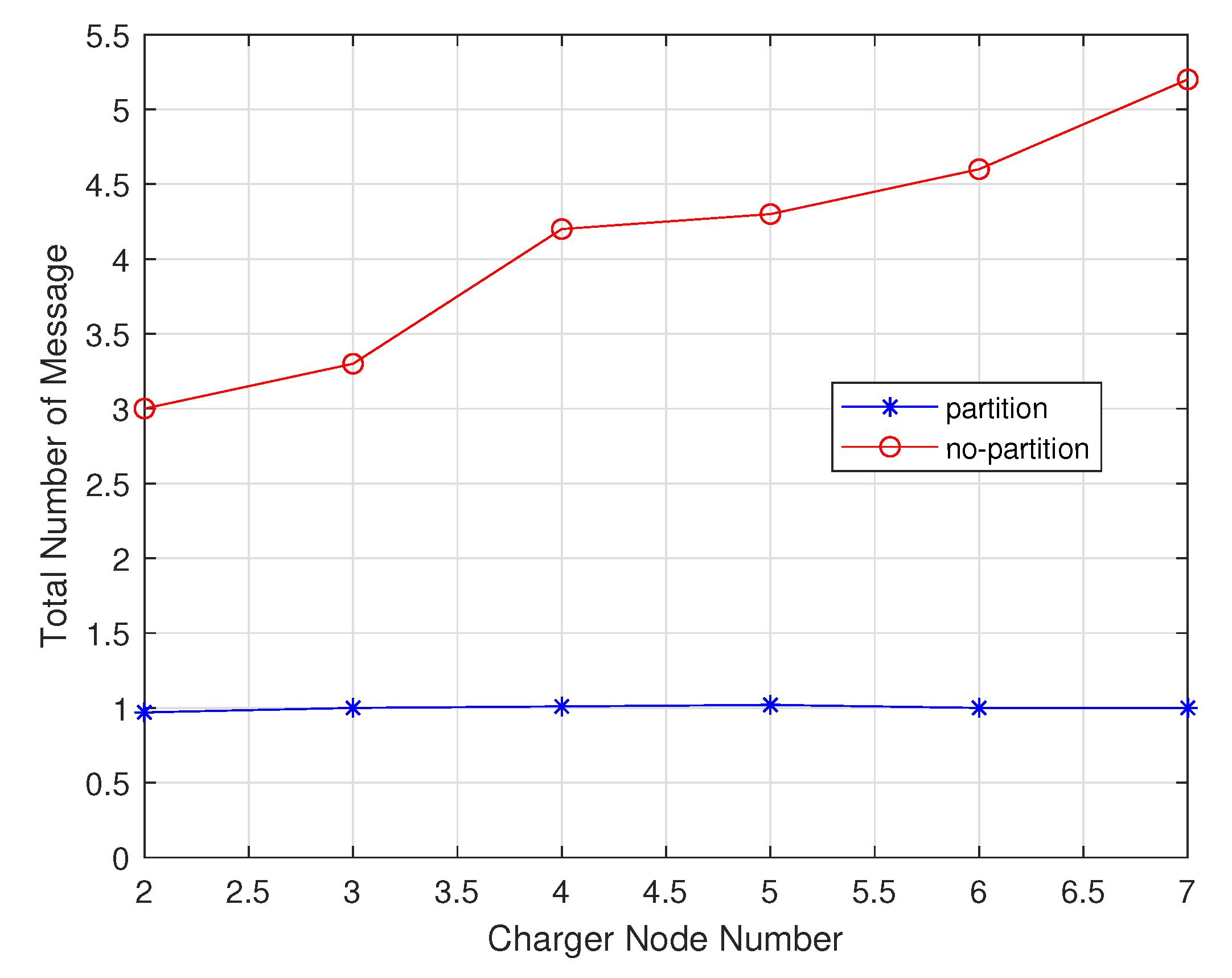
- The non-partition charging algorithm is designed based on the solution of Multiple Traveling salesman Problem with a fixed depot, which is better than the performance of the partition one. In this algorithm, the performance of the chargers is fully utilized relative to partition charging one.
- This paper proposes a safe charging algorithm based on multiple mobile chargers, which can minimize total charge time and improve some performance, ensuring electromagnetic radiation below the safe threshold.
2. Model and Algorithm
2.1. Basic Model
2.2. Node Position Correction
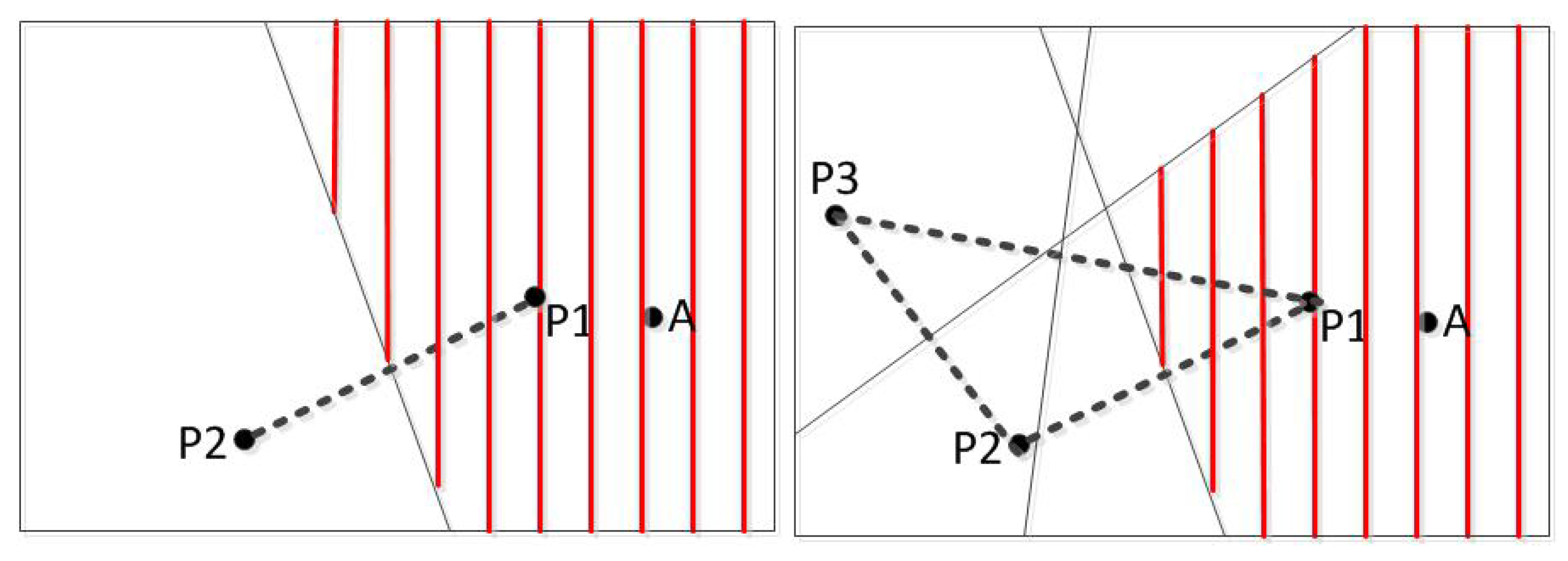
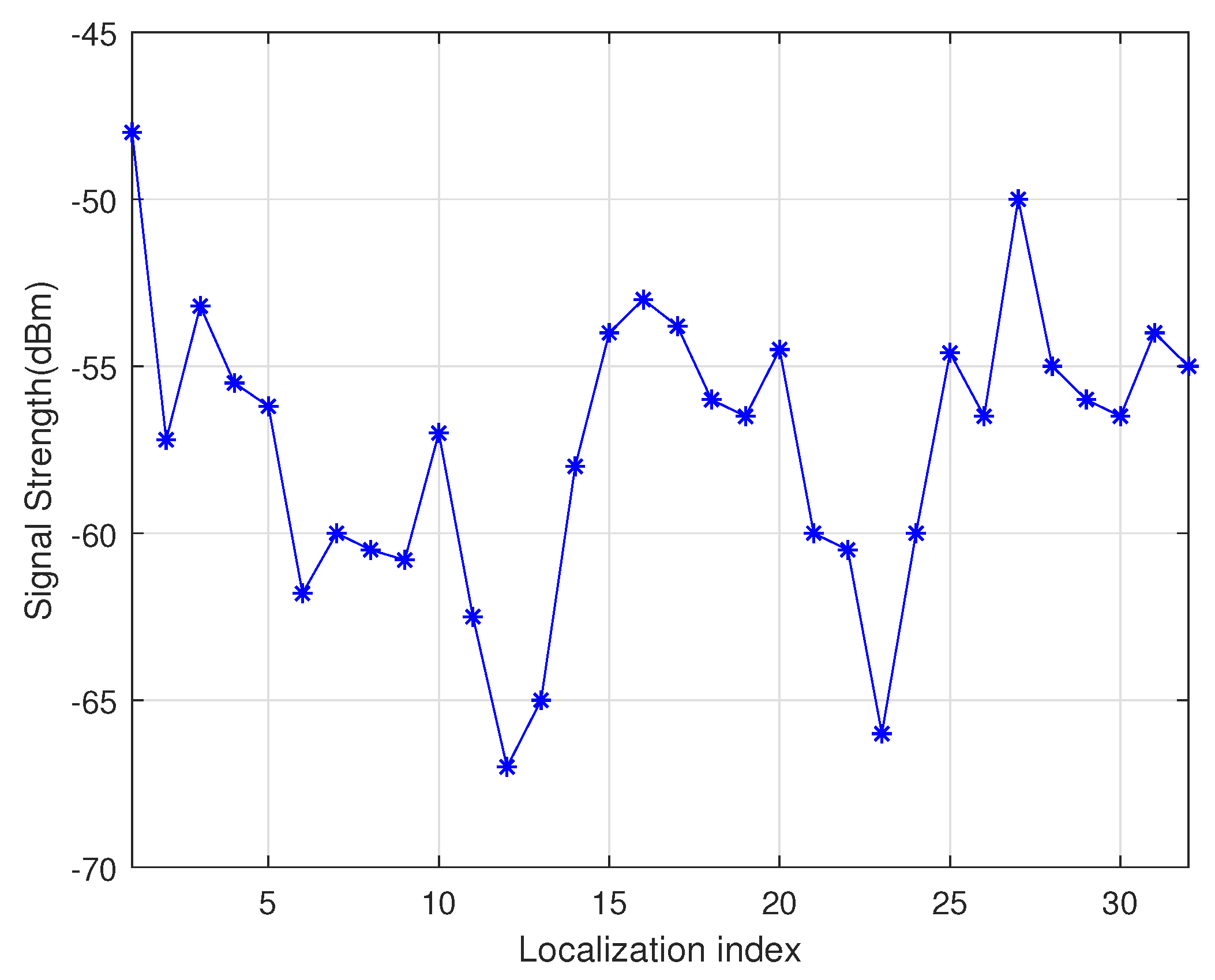
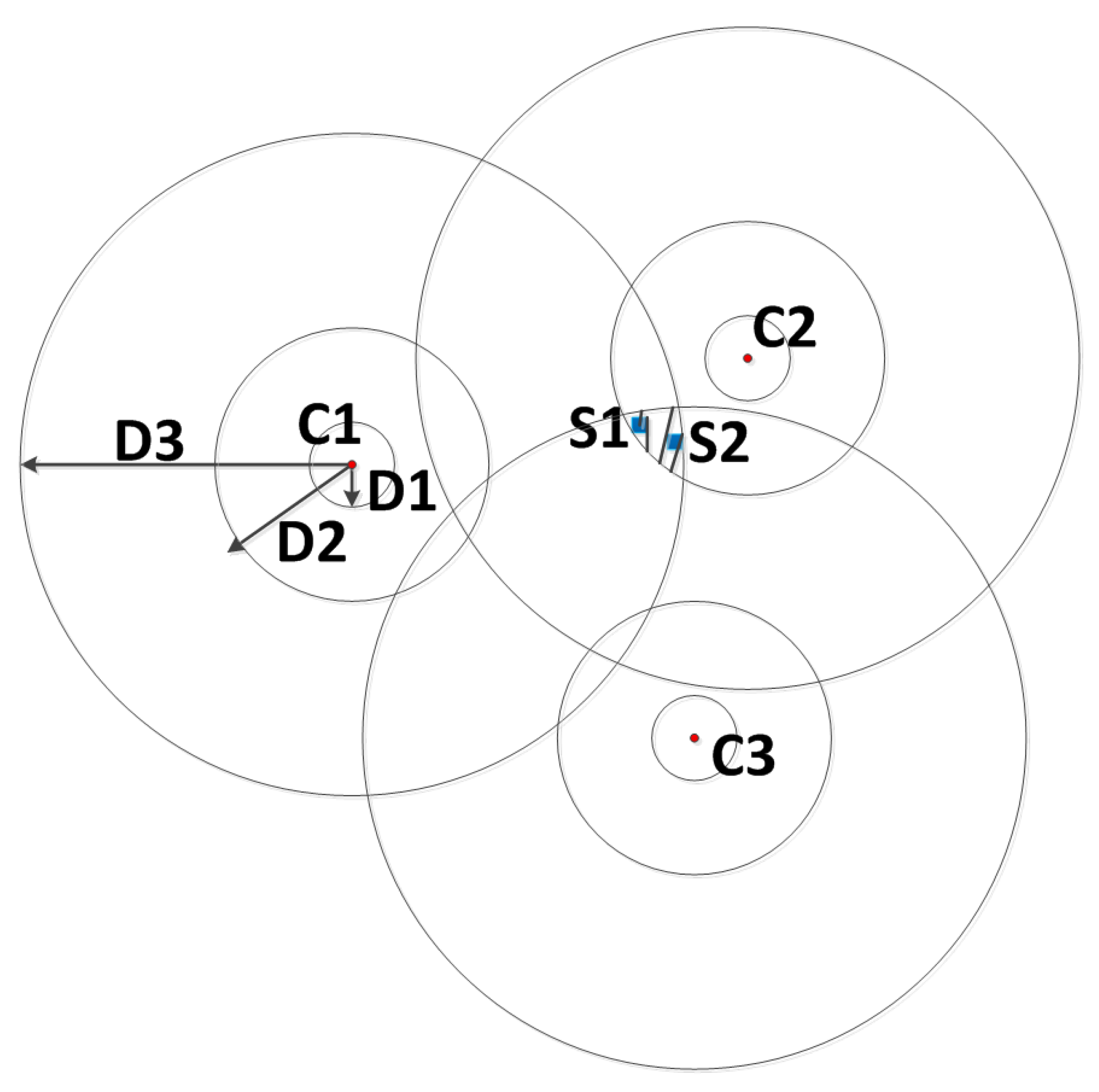
2.2.1. Localization Using Charging Time
2.2.2. Localization Using Antenna Waveform
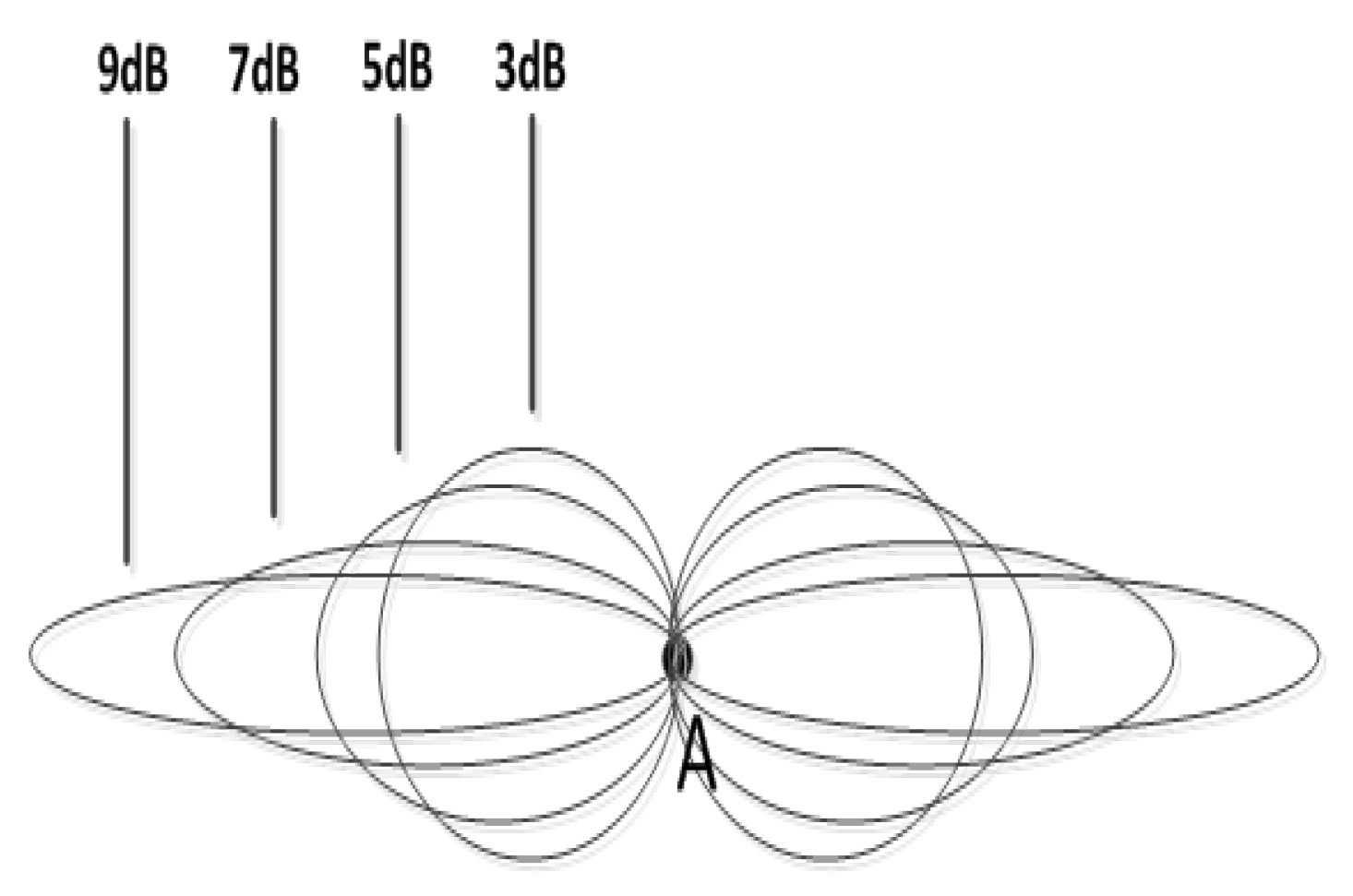
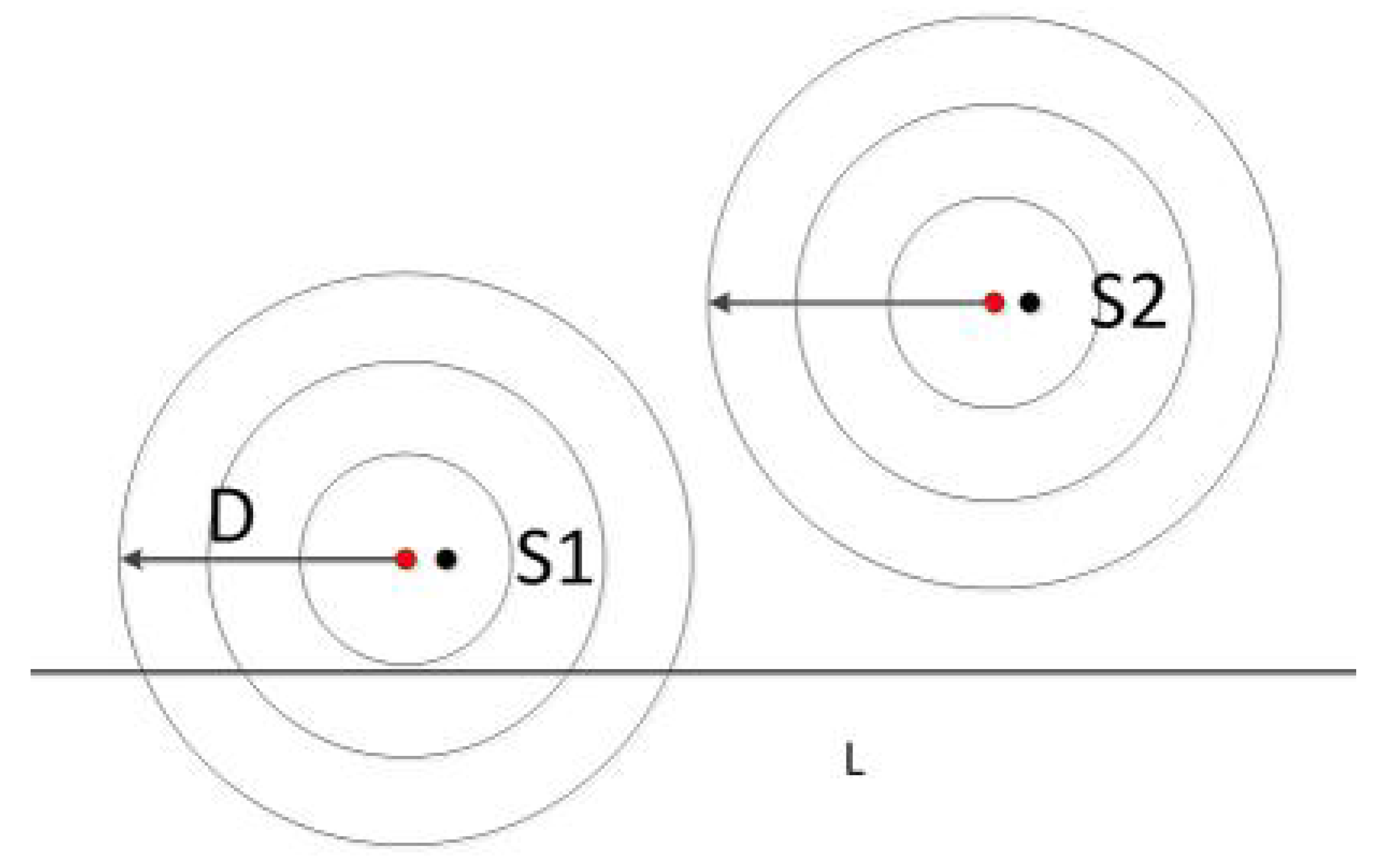
2.3. Network Radiation Analysis
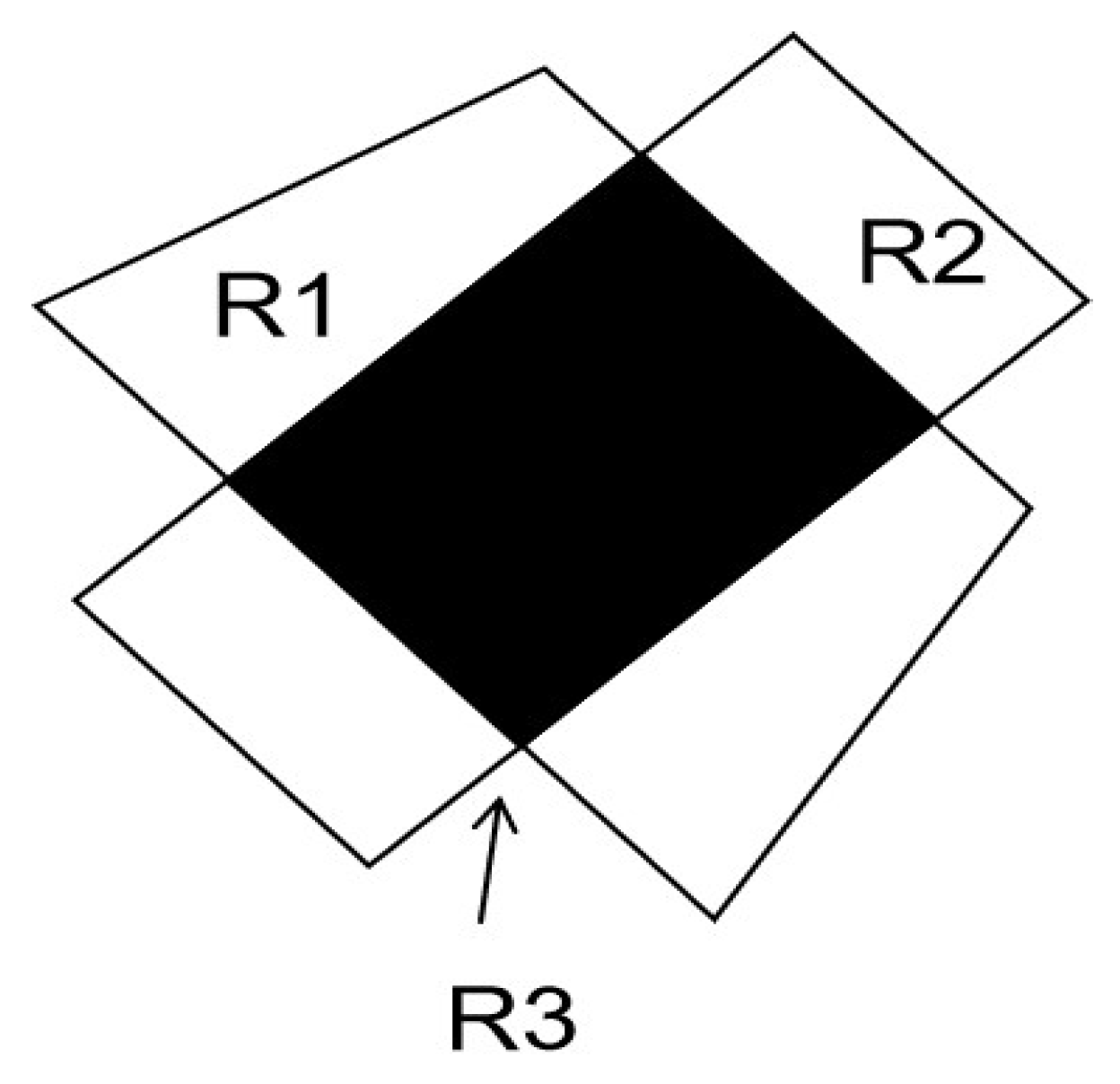
2.3.1. Charging Area Discretization
2.3.2. Radiation Analysis
2.4. Partition Charging Algorithm
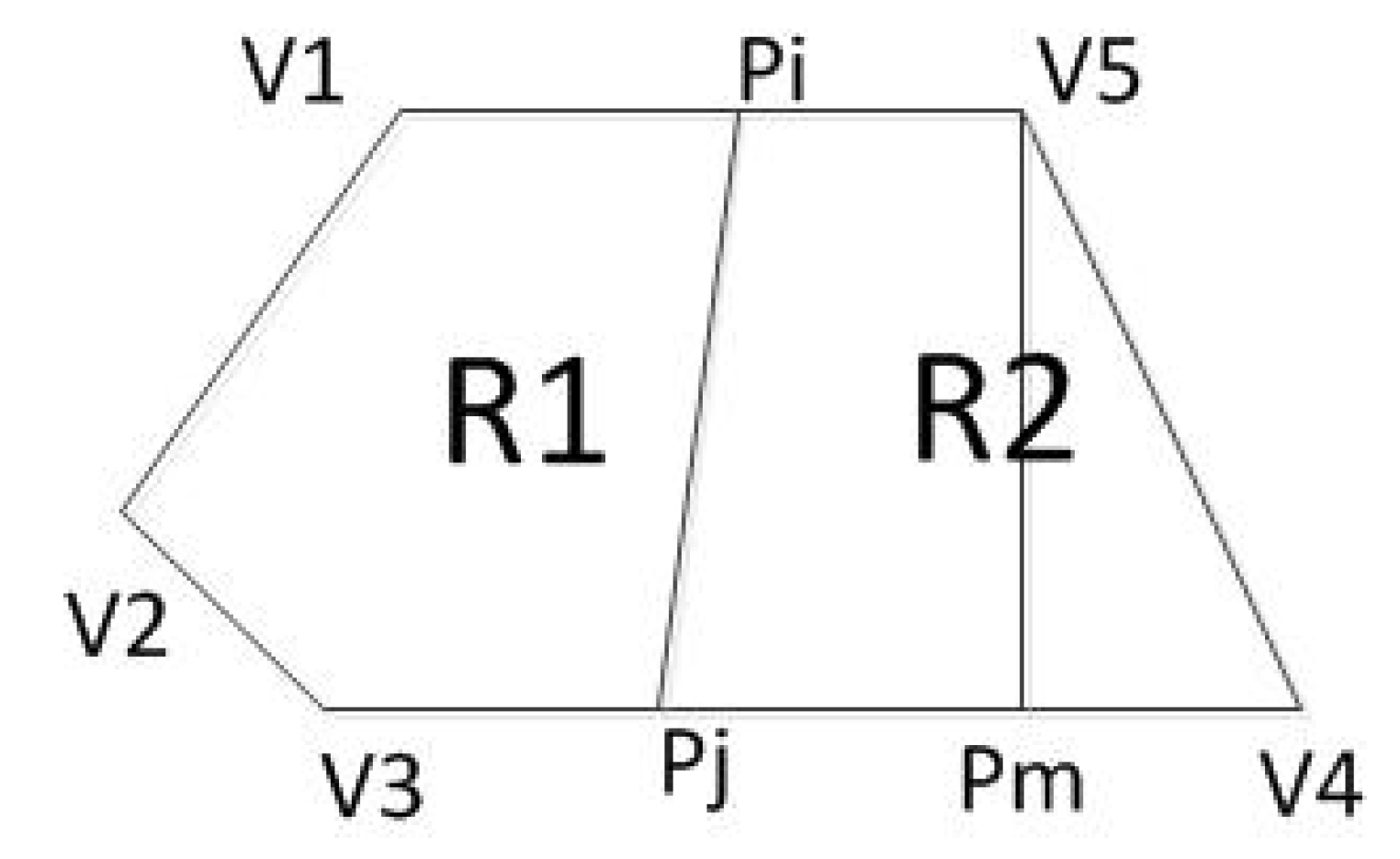
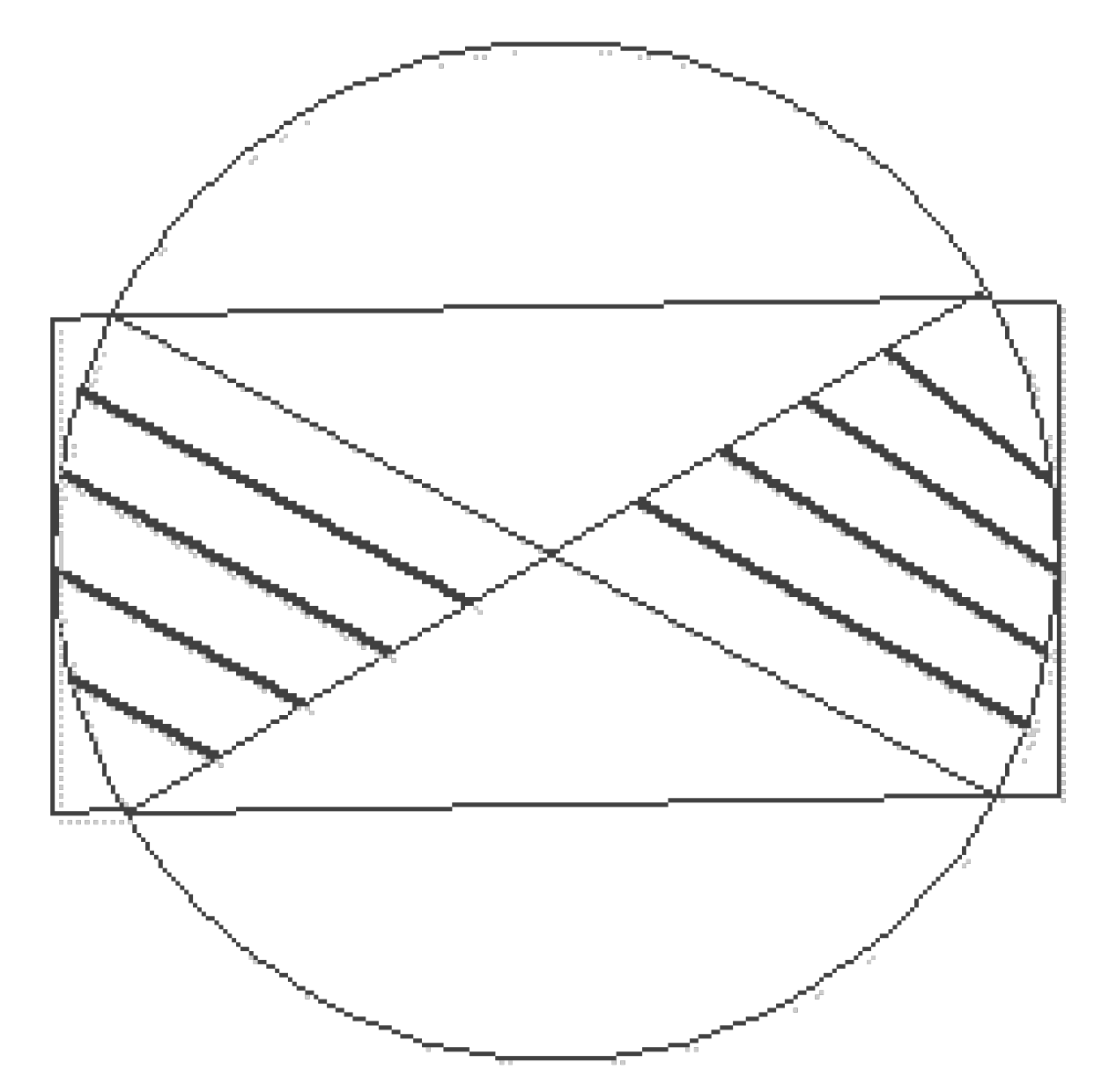
2.4.1. Edge Node Definition
2.4.2. Single Partition Path Plan
2.4.3. Overall Area Path Plan
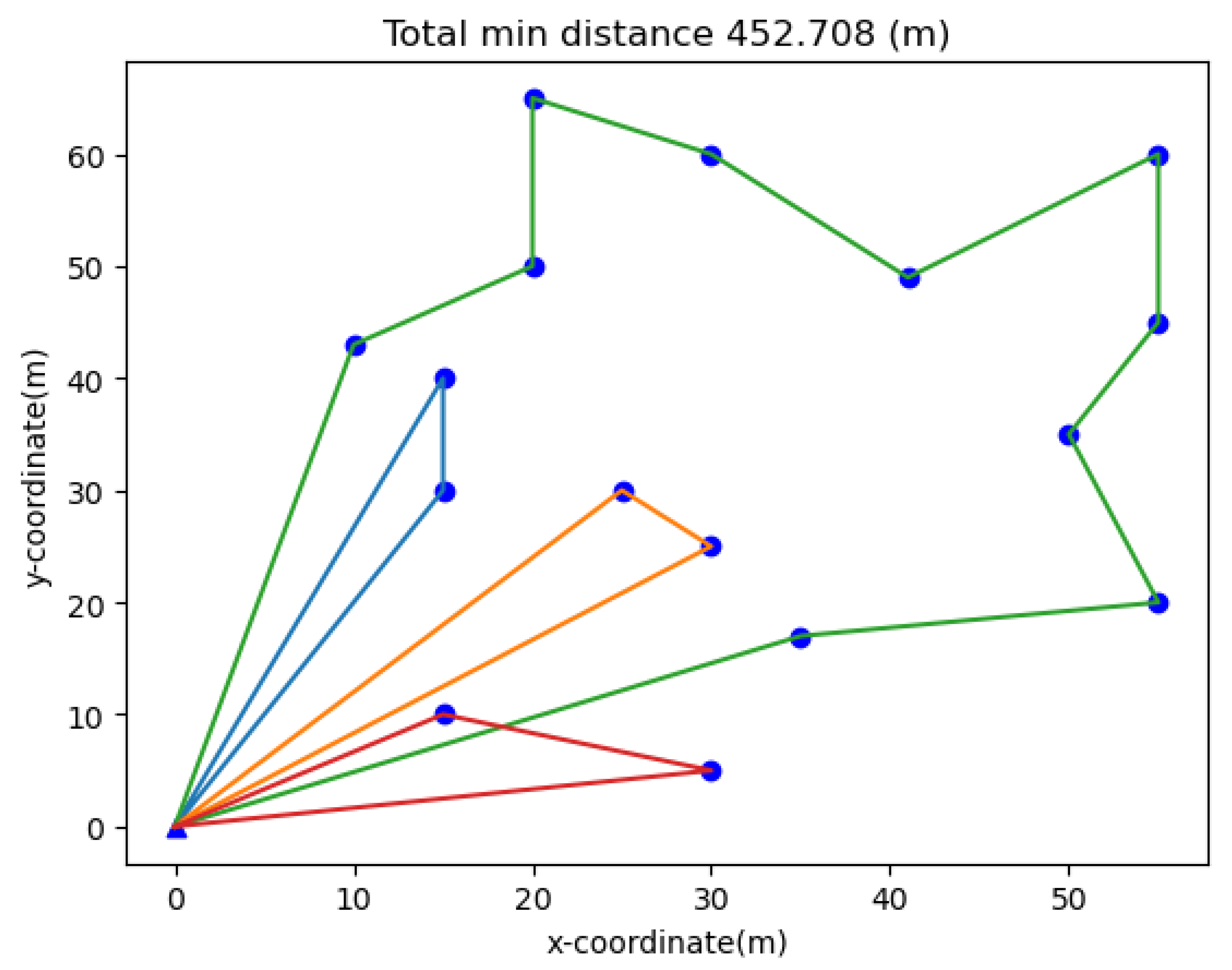
2.5. Non-Partition Charging Algorithm
2.5.1. Charging Path Calculation
2.5.2. Charging Path Allocation
3. Algorithm Descriptions
| Algorithm 1: SCBMC algorithm based on MTSP-fixed. |
 |
4. Simulation Test and Performance Analysis
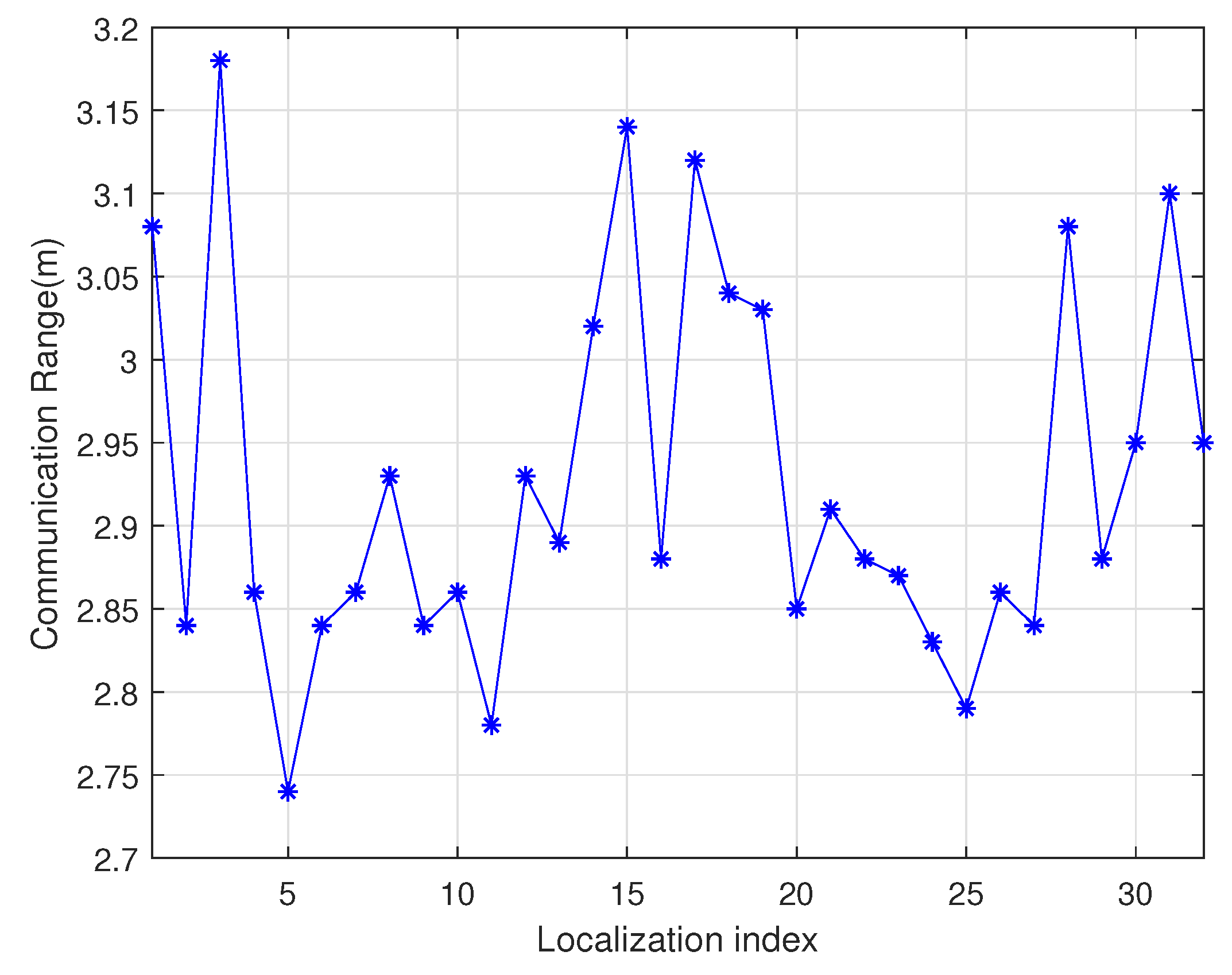
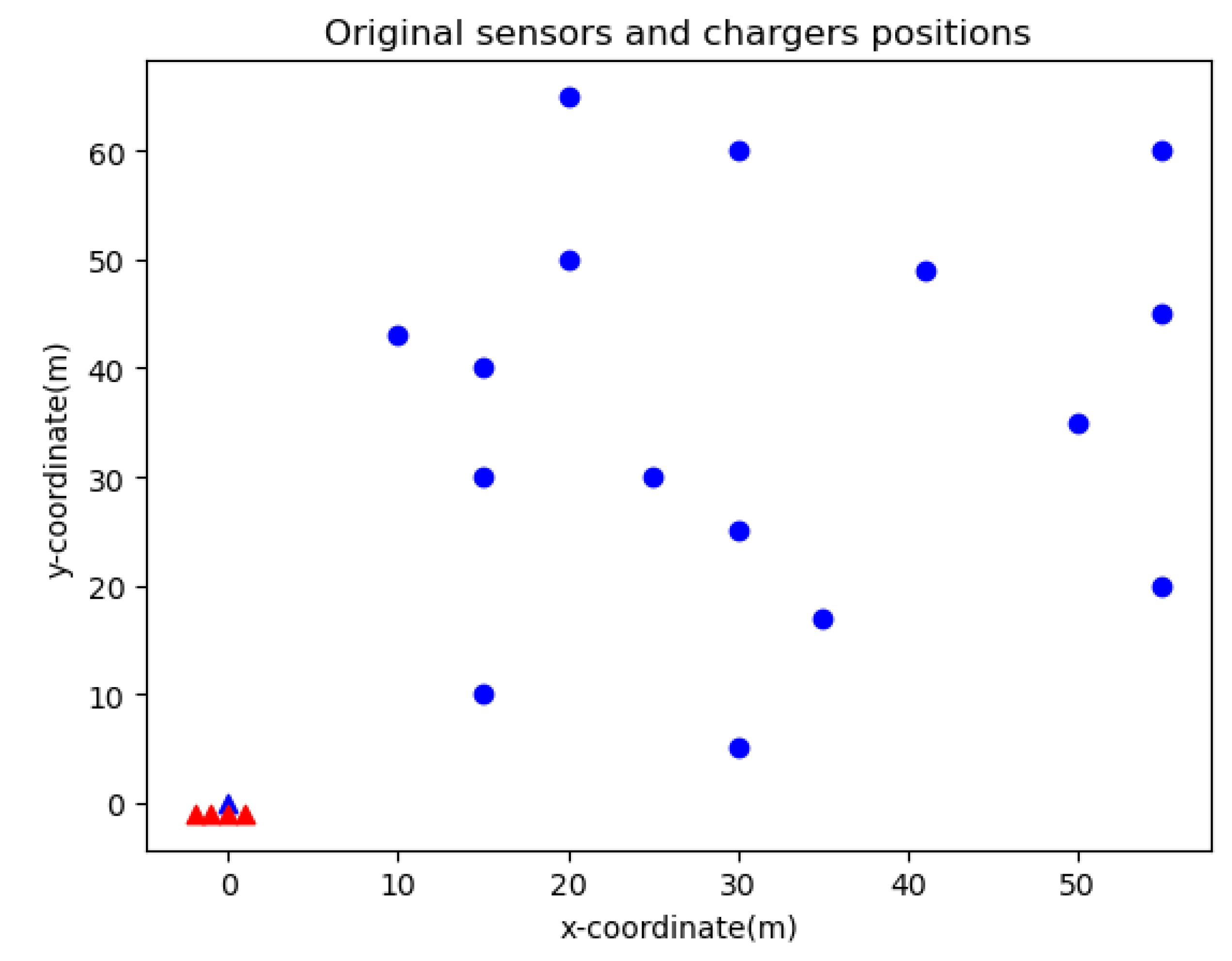
4.1. Simulation Experiment Data Analysis
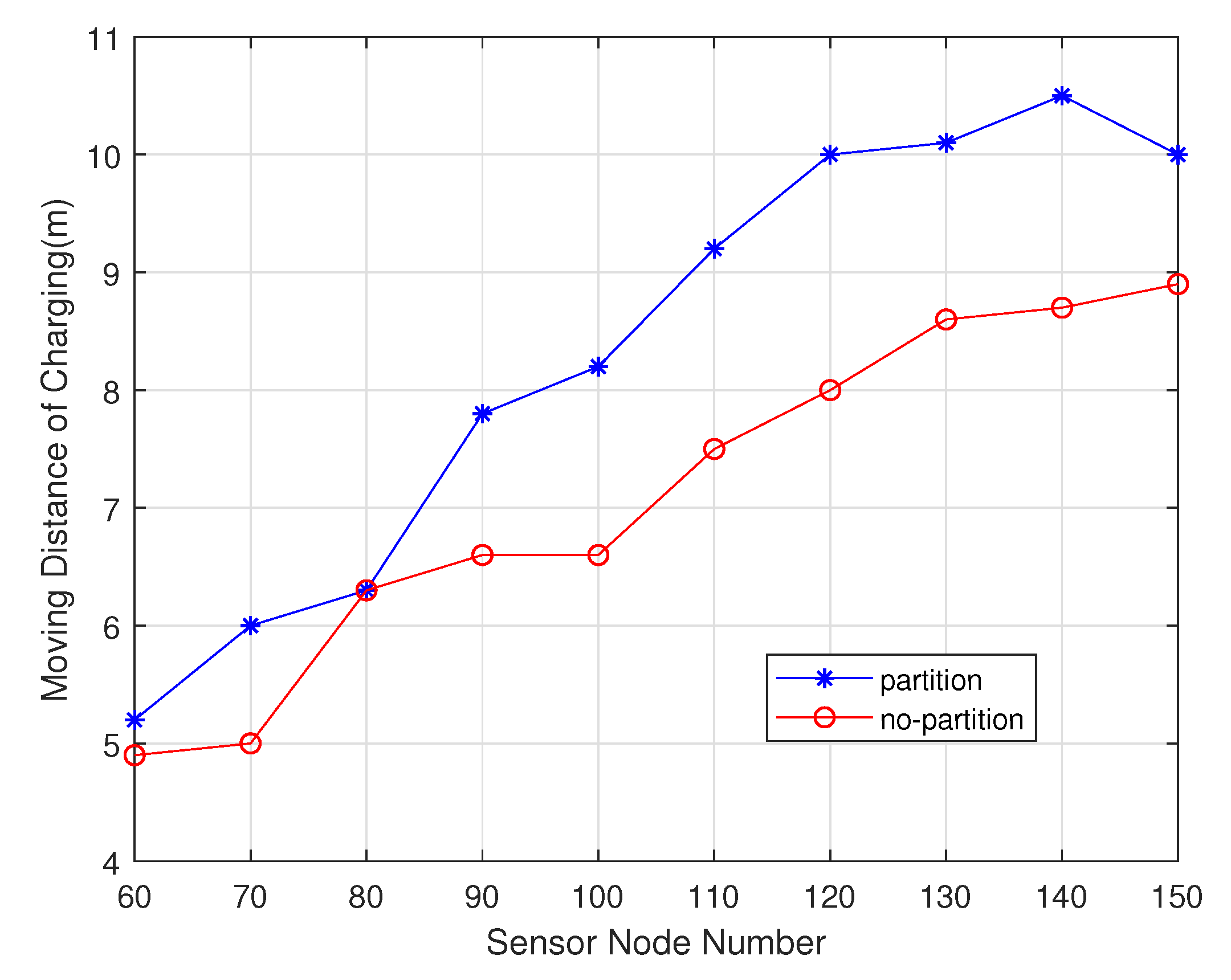
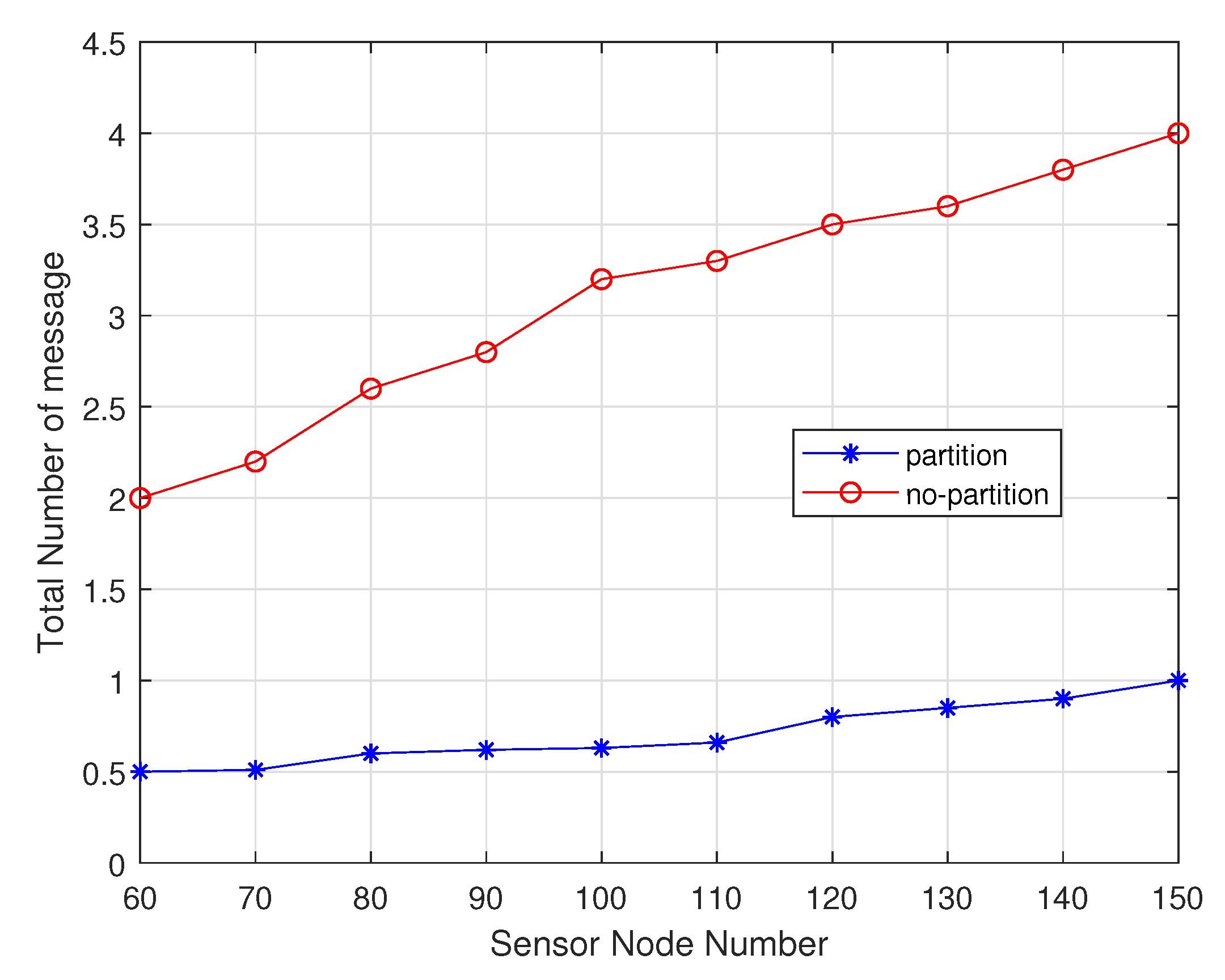
4.1.1. Performance Comparison with Sensor Node Number Change
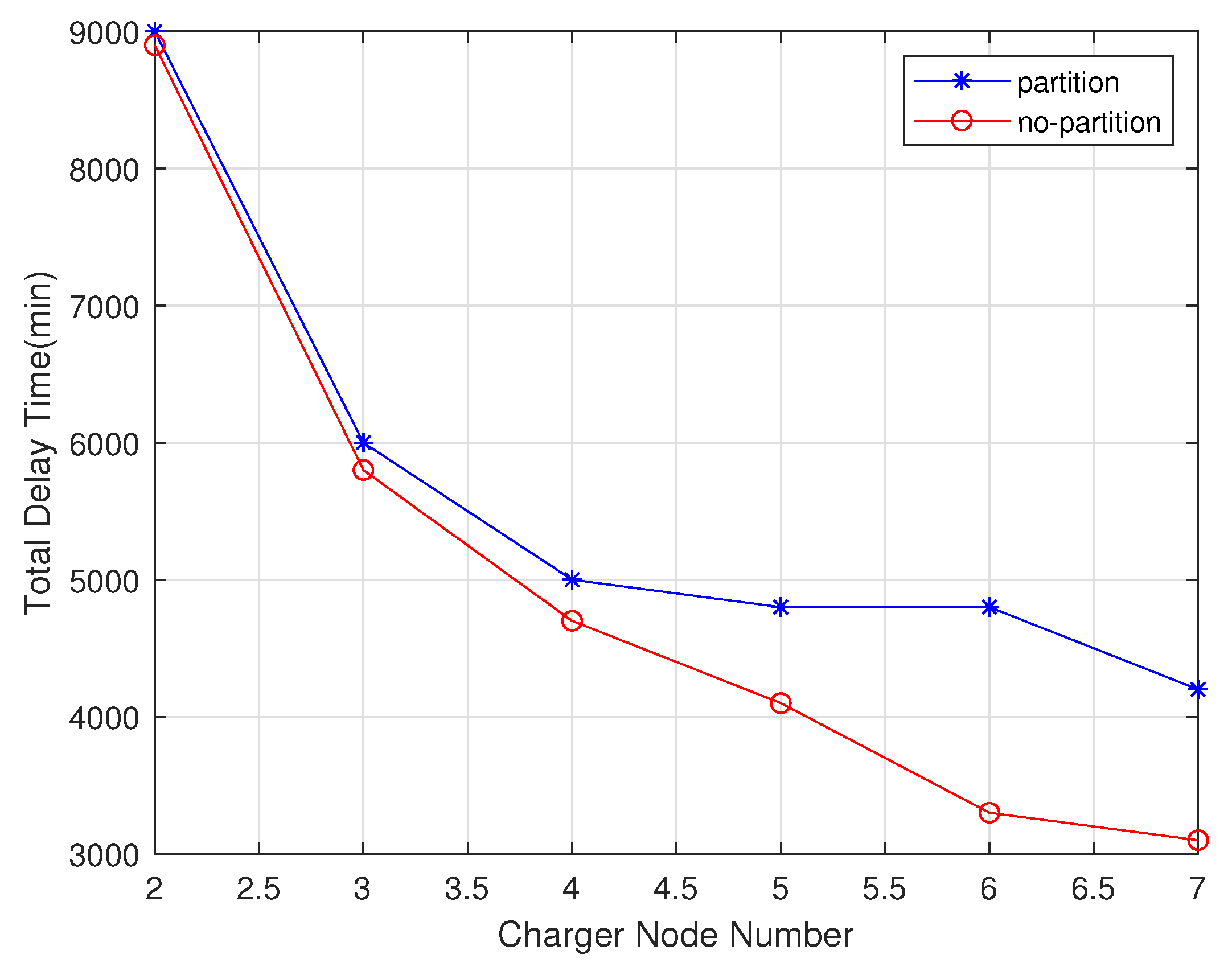
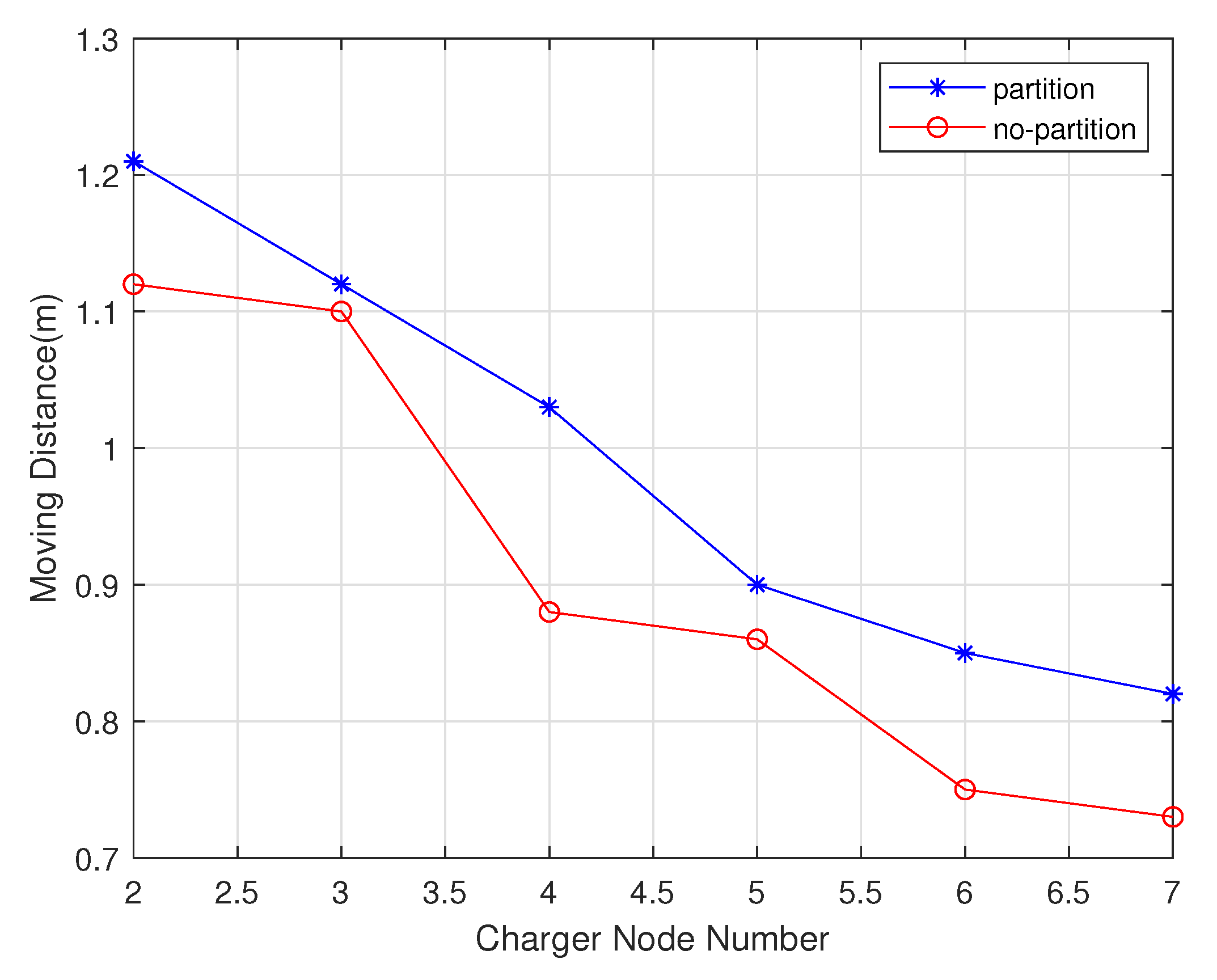
4.1.2. Performance Comparison with Chargers Number Change
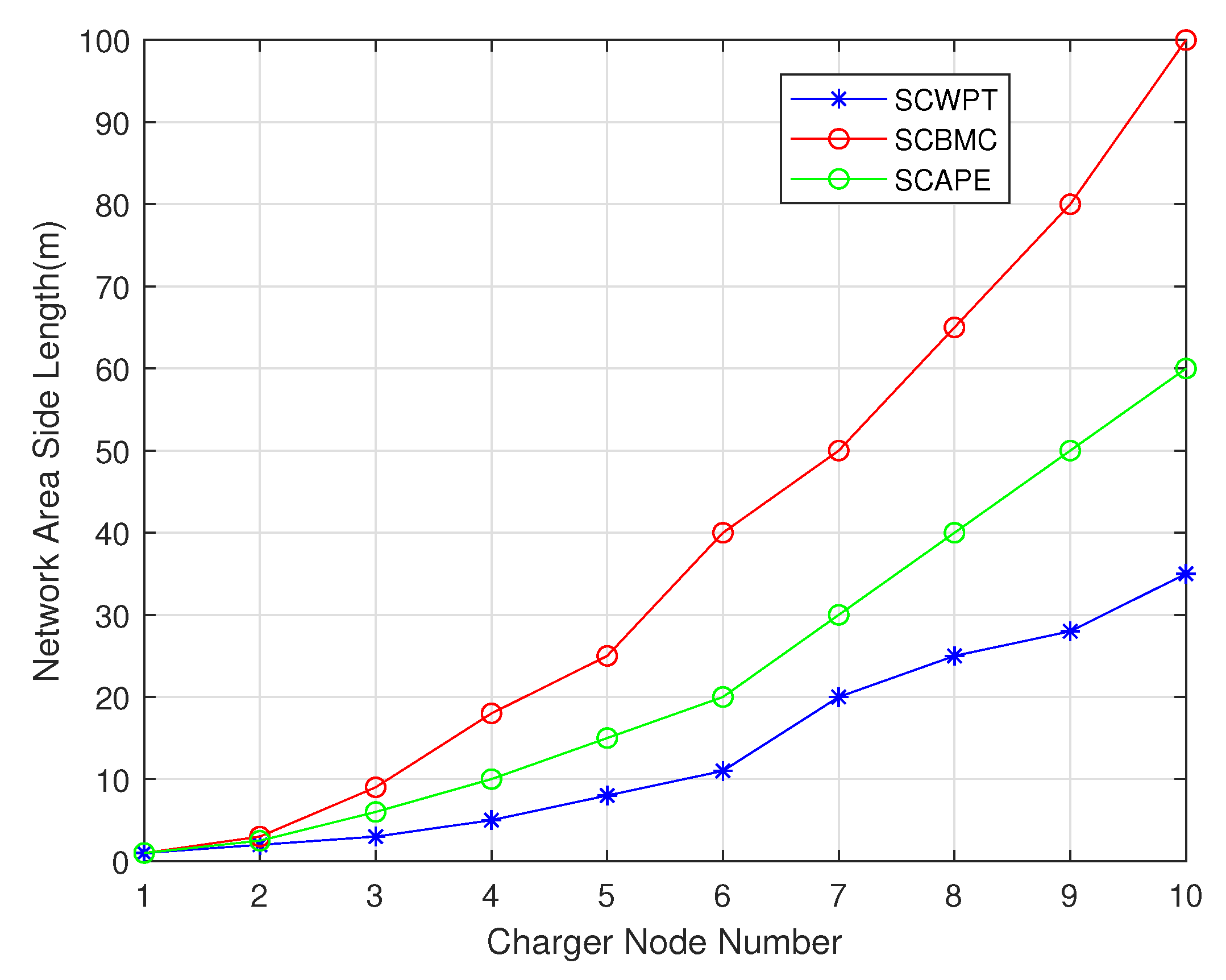
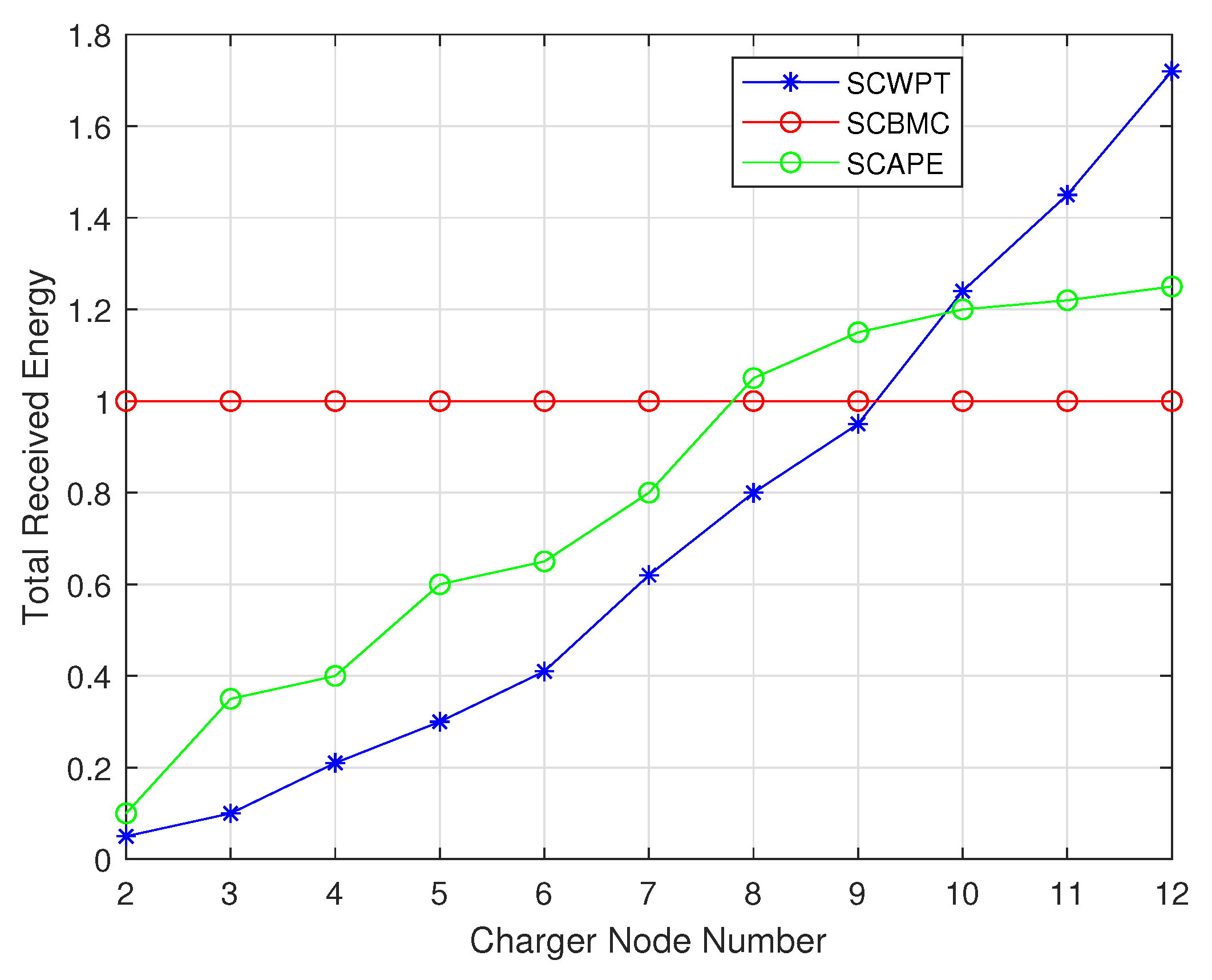
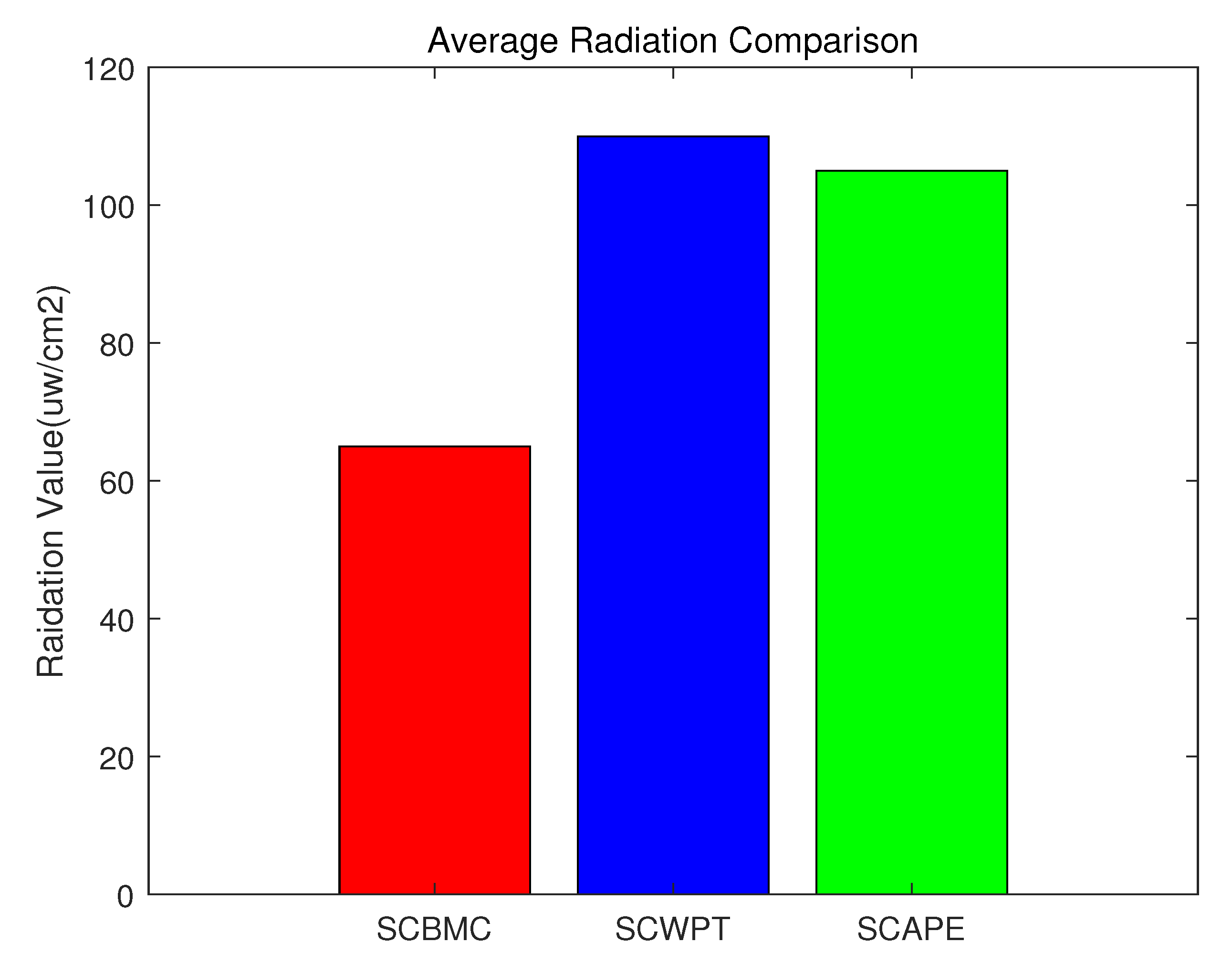
4.2. Comparison between SCBMC, SCWPT and SCAPE
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Engmann, F.; Katsriku, F.A.; Abdulai, J.-D.; Adu-Manu, K.S.; Banaseka, F.K. Prolonging the Lifetime of Wireless Sensor Networks: A Review of Current Techniques. Wirel. Commun. Mob. Comput. 2018, 2018, 8035065. [Google Scholar] [CrossRef]
- Mo, Y.; Shi, L.; Ambrosino, R.; Sinopoli, B. Network lifetime maximization via sensor selection. In Proceedings of the 2009 7th Asian Control Conference, Hong Kong, China, 27–29 August 2009; pp. 441–446. [Google Scholar]
- Akyildiz, I.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar] [CrossRef]
- Powers, R. Batteries for low power electronics. Proc. IEEE 1995, 83, 687–693. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.; Fisher, P.; Soljačić, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Liu, X.; Hackworth, S.; Sclabassi, R.; Sun, M. Wireless energy delivery and data communication for biomedical sensors and implantable devices. In Proceedings of the 2009 IEEE 35th Annual Northeast Bioengineering Conference, Boston, MA, USA, 3–5 April 2009; pp. 1–2. [Google Scholar]
- He, S.; Chen, J.; Jiang, F.; Yau, D.; Xing, G.; Sun, Y. Energy provisioning in wireless rechargeable sensor networks. IEEE Trans. Mob. Comput. 2012, 12, 1931–1942. [Google Scholar] [CrossRef]
- Dai, H.; Xu, L.; Wu, X.; Dong, C.; Chen, G. Impact of mobility on energy provisioning in wireless rechargeable sensor networks. In Proceedings of the 2013 IEEE Wireless Communications And Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 962–967. [Google Scholar]
- Chiu, T.; Shih, Y.; Pang, A.; Jeng, J.; Hsiu, P. Mobility-aware charger deployment for wireless rechargeable sensor networks. In Proceedings of the 2012 14th Asia-Pacific Network Operations and Management Symposium (APNOMS), Seoul, Korea, 25–27 September 2012; pp. 1–7. [Google Scholar]
- Dai, H.; Wu, X.; Xu, L.; Chen, G.; Lin, S. Using minimum mobile chargers to keep large-scale wireless rechargeable sensor networks running forever. In Proceedings of the 2013 22nd International Conference on Computer Communication and Networks (ICCCN), Nassau, Bahamas, 30 July–2 August 2013; pp. 1–7. [Google Scholar]
- Fu, L.; Cheng, P.; Gu, Y.; Chen, J.; He, T. Minimizing charging delay in wireless rechargeable sensor networks. In Proceedings of the 2013 Proceedings IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 2922–2930. [Google Scholar]
- Dai, H.; Liu, Y.; Chen, G.; Wu, X.; He, T.; Liu, A.; Ma, H. Safe charging for wireless power transfer. IEEE/ACM Trans. Netw. 2017, 25, 3531–3544. [Google Scholar] [CrossRef]
- Fu, L.; Cheng, P.; Gu, Y.; Chen, J.; He, T. Optimal charging in wireless rechargeable sensor networks. IEEE Trans. Veh. Technol. 2015, 65, 278–291. [Google Scholar] [CrossRef]
- Lin, C.; Han, D.; Deng, J.; Wu, G. P2S: A Primary and Passer-By Scheduling Algorithm for On-Demand Charging Architecture in Wireless Rechargeable Sensor Networks. IEEE Trans. Veh. Technol. 2017, 66, 8047–8058. [Google Scholar] [CrossRef]
- Zheng, K.; Wang, H.; Li, H.; Xiang, W.; Lei, L.; Qiao, J.; Shen, X. Energy-efficient localization and tracking of mobile devices in wireless sensor networks. IEEE Trans. Veh. Technol. 2016, 66, 2714–2726. [Google Scholar] [CrossRef]
- Ntzouni, M.; Skouroliakou, A.; Kostomitsopoulos, N.; Margaritis, L. Transient and cumulative memory impairments induced by GSM 1.8 GHz cell phone signal in a mouse model. Electromagn. Biol. Med. 2013, 32, 95–120. [Google Scholar] [CrossRef] [PubMed]
- Olteanu, M.; Marincas, C.; Rafiroiu, D. Dangerous temperature increase from em radiation around metallic implants. Acta Electroteh. 2012, 2, 175–180. [Google Scholar]
- Havas, M.; Marrongelle, J.; Pollner, B.; Kelley, E.; Rees, C.R.; Tully, L. Provocation study using heart rate variability shows microwave radiation from 2.4 GHz cordless phone affects autonomic nervous system. Eur. J. Oncol. 2010, 1638, 187–218. [Google Scholar]
- Edwards, M.; Saunders, R.; Shiota, K. Effects of heat on embryos and foetuses. Int. J. Hyperth. 2003, 19, 295–324. [Google Scholar] [CrossRef] [PubMed]
- Gandhi, O.; Morgan, L.; Desalles, A.; Han, Y.; Herberman, R.; Davis, D. Exposure limits: The underestimation of absorbed cell phone radiation, especially in children. Electromagn. Biol. Med. 2012, 31, 34–51. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; Liu, Y.; Chen, G.; Wu, X.; He, T.; Liu, A.; Zhao, Y. SCAPE: Safe charging with adjustable power. IEEE/ACM Trans. Netw. 2018, 26, 520–533. [Google Scholar] [CrossRef]
- Li, L.; Dai, H.; Chen, G.; Zheng, J.; Yang, Z.; Zeng, P. Radiation Constrained Fair Wireless Charging. In Proceedings of the 2017 14th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), San Diego, CA, USA, 12–14 June 2017. [Google Scholar]
- Lin, C.; Hua, H.; Shan, L.; Mamat, A.; Jie, W. Dynamic Mobile Charger Scheduling in Heterogeneous Wireless Sensor Networks. In Proceedings of the 2015 IEEE 12th International Conference on Mobile Ad Hoc and Sensor Systems, Dallas, TX, USA, 19–22 October 2015. [Google Scholar]
- Han, G.J.; Wu, J.W.; Wang, H.; Guizani, M.; Ansere, J.A.; Zhang, W.B. A Multicharger Cooperative Energy Provision Algorithm Based on Density Clustering in the Industrial Internet of Things. IEEE Internet Things J. 2019, 6, 9165–9174. [Google Scholar] [CrossRef]
- Franek, O. Phasor Alternatives to Friis’ Transmission Equation. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 90–93. [Google Scholar] [CrossRef]
- Shu, Y.; Cheng, P.; Gu, Y.; Chen, J.; He, T. TOC: Localizing wireless rechargeable sensors with time of charge. ACM Trans. Sens. Netw. 2015, 11, 1–22. [Google Scholar] [CrossRef]
- Tang, H.; Tan, K.; Yi, Z. Columnar competitive model for solving multi-traveling salesman problem. Neural Netw. Comput. Models Appl. 2007, 53, 145–160. [Google Scholar]
- Gurobi. Gurobi Optimization. Available online: www.gurobi.com (accessed on 10 April 2020).




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Jing, H.; Liao, J.; Yin, F.; Yuan, P.; Chen, L. A Safe Charging Algorithm Based on Multiple Mobile Chargers. Sensors 2020, 20, 2937. https://doi.org/10.3390/s20102937
Wang W, Jing H, Liao J, Yin F, Yuan P, Chen L. A Safe Charging Algorithm Based on Multiple Mobile Chargers. Sensors. 2020; 20(10):2937. https://doi.org/10.3390/s20102937
Chicago/Turabian StyleWang, Wei, Haoran Jing, Junhua Liao, Feng Yin, Ping Yuan, and Liangyin Chen. 2020. "A Safe Charging Algorithm Based on Multiple Mobile Chargers" Sensors 20, no. 10: 2937. https://doi.org/10.3390/s20102937
APA StyleWang, W., Jing, H., Liao, J., Yin, F., Yuan, P., & Chen, L. (2020). A Safe Charging Algorithm Based on Multiple Mobile Chargers. Sensors, 20(10), 2937. https://doi.org/10.3390/s20102937




