Adaptive Robust Unscented Kalman Filter for AUV Acoustic Navigation
Abstract
1. Introduction
2. Unscented Kalman Filter (UKF)
3. Adaptive Robust Kalman Filter
3.1. Adaptive UKF Based on the Sage-Husa Filter
3.2. Adaptive Robust UKF Algorithm
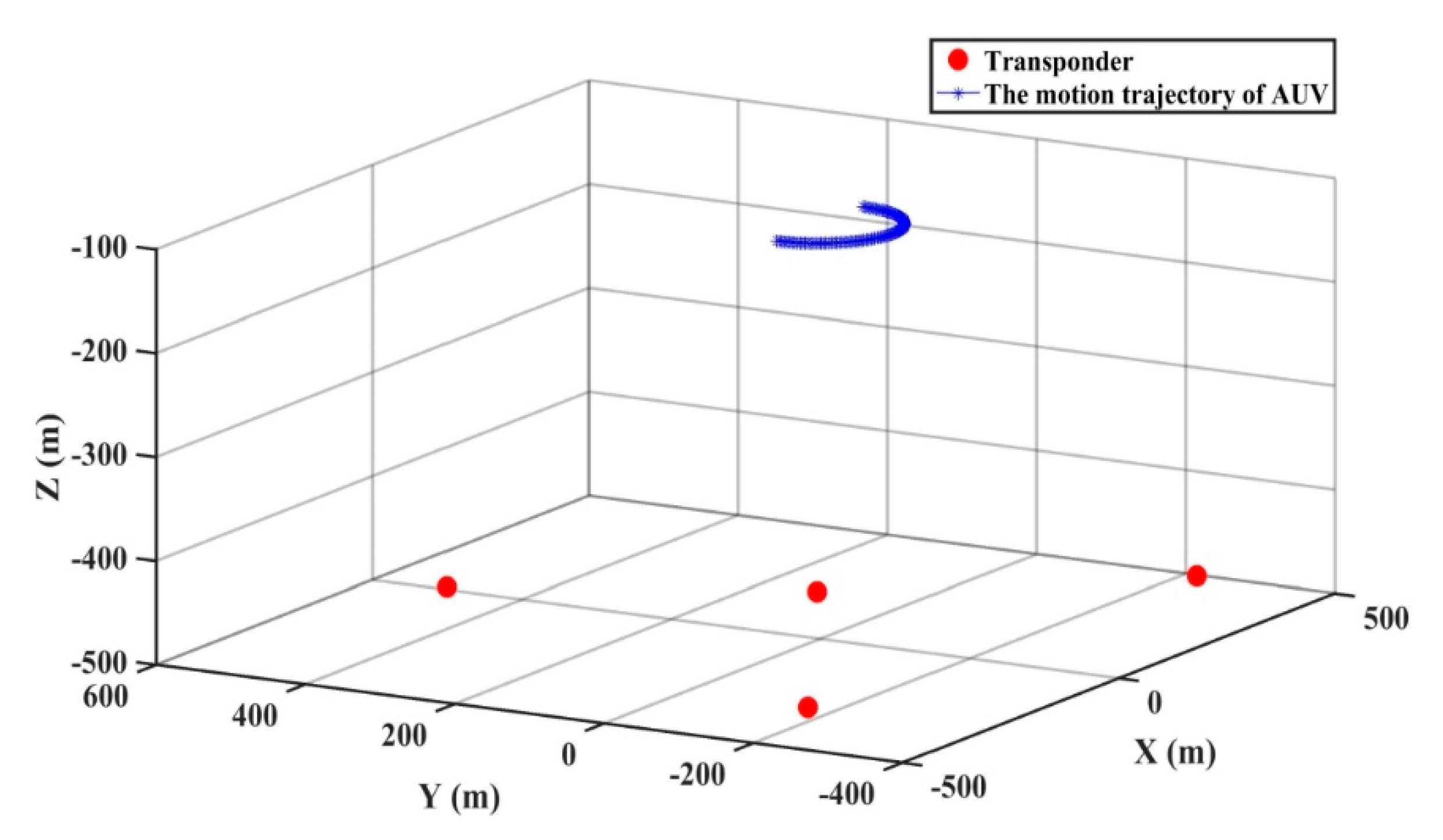
4. Experiments and Analysis
4.1. Comparison of UKF and Adaptive UKF
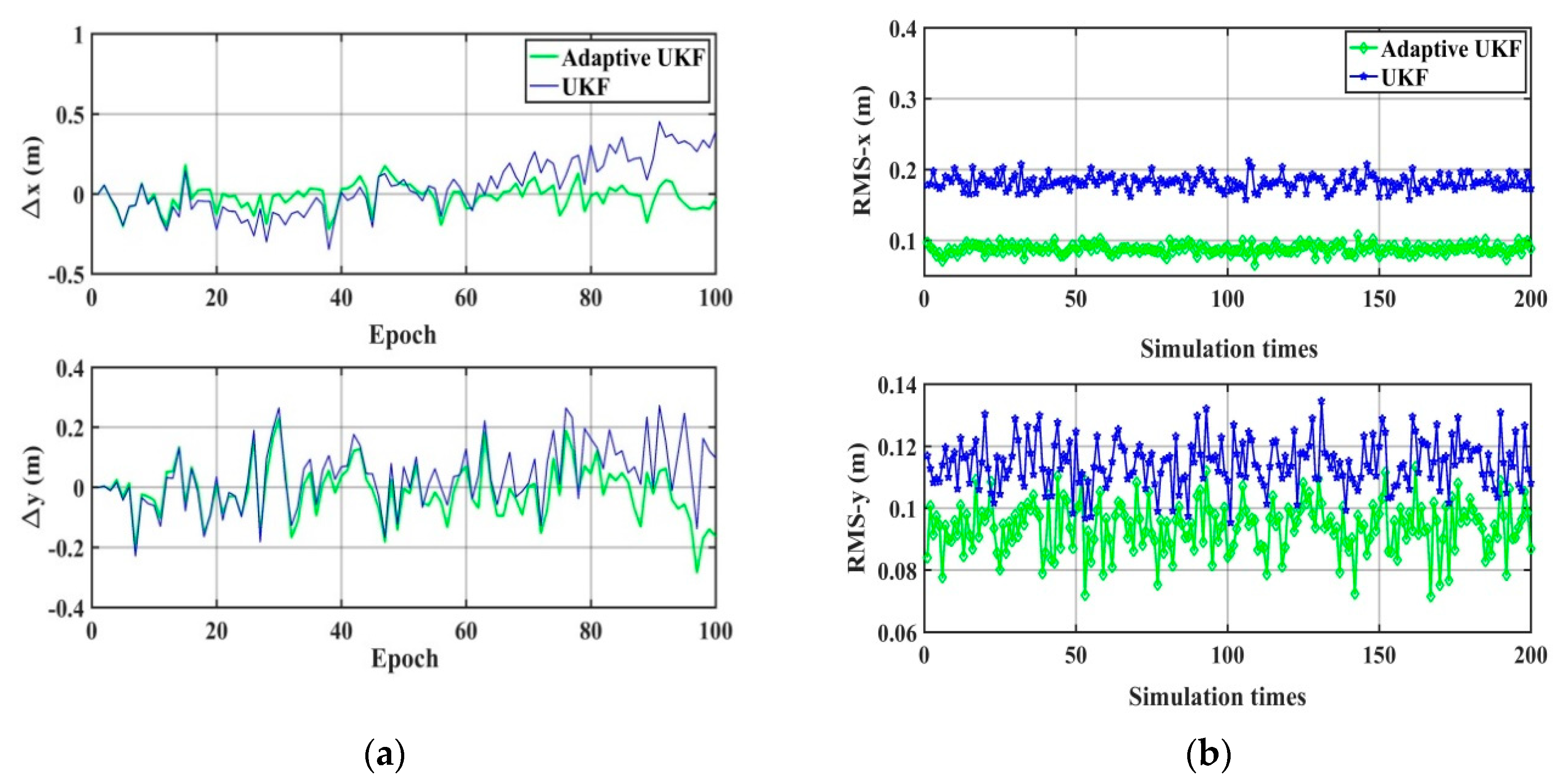
4.1.1. Simulation Experiment and Analysis
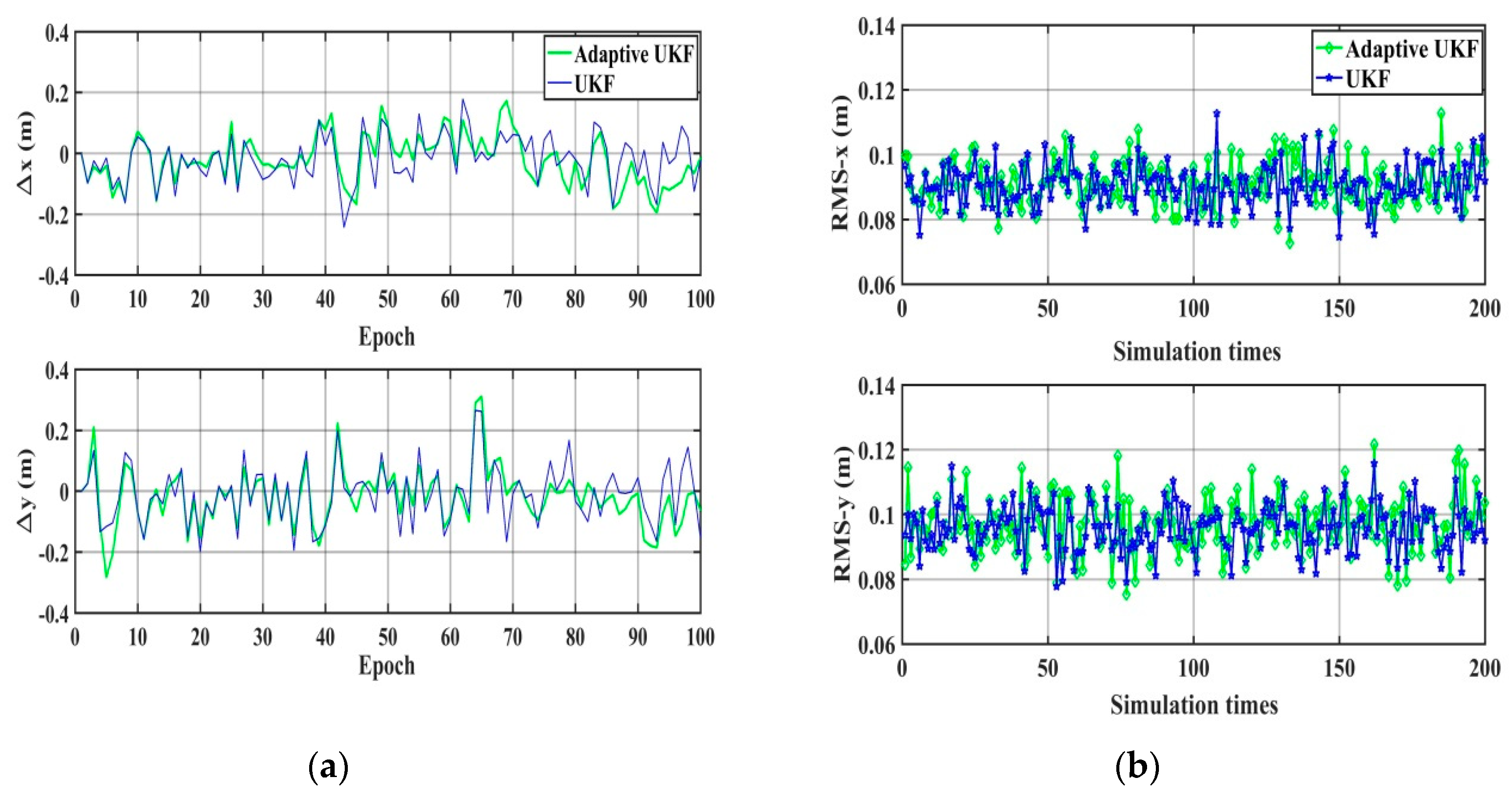
4.1.2. Real Experiment and Analysis
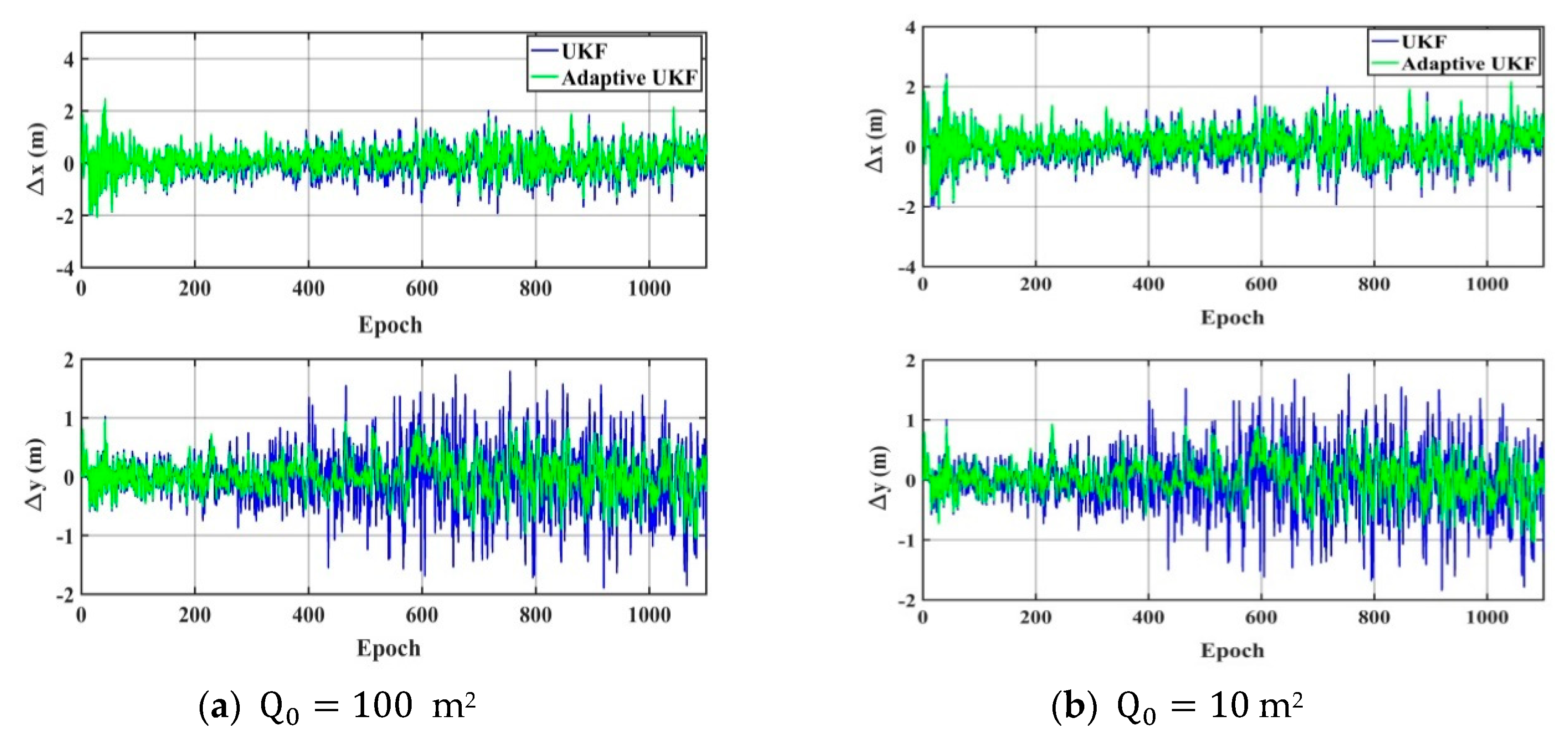
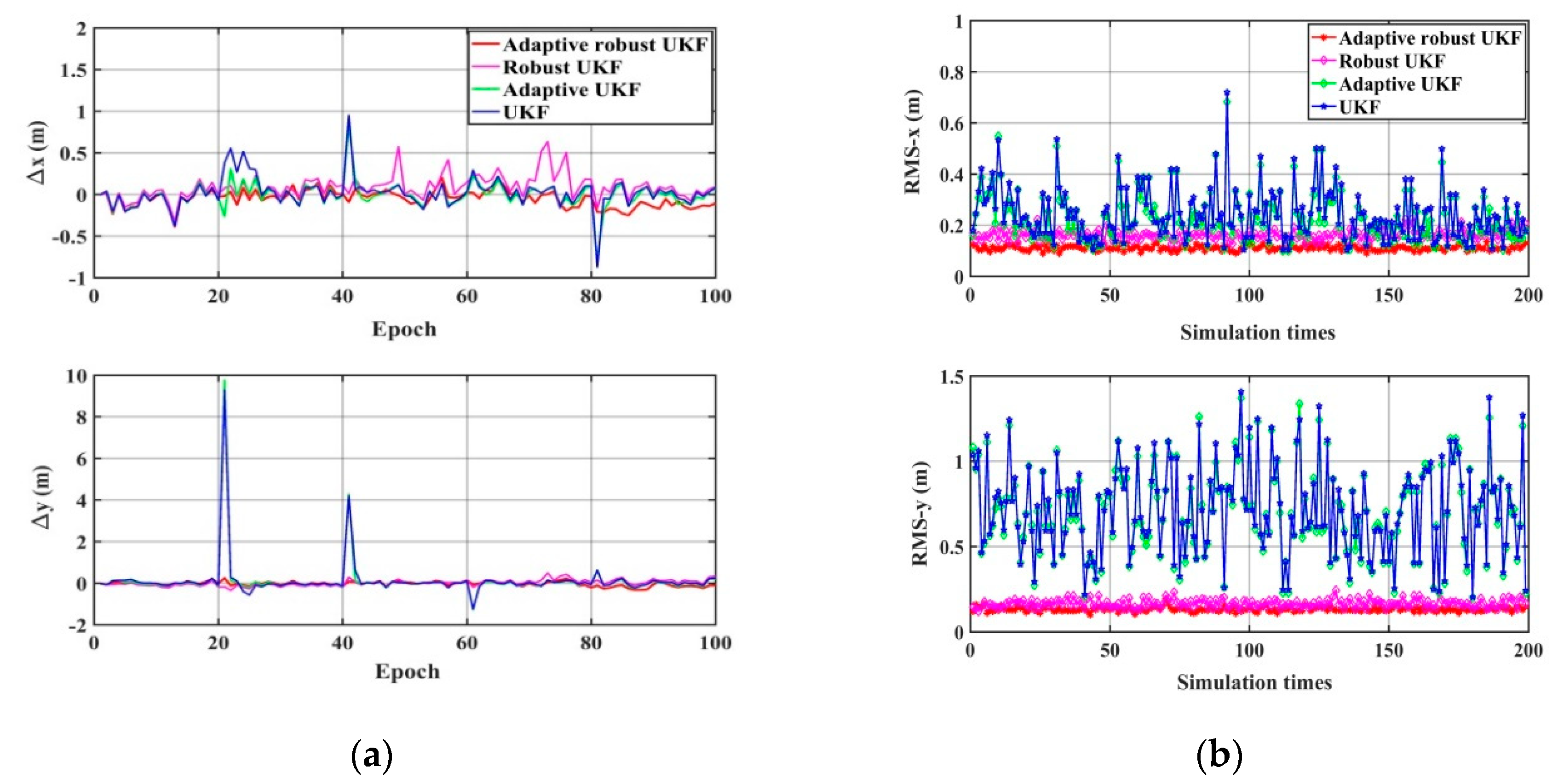
4.2. Validation of Adaptive Robust UKF
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV Navigation and Localization: A Review. IEEE J. Ocean. Eng. 2014, 39, 131–149. [Google Scholar] [CrossRef]
- Fiorelli, E.; Leonard, N.E.; Bhatta, P.; Paley, D.A.; Bachmayer, R.; Fratantoni, D.M. Multi-AUV Control and Adaptive Sampling in Monterey Bay. IEEE J. Ocean. Eng. 2007, 31, 935–948. [Google Scholar] [CrossRef]
- Zhang, T.; Shi, H.; Chen, L.; Li, Y.; Tong, J. AUV Positioning Method Based on Tightly Coupled SINS/LBL for Underwater Acoustic Multipath Propagation. Sensors 2016, 16, 357. [Google Scholar] [CrossRef] [PubMed]
- Thomson, D.J.M.; Dosso, S.E.; Barclay, D.R. Modeling AUV Localization Error in a Long Baseline Acoustic Positioning System. IEEE J. Ocean. Eng. 2017, 43, 955–968. [Google Scholar] [CrossRef]
- Ma, S.; Liu, G.; Yang, D.; Wang, Y. Research on acoustic positioning system in the process of AUV recovery. In Proceedings of the International Conference on Advanced Mechatronic Systems, Tokyo, Japan, 18–21 September 2012; pp. 447–451. [Google Scholar]
- Dong, Y.K.; Liu, M.Y.; Hu, J.W. An Novel Method of Integrated Navigation for AUV Based on Nonlinear Filter. Fire Control Command Control 2011, 36, 95–98. [Google Scholar]
- Allotta, B.; Caiti, A.; Costanzi, R.; Fanelli, F.; Fenucci, D.; Meli, E.; Ridolfi, A. A new AUV navigation system exploiting unscented Kalman filter. Ocean Eng. 2016, 113, 121–132. [Google Scholar] [CrossRef]
- Julier, S.J. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Koch, K.R.; Yang, Y. Robust Kalman filter for rank deficient observation models. J. Geod. 1998, 72, 436–441. [Google Scholar] [CrossRef]
- Mirzaee, A.; Salahshoor, K. Fault diagnosis and accommodation of nonlinear systems based on multiple-model adaptive unscented Kalman filter and switched MPC and H-infinity loop-shaping controller. J. Process Control 2012, 22, 626–634. [Google Scholar] [CrossRef]
- Jwo, D.J.; Weng, T.P. An Adaptive Sensor Fusion Method with Applications in Integrated Navigation. J. Navig. 2008, 61, 705. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman Filtering for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Chang, G. Kalman filter with both adaptivity and robustness. J. Process Control 2014, 24, 81–87. [Google Scholar] [CrossRef]
- Ozbek, L.; Aliev, F.A. Adaptive Fading Kalman Filter with an Application. Automatica 1998, 34, 1179–1182. [Google Scholar]
- Gao, X.; You, D.; Katayama, S. Seam Tracking Monitoring Based on Adaptive Kalman Filter Embedded Elman Neural Network During High-Power Fiber Laser Welding. IEEE Trans. Ind. Electron. 2012, 59, 4315–4325. [Google Scholar] [CrossRef]
- Guo, H.; Guo, J.; Yu, M.; Hong, H.; Xiong, J.; Tian, B.A. weighted combination filter with nonholonomic constrains for integrated navigation systems. Adv. Space Res. 2015, 55, 1470–1476. [Google Scholar] [CrossRef]
- Banda, S.S. Multiple model adaptive algorithms for detecting and compensating sensor and actuator/surface failures in aircraft flight control systems. Int. J. Robust Nonlinear Control 2015, 9, 1051–1070. [Google Scholar]
- Hajiyev, C. Adaptive filtration algorithm with the filter gain correction applied to integrated INS/radar altimeter. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2007, 221, 847–855. [Google Scholar] [CrossRef]
- Baarda, W. A testing procedure for use in geodetic networks. Available online: http://www.ncgeo.nl/downloads/09Baarda.pdf (accessed on 20 December 2019).
- Chen, Y.; Wenzhong, S.; Wu, C. Robust M-M unscented Kalman filtering for GPS/IMU navigation. J. Geod. Geodyn. 2019, 93, 1093–1194. [Google Scholar]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Bickel, P.J. On Some Analogues to Linear Combinations of Order Statistics in the Linear Model. Ann. Stat. 1973, 1, 597–616. [Google Scholar] [CrossRef]
- Ruppert, D. Robust Statistics: The Approach Based on Influence Functions. Technometrics 1987, 29, 240–241. [Google Scholar] [CrossRef]
- Jiangwen, Z. Classical Theory of Errors and Robust Estimation. Acta Geod. Et Cartogr. Sin. 1989, 18, 115–120. [Google Scholar]
- Yang, Y.X. Adaptive Navigation and Kinematic Positioning; Surveying and Mapping Press: Beijing, China, 2006; pp. 51–68. [Google Scholar]
- Xiaoyun, Y.; Heng, H. GPS/DR integrated navigation system based on adaptive robust Kalman filtering. In Proceedings of the International Conference on Microwave & Millimeter Wave Technology, Nanjing, China, 21–24 April 2008. [Google Scholar]
- Hajiyev, C.; Vural, S.Y.; Hajiyeva, U. Adaptive Fading Kalman Filter with Q-adaptation for estimation of AUV dynamics. In Proceedings of the Control & Automation, Nanjing, China, 21–24 April 2008. [Google Scholar]
- Costanzi, R.; Fanelli, F.; Meli, E.; Ridolfi, A.; Caiti, A.; Allotta, B. UKF-Based Navigation System for AUVs: Online Experimental Validation. IEEE J. Ocean. Eng. 2018, 44, 633–641. [Google Scholar] [CrossRef]
- Zheng, B.; Fu, P.; Li, B.; Yuan, X. A Robust Adaptive Unscented Kalman Filter for Nonlinear Estimation with Uncertain Noise Covariance. Sensors 2018, 18, 808. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Huang, X.G. An improved Sage-Husa adaptive filter algorithm. Electron. Instrum. Cust. 2009, 16, 71–73. [Google Scholar]
- Xue, L.; Gao, S.S.; Hu, G.G. Adaptive Sage-Husa particle filtering and its application in integrated navigation. Zhongguo Guanxing Jishu Xuebao/J. Chin. Inert. Technol. 2013, 21, 84–88. [Google Scholar]
- Sage, A.P.; Husa, G.W. Adaptive filtering with unknown prior statistics. In Joint Automatic Control Conference; IEEE: Piscataway, NJ, USA, 1969; Volume 7, pp. 760–769. [Google Scholar] [CrossRef]
- Ahmad, M.S.; Kukrer, O.; Hocanin, A. The effect of the forgetting factor on the RI adaptive algorithm in system identification. In Proceedings of the International Symposium on Signals, Circuits and Systems, Lasi, Romania, 30 June–1 July 2011; pp. 1–4. [Google Scholar]
- Song, Y.S.; Arshad, M.R. Tracking control design for autonomous underwater vehicle using robust filter approach. In Proceedings of the Autonomous Underwater Vehicles, Tokyo, Japan, 6–9 November 2016; pp. 374–380. [Google Scholar]
- Fakharian, A.; Gustafsson, T.; Mehrfam, M. Adaptive Kalman filtering based navigation: An IMU/GPS integration approach. In Proceedings of the 8th IEEE International Conference on Networking, Sensing and Control, Delft, Netherlands, 11–13 April 2011. [Google Scholar]
- Garrett, C.; Munk, W. Internal Waves in the Ocean. Annu. Rev. Fluid Mech. 1979, 11, 339–369. [Google Scholar] [CrossRef]
- Xu, P.; Ando, M.; Tadokoro, K. Precise three-dimensional seafloor geodetic deformation measurements using difference techniques. Earth Planets Space 2005, 57, 795–808. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Z.; Zhao, S.; He, K. Accurate Multiple Ocean Bottom Seismometer Positioning in Shallow Water Using GNSS/Acoustic Technique. Sensors 2019, 19, 1406. [Google Scholar] [CrossRef]


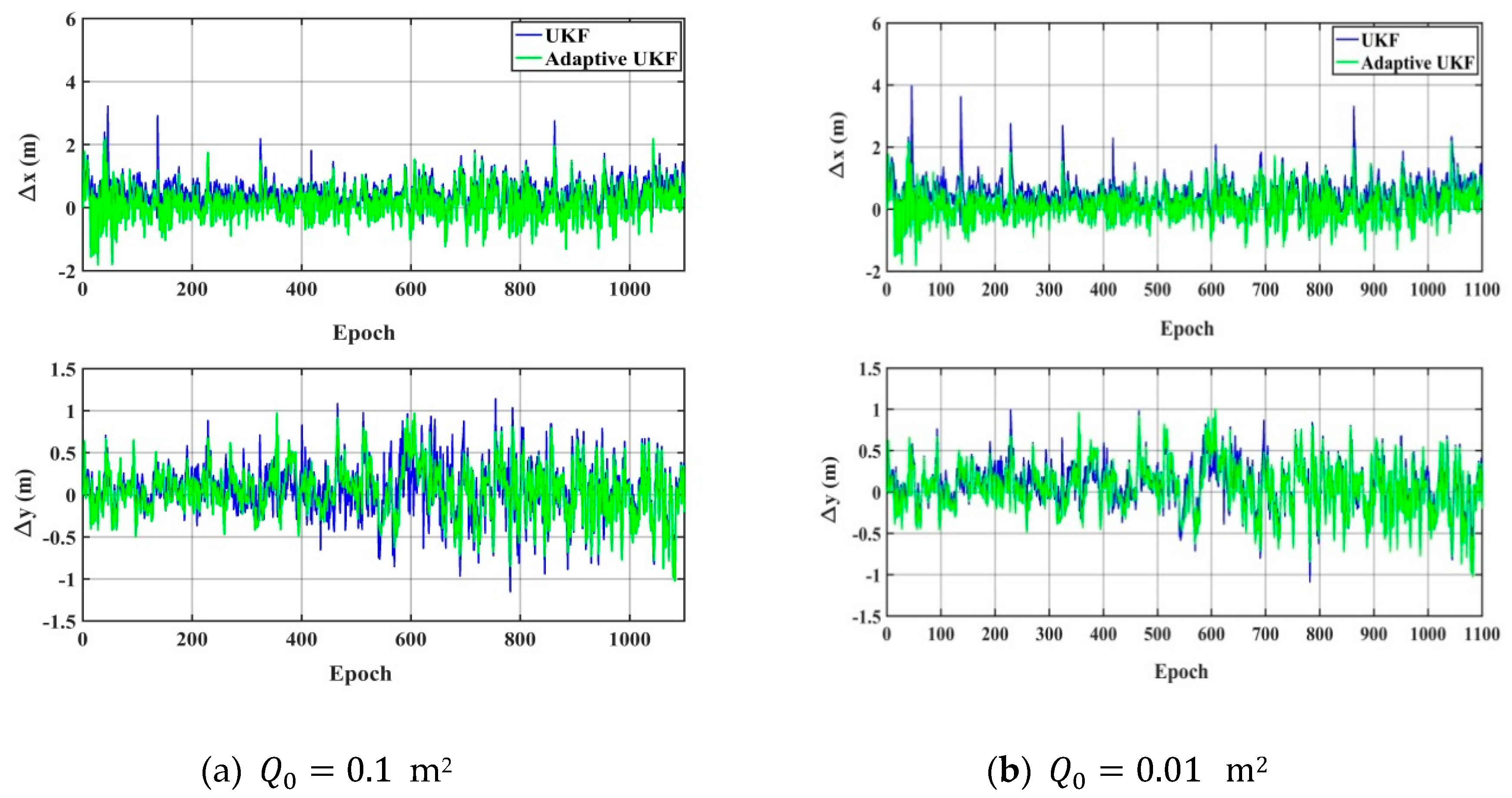



| Statistics | Method | RMS-x (m) | RMS-y (m) | |
|---|---|---|---|---|
| 1 | Mean | UKF | 0.182 | 0.114 |
| adaptive UKF | 0.088 | 0.094 | ||
| Max. | UKF | 0.212 | 0.134 | |
| adaptive UKF | 0.107 | 0.113 | ||
| Min. | UKF | 0.158 | 0.095 | |
| adaptive UKF | 0.006 | 0.071 | ||
| 0.1 | Mean | UKF | 0.090 | 0.095 |
| adaptive UKF | 0.091 | 0.097 | ||
| Max. | UKF | 0.112 | 0.115 | |
| adaptive UKF | 0.112 | 0.121 | ||
| Min. | UKF | 0.074 | 0.077 | |
| adaptive UKF | 0.072 | 0.075 |
| Method | RMS-x (m) | RMS-y (m) | |
|---|---|---|---|
| 1000 | UKF | 0.612 | 0.546 |
| Adaptive UKF | 0.561 | 0.363 | |
| 500 | UKF | 0.612 | 0.546 |
| Adaptive UKF | 0.557 | 0.347 | |
| 100 | UKF | 0.612 | 0.544 |
| Adaptive UKF | 0.553 | 0.313 | |
| 50 | UKF | 0.611 | 0.543 |
| Adaptive UKF | 0.550 | 0.303 | |
| 10 | UKF | 0.607 | 0.531 |
| Adaptive UKF | 0.547 | 0.303 | |
| 5 | UKF | 0.600 | 0.519 |
| Adaptive UKF | 0.546 | 0.301 | |
| 1 | UKF | 0.554 | 0.458 |
| Adaptive UKF | 0.548 | 0.297 | |
| 0.5 | UKF | 0.556 | 0.418 |
| Adaptive UKF | 0.548 | 0.297 | |
| 0.1 | UKF | 0.654 | 0.329 |
| Adaptive UKF | 0.580 | 0.300 | |
| 0.05 | UKF | 0.680 | 0.312 |
| Adaptive UKF | 0.550 | 0.302 | |
| 0.01 | UKF | 0.735 | 0.296 |
| Adaptive UKF | 0.550 | 0.302 | |
| 0.005 | UKF | 0.767 | 0.292 |
| Adaptive UKF | 0.551 | 0.304 | |
| 0.001 | UKF | 0.844 | 0.313 |
| Adaptive UKF | 0.551 | 0.303 |
| Statistics | Method | RMS-x (m) | RMS-y (m) |
|---|---|---|---|
| Mean | UKF | 0.264 | 0.651 |
| Robust UKF | 0.103 | 0.135 | |
| Max. | UKF | 0.839 | 1.827 |
| Robust UKF | 0.130 | 0.175 | |
| Min. | UKF | 0.101 | 0.183 |
| Robust UKF | 0.085 | 0.102 |
| System Noise Q0 (m2) | Statistics | Methods | RMS-x (m) | RMS-y (m) |
|---|---|---|---|---|
| 1 | Mean | UKF | 0.324 | 0.801 |
| Adaptive UKF | 0.232 | 0.730 | ||
| Robust UKF | 0.122 | 0.286 | ||
| Adaptive robust UKF | 0.101 | 0.106 | ||
| Max. | UKF | 0.912 | 2.287 | |
| Adaptive UKF | 0.719 | 2.197 | ||
| Robust UKF | 0.196 | 0.557 | ||
| Adaptive robust UKF | 0.124 | 0.289 | ||
| Min. | UKF | 0.144 | 0.226 | |
| Adaptive UKF | 0.099 | 0.197 | ||
| Robust UKF | 0.094 | 0.121 | ||
| Adaptive robust UKF | 0.074 | 0.100 | ||
| 0.1 | Mean | UKF | 0.248 | 0.716 |
| Adaptive UKF | 0.226 | 0.704 | ||
| Robust UKF | 0.163 | 0.167 | ||
| Adaptive robust UKF | 0.112 | 0.134 | ||
| Max. | UKF | 0.720 | 1.408 | |
| Adaptive UKF | 0.683 | 1.370 | ||
| Robust UKF | 0.224 | 0.245 | ||
| Adaptive robust UKF | 0.137 | 0.196 | ||
| Min. | UKF | 0.104 | 0.203 | |
| Adaptive UKF | 0.100 | 0.201 | ||
| Robust UKF | 0.124 | 0.121 | ||
| Adaptive robust UKF | 0.091 | 0.100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Xu, T.; Wang, Z. Adaptive Robust Unscented Kalman Filter for AUV Acoustic Navigation. Sensors 2020, 20, 60. https://doi.org/10.3390/s20010060
Wang J, Xu T, Wang Z. Adaptive Robust Unscented Kalman Filter for AUV Acoustic Navigation. Sensors. 2020; 20(1):60. https://doi.org/10.3390/s20010060
Chicago/Turabian StyleWang, Junting, Tianhe Xu, and Zhenjie Wang. 2020. "Adaptive Robust Unscented Kalman Filter for AUV Acoustic Navigation" Sensors 20, no. 1: 60. https://doi.org/10.3390/s20010060
APA StyleWang, J., Xu, T., & Wang, Z. (2020). Adaptive Robust Unscented Kalman Filter for AUV Acoustic Navigation. Sensors, 20(1), 60. https://doi.org/10.3390/s20010060





