Anomaly Detection Based Latency-Aware Energy Consumption Optimization For IoT Data-Flow Services
Abstract
1. Introduction
- We developed a formal model for energy-efficient CDF optimization. This is a model that is composed of four level entities in IFEC computing. This model is used to formulate an optimal problem that minimizes the energy consumption subject to the latency constraints and with the anomalous fog or MEC nodes existing in systems.
- We proposed a novel lightweight anomalous nodes detection strategy for latency-aware CDF optimization.
- We designed a block coordinate descend-based max-flow algorithm to solve latency-aware energy-efficient CDF problem iteratively.
- The performance of proposed model and algorithm was evaluated by simulations based on real-life datasets.
2. Motivation Scenario
3. System Model
- IoT end level: The IoT end devices belongs to this level, such as sensors, RFID, etc. which are used to collect the raw data in IoT.
- Fog level: The fog nodes with very limited communication and computation capability belong to this level, such as the IoT gateway.
- MEC level: The server clusters with limited computation capability belong to this level, which are deployed at places in proximity to access points of mobile networks, such as at the macro LTE base stations, at a multi-Radio Access Technology cell aggregation site, etc. [5].
- Cloud level: There are only data centers at this level.
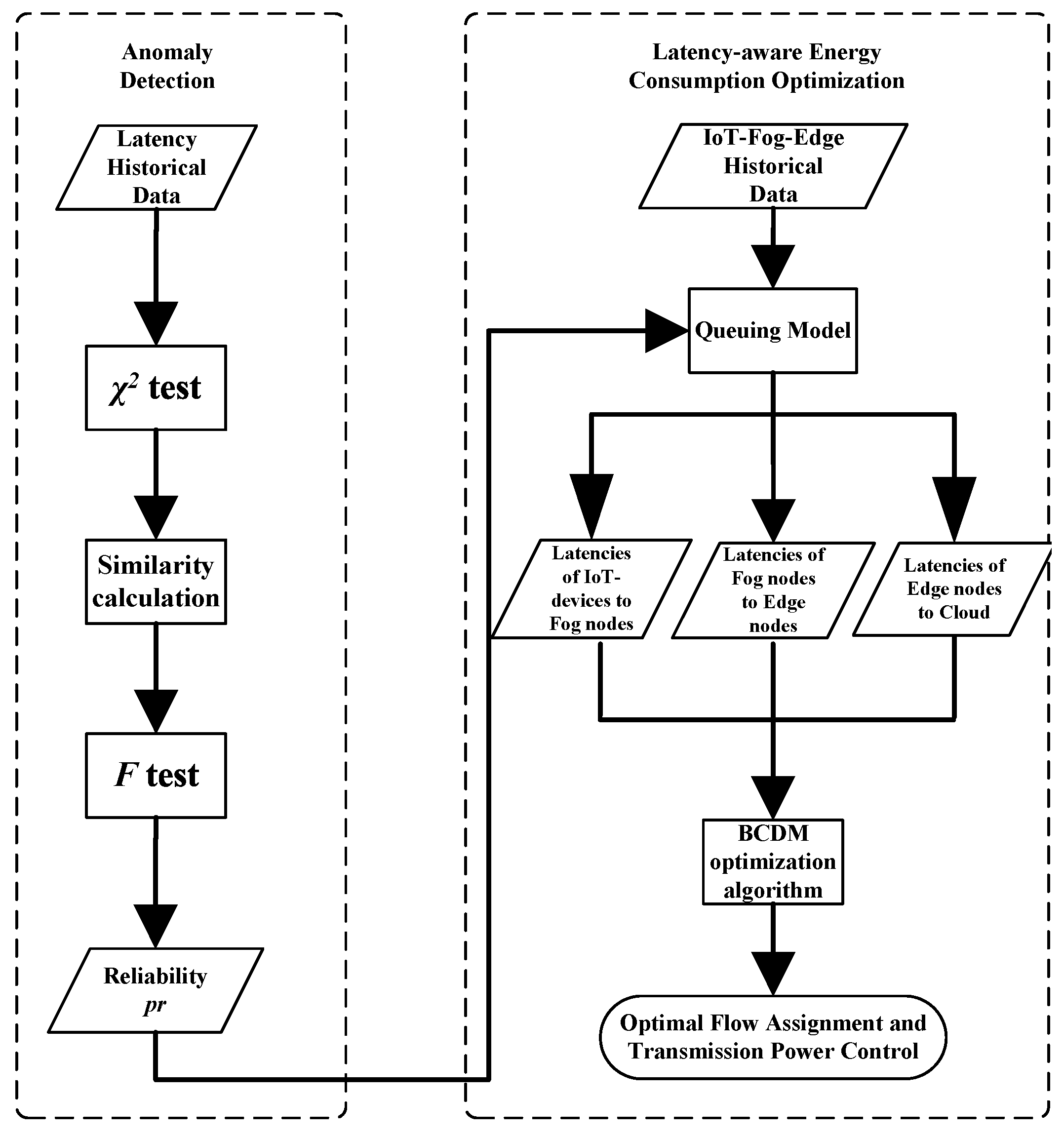
3.1. Anomalous Nodes Discovery and Confidence Evaluation
3.1.1. Chi-Square Test and Similarity Measurement
3.1.2. F-Test
3.1.3. Put It All Together
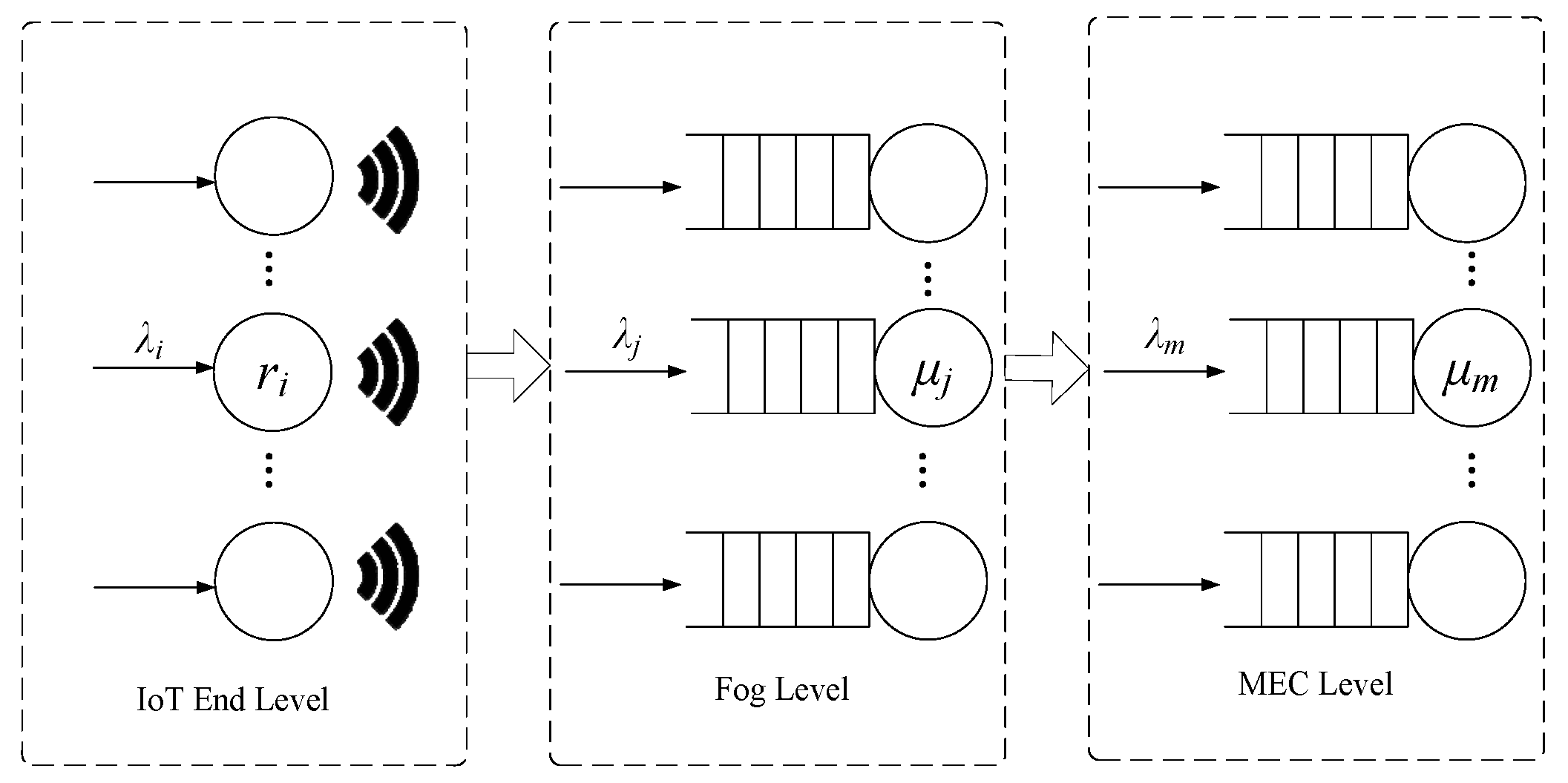
3.2. Tandem Queue Model
3.2.1. Latency in IoT End Level
3.2.2. Latency in Fog and MEC Level
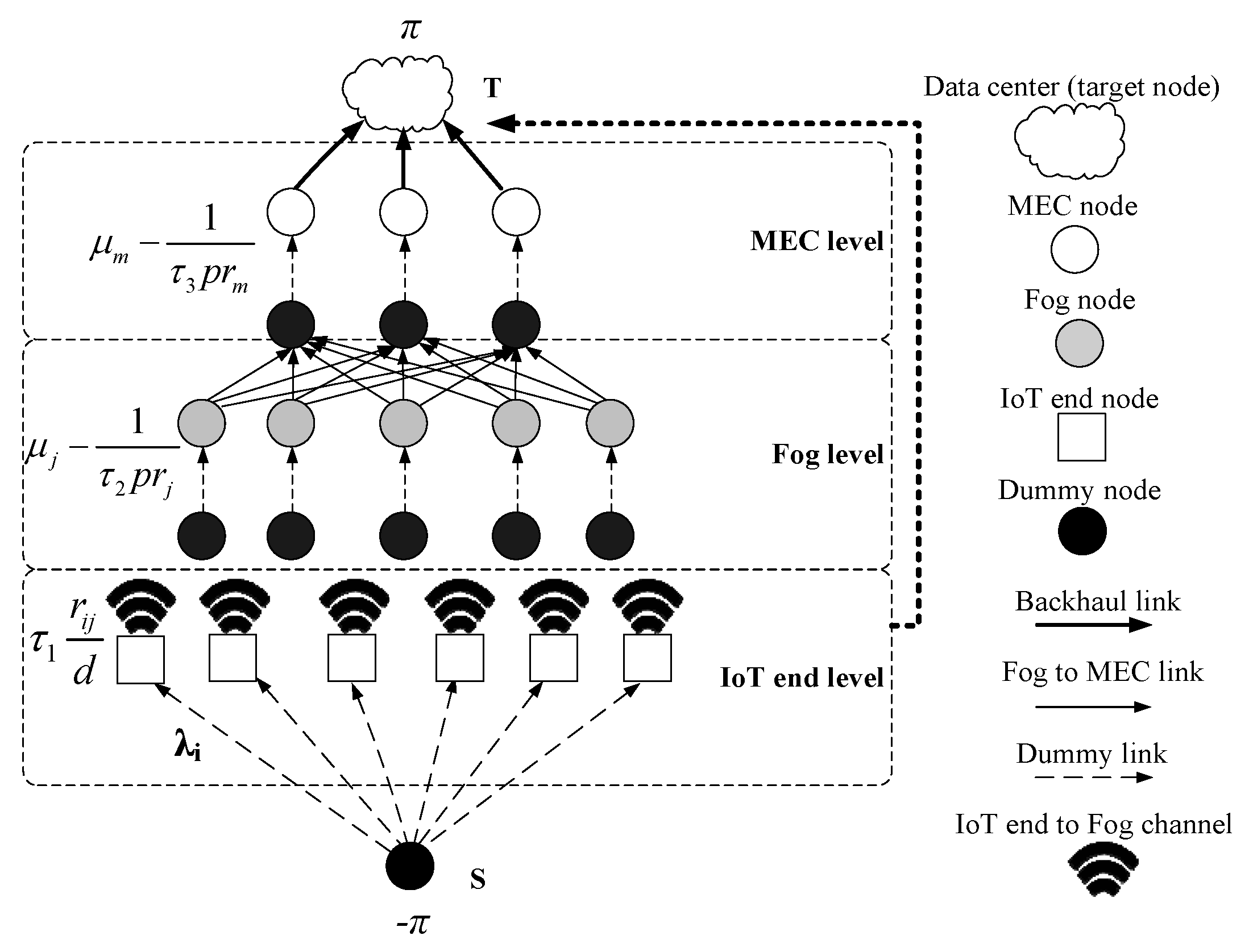
3.3. Problem Formulation
4. Solutions
4.1. Block Coordinate Descent Based Multi-Flow Algorithm
| Algorithm 1 Block Coordinate Descent based Multi-flow Algorithm |
|
4.2. Best-Effort Algorithm
| Algorithm 2 Best-effort Algorithm |
|
5. Simulations
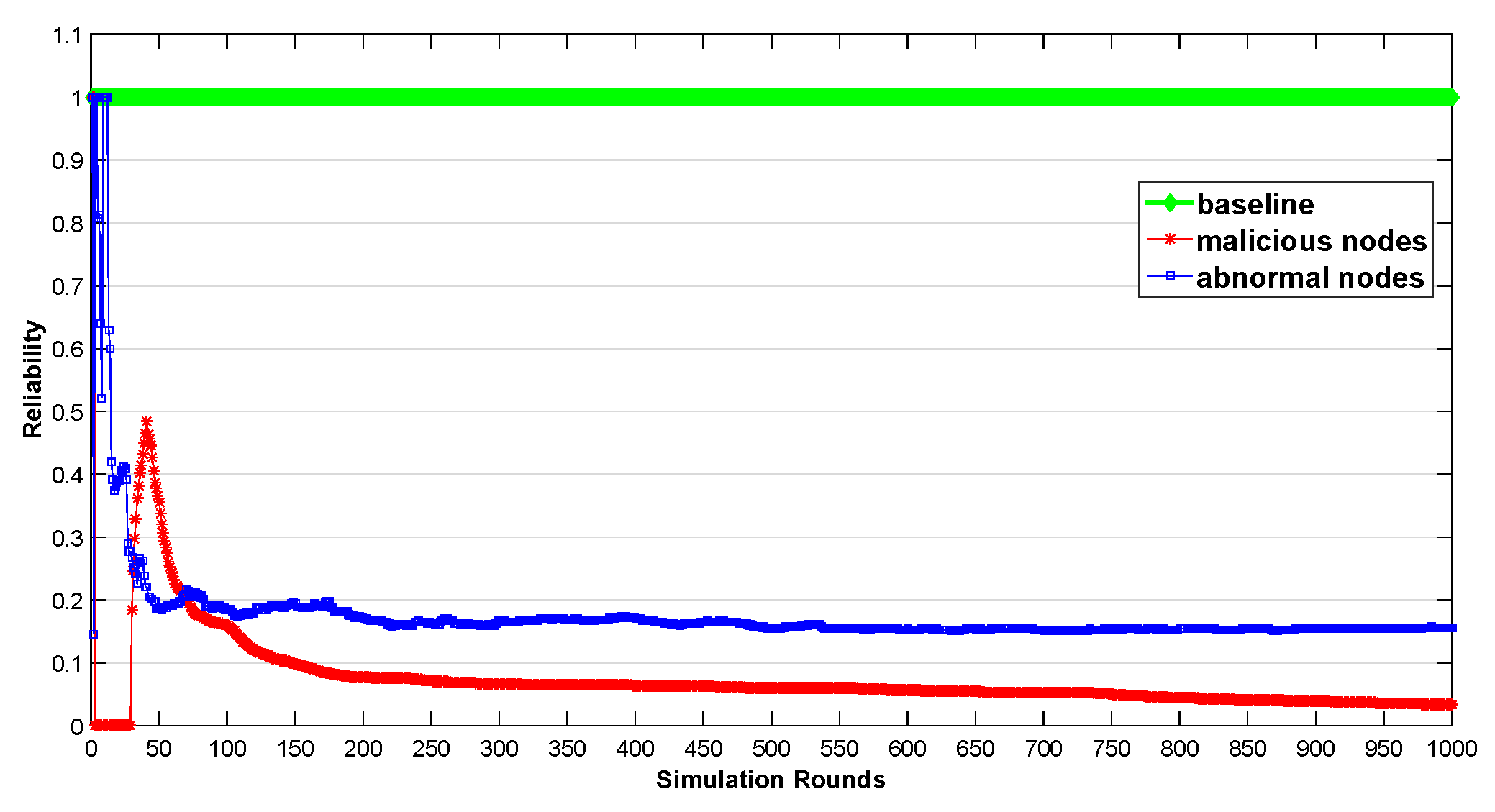
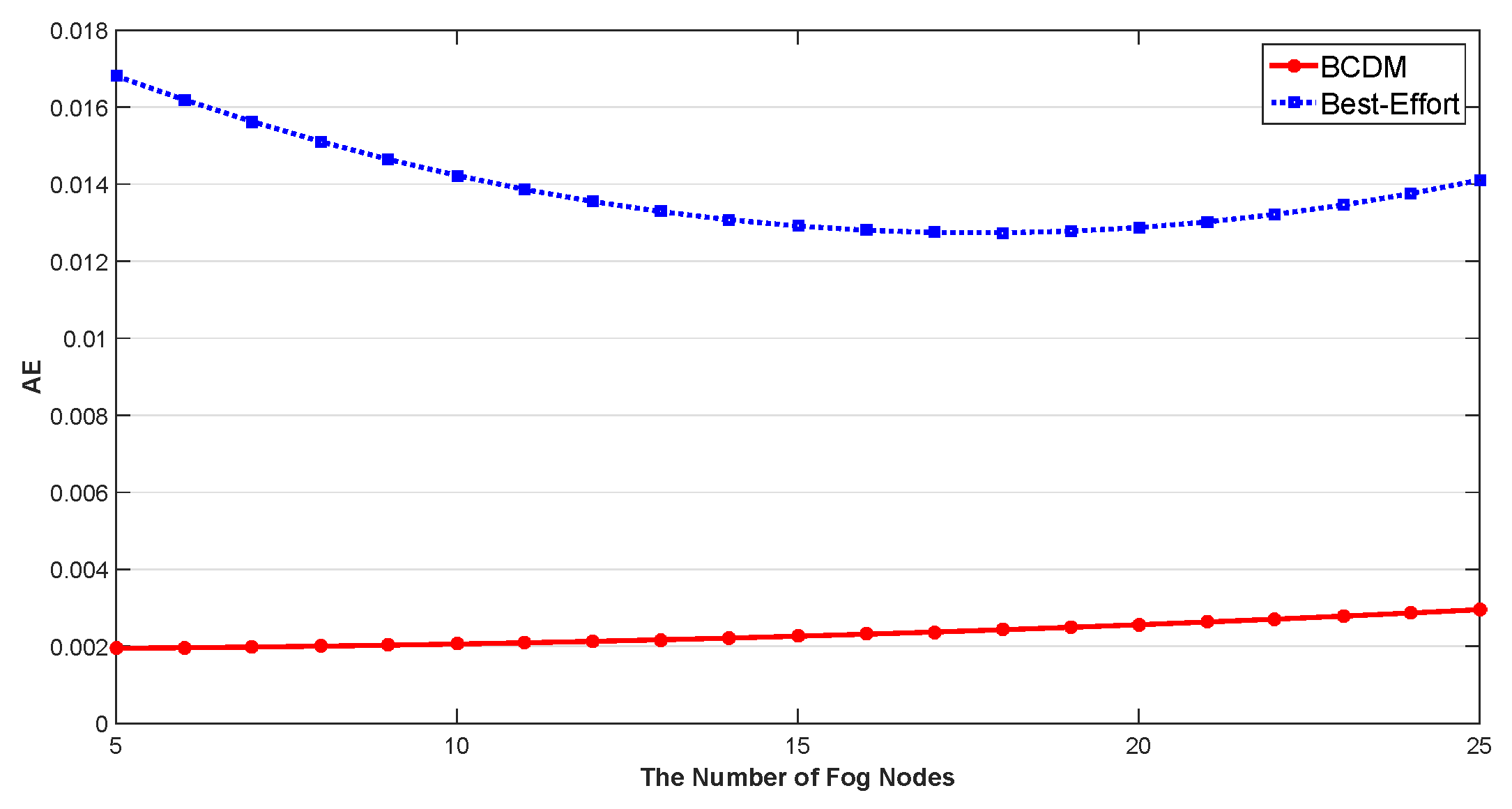
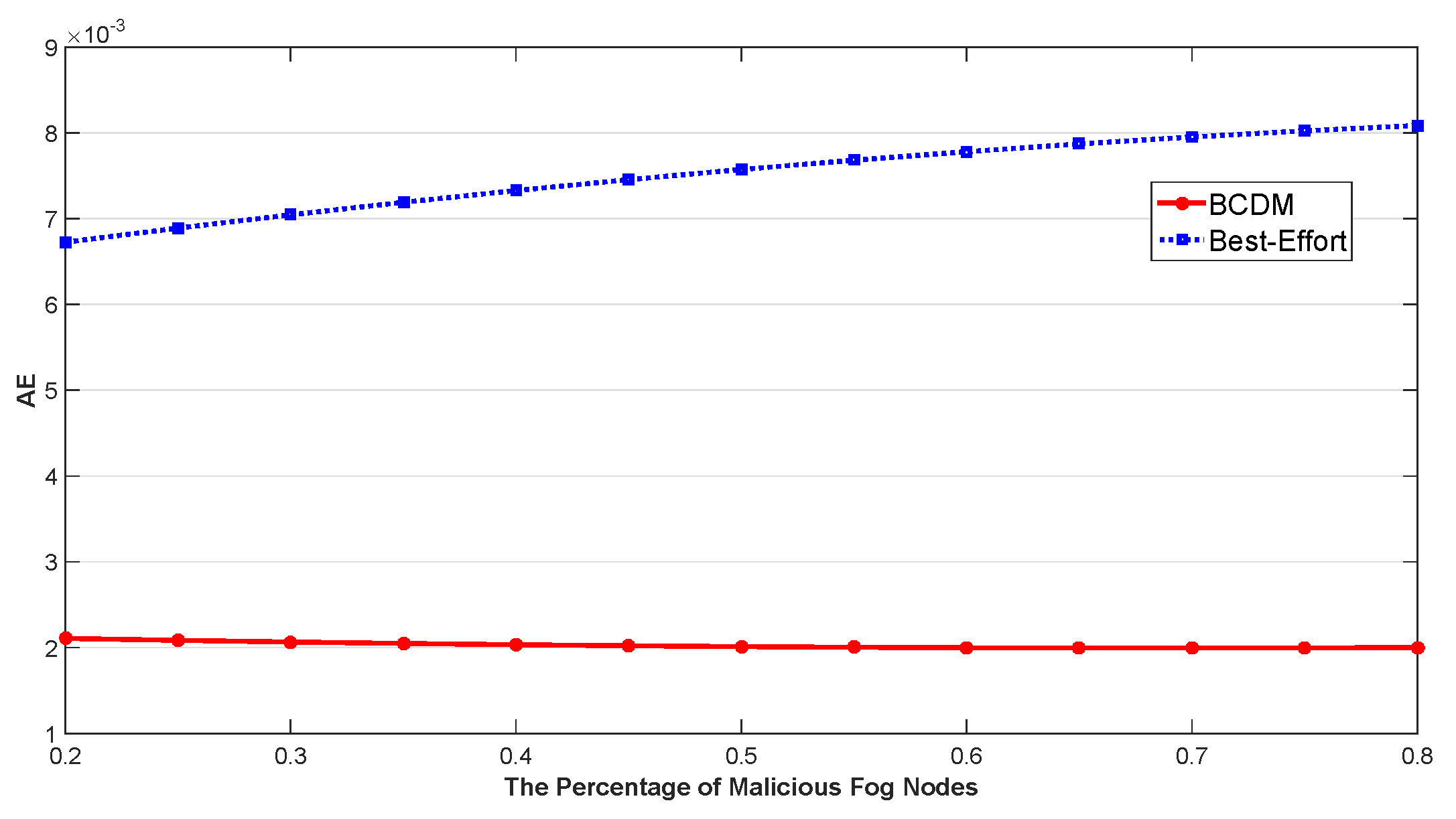
5.1. Anomaly Detection Based Latency Awareness
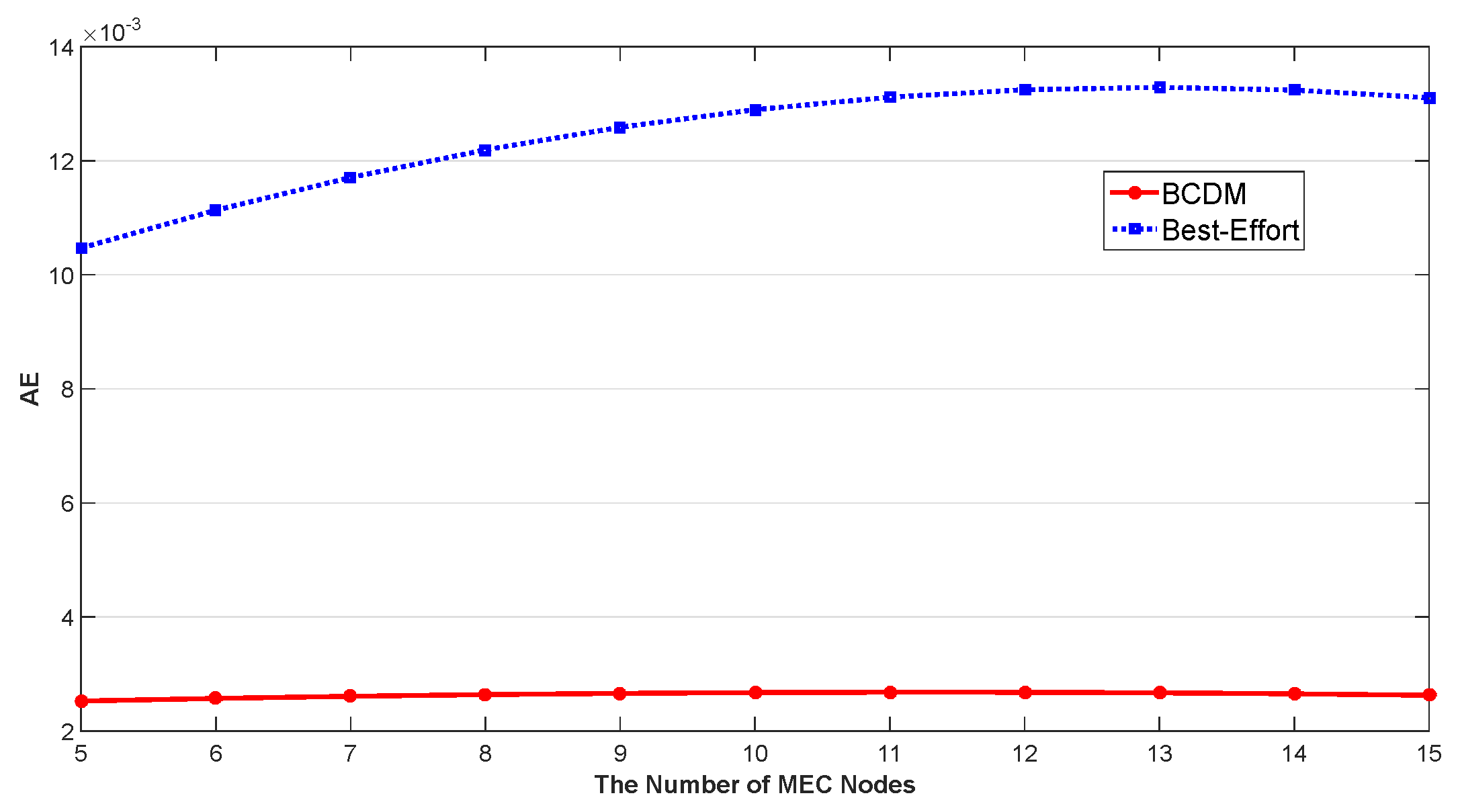
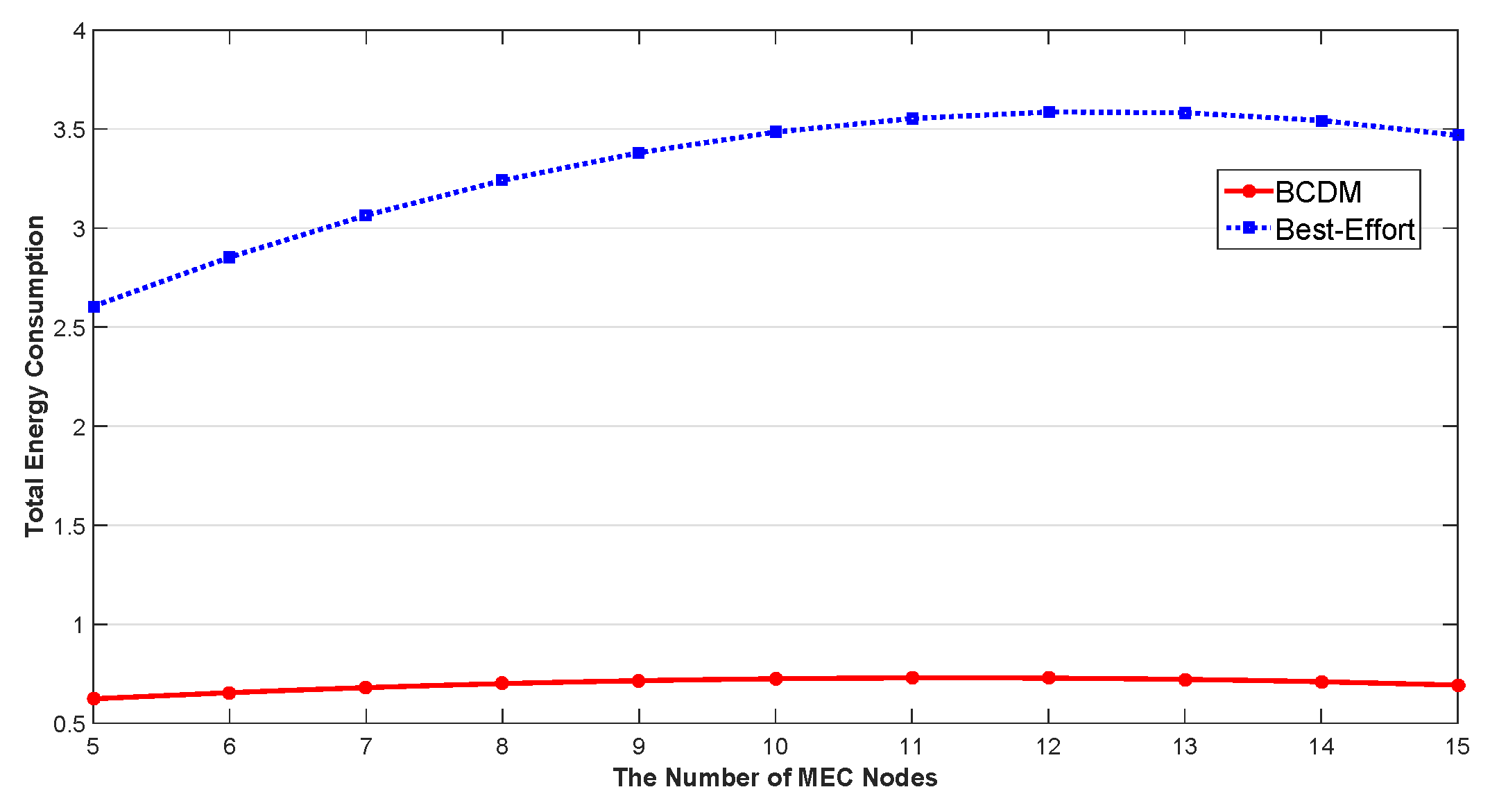
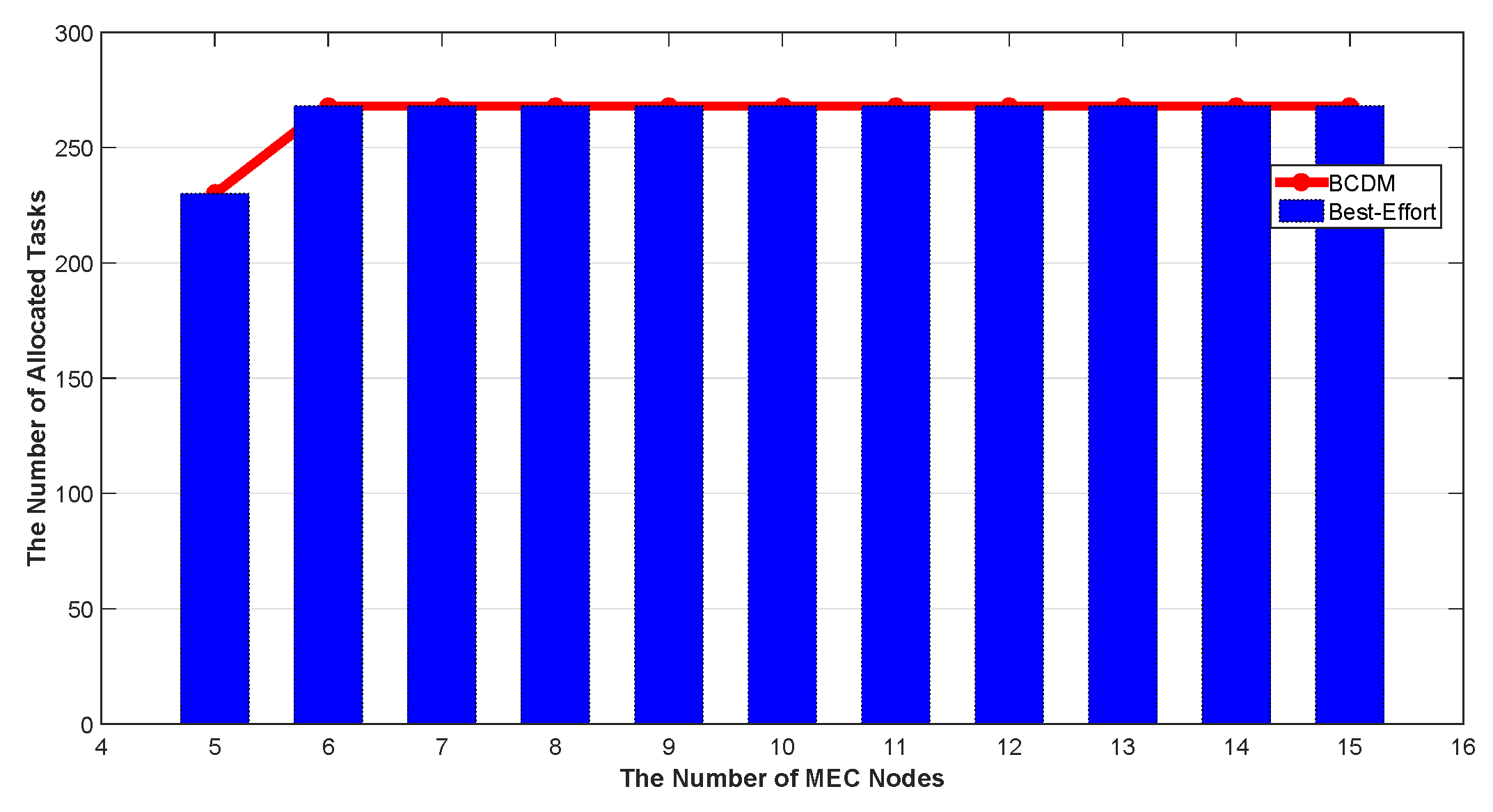
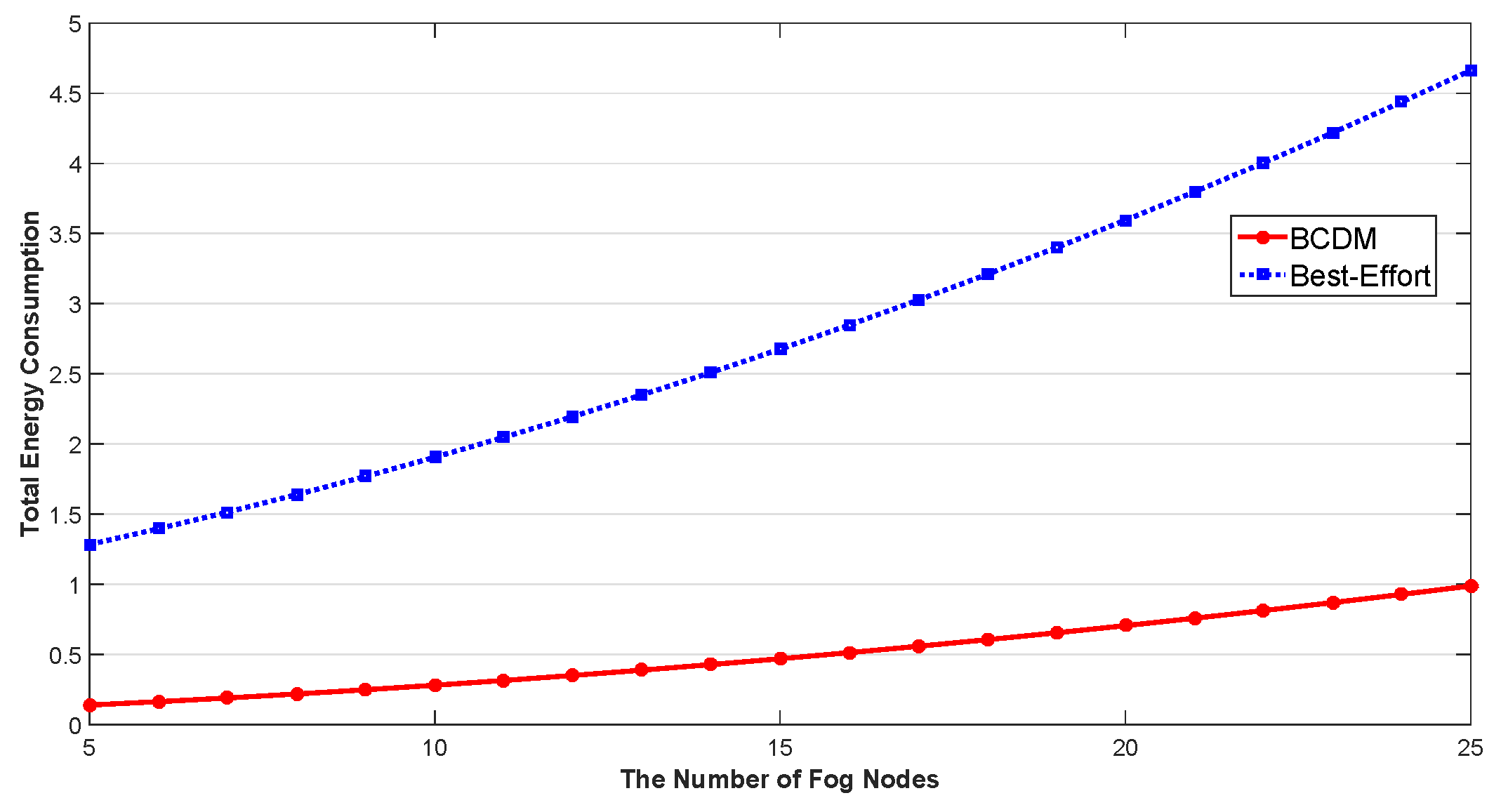
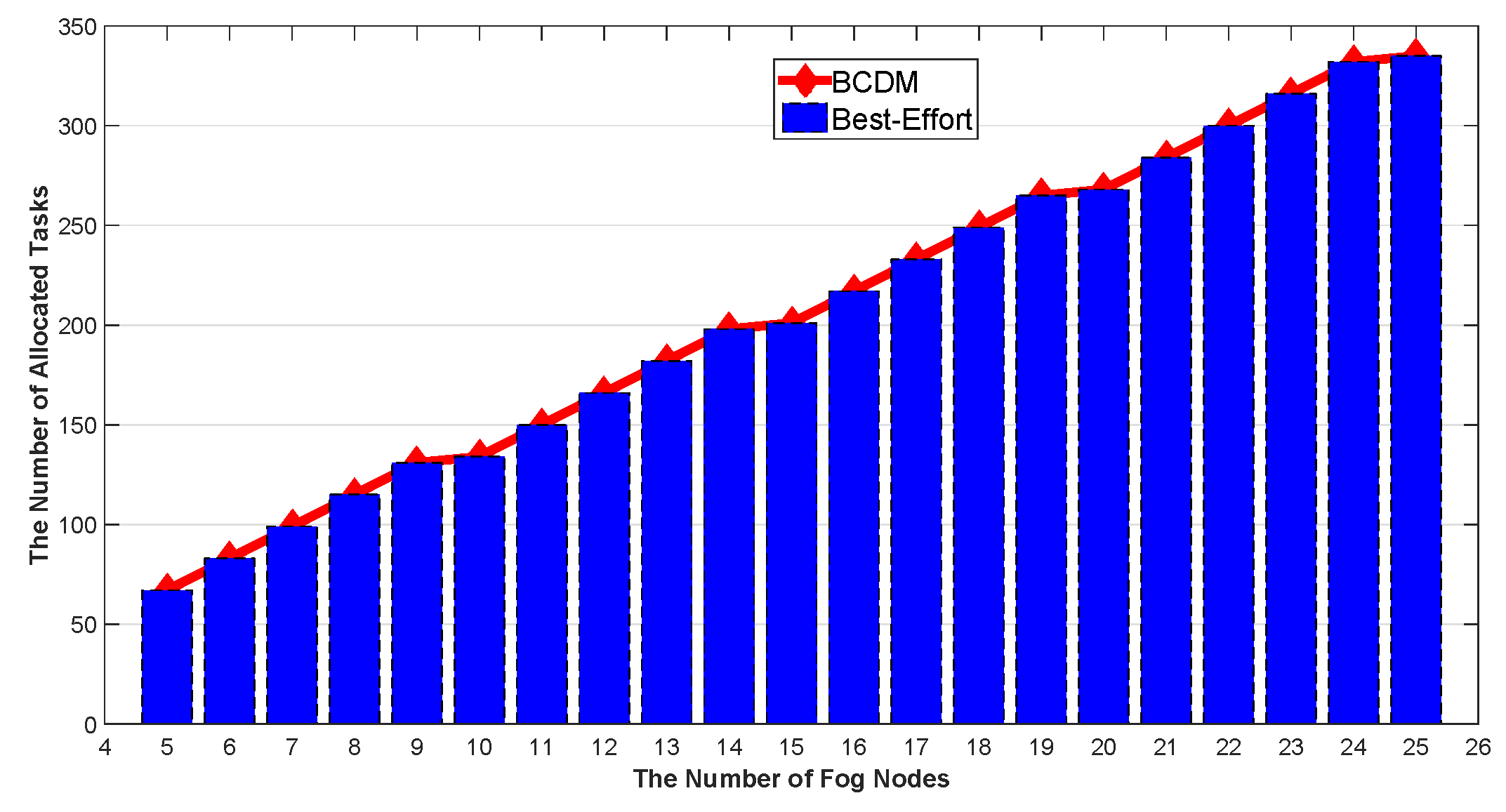
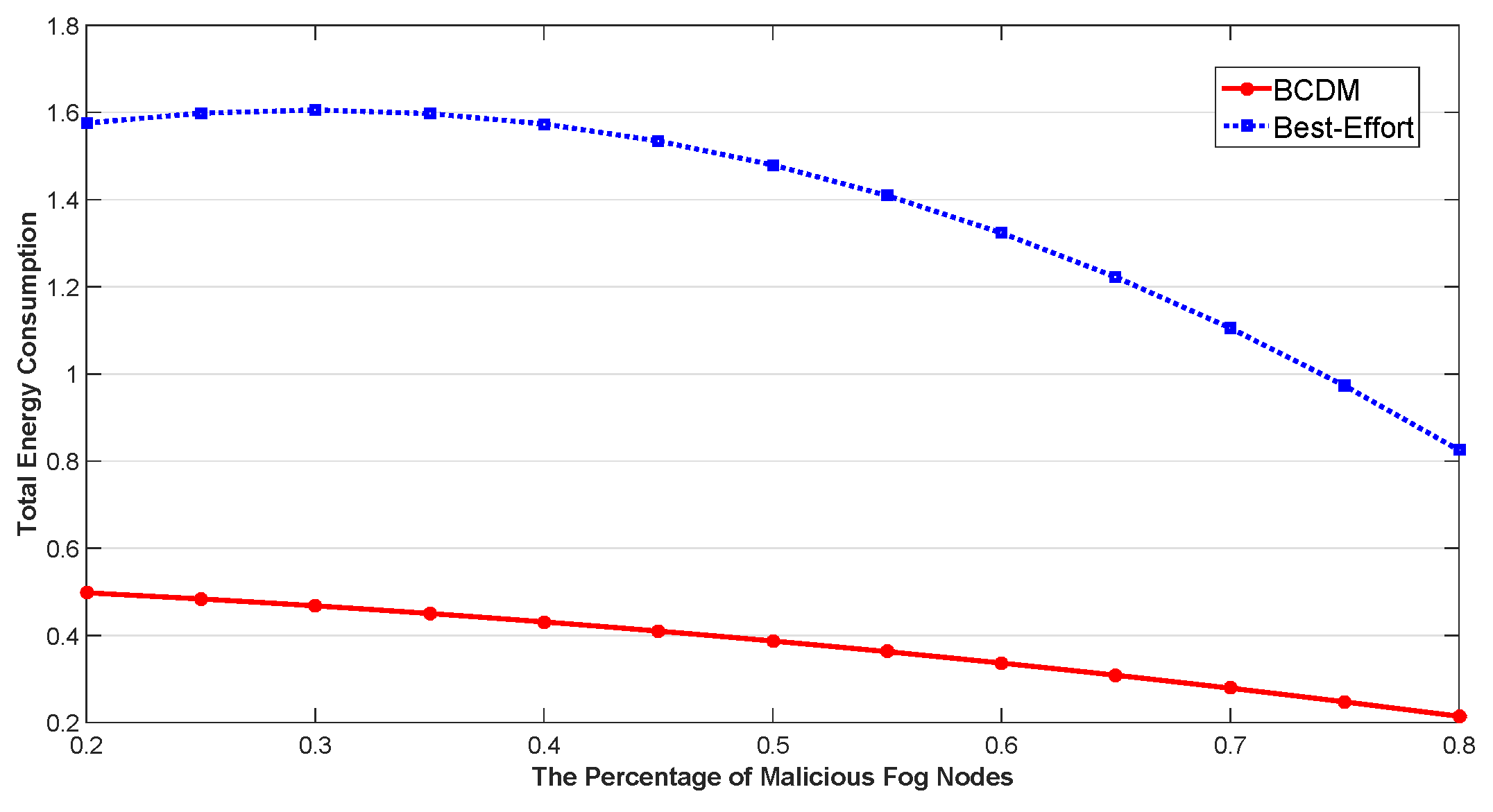
5.2. Energy Efficient Optimization for IoT Continuous Data-Flow Services
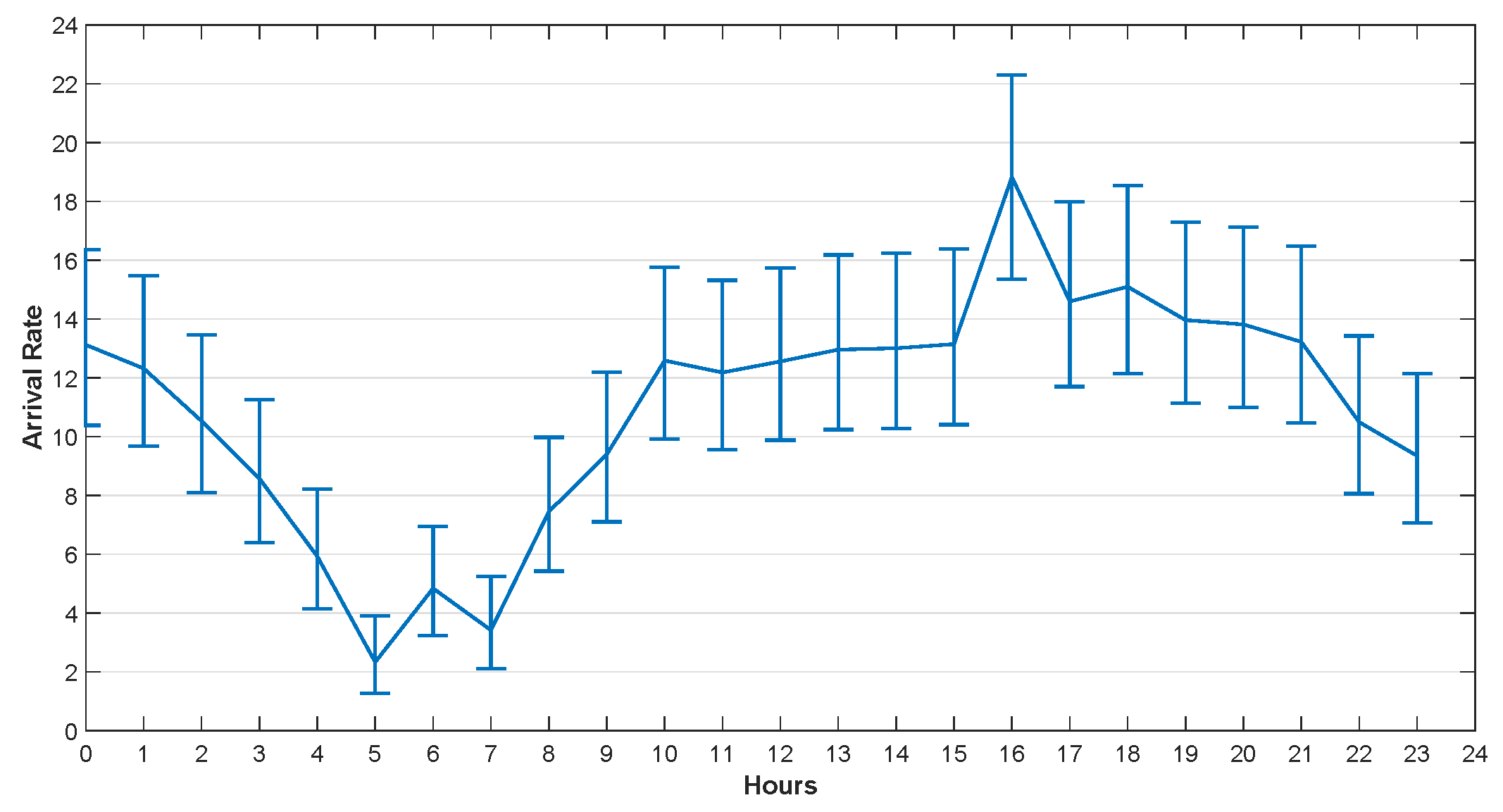
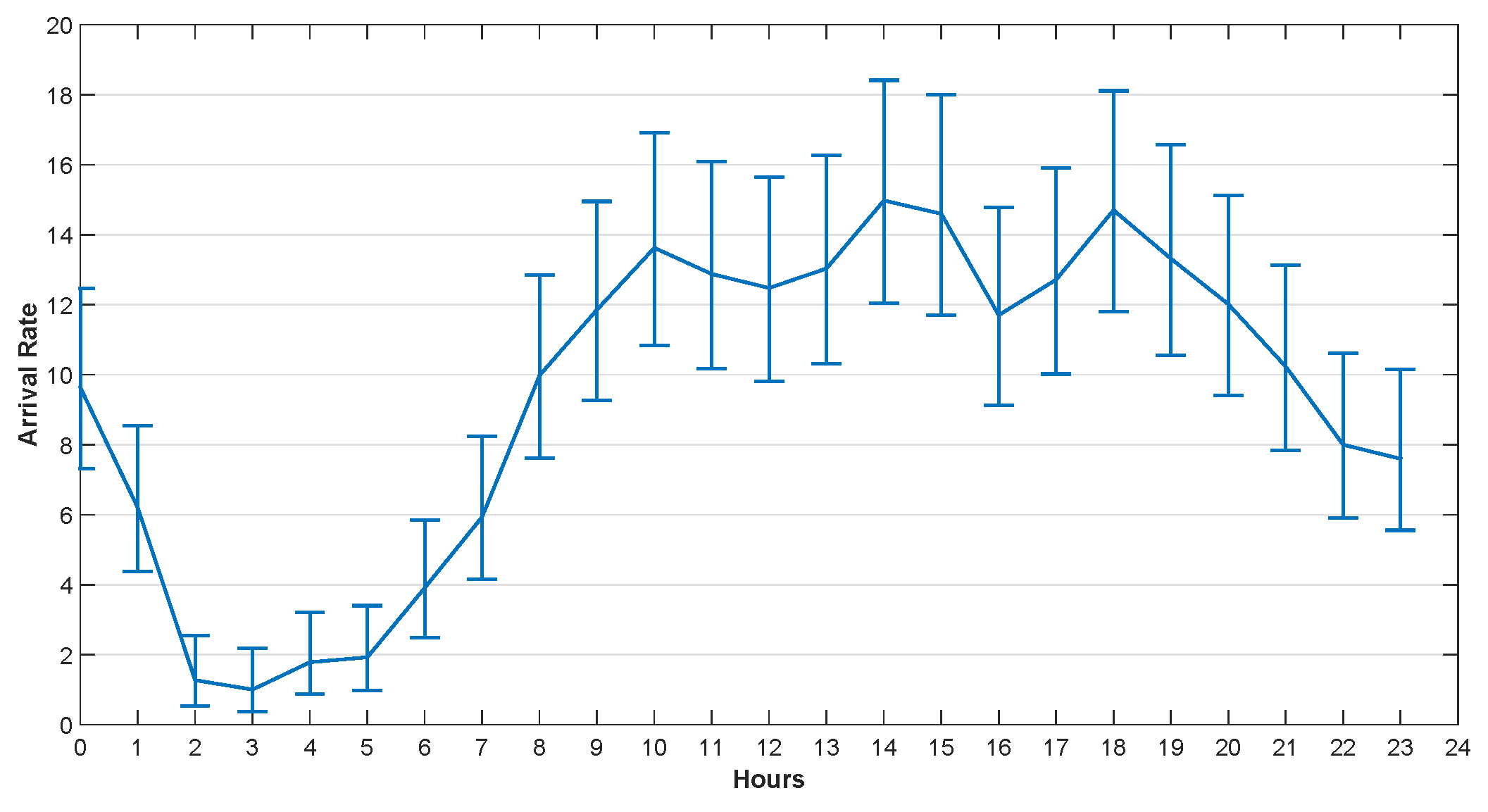
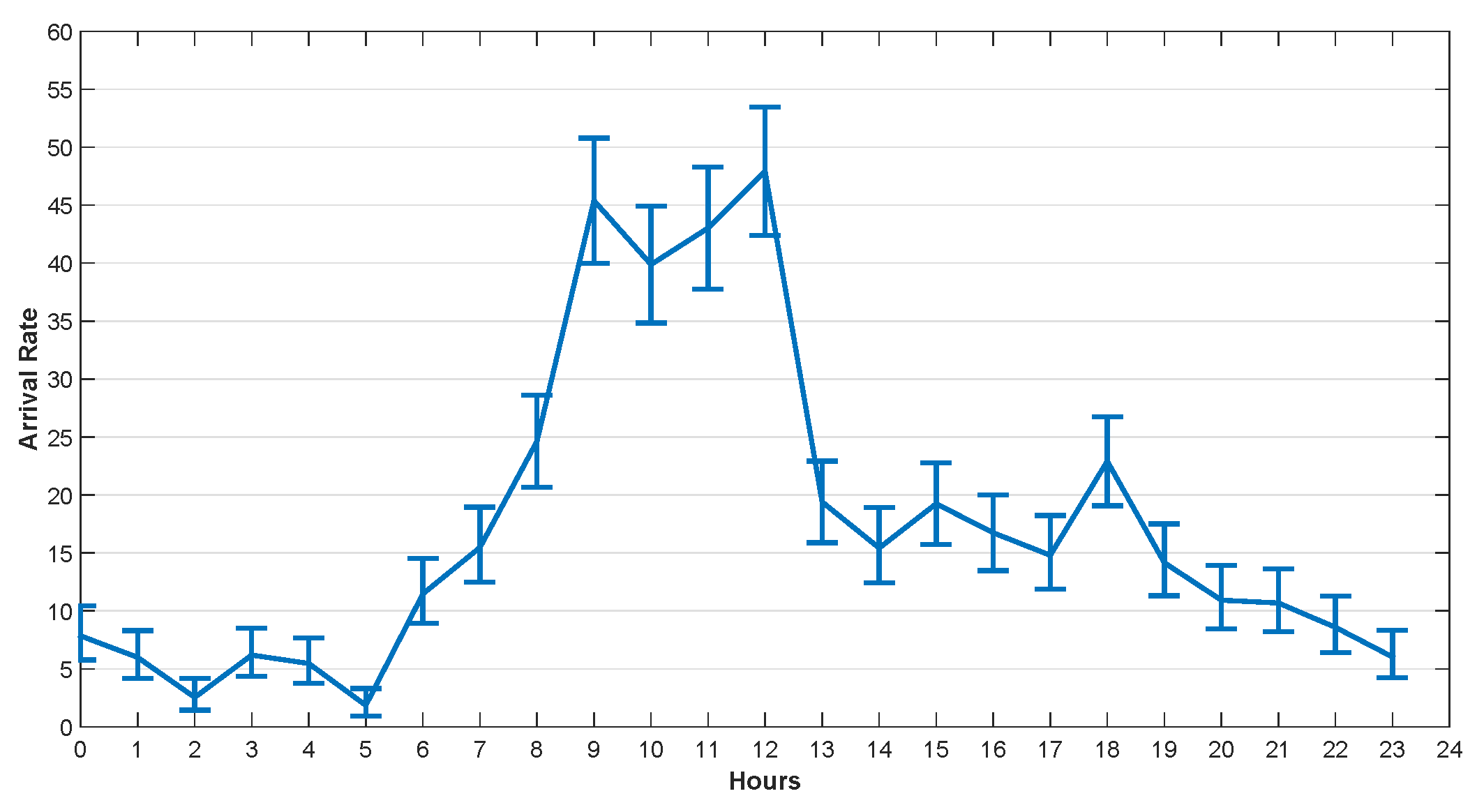
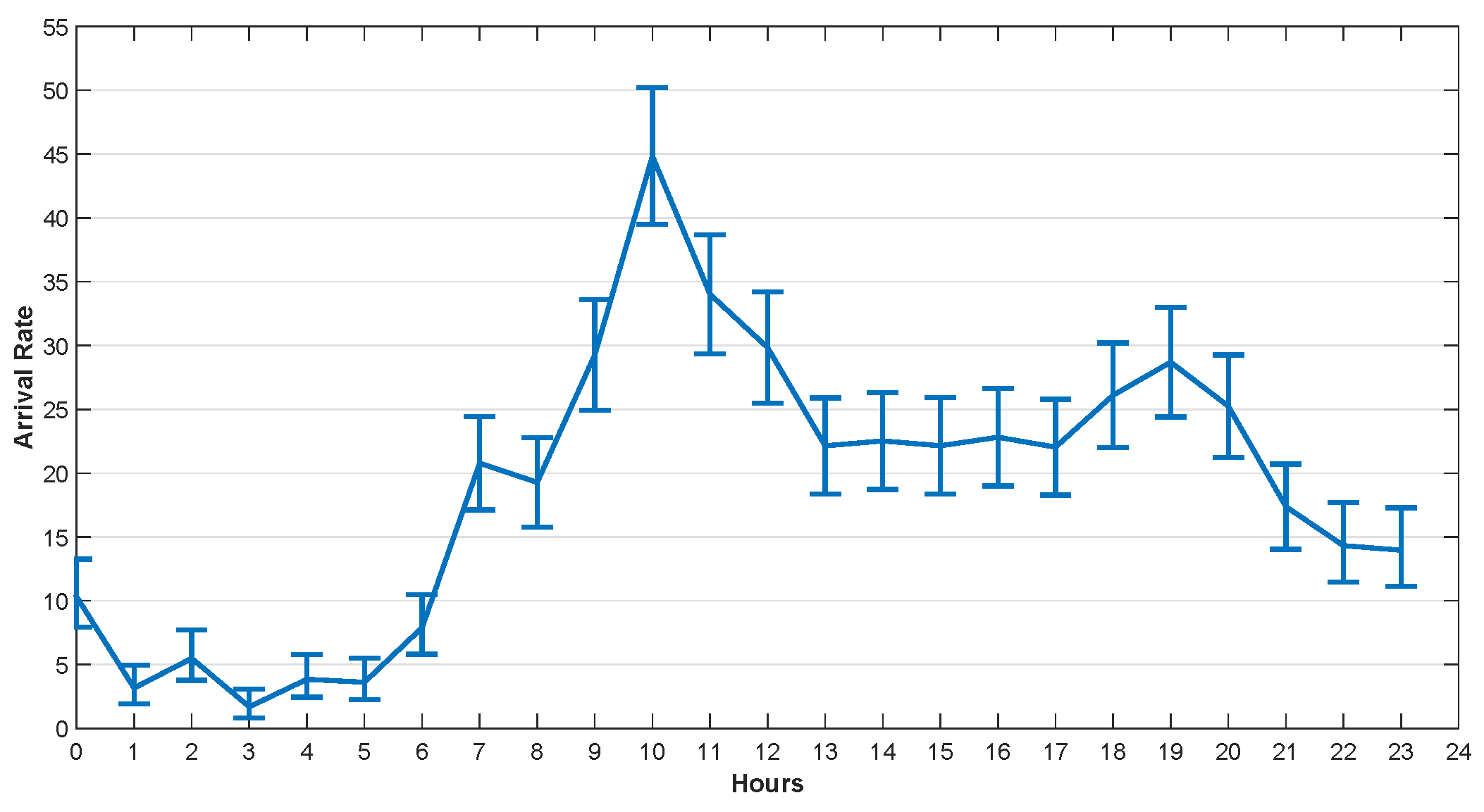
5.2.1. Task Arrival Rate Analysis
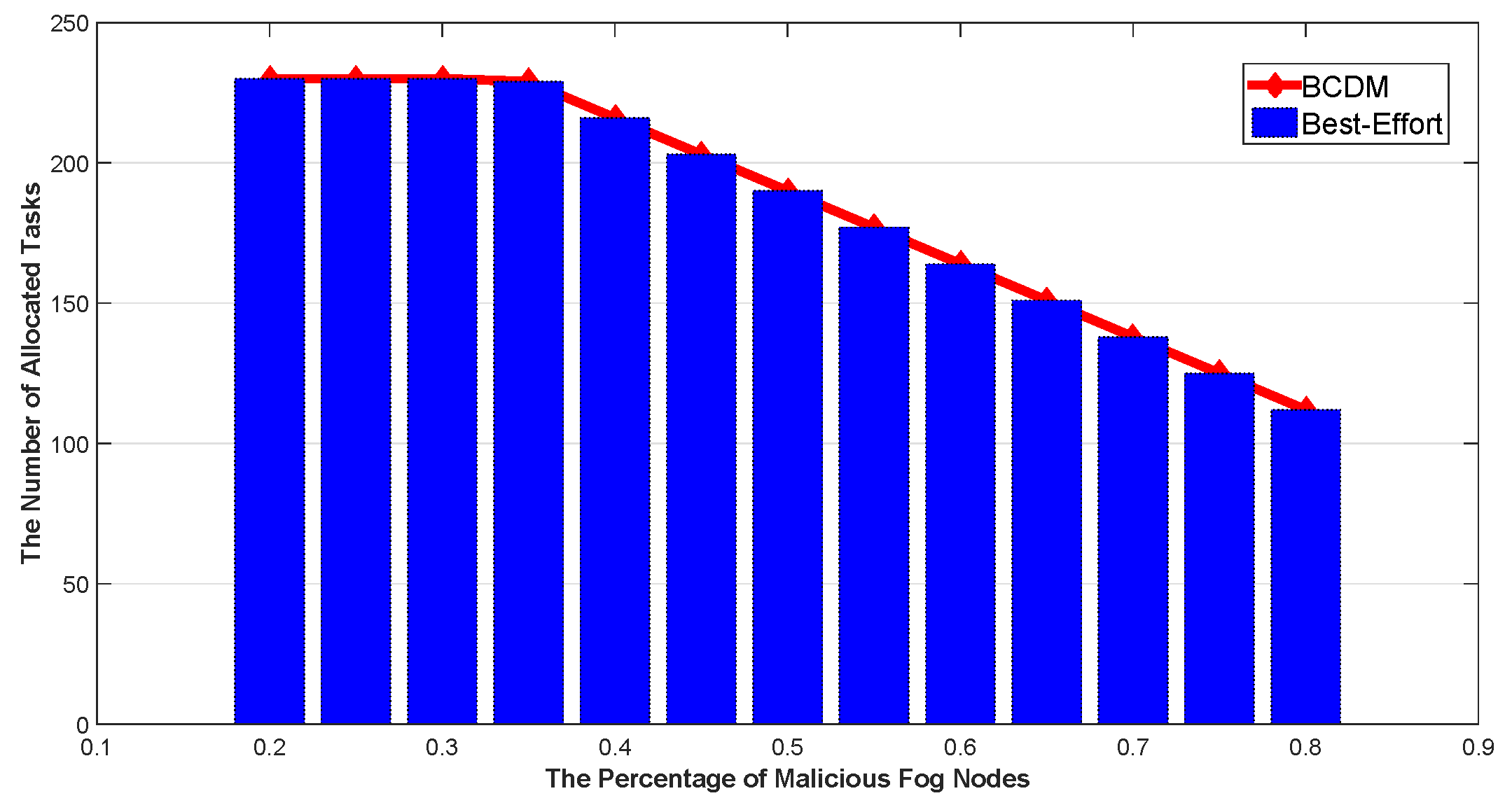
5.2.2. Verification of the Proposed Algorithm
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, W.; Chen, Z.; Gao, X.; Liu, W.; Wang, J. Multi-model framework for indoor localization under mobile edge computing environment. IEEE Internet Things J. 2018, 6, 4844–4853. [Google Scholar] [CrossRef]
- Lu, X.; Qian, X.; Li, X.; Miao, Q.; Peng, S. DMCM: A Data-adaptive Mutation Clustering Method to identify cancer-related mutation clusters. Bioinformatics 2018, 35, 389–397. [Google Scholar] [CrossRef] [PubMed]
- Aazam, M.; Zeadally, S.; Harras, K.A. Deploying fog computing in industrial internet of things and industry 4.0. IEEE Trans. Ind. Inform. 2018, 14, 4674–4682. [Google Scholar] [CrossRef]
- Pan, J.; Liu, Y.; Wang, J.; Hester, A. Key Enabling Technologies for Secure and Scalable Future Fog-IoT Architecture: A Survey. arXiv 2018, arXiv:1806.06188. [Google Scholar]
- Hu, Y.C.; Patel, M.; Sabella, D.; Sprecher, N.; Young, V. Mobile edge computing—A key technology towards 5G. ETSI White Pap. 2015, 11, 1–16. [Google Scholar]
- Morris, I. ETSI Drops “Mobile” from MEC; Light Reading: New York, NY, USA, 2016. [Google Scholar]
- Kaur, K.; Garg, S.; Aujla, G.S.; Kumar, N.; Rodrigues, J.J.; Guizani, M. Edge computing in the industrial internet of things environment: Software-defined-networks-based edge-cloud interplay. IEEE Commun. Mag. 2018, 56, 44–51. [Google Scholar] [CrossRef]
- Pinto, S.; Gomes, T.; Pereira, J.; Cabral, J.; Tavares, A. IIoTEED: An enhanced, trusted execution environment for industrial IoT edge devices. IEEE Internet Comput. 2017, 21, 40–47. [Google Scholar] [CrossRef]
- Mäkitalo, N.; Ometov, A.; Kannisto, J.; Andreev, S.; Koucheryavy, Y.; Mikkonen, T. Safe and secure execution at the network edge: A framework for coordinating cloud, fog, and edge. IEEE Softw. 2018, 35, 30–37. [Google Scholar] [CrossRef]
- Guo, M.; Li, L.; Guan, Q. Energy-Efficient and Delay-Guaranteed Workload Allocation in IoT-Edge-Cloud Computing Systems. IEEE Access 2019, 7, 78685–78697. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, K.; Xuan, D.; Yang, K. Optimal task allocation in near-far computing enhanced C-RAN for wireless big data processing. IEEE Wirel. Commun. 2018, 25, 50–55. [Google Scholar] [CrossRef]
- Chen, M.H.; Liang, B.; Dong, M. Joint offloading and resource allocation for computation and communication in mobile cloud with computing access point. In Proceedings of the IEEE INFOCOM 2017-IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Pereira, C.; Pinto, A.; Ferreira, D.; Aguiar, A. Experimental characterization of mobile iot application latency. IEEE Internet Things J. 2017, 4, 1082–1094. [Google Scholar] [CrossRef]
- Santos, G.L.; Endo, P.T.; da Silva Lisboa, M.F.F.; da Silva, L.G.F.; Sadok, D.; Kelner, J.; Lynn, T. Analyzing the availability and performance of an e-health system integrated with edge, fog and cloud infrastructures. J. Cloud Comput. 2018, 7, 16–37. [Google Scholar] [CrossRef]
- Farahani, B.; Firouzi, F.; Chang, V.; Badaroglu, M.; Constant, N.; Mankodiya, K. Towards fog-driven IoT eHealth: Promises and challenges of IoT in medicine and healthcare. Future Gener. Comput. Syst. 2018, 78, 659–676. [Google Scholar] [CrossRef]
- Rahmani, A.M.; Gia, T.N.; Negash, B.; Anzanpour, A.; Azimi, I.; Jiang, M.; Liljeberg, P. Exploiting smart e-Health gateways at the edge of healthcare Internet-of-Things: A fog computing approach. Future Gener. Comput. Syst. 2018, 78, 641–658. [Google Scholar] [CrossRef]
- Ibidunmoye, O.; Hernández-Rodriguez, F.; Elmroth, E. Performance anomaly detection and bottleneck identification. ACM Comput. Surv. (CSUR) 2015, 48, 4–40. [Google Scholar] [CrossRef]
- Khalil, I.; Bagchi, S. Stealthy attacks in wireless ad hoc networks: Detection and countermeasure. IEEE Trans. Mob. Comput. 2010, 10, 1096–1112. [Google Scholar] [CrossRef]
- Xie, K.; Li, X.; Wang, X.; Cao, J.; Xie, G.; Wen, J.; Zhang, D.; Qin, Z. On-line anomaly detection with high accuracy. IEEE/ACM Trans. Netw. 2018, 26, 1222–1235. [Google Scholar] [CrossRef]
- Xie, K.; Li, X.; Wang, X.; Xie, G.; Wen, J.; Zhang, D. Graph based tensor recovery for accurate Internet anomaly detection. In Proceedings of the IEEE INFOCOM 2018-IEEE Conference on Computer Communications, Honolulu, HI, USA, 16–19 April 2018; pp. 1502–1510. [Google Scholar]
- Xie, G.; Xie, K.; Huang, J.; Wang, X.; Chen, Y.; Wen, J. Fast low-rank matrix approximation with locality sensitive hashing for quick anomaly detection. In Proceedings of the IEEE INFOCOM 2017-IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- He, S.; Xie, K.; Xie, K.; Xu, C.; Wang, J. Interference-Aware Multisource Transmission in Multiradio and Multichannel Wireless Network. IEEE Syst. J. 2019, 13, 2507–2518. [Google Scholar] [CrossRef]
- Sohal, A.S.; Sandhu, R.; Sood, S.K.; Chang, V. A cybersecurity framework to identify malicious edge device in fog computing and cloud-of-things environments. Comput. Secur. 2018, 74, 340–354. [Google Scholar] [CrossRef]
- Li, W.; Song, H.; Zeng, F. Policy-Based Secure and Trustworthy Sensing for Internet of Things in Smart Cities. IEEE Internet Things J. 2018, 5, 716–723. [Google Scholar] [CrossRef]
- Brogi, A.; Forti, S.; Guerrero, C.; Lera, I. How to Place Your Apps in the Fog-State of the Art and Open Challenges. arXiv 2019, arXiv:1901.05717. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Common throughput maximization in UAV-enabled OFDMA systems with delay consideration. IEEE Trans. Commun. 2018, 66, 6614–6627. [Google Scholar] [CrossRef]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint trajectory and communication design for multi-UAV enabled wireless networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Sun, X.; Ansari, N. Edgeiot Mobile edge computing for the internet of things. IEEE Commun. Mag. 2016, 54, 22–29. [Google Scholar] [CrossRef]
- He, Q.Q.; Yang, W.C.; Hu, Y.X. Accurate method to estimate EM radiation from a GSM base station. Prog. Electromagn. Res. 2014, 34, 19–27. [Google Scholar] [CrossRef][Green Version]
- Das, K.; Schneider, J.; Neill, D.B. Anomaly pattern detection in categorical datasets. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 169–176. [Google Scholar]
- Dutta, S.; Nayek, P.; Bhattacharya, A. Neighbor-aware search for approximate labeled graph matching using the chi-square statistics. In Proceedings of the 26th International Conference on World Wide Web. International World Wide Web Conferences Steering Committee, Perth, Australia, 3–7 April 2017; pp. 1281–1290. [Google Scholar]
- Wang, Y.T.; Bagrodia, R. ComSen: A detection system for identifying compromised nodes in wireless sensor networks. In Proceedings of the Sixth International Conference on Emerging Security Information, Systems and Technologies, Rome, Italy, 19–24 August 2012; pp. 148–156. [Google Scholar]
- Kumar, S.; Dutta, K. Intrusion detection in mobile ad hoc networks: Techniques, systems, and future challenges. Secur. Commun. Netw. 2016, 9, 2484–2556. [Google Scholar] [CrossRef]
- Kathiroli, R.; Arivudainambi, D. Election of Guard Nodes to Detect Stealthy Attack in MANET. In Wireless Communications, Networking and Applications; Springer: New Delhi, India, 2016; pp. 127–140. [Google Scholar]
- Floudas, C.A. Nonlinear and Mixed-Integer Programming-Fundamentals and Applications; Oxford University Press: Oxford, UK, 1995; Volume 4, pp. 249–281. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Grippo, L.; Sciandrone, M. On the convergence of the block nonlinear Gauss–Seidel method under convex constraints. Oper. Res. Lett. 2000, 26, 127–136. [Google Scholar] [CrossRef]
- Li, W.; Song, H. ART: An attack-resistant trust management scheme for securing vehicular ad hoc networks. IEEE Trans. Intell. Transp. Syst. 2015, 17, 960–969. [Google Scholar] [CrossRef]
- Barlacchi, G.; De Nadai, M.; Larcher, R.; Casella, A.; Chitic, C.; Torrisi, G.; Antonelli, F.; Vespignani, A.; Pentland, A.; Lepri, B. A multi-source dataset of urban life in the city of Milan and the Province of Trentino. Sci. Data 2015, 2, 150055. [Google Scholar] [CrossRef]
- Zeng, F.; Yao, L.; Wu, B.; Li, W.; Meng, L. Dynamic human contact prediction based on naive Bayes algorithm in mobile social networks. Softw. Pract. Exp. 2019. [Google Scholar] [CrossRef]
- Li, W.; Xu, H.; Li, H.; Yang, Y.; Sharma, P.K.; Wang, J.; Singh, S. Complexity and Algorithms for Superposed Data Uploading Problem in Networks with Smart Devices. IEEE Internet Things J. 2019. [Google Scholar] [CrossRef]
- Zeng, F.; Ren, Y.; Deng, X.; Li, W. Cost-effective edge server placement in wireless metropolitan area networks. Sensors 2019, 19, 32. [Google Scholar] [CrossRef] [PubMed]
- Perez, D.A.; Velasquez, K.; Curado, M.; Monteiro, E. A Comparative Analysis of Simulators for the Cloud to Fog Continuum. Simul. Model. Pract. Theory 2019, 102029. [Google Scholar] [CrossRef]
- Lera, I.; Guerrero, C.; Juiz, C. YAFS: A Simulator for IoT Scenarios in Fog Computing. IEEE Access 2019, 7, 91745–91758. [Google Scholar] [CrossRef]
| Symbol | Description |
|---|---|
| U | Utility function |
| I | the amount of IoT-End nodes |
| M | the amount of MEC nodes |
| J | the amount of Fog nodes |
| arrival rate of tasks | |
| latency constraint | |
| service rate of fog and MEC nodes | |
| B | bandwidth of wireless channel |
| H | channel gains |
| Gaussian white noise |
| Parameter Name | Parameter Value (Unit) |
|---|---|
| Latency between GW and NSCL | |
| Latency between NSCL and DP | |
| Latency between DP and EHR |
| Parameter Name | Parameter Value (Unit) |
|---|---|
| The Distance from IoT-End Nodes to Access Points | 100–500 m |
| The Default Number of IoT-End Nodes | 60 |
| The Default Number of Fog Nodes | 20 |
| The Default Number of MEC Nodes | 10 |
| Bandwidth of Wireless Channel | Hz |
| Default Processing Capacity of MEC Nodes | 50/sec |
| Default Processing Capacity of Fog Nodes | 20/sec |
| The Data Size of a Task d | Bit |
| Latency Constraint | s |
| Default Task Arrival Rate of Each IoT-Fog Node | 10/sec |
| The Reliability of Normal Fog Nodes | |
| The Reliability of Normal MEC Nodes | |
| Default Percentage of Malicious Fog Nodes | |
| Default Percentage of Malicious MEC Nodes | |
| Default Reliability of Malicious Fog Nodes | |
| Default Reliability of Malicious MEC Nodes | |
| Background Noise | (dBm) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Li, W.; Qiu, S. Anomaly Detection Based Latency-Aware Energy Consumption Optimization For IoT Data-Flow Services. Sensors 2020, 20, 122. https://doi.org/10.3390/s20010122
Luo Y, Li W, Qiu S. Anomaly Detection Based Latency-Aware Energy Consumption Optimization For IoT Data-Flow Services. Sensors. 2020; 20(1):122. https://doi.org/10.3390/s20010122
Chicago/Turabian StyleLuo, Yuansheng, Wenjia Li, and Shi Qiu. 2020. "Anomaly Detection Based Latency-Aware Energy Consumption Optimization For IoT Data-Flow Services" Sensors 20, no. 1: 122. https://doi.org/10.3390/s20010122
APA StyleLuo, Y., Li, W., & Qiu, S. (2020). Anomaly Detection Based Latency-Aware Energy Consumption Optimization For IoT Data-Flow Services. Sensors, 20(1), 122. https://doi.org/10.3390/s20010122






