1. Introduction
Recently, distributed state estimation has been a hot topic in the field of target tracking in sensor networks [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19]. As a traditional method, the centralized scheme needs to simultaneously process the local measurements from all sensors in the fusion center at each time instant [
3,
15]. This scheme guarantees the optimality of estimates, but a lot of communication and a powerful fusion center are required to maintain the operation, which may give rise to problems when the network size is increased or the communication resources are restricted.
Unlike the centralized scheme, the distributed mechanism tries to recover the centralized performance via local communications between neighboring nodes. Specifically, each node in the network only exchanges information with its immediate neighbors to achieve a comparable performance to its centralized counterpart, which reduces communication cost and makes the network robust against possible failures of some nodes [
8]. The consensus filter, which computes the average of interested values in a distributed manner, has attracted immense popularity for distributed state estimation [
4,
5,
6,
7,
9,
10,
11,
12,
13,
14,
16,
17,
18,
19,
20,
21,
22]. Recently, in [
23,
24], the multiscale consensus scheme, in which the local estimated states achieve asymptotically prescribed ratios in terms of multiple scales, has been discussed and analyzed. The well-known Kalman consensus filter (KCF) [
4,
5,
6,
9,
14] combines the local Kalman filter with the average consensus protocol together to update the posterior state. In the update stage, each node exploits the measurement innovations as well as the prior estimates from its inclusive neighbors (including the node itself and its immediate neighbors) to correct its prior estimate. However, the prior estimates from its immediate neighbors are assigned with same weights. This may ensure consensus on the estimates from different nodes after a period of time, but the estimation accuracy is not guaranteed. It is very likely that a target is neither observed by a certain node nor observed by any of its immediate neighbors. That is, there is no measurement in the inclusive neighborhood of the node, and it is naive about the target’s state. Similar to [
16,
22], such a node is referred as a naive node. Since a naive node contains less information about the target, it usually results in an inaccurate estimate. If a naive node is given an identical weight to the informed nodes, the final estimate will be severely contaminated, which may even cause the final estimates to diverge [
9,
13]. In addition, the cross covariances among different nodes are ignored in the derivation of KCF for computational and bandwidth requirements, and thus the covariance of each node is updated without regard to its neighbor’s prior covariance during the consensus step. Given no naive nodes in the network, KCF is able to provide satisfactory results. However, due to limited sensing abilities or constrained communication resources, a network often consists of some naive nodes. Especially in sparse sensor networks, this phenomenon is even more serious. In such a case, KCF would result in poor estimates [
3]. To solve this problem, before updating the posterior estimate, the generalized Kalman consensus filter (GKCF) performs consensus on the prior information vectors and information matrices within the inclusive neighborhood of each node [
4,
16,
19]. As is analyzed in [
4], this procedure greatly improves the estimation performance in presence of naive nodes. GKCF updates current state based on consensus on prior estimates, but the current measurements are not considered for naive nodes. Each naive node only has access to measurements of the previous time instant existing in prior estimates. Therefore, there is a delay for naive nodes to access current measurements. On the contrary, consensus on measurements algorithm (CM) performs consensus on measurements [
5,
25,
26,
27], which can achieve the centralized performance with infinite consensus iterations. However, the stability is not guaranteed unless the number of consensus iterations is large enough [
26]. Consensus on information algorithm (CI) performs consensus on both prior estimates and measurements [
26,
27,
28], which can be viewed as a generalization of the covariance intersection fusion rule to multiple iterations [
29]. CI guarantees stability for any number of consensus iterations, but its estimation confidence can be degraded as a conservative rule is adopted by assuming that the correlation between estimates from different nodes are completely unknown [
26,
28,
30].
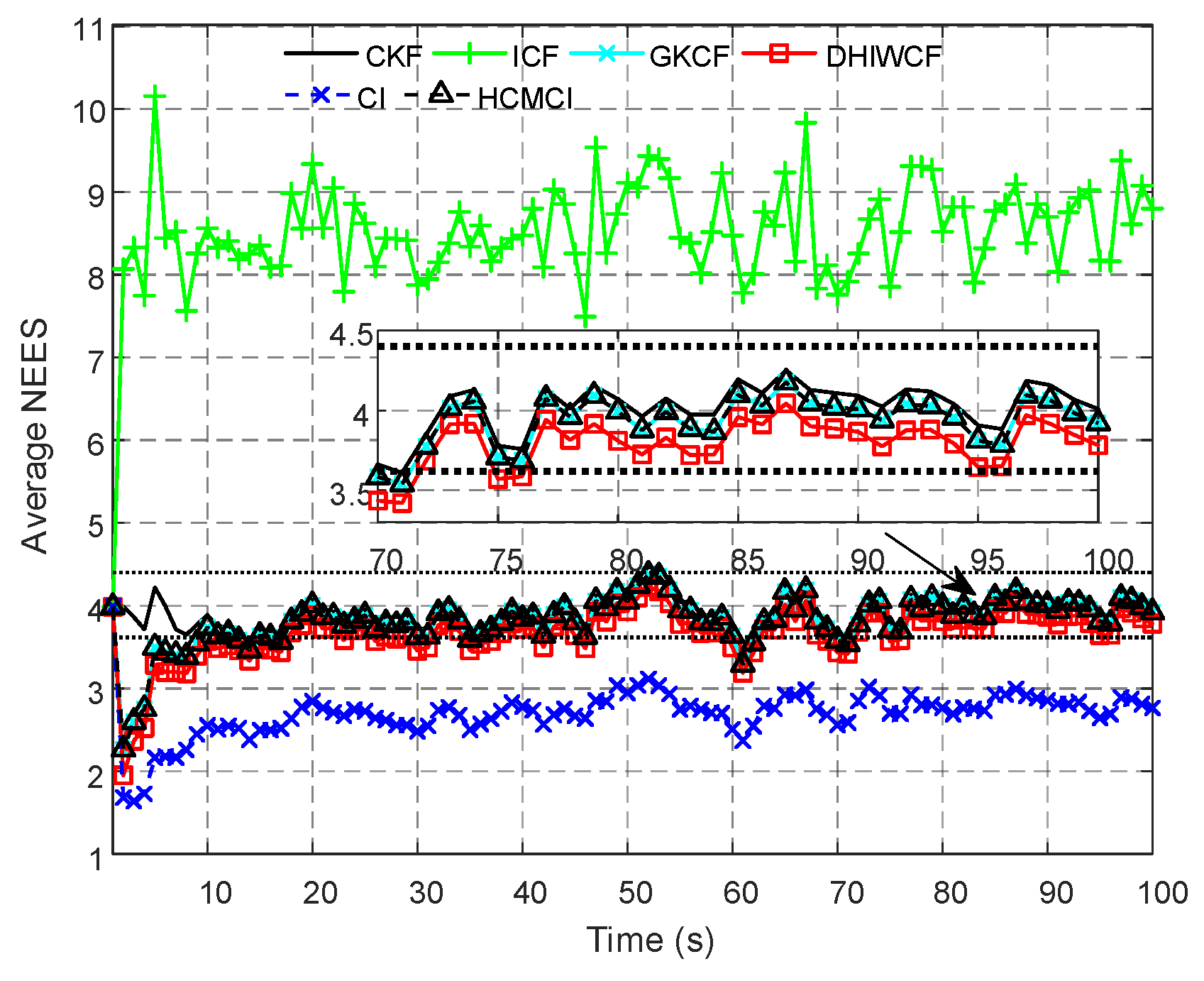
With more consensus iterations carried out, estimates from different nodes achieve a reasonable consensus. Therefore, each node has almost completely redundant or same prior information, and hence the prior estimation errors between nodes are highly correlated. In this situation, the algorithms such as KCF, GCKF, or CM, which do not take the cross-covariance into account, are sub-optimal [
16,
17]. Note that the redundant information only exists in the prior estimates, which come from the converged results in the previous time instant. Using this property, the information weighted consensus filter (ICF) [
18,
20,
21] divides the prior information of each node by
where
is the total number of nodes in the network. If each node can interact with its neighbors for infinite times, ICF will achieve the optimal estimation performance as the centralized Kalman consensus filter (CKF). In addition, ICF performs better than KCF, GKCF, CI, and CM under the same consensus iterations, which has been validated in [
16,
22,
26]. As is pointed out in [
26,
30,
31], the correction step by multiplying
may cause an overestimation of the measurement innovation for some nodes, which is often the case in sparse sensor networks. As a consequence, the estimates of some nodes may be too optimistic such that the estimation consistency will be lost, which should be avoided in recursive estimation. To address this problem, HCMCI algorithm combines the positive features of both CM and CI is proposed. It should be noted that HCMCI represents a family of different distributed algorithms dependent on the selection of scalar weights. Both CI and ICF are special cases of HCMCI. To preserve consistency of local filters as well as improve the estimation performance, the so-called normalization factor is introduced. If the network topology is fixed, the normalization factor can be computed offline to save bandwidth. In [
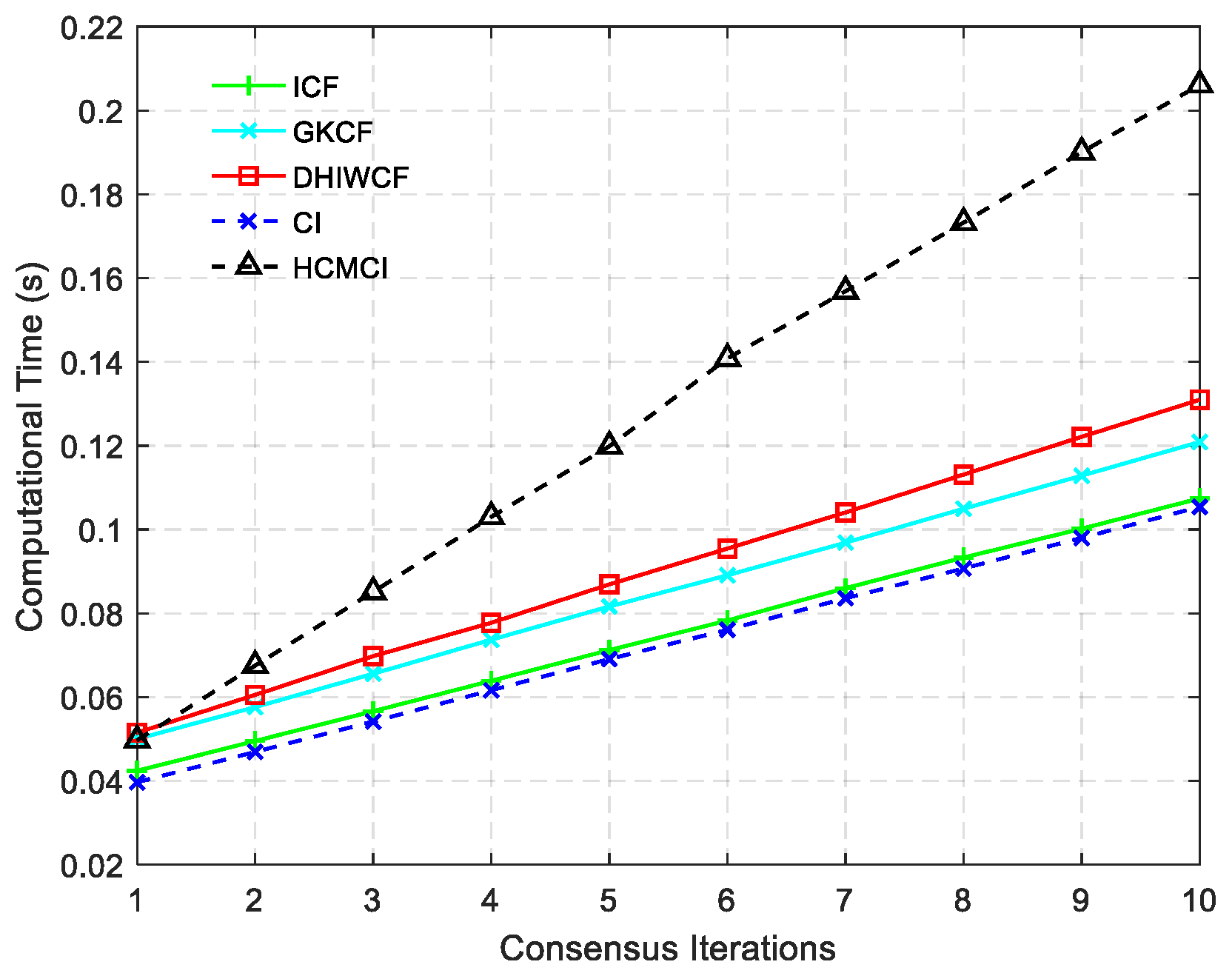
32], a novel distributed set-theoretic information flooding (DSIF) protocol is proposed. The DSIF protocol benefits from avoiding the reuse of information and offering the highest converging efficiency for network consensus, but it suffers from growing requirements of node-storage, more communication iterations, and higher communication load.
However, it takes sufficient consensus iterations for the algorithms discussed above to achieve an expected estimation performance. In practical applications, only a limited number of consensus iterations is allowed, and thus the performance of the afore-mentioned algorithms is corrupted. In addition, the estimation performance of the afore-mentioned algorithms depends closely on the selection of consensus weights. Inappropriate consensus weights may cause the algorithms to diverge or require more iterations to achieve consensus on the local estimates [
9]. It is a common way to set the weights as a constant value as discussed in [
6], which is an intuitive choice to maintain the stability of the error dynamics. However, the constant value needs the knowledge of maximum degree across the entire sensor network. Even the maximum degree is available, it remains a problem how to determine a proper constant weight to achieve the best performance while preserving the property of consistency. In addition, the initial consensus terms determined in ICF require the knowledge of the total number of nodes in the network. The global parameters, such as the maximum degree or the total number of nodes, may vary over time when the communication topology is changed, some new nodes are joined, or some existing nodes fail to communicate with others. Without the accurate knowledge of these global parameters, each node would either overestimate or underestimate the state of interest.
To deal with the problems analyzed above, a novel distributed hybrid information weighted consensus filter (DHIWCF) is proposed in this paper. Firstly, different from the previous work [
4,
5,
6,
16,
18,
22], each node assigns consensus weights to its neighbors based on their local degrees, which is fully distributed with no requirement for any knowledge of the global parameters. Secondly, the prior estimate information and measurement information at current time instant within the inclusive neighborhood are, respectively, combined together to form the local generalized prior estimate equation and the local generalized measurement equation. Then, a distributed local MAP estimator is derived with some reasonable approximations of the error covariance matrices, which achieves higher accuracy than the approaches introduce in [
4,
5,
6,
11,
16,
18,
19,
25,
26,
27,
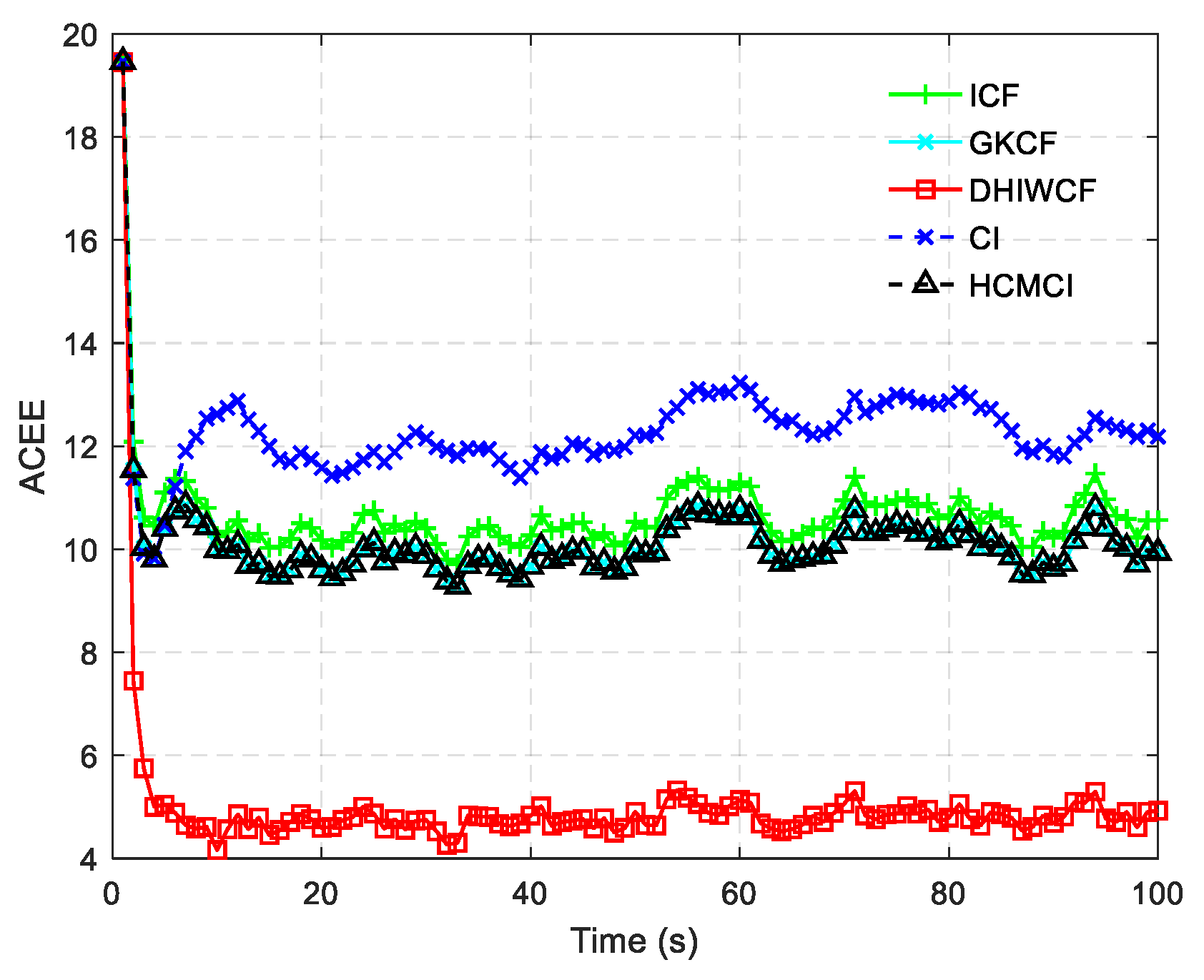
28]. Finally, the average consensus protocol with the aforementioned consensus weights is incorporated into the estimation framework, and the proposed DHIWCF is obtained. In addition, the theoretical analysis on consistency of the local estimates, stability and convergence of the estimator is performed. The comparative experiments on three different target tracking scenarios validate the effectiveness and feasibility of the proposed DHIWCF. Even with a single consensus iteration, the DHIWCF is still able to achieve acceptable estimation performance.
The remainder of this paper is organized as follows.
Section 2 formulates the problem of distributed state estimation in sensor networks. The distributed local MAP estimator is derived in
Section 3.
Section 4 presents distributed hybrid information weighted consensus filter. The theoretical analysis on the consistency of estimates, stability and convergence of the estimator is provided in
Section 5. The experimental results and analysis are considered in
Section 6. The concluded remarks are given in
Section 7.
Notation: denotes the n-dimensional Euclidean space. is the Euclidean norm in . For arbitrary matrix , and are respectively its inverse and transpose. means is positive definite, and is the shorthand for the trace of . denotes a block diagonal matrix with its main diagonal block being . represents the identity matrix. For a set , means the cardinality of . is the expectation operator.
3. Distributed Local MAP Estimation
This section starts with the centralized MAP estimator. Then we formulate the local generalized prior estimate equation based on prior estimates from the inclusive neighbors and the local generalized measurement equation based on the current measurements from the inclusive neighbors. By maximizing the local posterior probability, the local MAP estimator is derived. To implement the estimation steps in a distributed manner, approximation of the error cross covariance is required. Two special cases, where the prior errors from neighboring nodes are uncorrelated or completely identical, are considered here. The practical importance of such an approximation can be seen from the numerical examples in
Section 6, which indicate that the proposed DHIWCF is effective even if the assumed cases are not fulfilled.
3.1. Global MAP Estimator
Assume
represents the collective measurements of the entire sensor network at time instant
. The stacked measurement matrix of all the nodes is denoted as
. The stacked measurement noise is
with block diagonal covariance matrix
. Then the global measurement model can be formulated as
Suppose the centralized prior estimate is
. The corresponding prior estimation error is
with covariance matrix
. Let
be the maximum a posterior (MAP) estimate, we have
where
is a normalization constant. Since the process noise and measurement noise are both Gaussian, then the conditional PDF
and
are also Gaussian. The explicit form of the prior PDF
and the likelihood PDF
is formed as
where
is a normalization constant. Since the process noise and measurement noise are both Gaussian, then the conditional PDF
and
are also Gaussian. The explicit form of the prior PDF
and the likelihood PDF
is formed as
where
. Based on Gaussian product in the numerator, the criterion in (7) can be reformulated by minimizing the following cost function.
Here, the cost function in (11) is strictly convex on
and hence the optimal
is available.
The corresponding posterior error covariance is
The equivalent information form of the estimate in (12) and (13) can be rewritten as
3.2. Local MAP Estimation
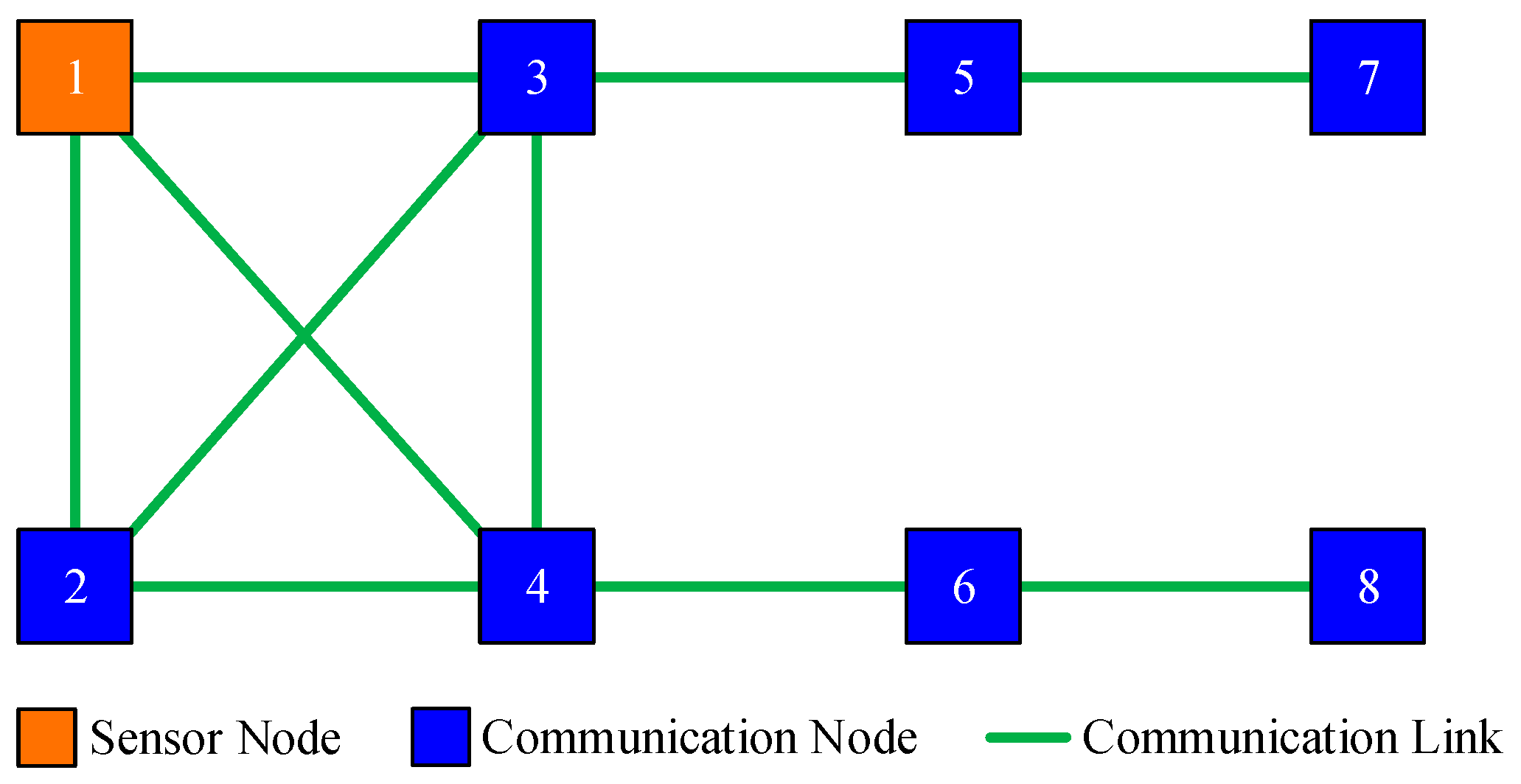
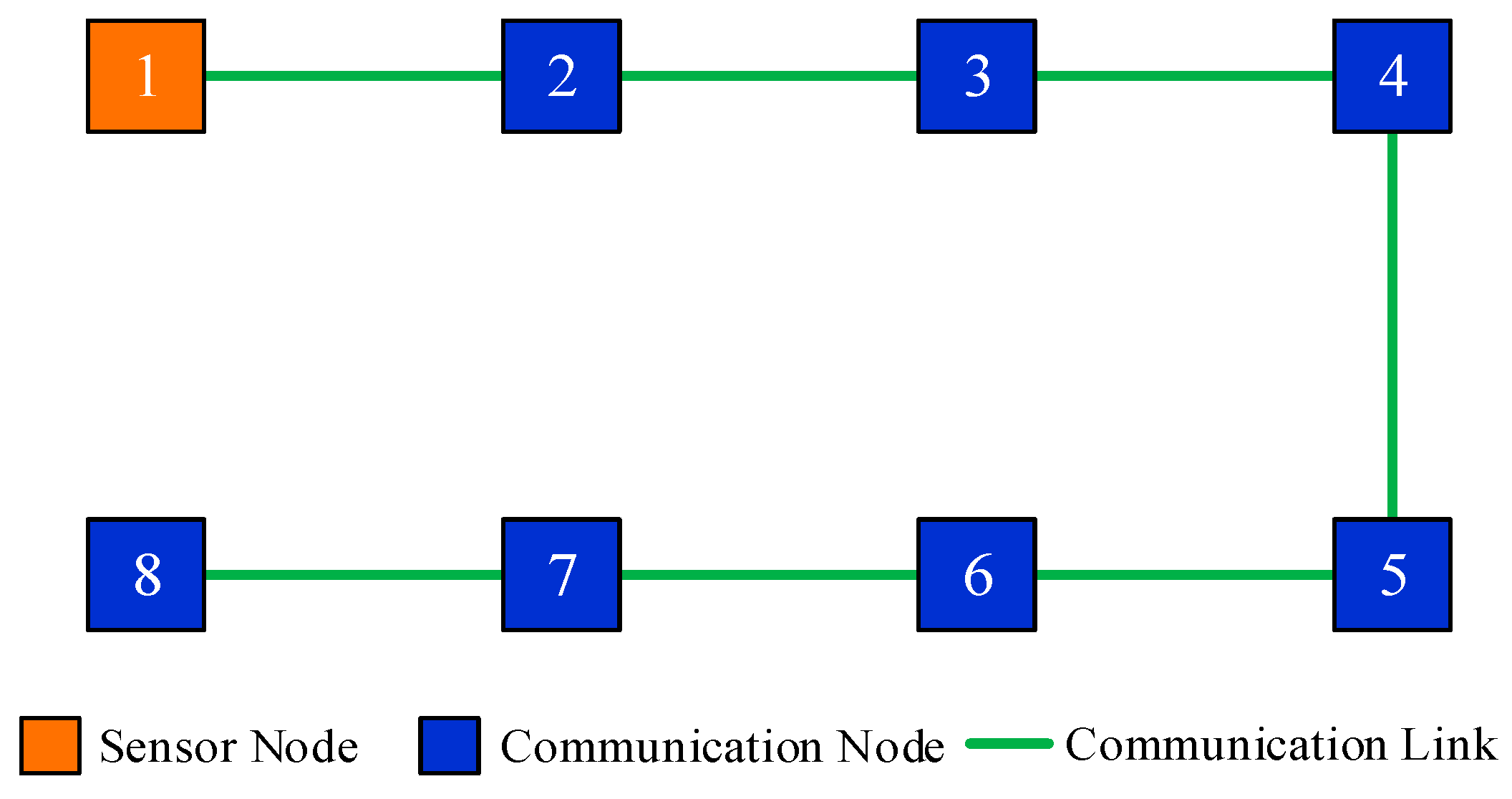
Assume that each node, for instance, node
, is able to receive its neighbor’s prior local estimate
and the corresponding covariance
, as well as its neighbor’s local measurement
and the corresponding noise covariance
by local communication. The local generalized prior estimate, denoted by
, is defined as
where
denotes the index of node
’s neighbors. Let
be the prior error of node
. The local collective prior error of node
with respect to its inclusive neighbors can be formulated as
. The local generalized prior estimate can be expressed by
where
is the matrix stacked by
identity matrices.
is the true state at time instant
. The local collective prior error covariance of node
can be written as
Here, the block matrix
.
Similarly, the local generalized measurement of node
with regard to its inclusive neighbors can be formulated as
Here, is the local generalized measurement. is the local generalized measurement matrix. denotes the local generalized measurement noise with covariance matrix .
Combining (17) and (19) together, one has
where the error covariance
Here the operator
denotes the block diagonal matrix.
According to the derivation of the global maximum a posterior estimator described in
Section 3.1, the updated local information matrix can be computed by
Similarly, the updated local information vector is
Here,
denotes the
-th block matrix of
. Similarly,
denotes the
-th block vector of
.
3.3. Approximation of
It is shown in (22) and (23) that the key to acquire the local posterior estimate is to compute the inverse of the local collective prior error covariance, that is,
. However, as is shown in (18), the computation of
requires the knowledge of cross-covariance between neighbors of node
. As is shown in [
6], to compute the cross-covariance matrix
, the information of the neighbors of node
is also required. Therefore, it is not practical to directly compute
due to the fact that large amounts of communication among neighboring nodes are required, which may cause tremendous burden on computation and communication for the networked system. Although some work has been done in [
35,
36] to incorporate cross-covariance information into the estimation framework, no technique for computing the required terms are offered and predefined values are used instead [
4].
Therefore, an approximation of in a distributed manner is necessary. In the following derivation, two special cases are discussed. The first case is that the prior estimates from different nodes are completely uncorrelated with each other. This is true at the beginning of the estimation procedure when the prior information are initialized with random quantities. The second case is for converged priors, which is critical for the reason that with sufficient consensus iterations, the prior estimates from all nodes will converge to the identical value.
3.3.1. Case 1: Uncorrelated Priors
In this case, the prior errors from different nodes are assumed to be uncorrelated with each other, i.e.,
. Hence,
in (18) turns into a block diagonal matrix
. The local posterior estimate in (22) and (23) can be approximated as
Note that after enough consensus iterations, the prior estimates of each node in the network asymptotically converges to the centralized result, i.e.,
and
. In such a case, the local prior information matrix in (25) turns into
. However, after convergence, the total amount of prior information in the network is
. That is, the local prior information matrix in the inclusive neighborhood is overestimated by a factor
. Therefore, the approximation of
should be modified by multiplying a factor
, which is
to avoid underestimation of the prior covariance. Hence, the results in (24) and (25) should be modified as
3.3.2. Case 2: Converged Priors
When the prior estimate of each node converges to the centralized result, one has
Note that for converged priors,
. Substituting this fact into (28), there is
Therefore, the estimated results in (22) and (23) can be transformed into the weighted summation of the prior information and current measurement innovations, which are the same forms as the results shown in (26) and (27).
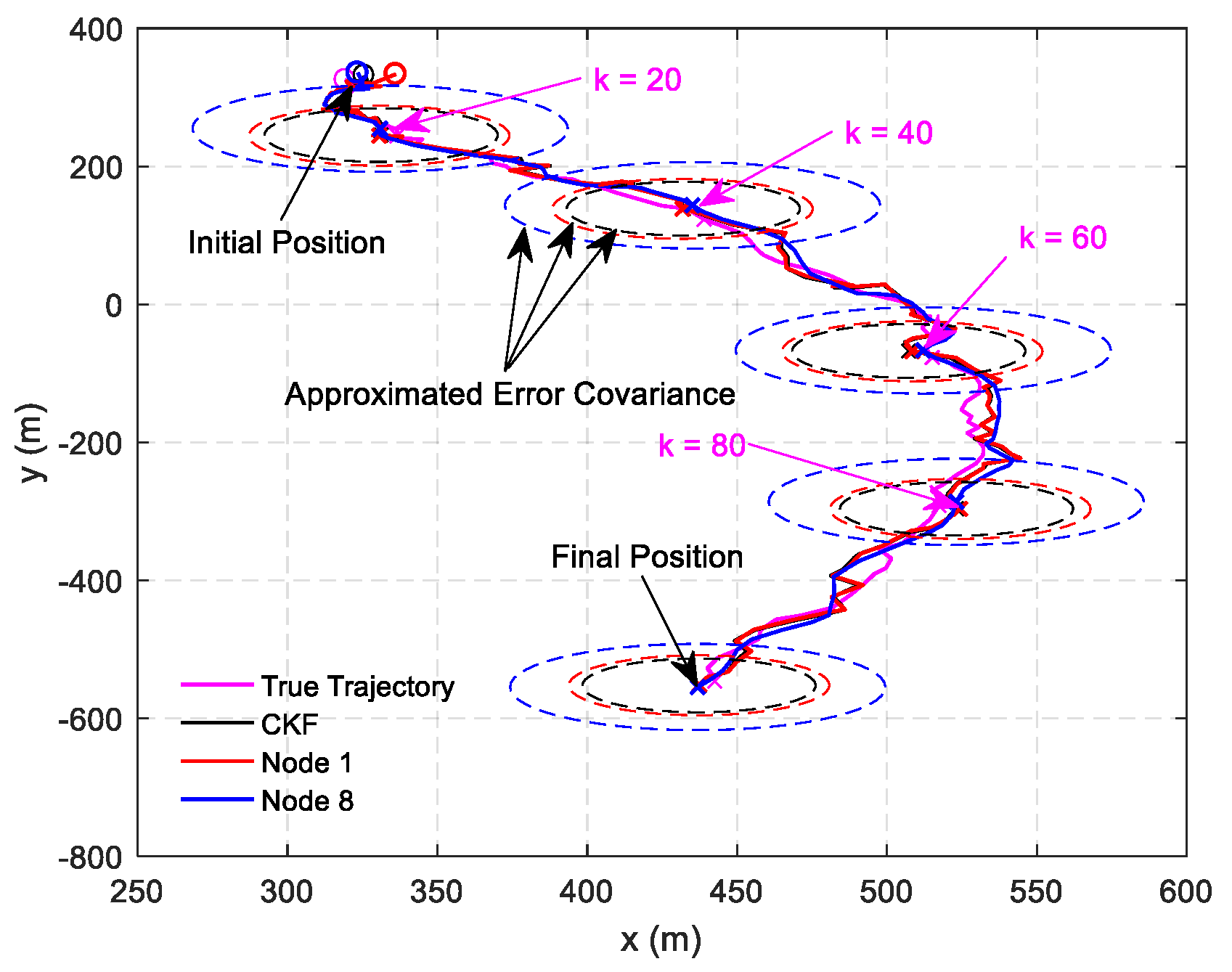
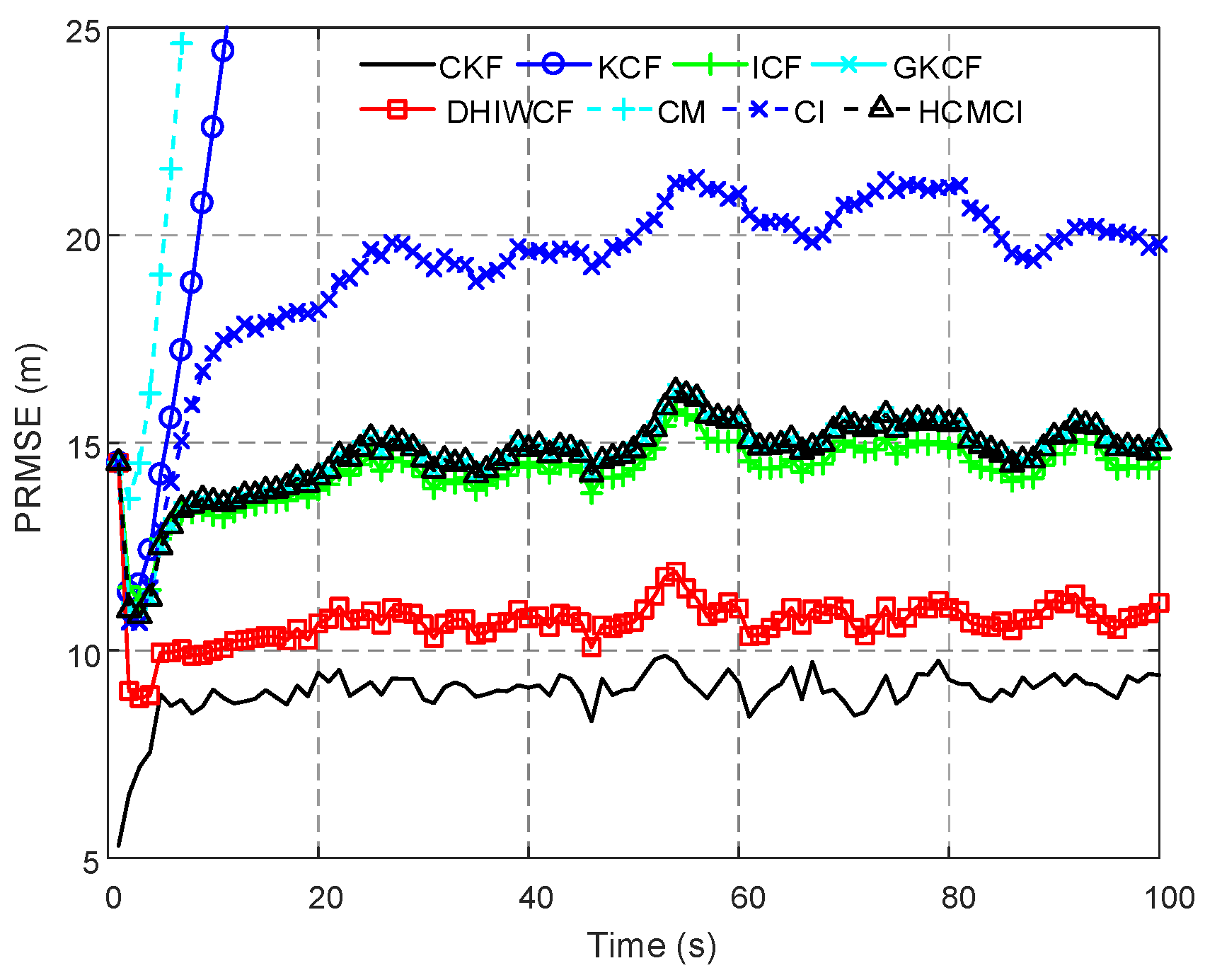
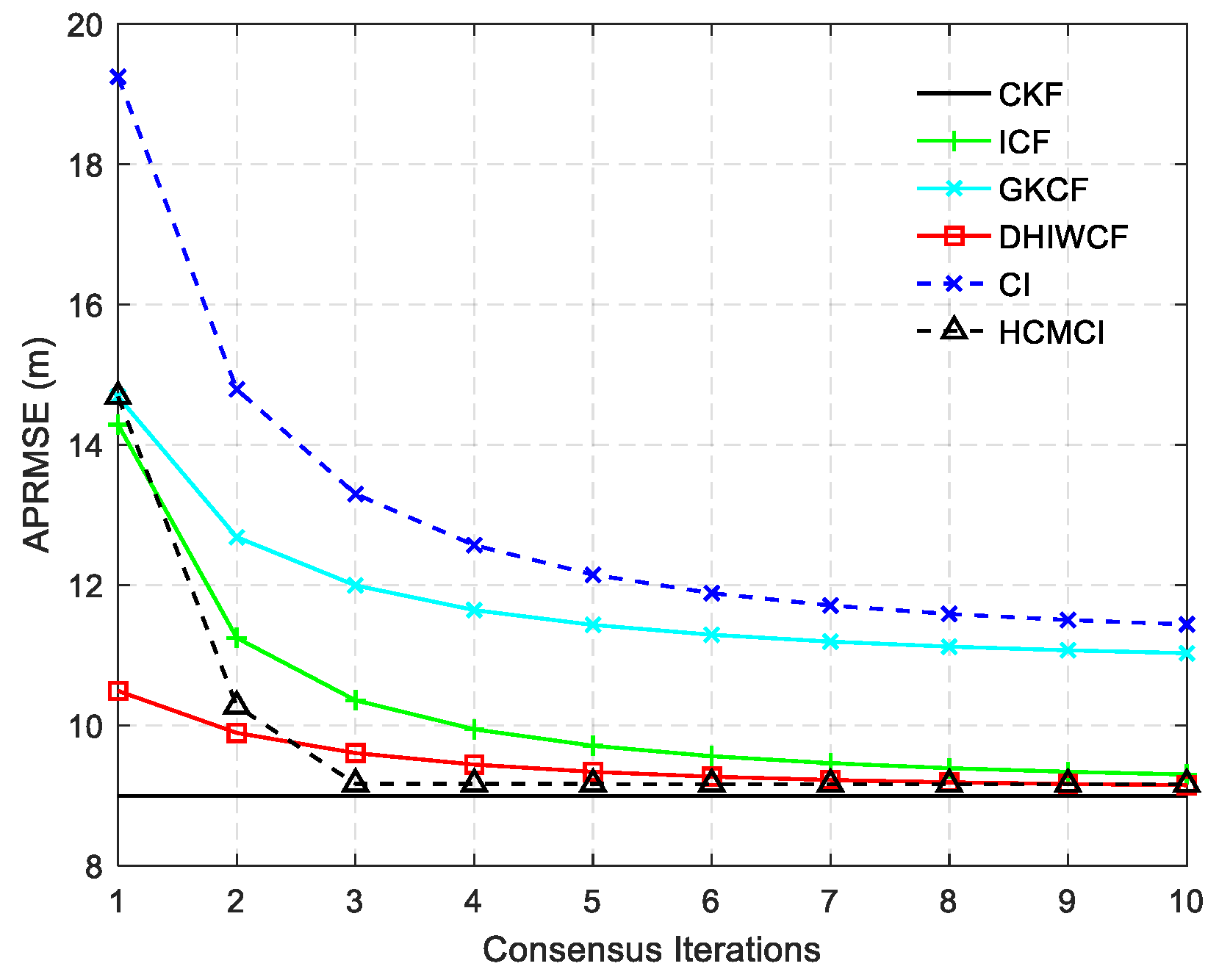
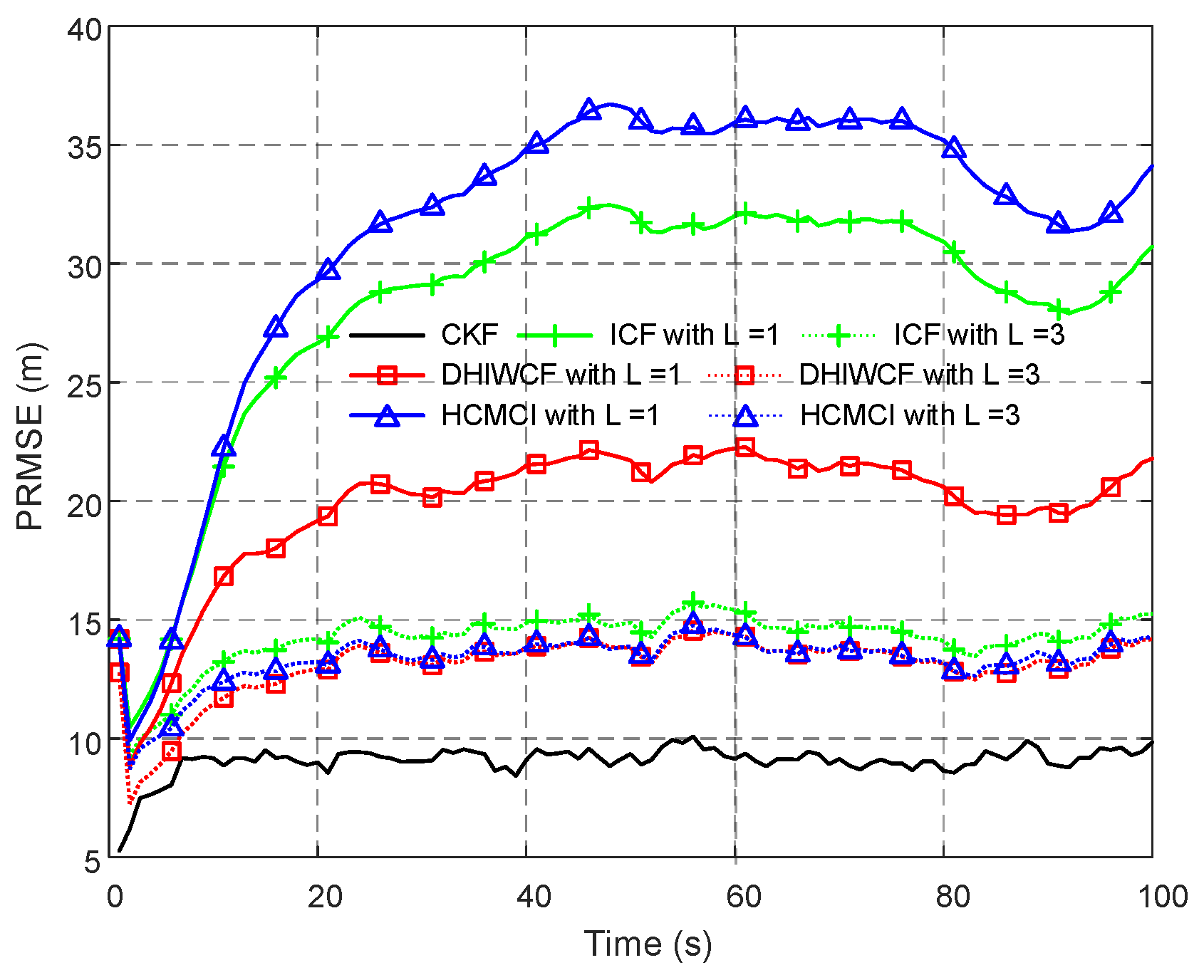
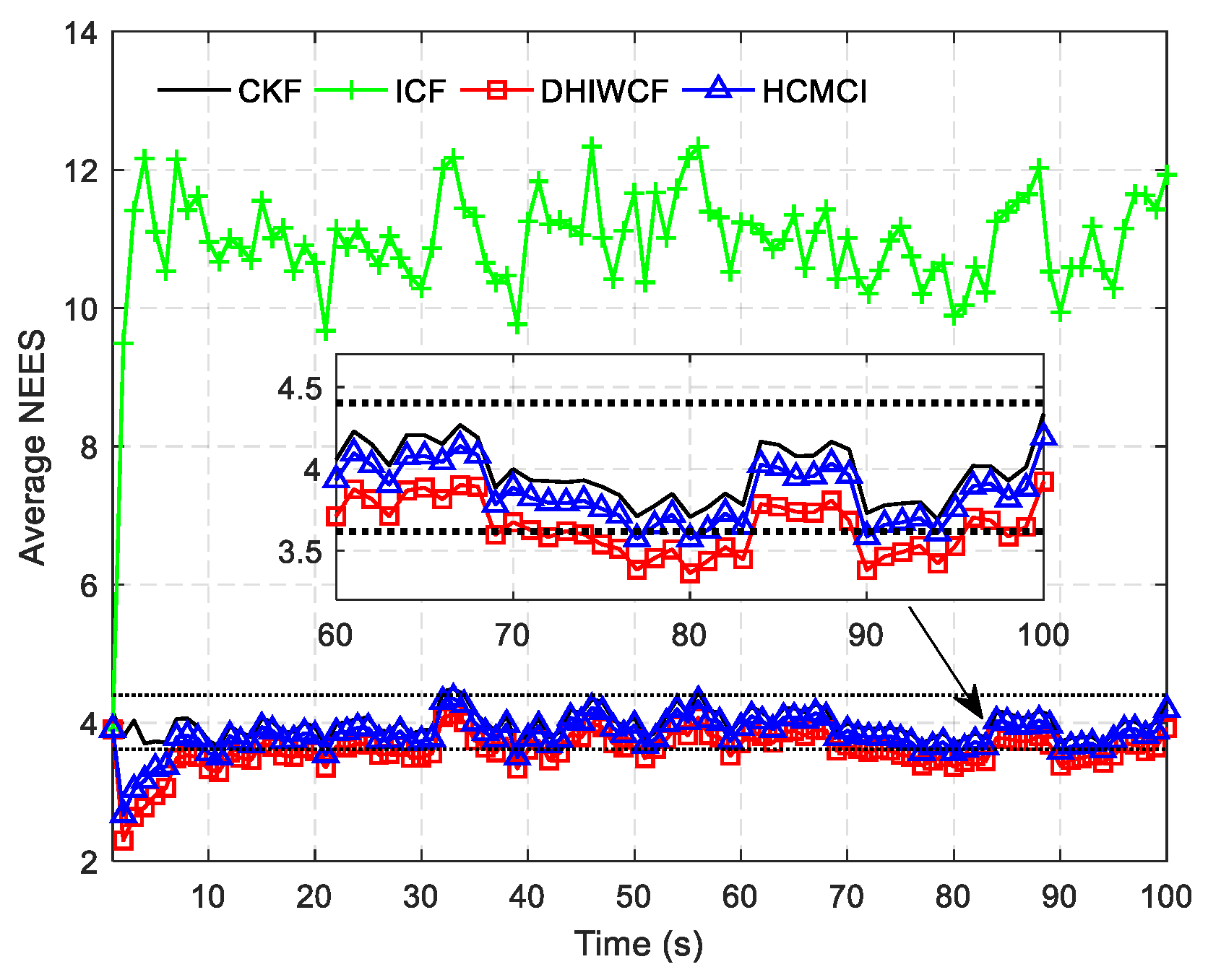
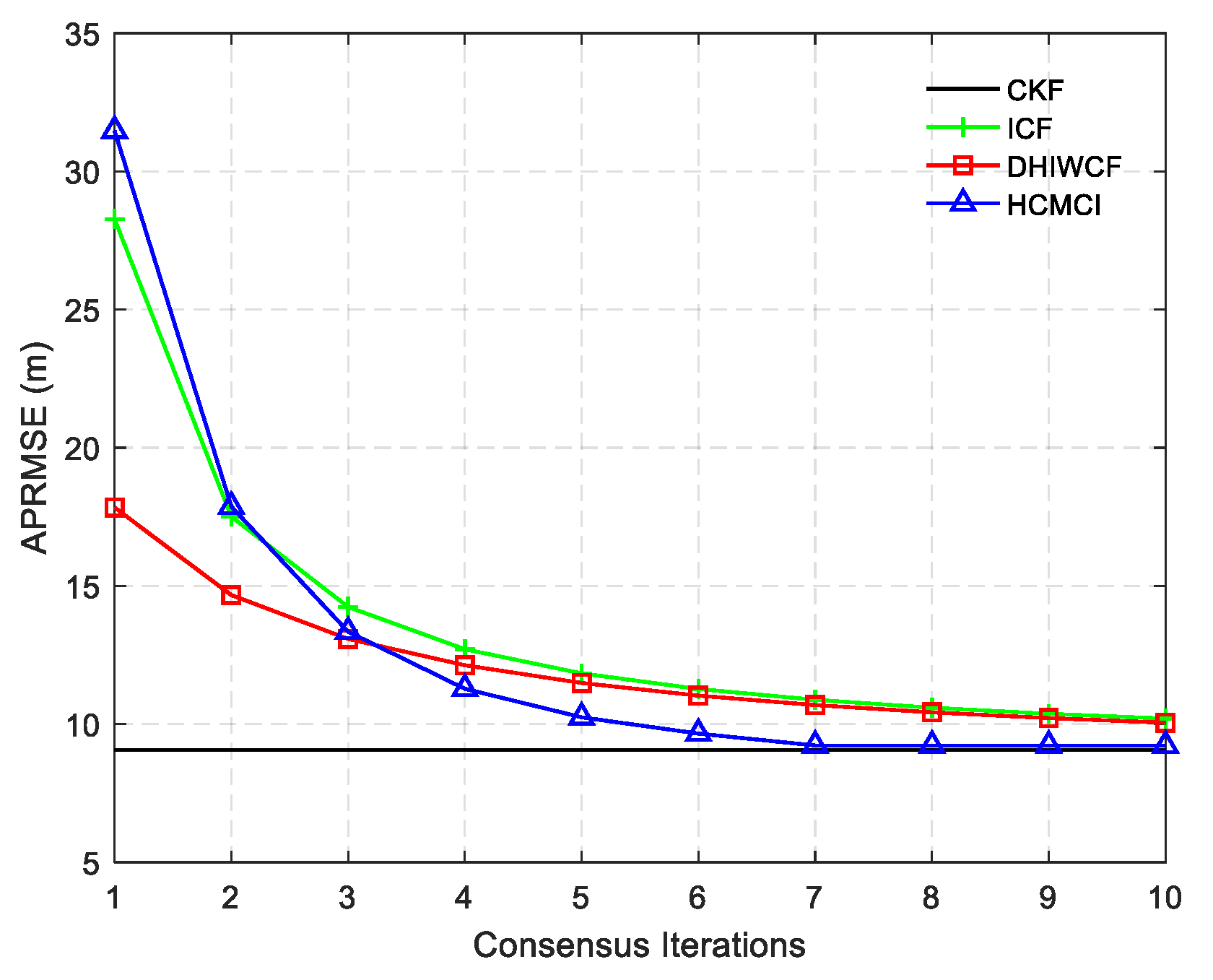
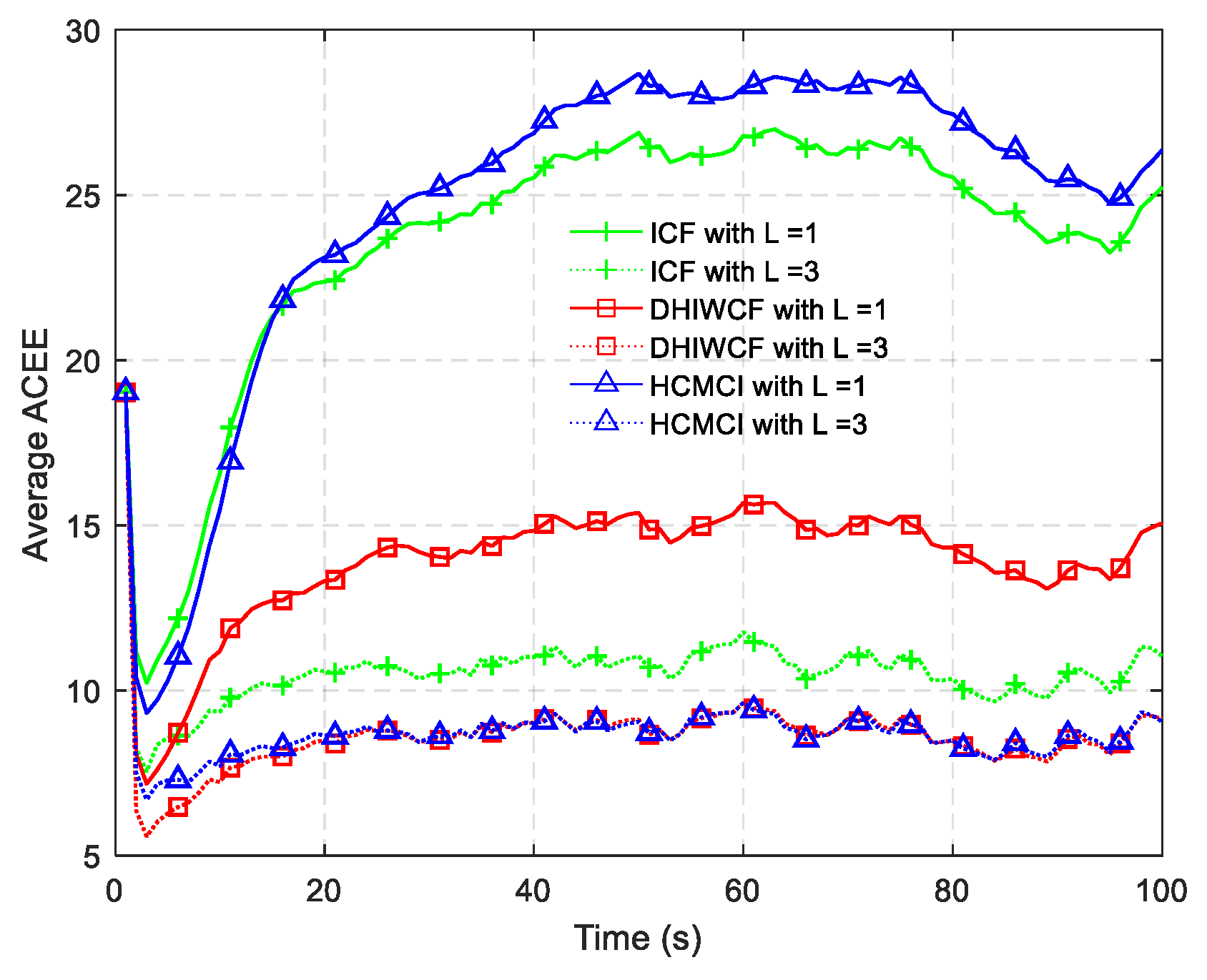
Remark 4. It should be noted that the assumed cases are not always satisfied in realistic applications, but it is still of great significance for distributed filtering algorithms. The effectiveness and feasibility of such an approximation is evaluated by numerical examples in Section 6. 5. Performance Analysis
5.1. Consistency of Estimates
One of the most fundamental but important properties of a recursive filtering algorithm is that the estimated error statistics should be consistent with the true estimation errors. The approximated error covariance of an inconsistent filtering algorithm is too small or optimistic, which does not really indicate the uncertainty of the estimate and may result in divergence since subsequent measurements in this case are prone to be neglected [
28].
Definition 2 [
28,
30,
37,
38]
. Consider a random vector . Let and be, respectively, the estimate of and the estimate of the corresponding error covariance. Then the pair is said to be consistent if It is shown in (38) that consistency requires that the true error covariance should be upper bounded (in the positive definite sense) by the approximated error covariance . In the distributed estimation paradigm, due to the unaware reuse of the redundant data in the consensus iteration and the possible correlation between measurements from different nodes, the filter may suffer from inconsistency and divergence. In such a case, preservation of consistency is even much more important.
For convenience, consider the information pair
, where
and
. The consistency defined by (38) can be rewritten as
Assumption 3. The initialized estimate of each node, represented by , is consistent. Equivalently, inequality holds for .
Remark 5. In general, Assumption 3 can be easily satisfied. The initial information on the state vector can be acquired in an off-line fashion before the fusion process. In the worst case where no prior information is available, each node can simply set the initialized information matrix as , which implies infinite estimate uncertainty in each node at the beginning so that Assumption 3 is fulfilled.
Assumption 4. The system matrix is invertible.
Lemma 1 [
28]
. Under Assumption 4, if two positive semidefinite matrices and satisfy , then . In other words, the function is monotonically nondecreasing for any . Theorem 1. Let Assumptions 1, 2, and 3 hold. Then, for each time instant and each node , the information pair of the DHIWCF is consistent in thatwith.
Proof. An inductive method is utilized here to prove this theorem. It is supposed that, at time instant
for any
. For brevity, the predicted information matrix in (31) can be rewritten as
On the basis of Lemma 1, it is immediate to see
According to (26) and (27), the local estimation error is
According to the consistency property of covariance intersection [
29,
38], it holds that
Then, exploiting (47) and (43) in (45), the following result is obtained.
Since the information pair
is computed based on the previous information pair
by (3), and the covariance intersection involved in (3) preserves the consistency of estimates [
29,
37,
38,
39], it can be concluded that
indicates
for any
. In other words, if the estimate obtained with
l consensus iterations is consistent, the estimate obtained with
l + 1 consensus iterations is also consistent. Therefore, it is straightforward to conclude that (40) holds with
and
. The proof is concluded since the initial estimate
is consistent. □
5.2. Boundedness of Error Covariances
According to the consistency of the proposed DHIWCF in Theorem 1, it is sufficient to prove that is lower bounded by a certain positive matrix (or equivalently, to prove is upper bounded by some constant matrix) for the proof of the boundedness of the error covariance . To derive the bounds for the information matrix , The following assumptions are required.
Assumption 5. The system is collectively observable. That is, the pair is observable where .
Let be the consensus matrix, whose elements are the consensus weights for any . Further, let be the -th element of , which is the -th power of .
Assumption 6. The consensus matrix is row stochastic and primitive.
Assumption 7. There exist real numbers and positive real numbers , , such that the following bounds are fulfilled for each . Lemma 2 [
28]
. Under Assumptions 4 and 5, and the proposed DHIWCF algorithm, if there exists a positive semidefinite matrix such that , then there always exists a strictly positive constant such that By virtue of Lemma 2, Theorem 2 which depicts the boundedness of error covariances is presented below.
Theorem 2. Let Assumptions 4–7 hold, there exist positive definite matrices and such thatwhere is the information matrix given by the proposed DHIWCF. Proof. For simplicity, the proof is concluded for the case
. The generalization for
can be directly derived in a similar way. According to the proposed DHIWCF, the information matrix for node
at time instant
can be written as
In view of Assumption 6, 7 and fact that
by (31), one can get
Hence, the upper bound is achieved. Next a lower bound will be guaranteed under Assumption 5.
According to Lemma 2 and Assumption 7 and (31), (53), it follows from (52) that
where
is a positive scalar with
. By recursively exploiting (52) and (54) for a certain number (denoted by
) of times, there is
where
is the
-th element of
.
is a matrix with elements
Note that the matrix
is constructed based on the network topology and is naturally stochastic. According to [
40,
41], as long as the undirected network is connected, similar to the definition of
,
is primitive. Therefore, there exist strictly positive integers
and
such that all the elements of
and
are positive for
. Let us define
It should be noted that, under Assumption 5, is definite positive for . Therefore, for , . Since is finite, for , there exists a constant positive definite matrix such that . Hence, there exists a positive definite matrix such that . The proof is now complete. □
Remark 6. The result shown in Theorem 2 is only dependent on collective observability. This is distinct from some algorithms that require some sort of local observability or detectability condition [5,6,8,11,25], which poses a great challenge to the sensing abilities of sensors and restricts the scope of application. 5.3. Convergence of Estimation Errors
In line with the boundedness of proven in Theorem 2, the convergence of local estimation errors obtained by the proposed DHIWCF is analyzed in this section. To facilitate the analysis, the following preliminary lemmas are required.
Lemma 3 [
26,
28,
31]
. Given an integer , positive definite matrices and vectors , the following inequality holds Lemma 4 [
26,
28]
. Under Assumptions 4 and 5, and the proposed DHIWCF algorithm, if there exists a positive semidefinite matrix such that , then there always exists a strictly positive scalar such that For the sake of simplicity, let us denote the prediction and estimation error at node by and , respectively. The collective forms are, respectively, and .
Theorem 3. Under Assumptions 4–6, the proposed DHIWCF algorithm yields an asymptotic estimate in each node of the network in that Proof. Under Assumptions 4–6, Theorem 2 holds. Therefore,
is uniformly lower and upper bounded. Let us define the following candidate Lyapunov function
By virtue of Lemma 2, it can be concluded that there exists a positive real number
such that
Since
, one can obtain
Here, pre-multiplying (65) by
and post-multiplying it by
yields
In a similar way, pre-multiplying (66) by
yields
According to (36), there is
Since
, one can get
Substituting (71) into (64) yields
Applying the fact that
and Lemma 3 to the right hand side of (72), one can obtain that
Writing (73) for
in a collective form, it turns out that
where
and
is a matrix with elements satisfying
Since the consensus matrix and the constructed matrix are both row stochastic, thus their spectral radiuses are both 1. As a consequence, for , the elements of vector vanishes as tends to infinity in that . Due to the equation and Assumption 4, it is straightforward to conclude that for any . □
Remark 7. The Lyapunov function defined in (61) plays a crucial role in the convergence proof of the proposed algorithm, which can be easily extended to stability analysis of Kalman-like consensus filters in other scenarios. The reason for the non-singularity requirements of in Theorem 3 is that the proof of the Lyapunov method depends on Lemma 4, the establishment of which needs the invertibility of .