Underwater Target Localization and Synchronization for a Distributed SIMO Sonar with an Isogradient SSP and Uncertainties in Receiver Locations
Abstract
1. Introduction
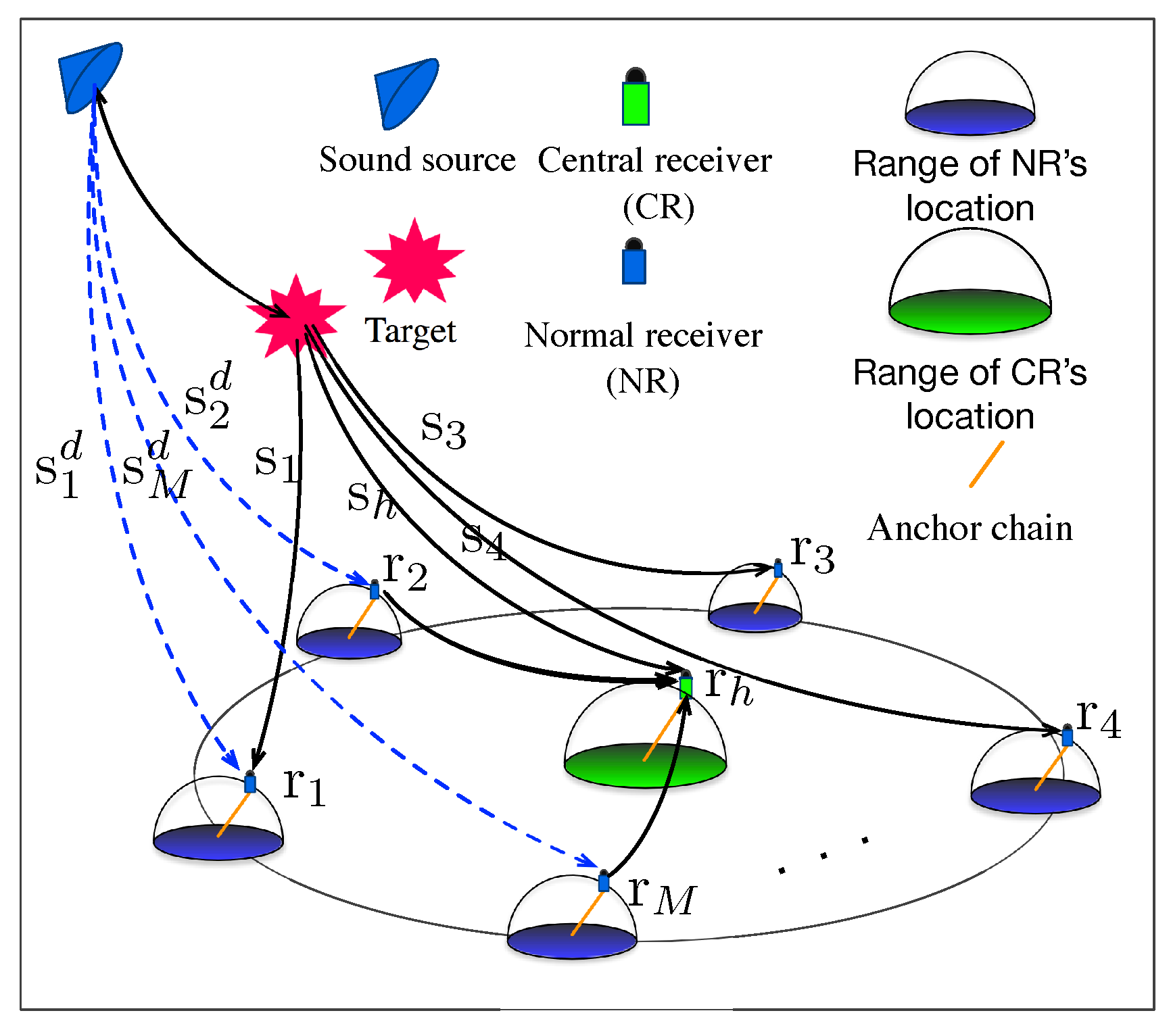
2. System Models
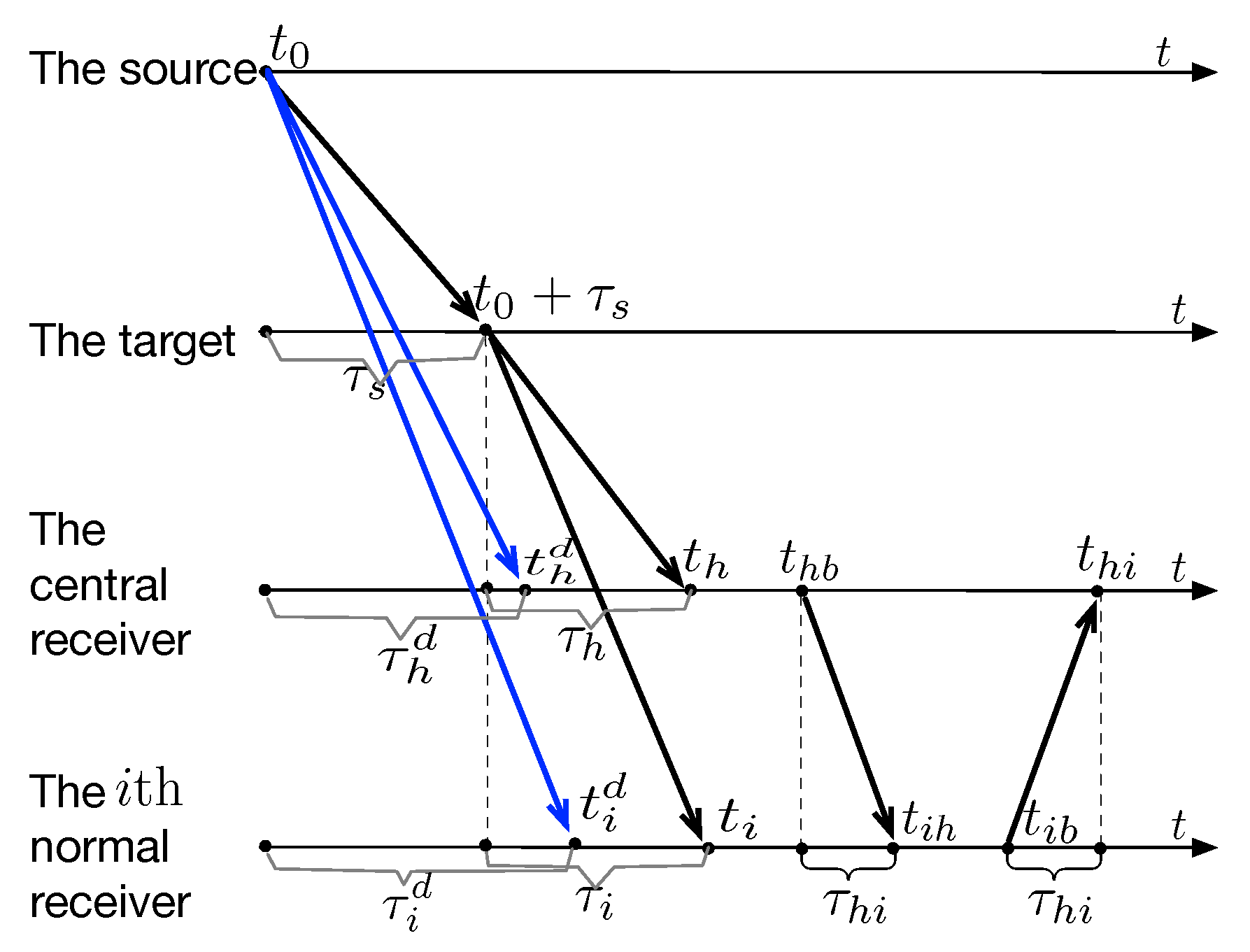
2.1. The Sound Speed and Time Delay Models
2.2. The Clock Model
2.3. The Uncertainty Model of the Receiver Locations
2.3.1. The Ocean Current Model
2.3.2. The Positions of Receivers
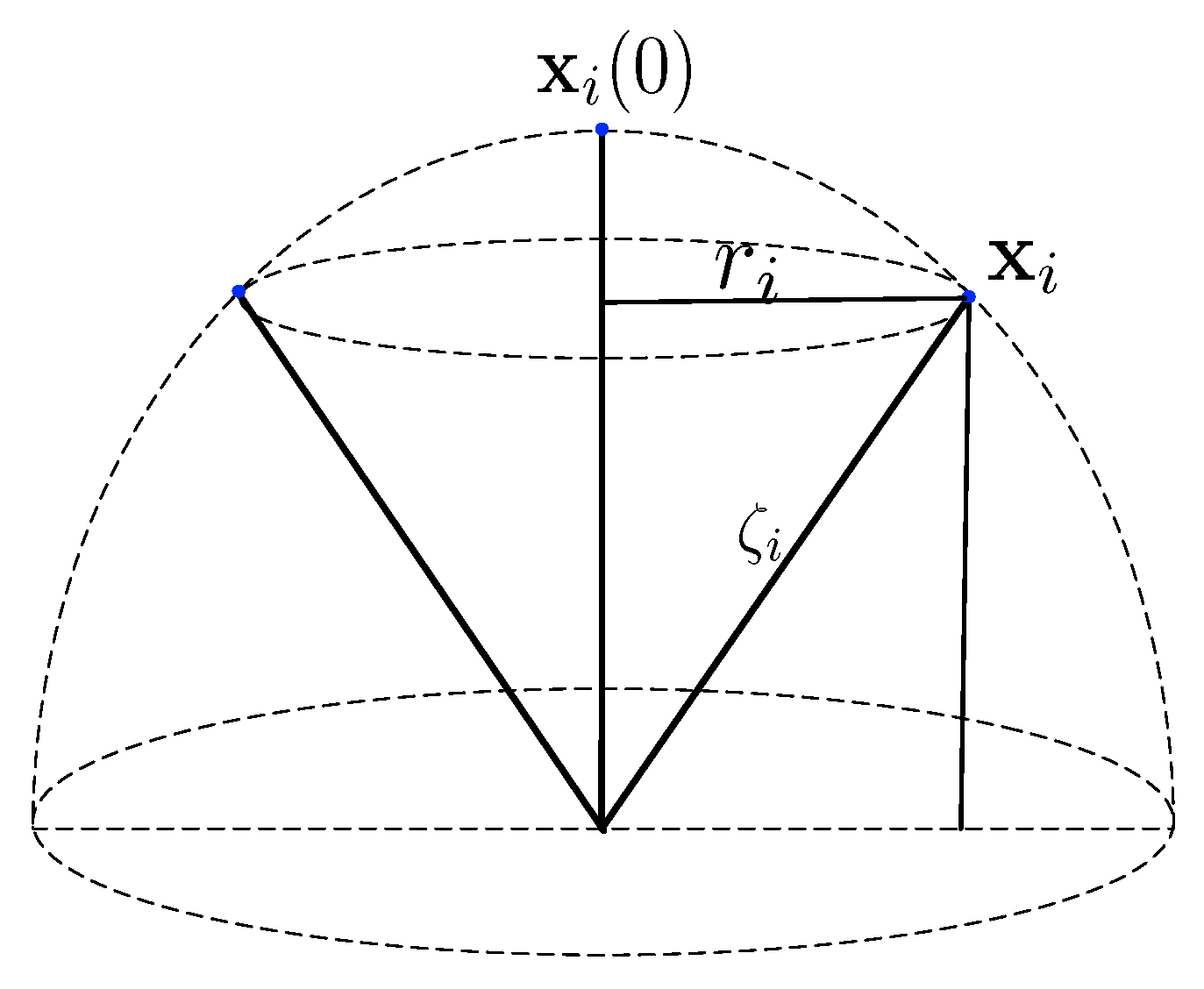
- In order to monitor the ocean more efficiently, the receivers need deploying at some special depths. Therefore, we assume that all the receivers are anchored at the bottom of the sea with anchor chains. The length of the i-th receiver chain is .
- All the receivers are equipped with buoyancy balls to keep them suspending underwater and straightening the anchor chains.
- All the receivers are equipped with pressure sensors to determine their depths.
- All the receivers can measure the BFVs around their positions by using an acoustic Doppler current profiler.
- The initial position of the i-th receiver is the receiver’s position when the anchor chain is perpendicular. The initial positions are known as prior information.
2.4. The TOA Measurement Models
3. The UTLS Algorithm
3.1. Time Synchronization
3.1.1. Estimation of the Clock Skews
| Algorithm 1: Expectation maximization (EM) based clock skews estimation algorithm. |
| Require:, , , , , Ensure:, 1: , , 2: whiledo 3: 4: linearize at according to (23) 5: E-Step: 6: calculate according to (A2) 7: calculate according to (A4) 8: M-Step: 9: calculate according to (35) 10: if then 11: , , 12: else 13: , , 14: end if 15: end while 16: , 17: return , . |
3.1.2. Estimation of the Clock Offsets
3.2. Target Localization
4. Numerical Simulations
4.1. Simulation Setup
4.2. Estimation Performance
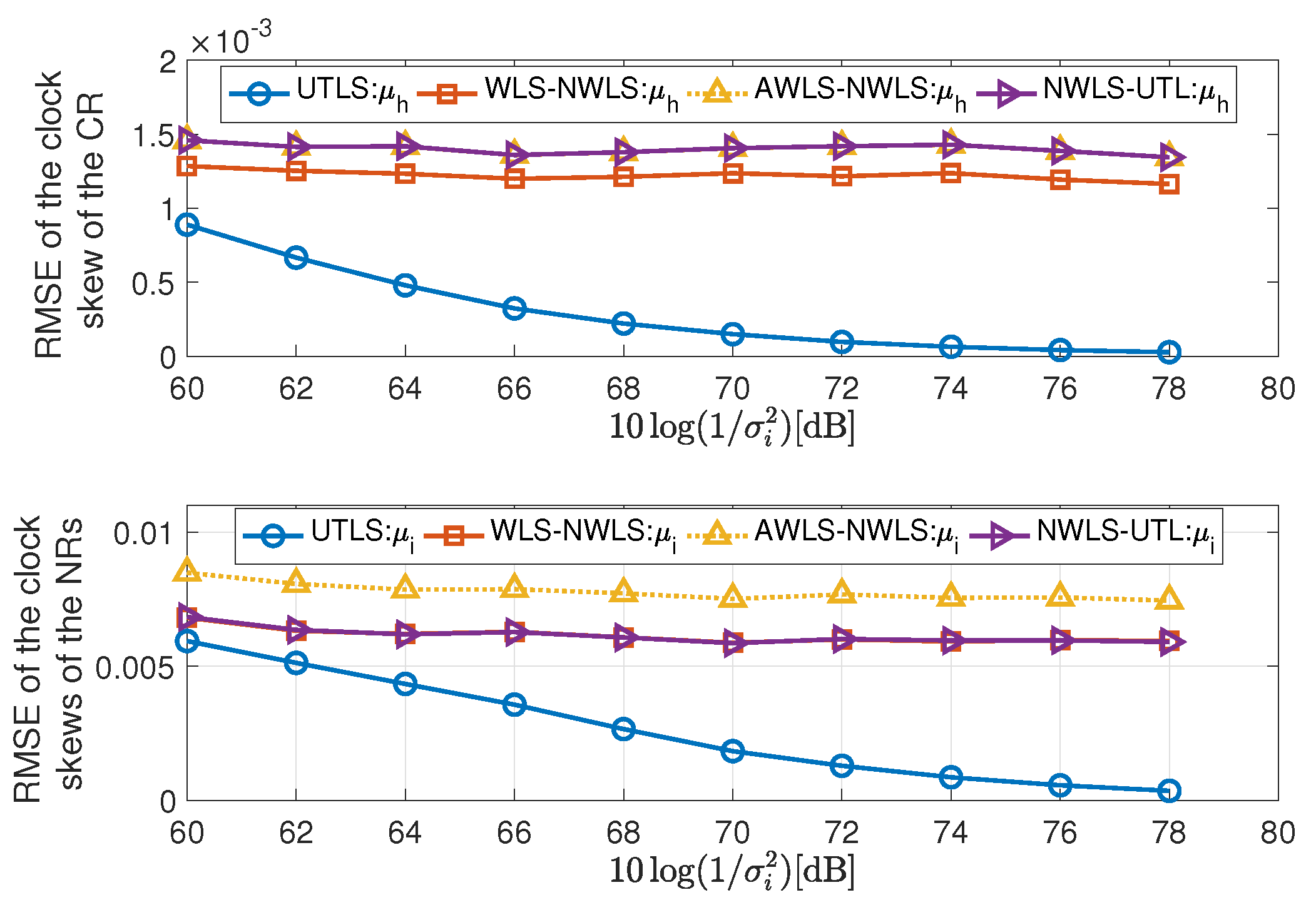
4.2.1. Performance of the Estimations of the Clock Skews and Locations of the Receivers
- The UTLS algorithm is the best one, the WLS-NWLS algorithm is the second one and the AWLS-NWLS is the worst one.
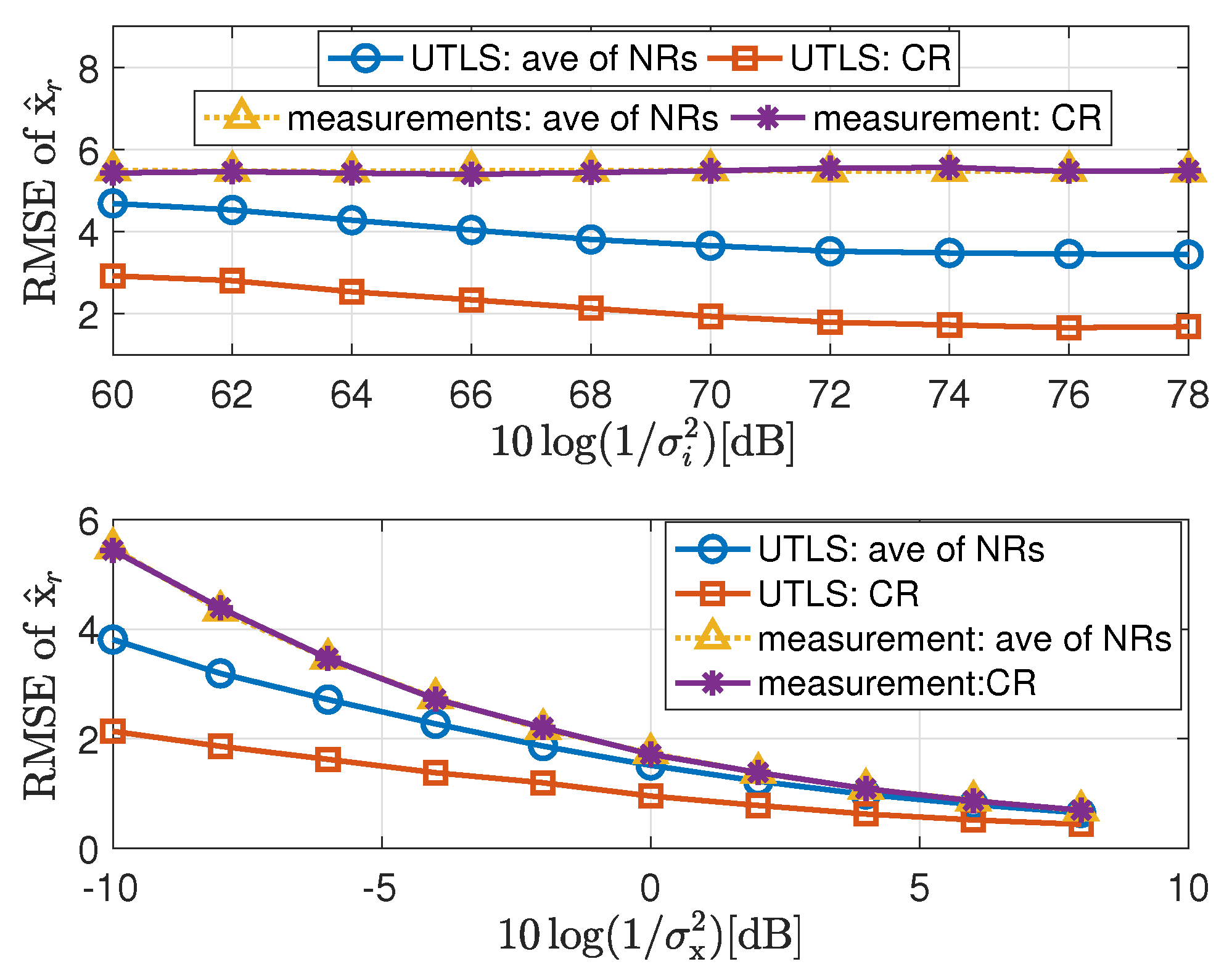
- The performance of the estimation of the clock skews can be improved by updating the locations of the receivers. The main difference between the EM algorithm of the UTLS algorithm and the WLS algorithm of the WLS-NWLS algorithm is that the EM algorithm estimates the locations of the receivers by calculating the conditional expectation and utilizes the estimates of the locations for the estimation of the clock skews, while the WLS algorithm of the WLS-NWLS algorithm only utilizes the statistical properties for the estimation of the clock skews. As shown in Figure 5, the UTLS algorithm is better than the WLS-NWLS algorithm and the difference increases with the decreasing of the variance . This is because that with a smaller variance , the UTLS algorithm obtains more accurate estimates of the locations of the receivers as shown in the upper subplot of Figure 7, with which the estimation accuracy of the clock skews can be improved.
- By utilizing the statistical properties of the locations of the receivers, the estimation performance of clock skews can be improved as shown in Figure 5. The main difference between the WLS algorithm of the WLS-NWLS algorithm and the AWLS algorithm of the AWLS-NWLS algorithm is that the WLS algorithm utilizes the statistical properties of the receivers’ locations, while the AWLS dose not. The performance superiority of the WLS-NWLS algorithm compared with the AWLS-NWLS algorithm arises from the utilizing of the statistical properties.
- In the NWLS-UTL algorithm, the clock offsets are eliminated by a designed subtraction of the time delay. The clock skews are estimated by a tailored WLS algorithm. Its. estimation performance of the clock skews is similar to the WLS-NWLS and the AWLS-NWLS algorithms and poorer than the UTLS algorithm.
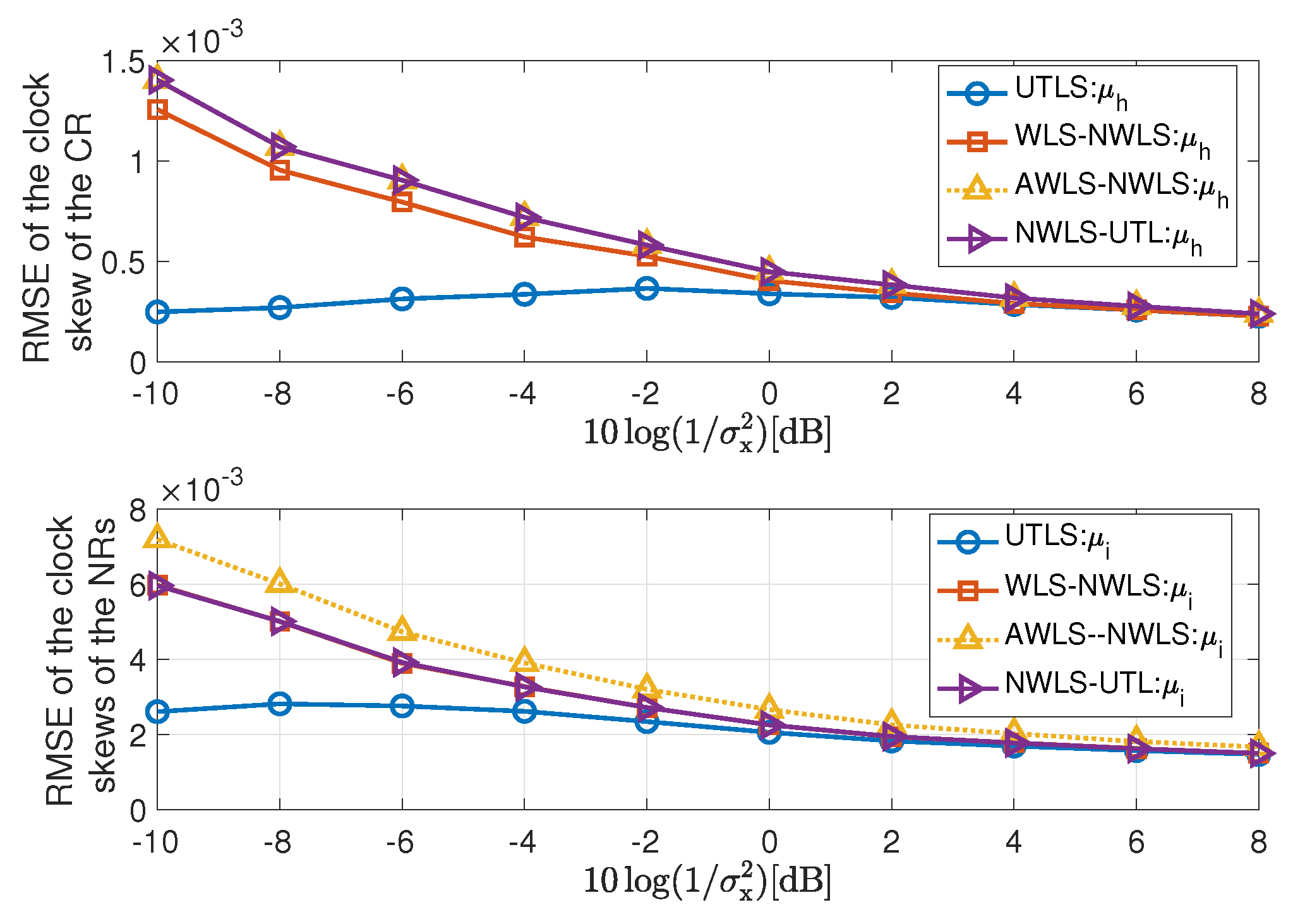
- As shown in Figure 6, the larger the variance of the receiver location noises, the greater the superiority of the UTLS algorithm.
- The UTLS algorithm is more robust against the location uncertainties of the receivers than the WLS-NWLS, the AWLS-NWLS and the NWLS-UTL algorithms. As shown in Figure 6 the performance of the UTLS algorithm decreases slowly with the increasing of the variance . While the WLS-NWLS, the AWLS-NWLS and the NWLS-UTL algorithms decrease faster than the UTLS algorithm with the increasing of the variance . The main reason is that the accuracy of the estimates of the receivers’ locations via the EM algorithm of the UTLS algorithm declines slowly with the increasing of the variance as shown in the lower subplot of Figure 7.
4.2.2. Performance of the Estimations of the Clock offsets of the Receivers
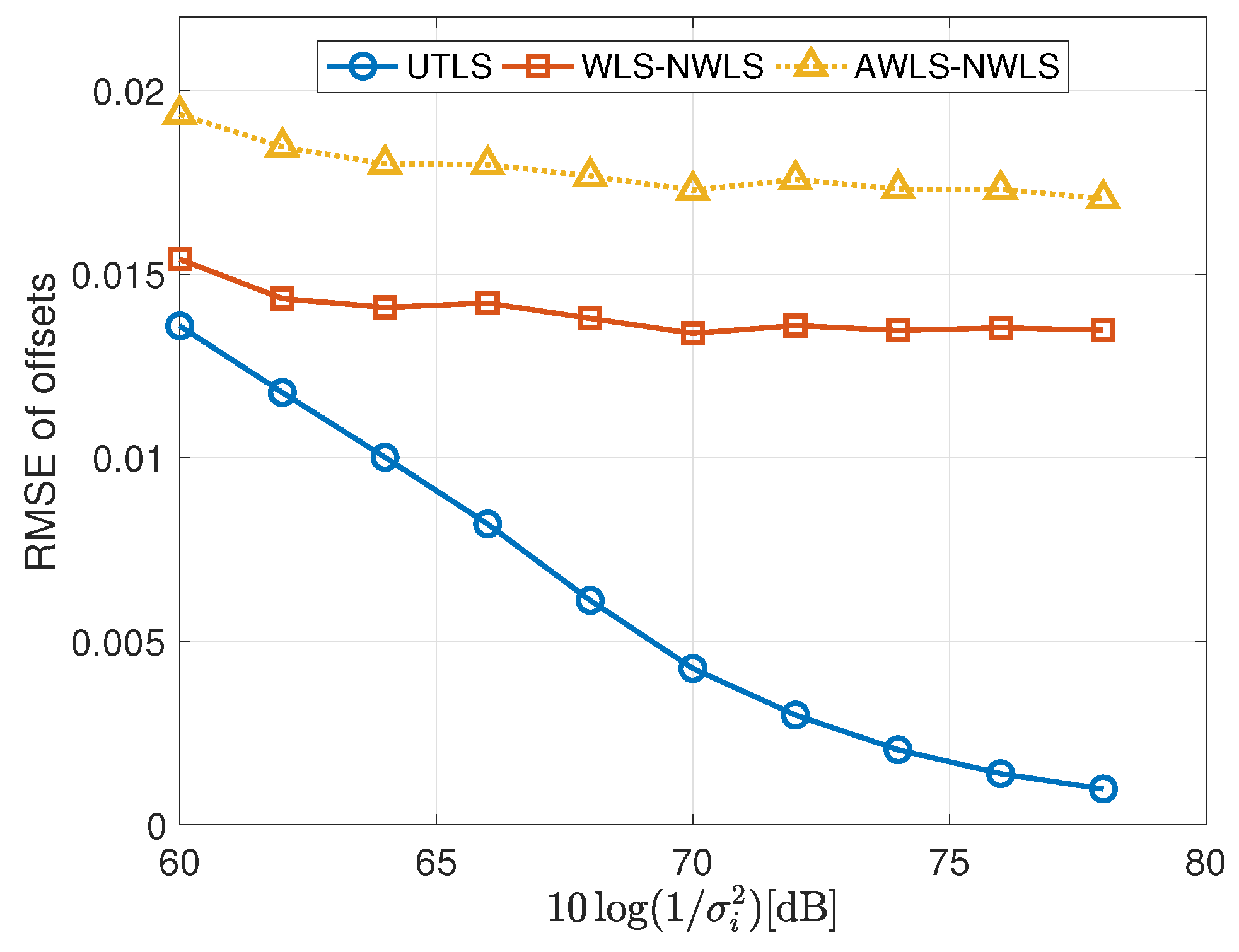
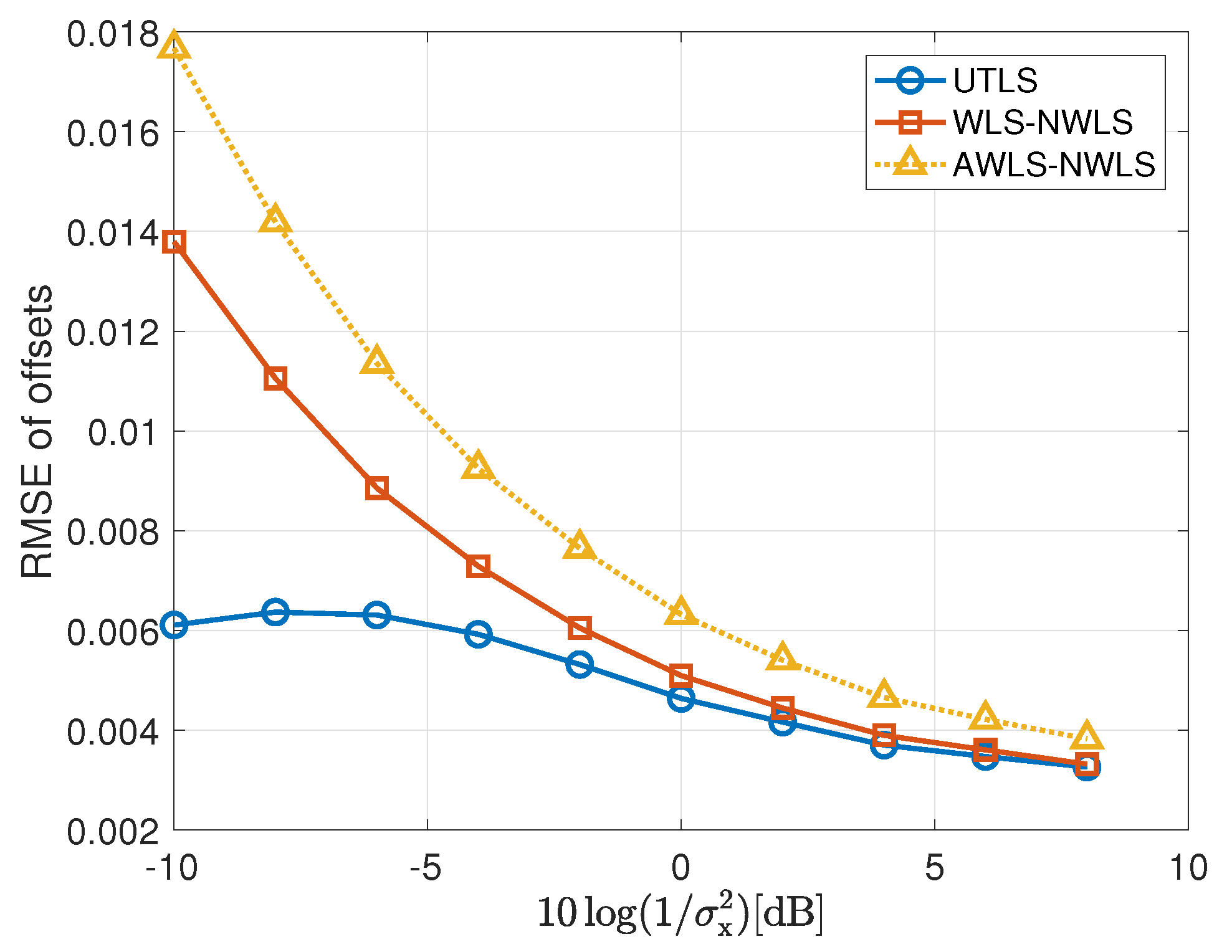
- For the estimation of the offsets of the receivers, the UTLS algorithm is the best and the differences between the UTLS algorithm and the other two algorithms increase with the decreasing of the variance as shown in Figure 8. There are two reasons. The first one is that the differences of the clock skew estimates between the EM algorithm of the UTLS algorithm and the other two algorithms increase with the decreasing of the variance . The second one is that the EM algorithm of the UTLS algorithm provides more accurate locations of the receivers for the WLS algorithm of the UTLS algorithm, and the estimation accuracy of the locations of the receivers increases with the decreasing of the variance .
- The performance superiority of the WLS algorithm of the WLS-NWLS algorithm compared with the WLS algorithm of the AWLS-NWLS algorithm arises from the utilizing of the statistical properties of the receivers’ locations as shown in Figure 8.
- As shown in Figure 9, the WLS algorithm of the UTLS algorithm is more robust against the uncertainty of the receivers’ locations. This characteristic is inherited from the EM algorithm of the UTLS algorithm.
4.2.3. Performance of the Estimation of the Location of the Target
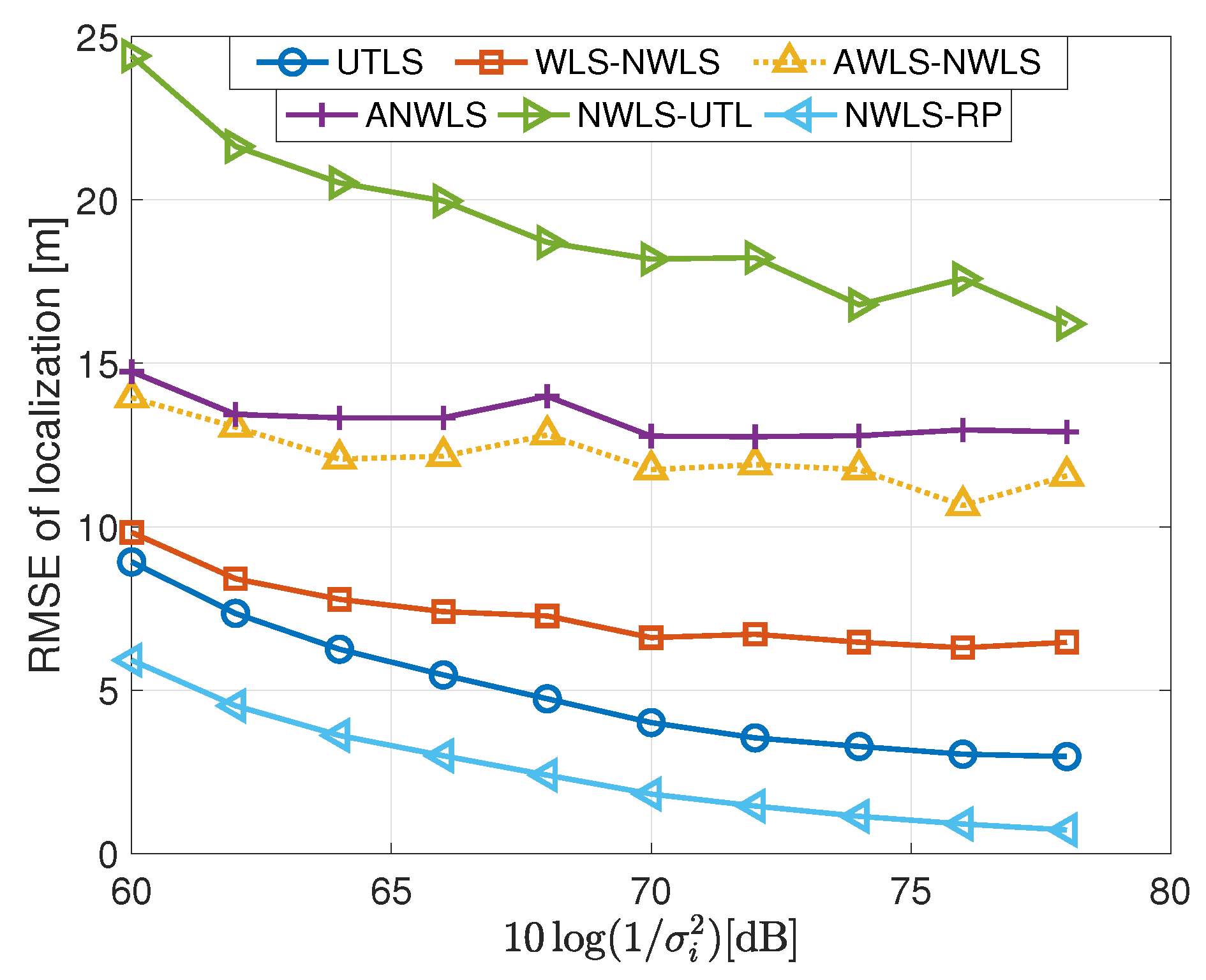
- The performance of the UTLS is the best compared with that of the WLS-NWLS, the AWLS-NWLS and the ANWLS algorithms as shown in Figure 10. The advantages of the UTLS arise from two reasons. First, the estimation accuracies of the clock skews and offsets carried out by the EM and WLS algorithms of the UTLS algorithm, respectively, are higher than that of the WLS-NWLS, the AWLS-NWLS and the ANWLS algorithms. Second, the estimation accuracy of the receivers’ locations by the EM algorithm of the UTLS algorithm is higher than the corresponding measurements of the receivers’ locations.
- The performance of the WLS-NWLS algorithm is better than the AWLS-NWLS and the ANWLS algorithms. This superiority of the WLS-NWLS arises from the WLS algorithms of the WLS-NWLS algorithm.
- As shown in Figure 10, the performance variation trend of the UTLS is almost the same as the NWLS-RP in which the real clock parameters and locations of the receivers are used. While the performance of the other algorithms almost do not vary with the variance of when the variance is small.
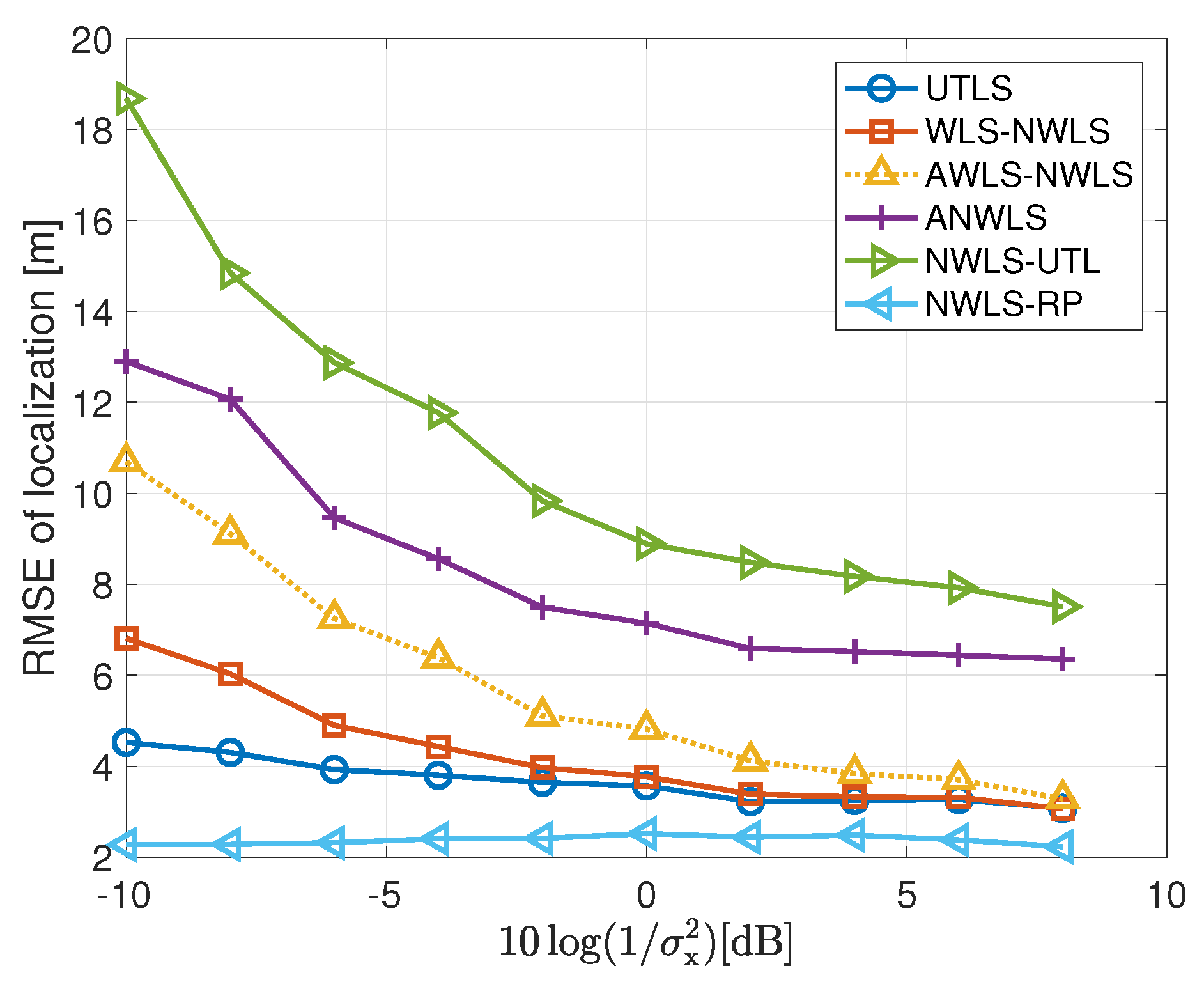
- The performance of the UTLS algorithm is almost the same as the WLS-NWLS algorithm when the variance is small as shown in Figure 11. The reasons can be stated as follows. As shown in the lower subplot of Figure 7, the difference between the estimated locations of the receivers and the measurements of the locations is small when the variance is small. As shown in Figure 6 and Figure 9, this phenomenon makes the performance superiority of the EM and WLS algorithms of our proposed UTLS algorithm small when compared to the WLS algorithms of the WLS-NWLS algorithm.
- The UTLS algorithm is still better than the AWLS-NWLS and ANWLS algorithms when the variance is small. The larger the variance , the greater the superiority of the UTLS algorithm.
- The localization performance of the NWLS-UTL algorithm is poor as shown in Figure 10. This phenomenon may arise from the fact that the NWLS-UTL algorithm is susceptible to the location uncertainties of the receivers as shown Figure 11. The clock offsets have been eliminated by the NWLS-UTL algorithm. Therefore, the computational cost is smaller because of the absence of the clock offset estimates.
- The localization performance of the NWLS-RP algorithm is better the our proposed UTLS algorithm. The reason is that the real clock parameters and receiver locations are employed in the NWLS-RP algorithm, which is impractical.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Kim, S.; Ku, B.; Hong, W.; Ko, H. Performance comparison of target localization for active sonar systems. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1371–1380. [Google Scholar]
- Dianat, M.; Taban, M.R.; Dianat, J.; Sedighi, V. Target localization using least squares estimation for MIMO radars with widely separated antennas. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2730–2741. [Google Scholar] [CrossRef]
- Pailhas, Y.; Petillot, Y. Large MIMO sonar systems: A tool for underwater surveillance. In Proceedings of the 2014 Sensor Signal Processing for Defence (SSPD), Edinburgh, UK, 8–9 September 2014. [Google Scholar]
- He, C.; Wang, Y.; Chen, C.; Guan, X. Target Localization for a Distributed SIMO Sonar with an Isogradient Sound Speed Profile. IEEE Access 2018, 6, 29770–29783. [Google Scholar] [CrossRef]
- Friedlander, B. On the relationship between MIMO and SIMO radars. IEEE Trans. Signal Process. 2009, 57, 394–398. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, S.; Song, H.; Lee, H.S. Wireless sensor network design for tactical military applications: Remote large-scale environments. In Proceedings of the MILCOM 2009-2009 IEEE Military Communications Conference, Boston, MA, USA, 18–21 October 2009; pp. 911–917. [Google Scholar]
- Noroozi, A.; Sebt, M.A. Target localization from bistatic range measurements in multi-transmitter multi-receiver passive radar. IEEE Signal Process. Lett. 2015, 22, 2445–2449. [Google Scholar] [CrossRef]
- Fioranelli, F.; Ritchie, M.; Gürbüz, S.Z.; Griffiths, H. Feature diversity for optimized human micro-Doppler classification using multistatic radar. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 640–654. [Google Scholar]
- Ehlers, F. Final Report On Deployable Multistatic Sonar Systems; NATO Undersea Research Centre: La Spezia, Italy, January 2009. [Google Scholar]
- Khan, H.; Hayat, M.N.; Rehman, Z.U. Wireless sensor networks free-range base localization schemes: A comprehensive survey. In Proceedings of the 2017 International Conference on Communication, Computing and Digital Systems (C-CODE), Islamabad, Pakistan, 8–9 March 2017; pp. 144–147. [Google Scholar]
- Garcia, M.; Tomas, J.; Boronat, F.; Lloret, J. The Development of Two Systems for Indoor Wireless Sensors Self-location. Ad Hoc Sens. Wirel. Netw. 2009, 8, 235–258. [Google Scholar]
- Maghdid, H.S.; Lami, I.A.; Ghafoor, K.Z.; Lloret, J. Seamless outdoors-indoors localization solutions on smartphones: Implementation and challenges. ACM Comput. Surv. 2016, 48, 53. [Google Scholar] [CrossRef]
- Rossi, M.; Haimovich, A.M.; Eldar, Y.C. Spatial compressive sensing for MIMO radar. IEEE Trans. Signal Process. 2014, 62, 419–430. [Google Scholar] [CrossRef]
- Liang, J.; Wang, D.; Su, L.; Chen, B.; Chen, H.; So, H.C. Robust MIMO radar target localization via nonconvex optimization. Signal Process. 2016, 122, 33–38. [Google Scholar]
- Kebkal, K.; Kebkal, O.; Glushko, E.; Kebkal, V.; Sebastiao, L.; Pascoal, A.; Gomes, J.; Ribeiro, J.; SIlva, H.; Ribeiro, M.; et al. Underwater acoustic modems with integrated atomic clocks for one-way travel time underwater vehicle positioning. In Proceedings of the Underwater Acoustics Conference and Exhibition, Skiathos Island, Greece, 3–8 September 2017. [Google Scholar]
- Dickinson, B. On Sale: The World’S Smallest Atomic Clock. Available online: http://www.zdnet.com/article/on-sale-the-worlds-smallest-atomic-clock/ (accessed on 5 May 2011).
- Liu, J.; Wang, Z.; Zuba, M.; Peng, Z.; Cui, J.H.; Zhou, S. DA-Sync: A Doppler-Assisted Time-Synchronization Scheme for Mobile Underwater Sensor Networks. IEEE Trans. Mob. Comput. 2014, 13, 582–595. [Google Scholar] [CrossRef]
- Pallares, O.; Bouvet, P.J.; del Rio, J. TS-MUWSN: Time Synchronization for Mobile Underwater Sensor Networks. IEEE J. Ocean. Eng. 2016, 41, 763–775. [Google Scholar] [CrossRef]
- Fresno, J.; Robles, G.; Martínez-Tarifa, J.; Stewart, B. Survey on the performance of source localization algorithms. Sensors 2017, 17, 2666. [Google Scholar] [CrossRef] [PubMed]
- Coraluppi, S. Multistatic sonar localization. IEEE J. Ocean. Eng. 2006, 31, 964–974. [Google Scholar] [CrossRef]
- Rui, L.; Ho, K.C. Elliptic localization: Performance study and optimum receiver placement. IEEE Trans. Signal Process. 2014, 62, 4673–4688. [Google Scholar] [CrossRef]
- Yin, J.; Wan, Q.; Yang, S.; Ho, K.C. A simple and accurate TDOA-AOA localization method using two stations. IEEE Signal Process. Lett. 2016, 23, 144–148. [Google Scholar] [CrossRef]
- Peters, D.J. A bayesian method for localization by multistatic active sonar. IEEE J. Ocean. Eng. 2017, 42, 135–142. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, L.; Ho, K.C. Moving target localization in multistatic sonar by differential delays and Doppler shifts. IEEE Signal Process. Lett. 2016, 23, 1160–1164. [Google Scholar]
- Shi, J.; Fan, L.; Zhang, X.; Shi, T. Multi-target positioning for passive sensor network via bistatic range space projection. Sci. China Inf. Sci. 2016, 59, 1–3. [Google Scholar] [CrossRef]
- Rui, L.; Ho, K.C. Efficient closed-form estimators for multistatic sonar localization. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 600–614. [Google Scholar] [CrossRef]
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2015, 53, 3010–3022. [Google Scholar] [CrossRef]
- Stoica, P.; Li, J. Lecture notes-source localization from range-difference measurements. IEEE Signal Process. Mag. 2006, 23, 63–66. [Google Scholar] [CrossRef]
- Ho, K.C.; Sun, M. Passive source localization using time differences of arrival and gain ratios of arrival. IEEE Trans. Signal Process. 2008, 56, 464–477. [Google Scholar] [CrossRef]
- Yardibi, T.; Li, J.; Stoica, P.; Xue, M.; Baggeroer, A.B. Source localization and sensing: A nonparametric iterative adaptive approach based on weighted least squares. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 425–443. [Google Scholar] [CrossRef]
- Sandys-Wunsch, M.; Hazen, M.G. Multistatic localization error due to receiver positioning errors. IEEE J. Ocean. Eng. 2002, 27, 328–334. [Google Scholar] [CrossRef]
- Ma, Z.; Ho, K.C. A study on the effects of sensor position error and the placement of calibration emitter for source localization. IEEE Trans. Wirel. Commun. 2014, 13, 5440–5452. [Google Scholar] [CrossRef]
- Ho, K.C.; Lu, X.; Kovavisaruch, L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: Analysis and solution. IEEE Trans. Signal Process. 2007, 55, 684–696. [Google Scholar] [CrossRef]
- Ho, K.C.; Yang, L. On the use of a calibration emitter for source localization in the presence of sensor position uncertainty. IEEE Trans. Signal Process. 2008, 56, 5758–5772. [Google Scholar] [CrossRef]
- Yang, L.; Ho, K.C. Alleviating sensor position error in source localization using calibration emitters at inaccurate locations. IEEE Trans. Signal Process. 2010, 58, 67–83. [Google Scholar] [CrossRef]
- Sun, M.; Ho, K.C. An asymptotically efficient estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of sensor location uncertainties. IEEE Trans. Signal Process. 2011, 59, 3434–3440. [Google Scholar]
- Wang, Y.; Ho, K.C. TDOA source localization in the presence of synchronization clock bias and sensor position errors. IEEE Trans. Signal Process. 2013, 61, 4532–4544. [Google Scholar] [CrossRef]
- Lee, K.H.; Jeong, E.C.; Kim, S.; Han, D.S. Robust localization using geographic information in bistatic sonar. Int. J. Distrib. Sens. Netw. 2017, 13, 1–9. [Google Scholar] [CrossRef]
- Beck, A.; Stoica, P.; Li, J. Exact and approximate solutions of source localization problems. IEEE Trans. Signal Process. 2008, 56, 1770–1778. [Google Scholar] [CrossRef]
- Ho, K.C.; Xu, W. An accurate algebraic solution for moving source location using TDOA and FDOA measurements. IEEE Trans. Signal Process. 2004, 52, 2453–2463. [Google Scholar] [CrossRef]
- Yang, L.; Ho, K.C. An approximately efficient TDOA localization algorithm in closed-form for locating multiple disjoint sources with erroneous sensor positions. IEEE Trans. Signal Process. 2009, 57, 4598–4615. [Google Scholar] [CrossRef]
- Ho, K.C. Bias reduction for an explicit solution of source localization using TDOA. IEEE Trans. Signal Process. 2012, 60, 2101–2114. [Google Scholar] [CrossRef]
- Sun, M.; Yang, L.; Ho, D.K.C. Efficient joint source and sensor localization in closed-form. IEEE Signal Process. Lett. 2012, 19, 399–402. [Google Scholar] [CrossRef]
- Porter, M.B. Acoustic models and sonar systems. IEEE J. Ocean. Eng. 1993, 18, 425–437. [Google Scholar] [CrossRef]
- Ramezani, H.; Jamali-Rad, H.; Leus, G. Localization and tracking of a mobile target for an isogradient sound speed profile. In Proceedings of the 2012 IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 10–15 June 2012; pp. 3654–3658. [Google Scholar]
- Ramezani, H.; Jamali-Rad, H.; Leus, G. Target localization and tracking for an isogradient sound speed profile. IEEE Trans. Signal Process. 2013, 61, 1434–1446. [Google Scholar] [CrossRef]
- Sendra, S.; Lloret, J.; Jimenez, J.M. Underwater acoustic modems. IEEE Sens. J. 2016, 16, 4063–4071. [Google Scholar] [CrossRef]
- Steven, M. Fundamentals of Statistical Signal Processing: Esitmation Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Aughenbaugh, J.M.; Cour, B.R.L.; Gelb, J.M. Interference Mitigation for Multistatic Active Sonar. IEEE J. Ocean. Eng. 2015, 40, 570–582. [Google Scholar] [CrossRef]
- Xu, L.; Li, J.; Jain, A. Impact of strong direct blast on active sonar systems. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 894–909. [Google Scholar] [CrossRef]
- Gianelli, C.; Xu, L.; Li, J. Active sonar systems in the presence of strong direct blast. In Proceedings of the OCEANS 2015-Genova, Genoa, Italy, 18–21 May 2015; pp. 1–10. [Google Scholar]
- Stojanovic, M.; Preisig, J. Underwater acoustic communication channels: Propagation models and statistical characterization. IEEE Commun. Mag. 2009, 47, 84–89. [Google Scholar] [CrossRef]
- Song, Z.; Mohseni, K. Cooperative mid-depth navigation aided by ocean current prediction. In Proceedings of the OCEANS 2017, Anchorage, AK, USA, 18–21 September 2017. [Google Scholar]
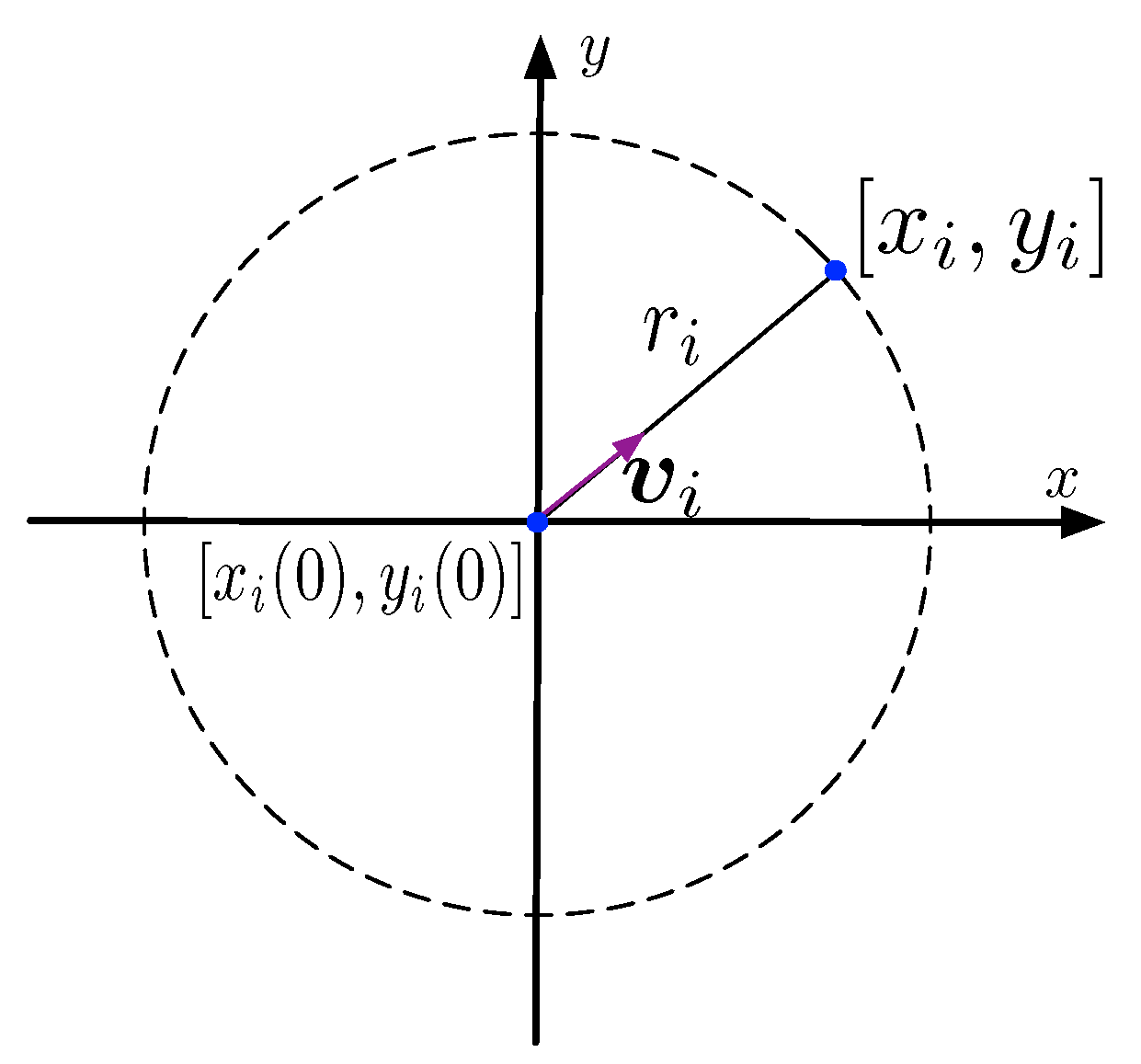
| Algorithms | Synchronization | Localization | |
|---|---|---|---|
| Clock Skew | Clock Offset | ||
| UTLS (proposed) | EM | WLS | NWLS |
| NWLS-UTL [4] | Tailored WLS | ∕ | Tailored NWLS |
| WLS-NWLS | WLS | WLS | NWLS |
| AWLS-NWLS | AWLS | WLS | NWLS |
| ANWLS | 1 | 0 | NWLS |
| NWLS-RP | real value | real value | NWLS |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, C.; Wang, Y.; Yu, W.; Song, L. Underwater Target Localization and Synchronization for a Distributed SIMO Sonar with an Isogradient SSP and Uncertainties in Receiver Locations. Sensors 2019, 19, 1976. https://doi.org/10.3390/s19091976
He C, Wang Y, Yu W, Song L. Underwater Target Localization and Synchronization for a Distributed SIMO Sonar with an Isogradient SSP and Uncertainties in Receiver Locations. Sensors. 2019; 19(9):1976. https://doi.org/10.3390/s19091976
Chicago/Turabian StyleHe, Chaofeng, Yiyin Wang, Wenbin Yu, and Lei Song. 2019. "Underwater Target Localization and Synchronization for a Distributed SIMO Sonar with an Isogradient SSP and Uncertainties in Receiver Locations" Sensors 19, no. 9: 1976. https://doi.org/10.3390/s19091976
APA StyleHe, C., Wang, Y., Yu, W., & Song, L. (2019). Underwater Target Localization and Synchronization for a Distributed SIMO Sonar with an Isogradient SSP and Uncertainties in Receiver Locations. Sensors, 19(9), 1976. https://doi.org/10.3390/s19091976





