Characterization and Design Improvement of a Thickness-Shear Lead Zirconate Titanate Transducer for Low Frequency Ultrasonic Guided Wave Applications
Abstract
1. Introduction
2. Analysis of a Current, State-of-the-Art, Generic, UGTW, Transducer, Design
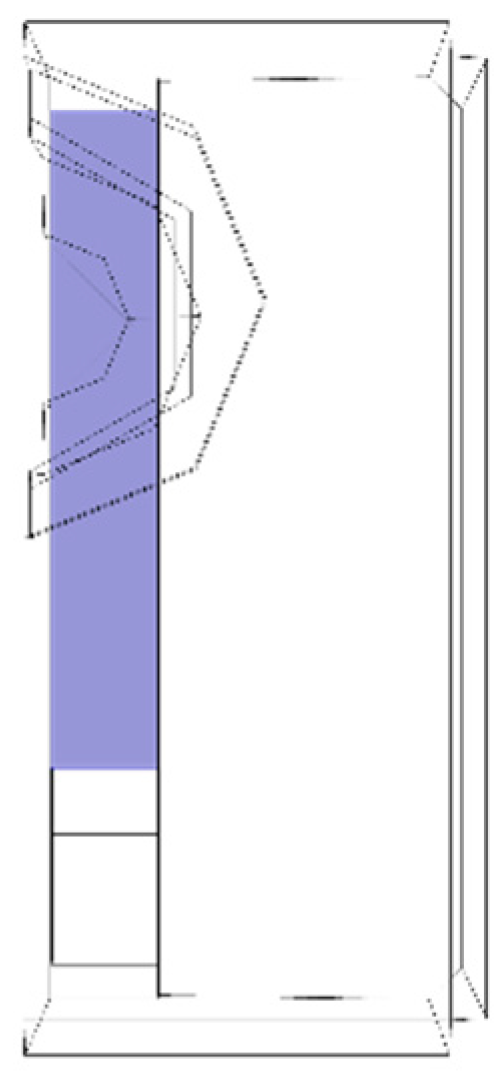
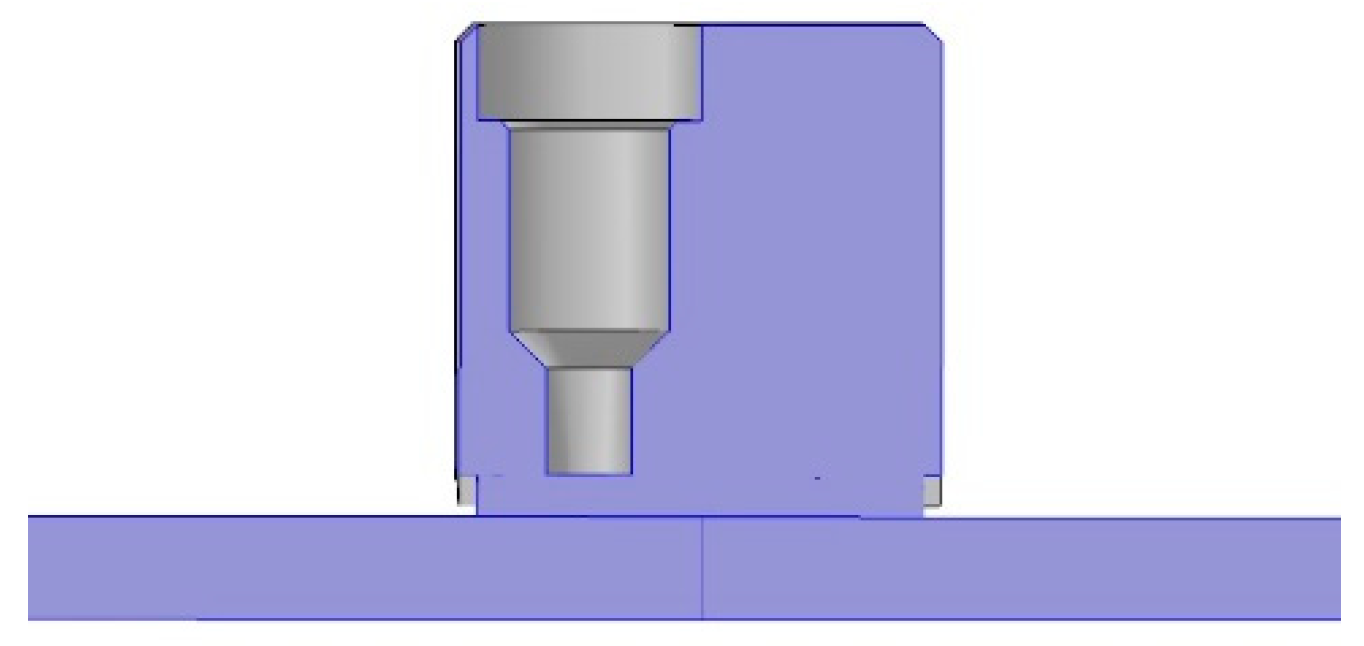
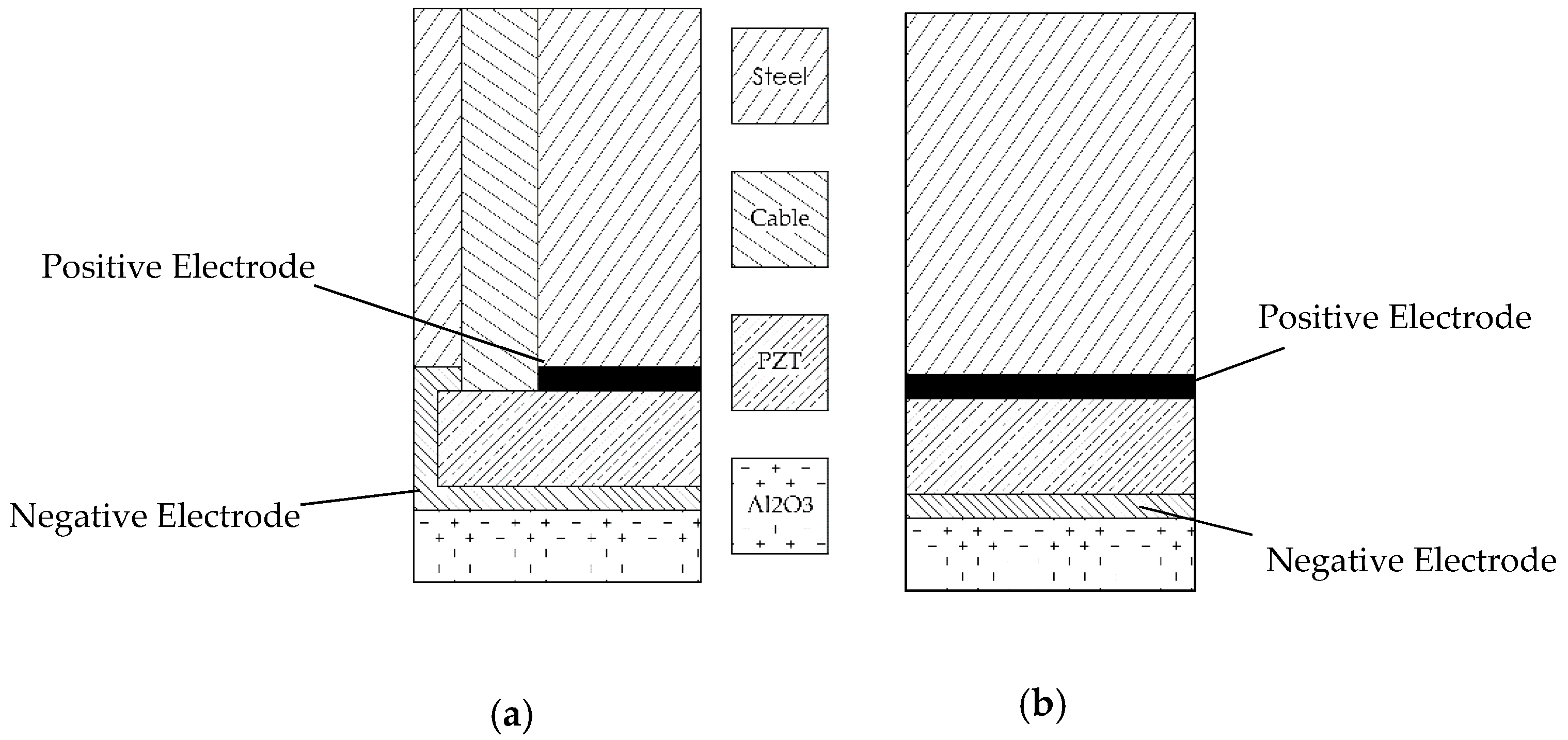
2.1. Design of the Transducers
2.2. Experimental Setup
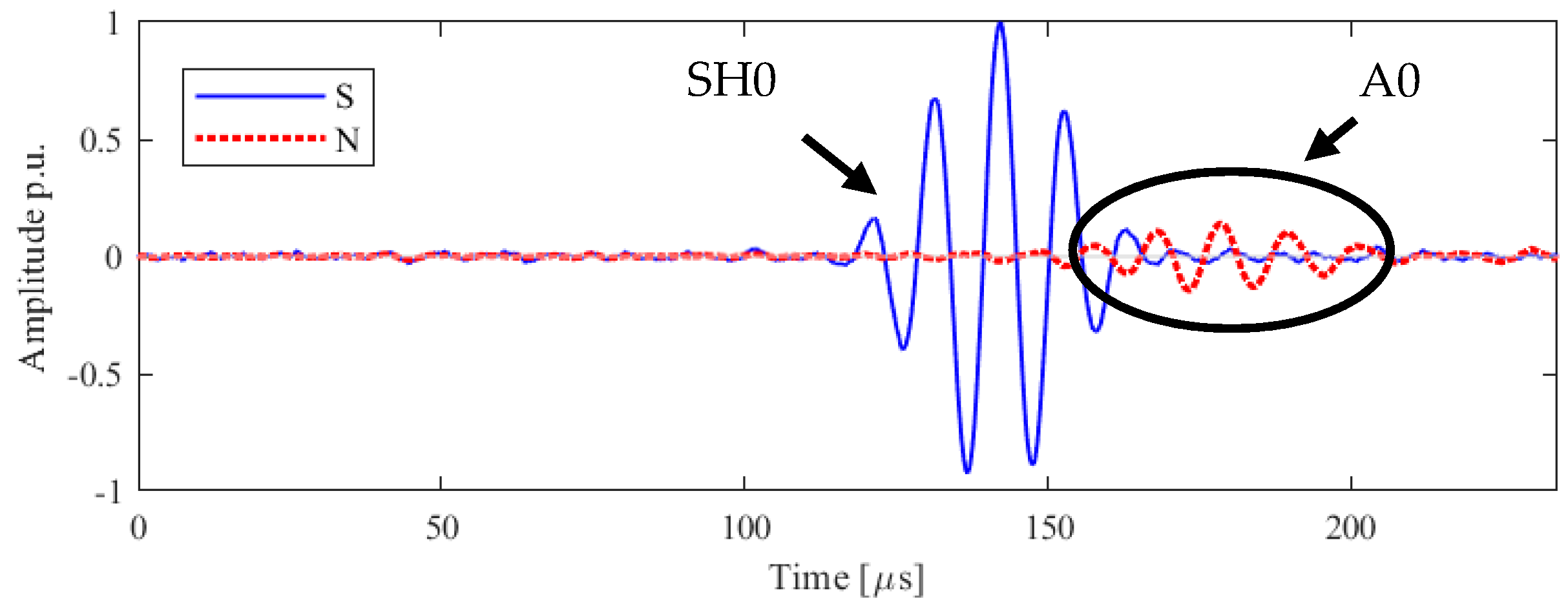
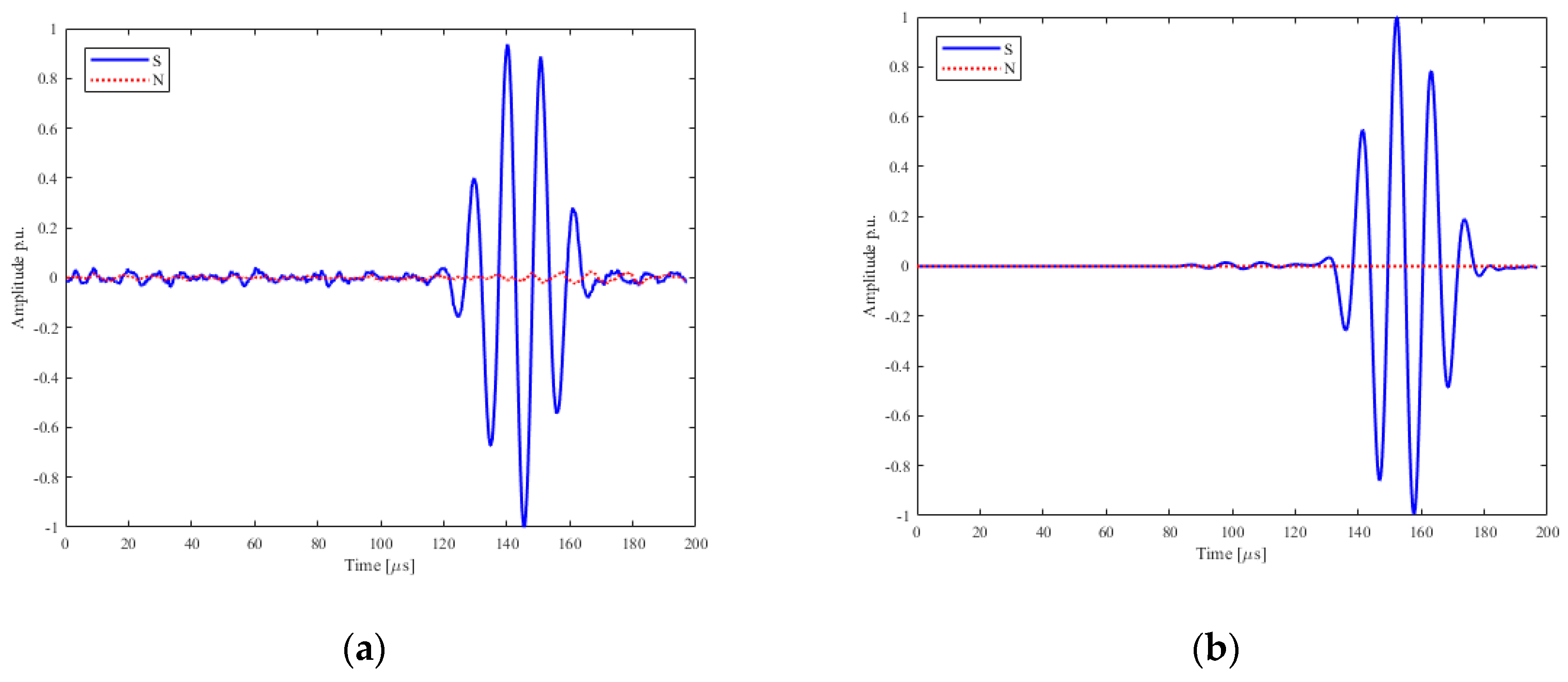
2.3. Experimental Results
3. Numerical Analysis of the Transient Behaviour for Configuration A
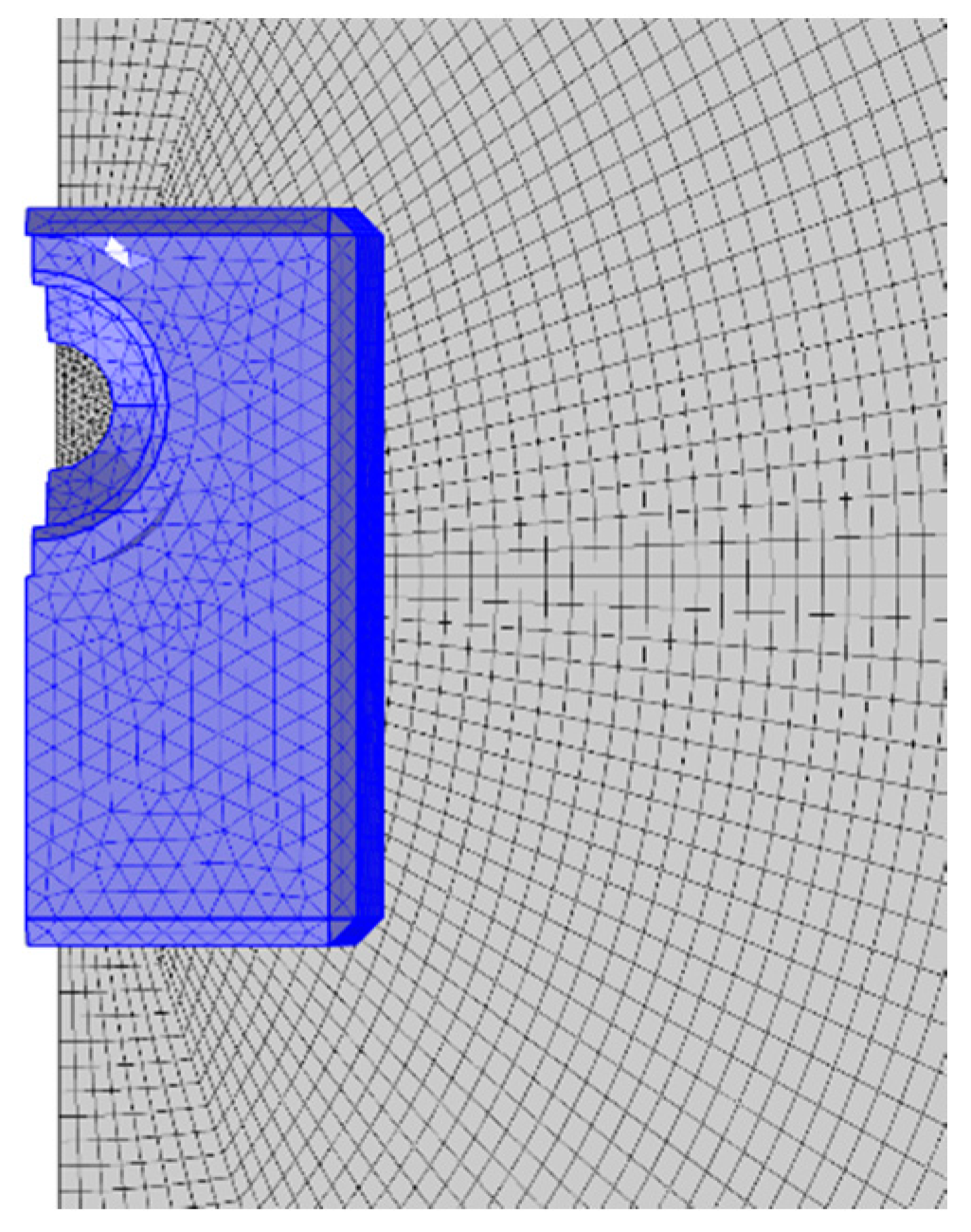
3.1. Background of the Model
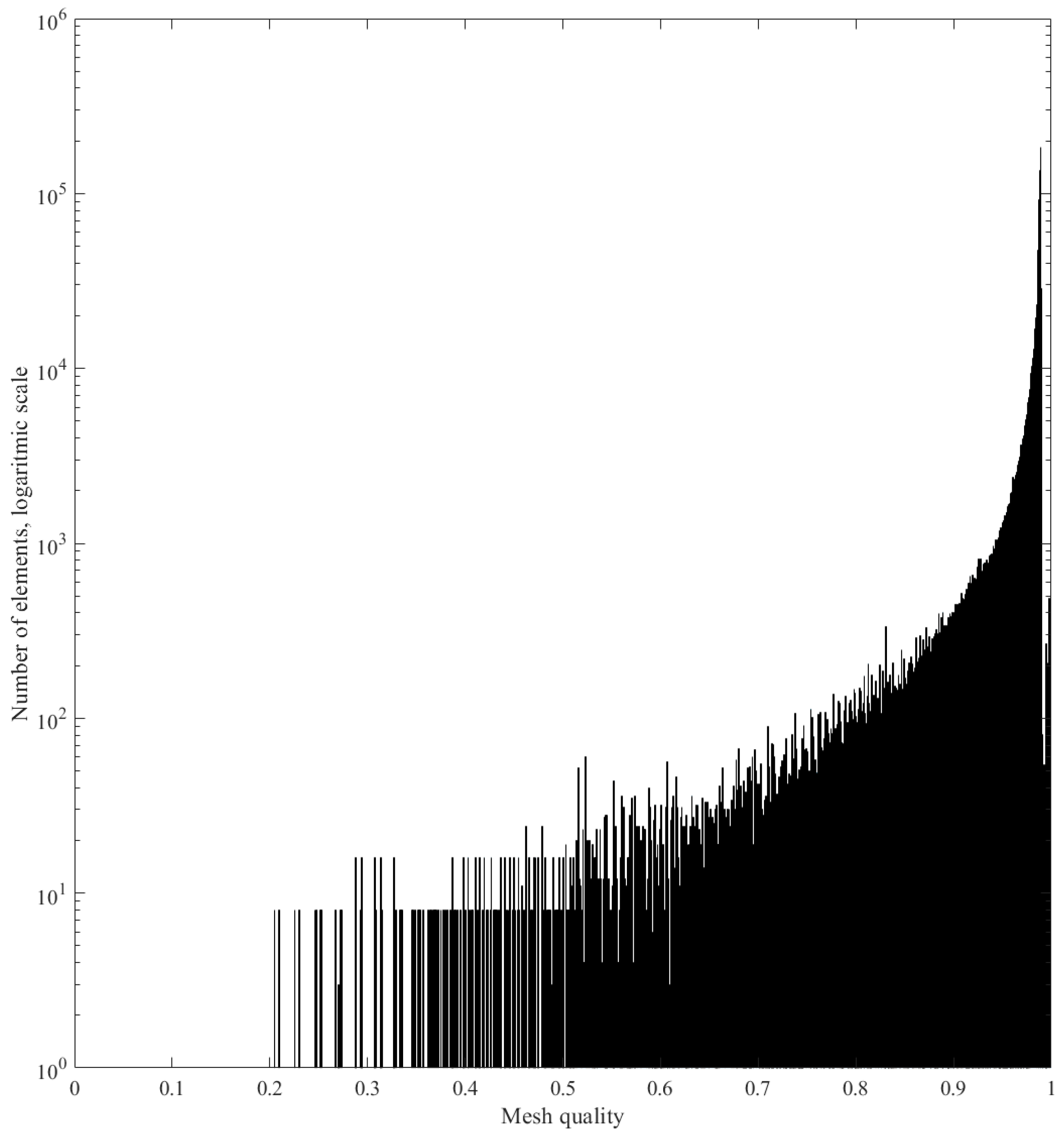
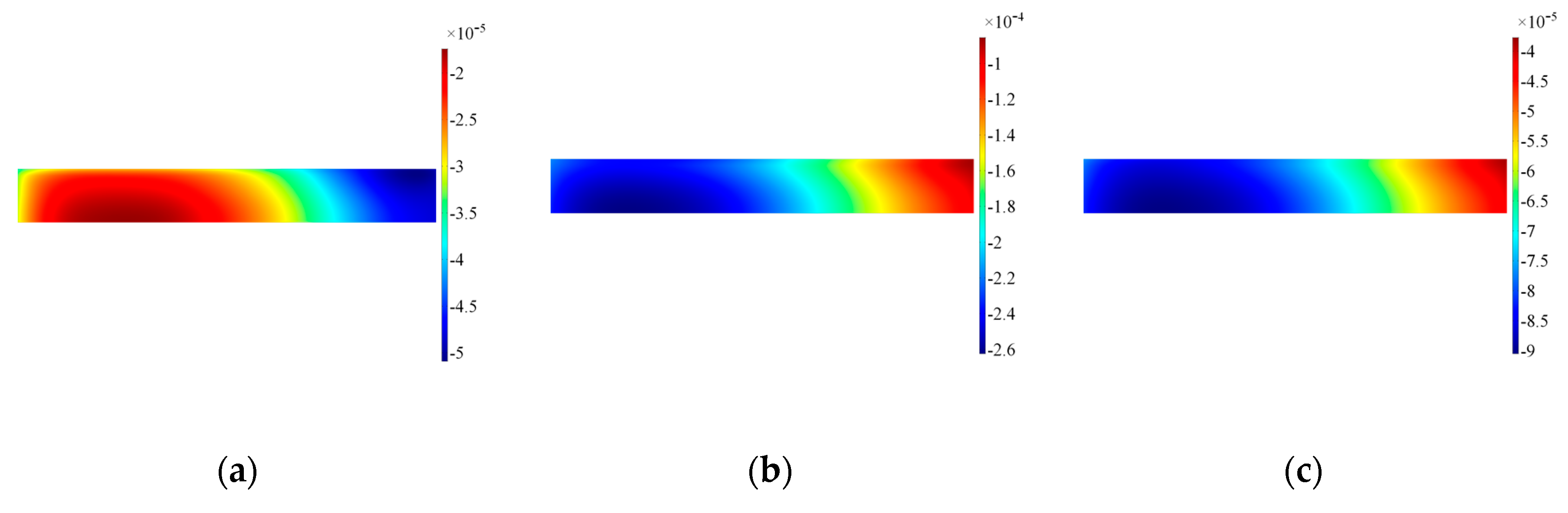
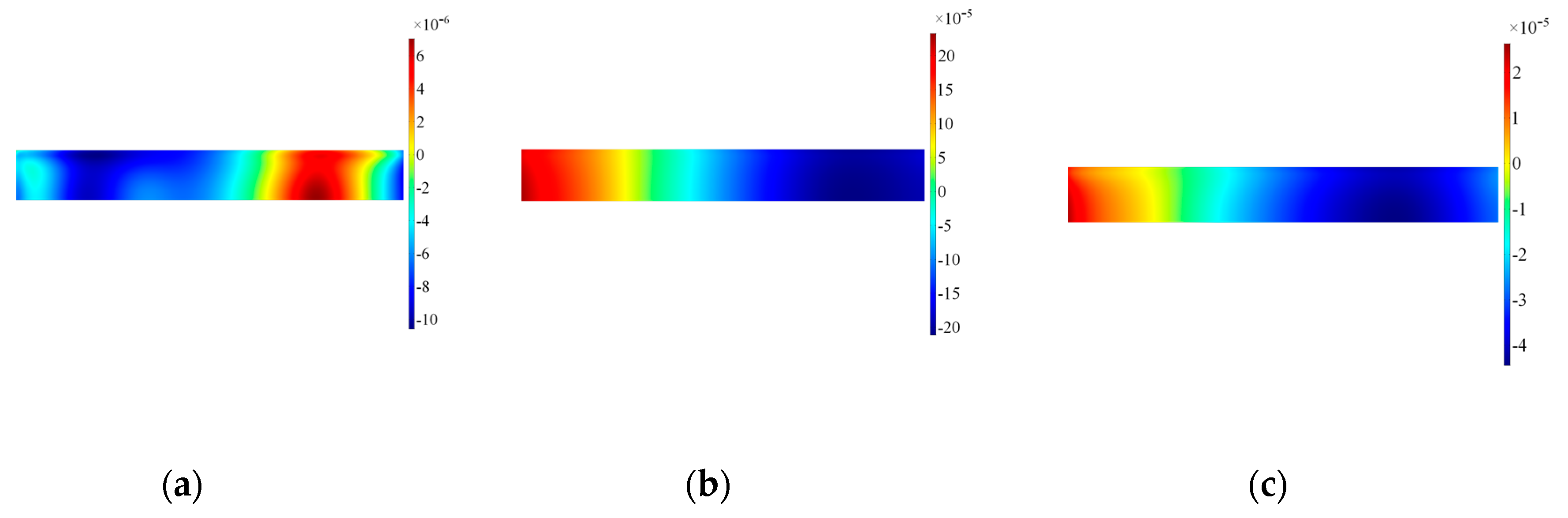
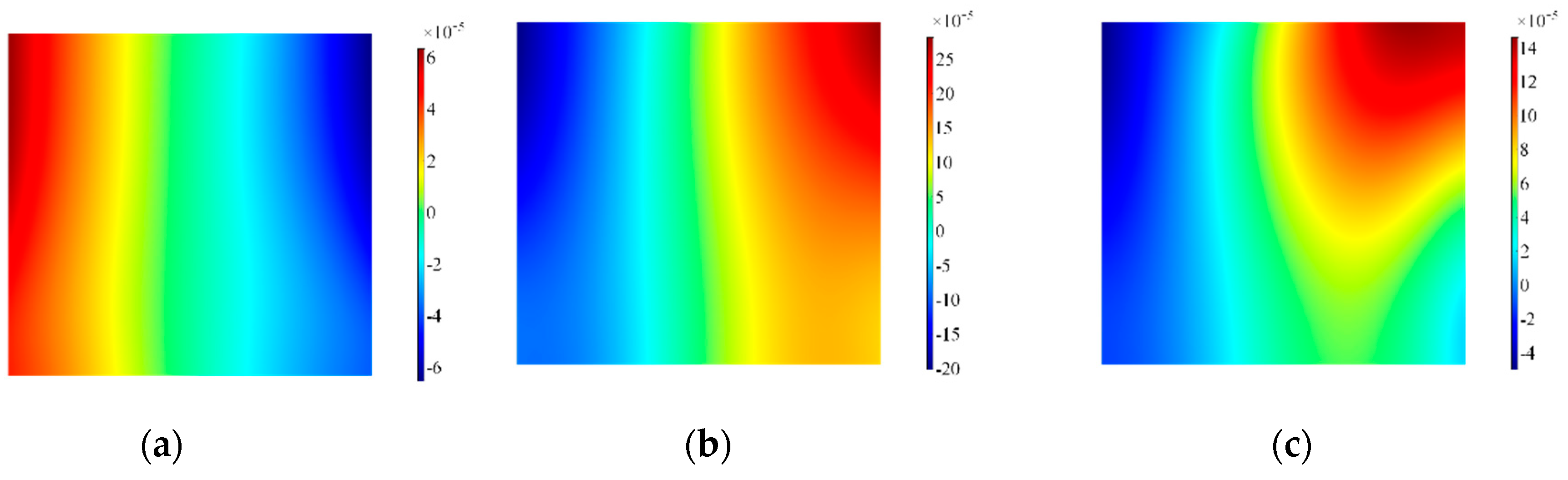
3.2. Numerical Results
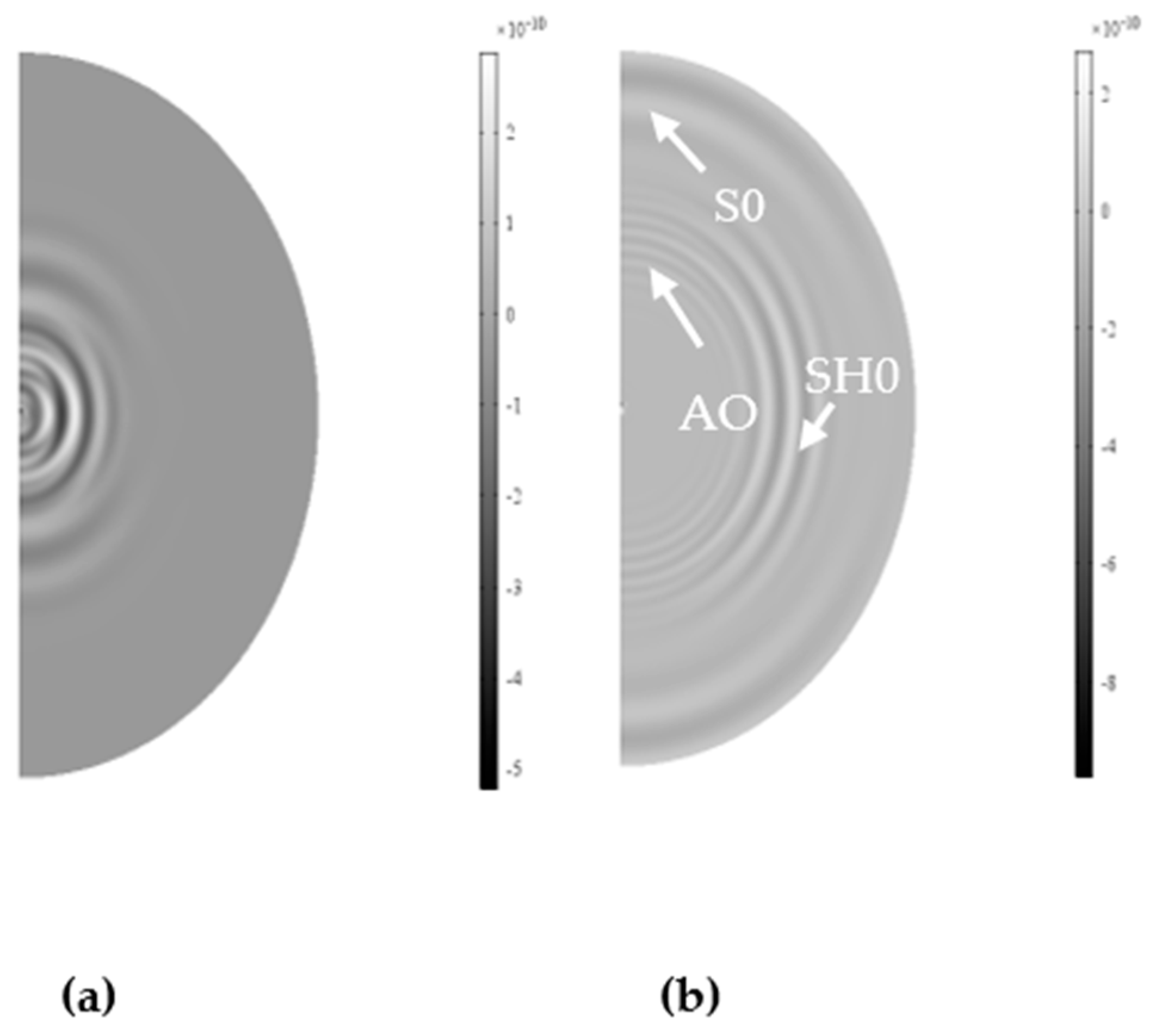
3.3. Physical Interpretation of the Pattern of the Transducer
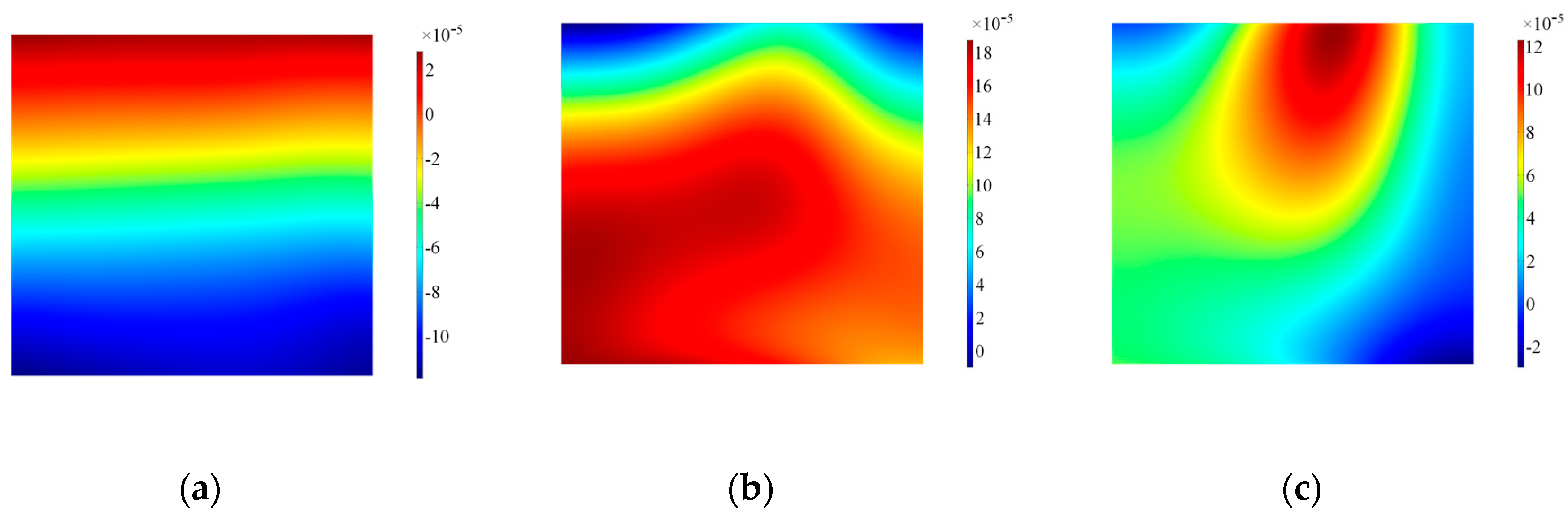
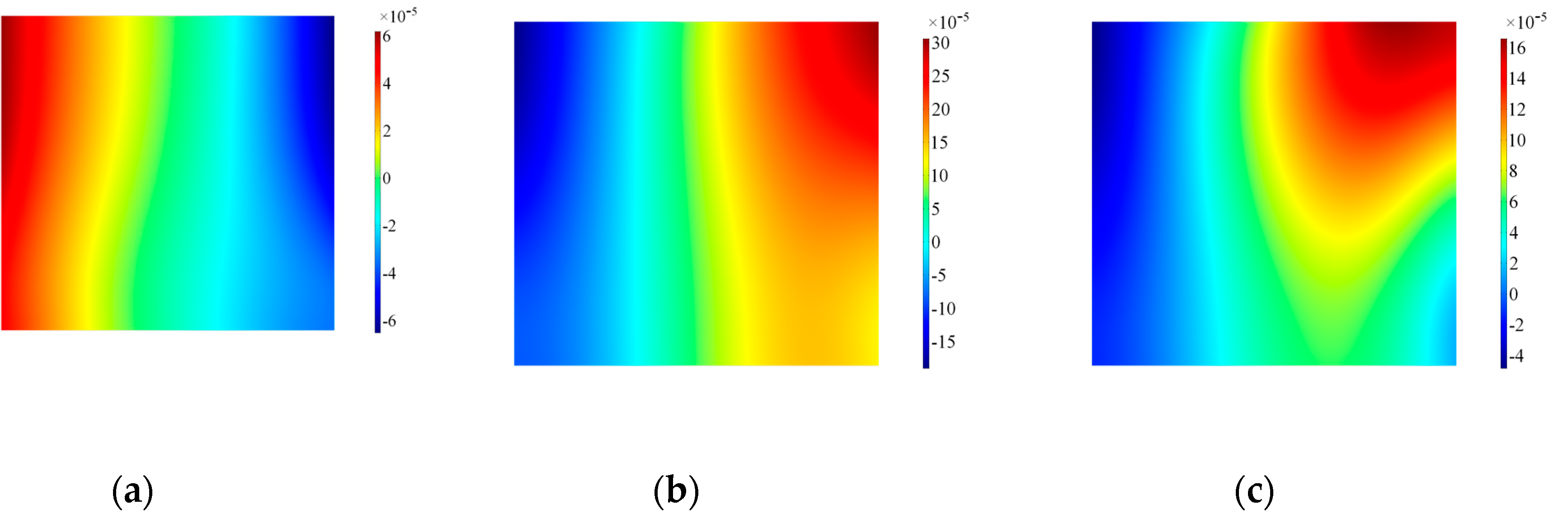
3.4. Numerical Results on a 3D Geometric Transducer without a Wraparound Electrode (Configuration A’)
4. Development and Testing of a New Configuration
Numerical Results on a 3D Geometric Transducer Without a Wraparound Electrode and with Geometry Modified (Configuration B)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bhaskaran, R.; Palaniswamy, N.; Rengaswamy, N.S.; Jayachandran, M. Global cost of corrosion—A historical review. Corros. Mater. 2005, 13, 621–628. [Google Scholar]
- Mudge, P.J. Field application of the Teletest long range ultrasonic testing technique. Insight 2001, 43, 3–96. [Google Scholar]
- Wilcox, P.D.; Lowe, M.J.S.; Cawley, P. Mode and transducer selection for long range Lamb wave inspection. J. Intell. Mater. Syst. Struct. 2001, 12, 553–565. [Google Scholar] [CrossRef]
- Lowe, P.S.; Sanderson, R.M.; Boulgouris, N.V.; Haig, A.G.; Balachandran, W. Inspection of cylindrical structures using the first longitudinal guided wave mode in isolation for higher flaw sensitivity. IEEE Sens. J. 2016, 16, 706–714. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Guided Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Lamb, H. On waves in an elastic plate. Proc. R. Soc. Lond. A Math. Phys. Sci. 1916, 93, 114–128. [Google Scholar] [CrossRef]
- Liu, Z.; He, Z.; Wu, C.; Wang, B.; Yang, X.S. Circumferential and longitudinal defect detection using T (0, 1) mode excited by thickness shear mode piezoelectric elements. Ultrasonics 2006, 44, 1135–1138. [Google Scholar] [CrossRef]
- Kamal, A.; Giurgiutiu, V. Shear horizontal wave excitation and reception with shear horizontal piezoelectric wafer active sensor (SH-PWAS). Smart Mater. Struct. 2014, 23, 085019. [Google Scholar] [CrossRef]
- Hongchen, M.; Huan, Q.; Wang, Q.; Li, F. Excitation and reception of single torsional wave T (0, 1) mode in pipes using face-shear d24 piezoelectric ring array. Smart Mater. Struct. 2017, 26, 025021. [Google Scholar]
- Lowe, P.S.; Scholehwar, T.; Yau, J.; Kanfoud, J.; Gan, T.; Selcuk, C. Flexible Shear Mode Transducer for Structural Health Monitoring using Ultrasonic Guided Waves. IEEE. Trans. Ind. Inform. 2018, 14, 2984–2993. [Google Scholar] [CrossRef]
- Belanger, P.; Boivin, G. Development of a low frequency omnidirectional piezoelectric shear horizontal wave transducer. Smart Mater. Struct. 2016, 25, 045024. [Google Scholar] [CrossRef]
- Boivin, G.; Viens, M.; Belanger, P. Plane wave SH0 piezoceramic transduction optimized using geometrical parameters. Sensors 2018, 18, 542. [Google Scholar] [CrossRef] [PubMed]
- Alleyne, D.N.; Cawley, P. The interaction of Lamb waves with defects. IEEE Trans. Ultrason. Ferroelect. Freq. Control 1992, 39, 381–397. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.B. Physical Principles of Measurement with EMAT Transducer. Phys. Acoust. 1990, 19, 157–200. [Google Scholar]
- Alleyne, D.N.; Cawley, P. The practical excitation and measurement of Lamb waves using piezoelectric transducers. In Review of Progress in Quantitative Nondestructive Evaluation; Springer: New York, NY, USA, 1994; Volume 13, pp. 181–185. [Google Scholar]
- Alleyne, D.N.; Cawley, P. The excitation of Lamb waves in pipes using dry coupled piezoelectric transducer. J. Nondestr. Eval. 1996, 15, 11–20. [Google Scholar] [CrossRef]
- Elborn, B.J. Performance Enhancements in an Ultrasonic Guilded Wave Pipe Inspection System. Master’s Dissertation, Dept. Mech. Aer. Civ. Eng., Brunel University London, Uxbridge, UK, 2015. [Google Scholar]
- Desilets, C.S.; Powell, D.J.; Abboud, N.; Wojcik, G.L. Effect of wraparound electrodes on ultrasonic array performance. In Proceedings of the Ultrasonics Symposium, Sendai, Japan, 5–8 October 1998; Volume 2, pp. 993–997. [Google Scholar]
- Engineer, B. The Mechanical and Resonant Behaviour of a Dry Coupled Thickness Shear PZT Transducer Used for Guided Wave Testing in Pipeline. Ph.D. Dissertation, Dept. Mech. Aer. Civ. Eng., Brunel University London, Uxbridge, UK, 2013. [Google Scholar]
- Lowe, P.S.; Fateri, S.; Sanderson, R.; Boulgouris, N.V. Finite element modelling of the interaction of ultrasonic guided waves with coupled piezoelectric transducers. Insight 2014, 56, 1–5. [Google Scholar] [CrossRef]
- Fateri, S.; Lowe, P.S.; Engineer, B.; Boulgouris, N.V. Investigation of Ultrasonic Guided Waves Interacting with Piezoelectric Transducers. IEEE Sens. J. 2015, 15, 4319–4328. [Google Scholar] [CrossRef]
- Marques, H.R. Omnidirectional and Unidirectional SH0 Mode Transducer Arrays for Guided Wave Evaluation of Plate-Like Structures. Ph.D. Dissertation, Dept. Mech. Aer. Civ. Eng., Brunel University London, Uxbridge, UK, 2016. [Google Scholar]
- Anurag, D.; Gan, T.H.; Mohimi, A.; Balachandran, W.; Kanfoud, J. Effect of Electrode Configuration on High Temperature Thickness Shear Gallium Phosphate Transducer. Proceedings 2017, 1, 381. [Google Scholar] [CrossRef]
- Zennaro, M.; Haig, A.G.; O’Boy, S.J.; Walsh, S.J. Experimental and numerical analysis of a transducer for the generation of guided waves. In Proceedings of the IXth NDT in Progress, Prague, Czech Republic, 9–11 October 2017. [Google Scholar]
- PI Ceramics. Piezoelectric Ceramic Components; PI Ceramics: Lederhose, Germany, 2007. [Google Scholar]
- Cao, W.; Jiu, S.; Jiang, B. Analysis of shear mode in a piezoelectric vibrator. J. Appl. Phys. 1998, 83, 4415–4420. [Google Scholar] [CrossRef][Green Version]
- Haig, A.G.; Sanderson, R.M.; Mudge, P.J.; Balachandran, W. Macro-fibre composite actuators for the transduction of Lamb and horizontal shear ultrasonic guided waves. Insight-Nondestr. Test. Cond. Monit. 2013, 55, 72–77. [Google Scholar] [CrossRef]
- COMSOL Multiphysics Reference Manual, Version 5.3a; COMSOL, Inc.: Burlington, MA, USA, 2015.
- Lais, H.; Lowe, P.S.; Gan, T.H.; Wrobel, L.C. Numerical modelling of acoustic pressure fields to optimize the ultrasonic cleaning technique for cylinder. Ultrason. Sonochem. 2018, 45, 7–16. [Google Scholar] [CrossRef]
- Baiyang, R.; Lissenden, C.J. Modeling guided wave excitation in plates with surface mounted piezoelectric elements: coupled physics and normal mode expansion. Smart Mater. Struct. 2018, 27, 045014. [Google Scholar]
- Zennaro, M.; Haig, A.G.; O’Boy, D.J.; Walsh, S.J.; Mudge, P. Parametric investigation of a transducer for guided wave applications. In Proceedings of the 12th ECNDT, Gothenburg, Sweden, 11–15 June 2018. [Google Scholar]
- Zennaro, M.; Haig, A.G.; O’Boy, D.J.; Walsh, S.J.; Mudge, P. An Investigation of ultrasonic transducer loading on a workpiece. In Proceedings of the Inter Noise, Chicago, IL, USA, 26–29 August 2018. [Google Scholar]


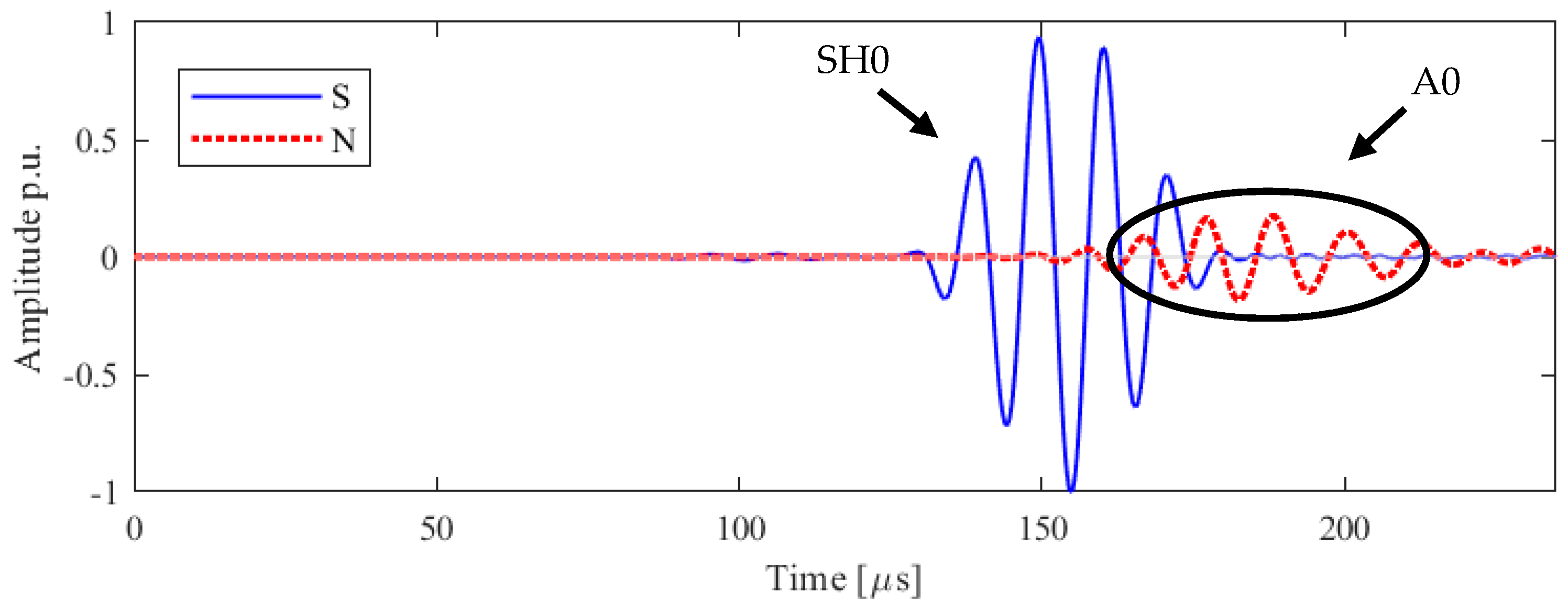
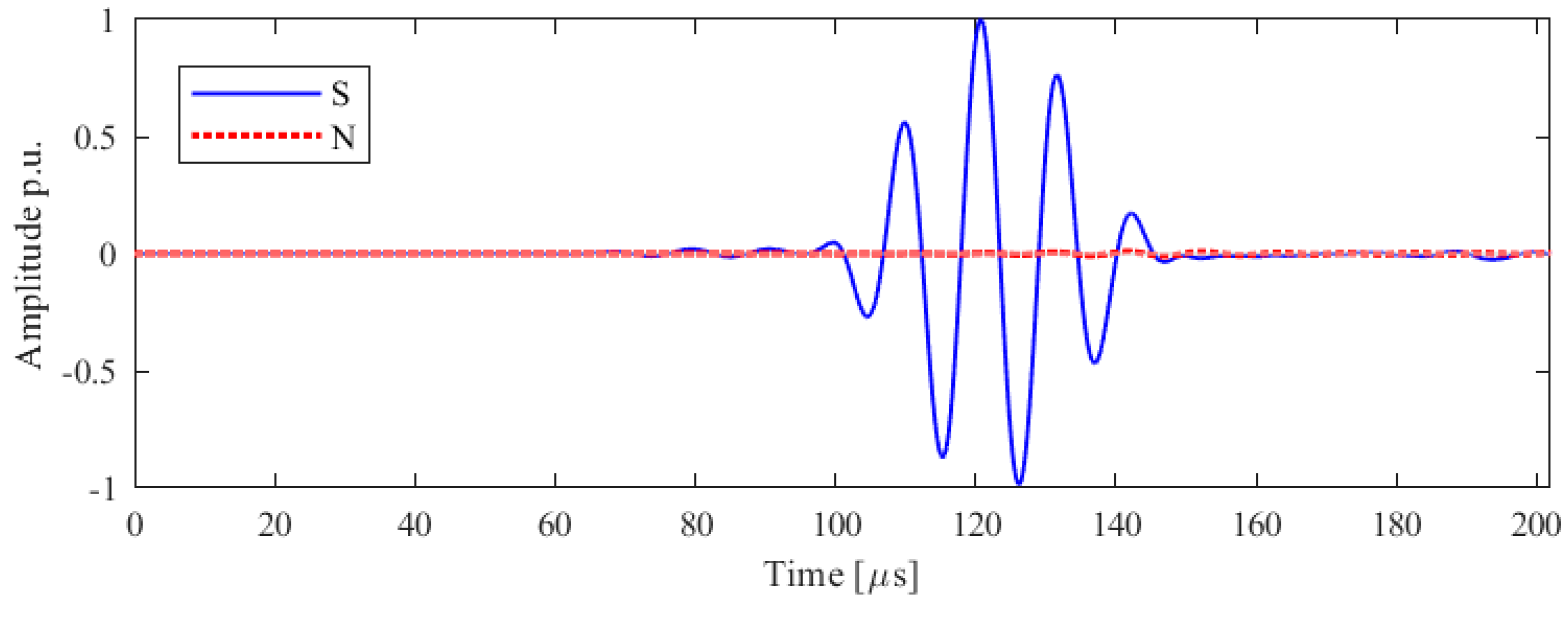
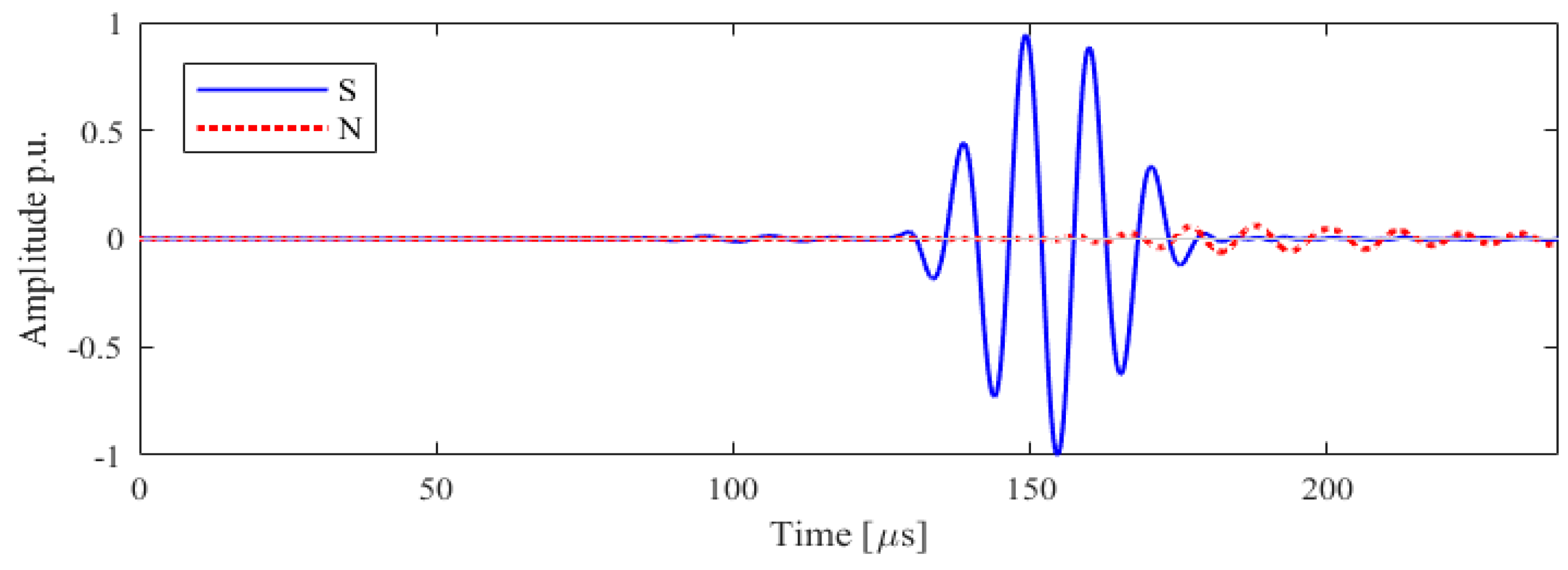
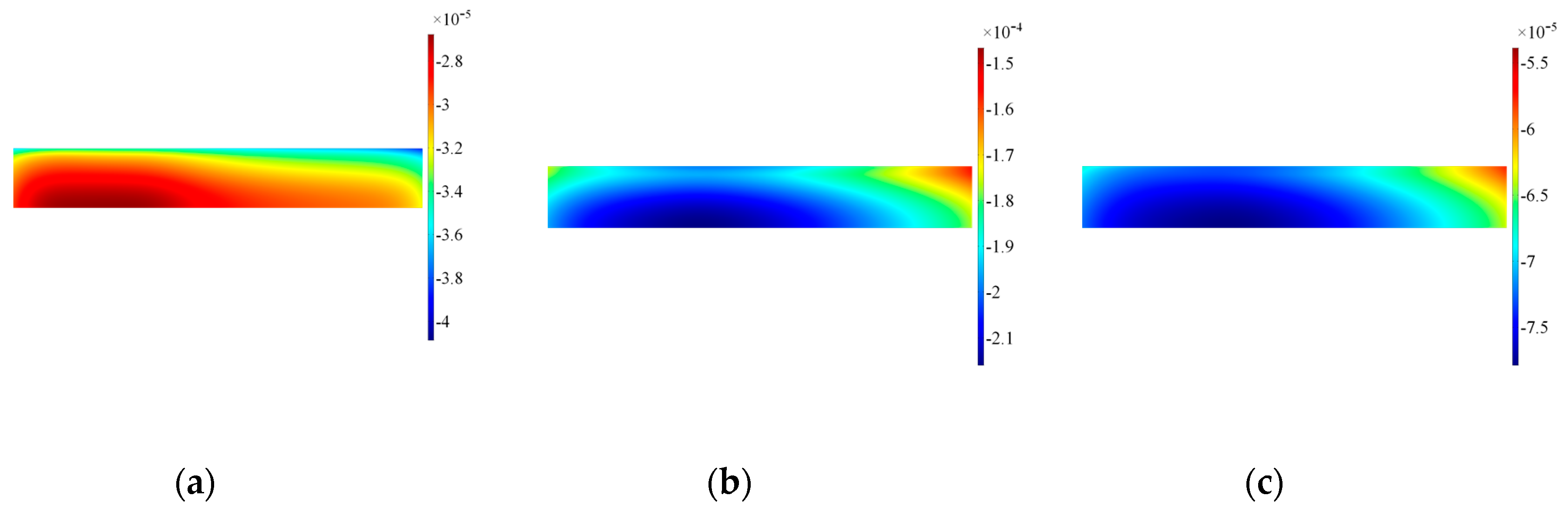
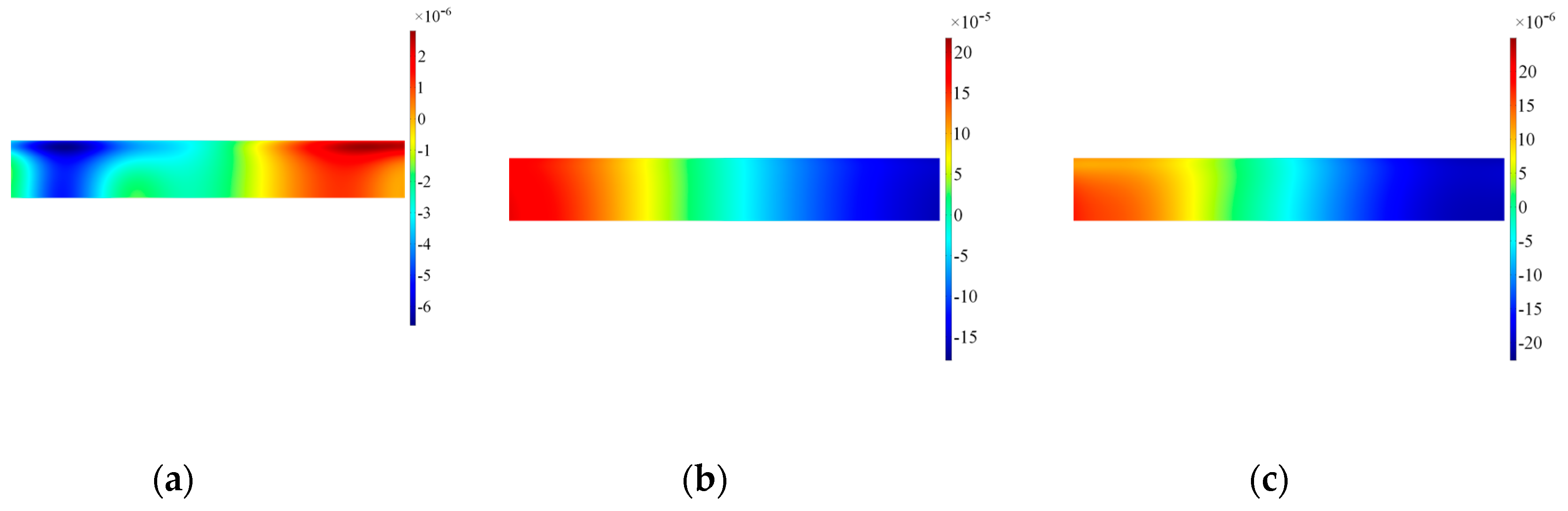
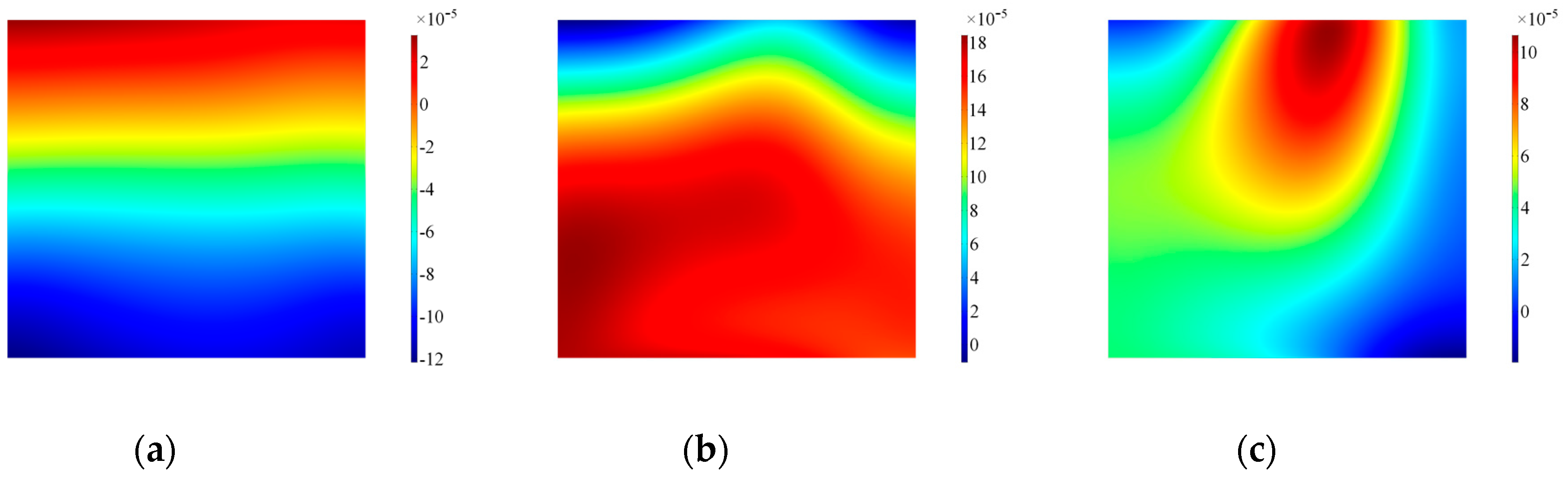
| Mode | Vgr [m/ms] | ToA [μs] |
|---|---|---|
| S0 | 5.4 | 74 |
| A0 | 2.6 | 153 |
| SH0 | 3.2 | 125 |
| Properties | Unit | Waveguide | Transducer | Block | Wear-Plate | Adhesive |
|---|---|---|---|---|---|---|
| Density | [kg/m3] | 7800 | 7800 | 8030 | 3960 | 752 |
| Young’s modulus | [Pa] | 207 × 109 | 110 × 109 | 193 × 109 | 370 × 109 | 1.47 × 109 |
| Poisson’s ratio | 0.3 | 0.36 | 0.25 | 0.22 | 0.4082 |
| Characteristics | A | B |
|---|---|---|
| Cable | Y | N |
| Wrap El. | Y | N |
| Continuous El. | N | Y |
| Copper tape | N | Y |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zennaro, M.; O’Boy, D.J.; Lowe, P.S.; Gan, T.-H. Characterization and Design Improvement of a Thickness-Shear Lead Zirconate Titanate Transducer for Low Frequency Ultrasonic Guided Wave Applications. Sensors 2019, 19, 1848. https://doi.org/10.3390/s19081848
Zennaro M, O’Boy DJ, Lowe PS, Gan T-H. Characterization and Design Improvement of a Thickness-Shear Lead Zirconate Titanate Transducer for Low Frequency Ultrasonic Guided Wave Applications. Sensors. 2019; 19(8):1848. https://doi.org/10.3390/s19081848
Chicago/Turabian StyleZennaro, Marco, Dan J. O’Boy, Premesh Shehan Lowe, and Tat-Hean Gan. 2019. "Characterization and Design Improvement of a Thickness-Shear Lead Zirconate Titanate Transducer for Low Frequency Ultrasonic Guided Wave Applications" Sensors 19, no. 8: 1848. https://doi.org/10.3390/s19081848
APA StyleZennaro, M., O’Boy, D. J., Lowe, P. S., & Gan, T.-H. (2019). Characterization and Design Improvement of a Thickness-Shear Lead Zirconate Titanate Transducer for Low Frequency Ultrasonic Guided Wave Applications. Sensors, 19(8), 1848. https://doi.org/10.3390/s19081848






