Modeling the Influence of Oil Film, Position and Orientation Parameters on the Accuracy of a Laser Triangulation Probe
Abstract
1. Introduction
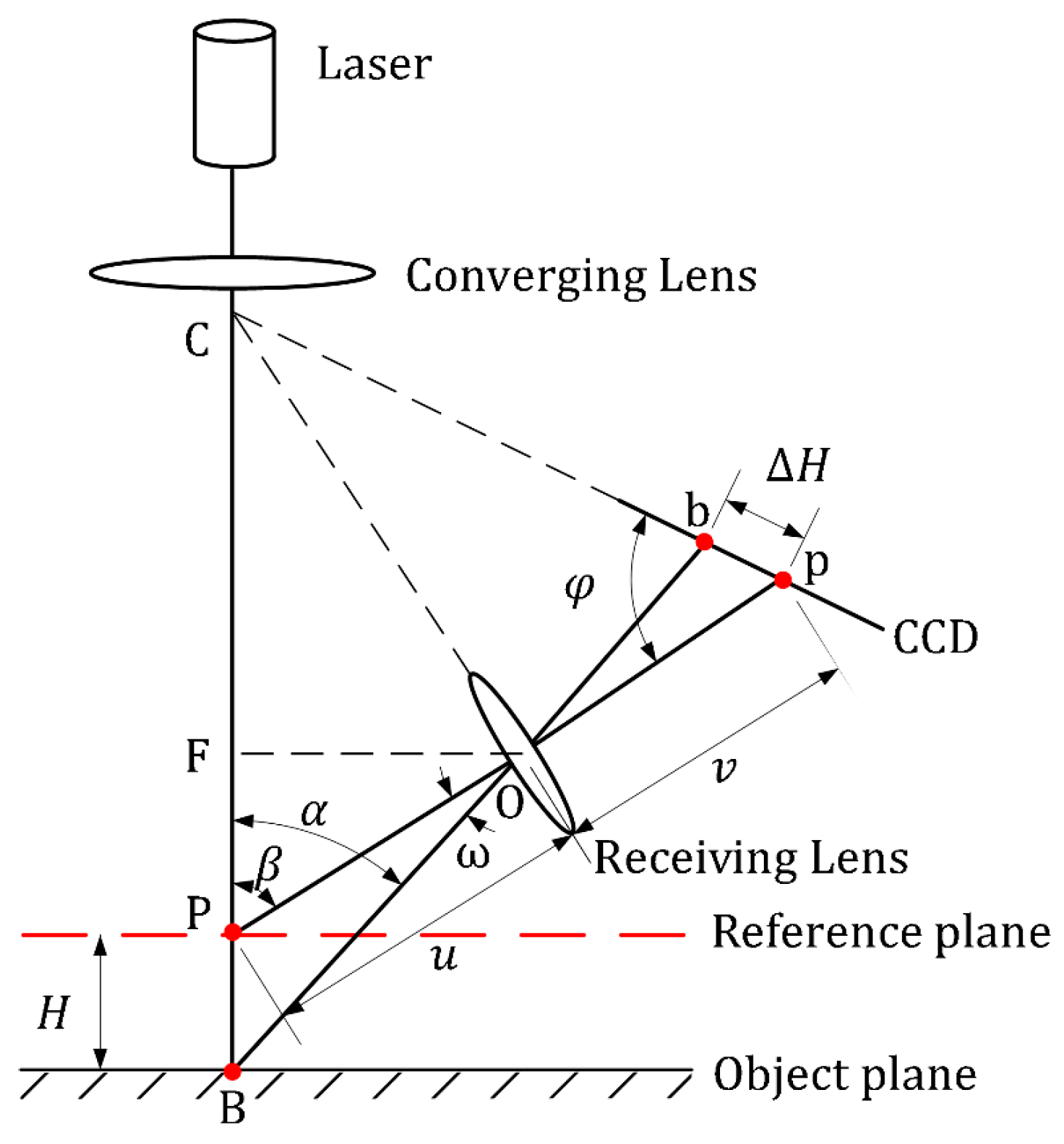
2. Measurement Principle
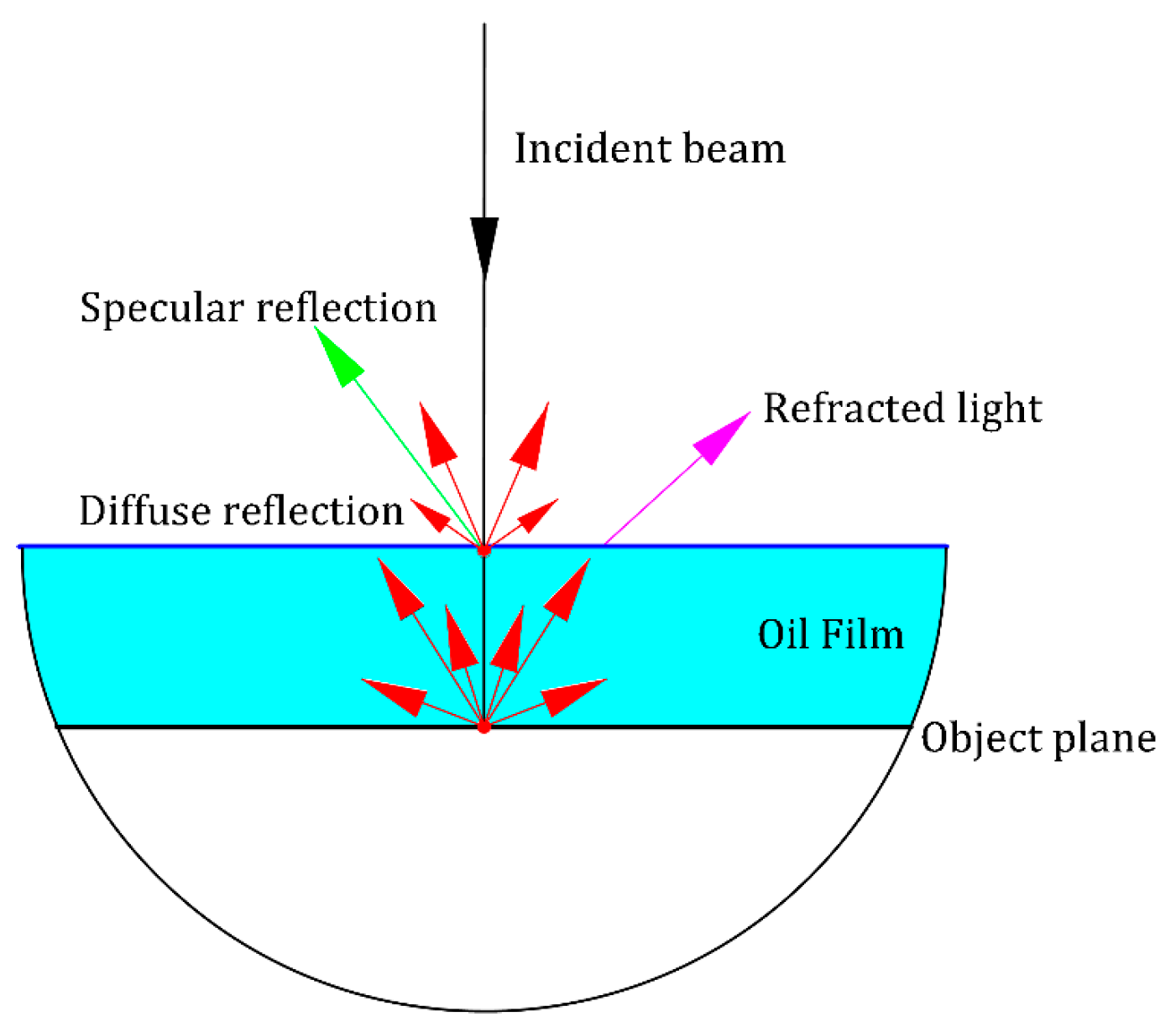
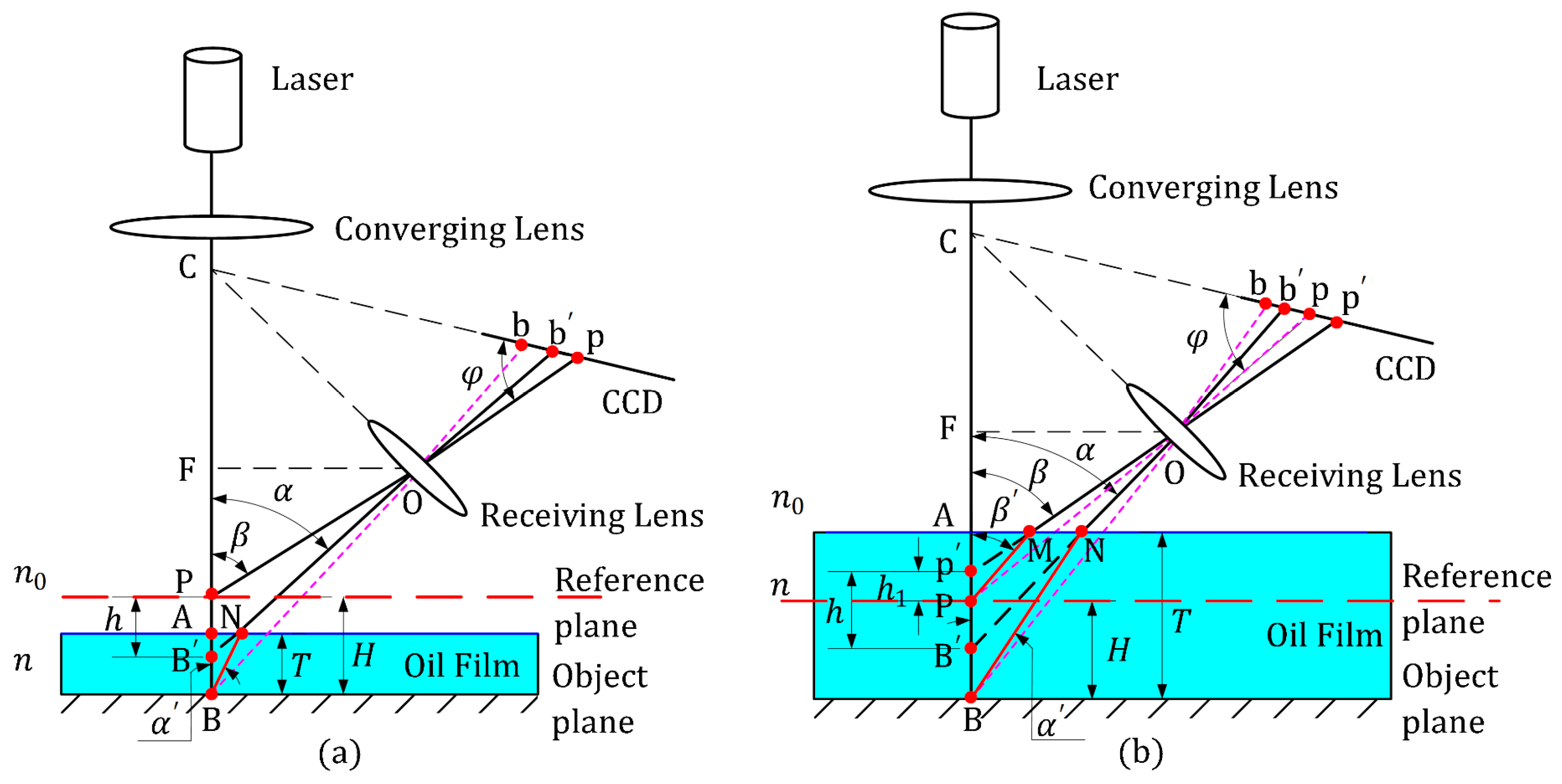
3. Influence of An Oil Film on Depth Measurement
Modeling Analysis
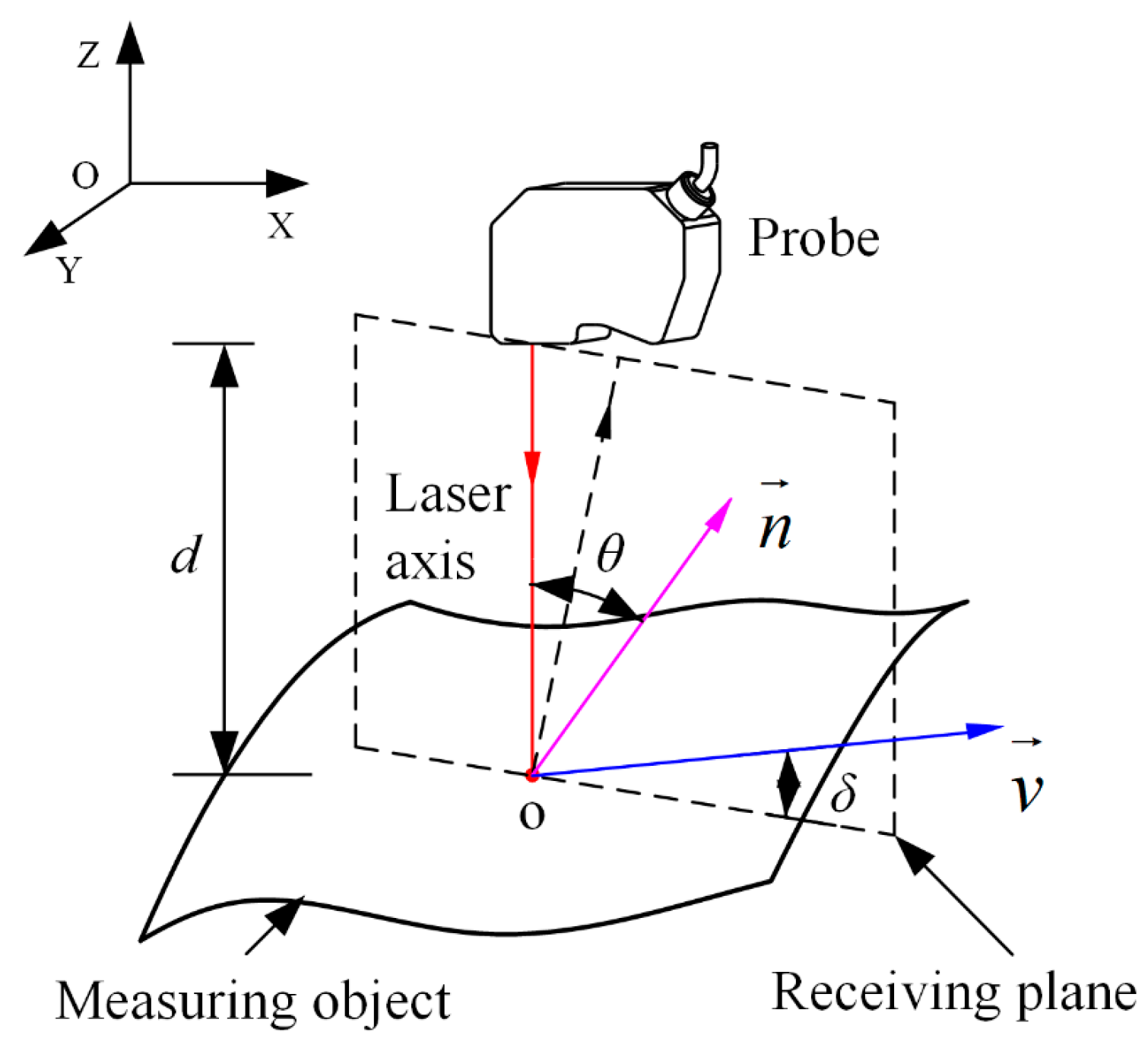
4. Influence of Probe’s Position and Orientation Parameters on Depth Measurement
- (1)
- d stands for the distance between the measurement point and the probe;
- (2)
- θ is the angle between the optical axis of probe’s converging lens and the normal vector at the measurement point;
- (3)
- δ is the angle between the probe’s moving direction and probe’s receiving plane. Where the receiving plane is composed of the incident beam and the optical axis of the receiving lens.
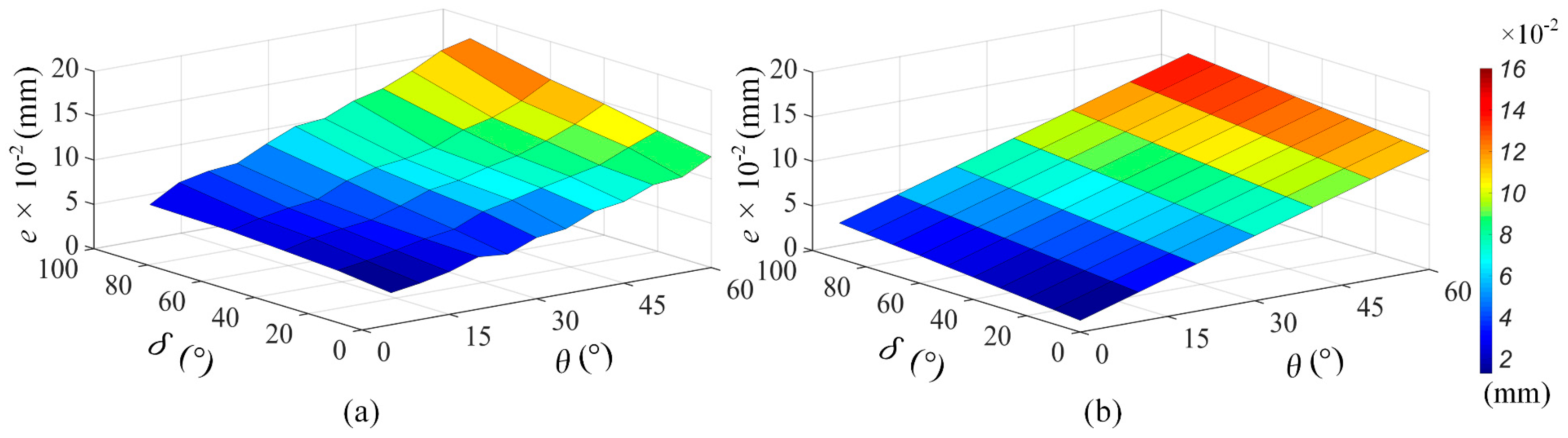
4.1. Error Evaluation
4.2. Modeling Analysis
5. Other Error Factors
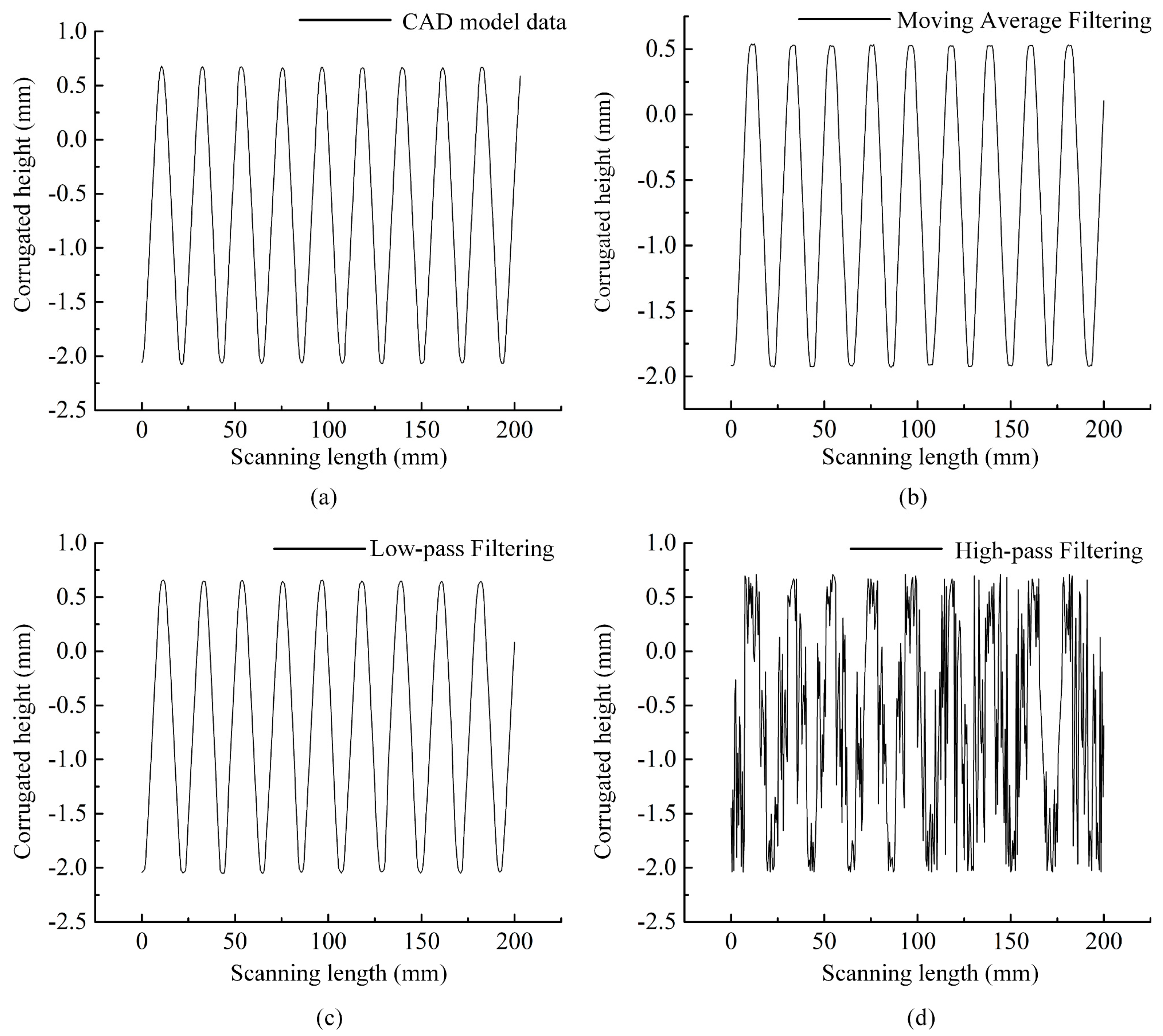
Filtering Processing
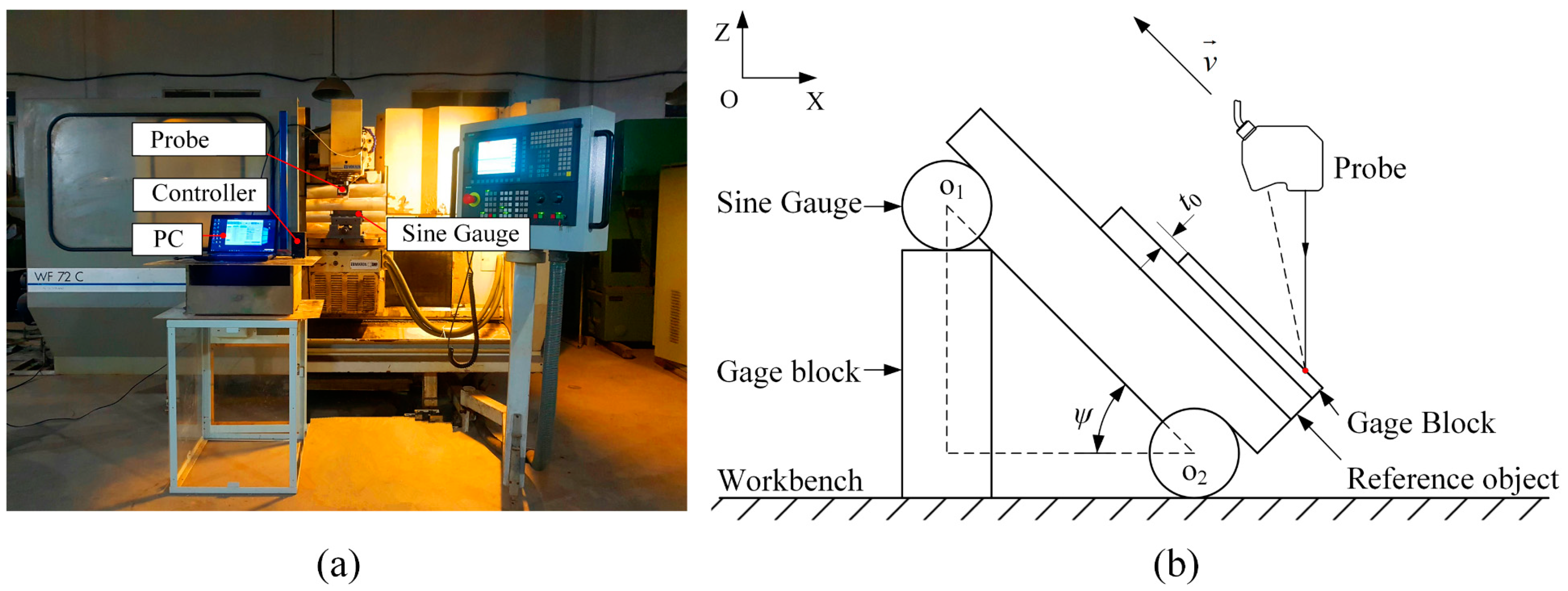
6. Experimental Verification
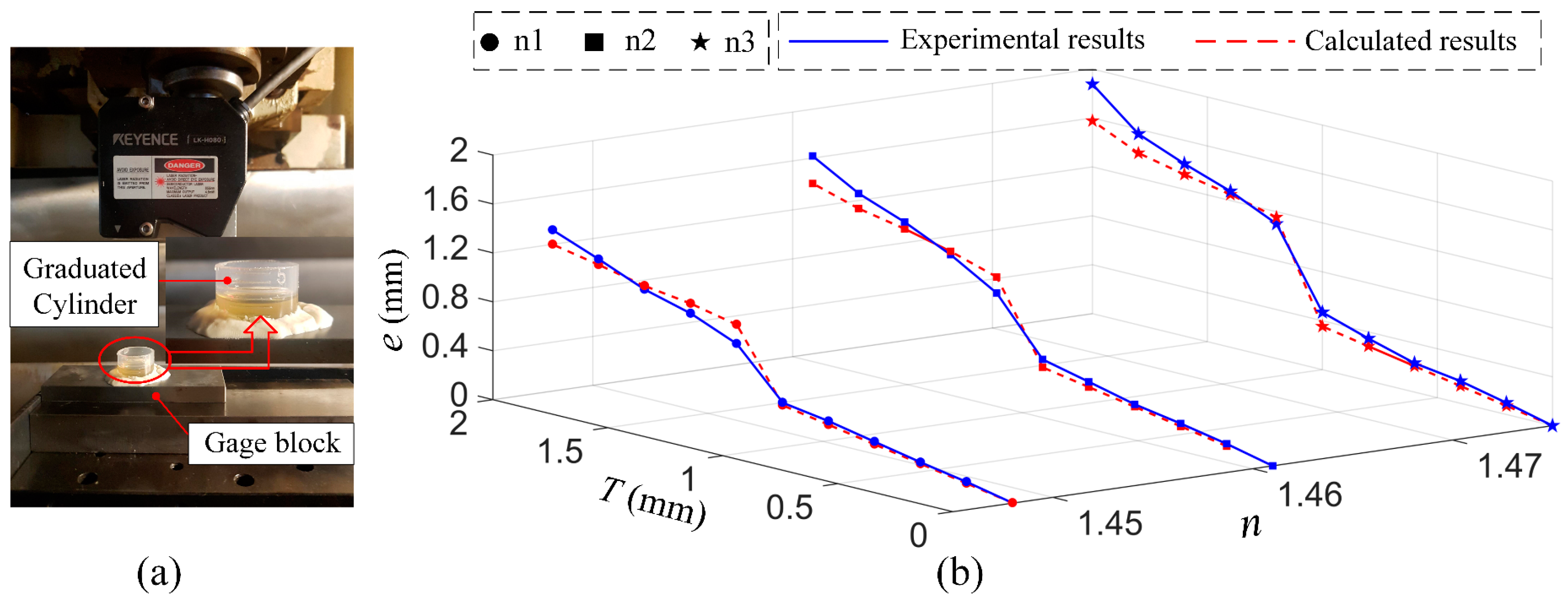
6.1. Measurement with the Presence of Oil Film
6.2. Measurement of the Free-Form Surface
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kulkarni, R.; Rastogi, P. Optical measurement techniques—A push for digitization. Opt. Lasers Eng. 2016, 87, 1–17. [Google Scholar] [CrossRef]
- Piskorski, K.; Niemiec, M.; Borowicz, L.; Przewlocki, H.M. A measurement system for the photoelectric and electrical characterization of modern semiconductor devices. Meas. Sci. Technol. 2017, 28, 055012. [Google Scholar] [CrossRef]
- Baqersad, J.; Poozesh, P.; Niezrecki, C.; Avitabile, P. Photogrammetry and optical methods in structural dynamics—A review. Mech. Syst. Signal Process. 2017, 86, 17–34. [Google Scholar] [CrossRef]
- Dong, Z.; Sun, X.; Chen, C.; Sun, M. A Fast and On-Machine Measuring System Using the Laser Displacement Sensor for the Contour Parameters of the Drill Pipe Thread. Sensors 2018, 18, 1192. [Google Scholar] [CrossRef]
- Giri, P.; Kharkovsky, S. Detection of surface crack in concrete using measurement technique with laser displacement sensor. IEEE Trans. Instrum. Meas. 2016, 65, 1951–1953. [Google Scholar] [CrossRef]
- Lu, Z.; Li, M.; Zheng, T.; Wang, L.; Tan, J. Measuring parallelism of two parallel narrow beams based on differential defocusing principle. Opt. Express 2016, 24, 15854–15862. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, D.; Li, J.; Born, R.; Curt Maxey, L.; Dinwiddie, R.B.; Daniel, C.; Wood III, D.L. Non-destructive evaluation of slot-die-coated lithium secondary battery electrodes by in-line laser caliper and IR thermography methods. Anal. Methods 2014, 6, 674–683. [Google Scholar] [CrossRef]
- Buzinski, M.; Levine, A.; Stevenson, W.H. Performance characteristics of range sensors utilizing optical triangulation. In Proceedings of the IEEE 1992 National Aerospace and Electronics Conference@ m_NAECON 1992, Dayton, OH, USA, 18–22 May 1992; pp. 1230–1236. [Google Scholar]
- Yafaev, D. Mathematical Scattering Theory: Analytic Theory; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Vukašinović, N.; Duhovnik, J. Optical 3D Geometry Measurments Based on Laser Triangulation. In Advanced CAD Modeling: Explicit, Parametric, Free-Form CAD and Re-Engineering; Springer International Publishing: Cham, Switzerland, 2019; pp. 191–216. ISBN 978-3-030-02399-7. [Google Scholar]
- Dorsch, R.G.; Häusler, G.; Herrmann, J.M. Laser triangulation: Fundamental uncertainty in distance measurement. Appl. Opt. 1994, 33, 1306–1314. [Google Scholar] [CrossRef]
- Mueller, T.; Poesch, A.; Reithmeier, E. Measurement Uncertainty of Microscopic Laser Triangulation on Technical Surfaces. Microsc. Microanal. 2015, 21, 1443–1454. [Google Scholar] [CrossRef] [PubMed]
- Paulus, S.; Eichert, T.; Goldbach, H.; Kuhlmann, H. Limits of Active Laser Triangulation as an Instrument for High Precision Plant Imaging. Sensors 2014, 14, 2489–2509. [Google Scholar] [CrossRef]
- Rico, J.C.; Valiño, G.; Fernández, P.; Zapico, P.; Blanco, D.; Mateos, S. Adjustment recommendations of a conoscopic holography sensor for a reliable scanning of surfaces with roughness grades obtained by different processes. Precis. Eng. 2015, 42, 335–345. [Google Scholar] [CrossRef]
- Lefebvre, D.; Doucet, M.; Duval, Y.; Roy, S. 3D Laser Triangulation Compensation for Non-Uniform Surfaces Reflectivity. In Proceedings of the Imaging and Applied Optics (2013), Arlington, VA, USA, 23–27 June 2013; p. ATu2B.3. [Google Scholar]
- Muralikrishnan, B.; Ren, W.; Everett, D.; Stanfield, E.; Doiron, T. Performance evaluation experiments on a laser spot triangulation probe. Measurement 2012, 45, 333–343. [Google Scholar] [CrossRef]
- Cuesta, E.; Rico, J.C.; Fernández, P.; Blanco, D.; Valiño, G. Influence of roughness on surface scanning by means of a laser stripe system. Int. J. Adv. Manuf. Technol. 2009, 43, 1157. [Google Scholar] [CrossRef]
- Vukašinović, N.; Bračun, D.; Možina, J.; Duhovnik, J. The influence of incident angle, object colour and distance on CNC laser scanning. Int. J. Adv. Manuf. Technol. 2010, 50, 265–274. [Google Scholar] [CrossRef]
- Li, S.; Jia, X.; Chen, M.; Yang, Y. Error analysis and correction for color in laser triangulation measurement. Optik 2018, 168, 165–173. [Google Scholar] [CrossRef]
- Dong, Z.; Sun, X.; Liu, W.; Yang, H. Measurement of free-form curved surfaces using laser triangulation. Sensors 2018, 18, 3527. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Li, F.; Liu, H.; Cai, H.; Mao, X.; Peng, F. A measurement strategy and an error-compensation model for the on-machine laser measurement of large-scale free-form surfaces. Meas. Sci. Technol. 2013, 25, 015204. [Google Scholar] [CrossRef]
- Sun, B.; Li, B. A Rapid Method to Achieve Aero-Engine Blade Form Detection. Sensors 2015, 15, 12782–12801. [Google Scholar] [CrossRef] [PubMed]
- Xi, F.; Liu, Y.; Feng, H.-Y. Error compensation for three-dimensional line laser scanning data. Int. J. Adv. Manuf. Technol. 2001, 18, 211–216. [Google Scholar] [CrossRef]
- Isheil, A.; Gonnet, J.-P.; Joannic, D.; Fontaine, J.-F. Systematic error correction of a 3D laser scanning measurement device. Opt. Lasers Eng. 2011, 49, 16–24. [Google Scholar] [CrossRef]
- Miks, A.; Novak, J.; Novak, P. Analysis of imaging for laser triangulation sensors under Scheimpflug rule. Opt. Express 2013, 21, 18225–18235. [Google Scholar] [CrossRef] [PubMed]
- OuYang, D.; Feng, H.-Y. On the normal vector estimation for point cloud data from smooth surfaces. Comput.-Aided Des. 2005, 37, 1071–1079. [Google Scholar] [CrossRef]
- Lou, S.; Zeng, W.-H.; Jiang, X.-Q.; Scott, P.J. Robust Filtration Techniques in Geometrical Metrology and Their Comparison. Int. J. Autom. Comput. 2013, 10, 1–8. [Google Scholar] [CrossRef]
- Destro, R.; Matakas, L.; Komatsu, W.; Ama, N.R.N. Implementation aspects of adaptive window moving average filter applied to PLLs—Comparative study. In Proceedings of the 2013 Brazilian Power Electronics Conference, Gramado, Brazil, 27–31 October 2013; pp. 730–736. [Google Scholar]
- Chowdhury, R.H.; Reaz, M.B.I.; Ali, M.A.B.M.; Bakar, A.A.A.; Chellappan, K.; Chang, T.G. Surface Electromyography Signal Processing and Classification Techniques. Sensors 2013, 13, 12431–12466. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Specifications |
|---|---|
| Installation mode | Diffuse reflection |
| Reference distance | 80 mm |
| Measuring range | ±18 mm |
| Beam diameter | 70 μm |
| Linearity | ±0.02 F.S. (Full Scale: F.S.; F.S. = 36 mm) |
| Repeatability | 0.1 μm |
| Resolution | 0.1 μm |
| Sampling frequency | 2.55/5/10/20/50/100/200/500/1000 μs |
| Temperature characteristic | 0.01 F.S./°C |
| Communication mode | RS232/USB/Ethernet |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Chen, B.; Ye, C.; Yan, X. Modeling the Influence of Oil Film, Position and Orientation Parameters on the Accuracy of a Laser Triangulation Probe. Sensors 2019, 19, 1844. https://doi.org/10.3390/s19081844
Wu C, Chen B, Ye C, Yan X. Modeling the Influence of Oil Film, Position and Orientation Parameters on the Accuracy of a Laser Triangulation Probe. Sensors. 2019; 19(8):1844. https://doi.org/10.3390/s19081844
Chicago/Turabian StyleWu, Chengxing, Baijin Chen, Chunsheng Ye, and Xiaopeng Yan. 2019. "Modeling the Influence of Oil Film, Position and Orientation Parameters on the Accuracy of a Laser Triangulation Probe" Sensors 19, no. 8: 1844. https://doi.org/10.3390/s19081844
APA StyleWu, C., Chen, B., Ye, C., & Yan, X. (2019). Modeling the Influence of Oil Film, Position and Orientation Parameters on the Accuracy of a Laser Triangulation Probe. Sensors, 19(8), 1844. https://doi.org/10.3390/s19081844





