Bandwidth Modeling of Silicon Retinas for Next Generation Visual Sensor Networks
Abstract
1. Introduction
1.1. Dynamic Vision Sensors
1.2. Scene Complexity
1.3. Motivation and Novelty
1.4. Contributions Provided in This Paper
- Which of the available scene complexity metrics shows the best correlation with the event rate?
- Can we define a novel scene complexity metric showing better correlation with the event rate?
- How can we model the relationship between the event rate and the scene complexity metric?
- How can we model the relationship between the event rate and the motion speed of the sensor?
- Finally, how can we model the neuromorphic data rate as a function of both the scene complexity metric and the motion speed of the sensor?
2. Materials and Methods
2.1. Dataset
- The asynchronous neuromorphic event stream in the form of the aforementioned tuple, i.e., .
- The frame-based output, in the form of intensity images, at approximately 24 frames per second. Each intensity image is precisely time stamped, which enables the recording of the number of neuromorphic events between any two intensity images.
- Inertial measurements in the form of a three-dimensional acceleration and velocity reported at a 1-ms interval. This information makes it possible to study the asynchronous event rate w.r.t. the three-dimensional velocity.
2.2. Methodology
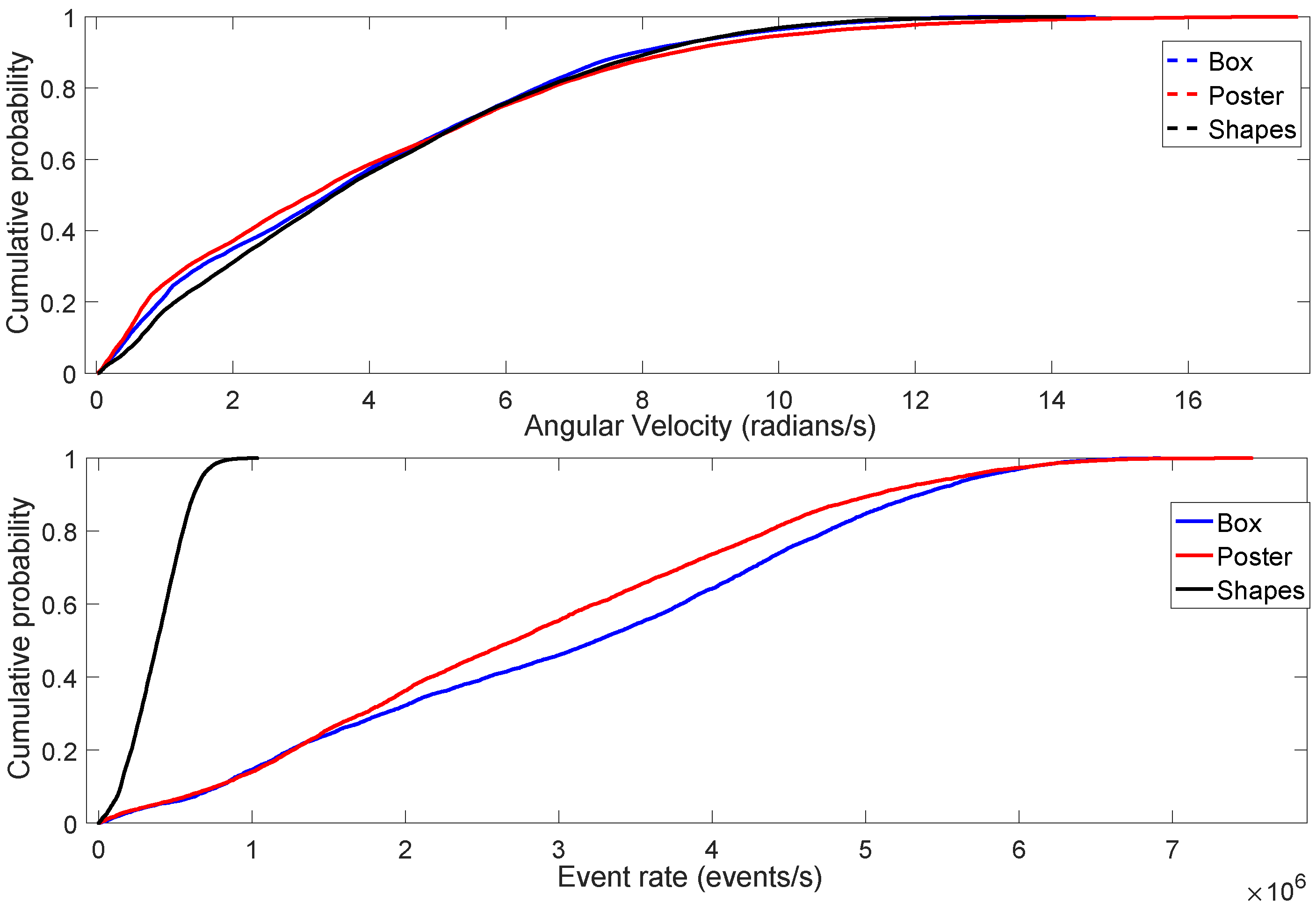
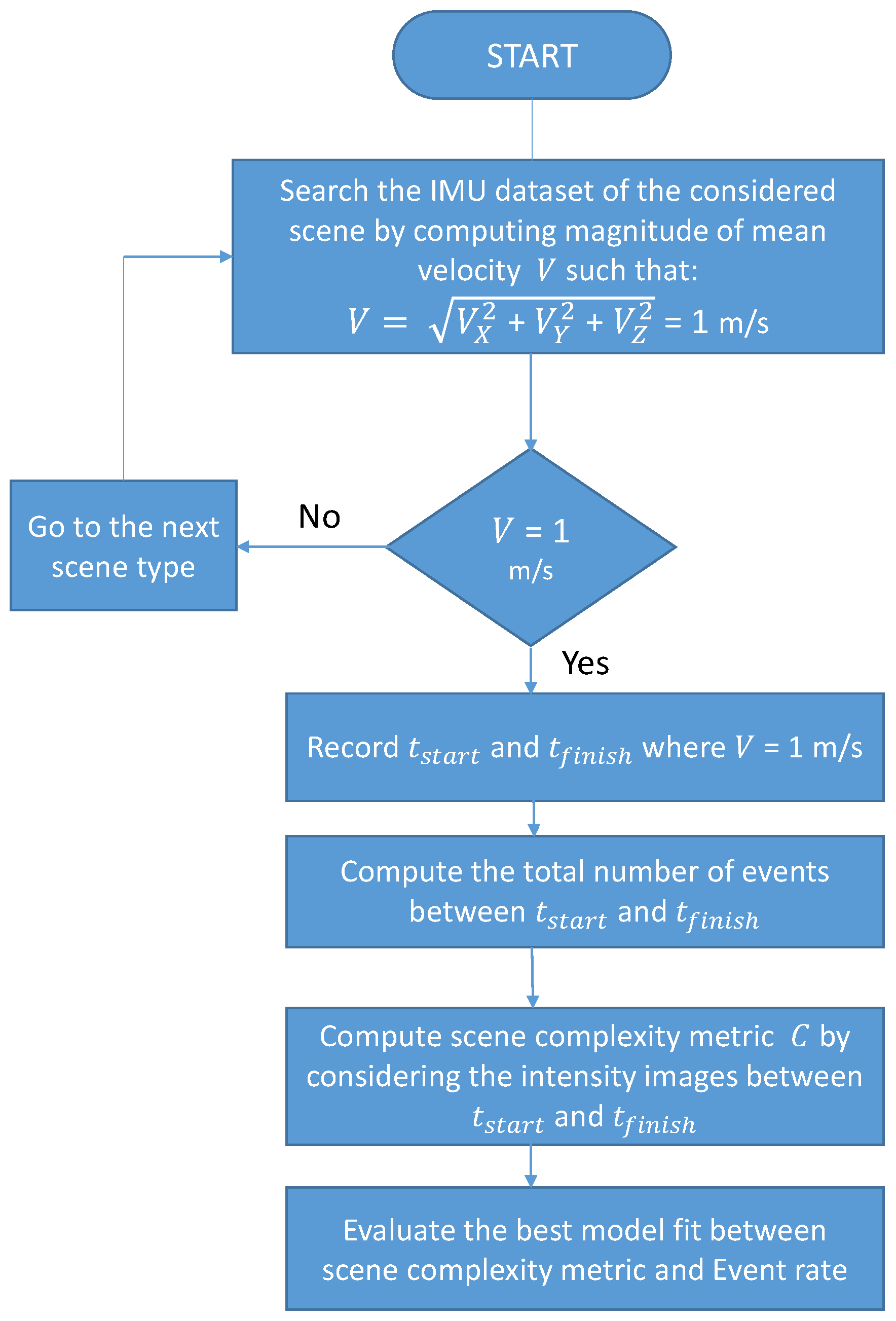
- Selection of data portions with similar speed of the capturing sensor: According to the analysis of the IMU dataset, the majority of the scene types comprised a magnitude of mean velocity of 1 m/s. Therefore, for every scene, we extracted the data (event rate and intensity images) such that the magnitude of mean velocity was 1 m/s. According to Figure 6, and are recorded for the extracted dataset of a scene. The spike events and images between and were utilized for the computation of event rate and scene complexity metrics.
- Event rate computation: We computed the total number of neuromorphic events generated, , for each type of scene. Since different scene types have different time durations, we computed the event rate by considering the duration, , for every type of scene, i.e., .
- Scene complexity metric computation: The neuromorphic event stream and intensity images were produced concurrently by the DAVIS camera. In the dataset, intensity images were precisely timestamped; therefore, we computed the scene complexity metric by utilizing the intensity images between and .
- Best model fit between scene complexity and event rate: Next, we found the best model (linear, exponential, power, etc.), for the relationship between scene complexity metric and event rate. Section 3 discusses the correlation performance of several scene complexity metrics w.r.t the neuromorphic event rate.
- Best model fit between motion and event rate: Our study of the correlation between scene complexity and event rate initially assumed the same mean sensor speed for the different scenes. On the other hand, in order to analyse the correlation performance between motion speed and event rate, the value assumed by the scene complexity metric must remain constant so that the event rate varies as a function of the sensor motion speed only. Section 4.1 studies the impact of motion on the event rate.
- In the final step, we propose a model for the neuromorphic event rate by utilizing the scene complexity metric and information on the motion of the camera (see Section 4.2).
3. Scene Complexity Metrics
3.1. Metrics Based on Gradient Approximation of Intensity Images
3.1.1. Sobel Filter
3.1.2. Prewitt Filter
3.1.3. Roberts Kernel
3.1.4. Computation Process for Spatial Content Metrics
| Algorithm 1 Computation process for the magnitude of the gradient of an intensity image. |
| Input: Intensity image having pixels |
| for to do |
| if then |
| Use symmetric padding of the border pixel to create |
| else |
| Construct a intensity matrix by considering a neighbourhood around pixel p |
| end if |
| Compute the gradient for pixel p in the horizontal direction according to (4) |
| Compute the gradient for pixel p in the vertical direction |
| Compute the magnitude of the gradient for pixel p according to (5) |
| end for |
| Output: Gradient magnitude image G. |
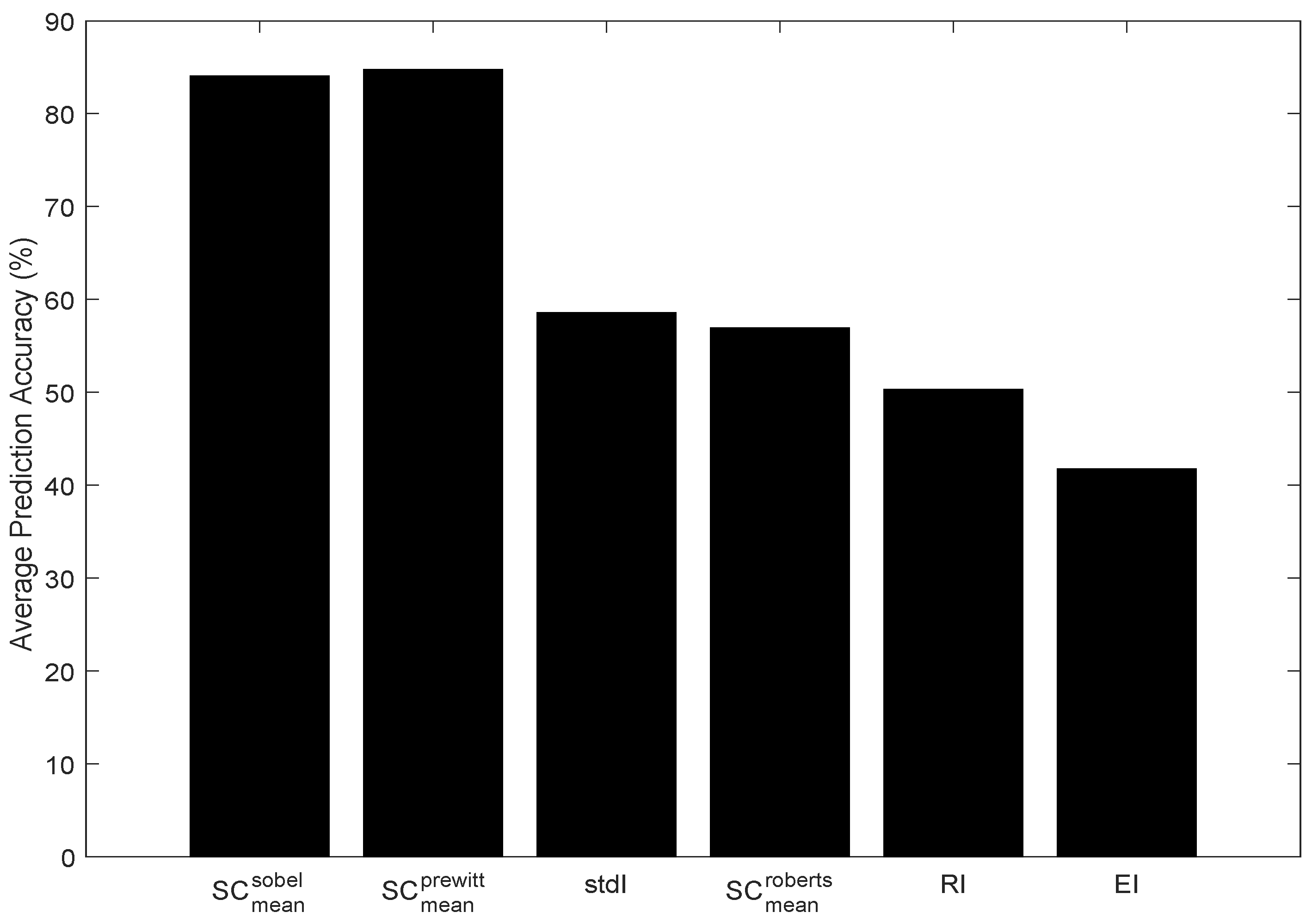
3.1.5. Correlation Performance Between Neuromorphic Event Rate and Spatial Content Metrics
3.2. Metrics Based on Binary Edge Detection
3.2.1. Edge Detection Based on a Single Threshold
3.2.2. Edge Detection Based on a Dual Threshold
- Applying the Gaussian filter to the intensity image. The main advantage of the filter is smoothing the image by removing any noise present in the image.
- Computation of the gradient magnitude image G based on the Sobel filter. This step is similar to the process reported in Section 3.1.
- The next step is to enhance the gradient approximation image by a process known as non-maxima suppression. This process enhances the gradient magnitude of all the pixels by further reducing the noise. The output of this step is a filtered pixel gradient.
- The last step is a dual threshold action known as hysteresis. In this step, a filtered pixel gradient higher than the upper threshold is marked as an edge pixel. On the other hand, a pixel gradient lower than the lower threshold is marked with zero. If the gradient is in between the two thresholds, then the pixel is marked as an edge pixel only when the neighbouring connected pixel’s gradient is above the higher threshold.
3.2.3. Correlation Performance Between Neuromorphic Event Rate and Binary Edge-Based Metrics
3.3. Metrics Based on Scene Texture
| Algorithm 2 Computation process of range, entropy and standard deviation indexes of the intensity image. |
| Input: Intensity image having pixels |
| for to do |
| if then |
| Use symmetric padding of the border pixel to create |
| else |
| Construct an intensity matrix by considering a neighbourhood around pixel p |
| end if |
| Compute the range of pixel p according to (13) |
| Compute the standard deviation of pixel p according to (14) |
| Compute the entropy of pixel p according to (15) |
| end for |
| Output: , and . |
| Compute the range index according to (16) |
| Compute the standard deviation index according to (17) |
| Compute the entropy index according to (18) |
Correlation Performance of Metrics Based on Scene Texture
4. Neuromorphic Data-Rate Model
4.1. Impact of Motion on Event Rate
4.1.1. Indoor Environment
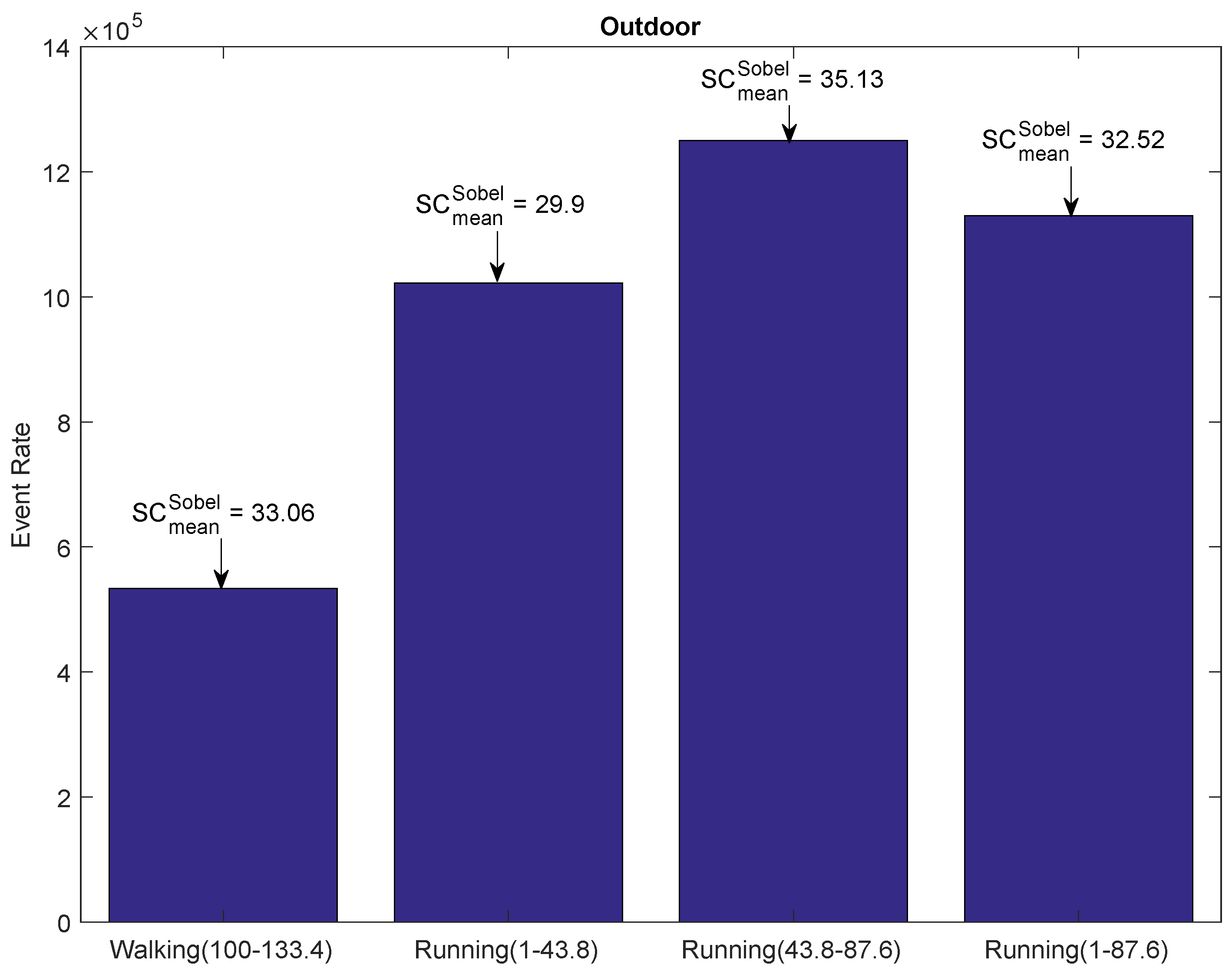
4.1.2. Outdoor Environment
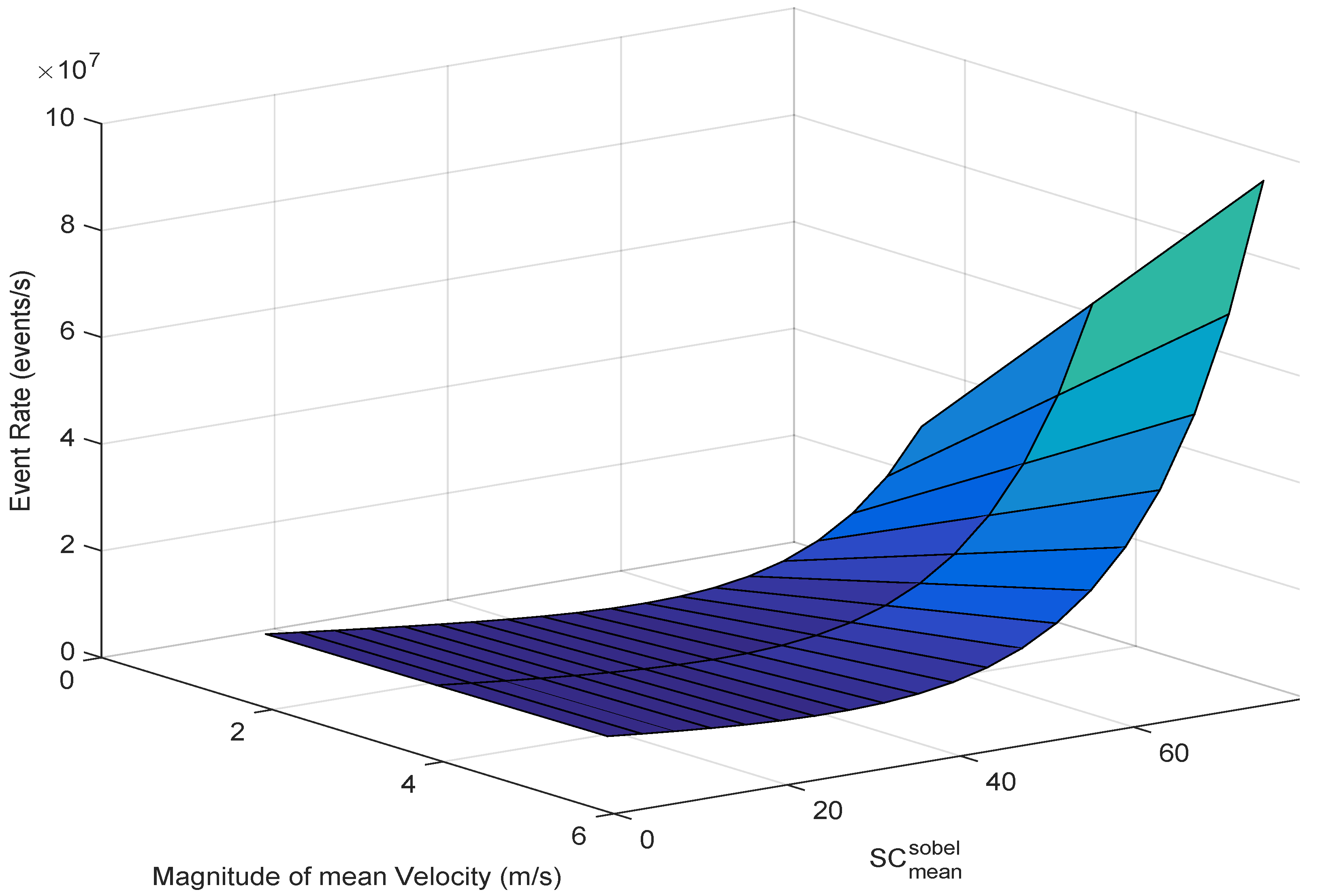
4.2. Model Formulation
4.3. Model Evaluation
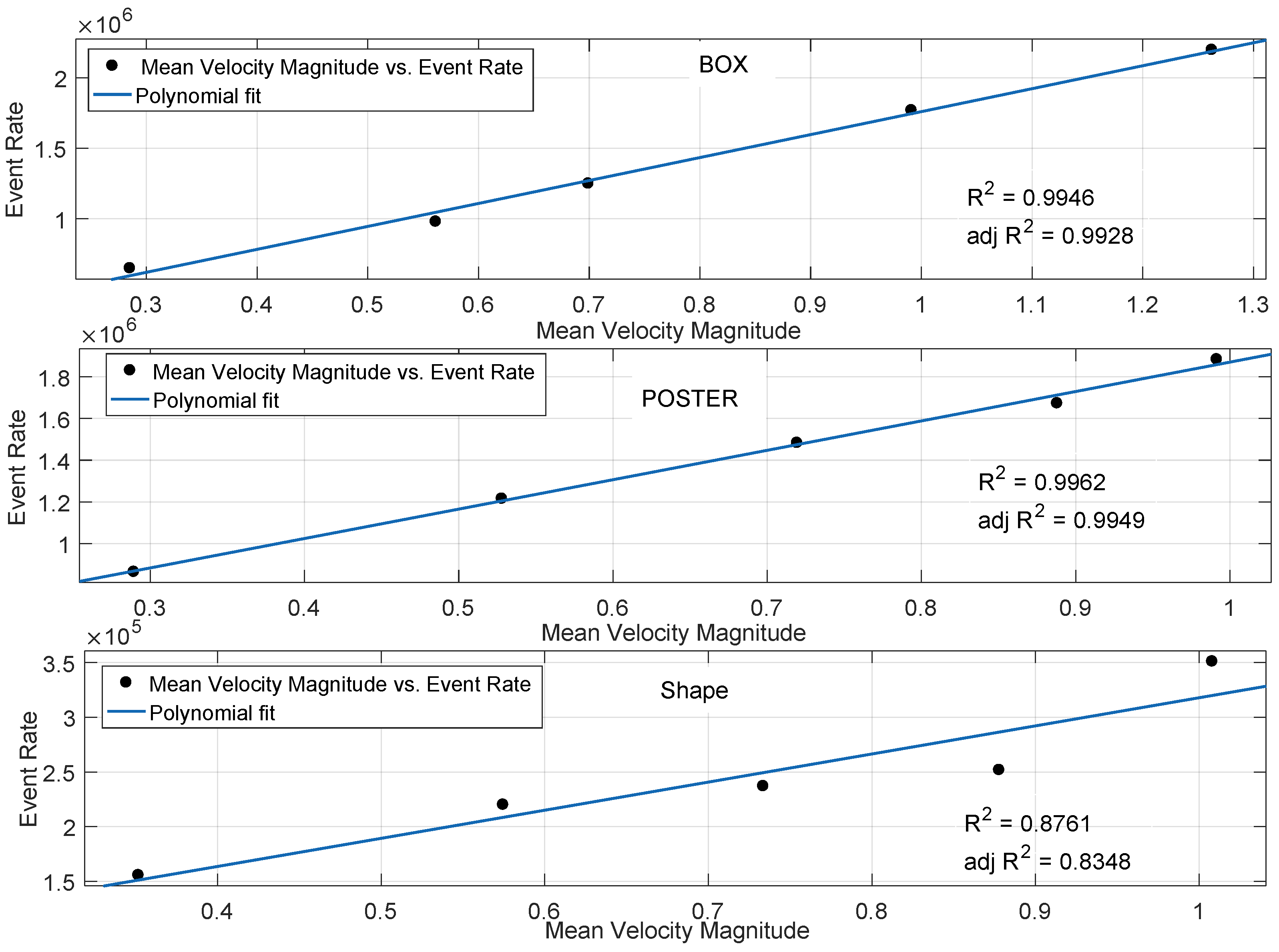
Impact of the Moving Objects in a Scene
5. Comparison of Neuromorphic Sensors and Conventional Ones for Sensor Network Devices
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Posch, C.; Benosman, R.; Cummings, R.E. Giving Machines Humanlike Vision similar to our own would let devices capture images more efficiently. IEEE Spectr. 2015, 52, 44–49. [Google Scholar] [CrossRef]
- Fukushima, K.; Yamaguchi, Y.; Yasuda, M.; Nagata, S. An electronic model of the retina. Proc. IEEE 1970, 58, 1950–1951. [Google Scholar] [CrossRef]
- Mead, C.; Mahowald, M. A silicon model of early visual processing. Proc. IEEE 1988, 1, 91–97. [Google Scholar] [CrossRef]
- Lichtsteiner, P.; Posch, C.; Delbruck, T. A 128 x 128 120 dB 15 μs Latency Asynchronous Temporal Contrast Vision Sensor. IEEE J. Solid-State Circuits 2008, 43, 566–576. [Google Scholar] [CrossRef]
- Lichtsteiner, P.; Posch, C.; Delbruck, T. A 128 × 128 120 dB 30 mW asynchronous vision sensor that responds to relative intensity change. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 6–9 February 2006. [Google Scholar]
- Mueggler, E.; Forster, C.; Baumli, N.; Gallego, G.; Scaramuzza, D. Lifetime estimation of events from Dynamic Vision Sensors. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Washington, DC, USA, 26–30 May 2015. [Google Scholar]
- Brandli, C.; Berner, R.; Yang, M.; Liu, S.; Delbruck, T. A 240 × 180 130 dB 3 μs Latency Global Shutter Spatiotemporal Vision Sensor. IEEE J. Solid-State Circuits 2014, 49, 2333–2341. [Google Scholar] [CrossRef]
- Sivilotti, M. Wiring Consideration in Analog VLSI Systems with Application to Field Programmable Networks. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1991. [Google Scholar]
- Barrios-Avilés, J.; Rosado-Muñoz, A.; Medus, L.D.; Bataller-Mompeán, M.; Guerrero-Martínez, J.F. Less Data Same Information for Event-Based Sensors: A Bioinspired Filtering and Data Reduction Algorithm. Sensors 2018, 18, 4122. [Google Scholar] [CrossRef] [PubMed]
- Chikhman, V.; Bondarko, V.; Danilova, M.; Goluzina, A.; Shelepin, Y. Complexity of images: Experimental and computational estimates compared. Perception 2012, 41, 631–647. [Google Scholar] [CrossRef] [PubMed]
- Cilibrasi, R.; Vitanyi, P.M.B. Clustering by compression. IEEE Trans. Inf. Theory 2005, 51, 1523–1545. [Google Scholar] [CrossRef]
- Yu, H.; Winkler, S. Image complexity and spatial information. In Proceedings of the IEEE International Conference on Quality of Multimedia Experience (QoMEX), Klagenfurt, Austria, 3–5 July 2013. [Google Scholar]
- ANSI T1.801.03. Digital Transport of One-Way Video Signals—Parameters for Objective Performance Assessment; Technical Report; American National Standards Institute: Washington, DC, USA, 1996. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2016. [Google Scholar]
- Li, M.; Chen, X.; Li, X.; Ma, B.; Vitanyi, P.M.B. The similarity metric. IEEE Trans. Inf. Theory 2004, 50, 863–872. [Google Scholar] [CrossRef]
- Cardaci, M.; Gesù, V.D.; Petrou, M.; Tabacchi, M.E. A fuzzy approach to the evaluation of image complexity. Fuzzy Sets Syst. 2009, 160, 1474–1484. [Google Scholar] [CrossRef]
- Perkio, J.; Hyvarinen, A. Modeling image complexity by independent component analysis, with application to content-based image retrieval. In Proceedings of the International Conference on Artificial Neural Networks (ICANN), Limassol, Cyprus, 14–17 September 2009. [Google Scholar]
- Romero, J.; Machado, P.; Carballal, A.; Santos, A. Using complexity estimates in aesthetic image classification. J. Math. Arts 2012, 6, 125–136. [Google Scholar] [CrossRef]
- Tedaldi, D.; Gallego, G.; Mueggler, E.; Scaramuzza, D. Feature Detection and Tracking with the Dynamic and Active-Pixel Vision Sensor. In Proceedings of the IEEE International Conference on Event-Based Control, Communication, and Signal Processing (EBCCSP), Krakow, Poland, 13–15 June 2016. [Google Scholar]
- Rigi, A.; Baghaei Naeini, F.; Makris, D.; Zweiri, Y. A Novel Event-Based Incipient Slip Detection Using Dynamic Active-Pixel Vision Sensor (DAVIS). Sensors 2018, 18, 333. [Google Scholar] [CrossRef] [PubMed]
- Maqueda, A.I.; Loquercio, A.; Gallego, G.; Garcia, N.; Scaramuzza, D. Event-Based Vision meets Deep Learning on Steering Prediction for Self-Driving Cars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Mueggler, E.; Huber, B.; Scaramuzza, D. Event-Based, 6-DOF Pose Tracking for High-Speed Maneuvers. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014. [Google Scholar]
- Khan, N.; Martini, M.G.; Staehle, D. QoS-aware composite scheduling using fuzzy proactive and reactive controllers. J. Wireless Com Network 2014, 2014, 1–21. [Google Scholar] [CrossRef][Green Version]
- Khan, N.; Martini, M.G.; Staehle, D. Opportunistic QoS-Aware Fair Downlink Scheduling for Delay Sensitive Applications Using Fuzzy Reactive and Proactive Controllers. In Proceedings of the IEEE Vehicular Technology Conference (VTC), Las Vegas, NV, USA, 2–5 September 2013. [Google Scholar]
- Nasralla, M.M.; Khan, N.; Martini, M.G. Content-aware downlink scheduling for LTE wireless systems: A survey and performance comparison of key approaches. Comput. Commun 2018, 130, 78–100. [Google Scholar] [CrossRef]
- Khan, N.; Martini, M.G. QoE-driven multi-user scheduling and rate adaptation with reduced cross-layer signaling for scalable video streaming over LTE wireless systems. J. Wireless Com Network 2016, 2016, 1–23. [Google Scholar] [CrossRef]
- Khan, N.; Martini, M.G. Data rate estimation based on scene complexity for dynamic vision sensors on unmanned vehicles. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Bologna, Italy, 9–12 September 2018. [Google Scholar]
- Mueggler, E.; Rebecq, H.; Gallego, G.; Delbruck, T.; Scaramuzza, D. The Event-Camera Dataset and Simulator: Event-Based Data for Pose Estimation, Visual Odometry, and SLAM. Int. J. Robot. Res. 2017, 36, 91–97. [Google Scholar] [CrossRef]
- Sobel, I.; Feldman, G. A 3 x 3 isotropic gradient operator for image processing, presented at a talk at the Stanford Artificial Project. In Pattern Classification and Scene Analysis; Duda, R., Hart, P., Eds.; John Wiley & Sons: New York, NY, USA, 1968; pp. 271–272. [Google Scholar]
- Prewitt, J.M.S. Object enhancement and extraction. In Picture Processing and Psychopictorics; Lipkin, B., Rosenfeld, A., Eds.; Academic Press: New York, NY, USA, 1970; pp. 75–149. [Google Scholar]
- Roberts, L.G. Machine Perception of Three-Dimensional Solids. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1963. [Google Scholar]
- Barman, N.; Martini, M.G. H.264/MPEG-AVC, H.265/MPEGHEVC and VP9 codec comparison for live gaming video streaming. In Proceedings of the IEEE International Conference on Quality of Multimedia Experience (QoMEX), Erfurt, Germany, 31 May–2 June 2017. [Google Scholar]
- Barman, N.; Zadtootaghaj, S.; Martini, M.G.; Moller, S.; Lee, S. A Comparative Quality Assessment Study for Gaming and Non-Gaming Videos. In Proceedings of the IEEE International Conference on Quality of Multimedia Experience (QoMEX), Sardinia, Italy, 29 May–1 June 2018. [Google Scholar]
- Haseeb, A.; Martini, M.G. Rate and distortion modeling for real-time MGS coding and adaptation. In Proceedings of the IEEE Wireless Advanced Conference (WiAd), London, UK, 25–27 June 2012. [Google Scholar]
- Parker, J.R. Algorithms for Image Processing and Computer Vision, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Canny, J.F. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef] [PubMed]
- Yap, F.G.H.; Yen, H.H. A Survey on Sensor Coverage and Visual Data Capturing/Processing/Transmission in Wireless Visual Sensor Networks. Sensors 2014, 14, 3506–3527. [Google Scholar] [CrossRef] [PubMed]
- Bi, Z.; Dong, S.; Tian, Y.; Huang, T. Spike Coding for Dynamic Vision Sensors. In Proceedings of the IEEE Data Compression Conference (DCC), Snowbird, UT, USA, 27–30 March 2018. [Google Scholar]



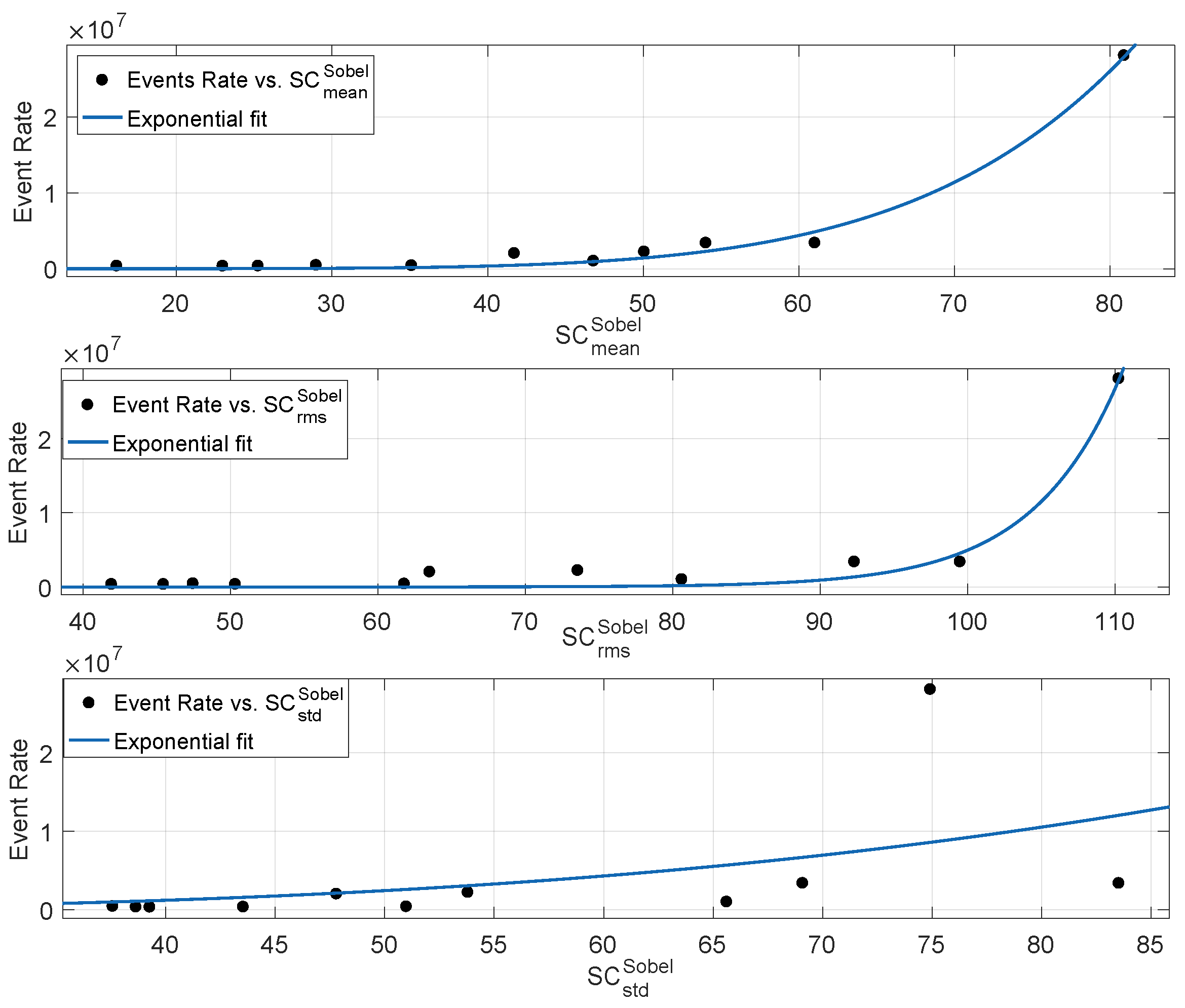
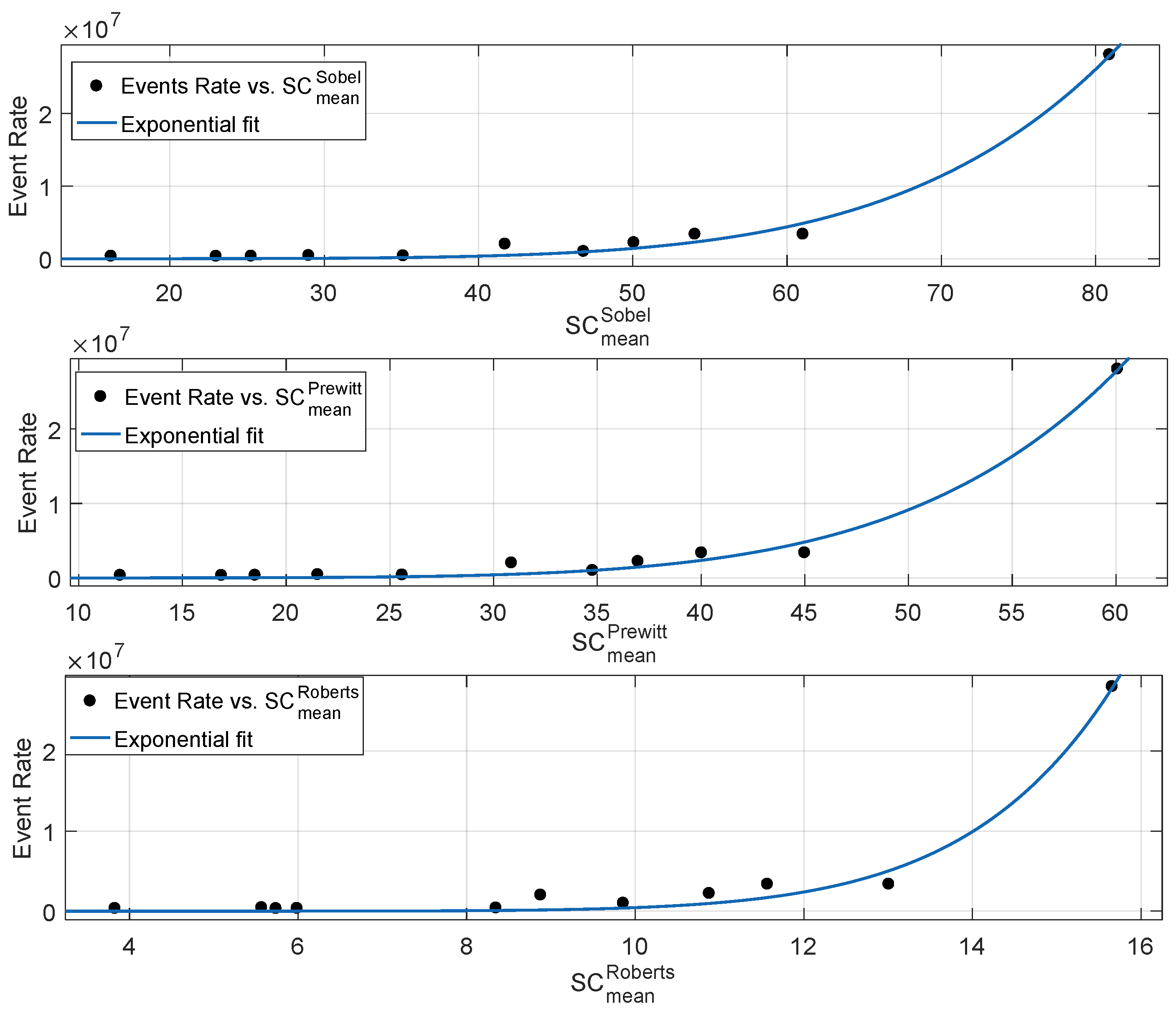
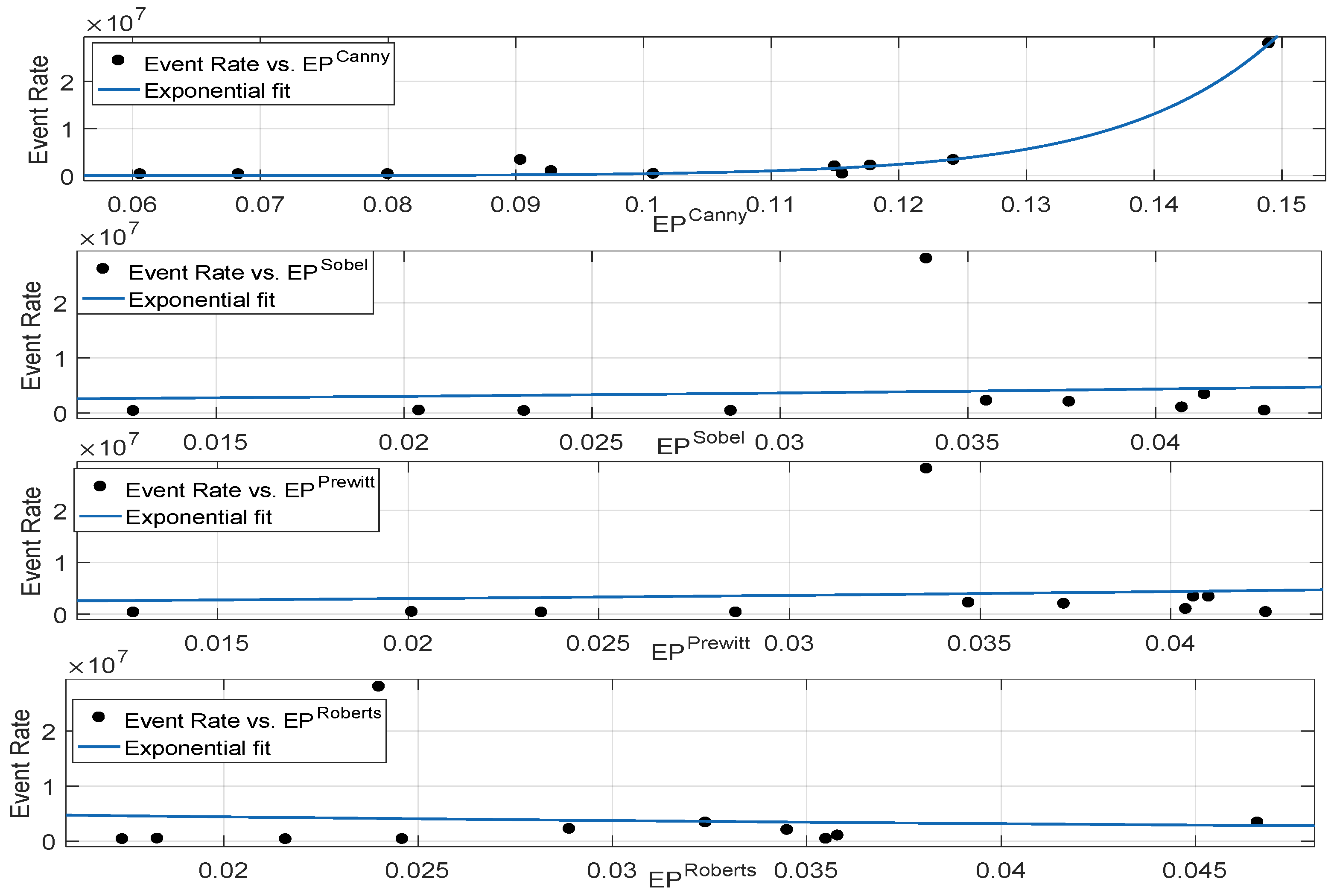
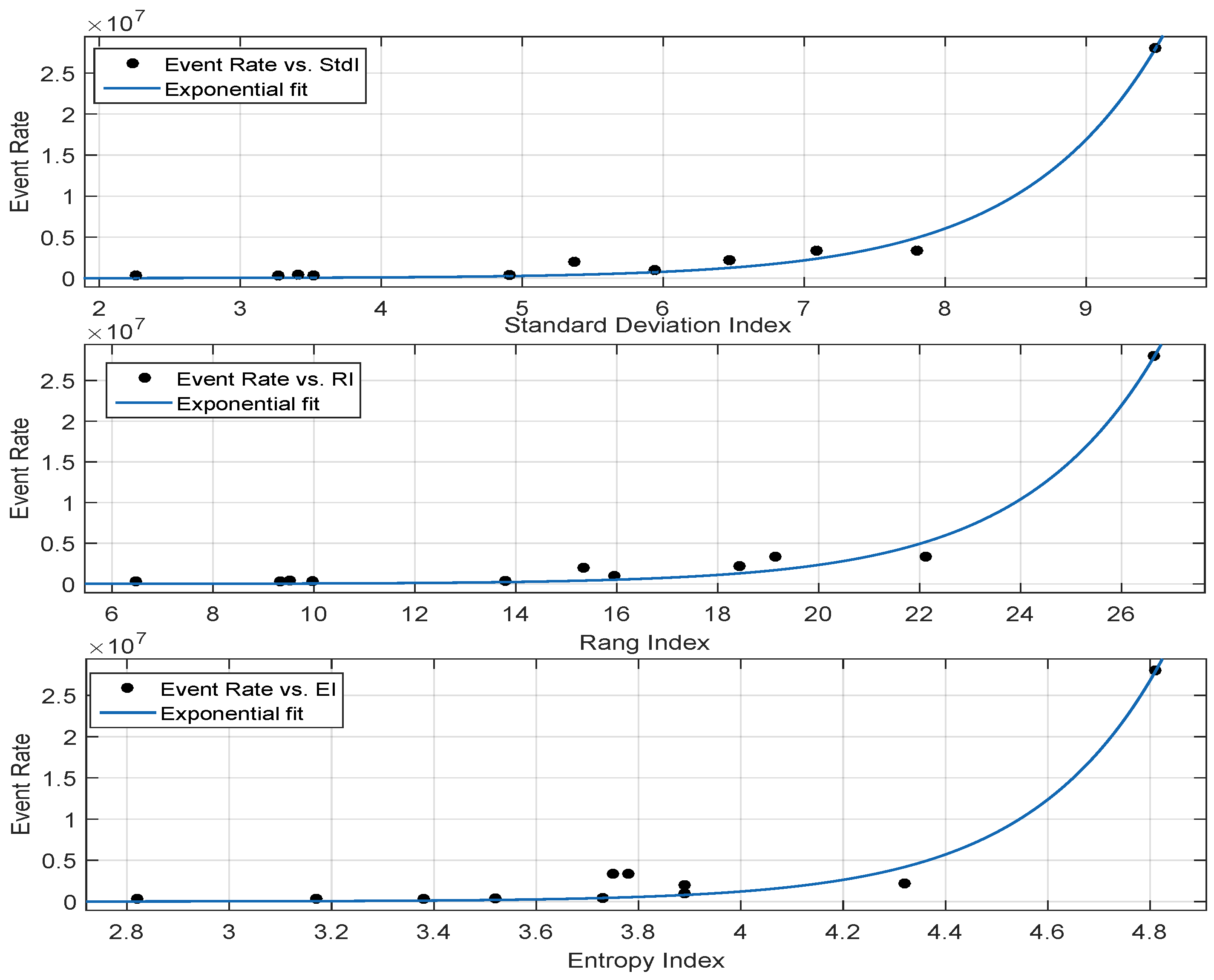
| Exponential Fit | ||||
|---|---|---|---|---|
| Metric | adj | RMSE | SSE | |
| 0.2252 | 0.1391 | 7.54 × 10 | 5.12 × 10 | |
| 0.9769 | 0.9743 | 1.3 × 10 | 1.53 × 10 | |
| 0.9935 | 0.9927 | 6.93 × 10 | 4.33 × 10 | |
| 0.9939 | 0.9933 | 6.67 × 10 | 4.01 × 10 | |
| 0.9866 | 0.9851 | 9.91 × 10 | 8.84 × 10 |
| Exponential Fit | ||||
|---|---|---|---|---|
| Metric | adj | RMSE | SSE | |
| 0.981 | 0.979 | 1.182 × 10 | 1.257 × 10 | |
| 0.01094 | −0.09896 | 8.521 × 10 | 6.535 × 10 | |
| 0.01091 | −0.09899 | 8.522 × 10 | 6.535 × 10 | |
| 0.006121 | −0.1043 | 8.542 × 10 | 6.567 × 10 |
| Exponential Fit | ||||
|---|---|---|---|---|
| Metric | adj | RMSE | SSE | |
| 0.9889 | 0.9876 | 9.04 × 10 | 7.35 × 10 | |
| 0.9848 | 0.9831 | 1.06 × 10 | 1.0 × 10 | |
| 0.9663 | 0.9626 | 1.57 × 10 | 2.22 × 10 |
| Extracted | Mean | Metric | Event Rate | Event Rate | Prediction |
|---|---|---|---|---|---|
| DAVIS | Velocity (V) | Model | Camera | Accuracy | |
| Dataset | (m/s) | (events/s) | (events/s) | ||
| Walking (100–133.4) | 1.42 | 33.06 | 97.77% | ||
| Running (1–43.5) | 3.1 | 29.9 | 83.82% | ||
| Running (43.5–87) | 3.1 | 35.13 | 90.4% | ||
| Running (1–87) | 3.1 | 32.52 | 97.12% | ||
| Urban (1–5) | 0.65 | 39.95 | 79.78% | ||
| Urban (5–10) | 0.65 | 41.85 | 81.9% | ||
| Box (1–25) | 0.57 | 50 | 89.81% | ||
| Slider far (1–6.4) | 0.16 | 60 | 75.47% | ||
| Slider depth (1–3.2) | 0.32 | 46.82 | 71.4% | ||
| Calibration (1–10) | 0.11 | 54.04 | 77.37% | ||
| Dynamic (1–30) | 0.85 | 34.3 | 80.6% | ||
| Dynamic (30–59) | 1.2 | 34.7 | 83% |
| Extracted | Data Rate | Data Rate | Data Rate | Data Rate |
|---|---|---|---|---|
| DAVIS | Events Camera | Conventional Camera | Events Camera | Conventional Camera |
| Dataset | 1000 fps (MB/s) | 1000 fps (MB/s) | 100 fps (MB/s) | 100 fps (MB/s) |
| Walking (100–133.4) | 1.066 | 43.2 | 0.152 | 4.32 |
| Running (1–43.5) | 2.04 | 43.2 | 0.255 | 4.32 |
| Running (43.5–87) | 2.5 | 43.2 | 0.334 | 4.32 |
| Running (1–87) | 2.26 | 43.2 | 0.322 | 4.32 |
| Urban (1–5) | 1.07 | 43.2 | 0.154 | 4.32 |
| Urban (5–10) | 1.25 | 43.2 | 0.176 | 4.32 |
| Box (1–25) | 2.16 | 43.2 | 0.27 | 4.32 |
| Slider far (1–6.4) | 1.076 | 43.2 | 0.154 | 4.32 |
| Slider depth (1–3.2) | 0.6344 | 43.2 | 0.09 | 4.32 |
| Calibration (1–10) | 0.698 | 43.2 | 0.107 | 4.32 |
| Dynamic (1–30) | 0.866 | 43.2 | 0.121 | 4.32 |
| Dynamic (30–59) | 1.196 | 43.2 | 0.171 | 4.32 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, N.; Martini, M.G. Bandwidth Modeling of Silicon Retinas for Next Generation Visual Sensor Networks. Sensors 2019, 19, 1751. https://doi.org/10.3390/s19081751
Khan N, Martini MG. Bandwidth Modeling of Silicon Retinas for Next Generation Visual Sensor Networks. Sensors. 2019; 19(8):1751. https://doi.org/10.3390/s19081751
Chicago/Turabian StyleKhan, Nabeel, and Maria G. Martini. 2019. "Bandwidth Modeling of Silicon Retinas for Next Generation Visual Sensor Networks" Sensors 19, no. 8: 1751. https://doi.org/10.3390/s19081751
APA StyleKhan, N., & Martini, M. G. (2019). Bandwidth Modeling of Silicon Retinas for Next Generation Visual Sensor Networks. Sensors, 19(8), 1751. https://doi.org/10.3390/s19081751





