Mini Inside-Out Nuclear Magnetic Resonance Sensor Design for Soil Moisture Measurements
Abstract
1. Introduction
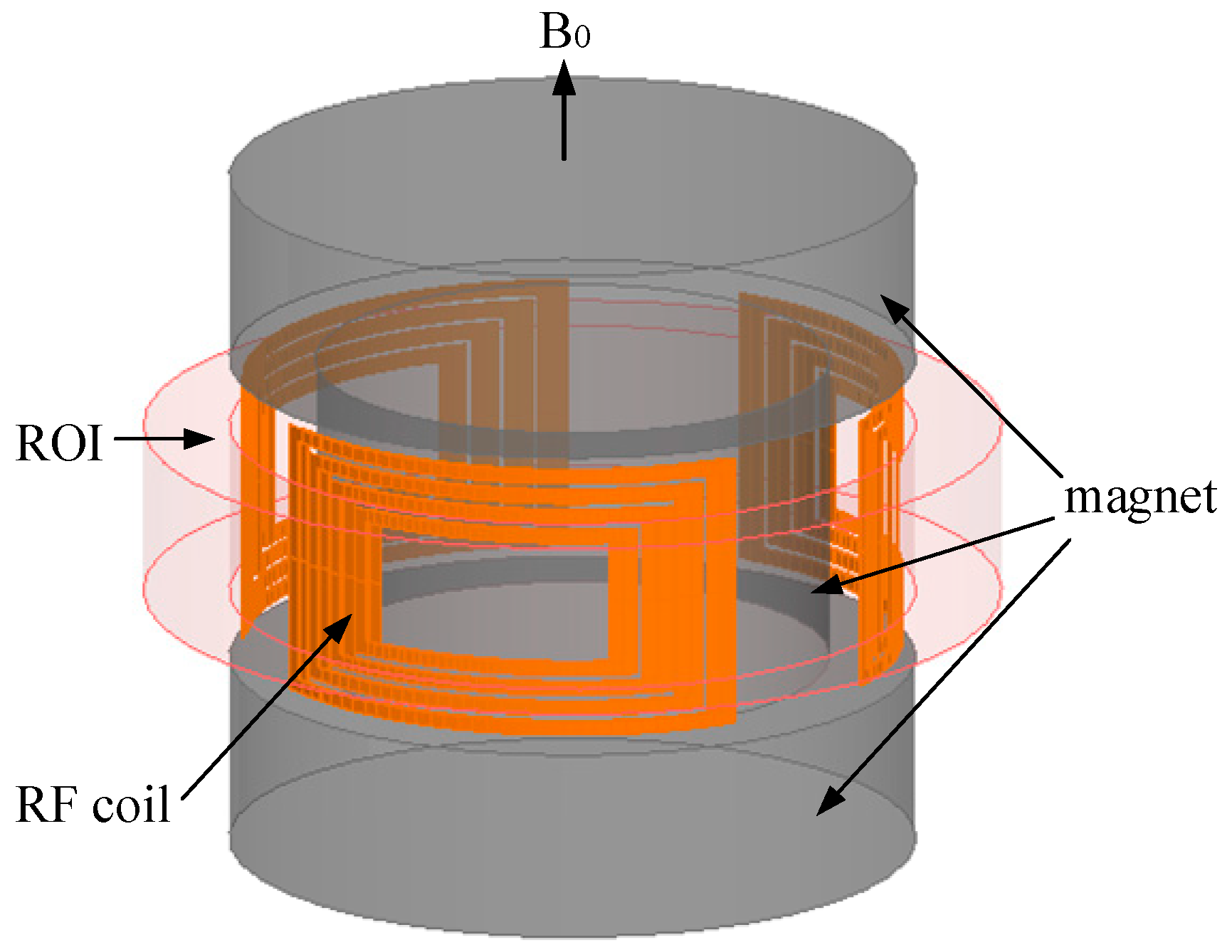
2. NMR Sensor Design
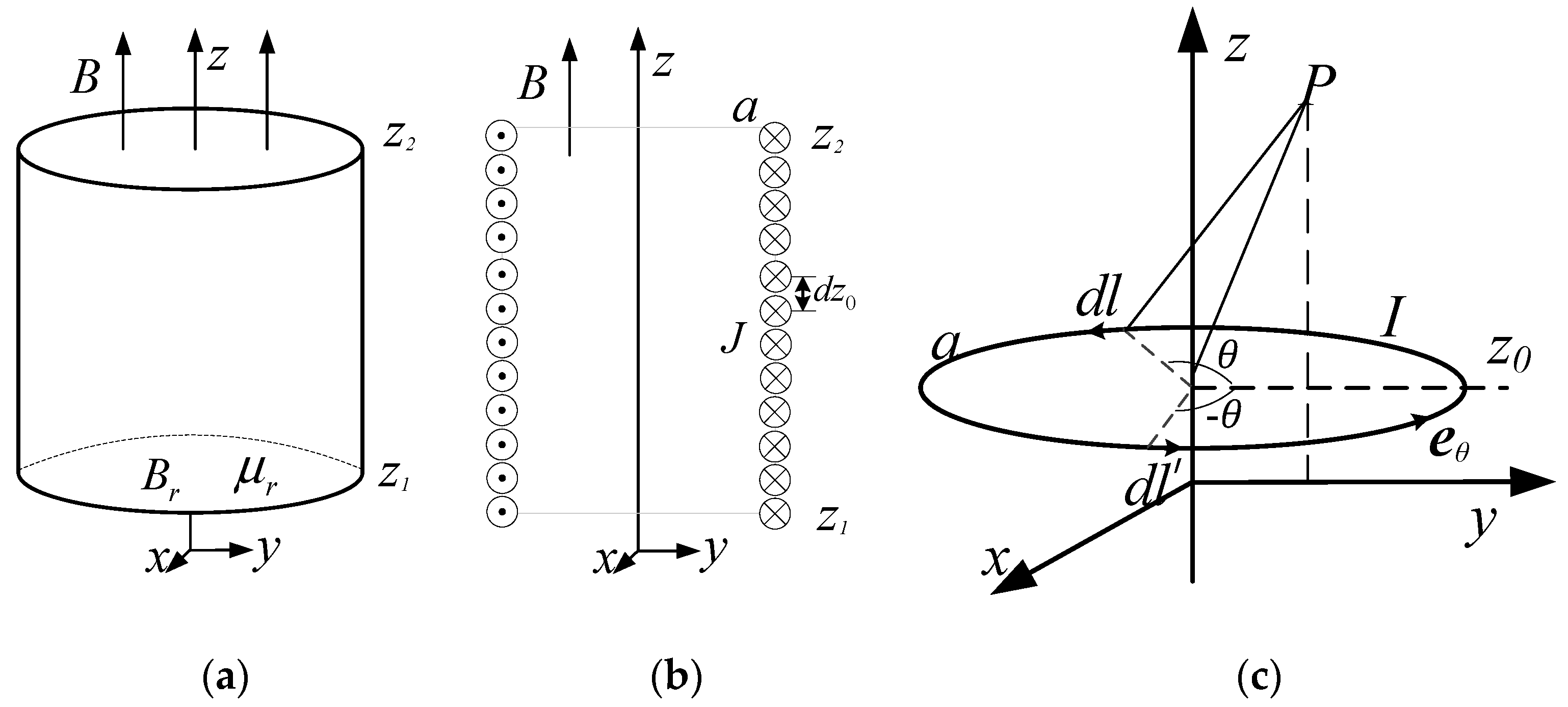
2.1. Magnetic Field Calculation
- , and I is the value of the current in the coil.
- is the first type of complete elliptic integral.
- is the second type of complete elliptic integral.
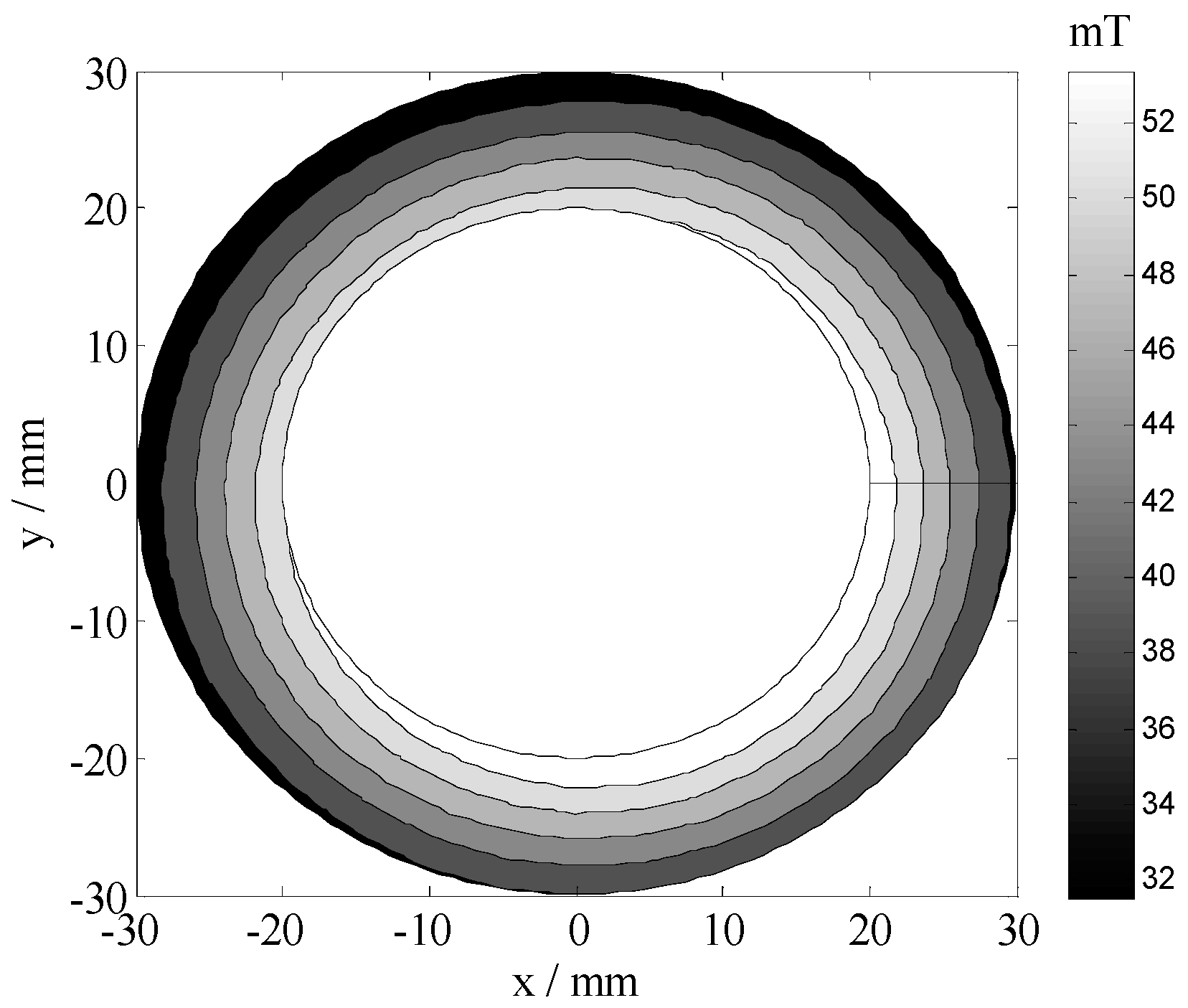
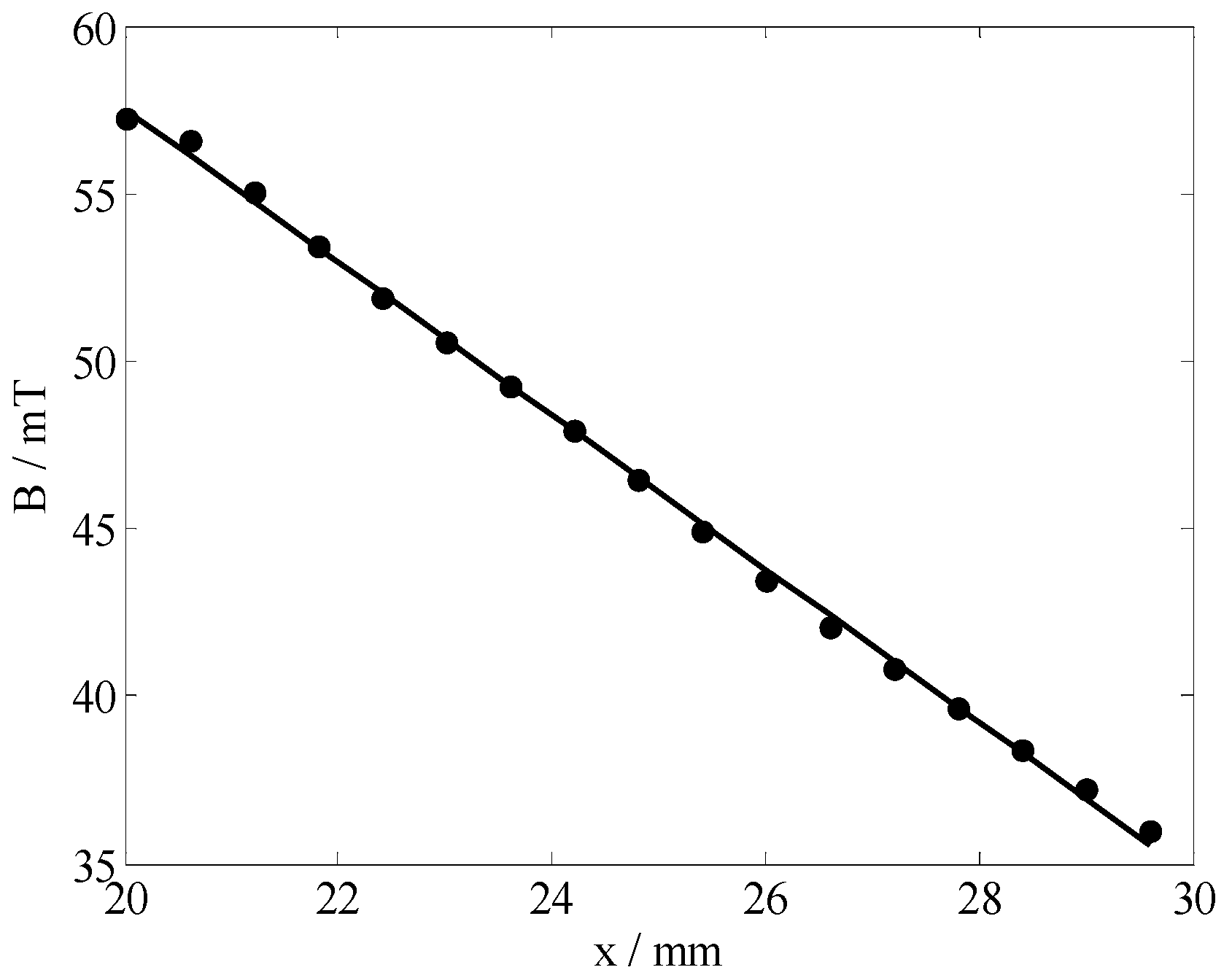
2.2. Magnet Structure Optimization and Field Measurement
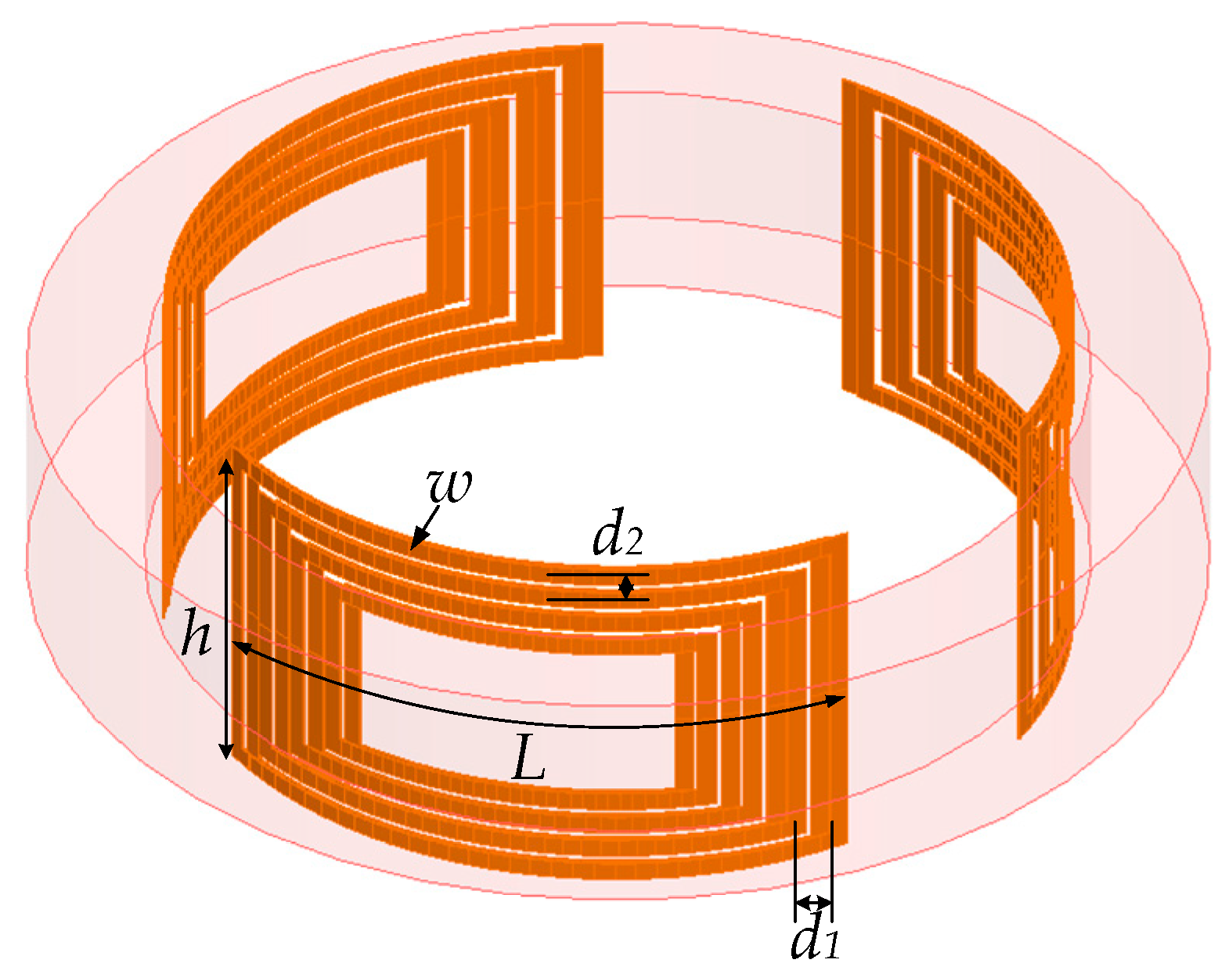
2.3. RF Coil Design
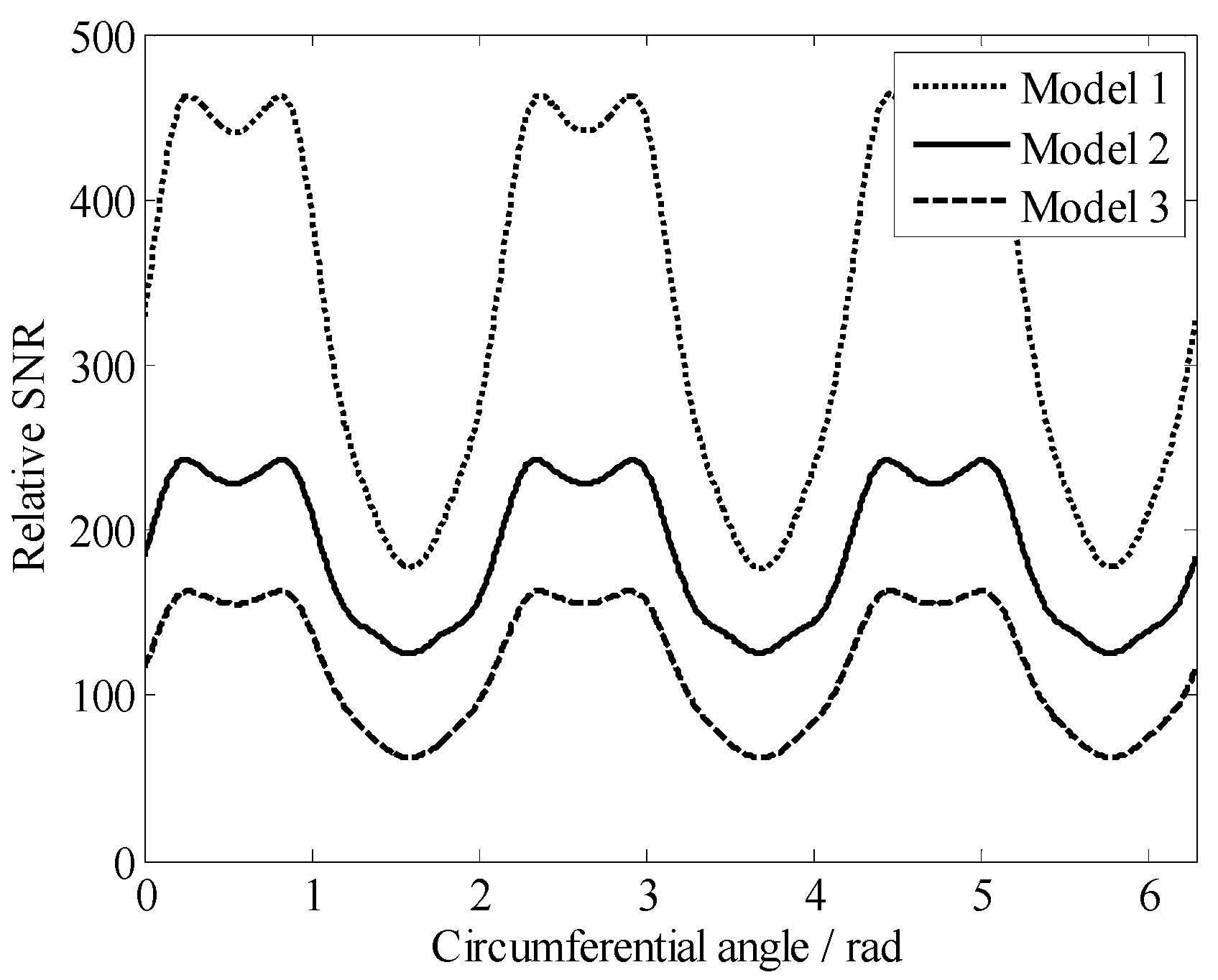
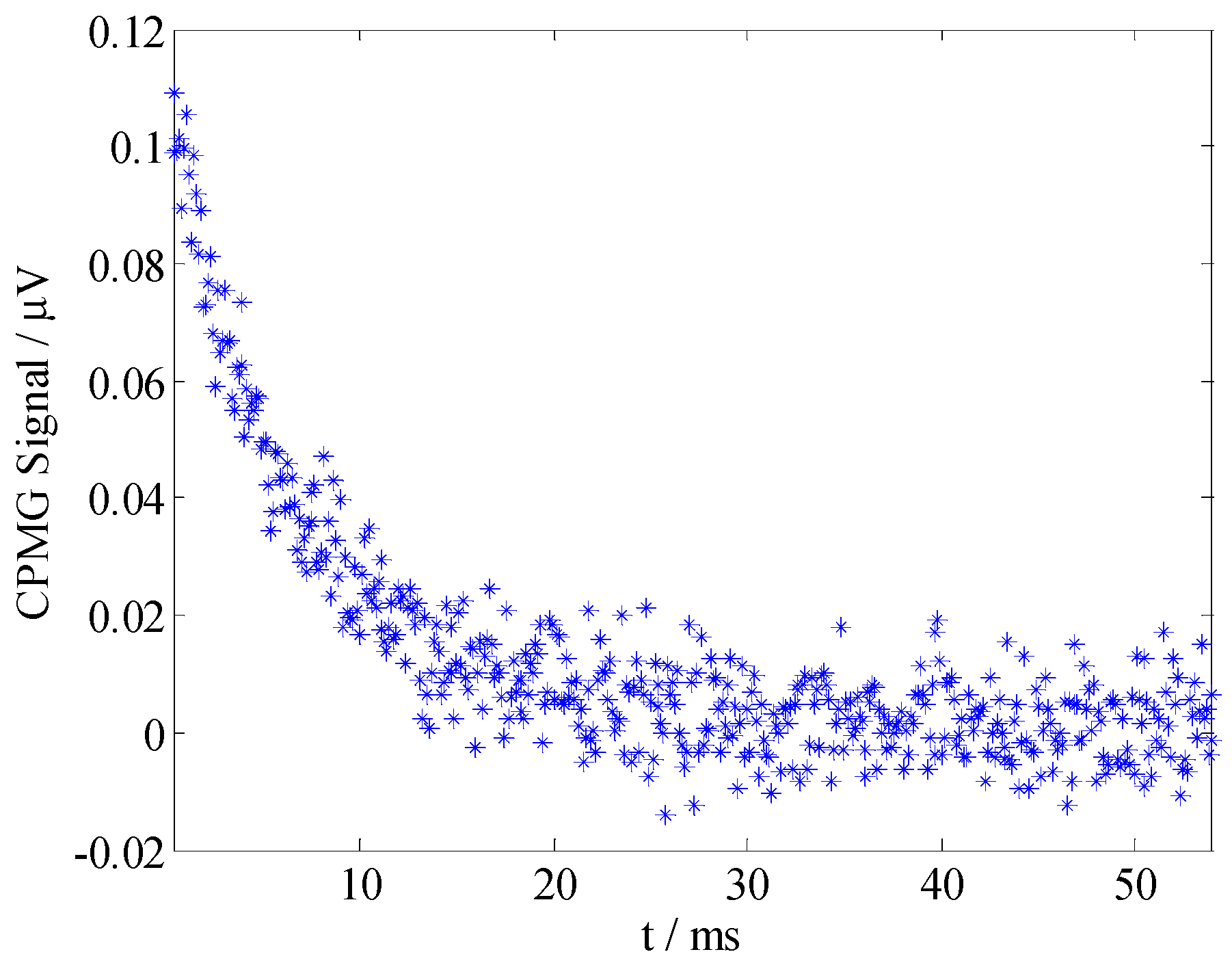
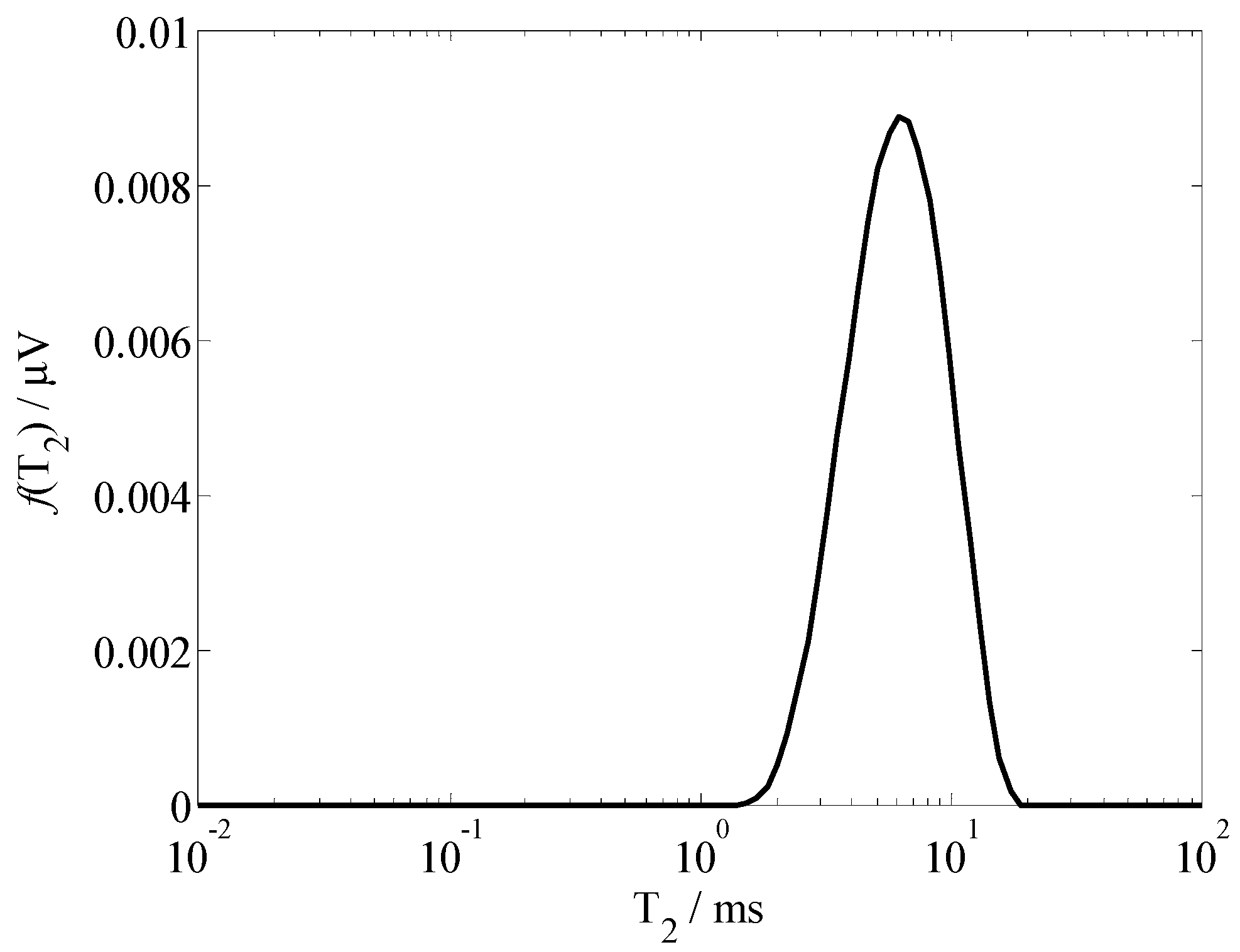
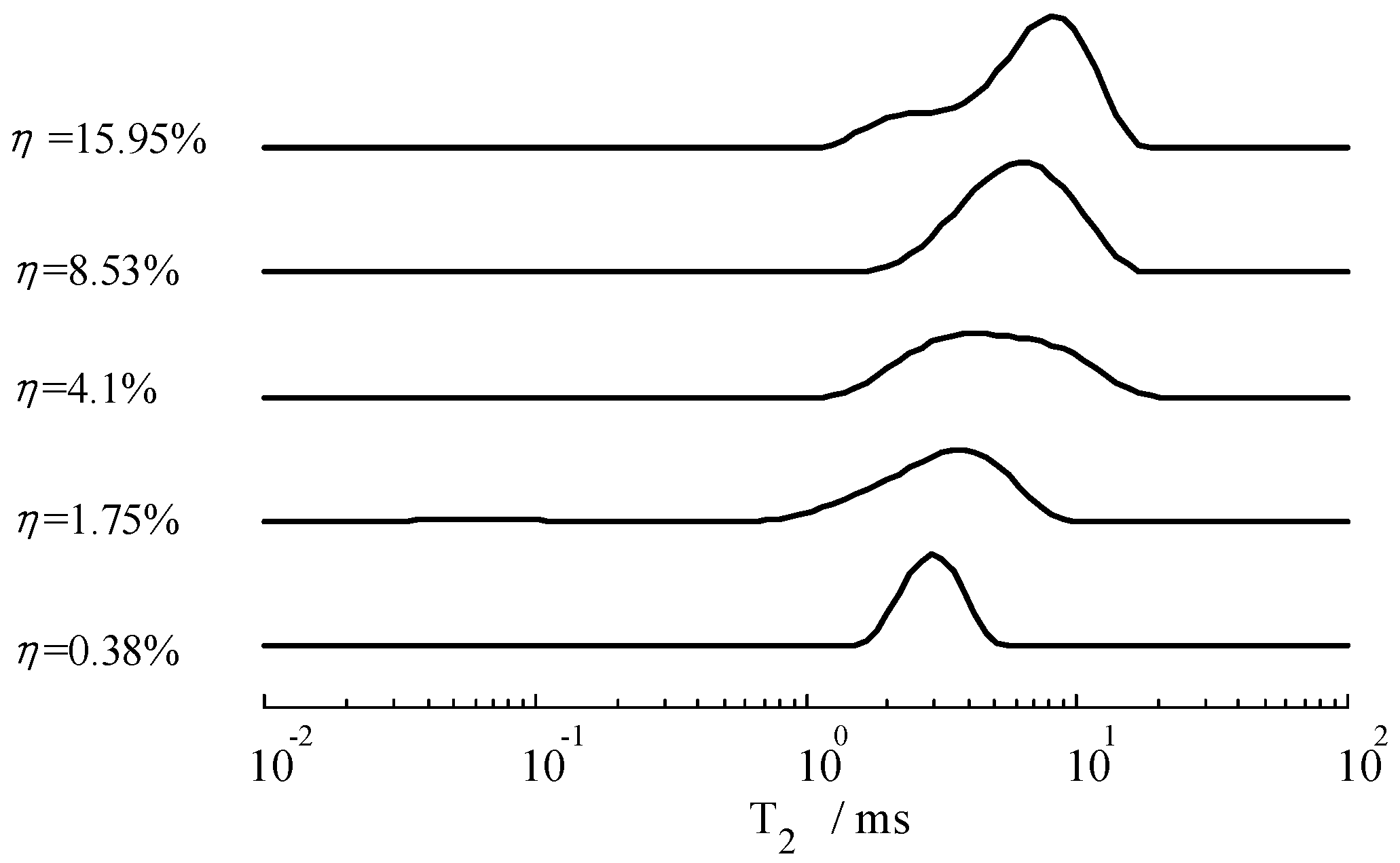
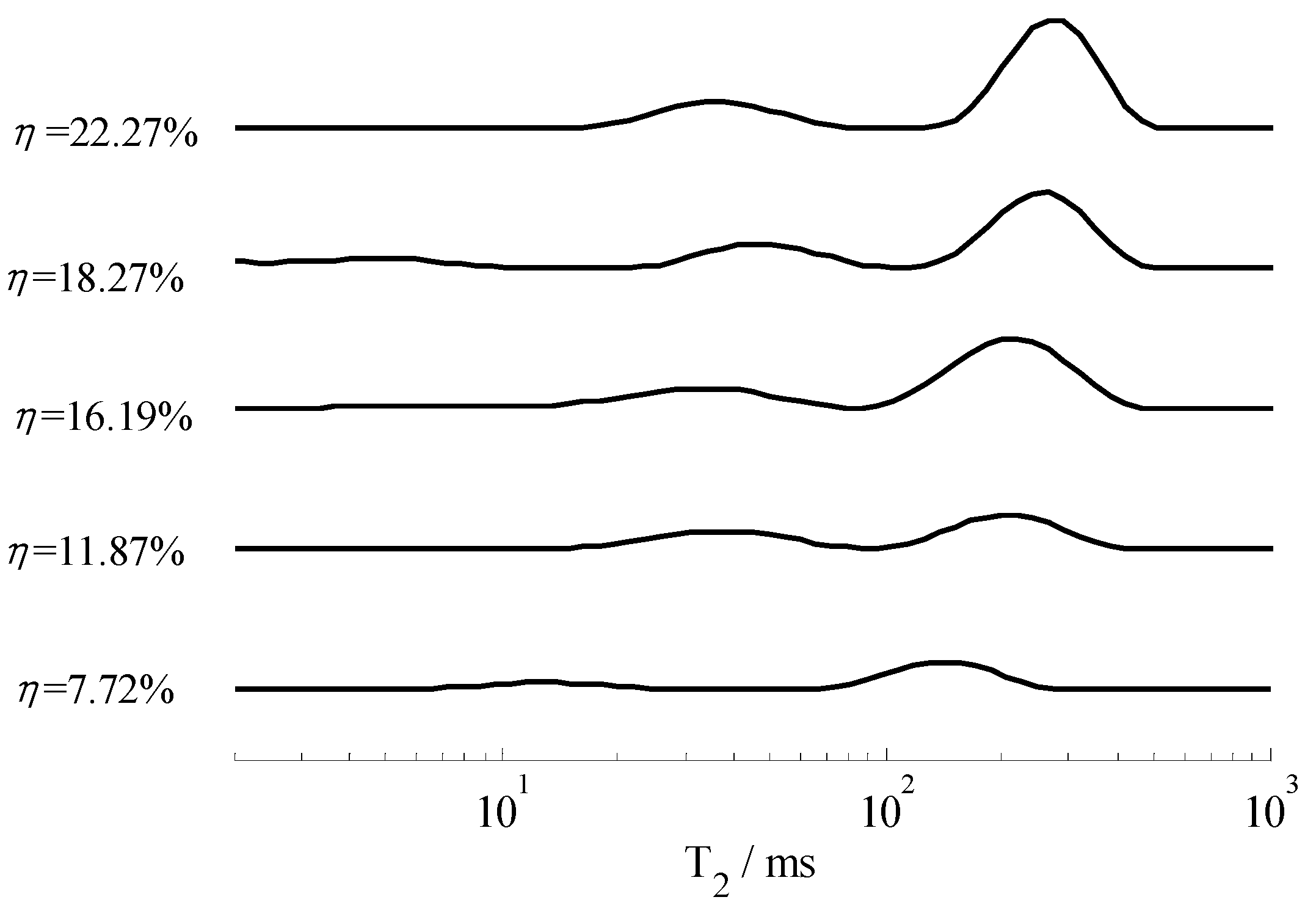
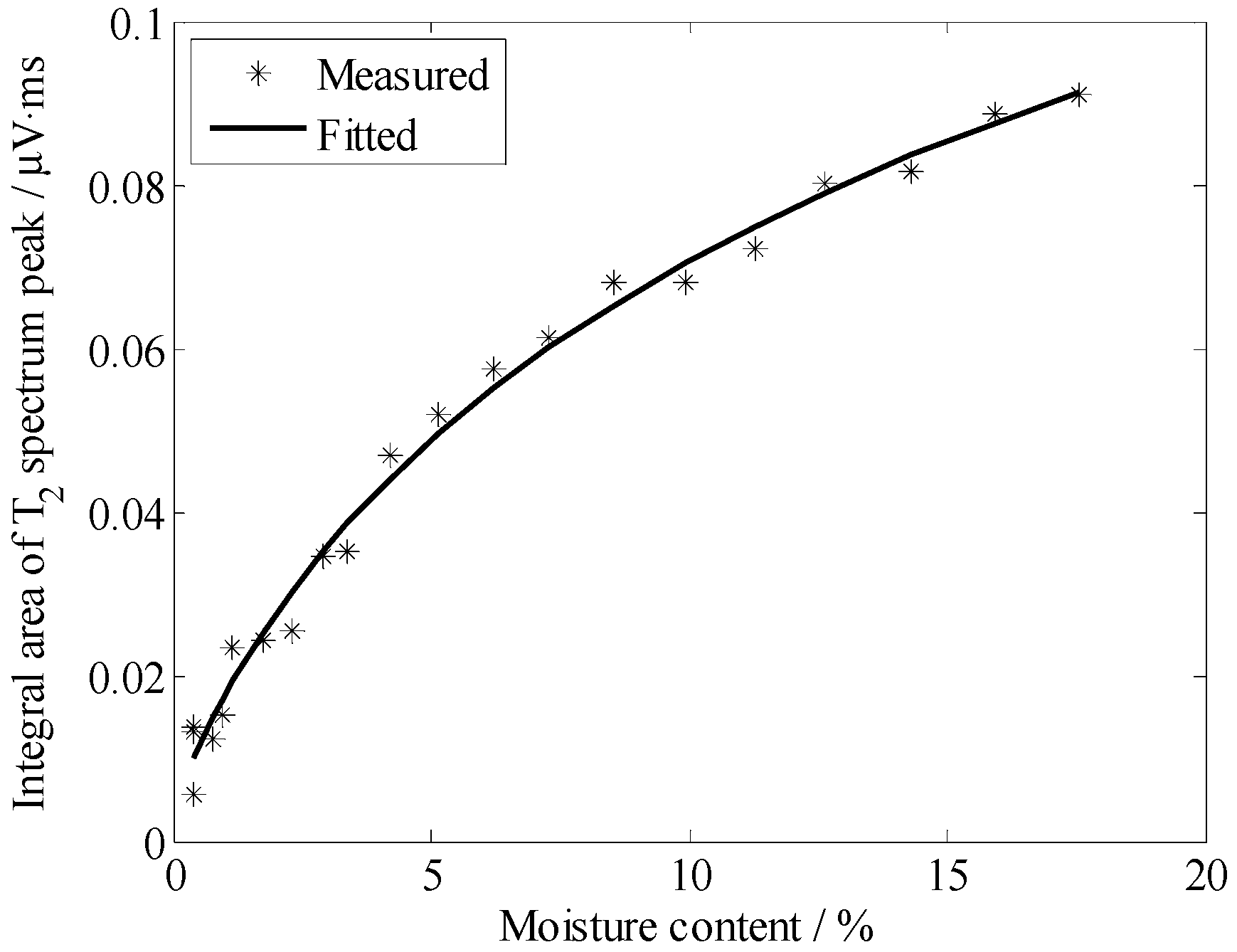
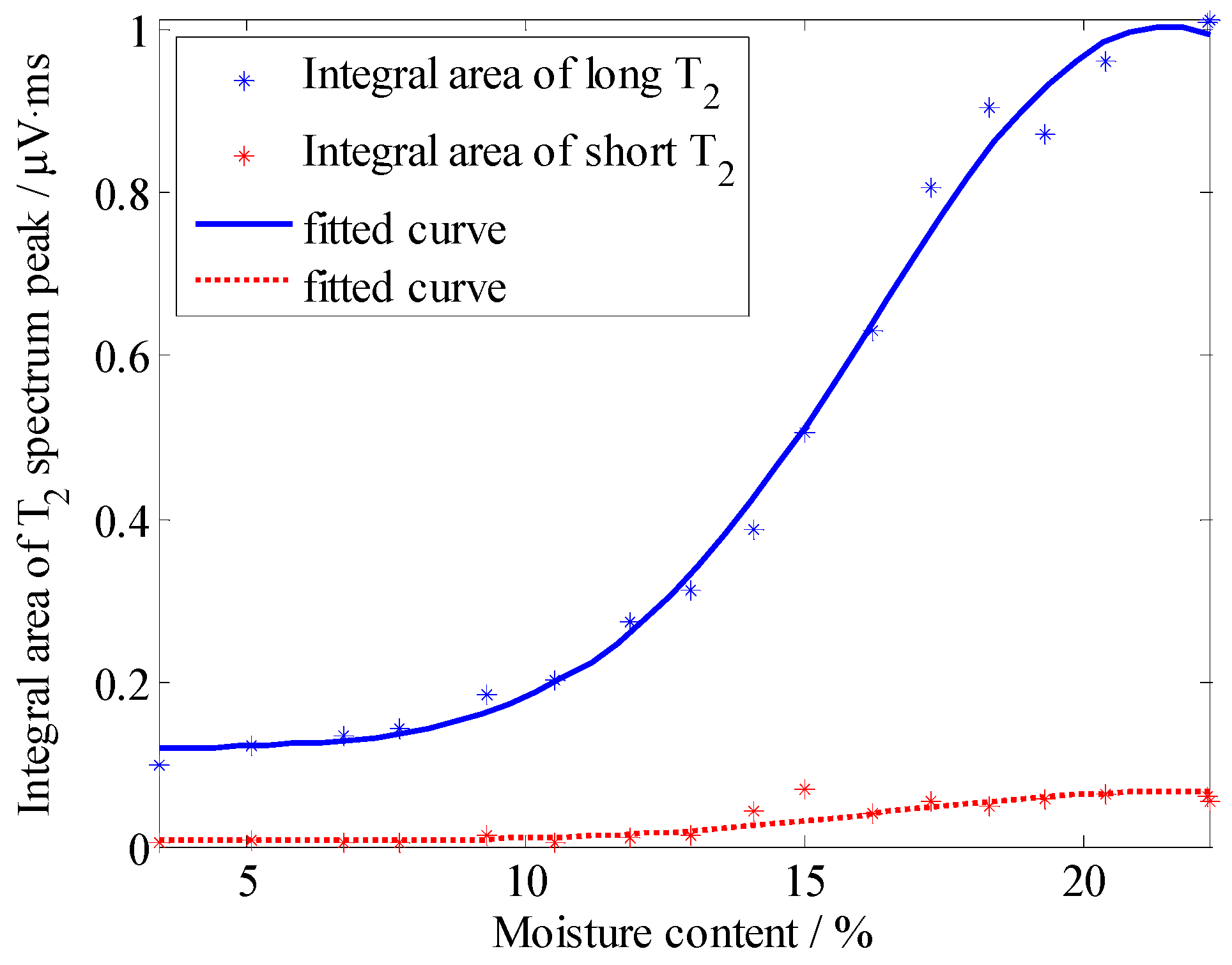
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sucre, O.; Pohlmeier, A.; Minière, A.; Blümich, B. Low-field NMR logging sensor for measuring hydraulic parameters of model soils. J. Hydrol. 2011, 406, 30–38. [Google Scholar] [CrossRef]
- Alvarado, R.J.; Damgaard, A.; Hansen, P.; Raven, M.; Heidler, R.; Hoshun, R.; Kovats, J.; Morriss, C.; Rose, D.; Wendt, W. Nuclear magnetic resonance logging while drilling. Oilfield Rev. 2003, 15, 40–51. [Google Scholar]
- Blümich, B.; Perlo, J.; Casanova, F. Mobile single-sided NMR. Prog. Nucl. Magn. Reson. Spectrosc. 2008, 52, 197–269. [Google Scholar] [CrossRef]
- Behroozmand, A.A.; Keating, K.; Auken, E. A Review of the principles and applications of the NMR technique for near-surface characterization. Surv. Geophys. 2015, 36, 27–85. [Google Scholar] [CrossRef]
- Blank, A.; Alexandrowicz, G.; Muchnik, L.; Tidhar, G.; Schneiderman, J.; Virmani, R.; Golan, E. Miniature self-contained intravascular magnetic resonance (IVMI) probe for clinical applications. Magn. Reson. Med. 2005, 54, 105–112. [Google Scholar] [CrossRef] [PubMed]
- Burnettt, L.J.; Jackson, J.A. Remote (inside-out) NMR. I. Remote production of a region of homogeneous magnetic field. J. Magn. Reson. 1980, 41, 406–410. [Google Scholar]
- Jackson, J.A.; Lowell, J.B.; Harmon, J.F. Remote (inside-out) NMR. III. Detection of nuclear magnetic resonance in a remotely produced region of homogeneous magnetic field. J. Magn. Reson. 1980, 41, 411–421. [Google Scholar] [CrossRef]
- Taicher, Z.; Shtrikman, S. Nuclear Magnetic Resonance Sensing Apparatus and Techniques. U.S. Patent No. 4,717,877, 5 January 1988. [Google Scholar]
- Kleinberg, R.L.; Sezginer, A.; Griffin, D.D.; Fukuhara, M. Novel NMR Apparatus for investigating an external sample. J. Magn. Reson. 1992, 97, 466–485. [Google Scholar] [CrossRef]
- Perlo, J.; Danieli, E.; Perlo, J.; Blümich, B.; Casanova, F. Optimized slim-line logging NMR tool to measure soil moisture in situ. J. Magn. Reson. 2013, 233, 74–79. [Google Scholar] [CrossRef] [PubMed]
- Marble, A.E.; Mastikhin, I.V.; Colpitts, B.G.; Balcom, B.J. A compact permanent magnet array with a remote homogeneous field. J. Magn. Reson. 2007, 186, 100–104. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.; He, W.; Juan, C.G.; Bruce, J.B. A New inside-out nuclear magnetic resonance sensor—Three-cylinder array. Trans. China Electrotech. Soc. 2016, 31, 96–101. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999; pp. 184–194. [Google Scholar]
- García-Naranjo, J.C.; Mastikhin, I.V.; Colpitts, B.G.; Balcom, B.J. A unilateral magnet with an extended constant magnetic field gradient. J. Magn. Reson. 2010, 207, 337–344. [Google Scholar] [CrossRef] [PubMed]
- Watzlaw, J.; Glöggler, S.; Blümich, B.; Mokwa, W.; Schnakenberg, U. Stacked planar micro coils for single-sided NMR applications. J. Magn. Reson. 2013, 230, 176–185. [Google Scholar] [CrossRef] [PubMed]
- Chelcea, R.I.; Fechete, R.; Culea, E.; Demco, D.E.; Blümich, B. Distributions of transverse relaxation times for soft-solids measured in strongly inhomogeneous magnetic fields. J. Magn. Reson. 2009, 196, 178–190. [Google Scholar] [CrossRef] [PubMed]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Guo, P.; Shen, S.; He, Y.; Huang, X.; Xu, Z. Mini Inside-Out Nuclear Magnetic Resonance Sensor Design for Soil Moisture Measurements. Sensors 2019, 19, 1682. https://doi.org/10.3390/s19071682
Wu J, Guo P, Shen S, He Y, Huang X, Xu Z. Mini Inside-Out Nuclear Magnetic Resonance Sensor Design for Soil Moisture Measurements. Sensors. 2019; 19(7):1682. https://doi.org/10.3390/s19071682
Chicago/Turabian StyleWu, Jiamin, Pan Guo, Sheng Shen, Yucheng He, Xin Huang, and Zheng Xu. 2019. "Mini Inside-Out Nuclear Magnetic Resonance Sensor Design for Soil Moisture Measurements" Sensors 19, no. 7: 1682. https://doi.org/10.3390/s19071682
APA StyleWu, J., Guo, P., Shen, S., He, Y., Huang, X., & Xu, Z. (2019). Mini Inside-Out Nuclear Magnetic Resonance Sensor Design for Soil Moisture Measurements. Sensors, 19(7), 1682. https://doi.org/10.3390/s19071682





