On the Combination of Multi-Cloud and Network Coding for Cost-Efficient Storage in Industrial Applications
Abstract
1. Introduction
2. Related Work
- Price: The user might specify a maximum price per instance/hour, bid. If the cost of the resource were greater than this price, the service would be interrupted.
- Capacity: A spot instance might suffer an interruption if there were not enough free EC2 capacity to meet the demand for the current instance.
- Constraints: When there is an additional constraint, such as a launch group or an availability zone group, the spot instance is terminated when it cannot be satisfied.
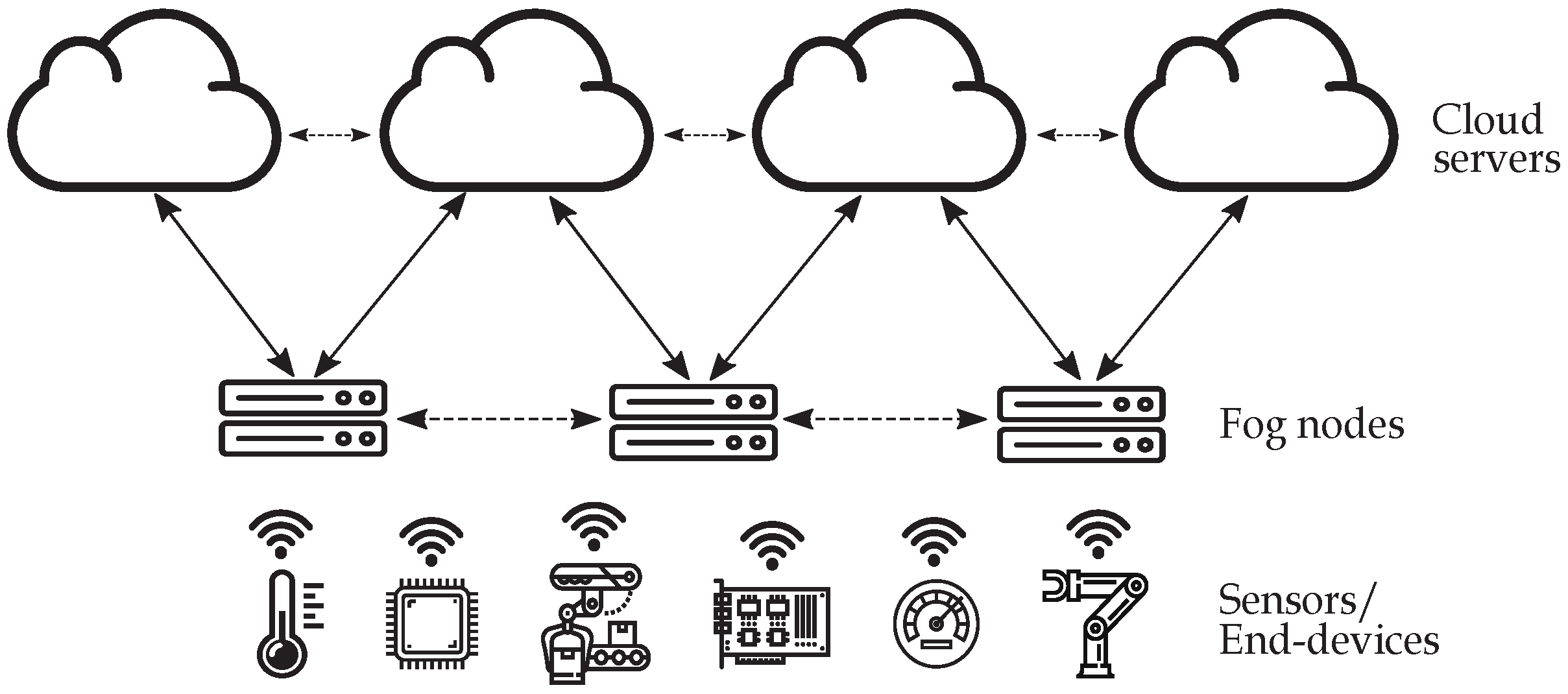
3. System Overview
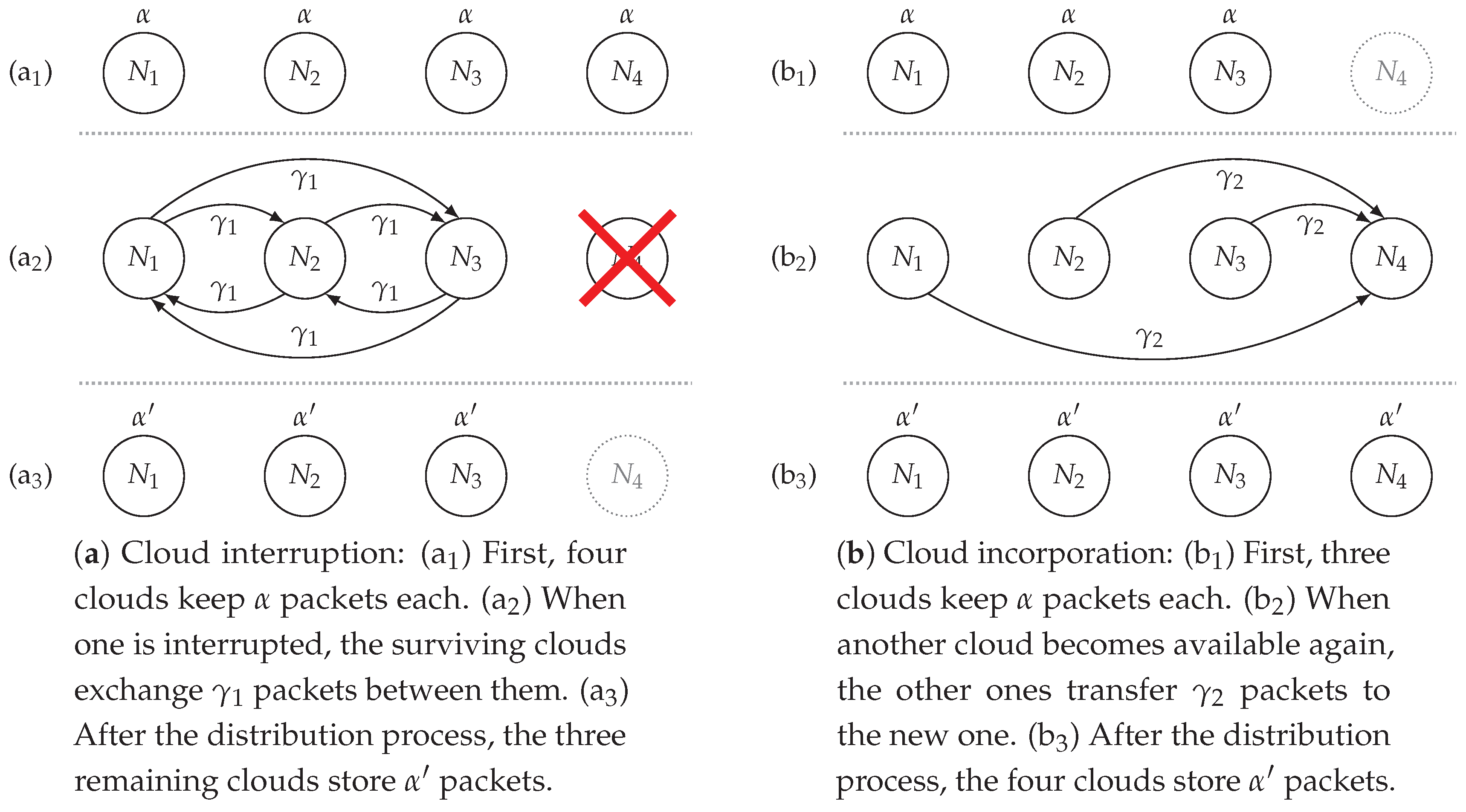
3.1. Proposed Scheme
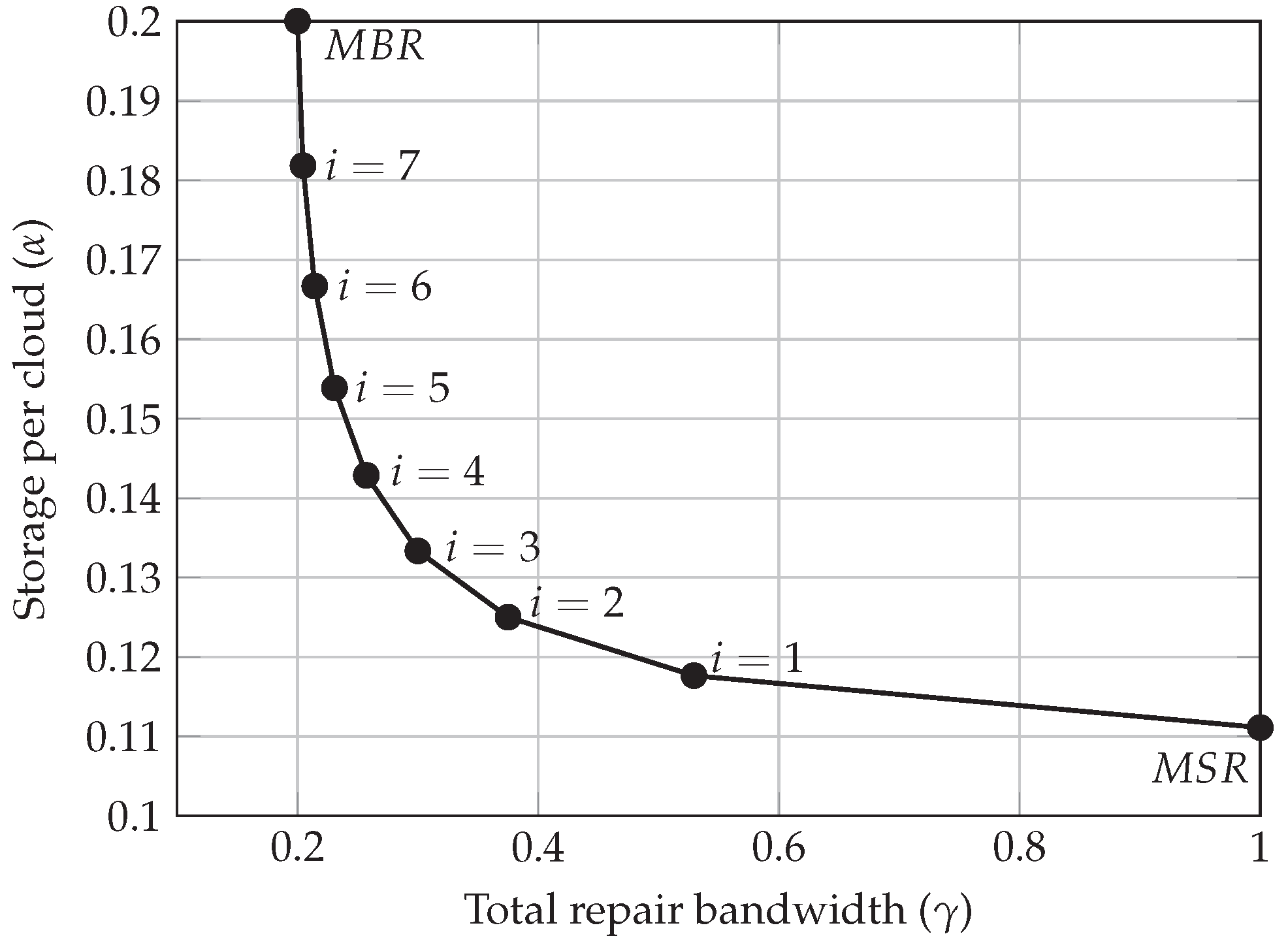
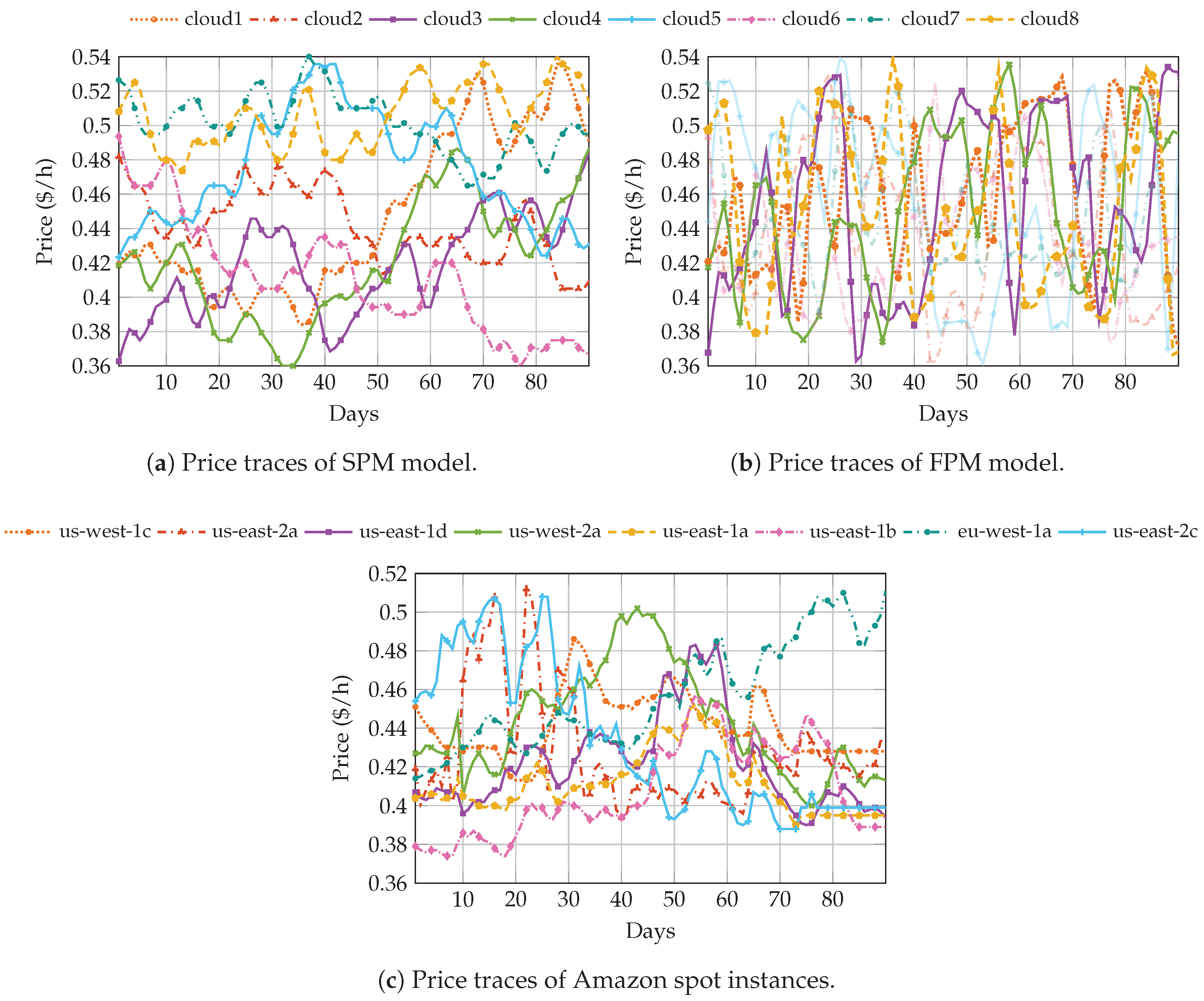
3.2. Pricing Model
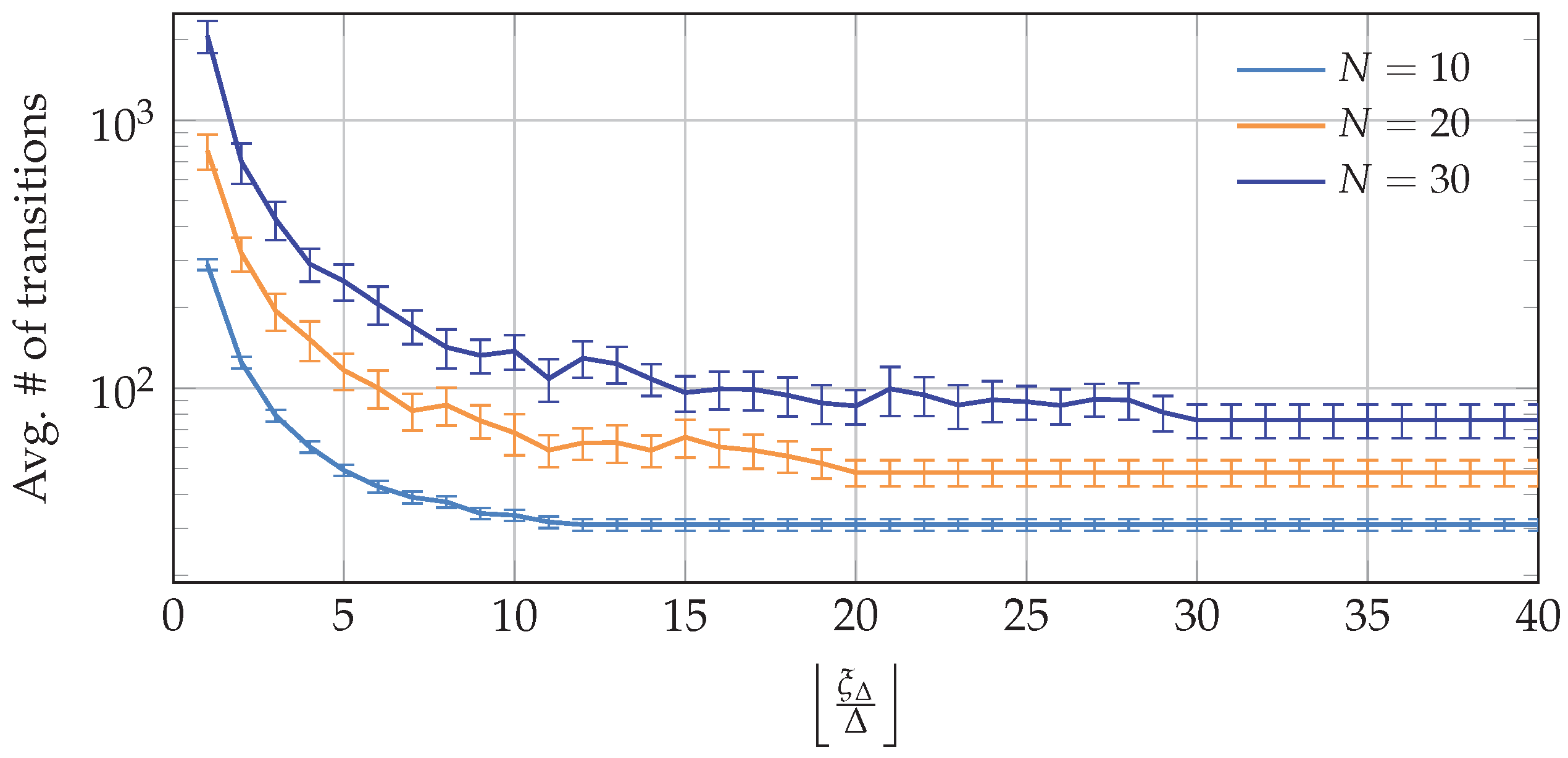
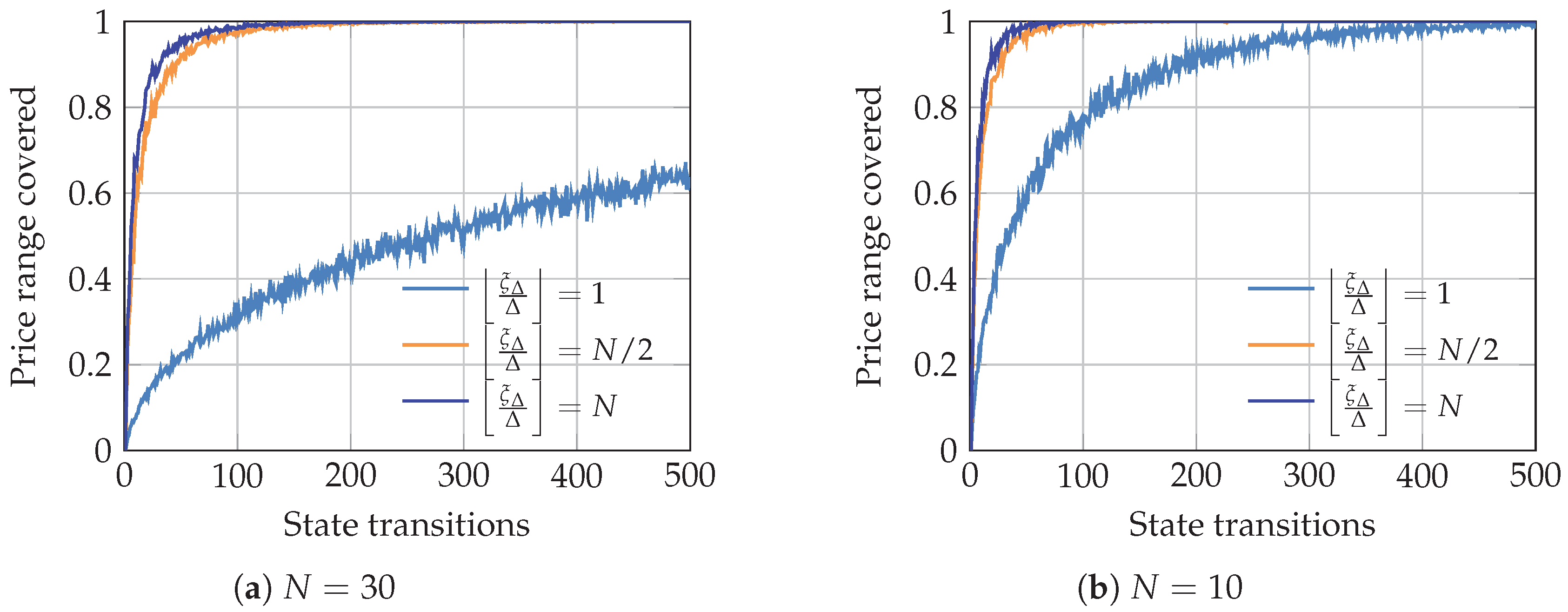
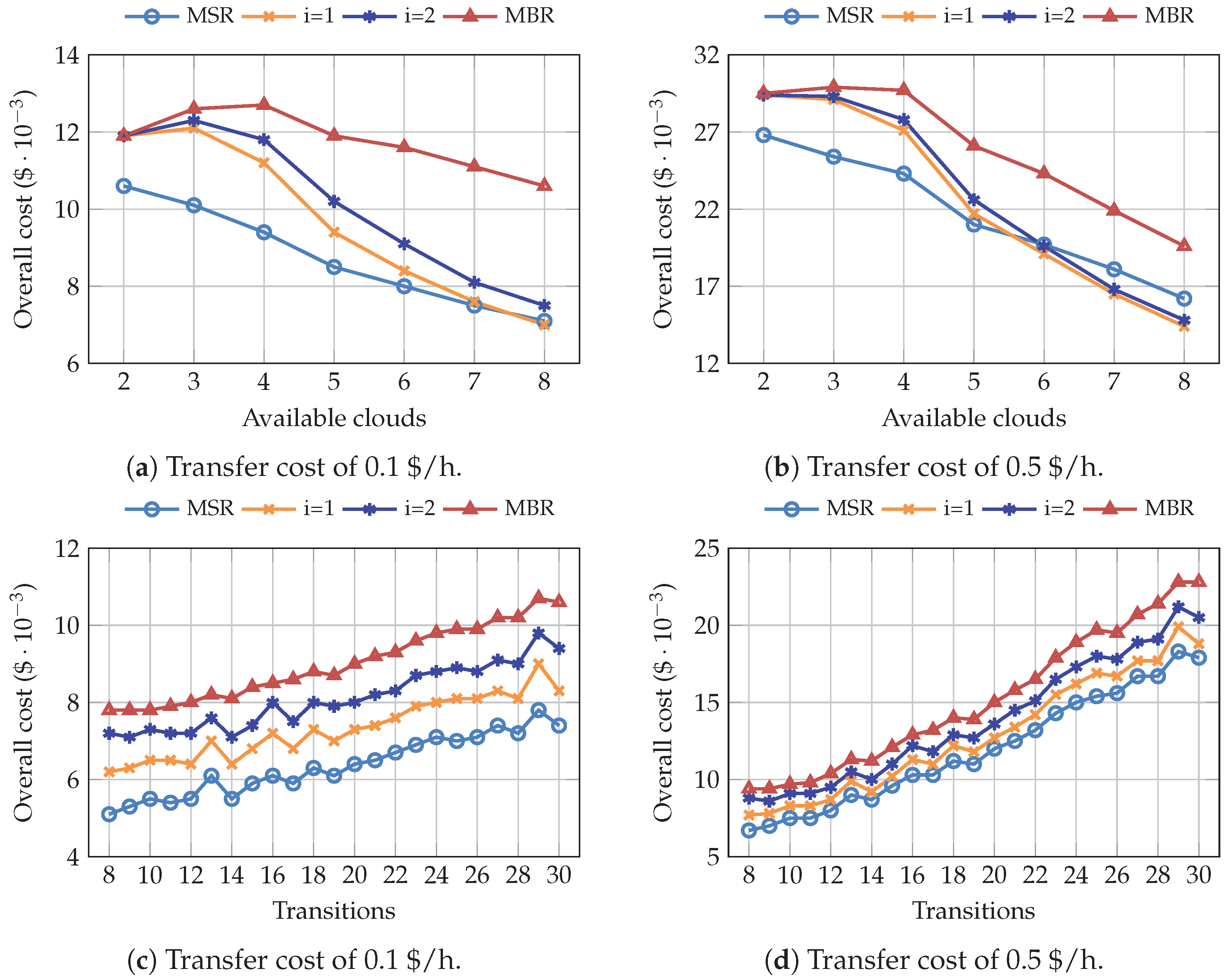
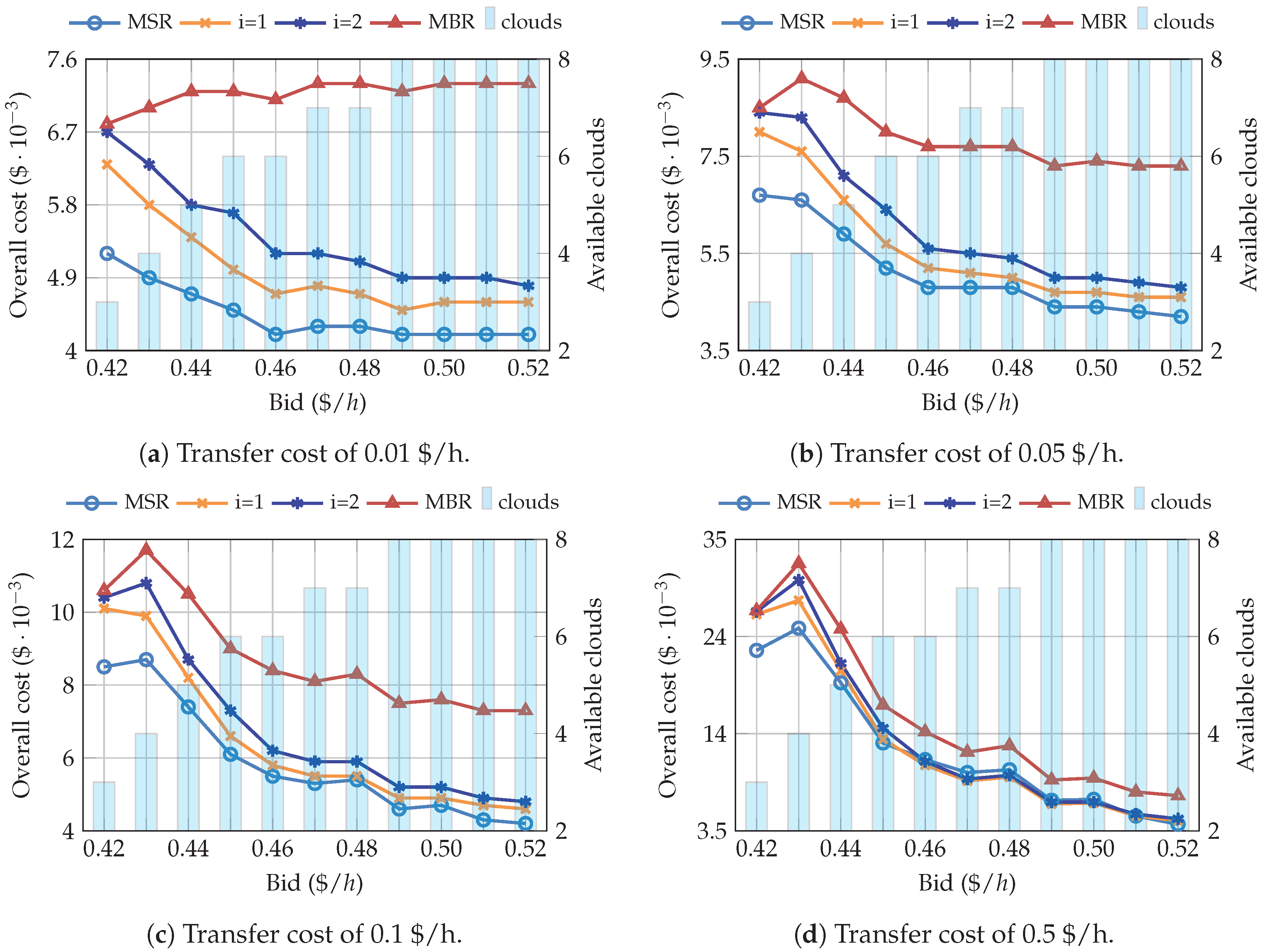
4. Results and Discussion
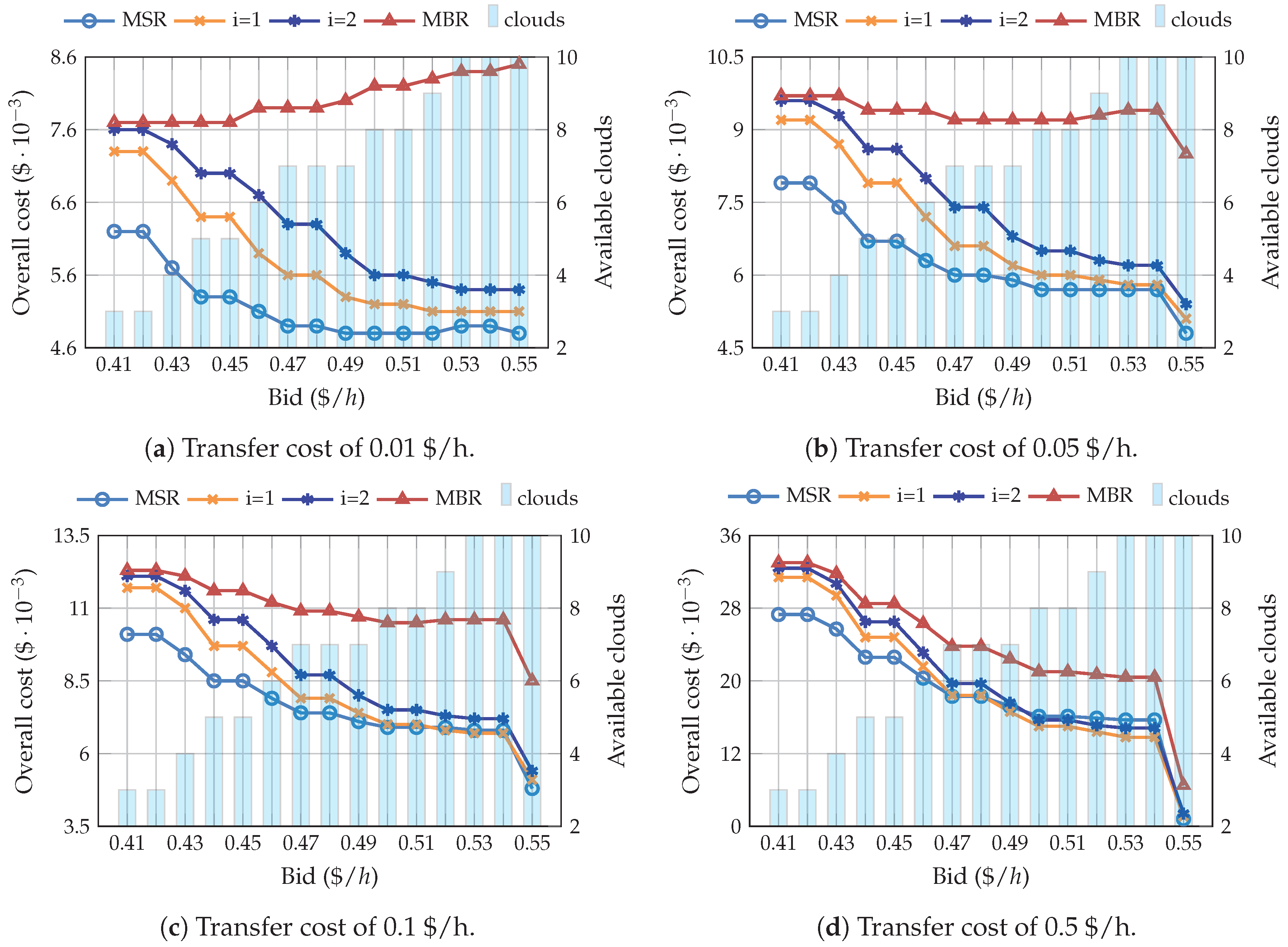
4.1. Simulations Using the Pricing Model
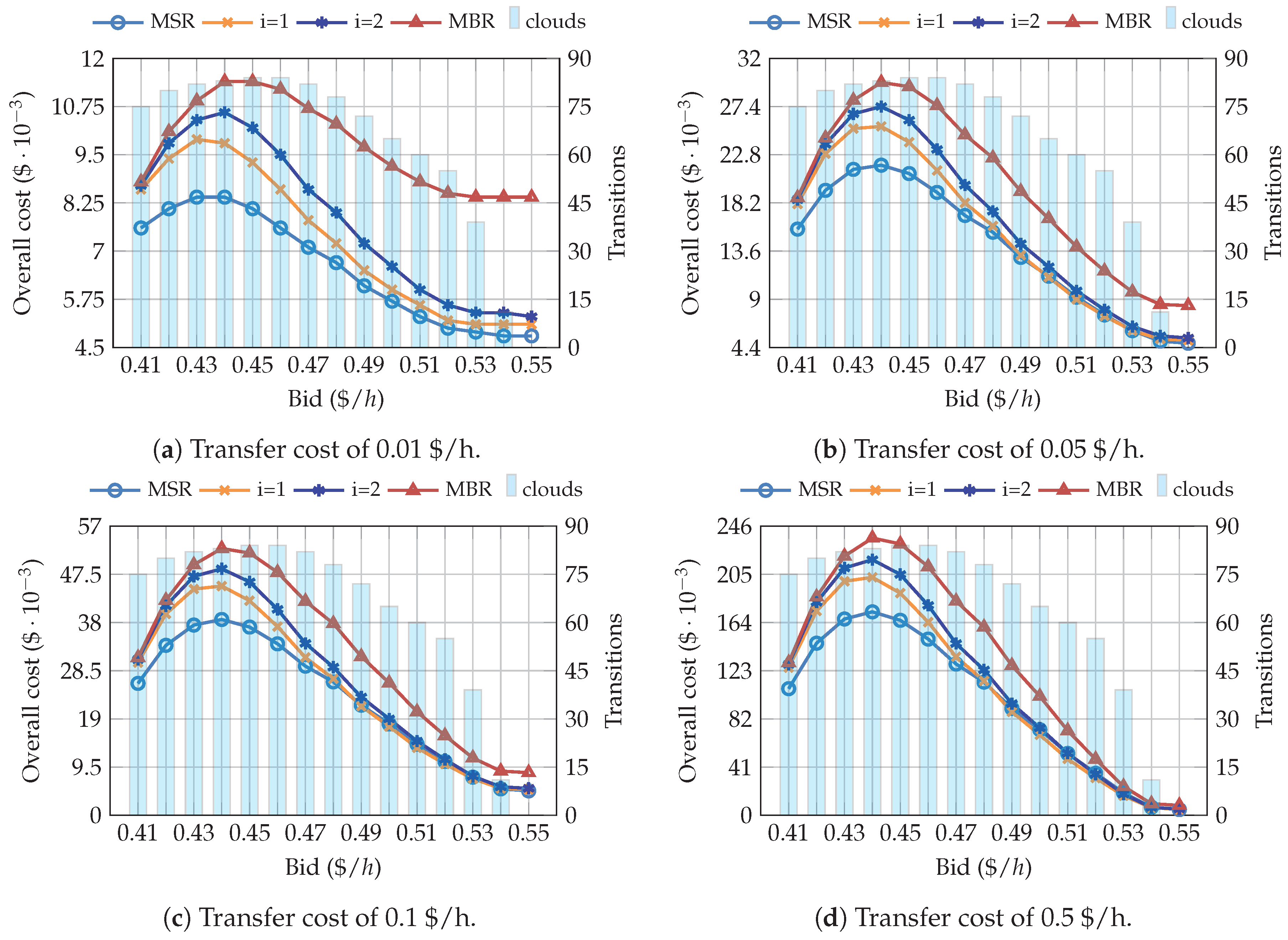
4.2. Simulations Using the Spot Pricing History
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Spot Pricing Model
- (i)
- and : in this case the transitions are not restricted, and any state can be reached from i, regardless of its value.
- (ii)
- and : the transitions to states are restricted, since we cannot reach a state j, in which . Such transition probabilities are 0, according to (A2) and are thus, not considered in the sum.
- (iii)
- and : transitions to states are restricted, since we cannot reach a state j, in which . Such transition probabilities are 0, according to (A2) and are thus, not considered in the sum.
- (iv)
- and : in this case both transitions, to and , are restricted.where is the harmonic number, i.e., the sum of the n first terms of the harmonic progression: .
References
- Lee, J.; Bagheri, B.; Kao, H.A. A Cyber–Physical Systems architecture for Industry 4.0-based manufacturing systems. Manuf. Lett. 2015, 3, 18–23. [Google Scholar] [CrossRef]
- Wollschlaeger, M.; Sauter, T.; Jasperneite, J. The Future of Industrial Communication: Automation Networks in the Era of the Internet-of-Things and Industry 4.0. IEEE Ind. Electron. Mag. 2017, 11, 17–27. [Google Scholar] [CrossRef]
- Wang, S.; Wan, J.; Li, D.; Zhang, C. Implementing Smart Factory of Industrie 4.0: An Outlook. Int. J. Distrib. Sens. Netw. 2016, 12, 3159805. [Google Scholar] [CrossRef]
- Yue, X.; Cai, H.; Yan, H.; Zou, C.; Zhou, K. Cloud-assisted industrial cyber–Physical systems: An insight. Microprocess. Microsyst. 2015, 39, 1262–1270. [Google Scholar] [CrossRef]
- Georgakopoulos, D.; Jayaraman, P.; Fazia, M.; Villari, M.; Ranjan, R. Internet-of-Things and Edge Cloud Computing Roadmap for Manufacturing. IEEE Cloud Comput. 2016, 3, 66–73. [Google Scholar] [CrossRef]
- Bonomi, F.; Milito, R.; Natarajan, P.; Zhu, J. Fog computing: A platform for Internet-of-Things and analytics. Stud. Comput. Intell. 2014, 546, 169–186. [Google Scholar]
- Chiang, M.; Zhang, T. Fog and IoT: An Overview of Research Opportunities. IEEE Internet Things J. 2016, 3, 854–864. [Google Scholar] [CrossRef]
- Peralta, G.; Iglesias-Urkia, M.; Barcelo, M.; Gomez, R.; Moran, A.; Bilbao, J. Fog computing based efficient IoT scheme for the Industry 4.0. In Proceedings of the 2017 IEEE International Workshop of Electronics, Control, Measurement, Signals and Their Application to Mechatronics (ECMSM), Donostia-San Sebastian, Spain, 24–26 May 2017; pp. 1–6. [Google Scholar]
- Masip-Bruin, X.; Marín-Tordera, E.; Tashakor, G.; Jukan, A.; Ren, G.J. Foggy clouds and cloudy fogs: A real need for coordinated management of fog-to-cloud computing systems. IEEE Wirel. Commun. 2016, 23, 120–128. [Google Scholar] [CrossRef]
- IDC. Worldwide Public Cloud Services Spending Forecast. Available online: https://www.idc.com/getdoc.jsp?containerId=prUS43511618 (accessed on 5 February 2019).
- AWS EC2 Spot Instances. Available online: https://aws.amazon.com/ec2/spot/?nc1=h_ls (accessed on 5 February 2019).
- Google Cloud Preemptible VM Instances. Available online: https://cloud.google.com/compute/docs/instances/preemptible (accessed on 5 February 2019).
- Microsoft Azure Low-Priority VMs. Available online: https://docs.microsoft.com/en-us/azure/virtual-machine-scale-sets/virtual-machine-scale-sets-use-low-priority (accessed on 5 February 2019).
- The Benefits of Multi-Cloud Computing. Available online: https://www.networkworld.com/article/3237184/cloud-computing/the-benefits-of-multi-cloud-computing.html (accessed on 5 February 2019).
- Ahlswede, R.; Cai, N.; Li, S.Y.; Yeung, R.W. Network Information Flow. IEEE Trans. Inf. Theory 2000, 46, 1204–1216. [Google Scholar] [CrossRef]
- Fragouli, C.; Le Boudec, J.Y.; Widmer, J. Network coding: An instant primer. SIGCOMM Comput. Commun. Rev. 2006, 36, 63–68. [Google Scholar] [CrossRef]
- Hansen, J.; Lucani, D.; Krigslund, J.; Médard, M.; Fitzek, F. Network coded software defined networking: Enabling 5G transmission and storage networks. IEEE Commun. Mag. 2015, 53, 100–107. [Google Scholar] [CrossRef]
- Bilbao, J.; Crespo, P.M.; Armendariz, I.; Médard, M. Network Coding in the Link Layer for Reliable Narrowband Powerline Communications. IEEE J. Sel. Areas Commun. 2016, 34, 1965–1977. [Google Scholar] [CrossRef]
- Szabo, D.; Gulyas, A.; Fitzek, F.H.P.; Lucani, D.E. Towards the Tactile Internet: Decreasing Communication Latency with Network Coding and Software Defined Networking. In Proceedings of the 21th European Wireless Conference on European Wireless, Budapest, Hungary, 20–22 May 2015; pp. 1–6. [Google Scholar]
- Dimakis, A.; Ramchandran, K.; Wu, Y.; Suh, C. A Survey on network codes for distributed storage. Proc. IEEE 2011, 99, 476–489. [Google Scholar] [CrossRef]
- Cabrera, J.A.; Lucani, D.E.; Fitzek, F.H.P. On network coded distributed storage: How to repair in a fog of unreliable peers. In Proceedings of the 2016 International Symposium on Wireless Communication Systems (ISWCS), Poznan, Poland, 20–23 September 2016. [Google Scholar]
- Dimakis, A.G.; Godfrey, P.B.; Wu, Y.; Wainwright, M.J.; Ramchandran, K. Network Coding for Distributed Storage Systems. IEEE Trans. Infor. Theory 2010, 56, 4539–4551. [Google Scholar] [CrossRef]
- Karlin, S.; Taylor, H.M. A First Course in Stochastic Processes, 2nd ed.; Academic Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Lu, Y. Industry 4.0: A survey on technologies, applications and open research issues. J. Ind. Inf. Integr. 2017, 6, 1–10. [Google Scholar] [CrossRef]
- Zhong, R.Y.; Xu, X.; Klotz, E.; Newman, S.T. Intelligent Manufacturing in the Context of Industry 4.0: A Review. Engineering 2017, 3, 616–630. [Google Scholar] [CrossRef]
- Fisher, O.; Watson, N.; Porcu, L.; Bacon, D.; Rigley, M.; Gomes, R. Cloud manufacturing as a sustainable process manufacturing route. J. Manuf. Syst. 2018, 47, 53–68. [Google Scholar] [CrossRef]
- Productive4.0. Available online: https://productive40.eu/ (accessed on 5 February 2019).
- DIGIMAN4.0. Available online: http://www.digiman4-0.mek.dtu.dk/ (accessed on 5 February 2019).
- Arrohead Framework. Available online: http://www.arrowhead.eu/ (accessed on 5 February 2019).
- C2NET. Available online: http://c2net-project.eu/home (accessed on 5 February 2019).
- CREMA. Available online: https://www.crema-project.eu/index.html (accessed on 5 February 2019).
- Wang, X.; Wang, L.; Mohammed, A.; Givehchi, M. Ubiquitous manufacturing system based on Cloud: A robotics application. Robot. Comput. Integr. Manuf. 2017, 45, 116–125. [Google Scholar] [CrossRef]
- Qu, T.; Lei, S.; Wang, Z.; Nie, D.; Chen, X.; Huang, G. IoT-based real-time production logistics synchronization system under smart cloud manufacturing. Int. J. Adv. Manuf. Technol. 2016, 84, 147–164. [Google Scholar] [CrossRef]
- Spot Instance Interruptions. Available online: https://docs.aws.amazon.com/AWSEC2/latest/UserGuide/spot-interruptions.html (accessed on 5 February 2019).
- Ekwe-Ekwe, N.; Barker, A. Location, Location, Location: Exploring Amazon EC2 Spot Instance Pricing Across Geographical Regions—Extended Version. arXiv, 2018; arXiv:1807.10507. [Google Scholar]
- Lumpe, M.; Chhetri, M.B.; Vo, Q.B.; Kowalcyk, R. On Estimating Minimum Bids for Amazon EC2 Spot Instances. In Proceedings of the 2017 17th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (CCGRID), Madrid, Spain, 14–17 May 2017; pp. 391–400. [Google Scholar]
- Domanal, S.G.; Reddy, G.R.M. An efficient cost optimized scheduling for spot instances in heterogeneous cloud environment. Future Gener. Comput. Syst. 2018, 84, 11–21. [Google Scholar] [CrossRef]
- Javadi, B.; Thulasiramy, R.K.; Buyya, R. Statistical modeling of spot instance prices in public cloud environments. In Proceedings of the 2011 Fourth IEEE International Conference on Utility and Cloud Computing, Victoria, NSW, Australia, 5–8 December 2011; pp. 219–228. [Google Scholar]
- Agmon Ben-Yehuda, O.; Ben-Yehuda, M.; Schuster, A.; Tsafrir, D. Deconstructing Amazon EC2 Spot Instance Pricing. ACM Trans. Econ. Comput. 2013, 1, 16:1–16:20. [Google Scholar] [CrossRef]
- Wang, L.; Wang, W.; Li, B. Towards Online Checkpointing Mechanism for Cloud Transient Servers. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Lee, K.; Son, M. DeepSpotCloud: Leveraging Cross-Region GPU Spot Instances for Deep Learning. In Proceedings of the 2017 IEEE 10th International Conference on Cloud Computing (CLOUD), Honolulu, CA, USA, 25–30 June 2017; pp. 98–105. [Google Scholar]
- Kumar, D.; Baranwal, G.; Raza, Z.; Vidyarthi, D.P. A Survey on Spot Pricing in Cloud Computing. J. Netw. Syst. Manag. 2018, 26, 809–856. [Google Scholar] [CrossRef]
- Bessani, A.; Correia, M.; Quaresma, B.; André, F.; Sousa, P. DepSky: Dependable and Secure Storage in a Cloud-of-Clouds. Trans. Storage 2013, 9, 12:1–12:33. [Google Scholar] [CrossRef]
- Grozev, N.; Buyya, R. Inter-Cloud architectures and application brokering: Taxonomy and survey. Softw. Pract. Exp. 2014, 44, 369–390. [Google Scholar] [CrossRef]
- Alshammari, M.M.; Alwan, A.A.; Nordin, A.; Al-Shaikhli, I.F. Disaster recovery in single-cloud and multi-cloud environments: Issues and challenges. In Proceedings of the 2017 4th IEEE International Conference on Engineering Technologies and Applied Sciences (ICETAS), Salmabad, Bahrain, 29 November–1 December 2017; pp. 1–7. [Google Scholar]
- Katti, S.; Rahul, H.; Hu, W.; Katabi, D.; Medard, M.; Crowcroft, J. XORs in the air: Practical wireless network coding. IEEE/ACM Trans. Netw. 2008, 16, 497–510. [Google Scholar] [CrossRef]
- Xie, L.; Chong, P.; Ho, I.; Guan, Y. A survey of inter-flow network coding in wireless mesh networks with unicast traffic. Comput. Netw. 2015, 91, 738–751. [Google Scholar] [CrossRef]
- Liu, A.; Zhang, Q.; Li, Z.; Choi, Y.J.; Li, J.; Komuro, N. A green and reliable communication modeling for industrial internet of things. Comput. Electr. Eng. 2017, 58, 364–381. [Google Scholar] [CrossRef]
- Oliveira, C.; Ghamri-Doudane, Y.; Brito, C.; Lohier, S. Optimal network coding-based in-network data storage and data retrieval for IoT/WSNs. In Proceedings of the 2015 IEEE 14th International Symposium on Network Computing and Applications, Cambridge, MA, USA, 28–30 September 2015; pp. 208–215. [Google Scholar]
- Sipos, M.; Fitzek, F.H.P.; Lucani, D.E.; Pedersen, M.V. Dynamic allocation and efficient distribution of data among multiple clouds using network coding. In Proceedings of the 2014 IEEE 3rd International Conference on Cloud Networking (CloudNet), Luxembourg, 8–10 October 2014; pp. 90–95. [Google Scholar]
- Sipos, M.; Heide, J.; Lucani, D.E.; Pedersen, M.V.; Fitzek, F.H.P.; Charaf, H. Adaptive Network Coded Clouds: High Speed Downloads and Cost-Effective Version Control. IEEE Trans. Cloud Comput. 2019, 7, 19–33. [Google Scholar] [CrossRef]
- Ho, T.; Medard, M.; Koetter, R.; Karger, D.R.; Effros, M.; Shi, J.; Leong, B. A Random Linear Network Coding Approach to Multicast. IEEE Trans. Inf. Theory 2006, 52, 4413–4430. [Google Scholar] [CrossRef]
- Zhao, X.; Lucani, D.; Shen, X.; Wang, H. Reliable IoT storage: Minimizing bandwidth use in storage without newcomer nodes. IEEE Commun. Lett. 2018, 22, 1462–1465. [Google Scholar] [CrossRef]
- Chen, H.C.H.; Hu, Y.; Lee, P.P.C.; Tang, Y. NCCloud: A Network-Coding-Based Storage System in a Cloud-of-Clouds. IEEE Trans. Comput. 2014, 63, 31–44. [Google Scholar] [CrossRef]
- AWS EC2 Instance Types. Available online: https://docs.aws.amazon.com/AWSEC2/latest/UserGuide/instance-types.html (accessed on 5 February 2019).
- Amazon EC2 I3 Instances. Available online: https://aws.amazon.com/ec2/instance-types/i3/?nc1=h_ls (accessed on 5 February 2019).
- Spot Instance Pricing History. Available online: https://docs.aws.amazon.com/AWSEC2/latest/UserGuide/using-spot-instances-history.html (accessed on 5 February 2019).
- Amazon EC2 Spot Instances Pricing. Available online: https://aws.amazon.com/es/ec2/spot/pricing/ (accessed on 5 February 2019).
- ELASTIC. Available online: https://elastic-project.eu/ (accessed on 5 February 2019).
- SAFIRE. Available online: https://www.safire-factories.org/ (accessed on 5 February 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peralta, G.; Garrido, P.; Bilbao, J.; Agüero, R.; Crespo, P.M. On the Combination of Multi-Cloud and Network Coding for Cost-Efficient Storage in Industrial Applications. Sensors 2019, 19, 1673. https://doi.org/10.3390/s19071673
Peralta G, Garrido P, Bilbao J, Agüero R, Crespo PM. On the Combination of Multi-Cloud and Network Coding for Cost-Efficient Storage in Industrial Applications. Sensors. 2019; 19(7):1673. https://doi.org/10.3390/s19071673
Chicago/Turabian StylePeralta, Goiuri, Pablo Garrido, Josu Bilbao, Ramón Agüero, and Pedro M. Crespo. 2019. "On the Combination of Multi-Cloud and Network Coding for Cost-Efficient Storage in Industrial Applications" Sensors 19, no. 7: 1673. https://doi.org/10.3390/s19071673
APA StylePeralta, G., Garrido, P., Bilbao, J., Agüero, R., & Crespo, P. M. (2019). On the Combination of Multi-Cloud and Network Coding for Cost-Efficient Storage in Industrial Applications. Sensors, 19(7), 1673. https://doi.org/10.3390/s19071673






