Research on Lane a Compensation Method Based on Multi-Sensor Fusion
Abstract
1. Introduction
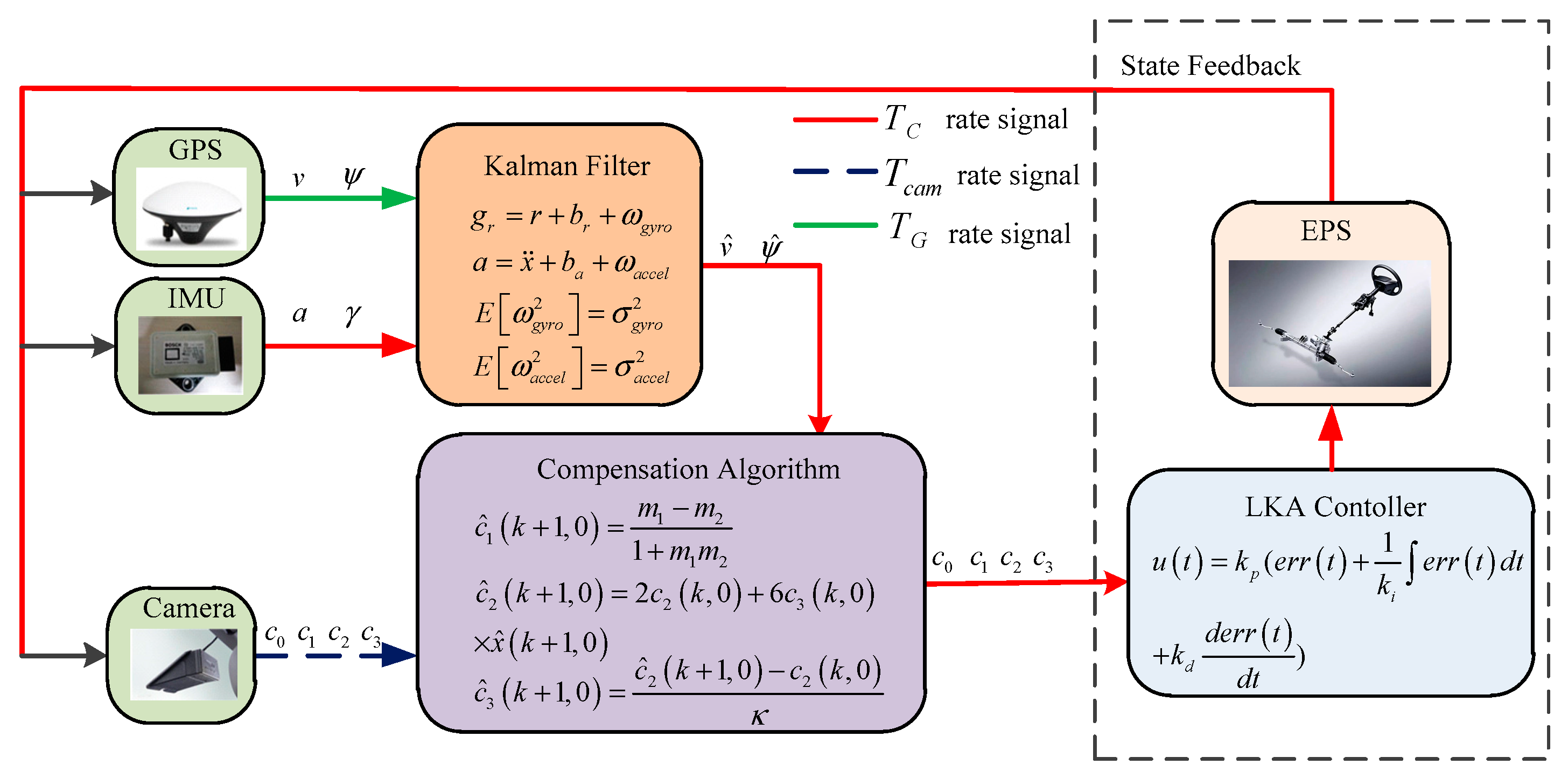
2. Sensor Fusion and Lane Modeling
2.1. Yaw Angle and Longitudinal Velocity Estimation
2.1.1. Gyro Modeling
2.1.2. Accelerometer Modeling
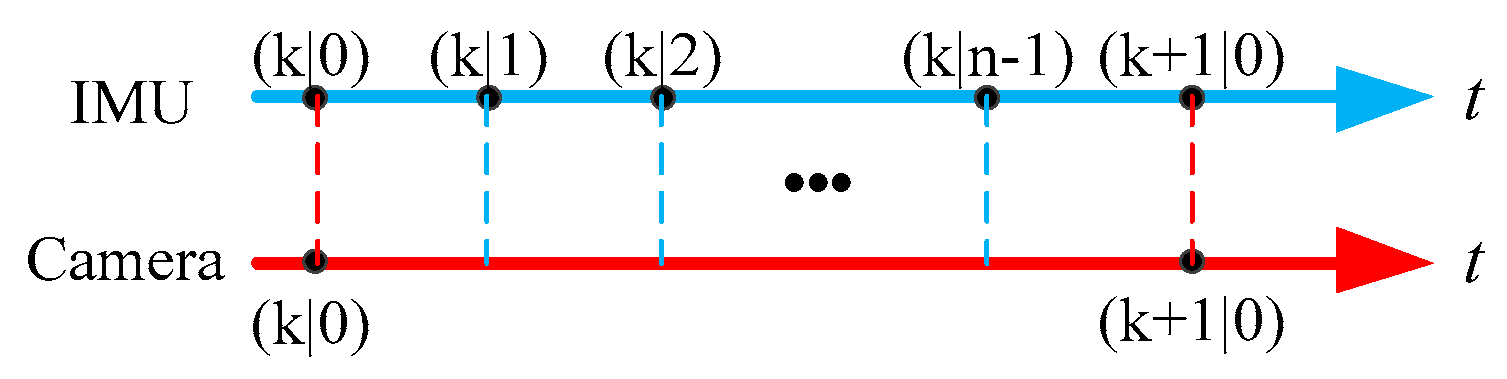
2.1.3. Kalman Filter Establishment
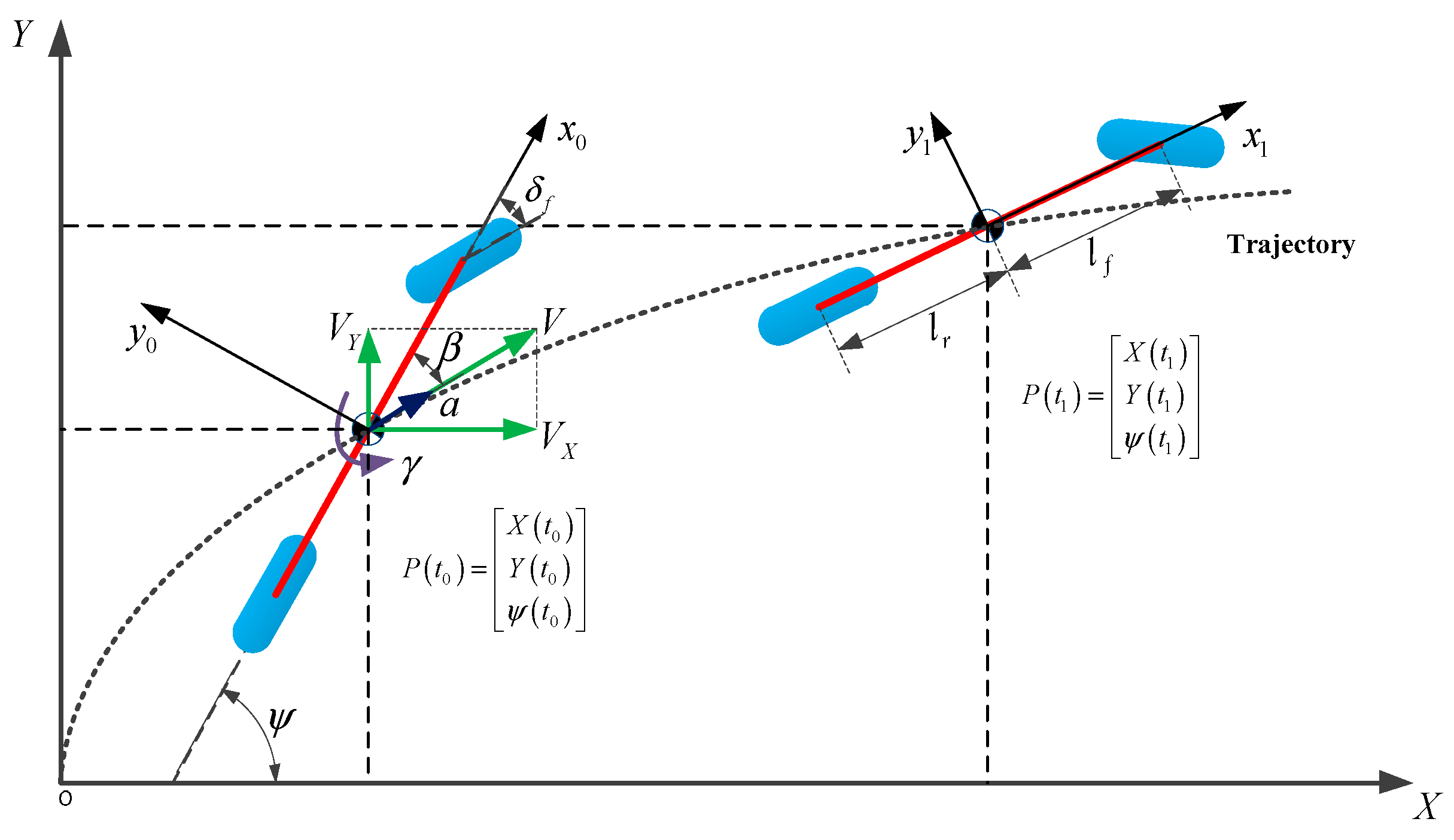
2.2. Vehicle Kinematics
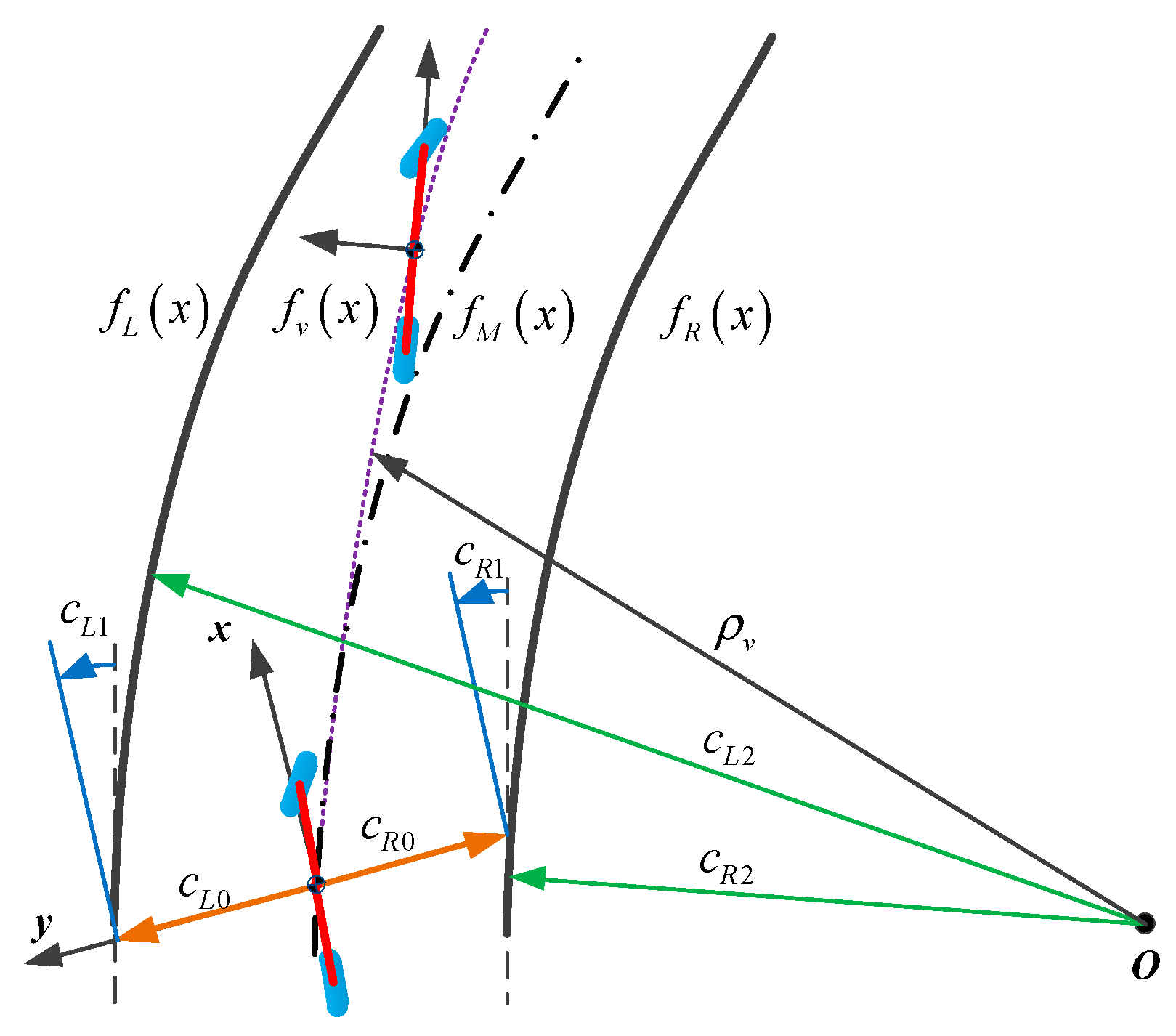
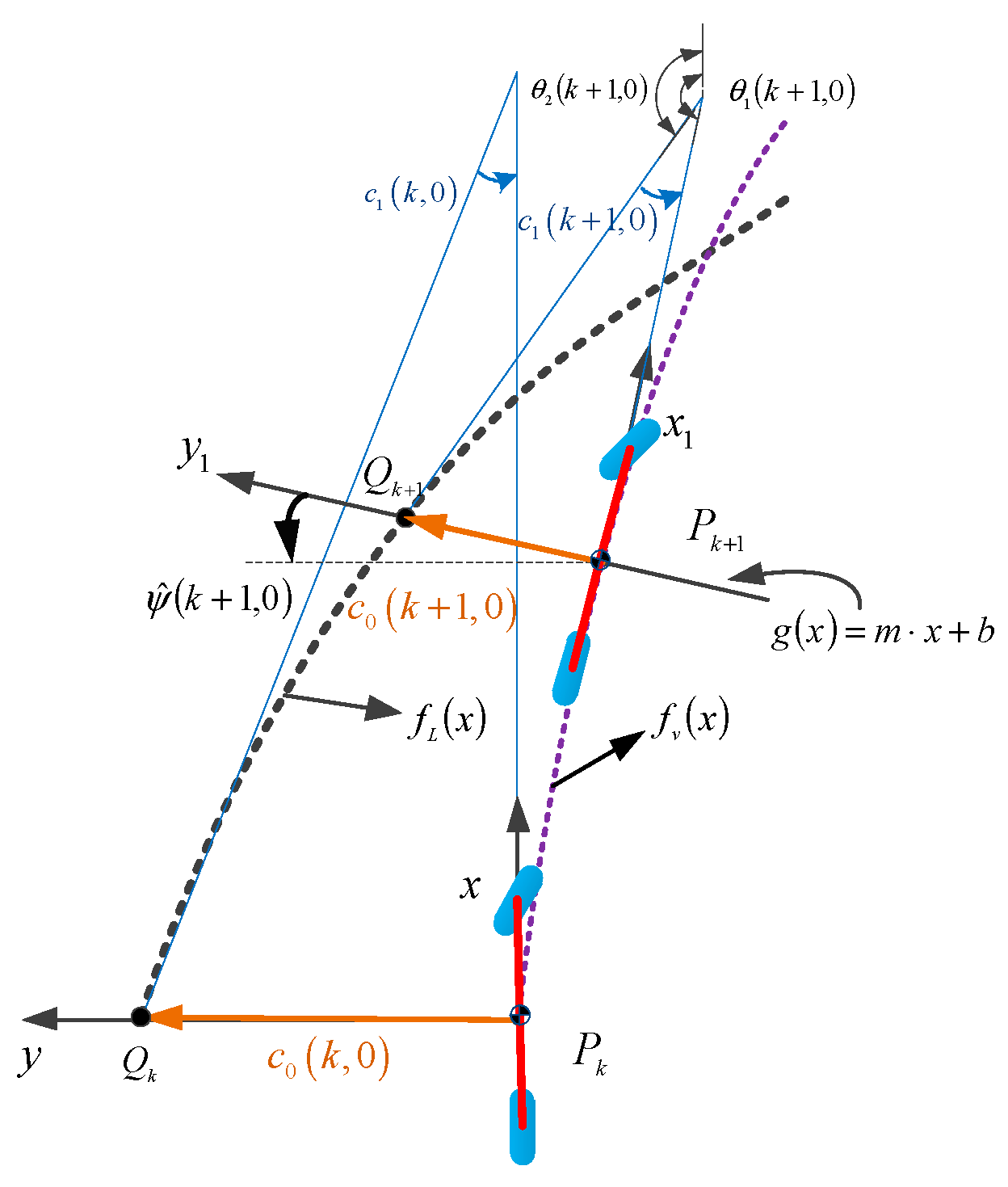
2.3. Vehicle Trajectory and Lane Polynomial
3. Lane Parameters Estimation
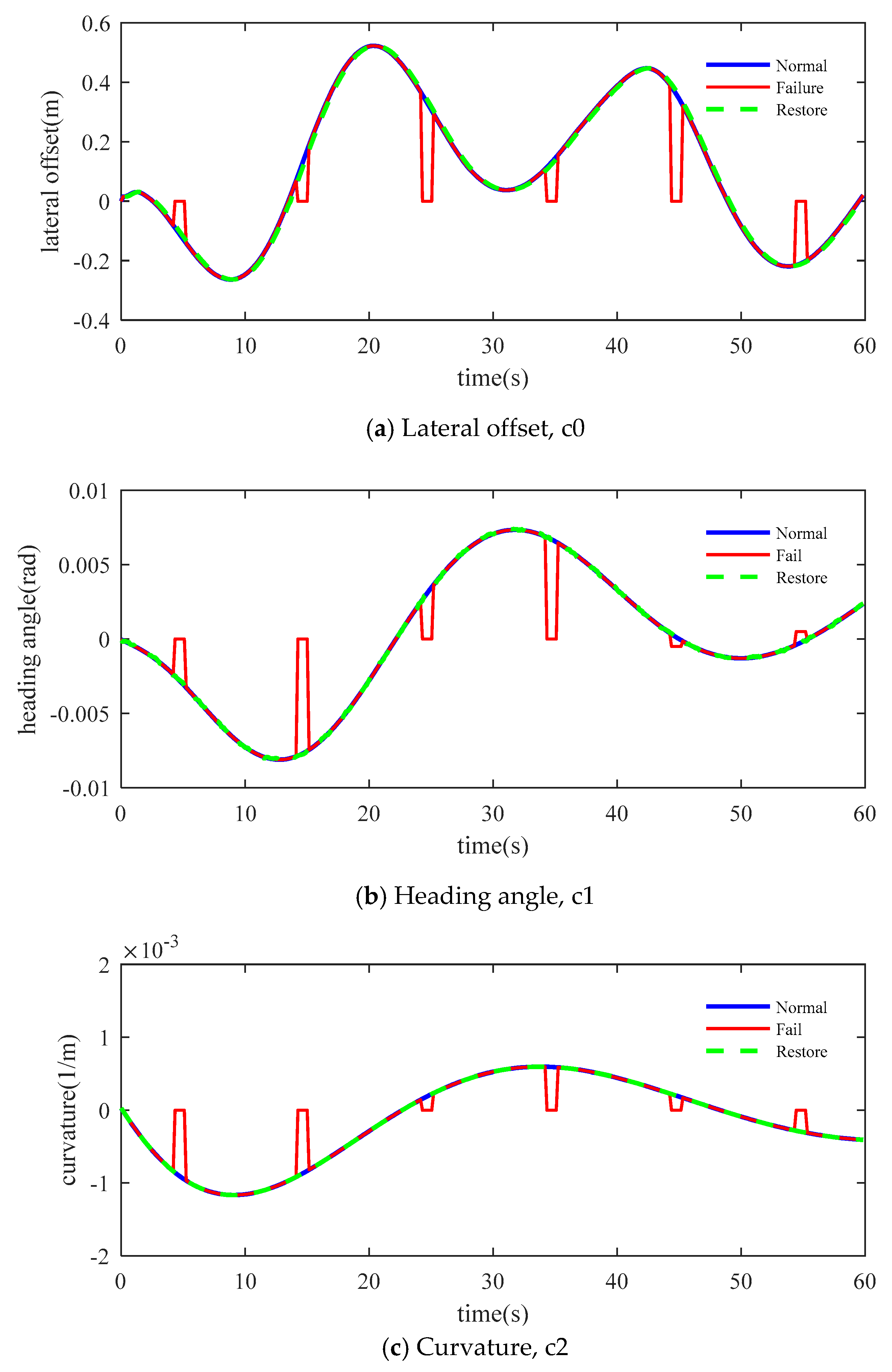
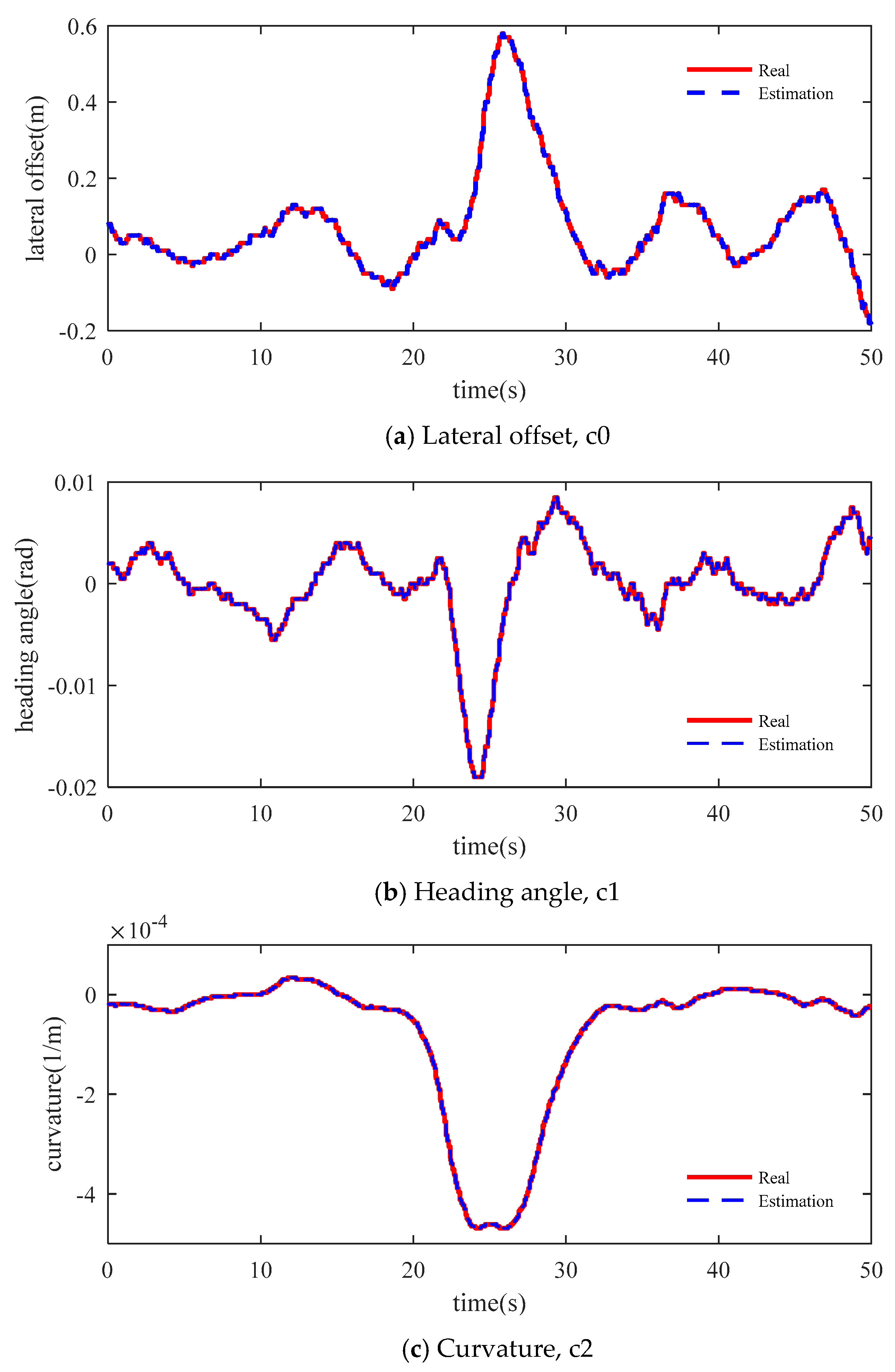
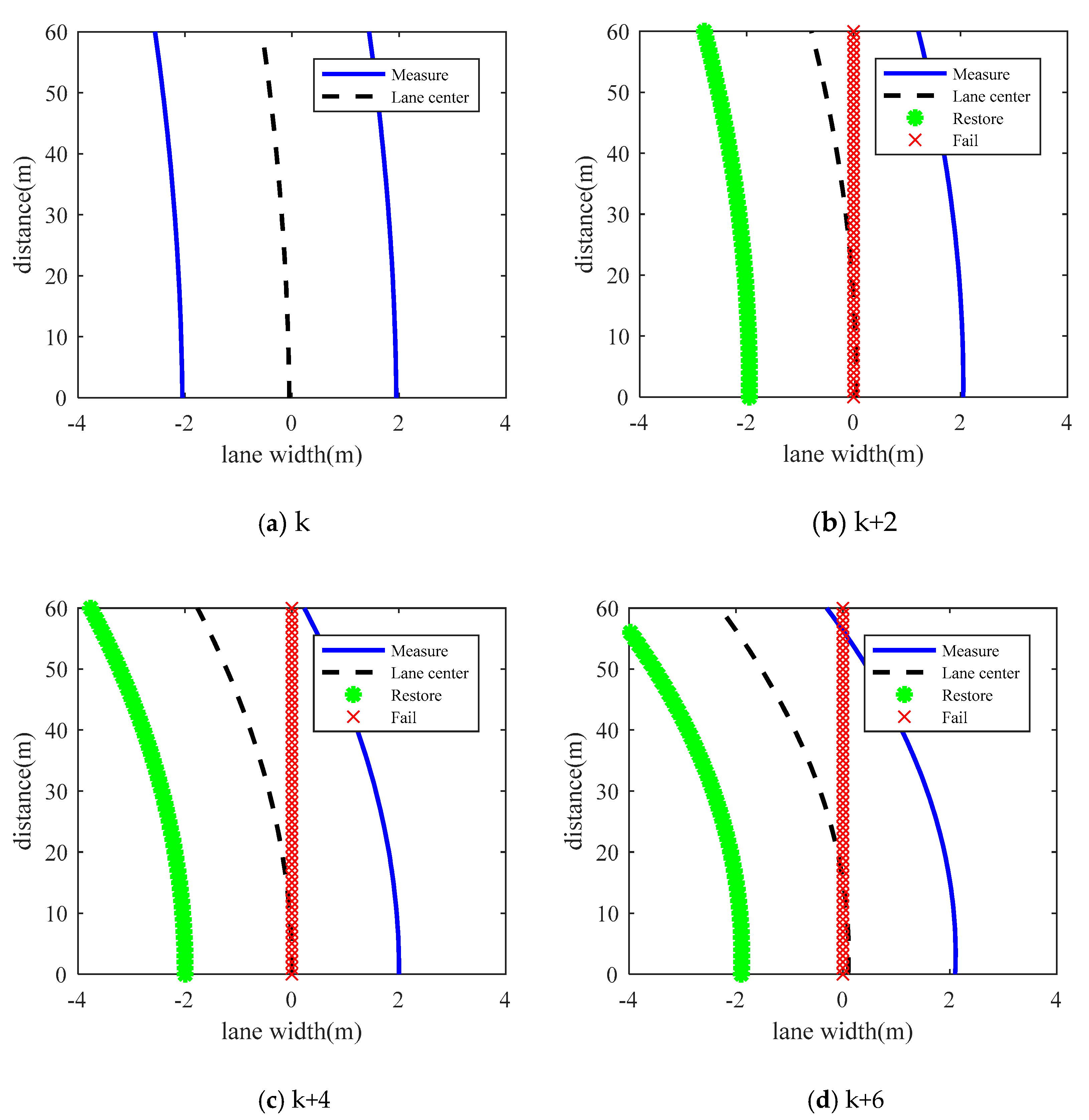
3.1. Lateral Offset Estimation
3.2. Heading Angle Estimation
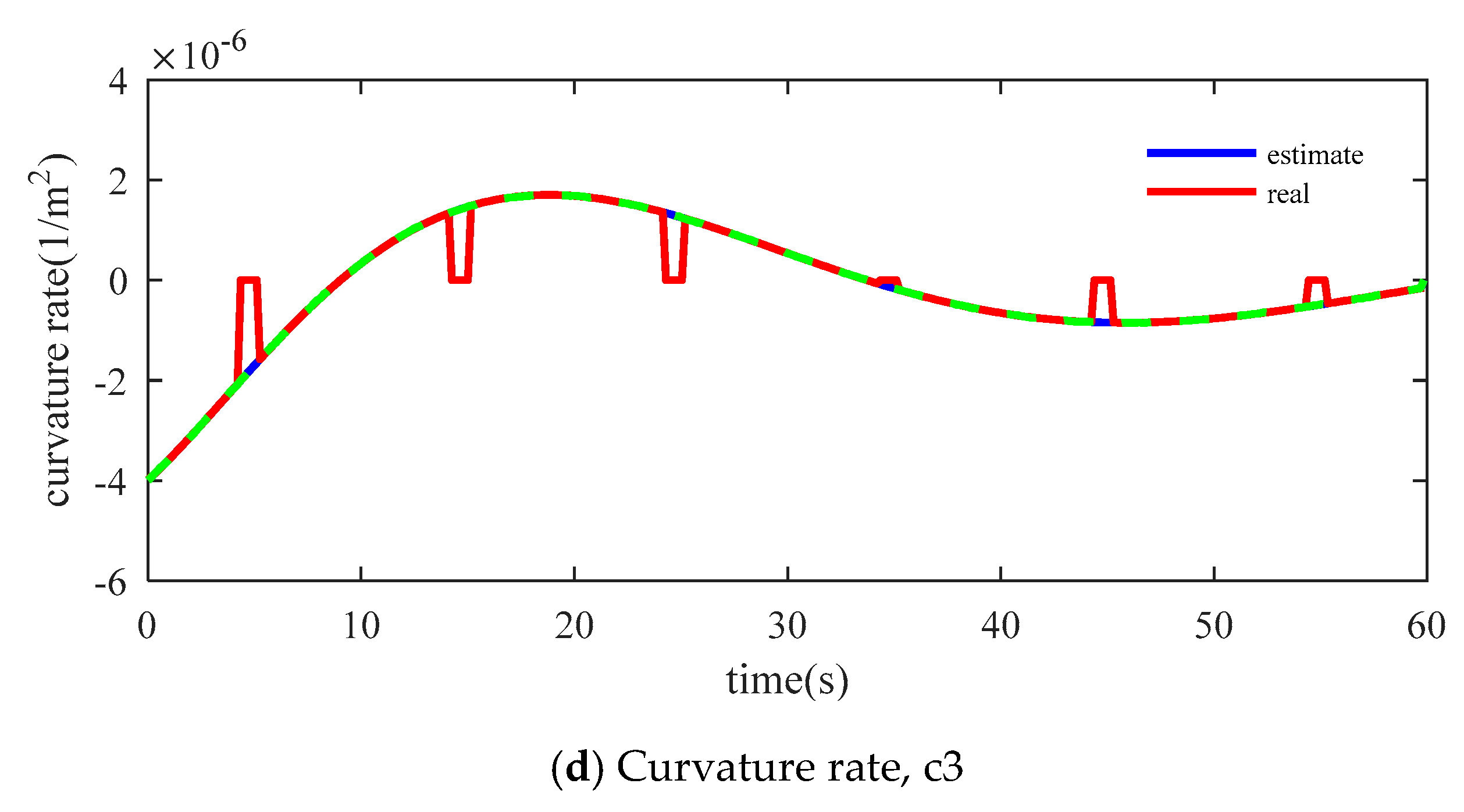
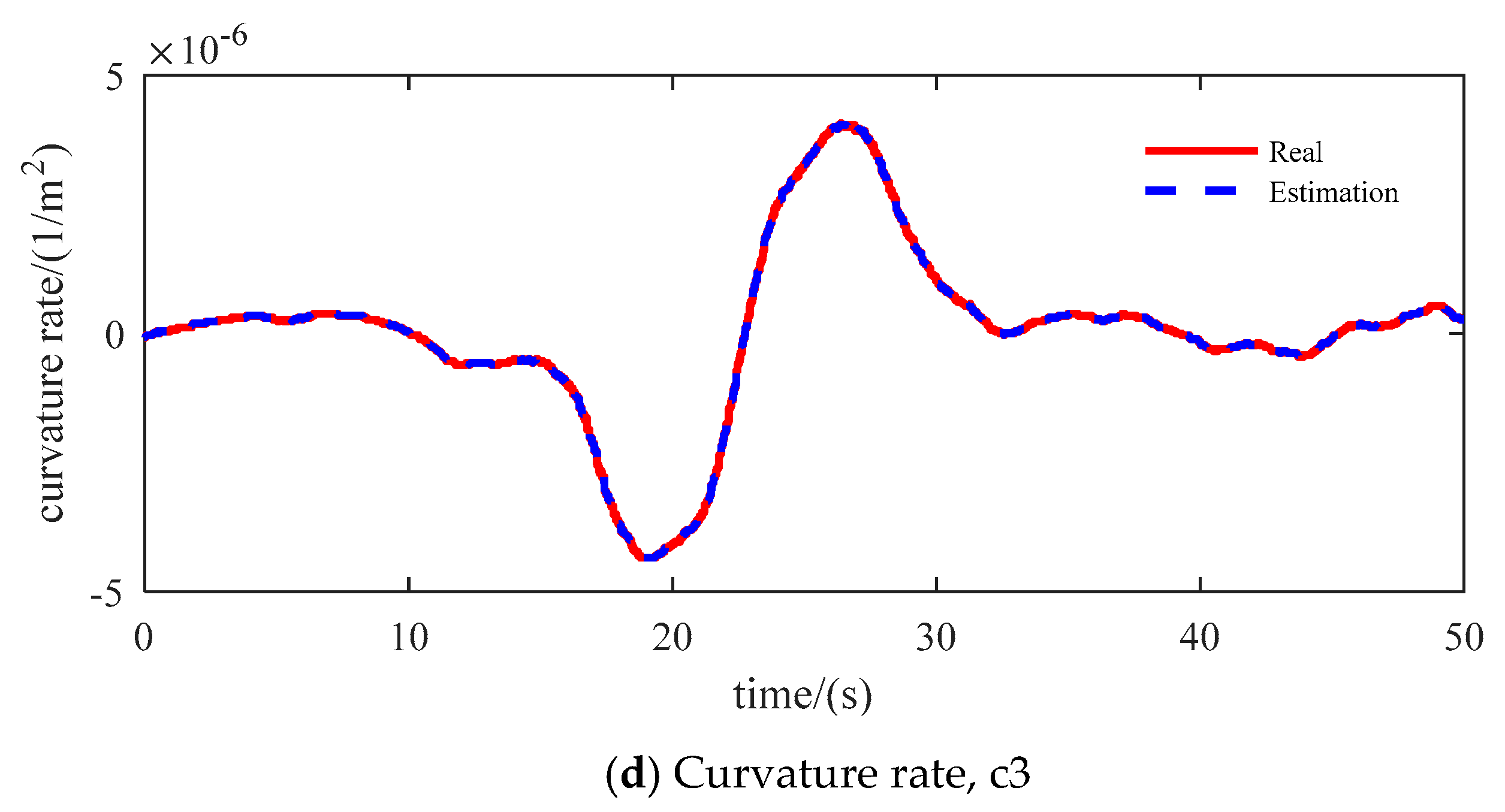
3.3. Curvature and Curvature Rate Estimation
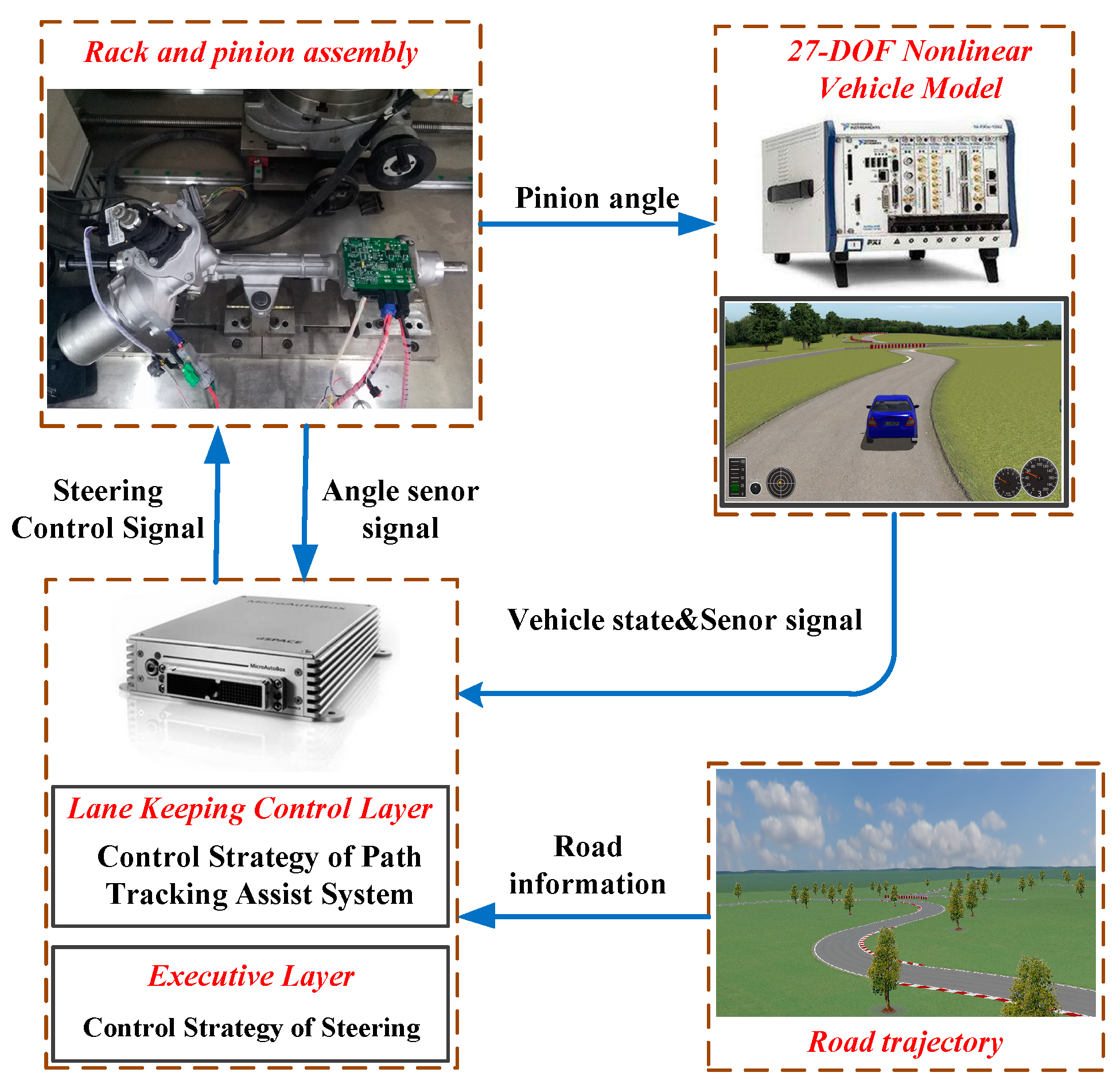
4. Experimental Results
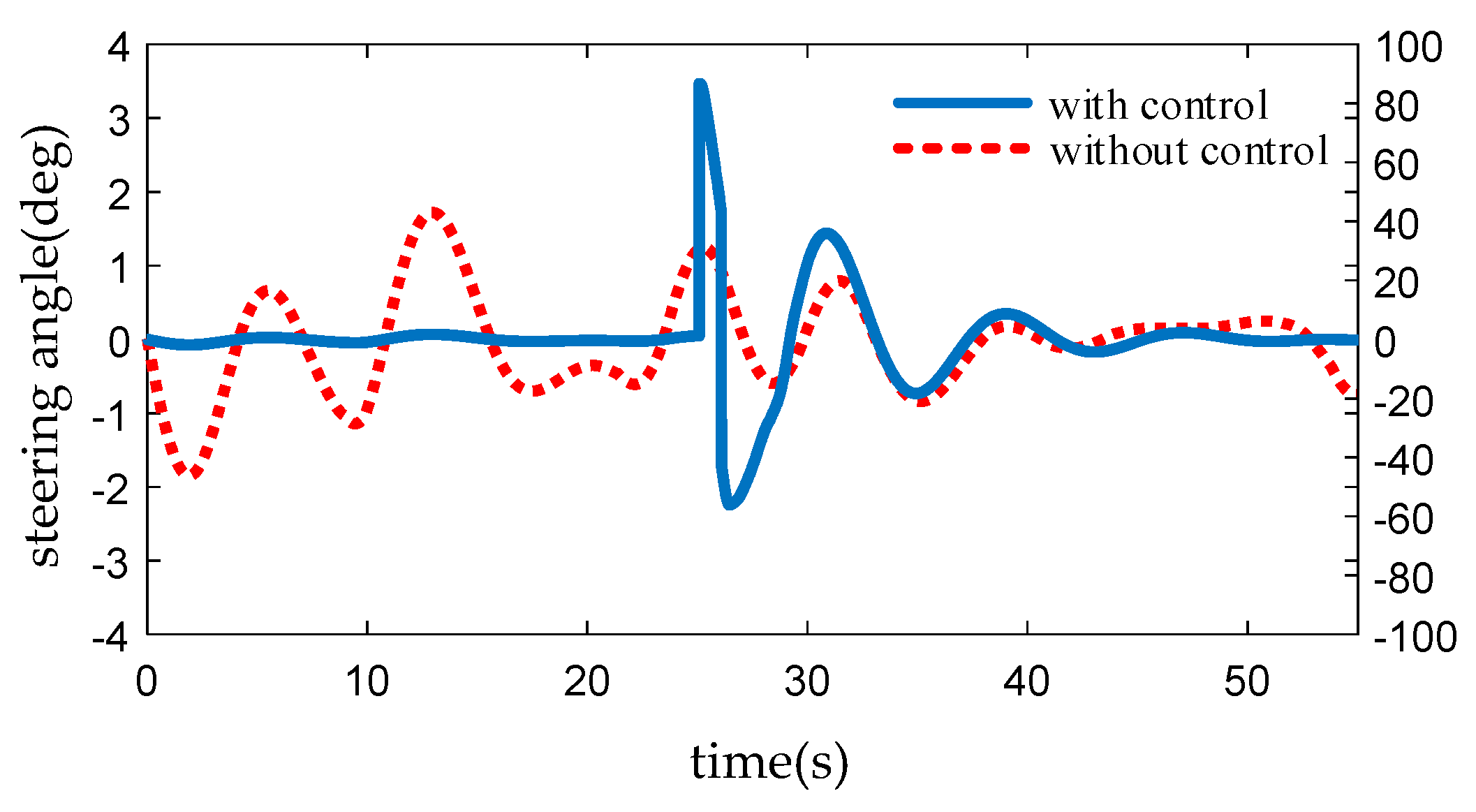
4.1. Simulation
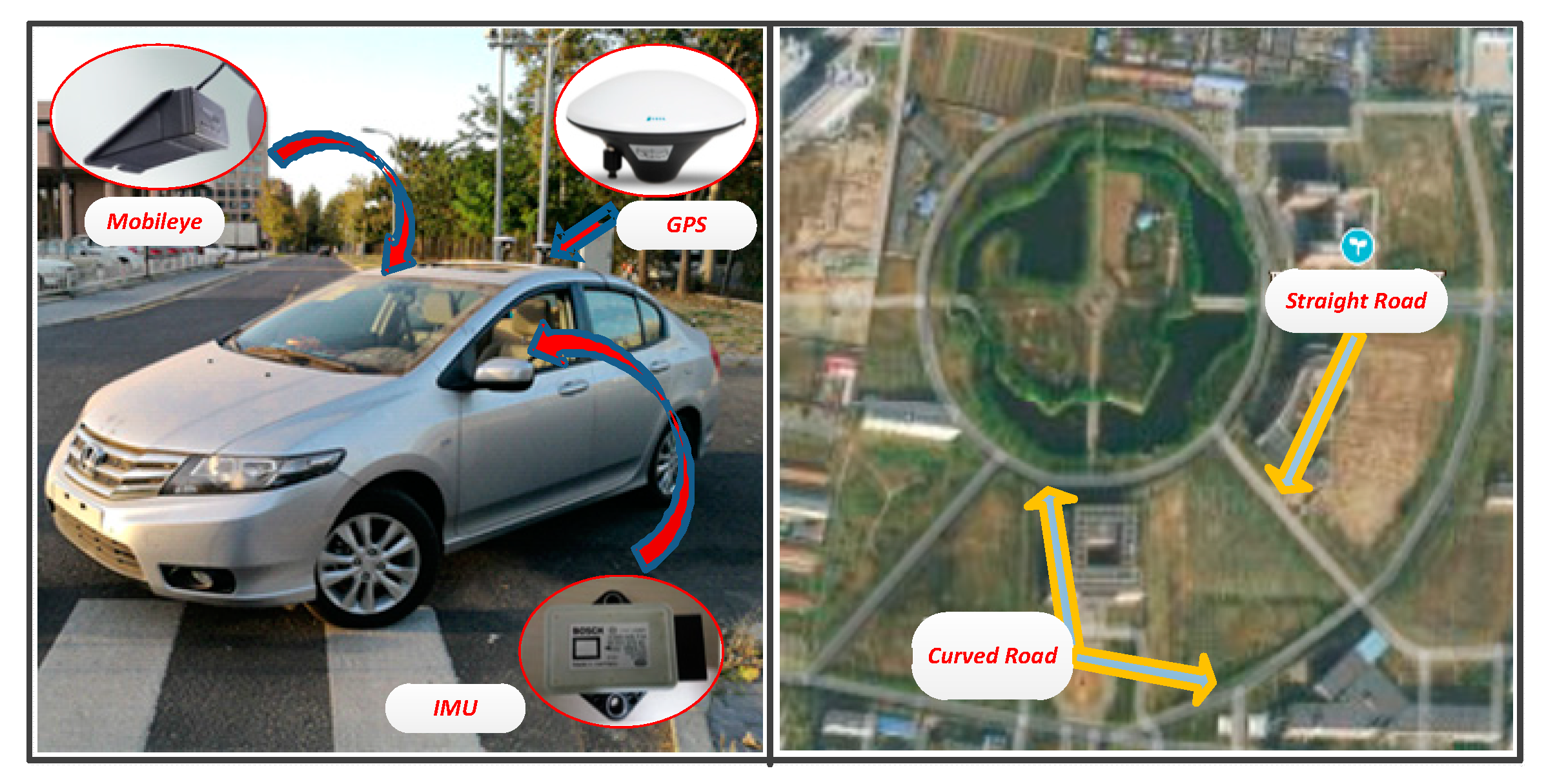
4.2. Vehicle Test
- Total length: 4000 m (straight line section: 1500 m; curve line section: 2500 m)
- Width: 2- lane (each lane width is 3.5 m)
- Curve radius: 250 m and 400 m.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chinese Society for Artificial Intelligence. China Artificial Intelligence Series White Paper Intelligent Driving; Chinese Society for Artificial Intelligence: Beijing, China, 2017; p. 11. [Google Scholar]
- Jung, S.; Youn, J.; Sull, S. Efficient Lane Detection Based on Spatiotemporal Images. IEEE Trans. Intell. Transp. Syst. 2015, 17, 289–295. [Google Scholar] [CrossRef]
- Sivaraman, S.; Trivedi, M.M. Integrated lane and vehicle detection, localization, and tracking: A synergistic approach. IEEE Trans. Intell. Transp. Syst. 2013, 14, 906–917. [Google Scholar] [CrossRef]
- Low, C.Y.; Zamzuri, H.; Mazlan, S.A. Simple robust road lane detection algorithm. In Proceedings of the 2014 5th International Conference on Intelligent and Advanced Systems (ICIAS), Kuala Lumpur, Malaysia, 3–5 June 2014. [Google Scholar]
- Tan, T.; Yin, S.; Quyang, P. Efficient lane detection system based on monocular camera. In Proceedings of the 2015 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 9–12 January 2015. [Google Scholar]
- Chen, Q.; Wang, H. A real-time lane detection algorithm based on a hyperbola-pair model. In Proceedings of the Intelligent Vehicles Symposium, Tokyo, Japan, 13–15 June 2006. [Google Scholar]
- Wang, Y.; Teoh, E.K.; Shen, D. Lane detection and tracking using B-Snake. Image Vis. Comput. 2004, 22, 269–280. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, D.; Teoh, E.K. Lane detection using spline model. Pattern Recognit. Lett. 2000, 21, 677–689. [Google Scholar] [CrossRef]
- Chiu, K.Y.; Lin, S.F. Lane detection using color-based segmentation. In Proceedings of the Intelligent Vehicles Symposium, Las Vegas, NV, USA, 6–8 June 2005. [Google Scholar]
- Ma, C.; Mao, L.; Zhang, Y.F. Lane detection using heuristic search methods based on color clustering. In Proceedings of the 2010 International Conference on Communications, Circuits and Systems (ICCCAS), Chengdu, China, 28–30 July 2010. [Google Scholar]
- Liu, G.; Li, S.; Liu, W. Lane detection algorithm based on local feature extraction. In Proceedings of the Chinese Automation Congress (CAC), Changsha, China, 7–8 November 2013. [Google Scholar]
- Wu, P.C.; Chang, C.Y.; Lin, C.H. Lane-mark extraction for automobiles under complex conditions. Pattern Recognit. 2014, 47, 2756–2767. [Google Scholar] [CrossRef]
- You, F.; Zhang, R.; Zhong, L.; Wang, H.; Xu, J. Lane detection algorithm for night-time digital image based on distribution feature of boundary pixels. J. Opt. Soc. Korea 2013, 17, 188–199. [Google Scholar] [CrossRef]
- Du, X.; Tan, K.K. Vision-based approach towards lane line detection and vehicle localization. Mach. Vis. Appl. 2016, 27, 175–191. [Google Scholar] [CrossRef]
- Hoang, T.M.; Baek, N.R.; Cho, S.W.; Kim, K.W.; Park, K.R. Road lane detection robust to shadows based on a fuzzy system using a visible light camera sensor. Sensors 2017, 17, 2475. [Google Scholar] [CrossRef] [PubMed]
- Lei, G.; Amp, W.J. Lane Detection Under Vehicles Disturbance. Automot. Eng. 2007, 29, 372–376. [Google Scholar]
- Kim, Z. Robust lane detection and tracking in challenging scenarios. IEEE Trans. Intell. Transp. Syst. 2008, 9, 16–26. [Google Scholar] [CrossRef]
- Assidiq, A.A.M.; Khalifa, O.O.; Islam, R.; Khan, S. Real time lane detection for autonomous vehicles. In Proceedings of the International Conference on Computer and Communication Engineering, Kuala Lumpur, Malaysia, 13–15 May 2008. [Google Scholar]
- Satzoda, R.K.; Sathyanarayana, S.; Srikanthan, T. Robust extraction of lane markings using gradient angle histograms and directional signed edges. In Proceedings of the Intelligent Vehicles Symposlum, Madrid, Spain, 3–7 June 2012; pp. 754–759. [Google Scholar]
- Niu, J.W.; Lu, J.; Xu, M.L.; Liu, P. Robust Lane Detection using Two-stage Feature Extraction with Curve Fitting. Pattern Recognit. 2016, 59, 225–233. [Google Scholar] [CrossRef]
- Tapia-Espinoza, R.; Torres-Torriti, M. Robust lane sensing and departure warning under shadows and occlusions. Sensors 2013, 13, 3270–3298. [Google Scholar] [CrossRef] [PubMed]
- Suhr, J.K.; Jang, J.; Min, D.; Jung, H.G. Sensor Fusion-Based Low-Cost Vehicle Localization System for Complex Urban Environments. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1–9. [Google Scholar] [CrossRef]
- Gu, Y.L.; Hsu, L.T.; Kamijo, S. Passive Sensor Integration for Vehicle Self-Localization in Urban Traffic Environment. Sensors 2015, 12, 30199–30220. [Google Scholar] [CrossRef]
- Kang, C.; Lee, S.H.; Chung, C.C. On-road vehicle localization with GPS under long term failure of a vision sensor. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems (ITSC), Gran Canaria, Spain, 15–18 September 2015. [Google Scholar]
- Hu, Z.C.; Uchimura, K. Fusion of Vision, GPS and 3D Gyro Data in Solving Camera Registration Problem for Direct Visual Navigation. Int. J. ITS Res. 2006, 4, 3–12. [Google Scholar]
- Tao, Z.; Bonnifait, P.; Frémont, V. Mapping and localization using GPS, lane markings and proprioceptive sensors. In Proceedings of the IEEE RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 406–412. [Google Scholar]
- Jung, J.; Bae, S.H. Real-Time Road Lane Detection in Urban Areas Using LiDAR Data. Electronics 2018, 7, 276. [Google Scholar] [CrossRef]
- Vivacqua, R.; Vassallo, R.; Martins, F. A low cost sensors approach for accurate vehicle localization and autonomous driving application. Sensors 2017, 17, 2359. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Liu, B. A robust vehicle localization approach based on gnss/imu/dmi/lidar sensor fusion for autonomous vehicles. Sensors 2017, 17, 2140. [Google Scholar] [CrossRef]
- Lee, G.I.; Kang, C.M.; Lee, S.H. Multi object-based predictive virtual lane. In Proceedings of the IEEE International Conference on Intelligent Transportation Systems, Yokohama, Japan, 16–19 October 2018. [Google Scholar]
- Song, M.; Kim, C.; Kim, M.; Yi, K. Robust lane tracking algorithm for forward target detection of automated driving vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018. [Google Scholar] [CrossRef]
- Kang, C.M.; Lee, S.H.; Chung, C.C. Lane estimation using a vehicle kinematic lateral motion model under clothoidal road constraints. In Proceedings of the 2014 IEEE 17th International Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014. [Google Scholar]
- Son, Y.S.; Kim, W.; Lee, S.H.; Chung, C.C. Robust multirate control scheme with predictive virtual lanes for lane-keeping system of autonomous highway driving. IEEE Trans. Veh. Technol. 2015, 64, 3378–3391. [Google Scholar] [CrossRef]
- Kang, C.M.; Lee, S.H.; Kee, S.C.; Chung, C.C. Kinematics-based Fault-tolerant Techniques: Lane Prediction for an Autonomous Lane Keeping System. Int. J. Control Autom. Syst. 2018, 16, 1293–1302. [Google Scholar] [CrossRef]
- Son, Y.S.; Lee, S.H.; Chung, C.C. Predictive virtual lane method using relative motions between a vehicle and lanes. Int. J. Control Autom. Syst. 2015, 13, 146–155. [Google Scholar] [CrossRef]
- Lee, S.H.; Chung, C.C. Robust multirate on-road vehicle localization for autonomous highway driving vehicles. IEEE Trans. Control Syst. Technol. 2017, 25, 577–589. [Google Scholar] [CrossRef]
- Adrian, Z.; Marc, W. Control algorithm for hands-off lane centering on motorways. In Proceedings of the Aachen Colloquium Automobile and Engine Technology, Aachen, Germany, 12 October 2011; pp. 1–13. [Google Scholar]
- Ji, X.; Wu, J.; Zhao, Y.; Liu, Y.; Zhan, X. A new robust control method for active front steering considering the intention of the driver. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2015, 229, 518–531. [Google Scholar] [CrossRef]
- Wu, J.; Cheng, S.; Liu, B.; Liu, C. A Human-Machine-Cooperative-Driving Controller Based on AFS and DYC for Vehicle Dynamic Stability. Energies 2017, 10, 1737. [Google Scholar] [CrossRef]
- Ji, X.; Liu, Y.; He, X.; Yang, K.; Na, X.; Lv, C. Interactive Control Paradigm based Robust Lateral Stability Controller Design for Autonomous Automobile Path Tracking with Uncertain Disturbance: A Dynamic Game Approach. IEEE Trans. Veh. Technol. 2018, 67, 6906–6920. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]

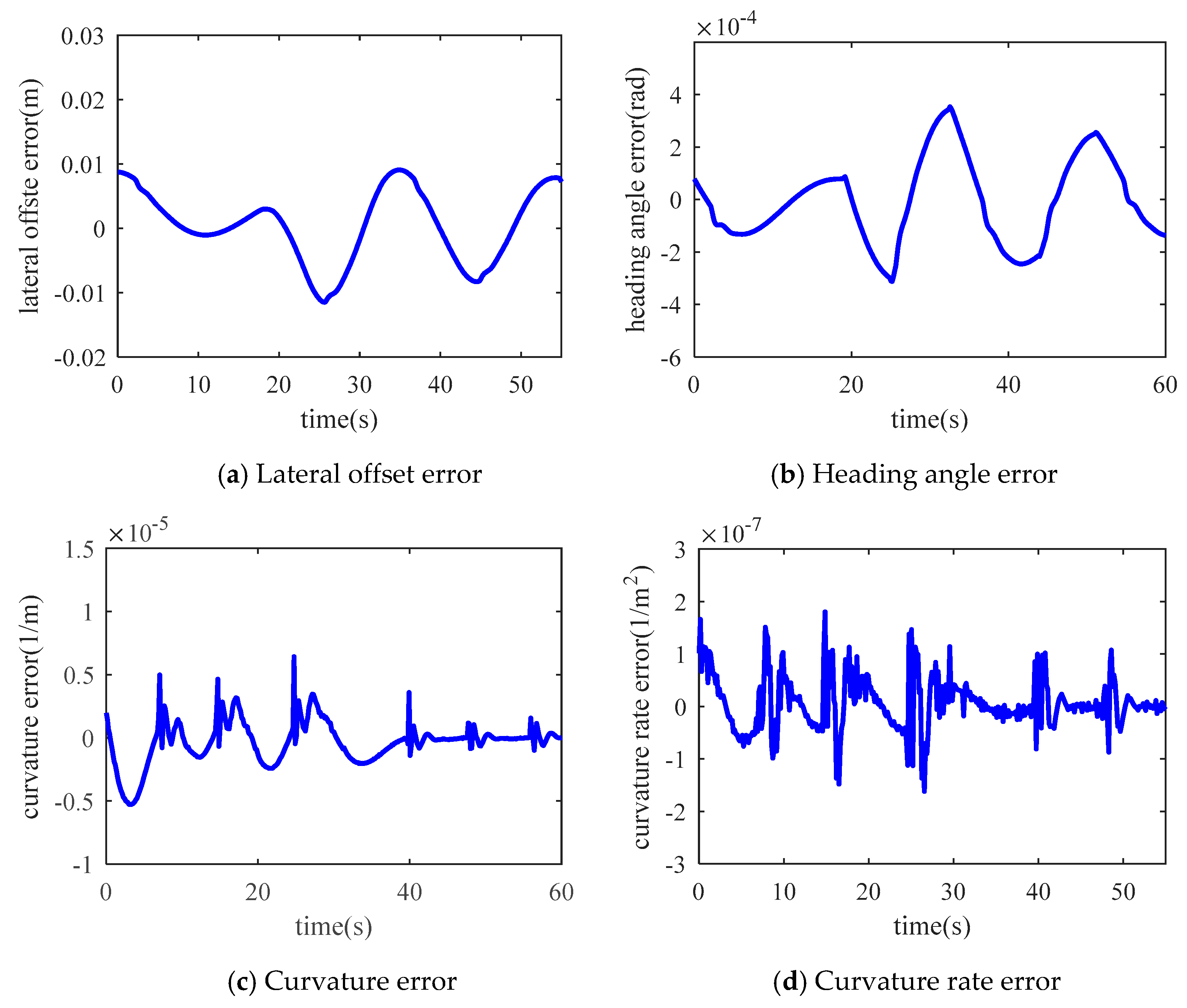
| Error Boundaries | RMSE | |
|---|---|---|
| Lateral offset [m] | 1 × 10−2 | 3.9 × 10−3 |
| Heading angle [rad] | 4 × 10−4 | 1.18 × 10−4 |
| Curvature [1/m] | 1.2 × 10−5 | 4 × 10−6 |
| Curvature rate [1/m2] | 1.5 × 10−7 | 3.24 × 10−8 |
| Sensor/Parameters | Update Period (ms) |
|---|---|
| ECU | 10 |
| Vision (Mobileye) | 70 |
| GPS (Trimble) | 500 |
| IMU (BOSCH) | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhang, W.; Ji, X.; Ren, C.; Wu, J. Research on Lane a Compensation Method Based on Multi-Sensor Fusion. Sensors 2019, 19, 1584. https://doi.org/10.3390/s19071584
Li Y, Zhang W, Ji X, Ren C, Wu J. Research on Lane a Compensation Method Based on Multi-Sensor Fusion. Sensors. 2019; 19(7):1584. https://doi.org/10.3390/s19071584
Chicago/Turabian StyleLi, Yushan, Wenbo Zhang, Xuewu Ji, Chuanxiang Ren, and Jian Wu. 2019. "Research on Lane a Compensation Method Based on Multi-Sensor Fusion" Sensors 19, no. 7: 1584. https://doi.org/10.3390/s19071584
APA StyleLi, Y., Zhang, W., Ji, X., Ren, C., & Wu, J. (2019). Research on Lane a Compensation Method Based on Multi-Sensor Fusion. Sensors, 19(7), 1584. https://doi.org/10.3390/s19071584





