Toward Sensor-Based Sleep Monitoring with Electrodermal Activity Measures
Abstract
1. Introduction
1.1. Sleep Monitoring Using Surveys and Sensors
1.2. Sleep Monitoring Using a Controlled Environment
2. Materials and Methods
2.1. Data Collection
2.2. Instrumentation
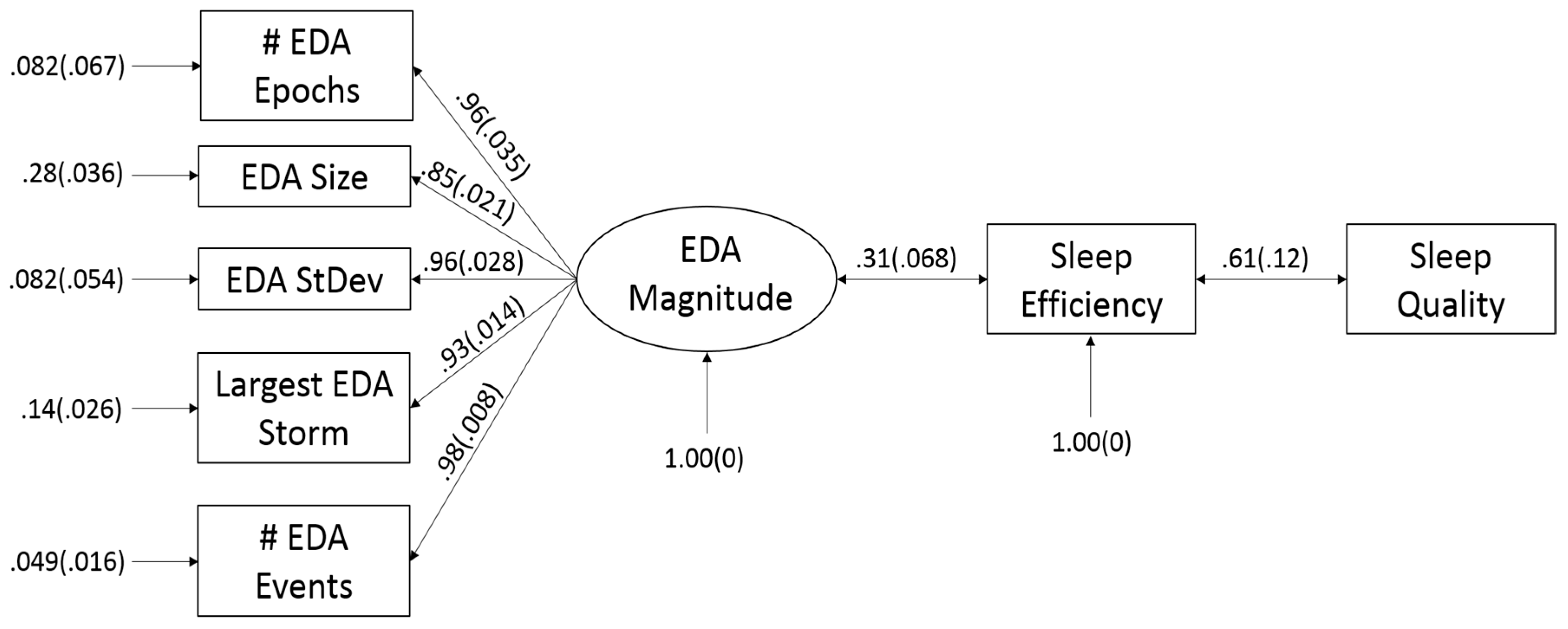
2.3. Creating Models for Sleep Efficiency (SE) and Sleep Quality (SQ)
2.3.1. Feature Extraction
2.3.2. Model Selection
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Human Subjects
References
- Minkel, J.D.; Banks, S.; Htaik, O.; Moreta, M.C.; Jones, C.W.; Mcglinchey, E.L.; Simpson, N.S.; Dinges, D.F. Sleep deprivation and stressors: Evidence for elevated negative affect in response to mild stressors when sleep deprived. Emotion 2012, 12, 1015–1020. [Google Scholar] [CrossRef] [PubMed]
- Daniela, T.; Alessandro, C.; Giuseppe, C.; Fabio, M.; Cristina, M.; Luigi, D.G.; Michele, F. Lack of sleep affects the evaluation of emotional stimuli. Brain Res. Bull. 2010, 82, 104–108. [Google Scholar] [CrossRef] [PubMed]
- Irwin, M.R. Why Sleep Is Important for Health: A Psychoneuroimmunology Perspective. Annu. Rev. Psychol. 2015, 66, 143–172. [Google Scholar] [CrossRef] [PubMed]
- Buysse, D.J.; Reynolds, C.F., III; Monk, T.H.; Berman, S.R.; Kupfer, D.J. The Pittsburgh Sleep Quality Index: A new instrument for psychiatric practice and research. Psychiatry Res. 1989, 28, 193–213. [Google Scholar] [CrossRef]
- Lane, N.; Mohammod, M.; Lin, M.; Yang, X.; Lu, H.; Ali, S.; Doryab, A.; Berke, E.; Choudhury, T.; Campbell, A. BeWell: A Smartphone Application to Monitor, Model and Promote Wellbeing. In Proceedings of the 5th International ICST Conference on Pervasive Computing Technologies for Healthcare, Dublin, Ireland, 23–26 May 2011. [Google Scholar]
- Chen, Z.; Lin, M.; Chen, F.; Lane, N.D.; Cardone, G.; Wang, R.; Li, T.; Chen, Y.; Choudhury, T.; Campbell, A.T. Unobtrusive Sleep Monitoring using Smartphones. In Proceedings of the 7th International Conference on Pervasive Computing Technologies for Healthcare, Venice, Italy, 5–8 May 2013; pp. 145–152. [Google Scholar]
- Hao, T.; Xing, G.; Zhou, G. iSleep: Unobtrusive SQ Monitoring using Smartphones. In Proceedings of the 11th ACM Conference on Embedded Networked Sensor Systems (SenSys’13), Roma, Italy, 11–15 November 2013. [Google Scholar]
- Douglas, N.; Thomas, S.; Jan, M. Clinical value of polysomnography. Lancet 1992, 339, 347–350. [Google Scholar] [CrossRef]
- Sano, A.; Picard, R.W.; Stickgold, R. Quantitative analysis of wrist electrodermal activity during sleep. Int. J. Psychophysiol. 2014, 94, 382–389. [Google Scholar] [CrossRef] [PubMed]
- Real-time Physiological Signals. E4 EDA/GSR Sensor. Empatica. Available online: https://www.empatica.com/en-eu/research/e4/ (accessed on 6 November 2018).
- Designer. Fitbit Blaze™ Smart Fitness Watch. Available online: https://www.fitbit.com/blaze (accessed on 20 January 2019).
- Times, T.N.Y.; Verge, T.; CNET. UP by Jawbone™. Find the Tracker That’s Right for You. Jawbone. Available online: https://jawbone.com/up/trackers (accessed on 20 January 2019).
- Muaremi, A.; Bexheti, A.; Gravenhorst, F.; Arnrich, B.; Troster, G. Monitoring the impact of stress on the sleep patterns of pilgrims using wearable sensors. In Proceedings of the IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI), Valencia, Spain, 1–4 June 2014; pp. 185–188. [Google Scholar]
- Beecroft, J.M.; Ward, M.; Younes, M.; Crombach, S.; Smith, O.; Hanly, P.J. Sleep monitoring in the intensive care unit: Comparison of nurse assessment, actigraphy and polysomnography. Intensive Care Med. 2008, 34, 2076–2083. [Google Scholar] [CrossRef] [PubMed]
- Boucsein, W. Electrodermal Activity; Plenum: New York, NY, USA, 1992. [Google Scholar]
- Cole, R.J.; Kripke, D.F.; Gruen, W.; Mullaney, D.J.; Gillin, J.C. Automatic Sleep/Wake Identification from Wrist Activity. Sleep 1992, 15, 461–469. [Google Scholar] [CrossRef] [PubMed]
- Henderson, D.A.; Denison, D.R. Stepwise regression in social and psychological research. Psychol. Rep. 1989, 64, 251–257. [Google Scholar] [CrossRef]
- Hendrickson, A.E.; White, P.O. Promax: A quick method for rotation to oblique simple structure. Br. J. Stat. Psychol. 1964, 17, 65–70. [Google Scholar] [CrossRef]
- Costello, A.B.; Osborne, J.W. Best practices in exploratory factor analysis: Four recommendations for getting the most from your analysis. Pract. Assess. Res. Eval. 2005, 10, 1–9. [Google Scholar]
- Glymour, C.; Scheines, R.; Spirtes, P.; Ramsey, J. TETRAD [Computer Software]. Center for Causal Discovery. 2016. Available online: http://www.phil.cmu.edu/tetrad/current.html (accessed on 12 October 2018).
- Ramsey, J.; Glymour, M.; Sanchez-Romero, R.; Glymour, C. A million variables and more: The Fast Greedy Equivalence Search algorithm for learning high-dimensional graphical causal models, with an application to functional magnetic resonance images. Int. J. Data Sci. Anal. 2017, 3, 121–129. [Google Scholar] [CrossRef]
- Klem, L. Path analysis. In Reading and Understanding Multivariate Statistics; Grimm, L.G., Yarnold, P.R., Eds.; American Psychological Association: Washington, DC, USA, 1995; pp. 65–97. [Google Scholar]
- Steiger, J.H. Understanding the limitations of global fit assessment in structural equation modeling. Pers. Individ. Differ. 2007, 42, 893–898. [Google Scholar] [CrossRef]
- Bentler, P.M. Comparative Fit Indexes in Structural Models. Psychol. Bull. 1990, 107, 238–246. [Google Scholar] [CrossRef] [PubMed]
- Muthén, B.O.; Muthén, L.K. Mplus 7 Base Program; Muthén & Muthén: Los Angeles, CA, USA, 2012. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Representation and Reasoning Series; Morgan Kaufmann: San Mateo, CA, USA, 1988. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge Academic: New York, NY, USA, 1988. [Google Scholar]
- Ng, A.Y.; Jordan, M.I. On discriminative vs. generative classifiers: A comparison of logistic regression and naive bayes. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Torniainen, J.; Cowley, B.; Henelius, A.; Lukander, K.; Pakarinen, S. Feasibility of an electrodermal activity ring prototype as a research tool. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 6433–6436. [Google Scholar]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
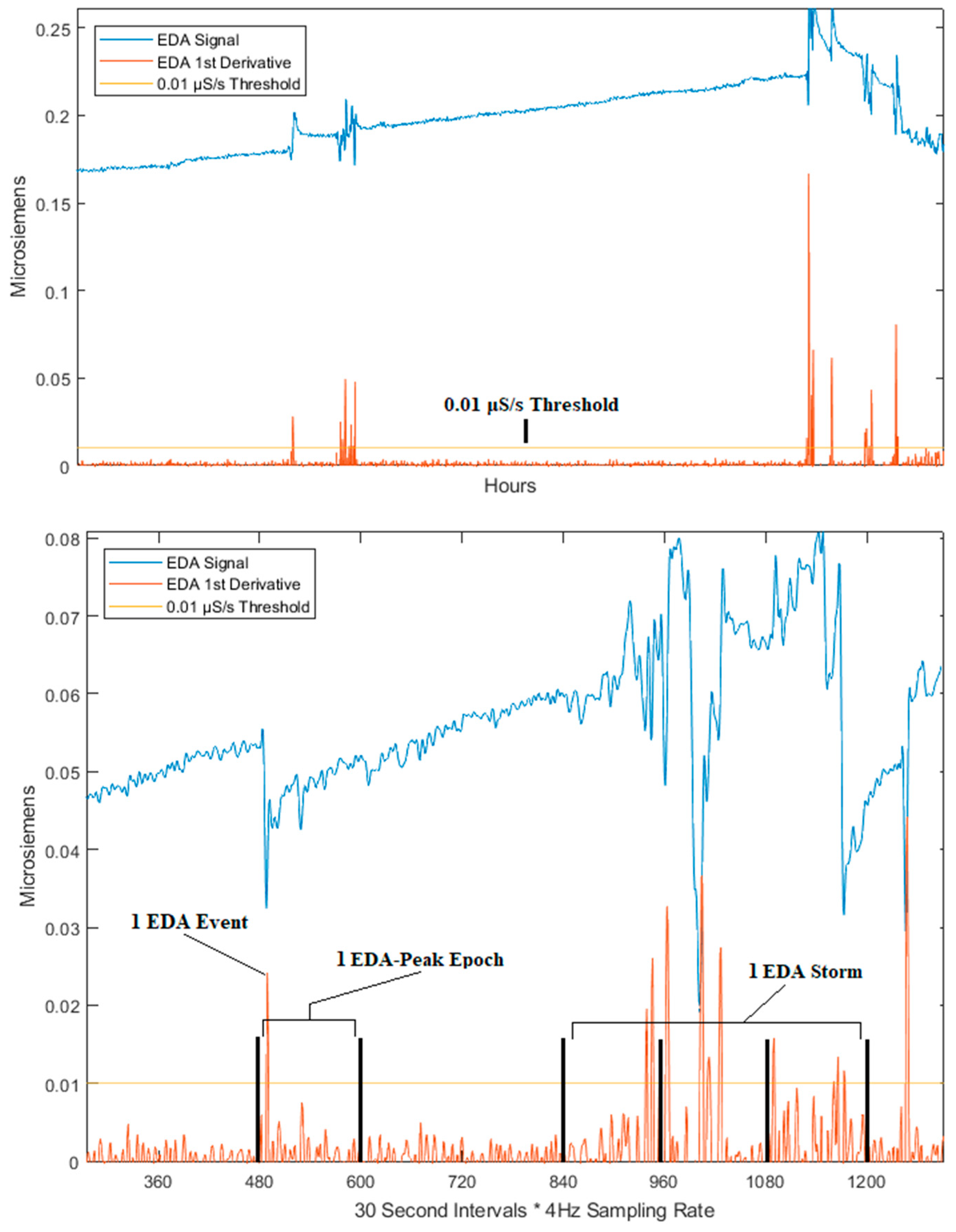
| Feature | Type | Description |
|---|---|---|
| Amount of Sleep Minutes | PSQI Feature | The number of minutes the participant was asleep. |
| Amount of Wake Minutes | PSQI Feature | The number of minutes the participant was awake. |
| Number of EDA Epochs | EDA Feature | The number of EDA epochs over the entire duration of sleep in a single night |
| Number of EDA Storms | EDA Feature | The number of EDA storms over the entire duration of sleep in a single night |
| Average Size of EDA Storms | EDA Feature | Mean number of epochs within an EDA storm across all EDA storms over a single night of sleep. |
| Standard Deviation of EDA Storms | EDA Feature | Standard deviation in the number of peak epochs within an EDA storm across all EDA storms over a single night of sleep. |
| Largest EDA Storm | EDA Feature | The number of peaks within the largest EDA storm in the signal for a single night of sleep. |
| Number of EDA Events | EDA Feature | Number of EDA events (peaks) in the signal over the entire duration of sleep in a single night. |
| SE | PSQI Feature | SE calculated using the daily-PSQI questions 1, 2, and 3. |
| SQ | PSQI Feature | SQ deduced using SQ rating scale from the daily-PSQI, creating a binary system where poor is 1–2 rating and good is 3–4 rating. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romine, W.; Banerjee, T.; Goodman, G. Toward Sensor-Based Sleep Monitoring with Electrodermal Activity Measures. Sensors 2019, 19, 1417. https://doi.org/10.3390/s19061417
Romine W, Banerjee T, Goodman G. Toward Sensor-Based Sleep Monitoring with Electrodermal Activity Measures. Sensors. 2019; 19(6):1417. https://doi.org/10.3390/s19061417
Chicago/Turabian StyleRomine, William, Tanvi Banerjee, and Garrett Goodman. 2019. "Toward Sensor-Based Sleep Monitoring with Electrodermal Activity Measures" Sensors 19, no. 6: 1417. https://doi.org/10.3390/s19061417
APA StyleRomine, W., Banerjee, T., & Goodman, G. (2019). Toward Sensor-Based Sleep Monitoring with Electrodermal Activity Measures. Sensors, 19(6), 1417. https://doi.org/10.3390/s19061417





