Sensing Region Characteristics of Smart Piezoelectric Interface for Damage Monitoring in Plate-Like Structures
Abstract
:1. Introduction
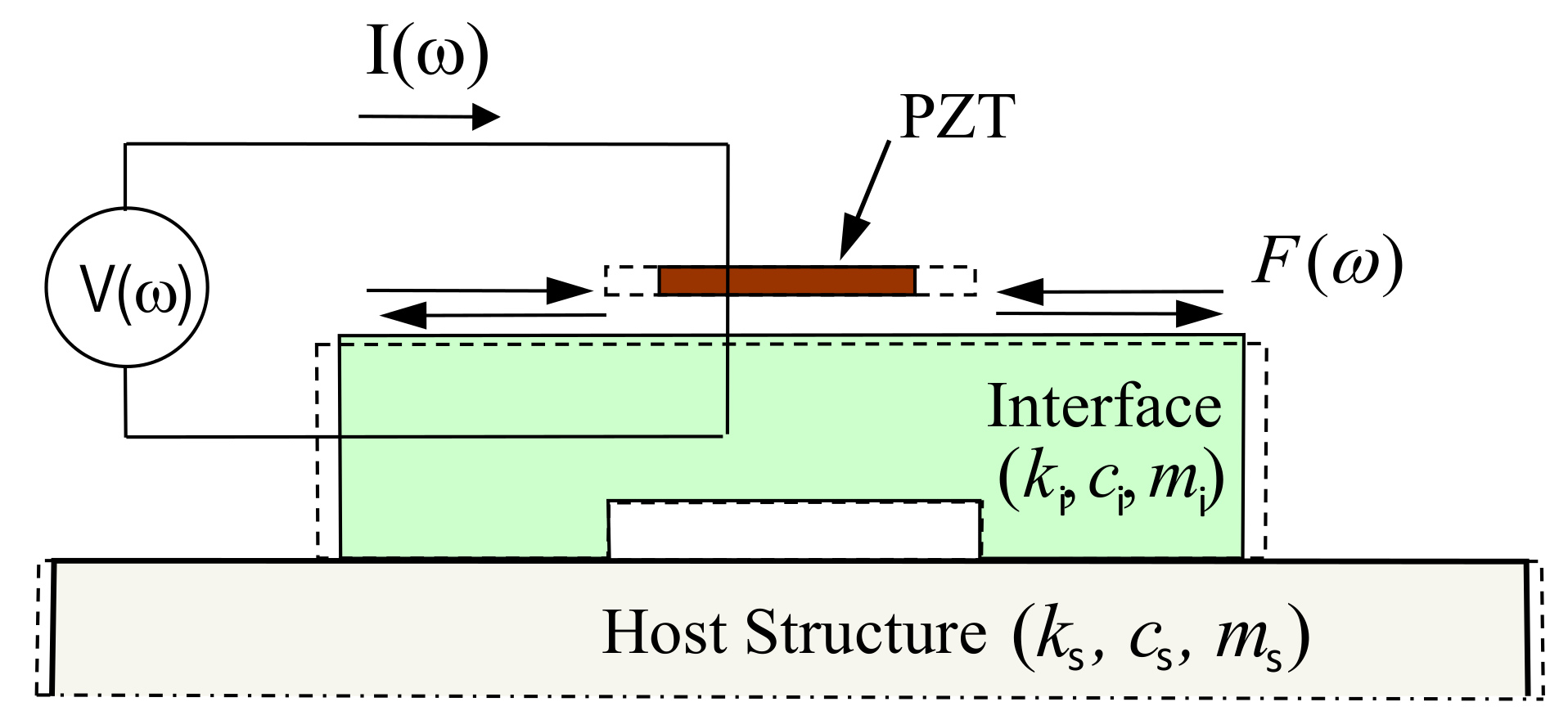
2. Piezoelectric Interface-Based Impedance Monitoring Technique
2.1. Impedance Monitoring via Piezoelectric Interface
2.2. Damage Classification Using Impedance Signatures
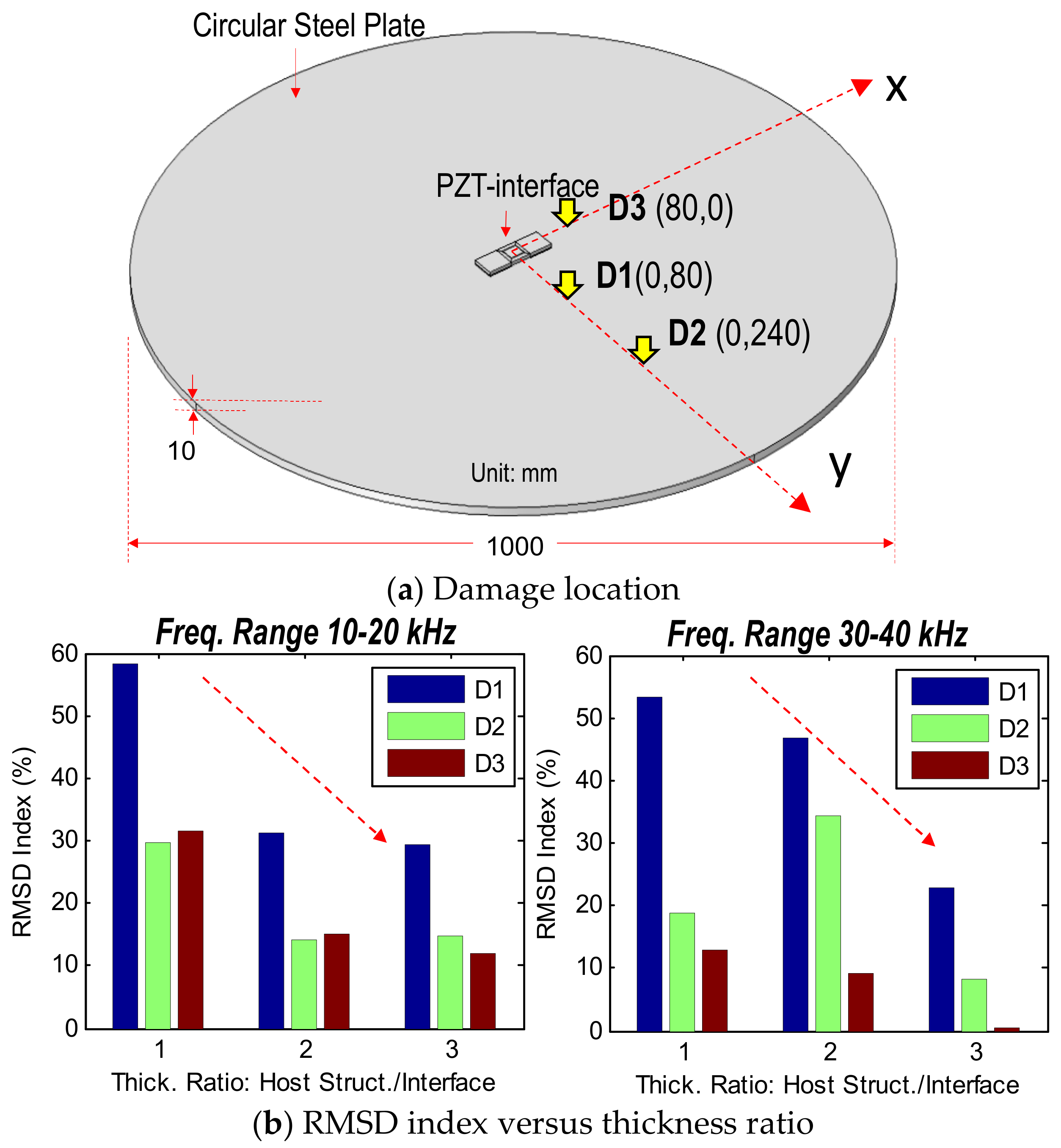
3. Sensing Region Characteristics of PZT Interface on a Numerical Plate Domain
3.1. FE Modeling
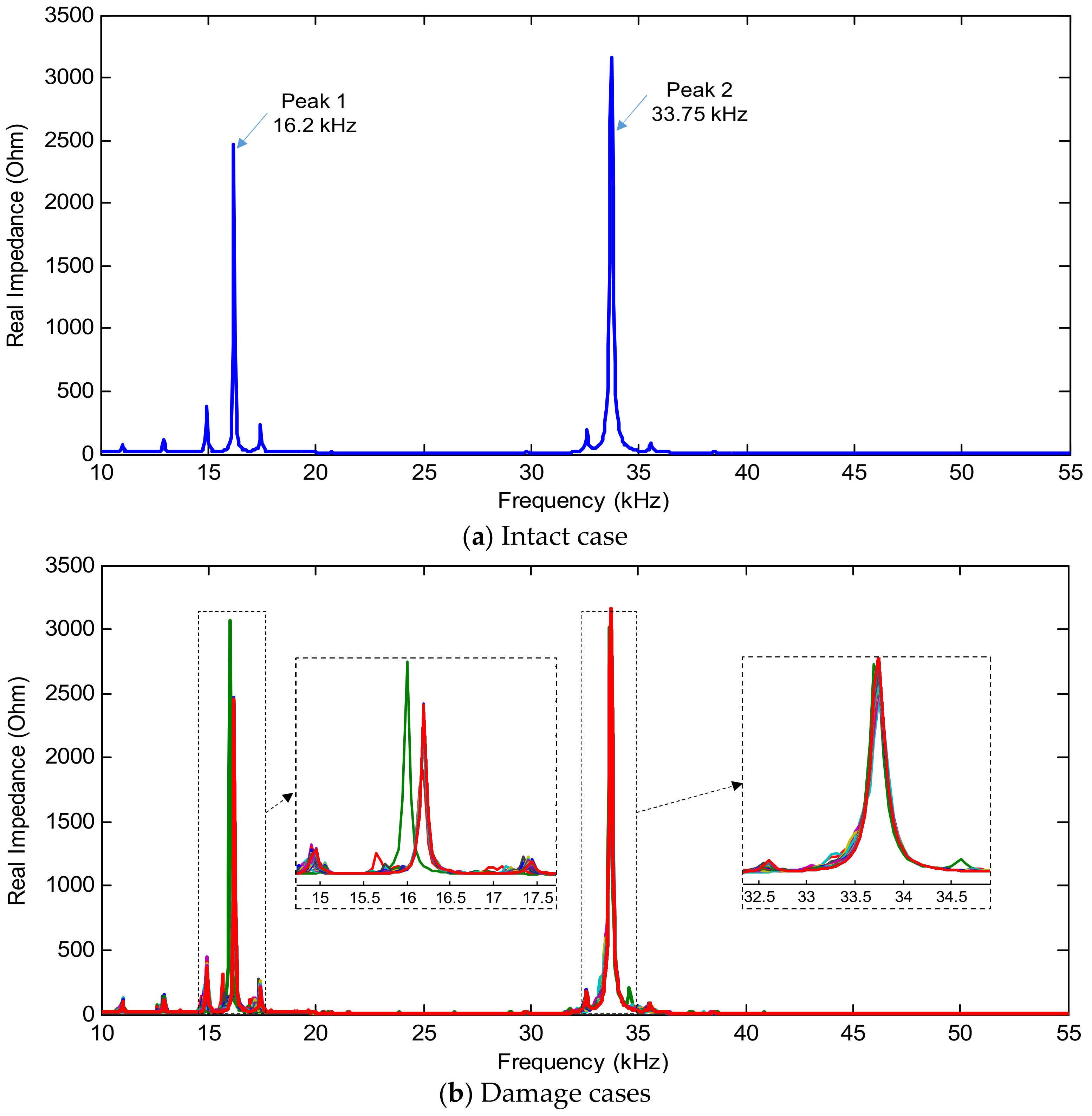
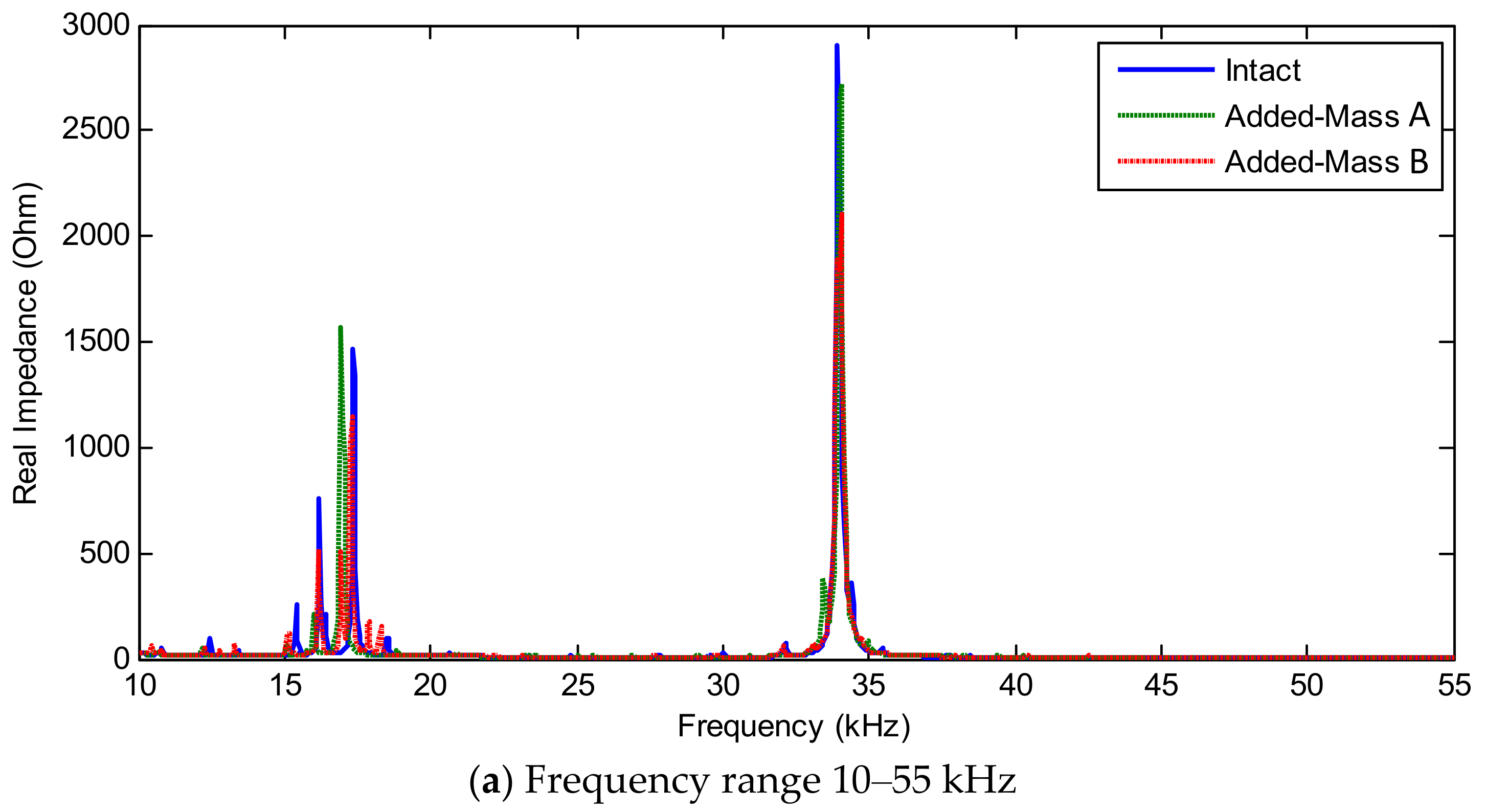
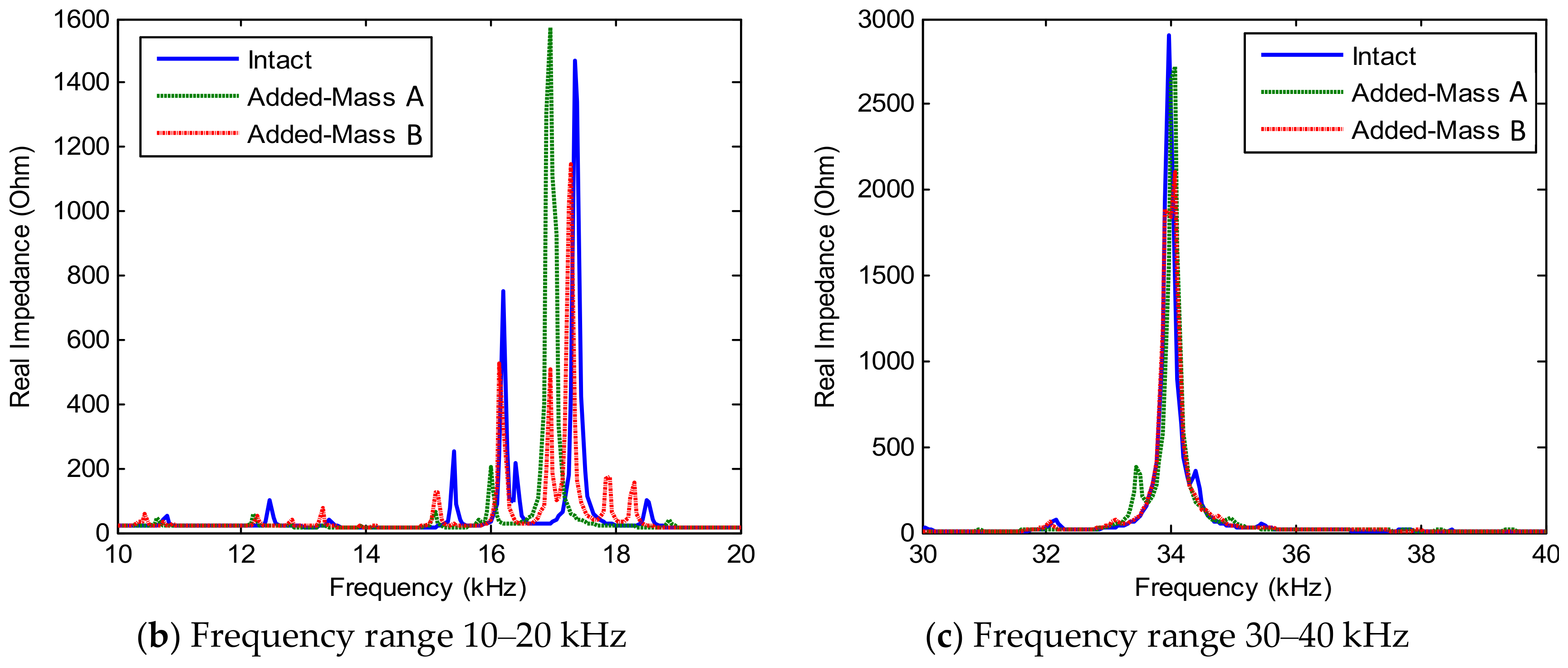
3.2. Numerical Impedance Responses
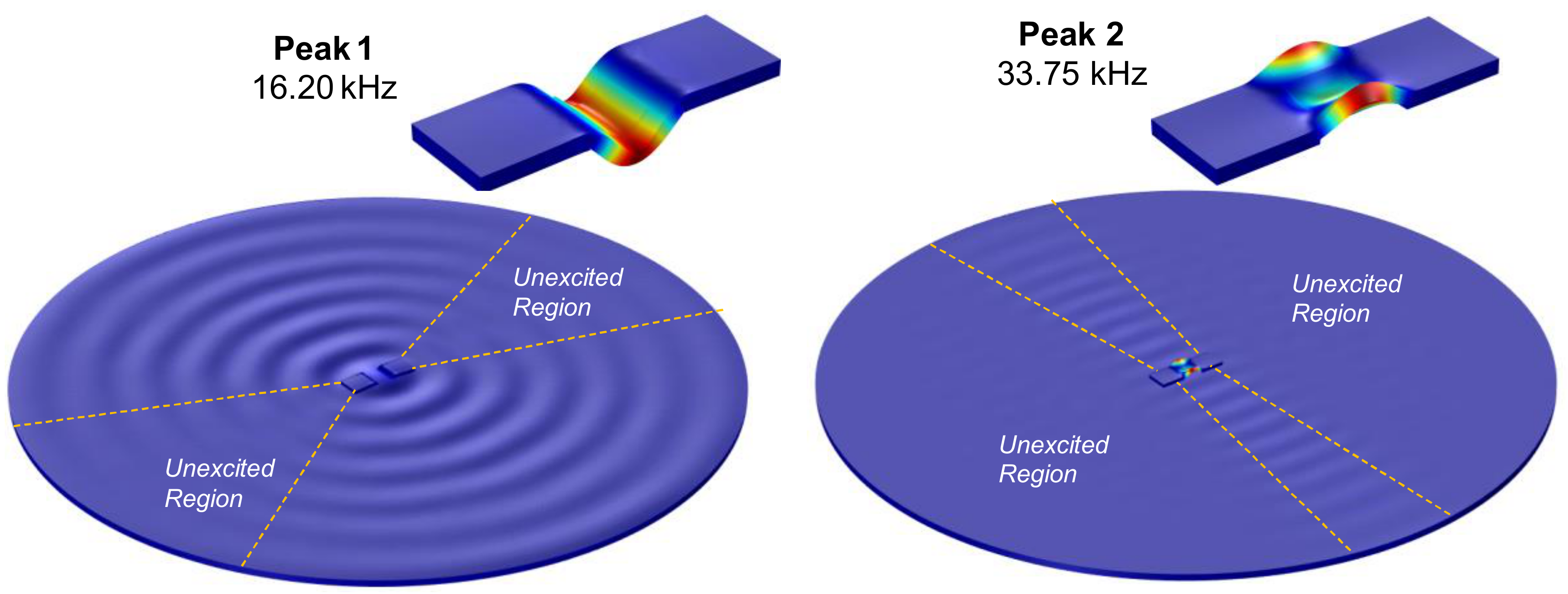
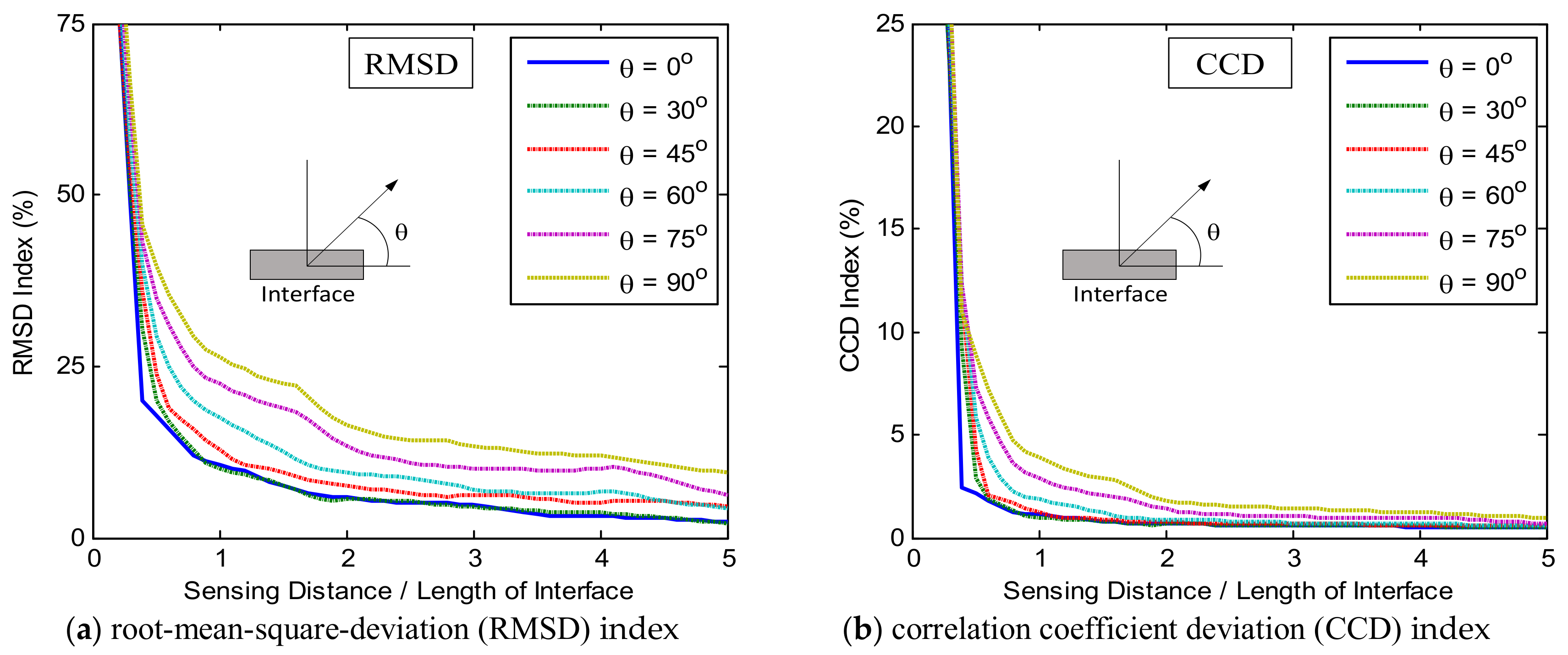
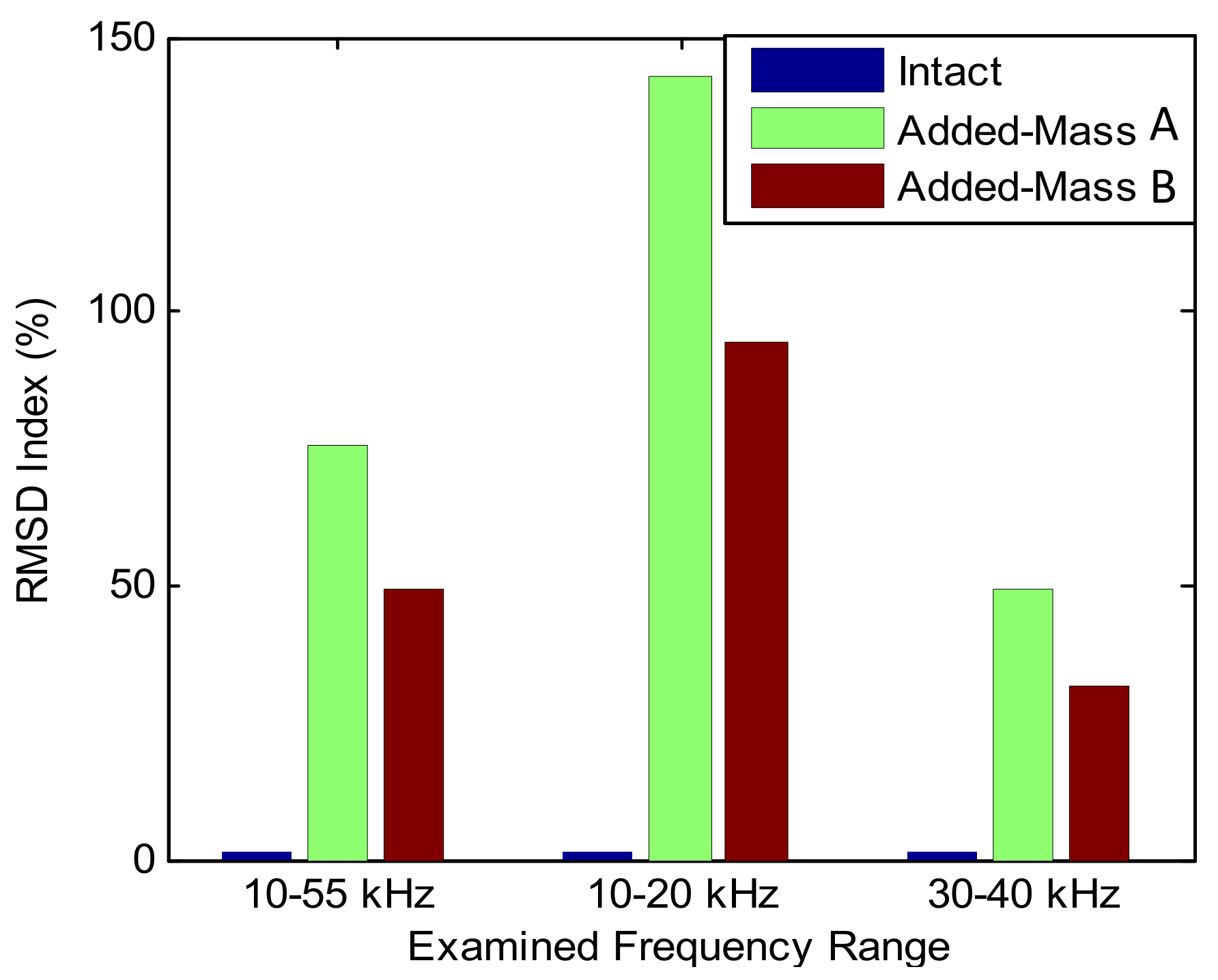
3.3. Numerical Characterization of Sensing Region
3.3.1. Sensitivity of Impedance Features with Respect to Damage Location
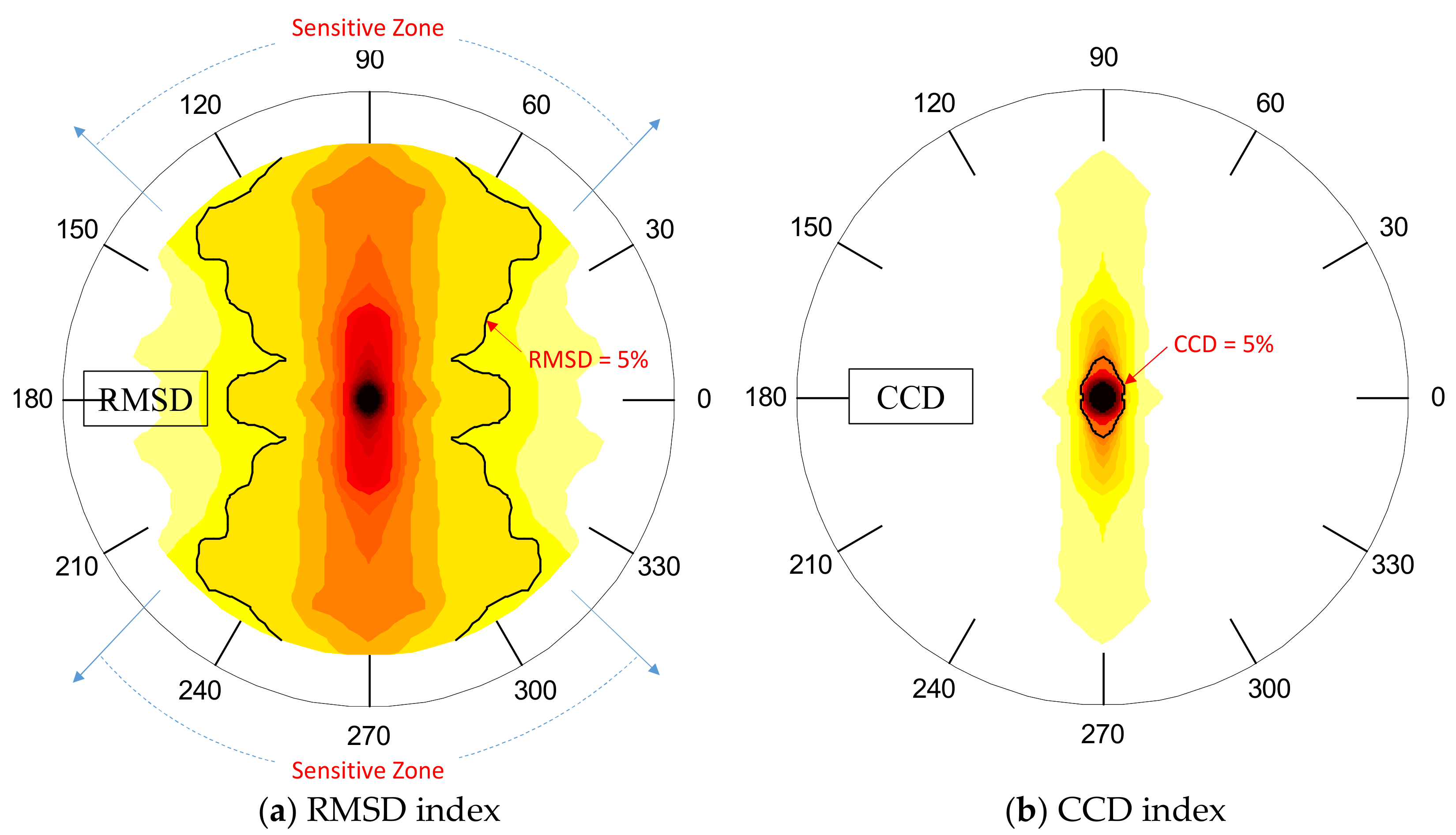
3.3.2. Detectable Zone of Piezoelectric Interface
3.3.3. Damage Detectability with Respect to Plate’s Thickness
4. Sensing Region Characteristics of PZT Interface on a Realistic Plate Structure
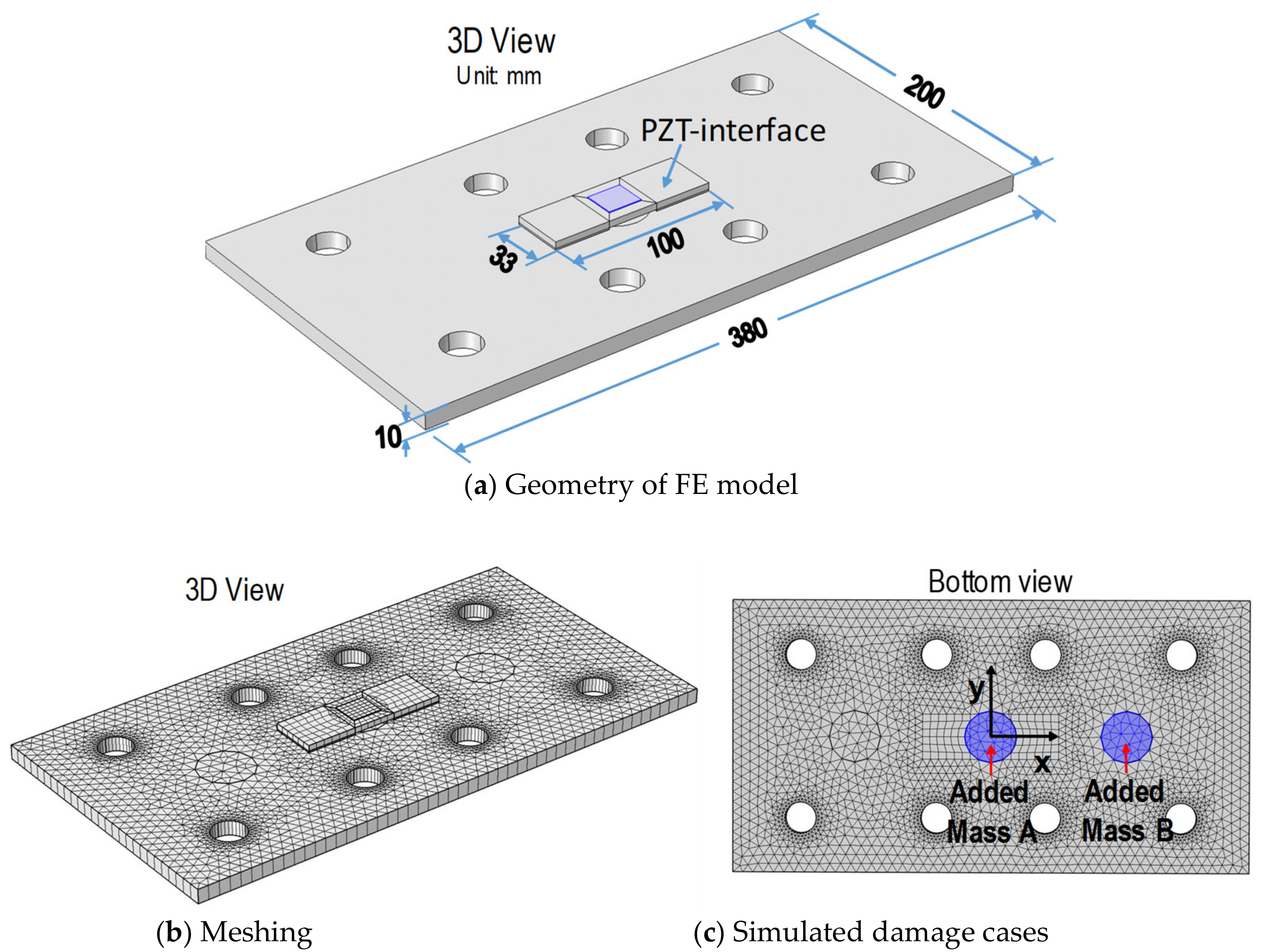
4.1. Test-Setup of Connection Splice Plate
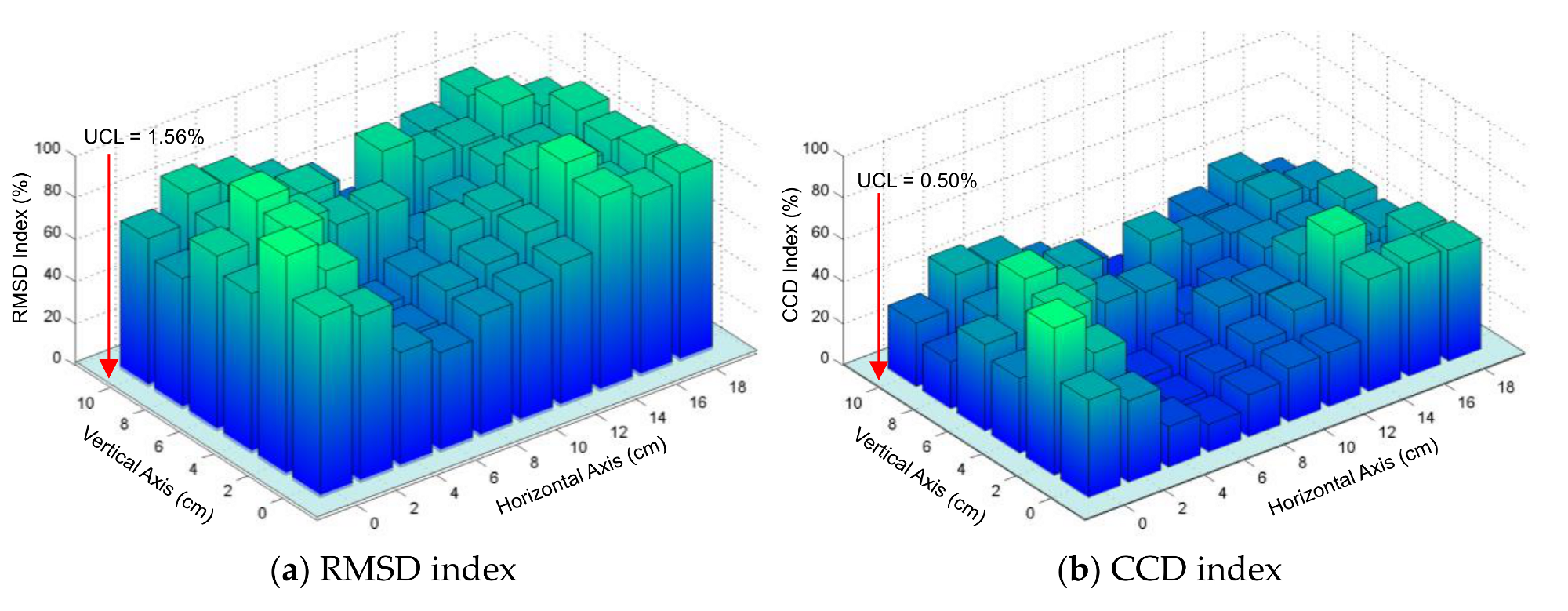
4.2. Experimental Characterization of Sensing Region on Connection Splice Plate
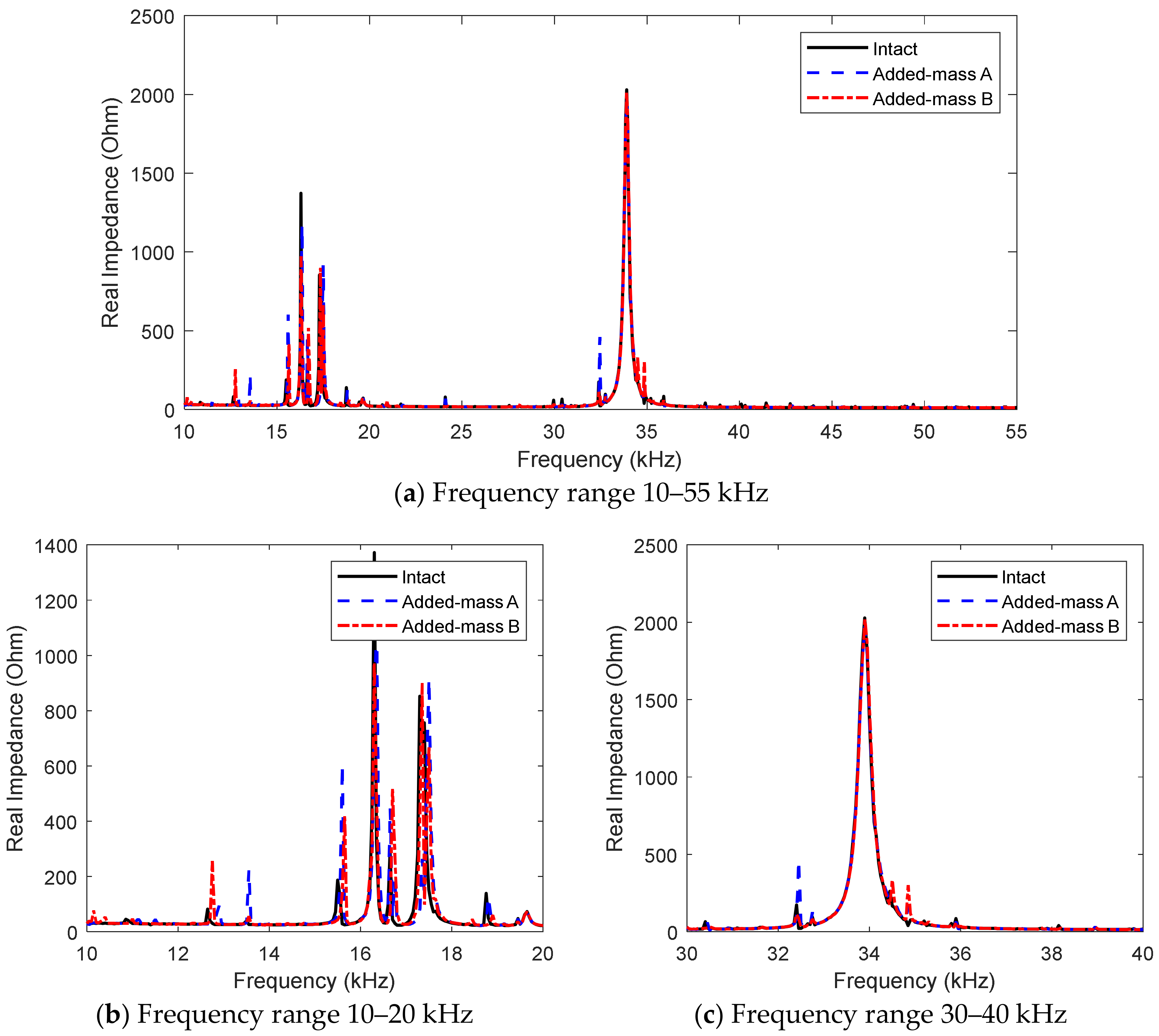
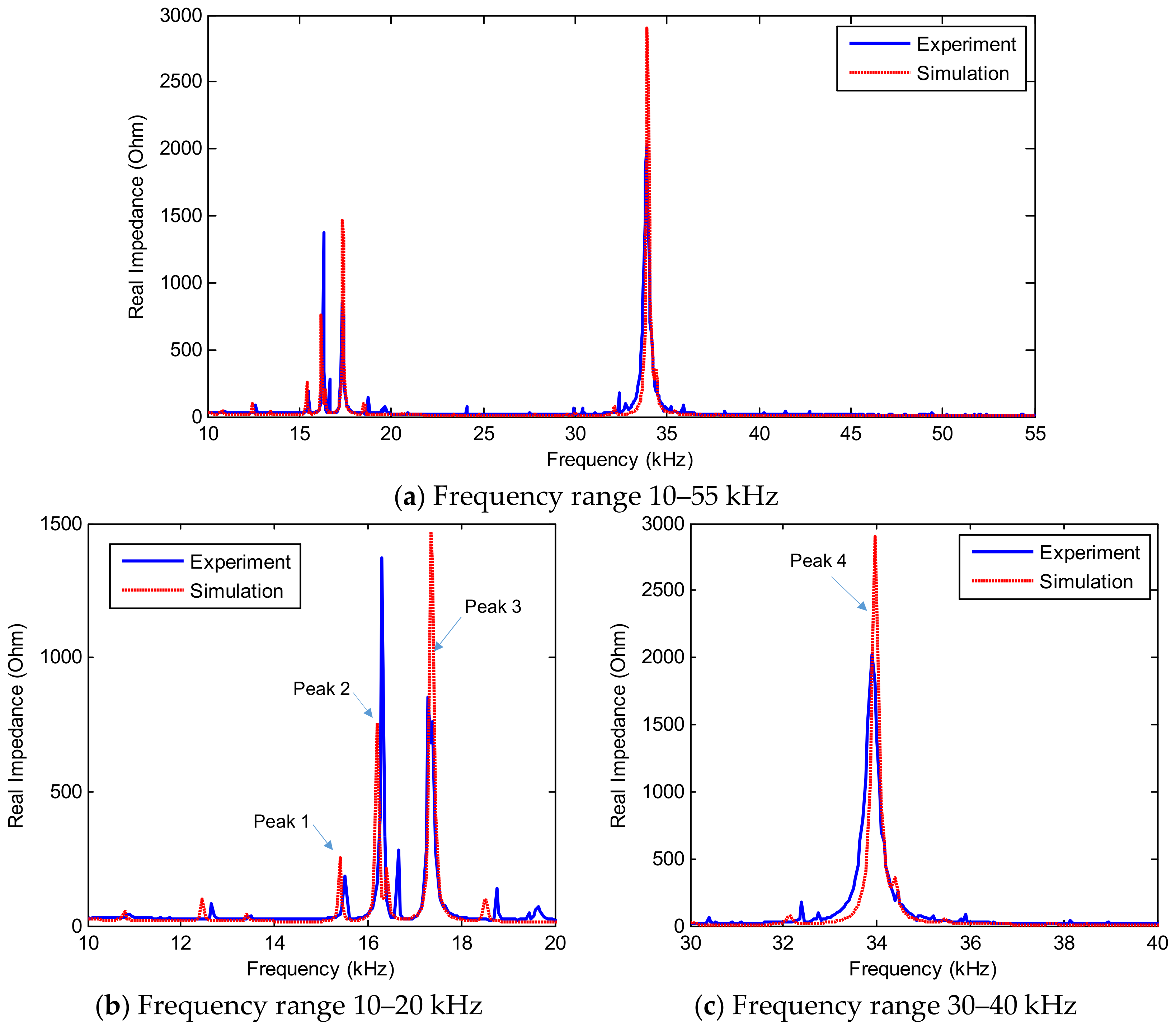
4.2.1. Experimental Impedance Signatures
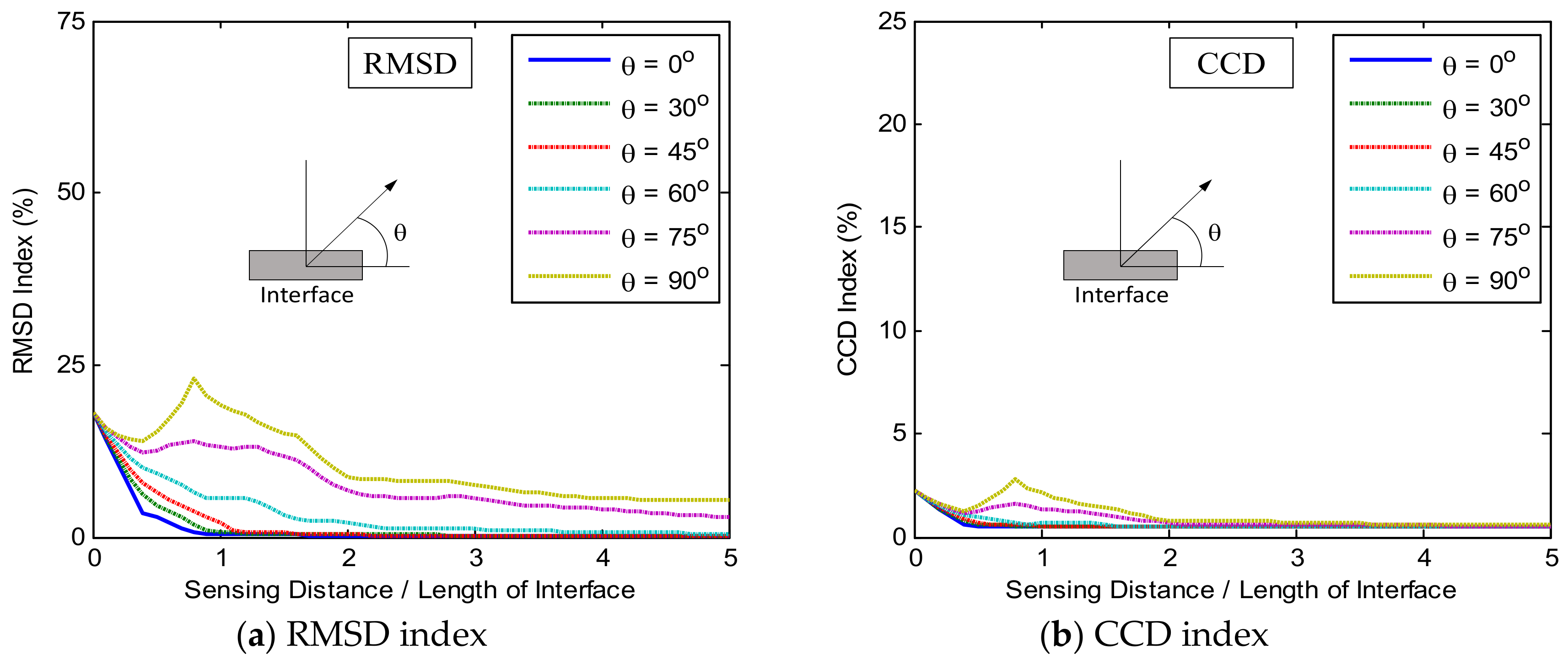
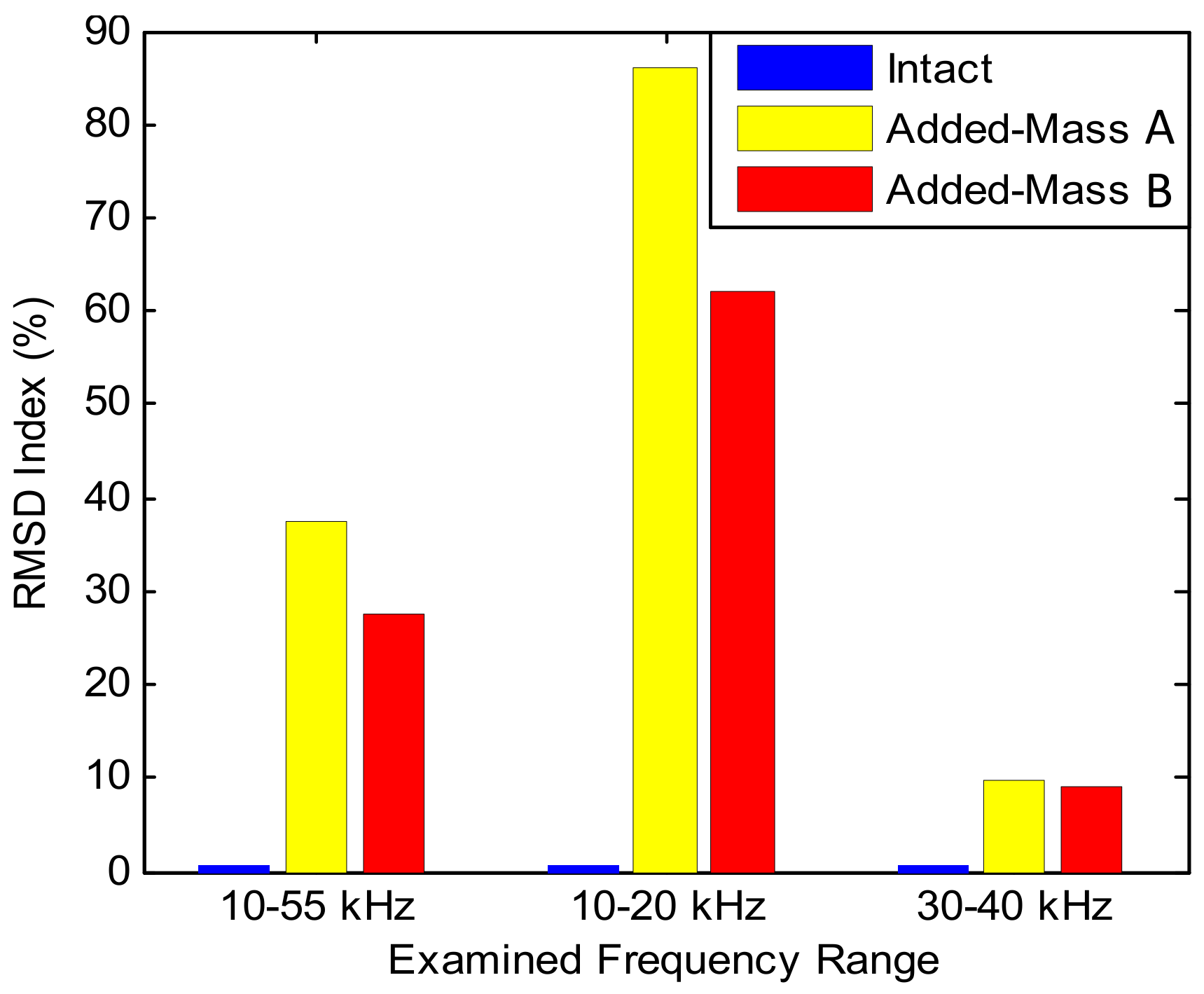
4.2.2. Sensitivity of Experimental Impedance Features with Respect to Damage Location
4.3. Numerical Validation of Sensing Region on Connection Splice Plate
4.3.1. FE Modeling
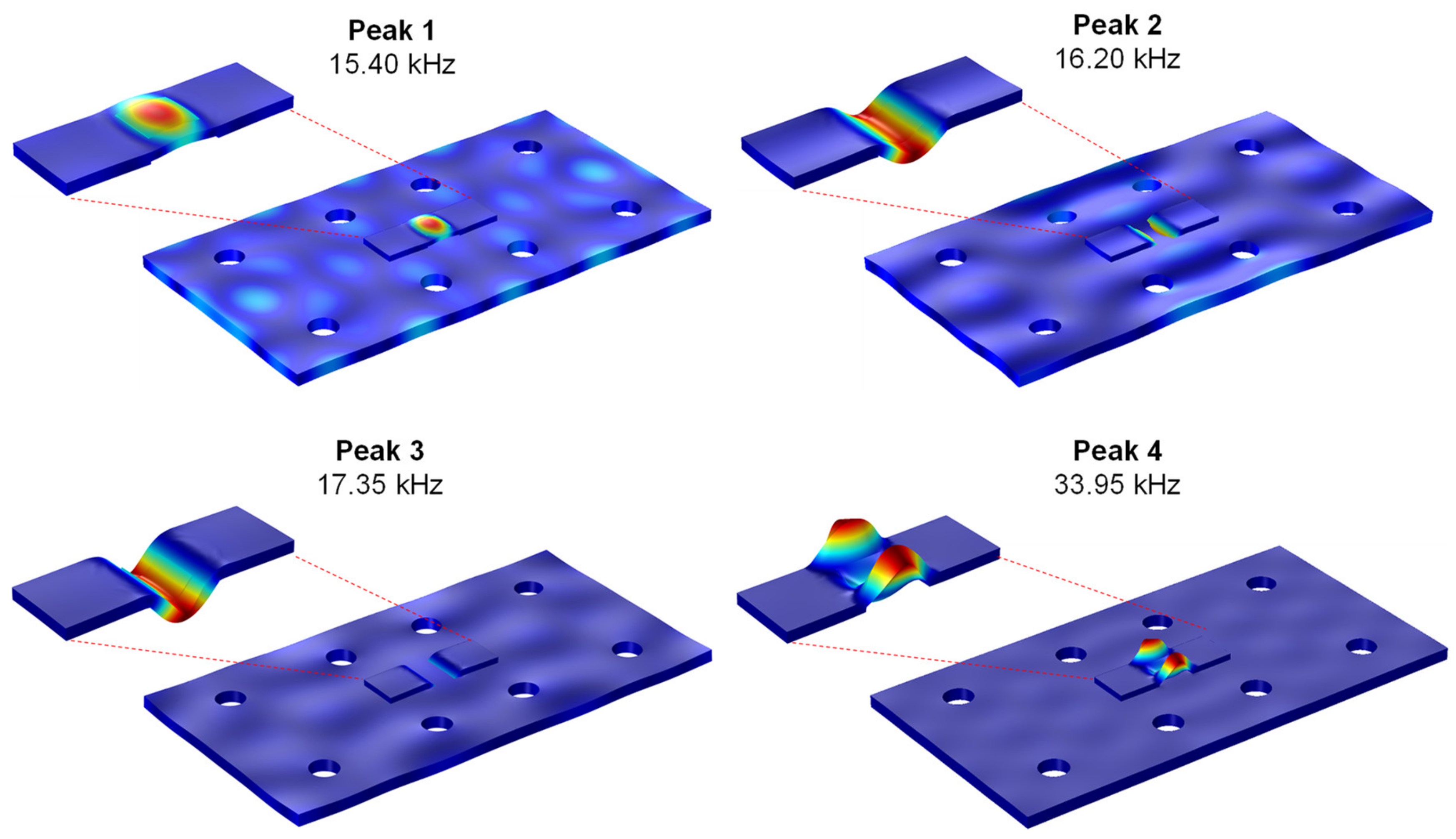
4.3.2. Numerical Impedance Signatures
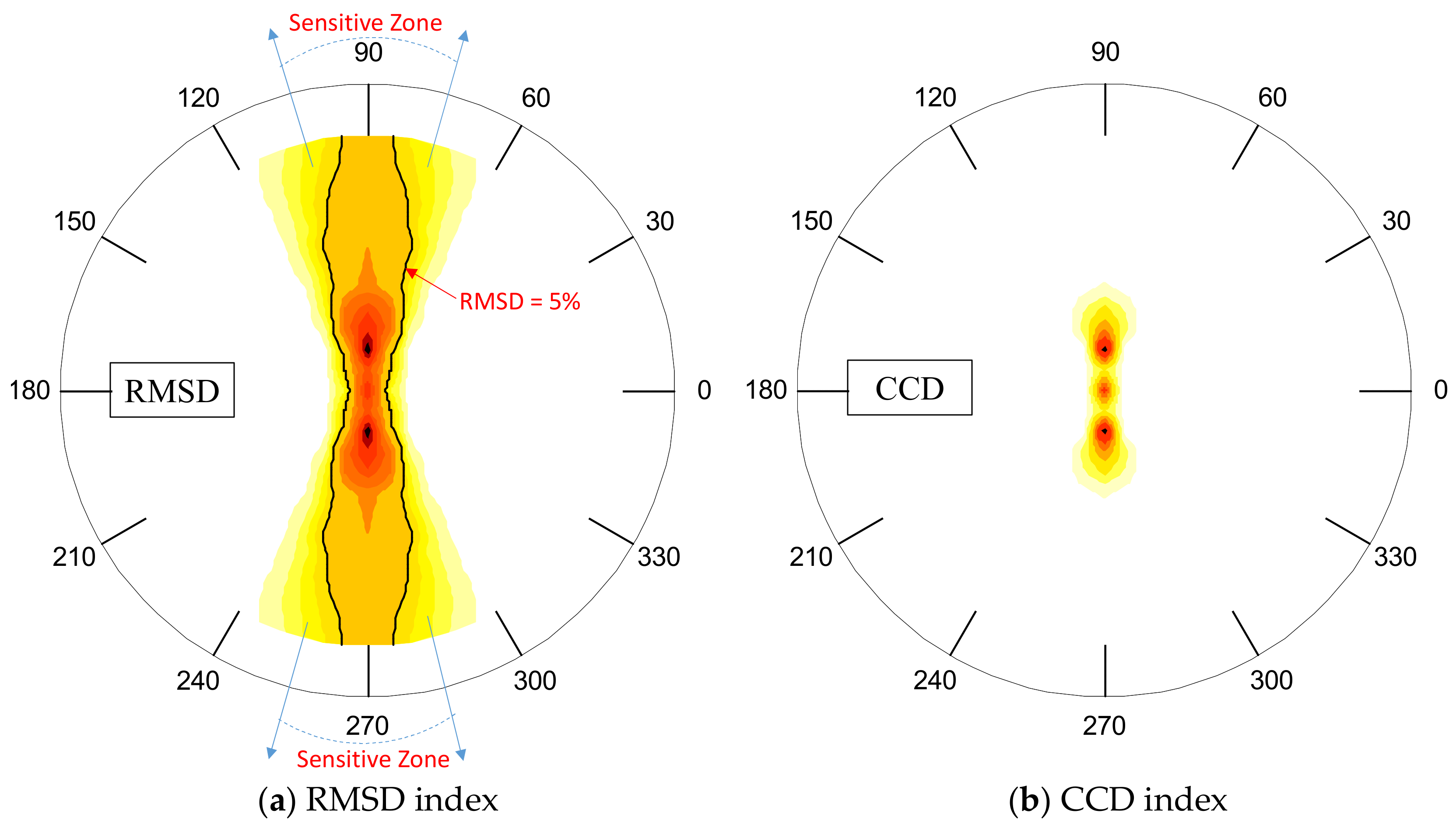
4.3.3. Sensitivity of Numerical Impedance Features with Respect to Damage Location
5. Conclusions
- (1)
- The sensing region characteristics of the PZT interface on the large plate domain was different with the limited plate domain such as the rectangular splice plate.
- (2)
- For the circular plate domain, the detectable distance of the PZT interface analyzed by RMSD was about five times of the interface’s length. The detectable orientation θ was within (45° to 135°) and (225° to 315°) for the range 10–20 kHz; and (75° to 105°) and (255° to 295°) for the range 30–40 kHz.
- (3)
- For the limited plate domain like the connection splice plate, the detectable zones of the PZT interface were the entire plate. The damage locations near the boundaries of the splice plate or at the angle θ ≈ 90° resulted in significant magnitudes of impedance features.
- (4)
- The numerical analyses of the coupled vibration modes of the PZT interface-host structure system can reveal an overall view on the detectable zones over the plate domain.
- (5)
- The frequency range containing the longitudinal flexural motion of the interface device (i.e., 10–20 kHz) had significant sensing regions.
Author Contributions
Funding
Conflicts of Interest
References
- Liang, C.; Sun, F.P.; Rogers, C.A. Coupled electro-mechanical analysis of adaptive matrial – Determination of the actuator power consumption and system energy transfer. J. Intel. Mat. Syst. Str. 1994, 5, 12–20. [Google Scholar] [CrossRef]
- Sun, F.P.; Chaudhry, Z.; Liang, C.; Rogers, C.A. Truss structure integrity identification using PZT sensor-actuator. J. Intell. Mater. Syst. Struct. 1995, 6, 134–139. [Google Scholar] [CrossRef]
- Zagrai, A.N.; Giurgiutiu, V. Electro-mechanical impedance method for crack detection in thin plates. J. Intell. Mater. Syst. Struct. 2001, 12, 709–718. [Google Scholar] [CrossRef]
- Fasel, T.R.; Sohn, H.; Park, G.; Farrar, C.R. Active sensing using impedance-based ARX models and extreme value statistics for damage detection. Earthq. Eng. Struct. Dyn. 2005, 34, 763–785. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, Y.; Lu, Y. Sensitivity of PZT impedance sensors for damage detection of concrete structures. Sensors 2008, 8, 327–346. [Google Scholar] [CrossRef] [PubMed]
- Schwankl, M.; Sharif-Khodaei, Z.; Aliabadi, M.H.; Weimer, C. Electro-mechanical impedance technique for structural health monitoring of composite panels. Key Eng. Mater. 2013, 525, 569–572. [Google Scholar] [CrossRef]
- Ho, D.D.; Ngo, T.M.; Kim, J.T. Impedance-based damage monitoring of steel column connection: Numerical simulation. Struct. Monit. Maint. 2014, 1, 339–356. [Google Scholar] [CrossRef]
- Park, J.H.; Huynh, T.C.; Kim, J.T. Temperature effect on wireless impedance monitoring in tendon anchorage of prestressed concrete girder. Smart Struct. Syst. 2015, 15, 1159–1175. [Google Scholar] [CrossRef]
- Zou, F.; Aliabadi, M.H. A boundary element method for detection of damages and self-diagnosis of transducers using electro-mechanical impedance. Smart Mater. Struct. 2015, 24, 095015. [Google Scholar] [CrossRef]
- Sharif-Khodaei, Z.; Ghajari, M.; Aliabadi, M.H. Impact damage detection in composite plates using a self-diagnostic electro-mechanical impedance based structural health monitoring system. J. Multiscale Model. 2016, 2016, P1550013. [Google Scholar] [CrossRef]
- Huynh, T.C.; Dang, N.L.; Kim, J.T. PCA-based filtering of temperature effect on impedance monitoring in prestressed tendon anchorage. Smart Struct. Syst. 2018, 22, 57–70. [Google Scholar]
- Ryu, J.Y.; Huynh, T.C.; Kim, J.T. Tension force estimation in axially loaded members using wearable piezoelectric interface technique. Sensors 2019, 19, 47. [Google Scholar] [CrossRef] [PubMed]
- Park, G.; Cudney, H.; Inman, D.J. Impedance-based health monitoring of civil structural components. J. Infrastruct. Syst. 2000, 6, 153–160. [Google Scholar] [CrossRef]
- Soh, C.K.; Tseng, K.K.; Bhalla, S.; Gupta, A. Performance of smart piezoceramic patches in health monitoring of a RC bridge. Smart Mater. Struct. 2000, 9, 533–542. [Google Scholar] [CrossRef]
- Kim, J.T.; Park, J.H.; Hong, D.S.; Park, W.S. Hybrid health monitoring of prestressed concrete girder bridges by sequential vibration-impedance approaches. Eng. Struct. 2010, 32, 115–128. [Google Scholar] [CrossRef]
- Huynh, T.C.; Kim, J.T. Impedance-based cable force monitoring in tendon-anchorage using portable PZT-interface technique. Math. Probl. Eng. 2014, 2014, 784731. [Google Scholar] [CrossRef]
- Annamdas, V.G.M.; Radhika, M.A.; Yang, Y. Easy installation method of piezoelectric (PZT) transducers for health monitoring of structures using electro-mechanical impedance technique. In Proceedings of the 16th International Symposium on: Smart Structures and Materials & Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 30 March 2009; Volume 7292, pp. 729227–729231. [Google Scholar]
- Kim, J.-T.; Huynh, T.-C.; Lee, S.-Y.; Ryu, J.-Y. Compensation of temperature effect on impedance-based damage monitoring in prestressed tendon-anchorage system. In Proceedings of the 7th International Conference on Advances in Experimental Structural Engineering 2017, Pavia, Italy, 6–8 September 2017; pp. 825–839. [Google Scholar]
- Huynh, T.C.; Kim, J.T. RBFN-based temperature compensation method for impedance monitoring in prestressed tendon anchorage. Struct. Control Health Monit. 2018, 25, e2173. [Google Scholar] [CrossRef]
- Huynh, T.C.; Dang, N.L.; Kim, J.T. Advances and challenges in impedance-based structural health monitoring. Struct. Monit. Maint. 2017, 4, 301–329. [Google Scholar]
- Pei, X.Y.; Yi, T.H.; Li, H.N. A multitype sensor placement method for the modal estimation of structure. Smart Struct. Syst. 2018, 21, 407–420. [Google Scholar]
- Chaudhry, Z.; Lalande, F.; Ganino, A.; Rogers, C. Monitoring the integrity of composite patch structural repair via piezoelectric actuators/sensors. In Proceedings of the 36th Structural Dynamics and Materials Conference, New Orleans, LA, USA, 10–13 April 1995. [Google Scholar]
- Esteban, J. Modeling of the Sensing Region of a Piezoelectric Actuator/Sensor. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1996. [Google Scholar]
- Park, G.; Sohn, H.; Farrar, C.; Inman, D. Overview of piezoelectric impedance-based health monitoring and path forward. Shock Vib. Dig. 2003, 35, 451–463. [Google Scholar] [CrossRef]
- Huynh, T.C.; Kim, J.T. Quantification of temperature effect on impedance monitoring via PZT interface for prestressed tendon anchorage. Smart Mater. Struct. 2017, 26, 125004. [Google Scholar] [CrossRef]
- Nguyen, K.D. Finite Element Analysis of EMI Signatures of DAMAGED structural Connection via High-Performance Interface Washer. Master’s Thesis, Department of Ocean Engineering, PKNU, Busan, Korea, 2011. [Google Scholar]
- Nesvijski, E.; Sahul, R. Modeling and simulation of piezoelectric materials for comparison to experimental data. In Proceedings of the 2013 COMSOL Conference, Boston, MA, USA, 23–25 October 2013. [Google Scholar]
- Dang, N.L.; Huynh, T.C.; Kim, J.T. Local strand-breakage detection in multi-strand anchorage system using an impedance-based stress monitoring method—Feasibility study. Sensors 2019, 19, 1054. [Google Scholar] [CrossRef]
- Ong, C.W.; Yang, Y.; Wong, Y.T.; Bhalla, S.; Lu, Y.; Soh, C.K. The effects of adhesive on the electro-mechanical response of a piezoceramic transducer coupled smart system. Proc. SPIE 2003, 5062, 241–247. [Google Scholar]
- Gresil, M.; Yu, L.; Giurgiutiu, V.; Sutton, M. Predictive modeling of electromechanical impedance spectroscopy for composite materials. Struct. Health Monit. 2012, 11, 671–683. [Google Scholar] [CrossRef]
- Huynh, T.C.; Dang, N.L.; Kim, J.T. Preload monitoring in bolted connection using piezoelectric-based smart interface. Sensors 2018, 18, 2766. [Google Scholar] [CrossRef]
- efunda Inc. eFunda: The Ultimate Online Reference for Engineers. Available online: http://www.efunda.com (accessed on 8 January 2019).
- Behmanesh, I.; Moaveni, B. Probabilistic identification of simulated damage on the Dowling Hall footbridge through Bayesian finite element model updating. Struct. Control Health Monit. 2015, 22, 463–483. [Google Scholar] [CrossRef]
- Rajendran, P.; Srinivasan, S.M. Identification of Added Mass in the Composite Plate Structure Based on Wavelet Packet Transform. Strain 2016, 52, 14–25. [Google Scholar] [CrossRef]
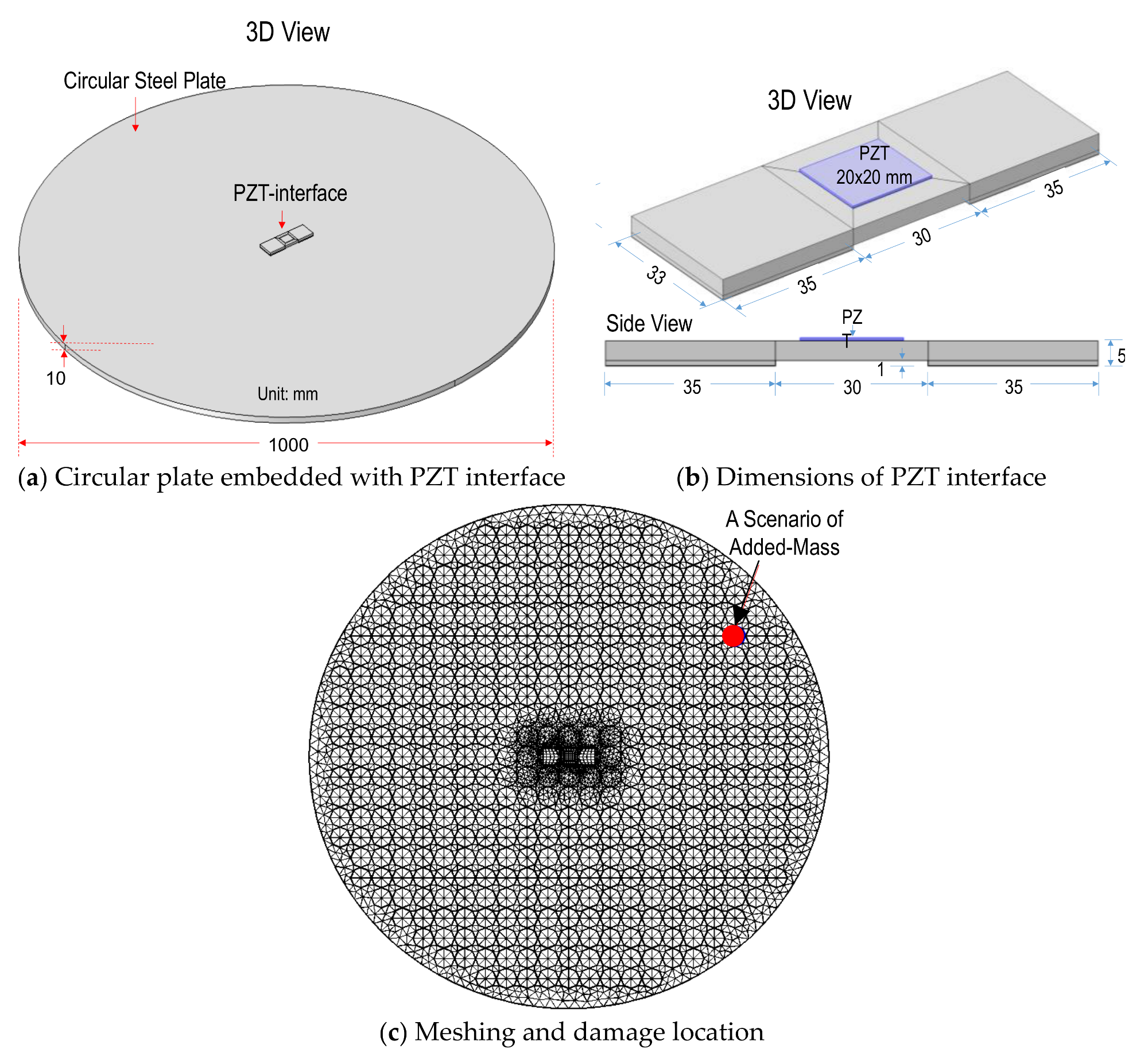


| Parameters | Aluminum Interface | Steel Circular Plate | Bonding Layer |
|---|---|---|---|
| Young’s modulus, E (GPa) | 70 | 200 | 6 |
| Poisson’s ratio, υ | 0.33 | 0.33 | 0.38 |
| Mass density, ρ (kg/m3) | 2700 | 7850 | 1700 |
| Damping loss factor, η | 0.004 | 0.004 | 0.004 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huynh, T.-C.; Lee, S.-Y.; Dang, N.-L.; Kim, J.-T. Sensing Region Characteristics of Smart Piezoelectric Interface for Damage Monitoring in Plate-Like Structures. Sensors 2019, 19, 1377. https://doi.org/10.3390/s19061377
Huynh T-C, Lee S-Y, Dang N-L, Kim J-T. Sensing Region Characteristics of Smart Piezoelectric Interface for Damage Monitoring in Plate-Like Structures. Sensors. 2019; 19(6):1377. https://doi.org/10.3390/s19061377
Chicago/Turabian StyleHuynh, Thanh-Canh, So-Young Lee, Ngoc-Loi Dang, and Jeong-Tae Kim. 2019. "Sensing Region Characteristics of Smart Piezoelectric Interface for Damage Monitoring in Plate-Like Structures" Sensors 19, no. 6: 1377. https://doi.org/10.3390/s19061377
APA StyleHuynh, T.-C., Lee, S.-Y., Dang, N.-L., & Kim, J.-T. (2019). Sensing Region Characteristics of Smart Piezoelectric Interface for Damage Monitoring in Plate-Like Structures. Sensors, 19(6), 1377. https://doi.org/10.3390/s19061377





