A Doppler Range Compensation for Step-Frequency Continuous-Wave Radar for Detecting Small UAV
Abstract
:1. Introduction
2. Materials and Methods
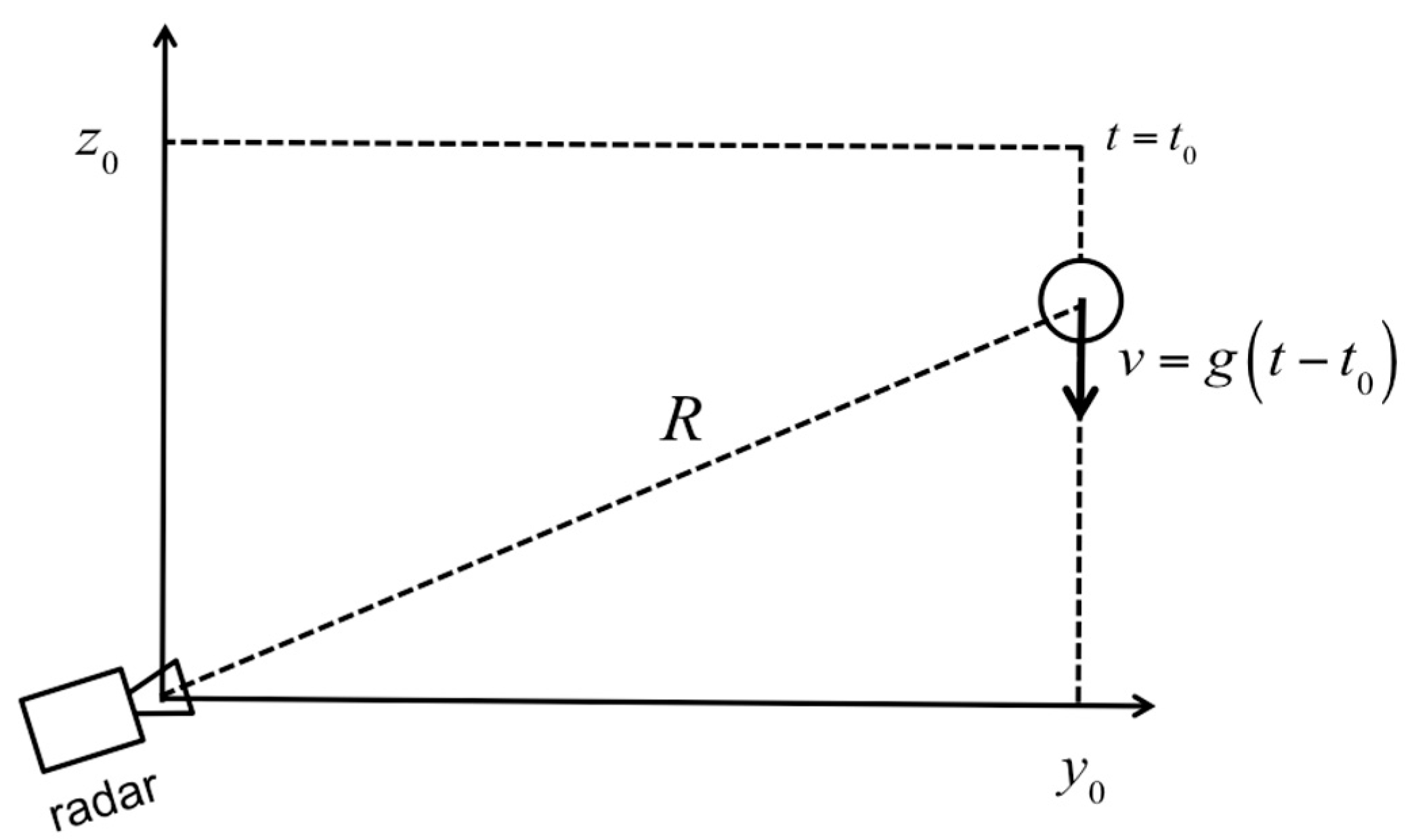
2.1. Theoretical Formulation of the Problem
- (1)
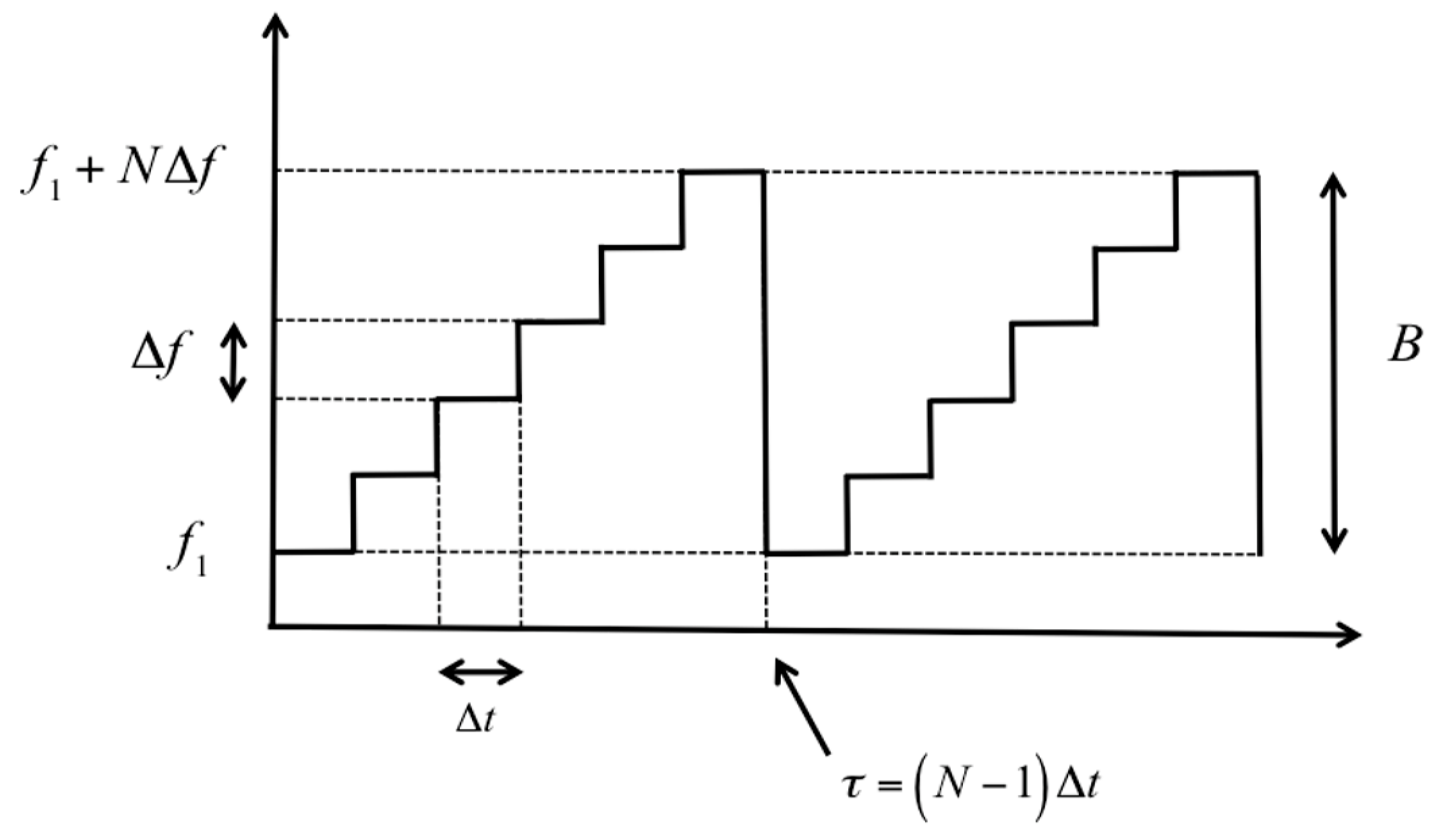
- The gathered data were disposed in a matrix Ei,k where the i index was relative to the frequency, and the k index was relative to time (that proceeded at step τ).
- (2)
- The matrix was windowed along the i-index with a Kaiser window with β = 10.
- (3)
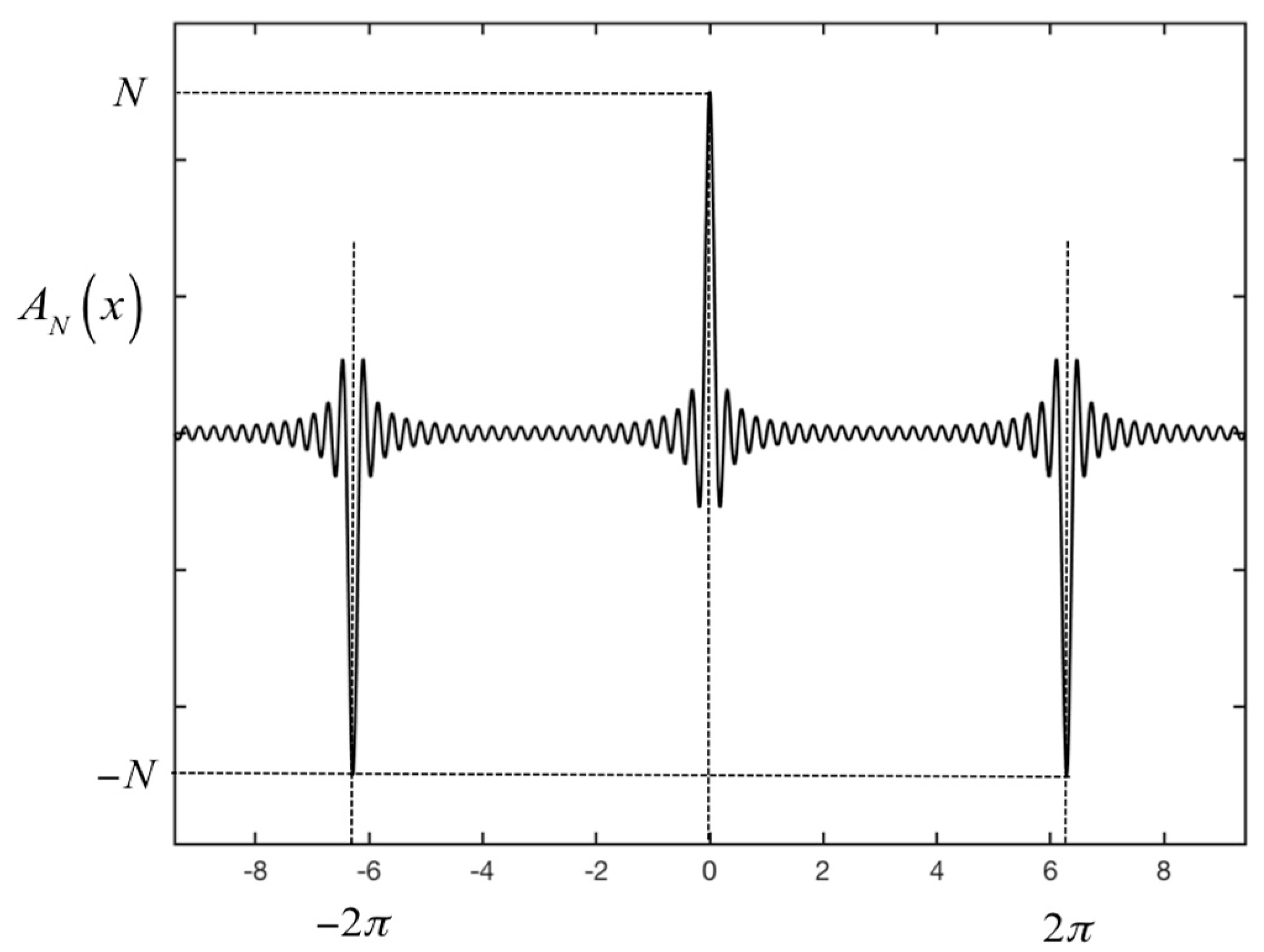
- We calculated the IFFT of each column (i-index) with a suitable padding factor (F = 50) [15]. The number of elements of each column was N × F, and the new index was ii. The range step was c/(2B × F).
- (4)
- We calculated the phase of the product between each column and the complex conjugate of the previous column.
- (5)
- Using Equation (13), we calculated the estimated speed at each range (identified by the index ii).
- (6)
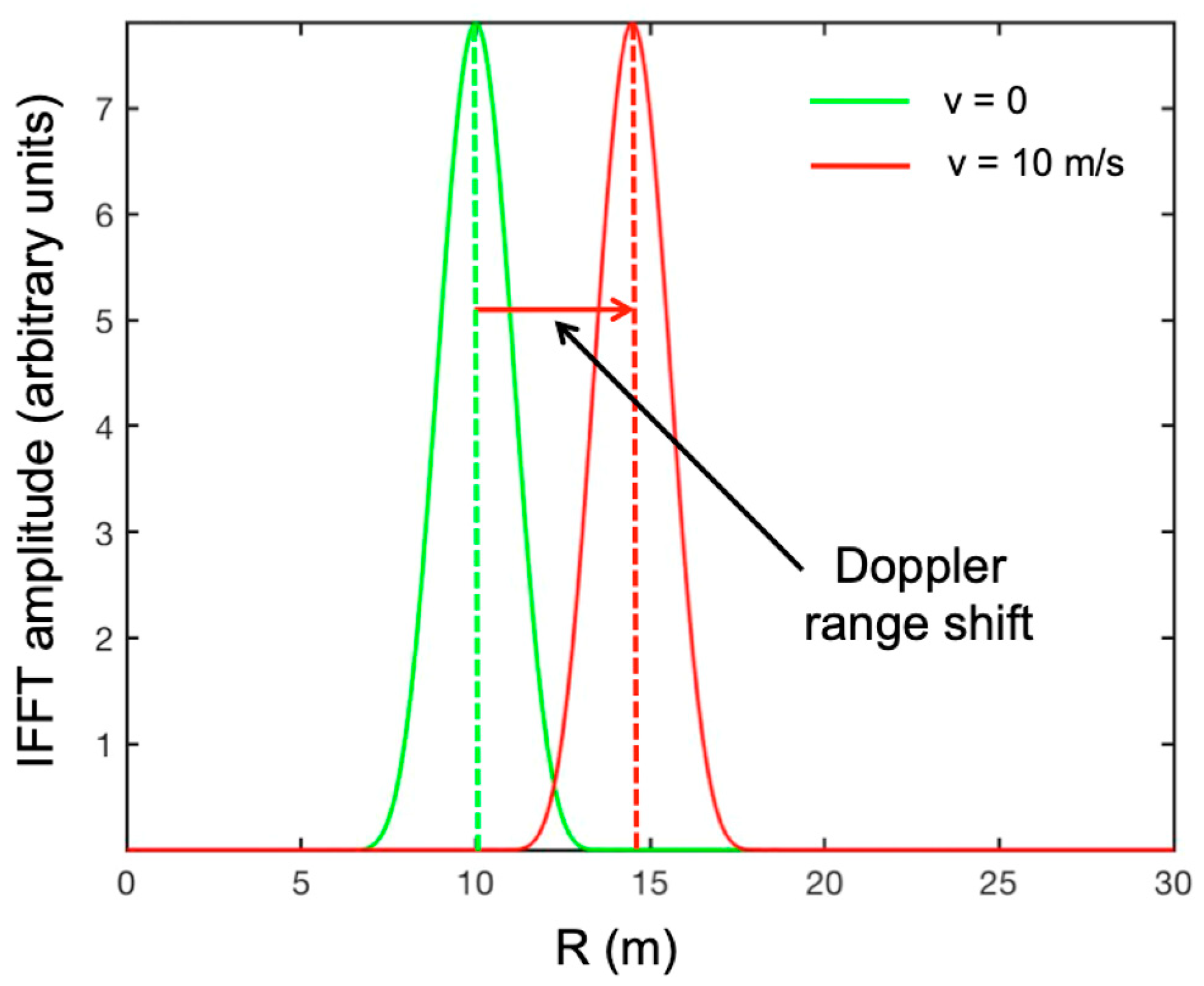
- Using Equation (9), we calculated the Doppler range shift and we divided it by the range step. We estimated the integer number m closer to that ratio.
- (7)
- The complex value of the IFFT at range ii was summed to the value at range ii + m.
- (8)
- We repeated steps 5–7 for all ii.
2.2. Simulation
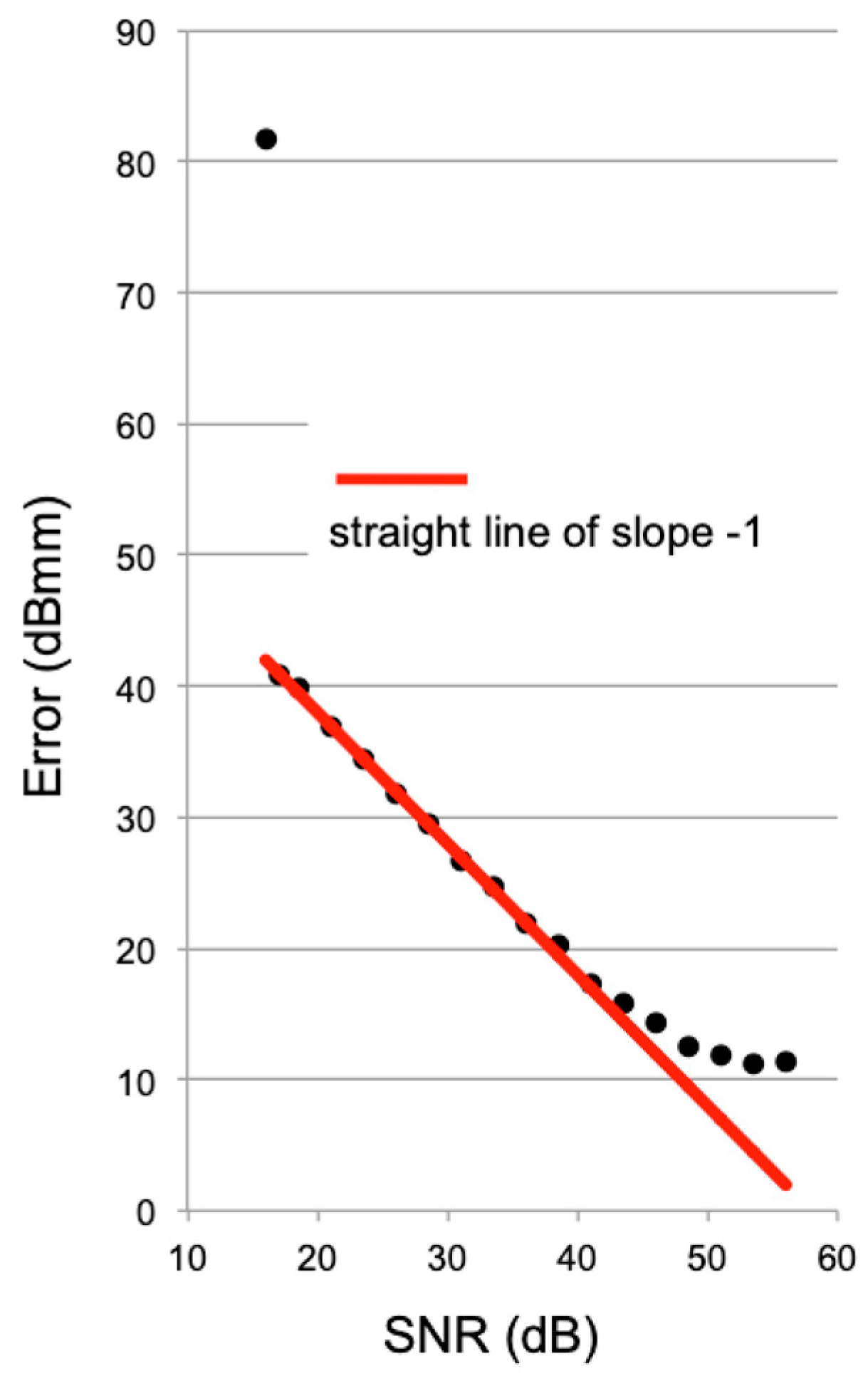
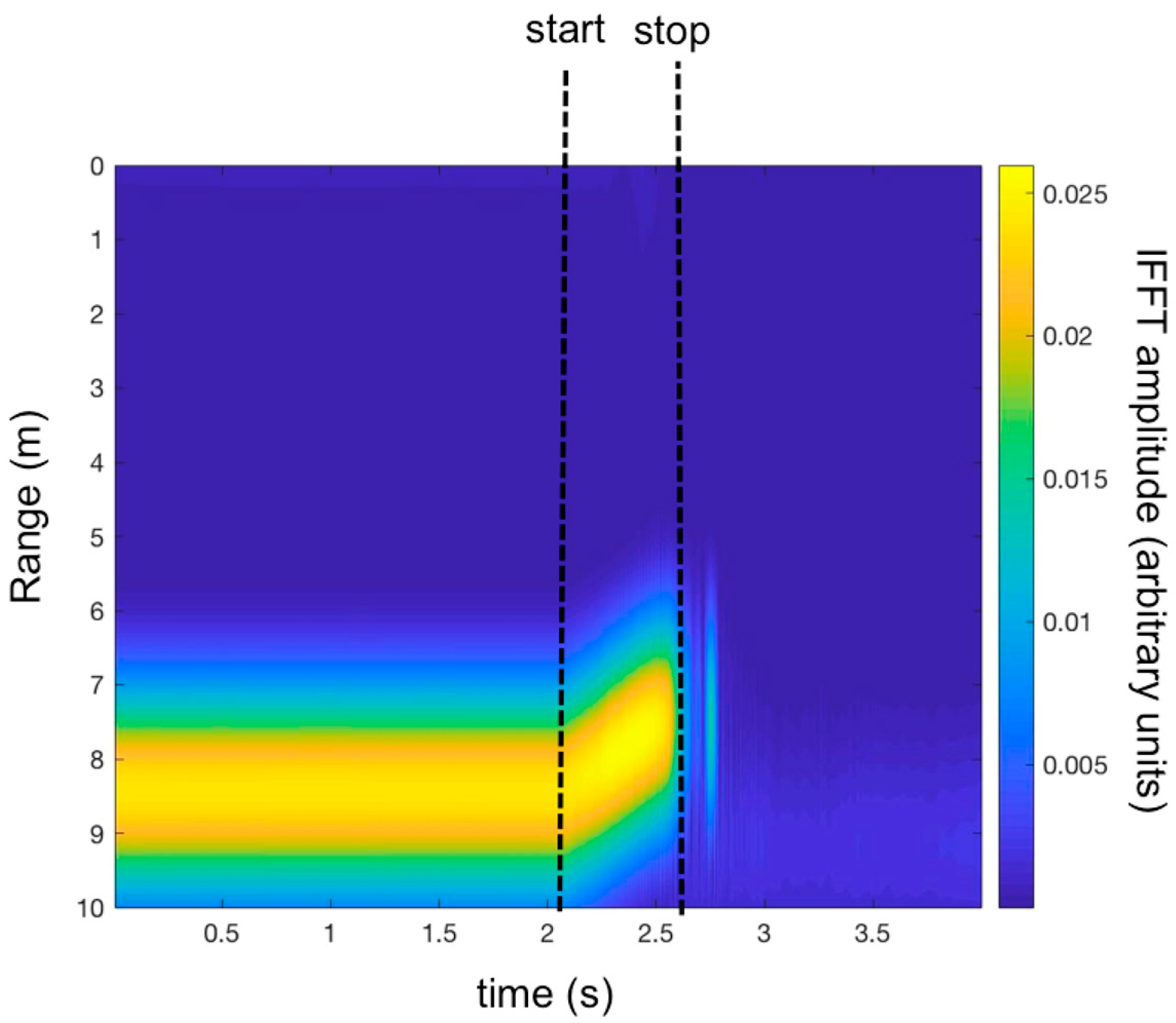
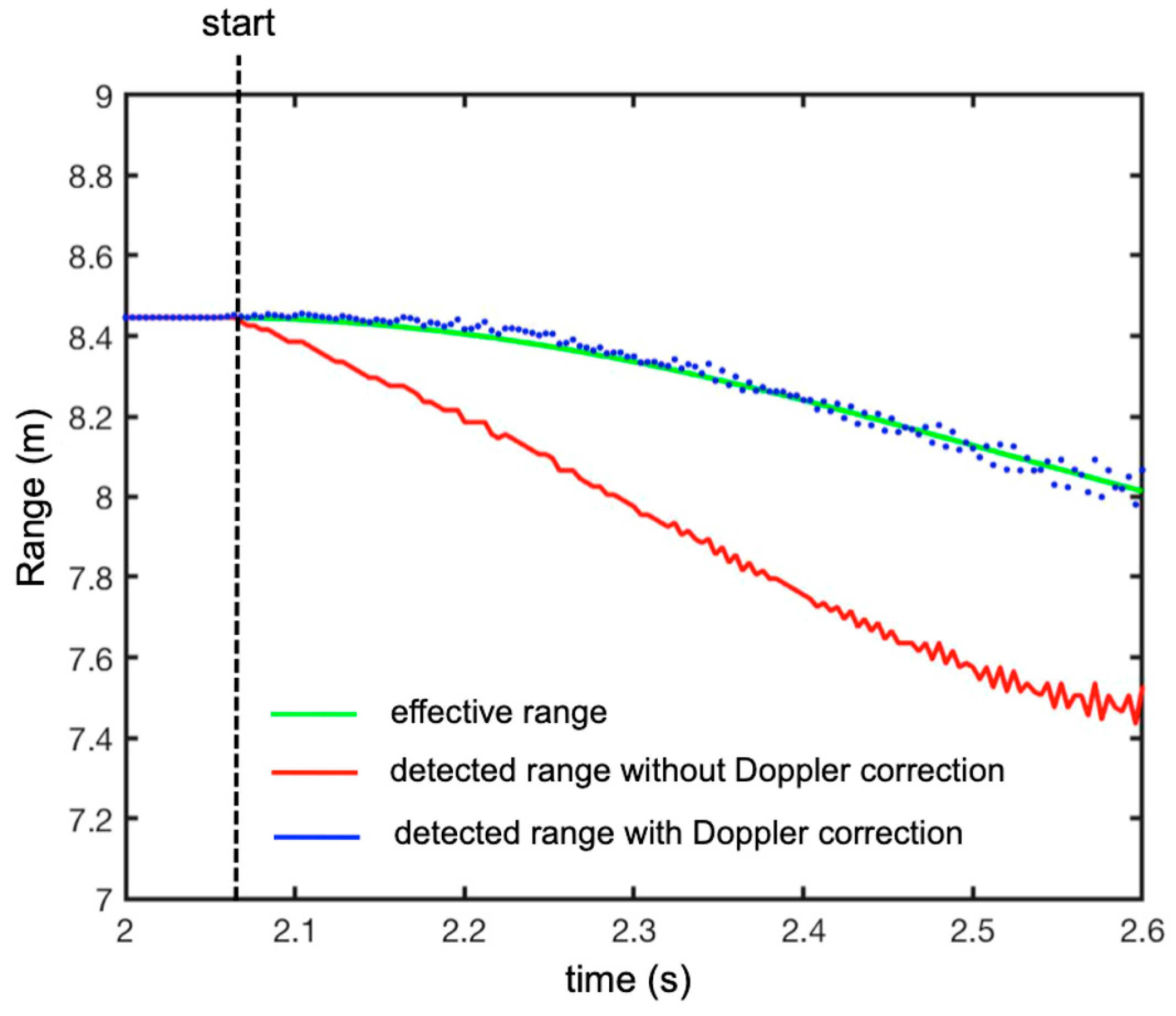
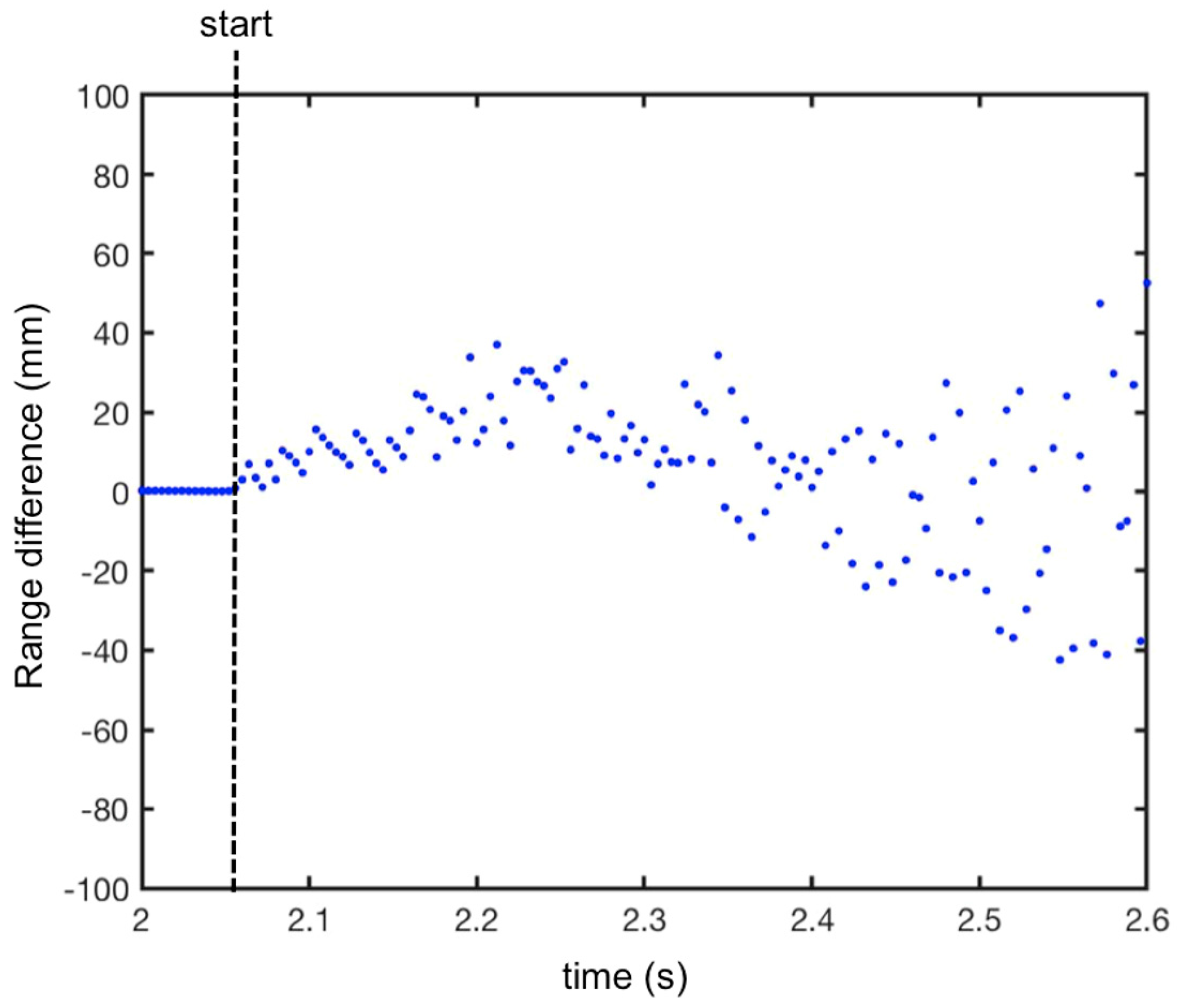
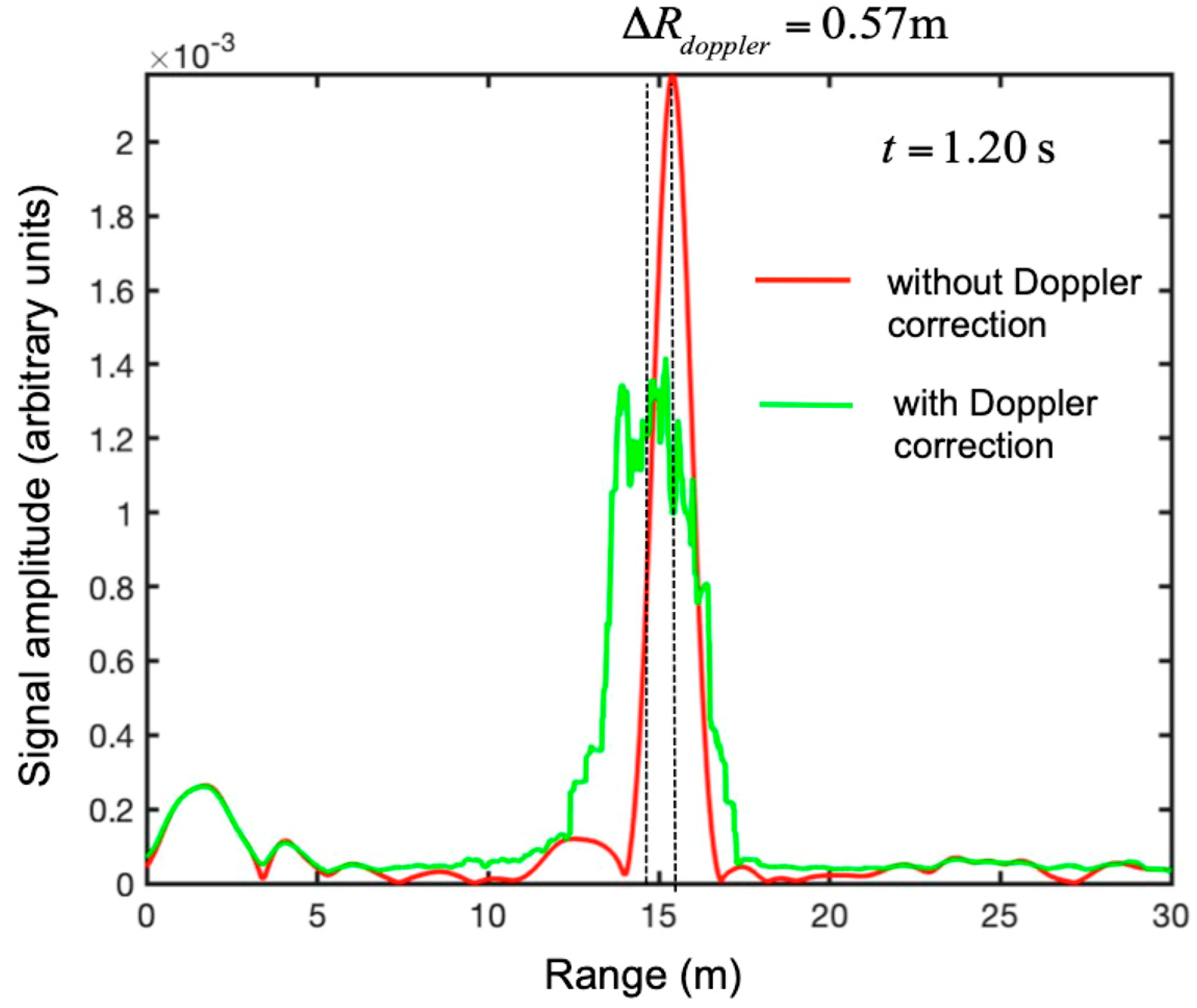
3. Results
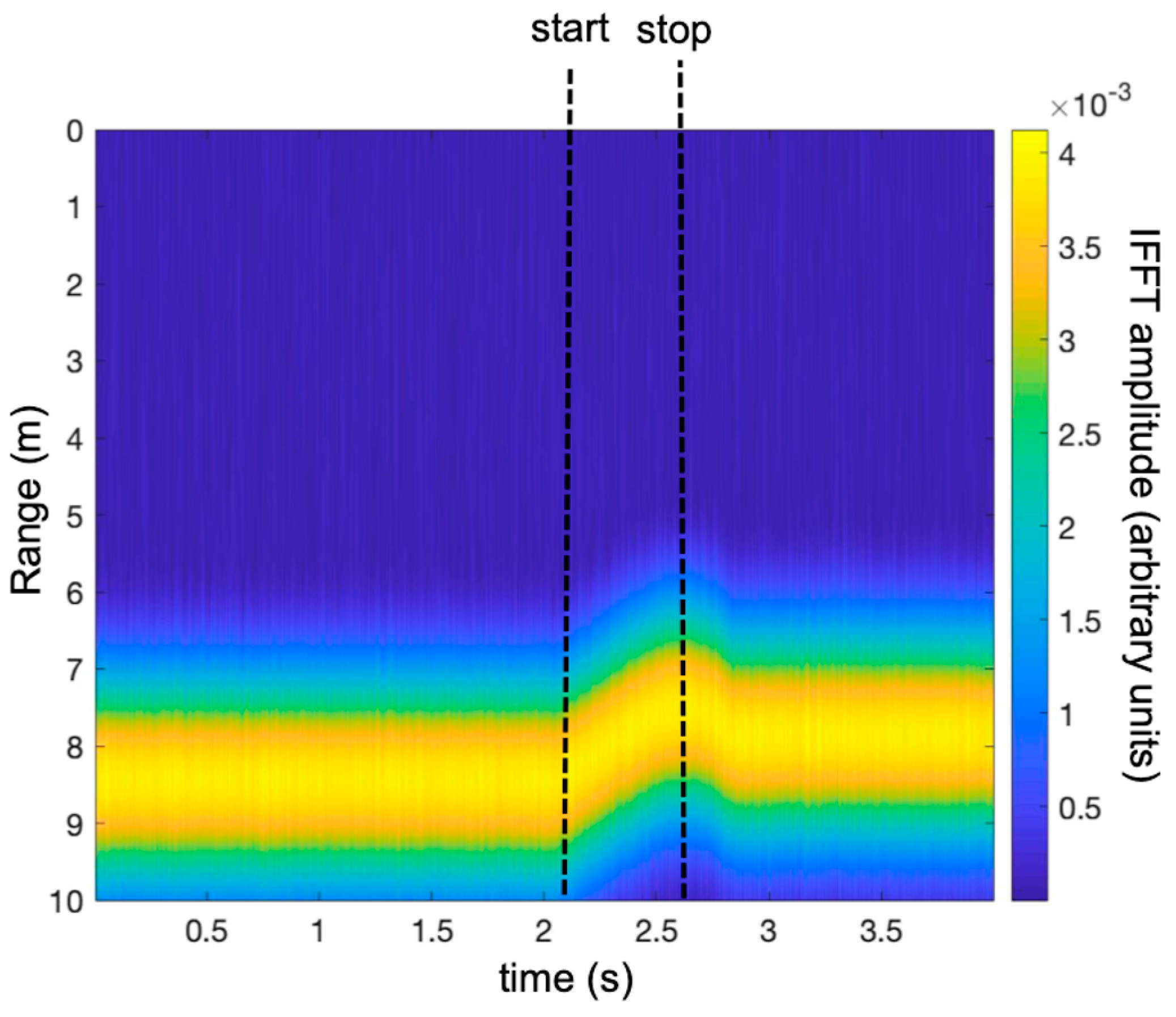
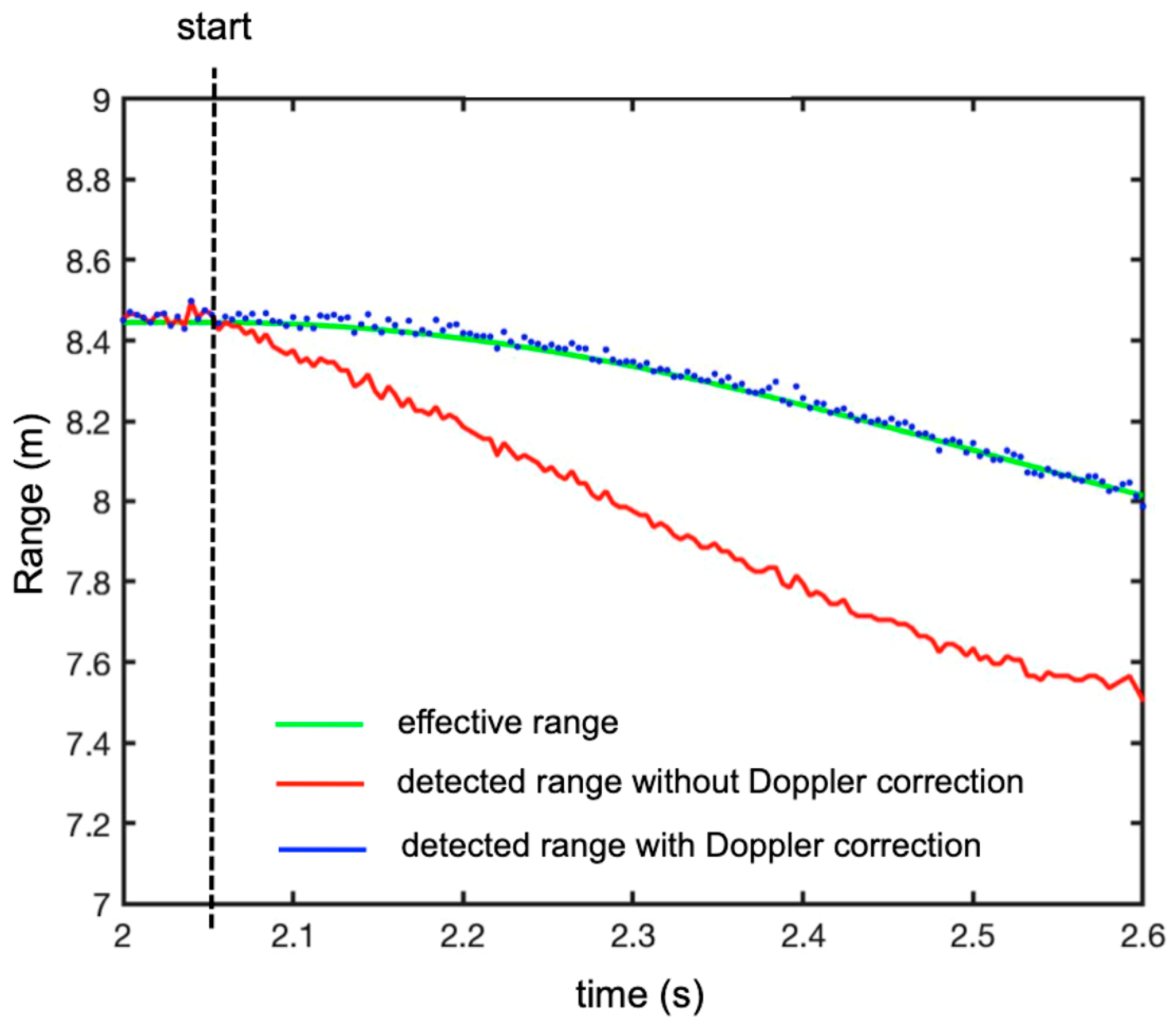
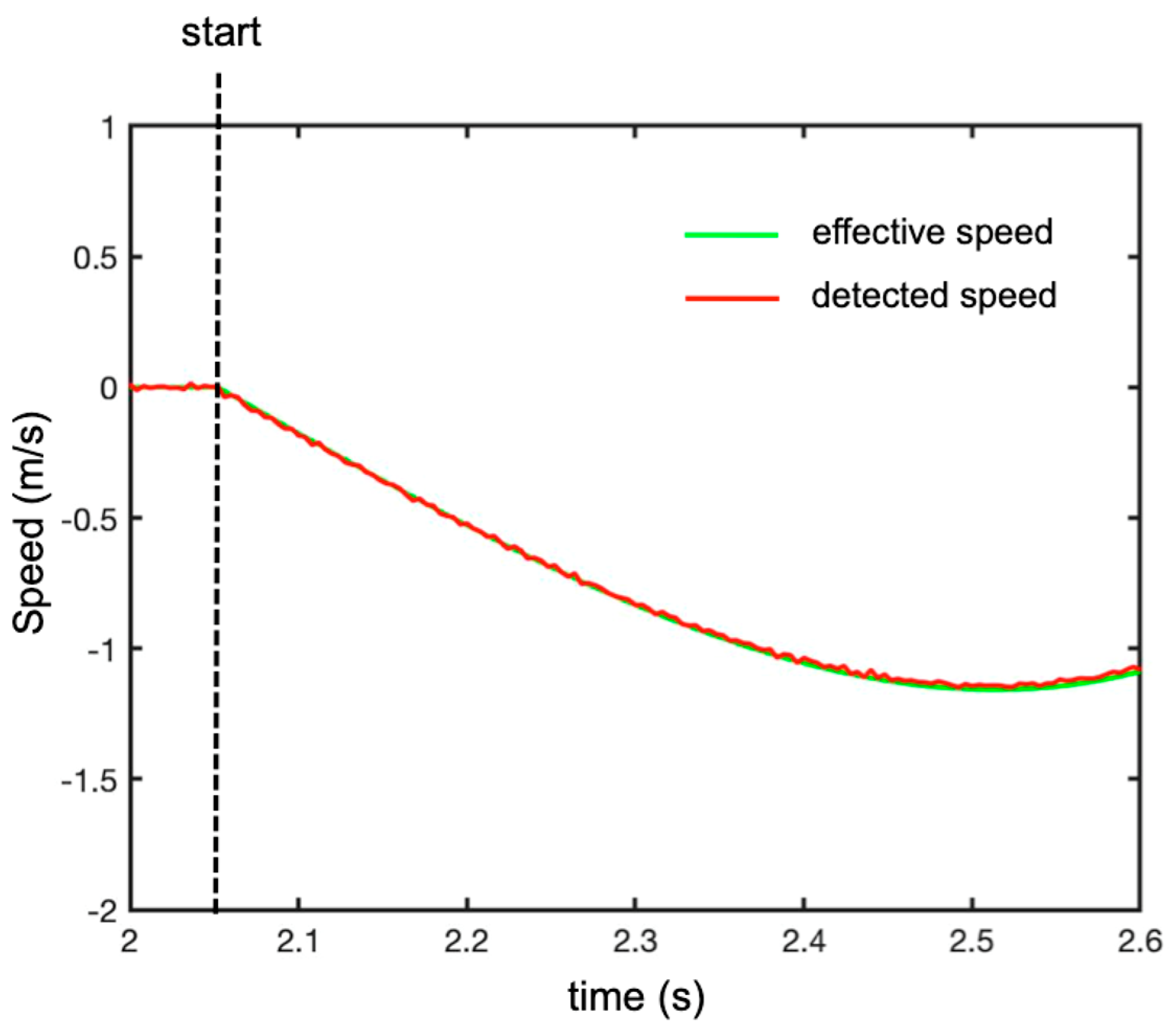
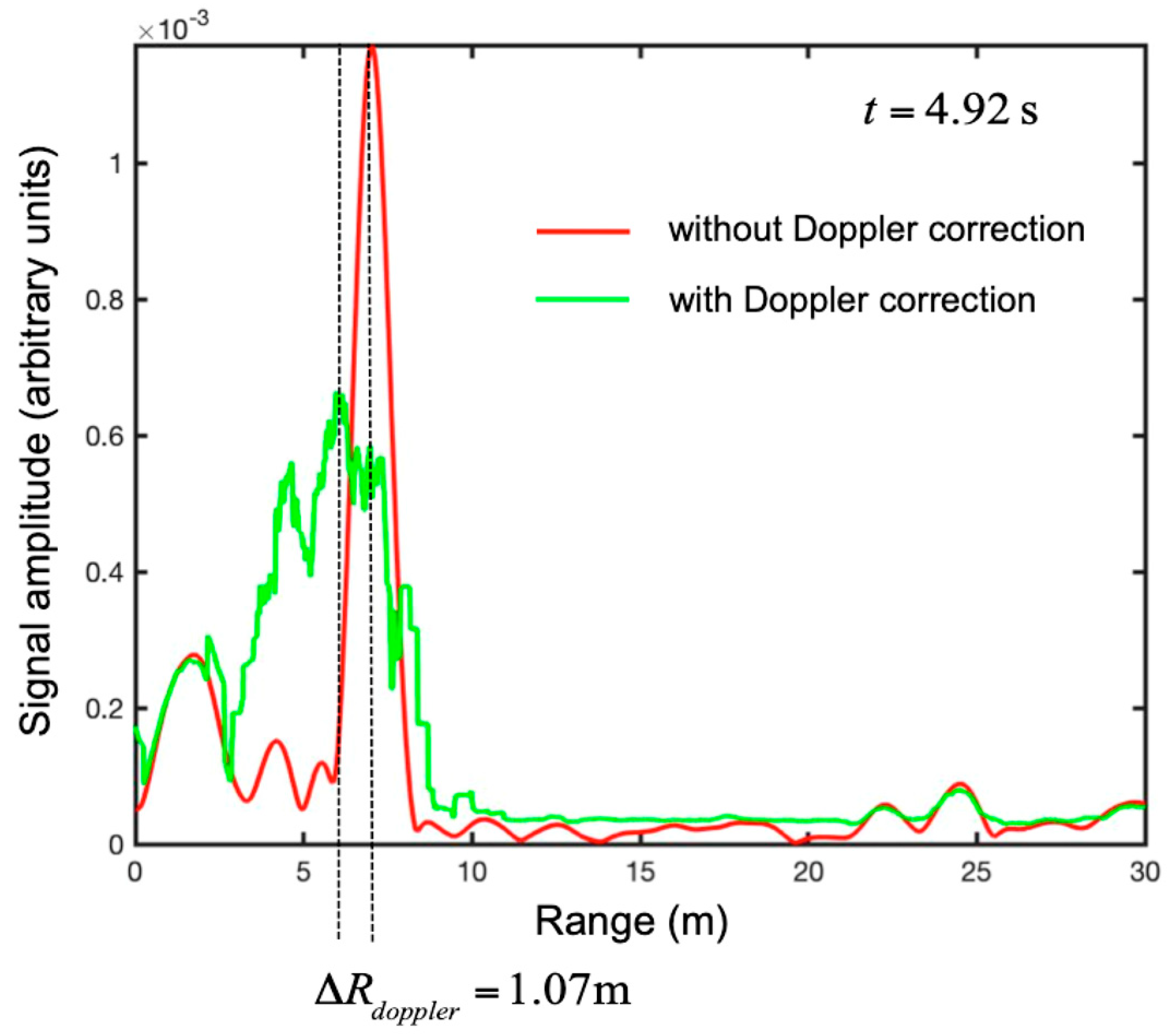
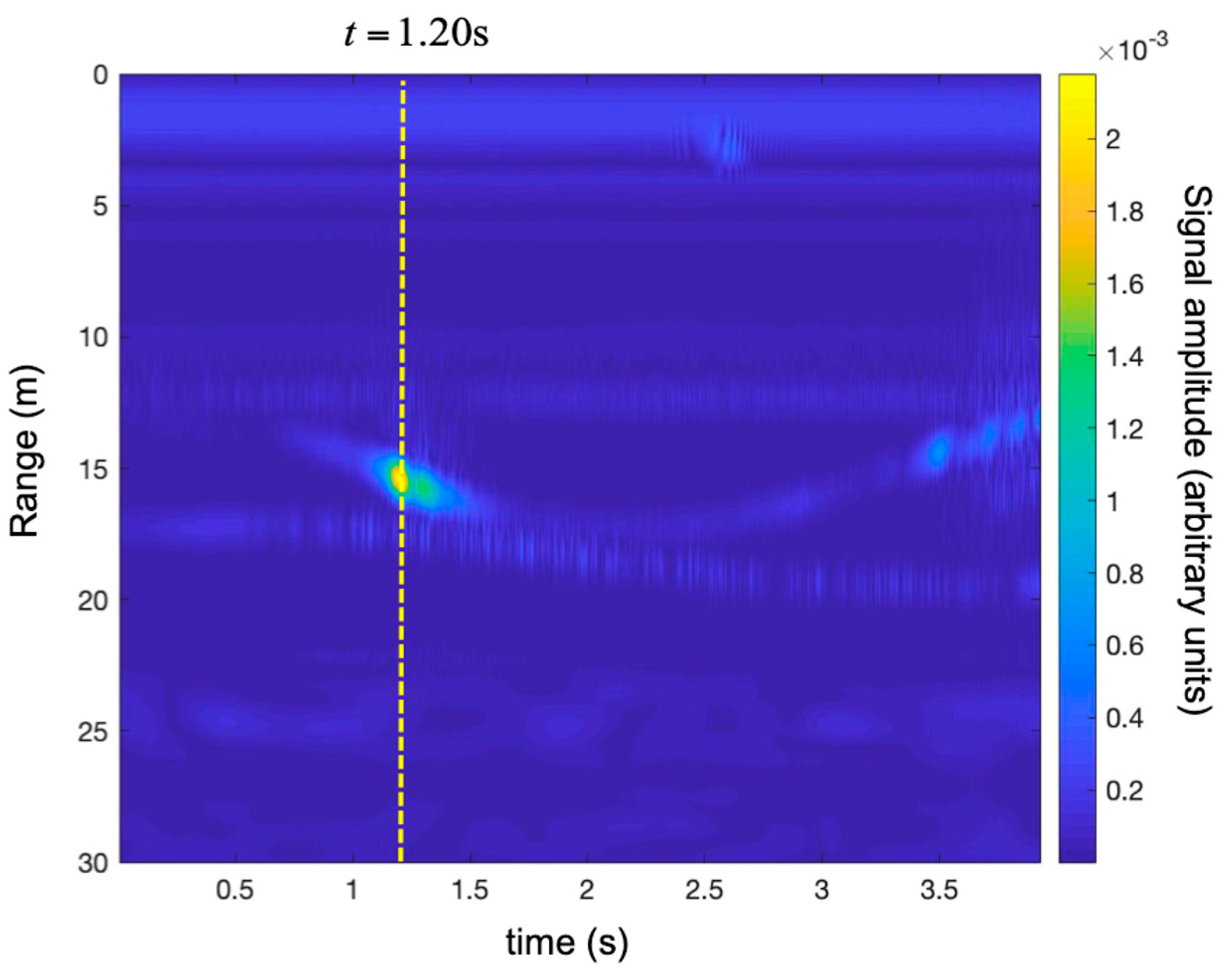
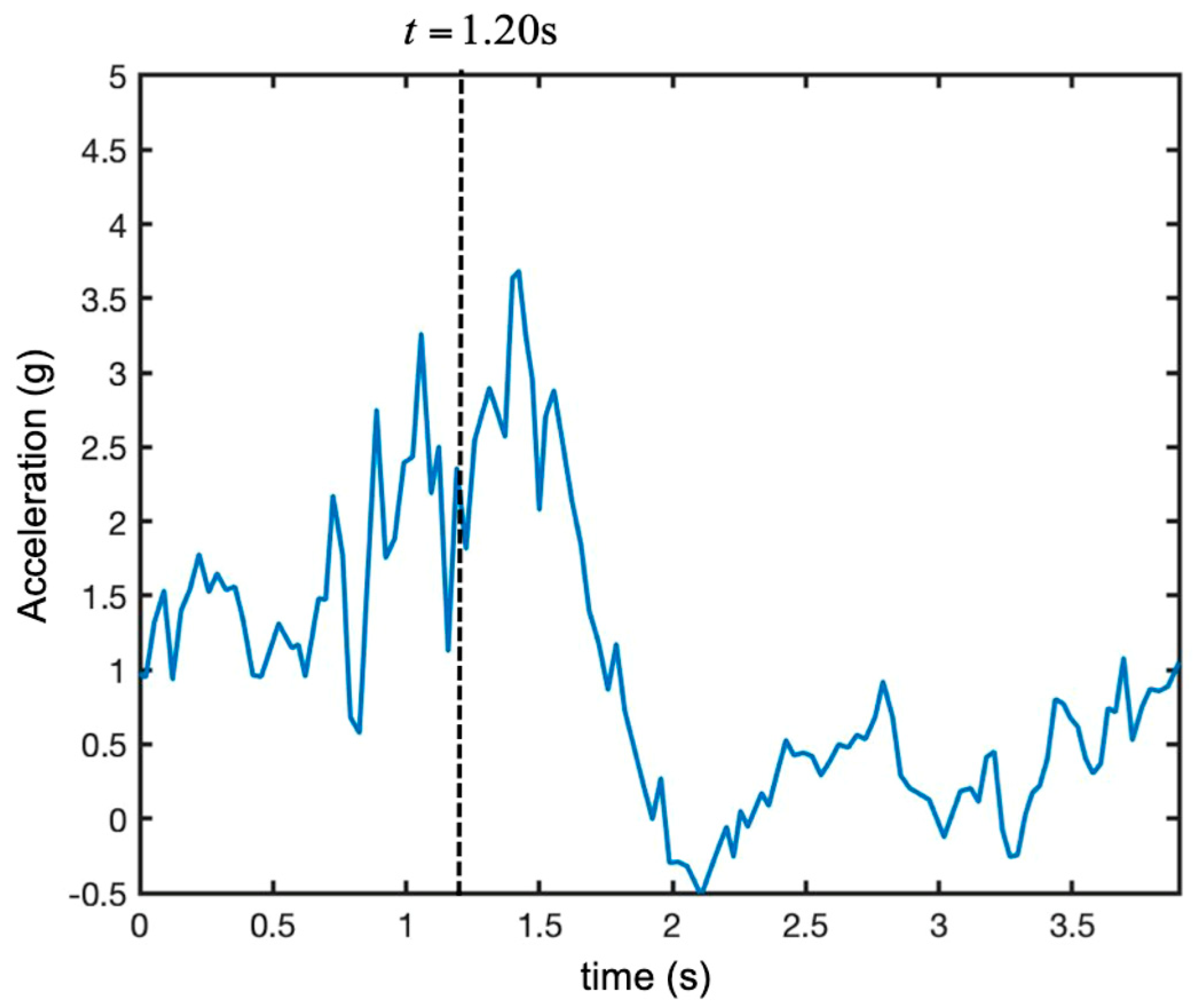
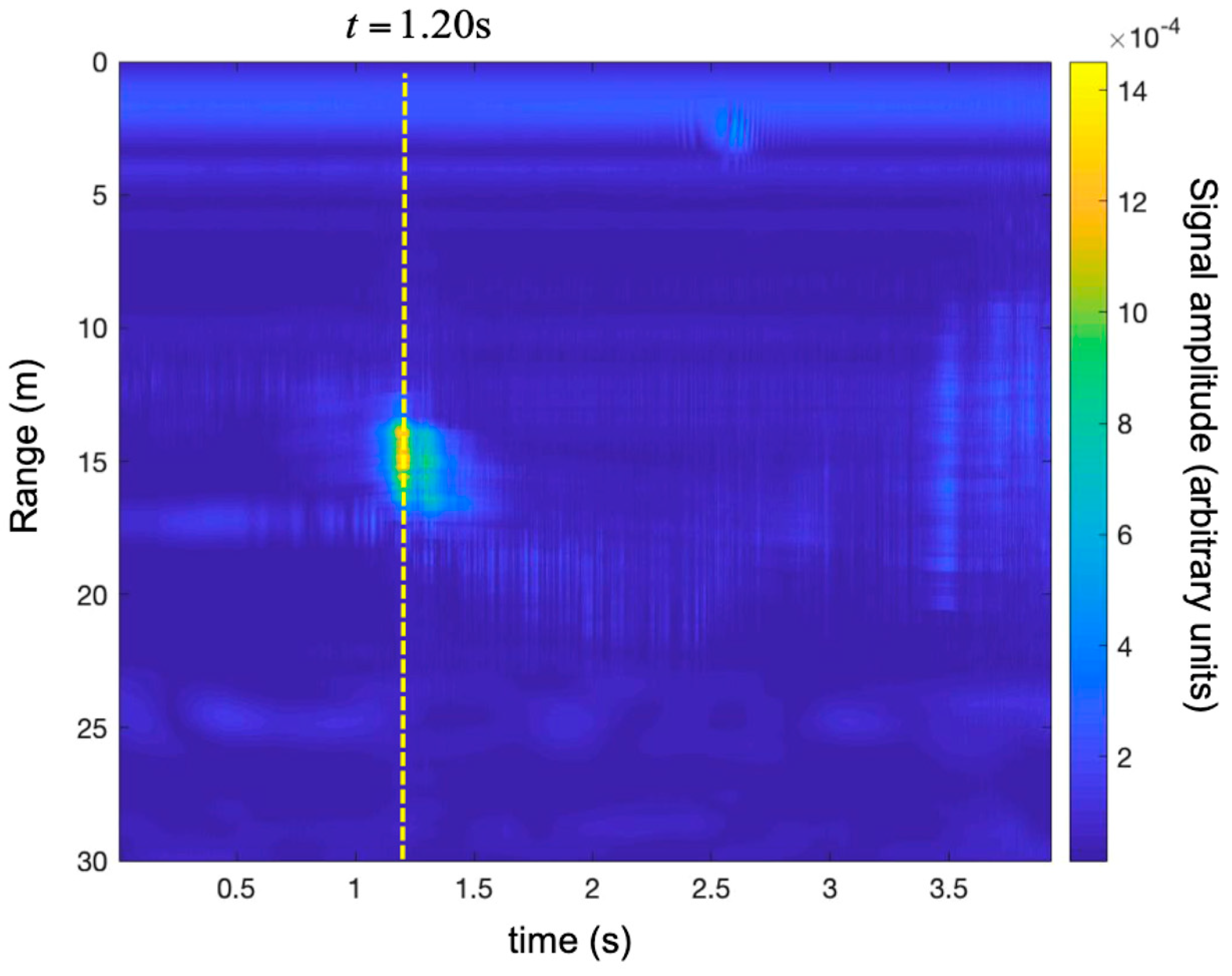
3.1. Falling Corner Reflector
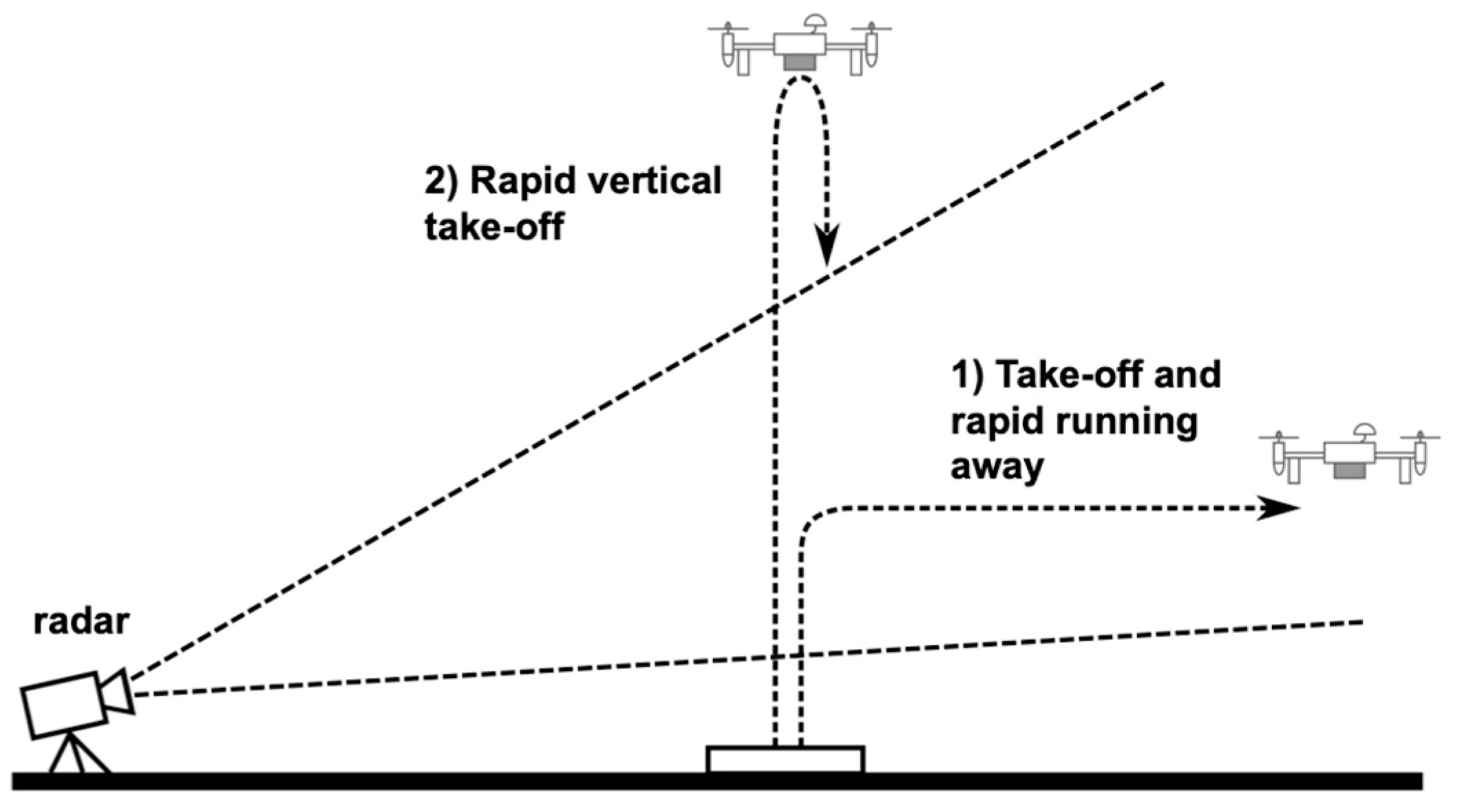
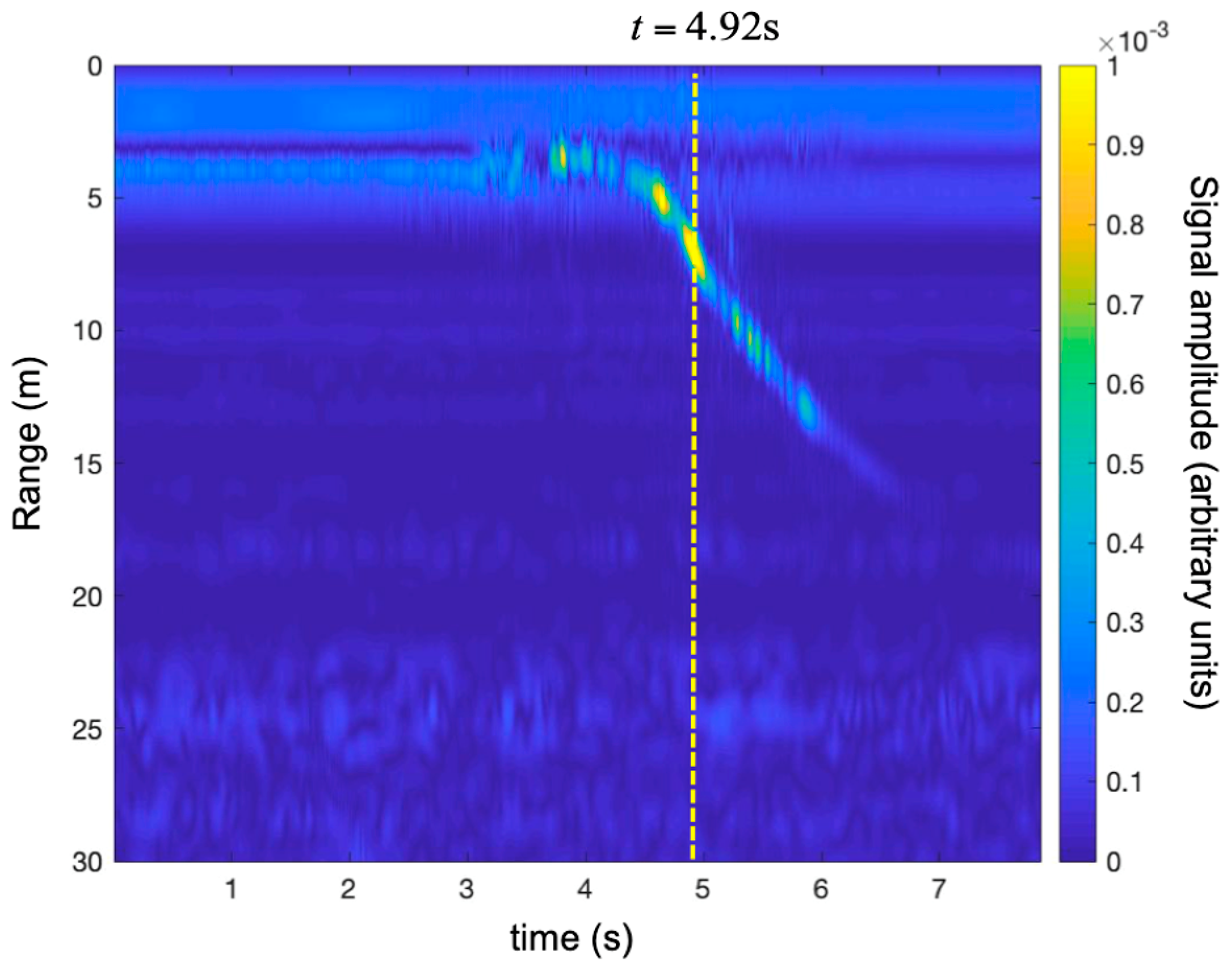
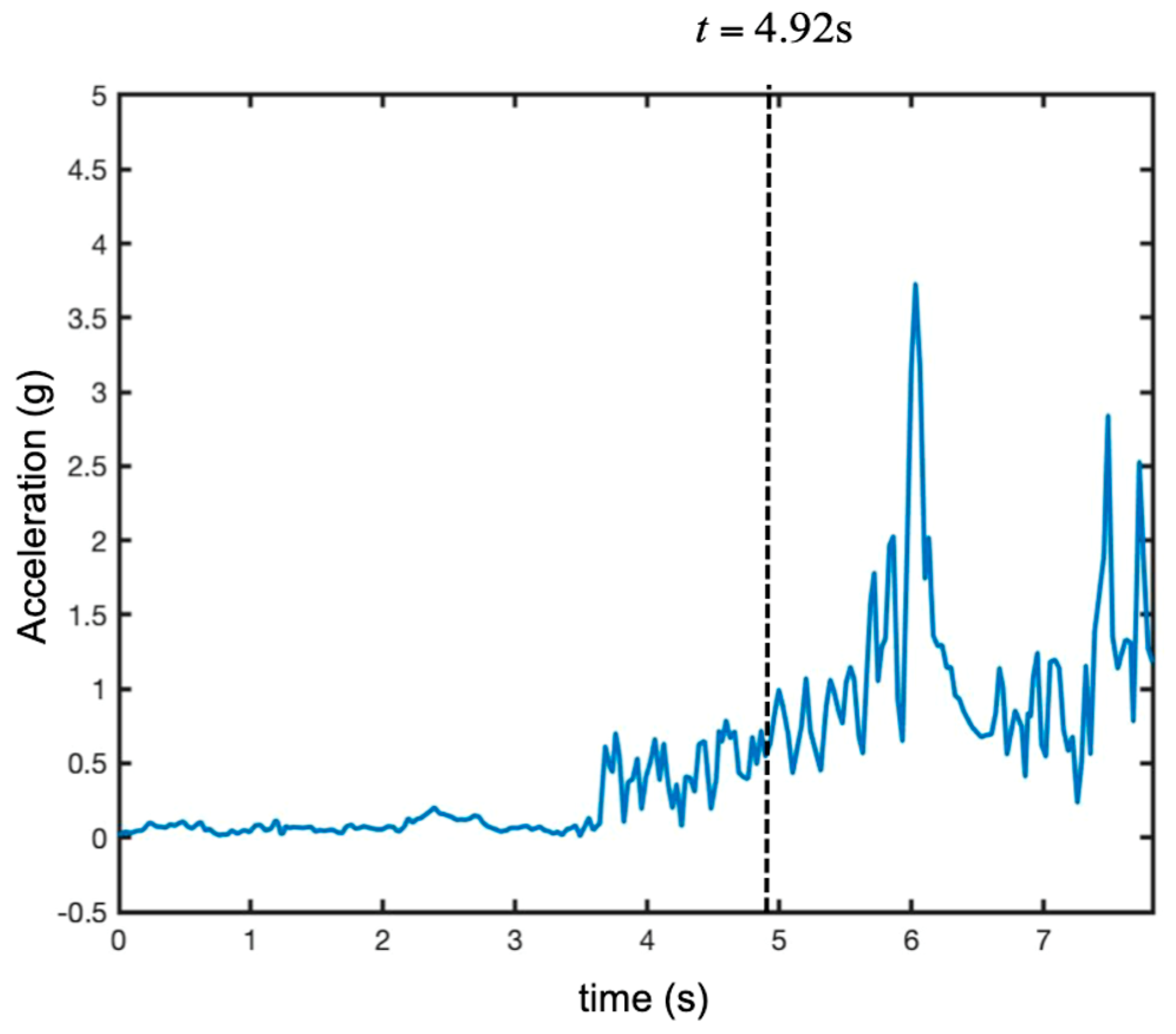
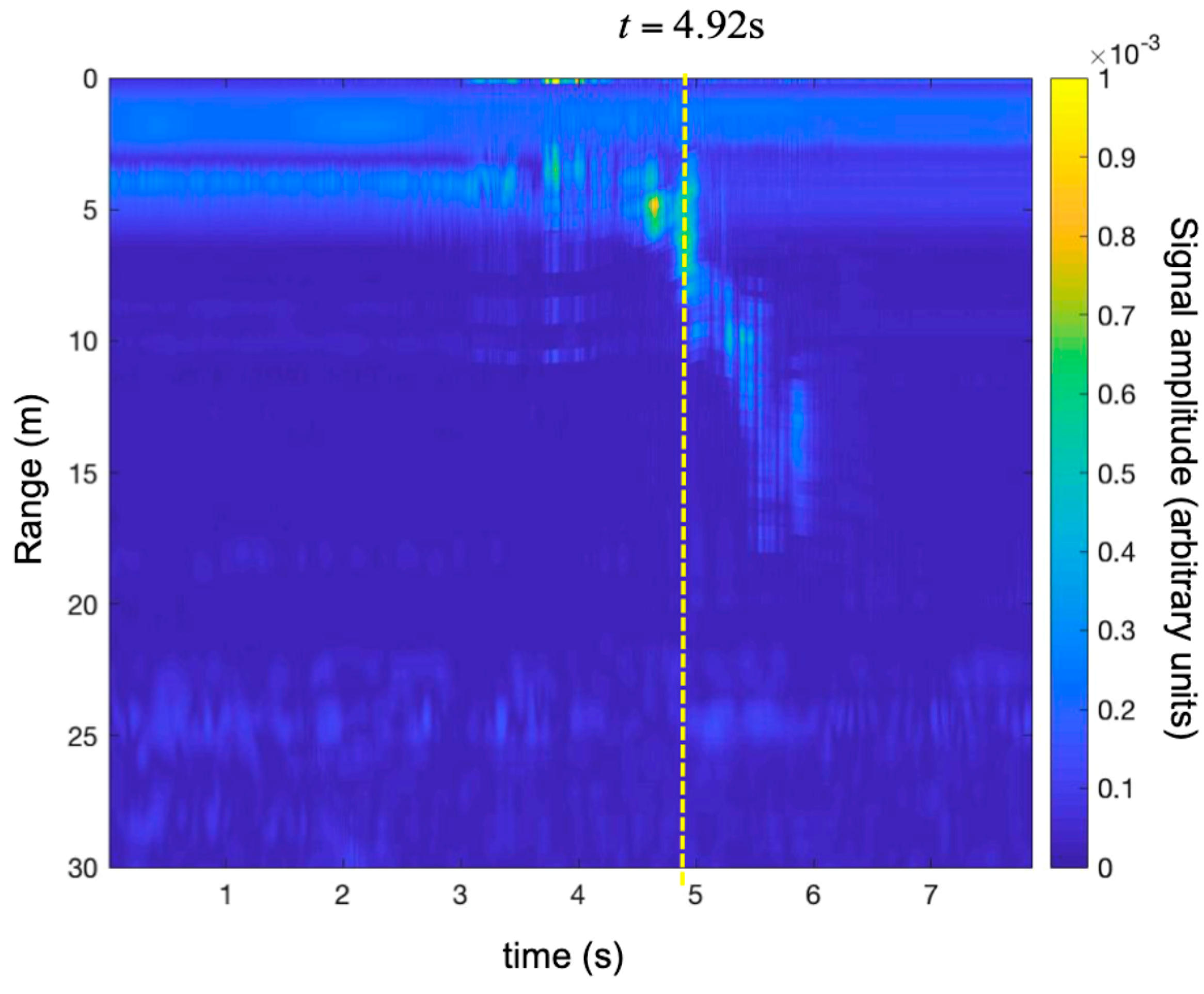
3.2. Detection of a Small UAV
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vattapparamban, E.; Güvenç, İ.; Yurekli, A.İ.; Akkaya, K.; Uluağaç, S. Drones for smart cities: Issues in cybersecurity, privacy, and public safety. In Proceedings of the 2016 International Wireless Communications and Mobile Computing Conference (IWCMC), Paphos, Cyprus, 5–9 September 2016; pp. 216–221. [Google Scholar]
- Pieraccini, M.; Miccinesi, L.; Rojhani, N. RCS measurements and ISAR images of small UAVs. IEEE Aerosp. Electron. Syst. Mag. 2017, 32, 28–32. [Google Scholar] [CrossRef]
- Weiss, M.; Knochel, R. A sub-millimeter accurate microwave multilevel gauging system for liquids in tanks. IEEE Trans. Microw. Theory Tech. 2001, 49, 381–384. [Google Scholar] [CrossRef]
- Pieraccini, M.; Mecatti, D.; Dei, D.; Parrini, F.; Macaluso, G.; Spinetti, A.; Puccioni, F. Microwave sensor for molten glass level measurement. Sens. Actuat. A Phys. 2014, 212, 52–57. [Google Scholar] [CrossRef]
- Oyan, M.J.; Hamran, S.E.; Hanssen, L.; Berger, T.; Plettemeier, D. Ultrawideband gated step frequency ground-penetrating radar. IEEE Trans. Geosci. Remote Sens. 2012, 50, 212–220. [Google Scholar] [CrossRef]
- Parrini, F.; Persico, R.; Pieraccini, M.; Spinetti, A.; Macaluso, G.; Fratini, M.; Manacorda, G. A reconfigurable stepped frequency gpr (gpr-r). In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2011), Vancouver, BC, Canada, 24–29 July 2011; pp. 67–70. [Google Scholar]
- Monserrat, O.; Crosetto, M.; Luzi, G. A review of ground-based SAR interferometry for deformation measurement. ISPRS J. Photogramm. Remote Sens. 2014, 93, 40–48. [Google Scholar] [CrossRef]
- Pieraccini, M.; Luzi, G.; Mecatti, D.; Noferini, L.; Atzeni, C. Ground-based SAR for short and long term monitoring of unstable slopes. In Proceedings of the 3rd European Radar Conference, Manchester, UK, 13–15 September 2006; pp. 92–95. [Google Scholar]
- Pieraccini, M. Noise performance comparison between continuous wave and stroboscopic pulse ground penetrating radar. IEEE Geosci. Remote Sens. Lett. 2018, 15, 222–226. [Google Scholar] [CrossRef]
- Pieraccini, M.; Miccinesi, L. CWSF radar for detecting small UAVs. In Proceedings of the 2017 IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems (COMCAS), Tel-Aviv, Israel, 13–15 November 2017. [Google Scholar]
- Skolnik, M.I. Radar Handbook; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Gill, G.S. Simultaneous pulse compression and Doppler processing with step frequency waveform. Electron. Let. 1996, 32, 2178–2179. [Google Scholar] [CrossRef]
- Haotian, Y.; Zhen, C.; Shuliang, W.; Jun, P. Study on radar target imaging and velocity measurement simultaneously based on step frequency waveforms. In Proceedings of the 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 5–9 November 2007; pp. 404–407. [Google Scholar]
- Chen, H.Y.; Liu, Y.X.; Jiang, W.D.; Guo, G.R. A new approach for synthesizing the range profile of moving targets via stepped-frequency waveforms. IEEE Geosci. Remote Sens. Lett. 2006, 3, 406–409. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Pieraccini, M.; Rojhani, N.; Miccinesi, L. Compressive sensing for ground based synthetic aperture radar. Remote Sens. 2018, 10, 1960. [Google Scholar] [CrossRef]
- Pieraccini, M.; Fratini, M.; Parrini, F.; Atzeni, C. Dynamic monitoring of bridges using a high-speed coherent radar. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3284–3288. [Google Scholar] [CrossRef]
- Pieraccini, M.; Parrini, F.; Fratini, M.; Atzeni, C.; Spinelli, P. In-service testing of wind turbine towers using a microwave sensor. Renew. Energy 2008, 33, 13–21. [Google Scholar] [CrossRef]
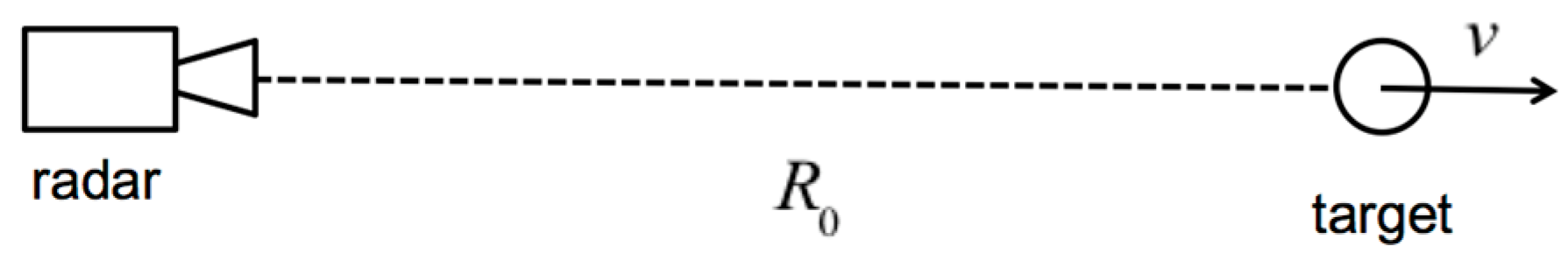



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pieraccini, M.; Miccinesi, L.; Rojhani, N. A Doppler Range Compensation for Step-Frequency Continuous-Wave Radar for Detecting Small UAV. Sensors 2019, 19, 1331. https://doi.org/10.3390/s19061331
Pieraccini M, Miccinesi L, Rojhani N. A Doppler Range Compensation for Step-Frequency Continuous-Wave Radar for Detecting Small UAV. Sensors. 2019; 19(6):1331. https://doi.org/10.3390/s19061331
Chicago/Turabian StylePieraccini, Massimiliano, Lapo Miccinesi, and Neda Rojhani. 2019. "A Doppler Range Compensation for Step-Frequency Continuous-Wave Radar for Detecting Small UAV" Sensors 19, no. 6: 1331. https://doi.org/10.3390/s19061331
APA StylePieraccini, M., Miccinesi, L., & Rojhani, N. (2019). A Doppler Range Compensation for Step-Frequency Continuous-Wave Radar for Detecting Small UAV. Sensors, 19(6), 1331. https://doi.org/10.3390/s19061331






