Effect of Uneven Electrostatic Forces on the Dynamic Characteristics of Capacitive Hemispherical Resonator Gyroscopes
Abstract
1. Introduction
2. Gyroscope Description and Theoretical Analysis
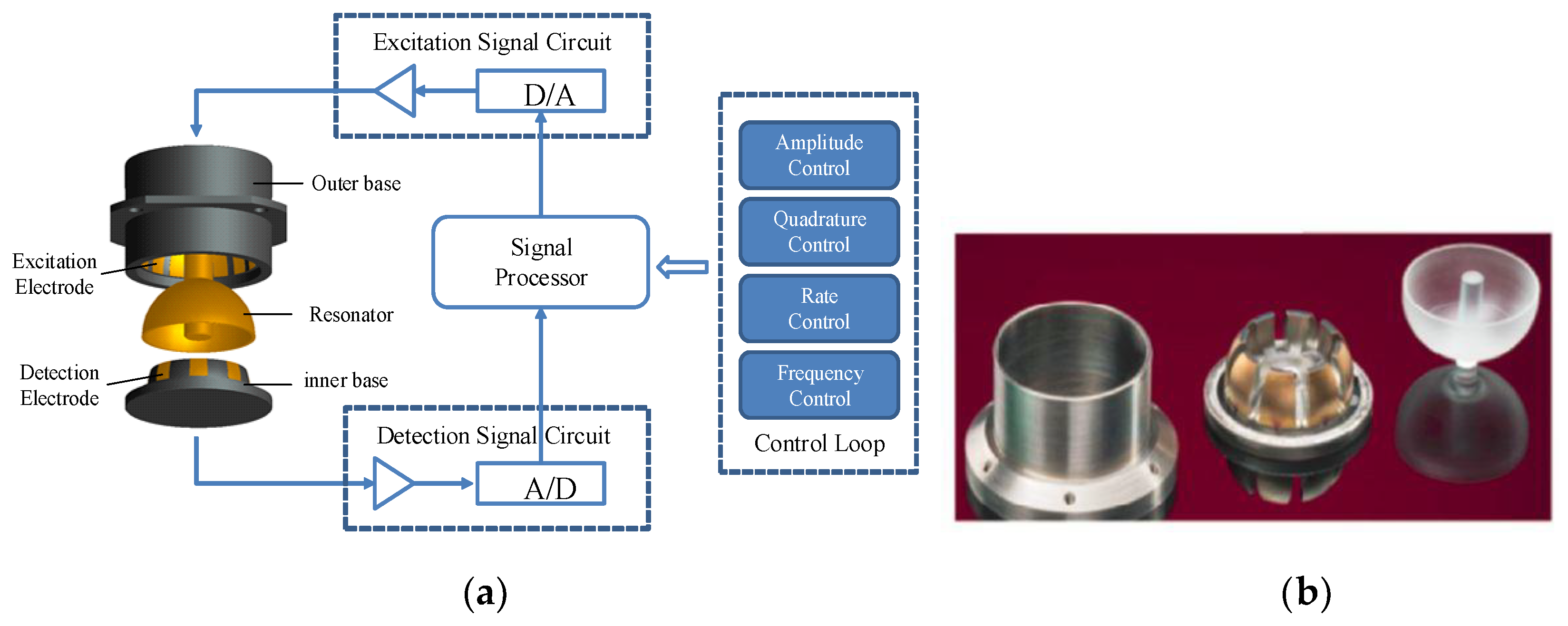
2.1. Gyroscope Structure
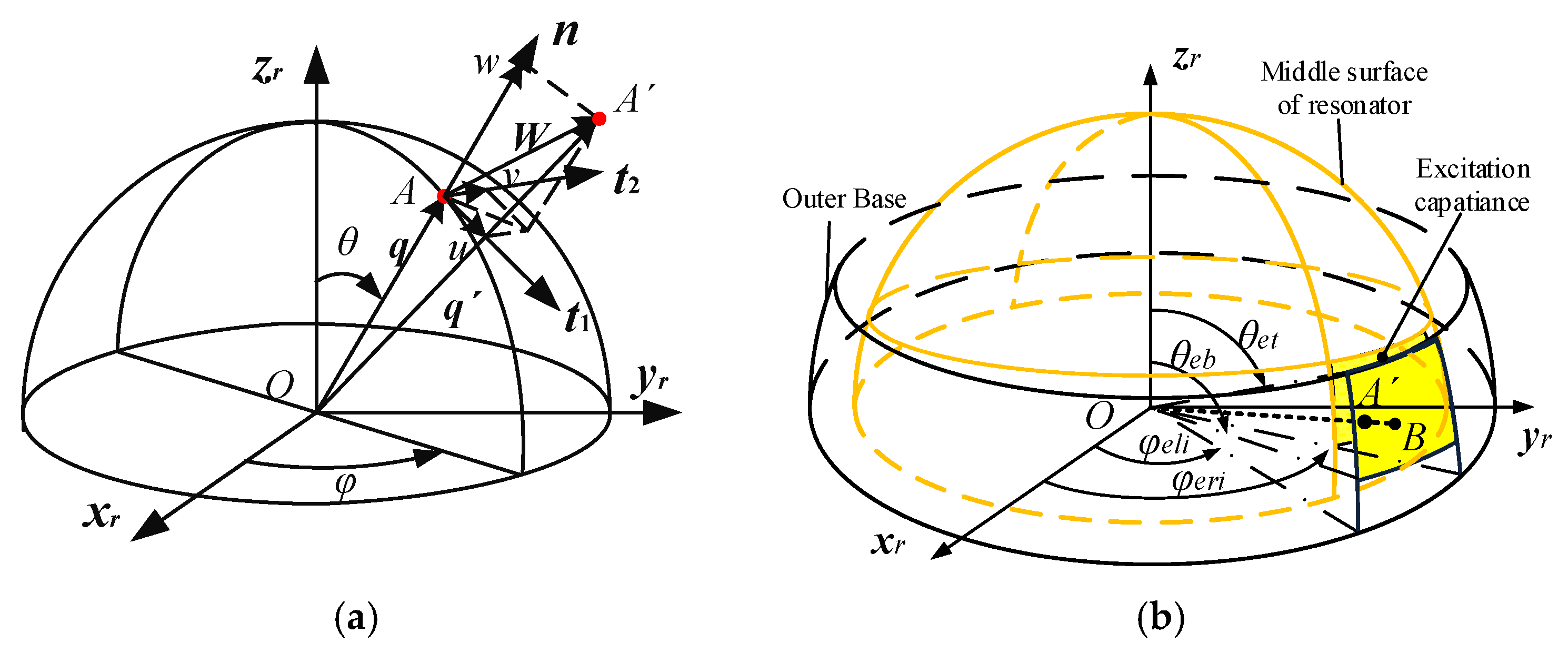
2.2. Theoretical Analysis
2.2.1. Uneven Electrostatic Forces
2.2.2. Resonator Deformation
3. Dynamic Model
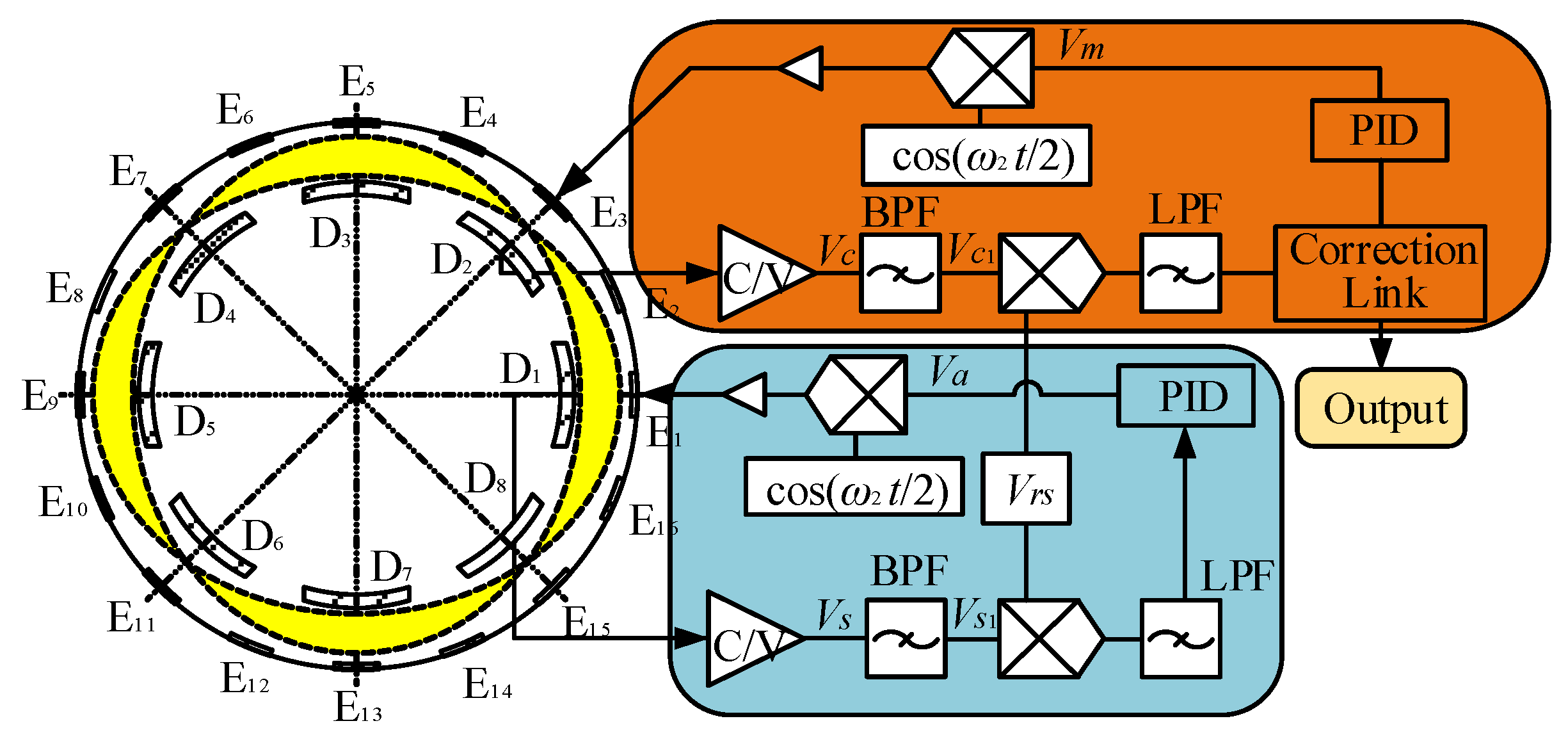
3.1. Dynamic Characteristics of Uneven Electrostatic Forces
3.2. Output Error Model
4. Simulation Analysis
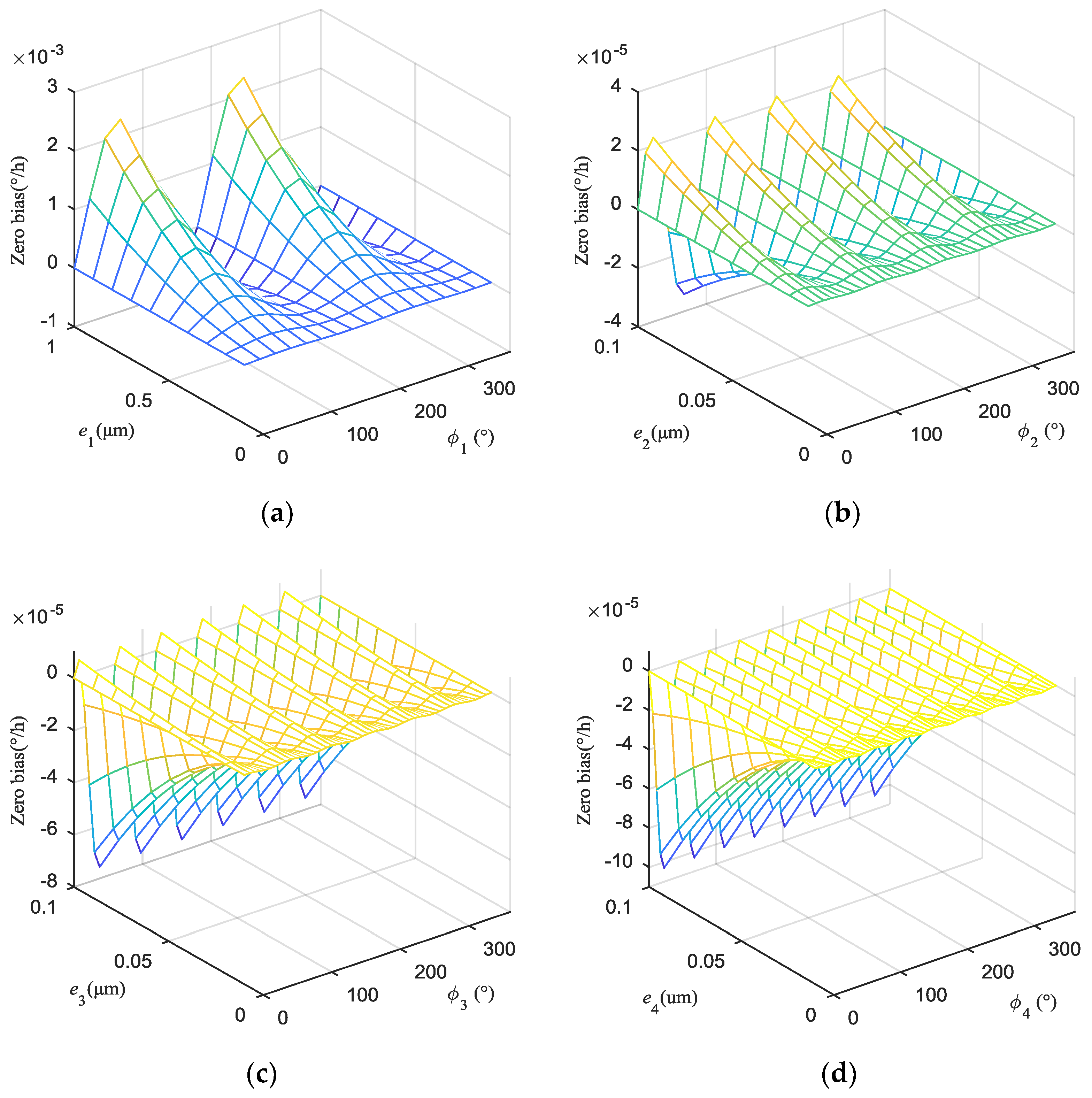
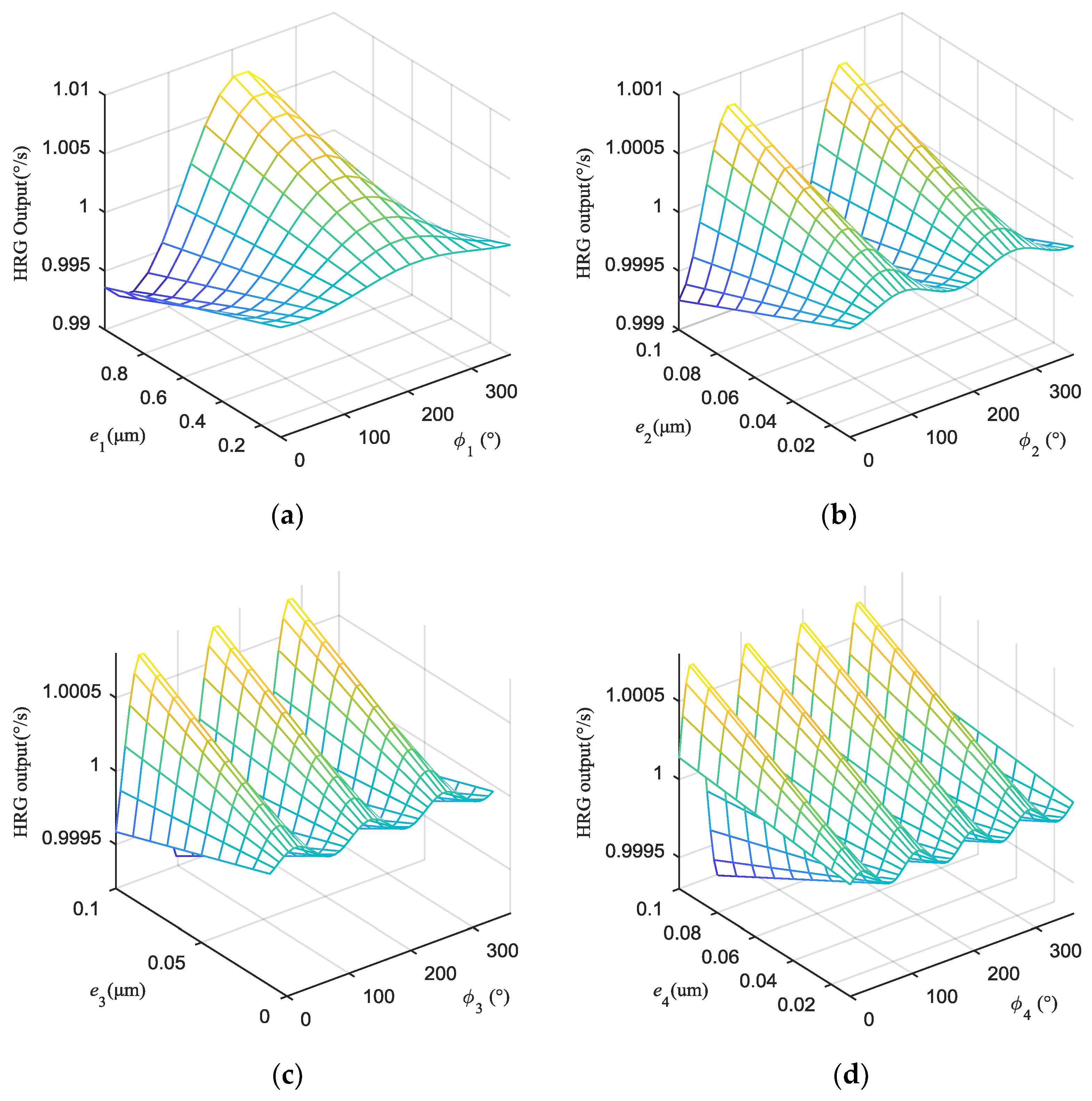
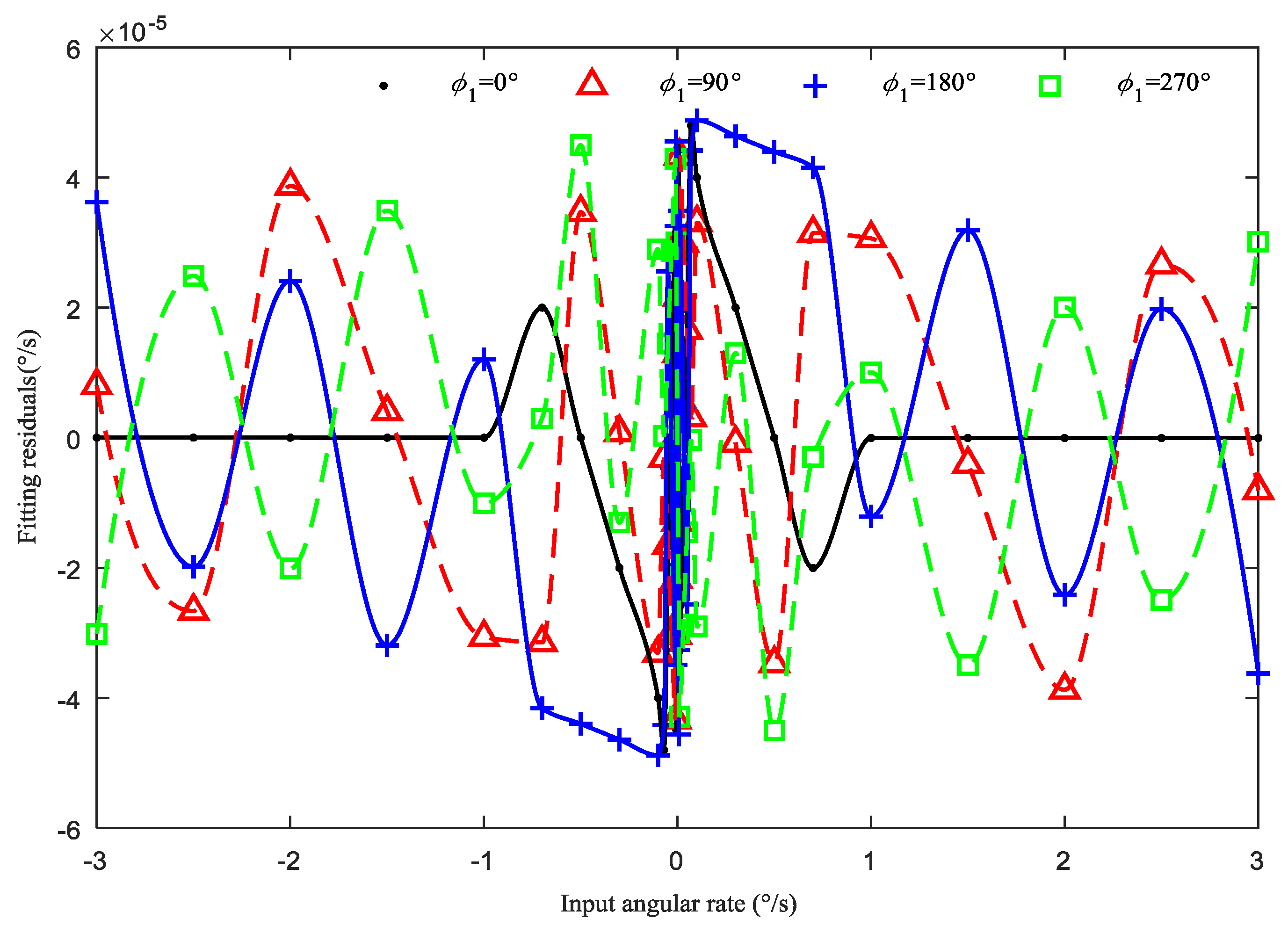
4.1. Effect of the First Four Harmonics
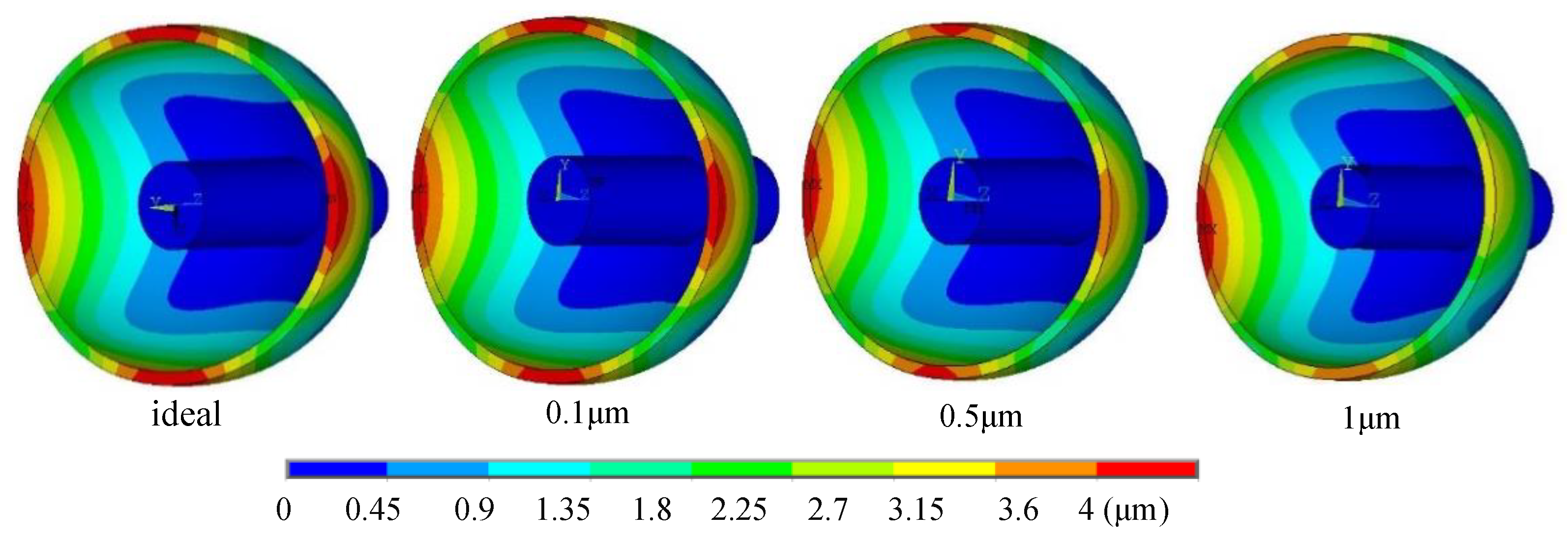
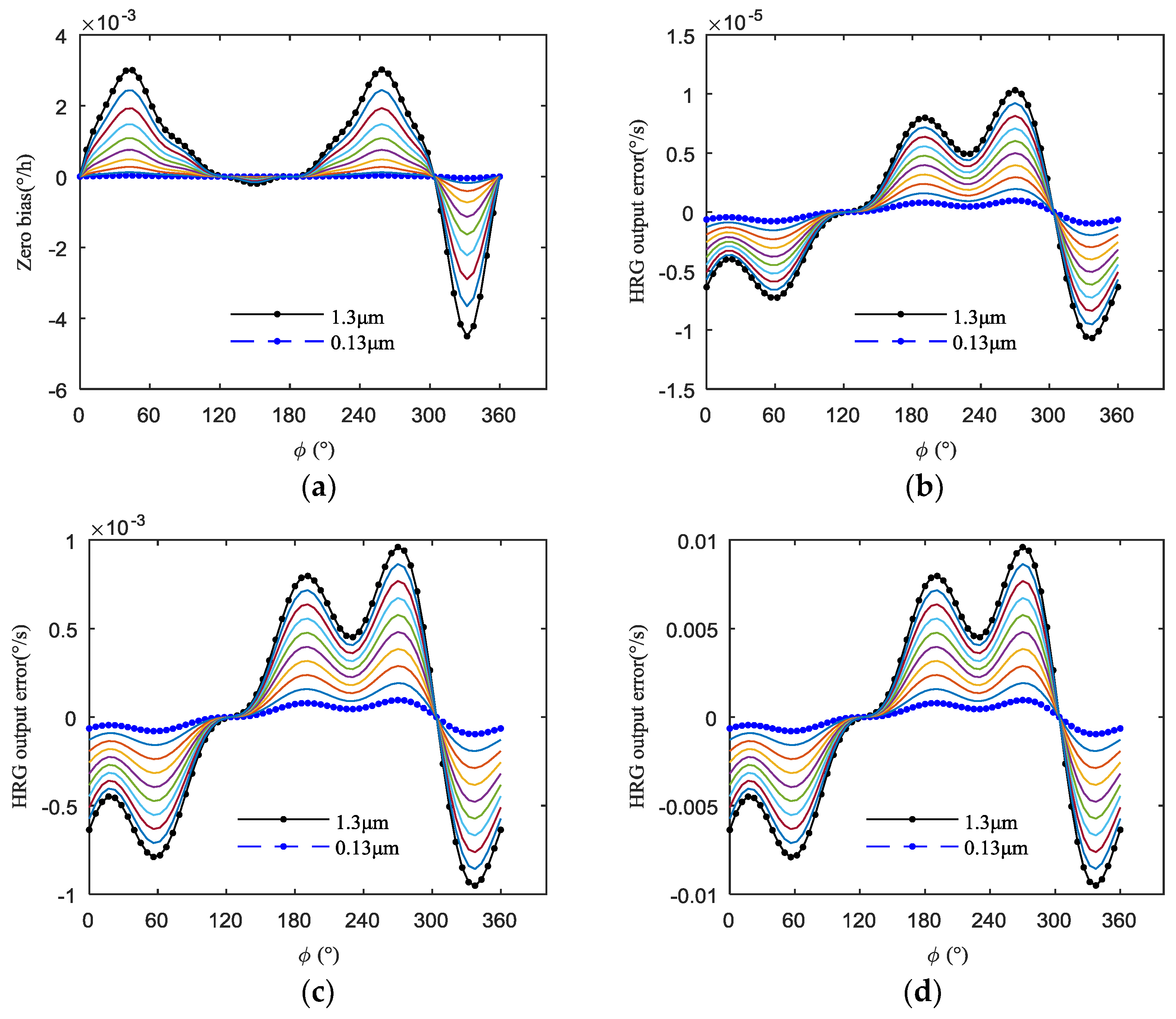
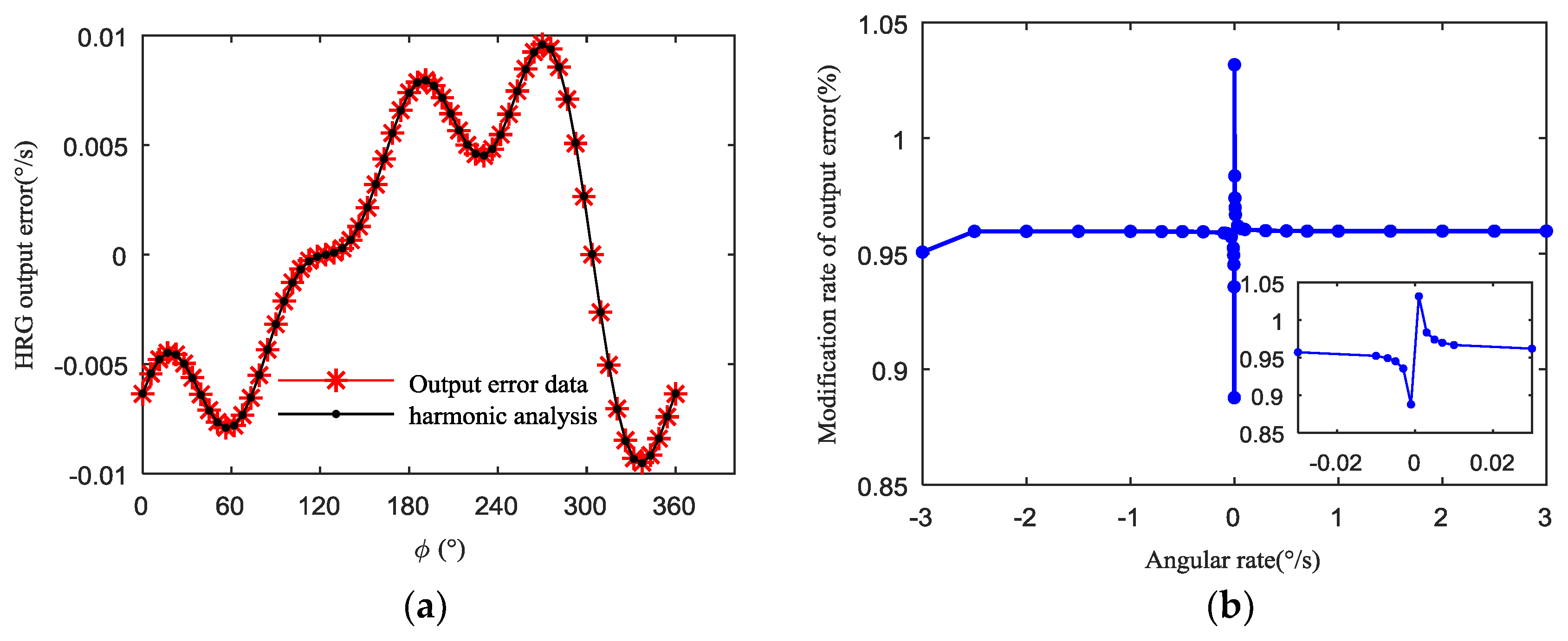
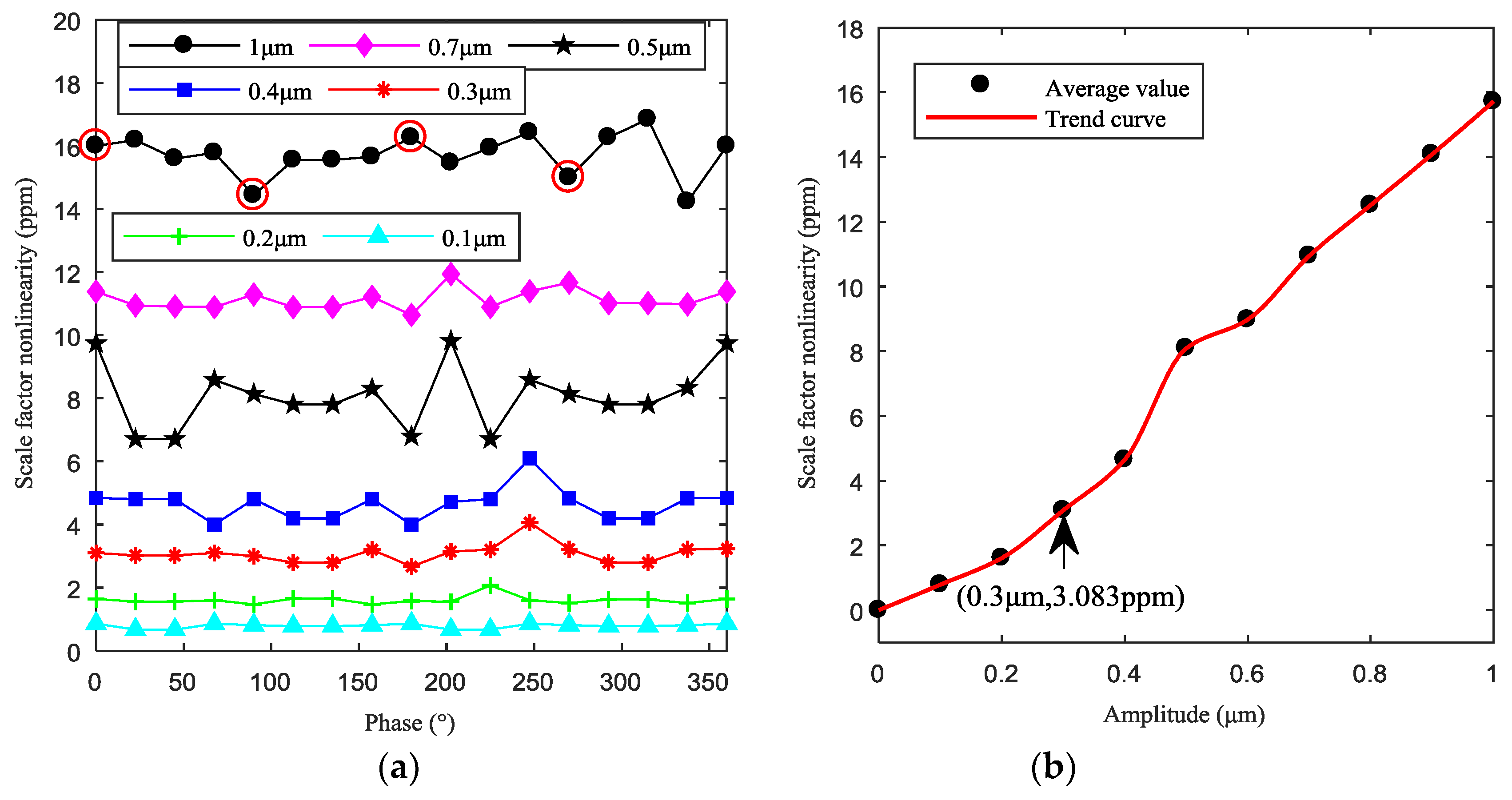
4.2. Effect of Uneven Electrostatic Forces
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brown, T.S. In-Flight Performance of the Cassini Hemispherical Quartz Resonator Gyro Inertial Reference Units. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Rozelle, D.M. The hemispherical resonator gyro: From wineglass to the planets. Adv. Astronaut. Sci. 2009, 134, 1157–1178. [Google Scholar]
- Delhaye, F. HRG by SAFRAN. In Proceedings of the 5th IEEE International Symposium on Inertial Sensors & System, Lake Como, Italy, 26–29 March 2018; pp. 149–152. [Google Scholar]
- Júnior, M.H.B.; Magalhães, A.L.; Bastos, A.M.; Sales, A.J.M.; Gouveia, D.X.; Kamshilin, A.A.; Ferreira, A.D.C.; Guimarães, G.D.F.; Sombra, A.S.B.; Menezes, J.W.M. Piezoelectric ceramic sensor (PZT) applied to electric current measurements. Microsyst. Technol. 2018. [Google Scholar] [CrossRef]
- Wang, X.; Wu, W.; Luo, B.; Fang, Z.; Li, Y.; Jiang, Q. Force to rebalance control of HRG and suppression of its errors on the basis of FPGA. Sensors 2011, 11, 11761–11773. [Google Scholar] [CrossRef]
- Minotti, P.; Dellea, S.; Mussi, G.; Bonfanti, A.; Facchinetti, S.; Tocchio, A.; Zega, V.; Comi, C.; Lacaita, A.L.; Langfelder, G. High scale-factor stability frequency-modulated MEMS gyroscopes: 3-axis sensor and integrated electronics design. IEEE Trans. Ind. Electron. 2018, 65, 5040–5050. [Google Scholar] [CrossRef]
- Weng, J.H.; Chieng, W.H.; Lai, J.M. Structural design and analysis of micromachined ring-type vibrating sensor of both yaw rate and linear acceleration. Sens. Actuators A Phys. 2005, 117, 230–240. [Google Scholar] [CrossRef]
- Kim, D.J.; M’Closkey, R.T. A systematic method for tuning the dynamics of electrostatically actuated vibratory gyros. IEEE Trans. Control Syst. Technol. 2006, 14, 69–81. [Google Scholar]
- Yang, M.Z.; Dai, C.L.; Hong, J.Y. Manufacture and characterization of high q-factor inductors based on cmos-mems techniques. Sensors 2011, 11, 9798–9806. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, D.Y.; Wang, Y.Y.; Liu, J.P.; Wu, S.Y.; Qu, T.L.; Yang, K.Y.; Luo, H. Monolithic cylindrical fused silica resonators with high Q factors. Sensors 2016, 16, 1185. [Google Scholar] [CrossRef]
- Lin, Z.; Fu, M.Y.; Deng, Z.H.; Liu, N.; Liu, H. Frequency split elimination method for a solid-state vibratory angular rate gyro with an imperfect axisymmetric-shell resonator. Sensors 2015, 15, 3204–3223. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.D.; Wu, Y.L.; Xi, X.; Zhang, Y.M.; Wu, X.Z. Analysis on node position of imperfect resonators for cylindrical shell gyroscopes. Sensors 2016, 16, 1206. [Google Scholar] [CrossRef]
- Ren, S.Q.; Li, W.; Zhao, H.B. The influence of alignment errors on the output accuracy of hemispherical resonator gyro. J. Vib. Measure. Diagnosis 2011, 31, 420–423, 532. [Google Scholar]
- Wu, H.; Yin, T.; Jiao, J.; Yang, H. Analysis of parasitic feed-through capacitance effect in closed-loop drive circuit design for capacitive micro-gyroscope. Microsyst. Technol. 2016, 22, 2201–2207. [Google Scholar] [CrossRef]
- Chouvion, B.; McWilliam, S.; Popov, A.A. Effect of nonlinear electrostatic forces on the dynamic behaviour of a capacitive ring-based Coriolis vibrating gyroscope under severe shock. Mecha. Syst. Signal Proc. 2018, 106, 395–412. [Google Scholar] [CrossRef]
- Sieberer, S. In-plane Shock Response of Capacitive MEMS Ring-Rate Sensors. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2014. [Google Scholar]
- Wang, R.X.; Bai, B.; Feng, H.Z.; Ren, Z.M.; Cao, H.L.; Xue, C.Y.; Zhang, B.Z.; Liu, J. Design and fabrication of micro hemispheric shell resonator with annular electrodes. Sensors 2016, 16, 1991. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.Y.; Yi, G.X.; Xie, Y.G.; Wei, Z.N.; Qi, Z.Y. Influence of external load on hemispherical resonator gyro feedback control system with state constraints. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 6217–6222. [Google Scholar]
- Sun, J.K.; Wu, Y.L.; Xi, X.; Zhang, Y.M.; Wu, X.Z. Analysis of the damping characteristics of cylindrical resonators influenced by piezoelectric electrodes. Sensors 2017, 17, 1017. [Google Scholar]
- Song, J.W.; Song, H.M.; Lee, Y.J.; Park, C.G.; Sung, S. Design of oscillation control loop with coarse-precision mode transition for solid-state resonant gyroscope. IEEE Sens. J. 2016, 16, 1730–1742. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Yi, G.X.; Xie, Y.G.; Wei, Z.N. Influence of acceleration on control system of hemispherical resonator gyro and its suppression method. J. Chin. Inert. Technol. 2018, 26, 63–68. [Google Scholar]
- Huang, J.M.; Liew, K.; Wong, C.; Rajendran, S.; Tan, M.; Liu, A. Mechanical design and optimization of capacitive micromachined switch. Sens. Actuators A Phys. 2001, 93, 273–285. [Google Scholar] [CrossRef]
- Liu, N.; Su, Z.; Li, Q.; Fu, M.Y.; Liu, H.; Fan, J.F. Characterization of the bell-shaped vibratory angular rate gyro. Sensors 2013, 13, 10123–10150. [Google Scholar] [CrossRef]
- Xi, X.; Wu, Y.L.; Wu, X.M.; Tao, Y.; Wu, X.Z. Modeling and analysis of the stress effects for trimmed cupped resonator under varying temperature. Sens. Actuators A Phys. 2013, 189, 429–440. [Google Scholar] [CrossRef]
- Zhbanov, Y.K.; Zhuravlev, V.P. Effect of movability of the resonator center on the operation of a hemispherical resonator gyro. Mecha. Solids 2007, 42, 851–859. [Google Scholar] [CrossRef]
- Kagawa, Y.; Tsuchiya, T.; Kawashima, T. Finite element simulation of piezoelectric vibrator gyroscopes. IEEE Trans. Ultrason. Ferroelect. Freq. Control 1996, 43, 509–518. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Yi, G.X.; Wei, Z.N.; Zhao, W.L. A dynamic modeling method for resonator of hemispherical resonator gyro. Acta Aeronua. Astronau. Sin. 2018, 39, 221624. [Google Scholar]
- Loveday, P.W.; Rogers, C.A. Modification of piezoelectric vibratory gyroscope resonator parameters by feedback control. IEEE Trans. Ultrason. Ferroelect. Freq. Control 1998, 45, 1211–1215. [Google Scholar] [CrossRef] [PubMed]
- Loveday, P.W.; Rogers, C.A. The influence of control system design on the performance of vibratory gyroscopes. J. Sound Vib. 2002, 255, 417–432. [Google Scholar] [CrossRef]
- Hu, Z.X.; Gallacher, B. A mode-matched force-rebalance control for a MEMS vibratory gyroscope. Sens. Actuators A Phys. 2018, 273, 1–11. [Google Scholar] [CrossRef]
- Li, Z.K.; Zhao, L.B.; Jiang, Z.D.; Ye, Z.Y.; Dai, L.; Zhao, Y.L. Mechanical behavior analysis on electrostatically actuated rectangular microplates. J. Micromech. Microeng. 2015, 25, 035007. [Google Scholar] [CrossRef]
- Ting, Y.; Huang, J.L.; Yang, C.M. Effect of polarized electric field on piezoelectric cylinder vibratory gyroscope. Sens. Actuators A Phys. 2006, 128, 248–256. [Google Scholar] [CrossRef]

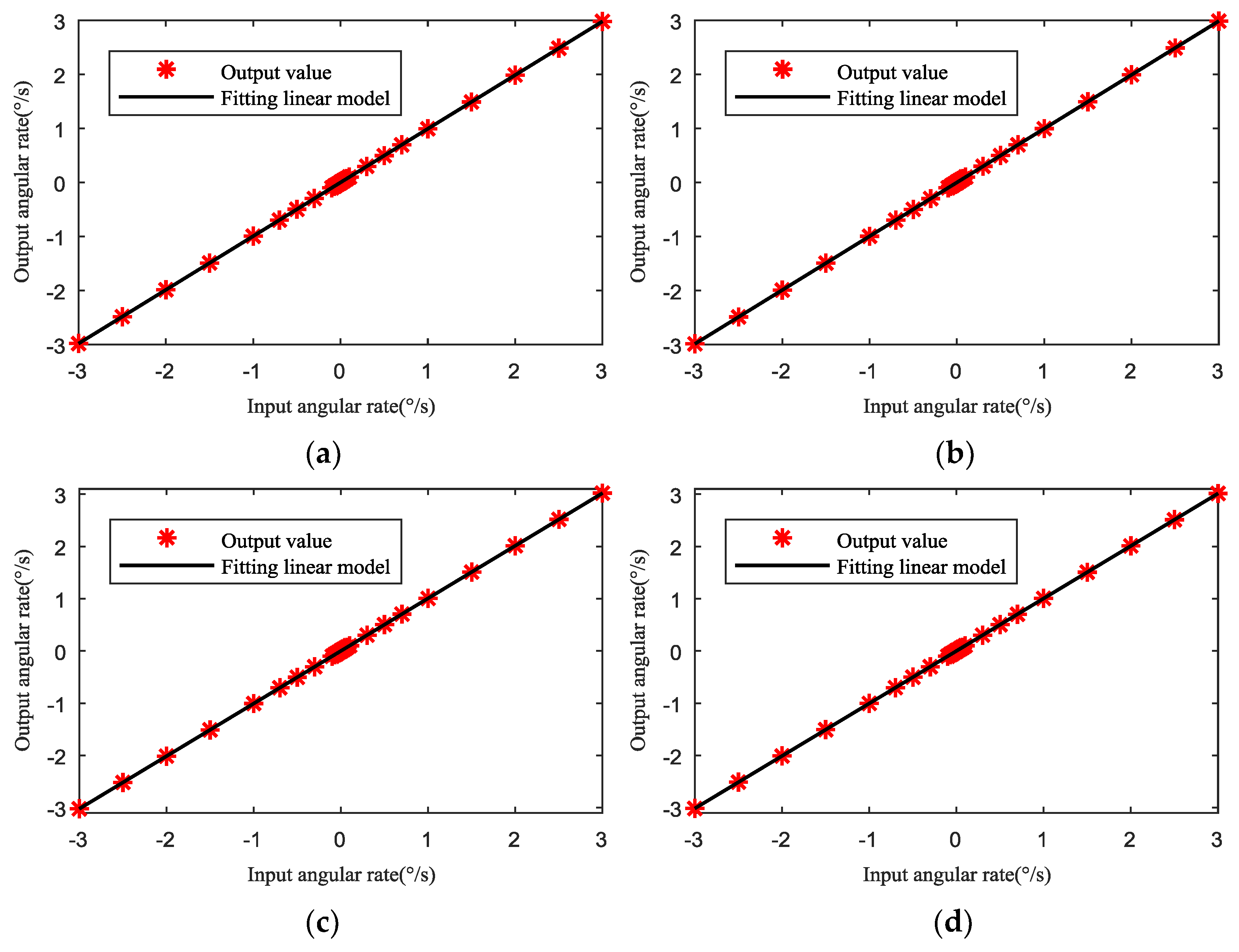
| Uneven Capacitance Gap | First Harmonic | Second Harmonic | Third Harmonic | Fourth Harmonic |
|---|---|---|---|---|
| Amplitude | 0.0078°/s | 0.0015°/s | 0.0021°/s | 0.0026°/s |
| Initial phase | 123.82° | 67.30° | 11.39° | 314.82° |
| Input Angular Rate (°/s) | Output Angular Rate (°/s) | Input Angular Rate (°/s) | Output Angular Rate (°/s) | Input Angular Rate (°/s) | Output Angular Rate (°/s) | Input Angular Rate (°/s) | Output Angular Rate (°/s) |
|---|---|---|---|---|---|---|---|
| −3 | −2.9808 | −0.07 | −0.0696 | 0.003 | 0.0030 | 0.5 | 0.4968 |
| −2.5 | −2.4840 | −0.05 | −0.0497 | 0.005 | 0.0050 | 0.7 | 0.6955 |
| −2 | −1.9872 | −0.03 | −0.0298 | 0.007 | 0.0070 | 1 | 0.9936 |
| −1.5 | −1.4904 | −0.01 | −0.0099 | 0.01 | 0.0099 | 1.5 | 1.4904 |
| −1 | −0.9936 | −0.007 | −0.0070 | 0.03 | 0.0298 | 2 | 1.9872 |
| −0.7 | −0.6955 | −0.005 | −0.0050 | 0.05 | 0.0497 | 2.5 | 2.4840 |
| −0.5 | −0.4968 | −0.003 | −0.0030 | 0.07 | 0.0696 | 3 | 2.9808 |
| −0.3 | −0.2981 | −0.001 | −0.0010 | 0.1 | 0.0994 | ||
| −0.1 | −0.0994 | 0.001 | 0.0010 | 0.3 | 0.2981 |
| First Harmonic | 1 μm–0° | 1 μm–90° | 1 μm–180° | 1 μm–270° |
|---|---|---|---|---|
| K1 | 0.9936 | 0.9957 | 1.0065 | 1.0043 |
| K2 | 0 | 2.7756 × 10−17 | 1.3878 × 10−17 | 2.7756 × 10−17 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Yi, G.; Er, M.J.; Huang, C. Effect of Uneven Electrostatic Forces on the Dynamic Characteristics of Capacitive Hemispherical Resonator Gyroscopes. Sensors 2019, 19, 1291. https://doi.org/10.3390/s19061291
Xu Z, Yi G, Er MJ, Huang C. Effect of Uneven Electrostatic Forces on the Dynamic Characteristics of Capacitive Hemispherical Resonator Gyroscopes. Sensors. 2019; 19(6):1291. https://doi.org/10.3390/s19061291
Chicago/Turabian StyleXu, Zeyuan, Guoxing Yi, Meng Joo Er, and Chao Huang. 2019. "Effect of Uneven Electrostatic Forces on the Dynamic Characteristics of Capacitive Hemispherical Resonator Gyroscopes" Sensors 19, no. 6: 1291. https://doi.org/10.3390/s19061291
APA StyleXu, Z., Yi, G., Er, M. J., & Huang, C. (2019). Effect of Uneven Electrostatic Forces on the Dynamic Characteristics of Capacitive Hemispherical Resonator Gyroscopes. Sensors, 19(6), 1291. https://doi.org/10.3390/s19061291





