A Novel Approach for 3D-Structural Identification through Video Recording: Magnified Tracking †
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodology
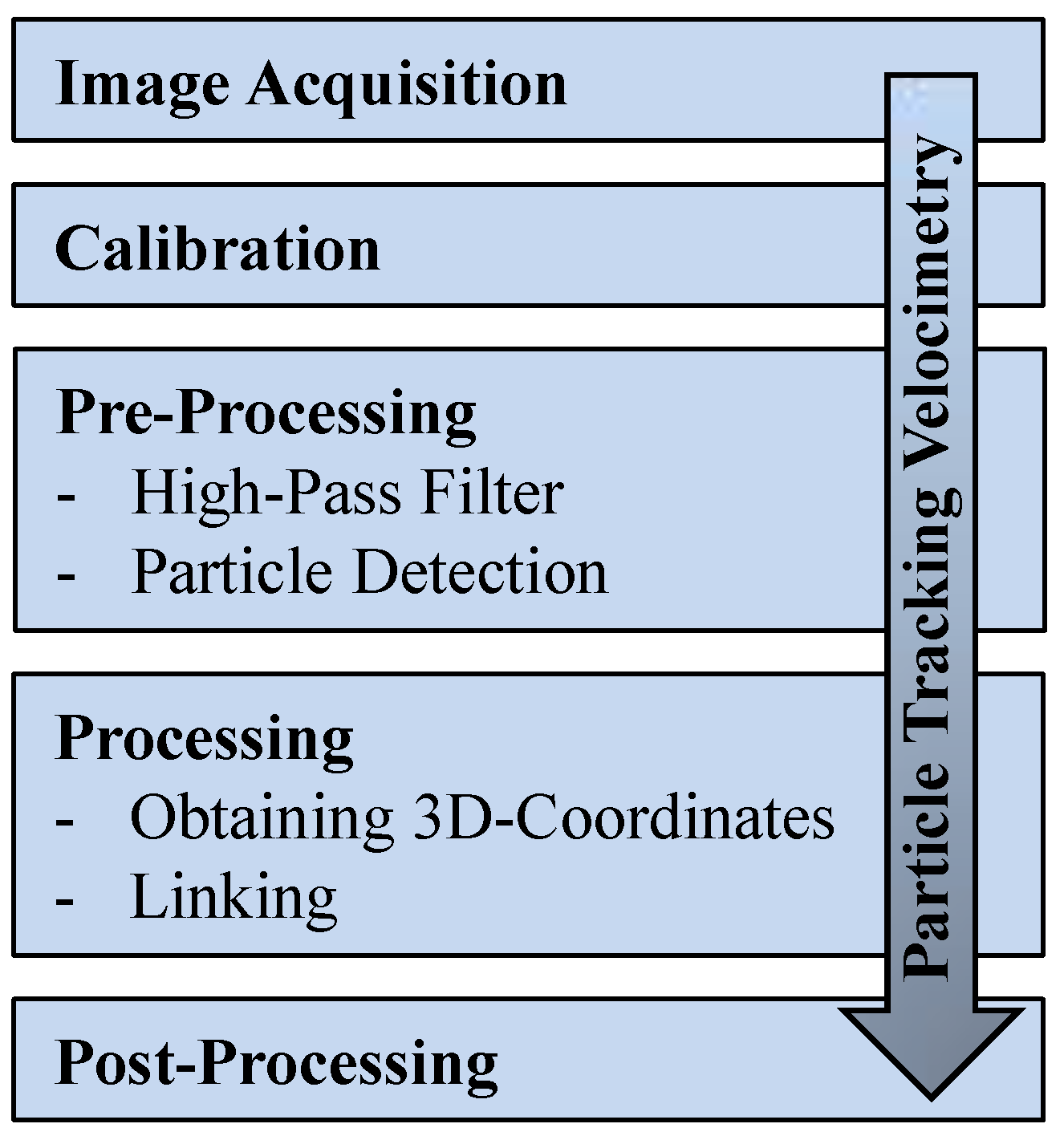
2.1.1. Particle Tracking Velocimetry
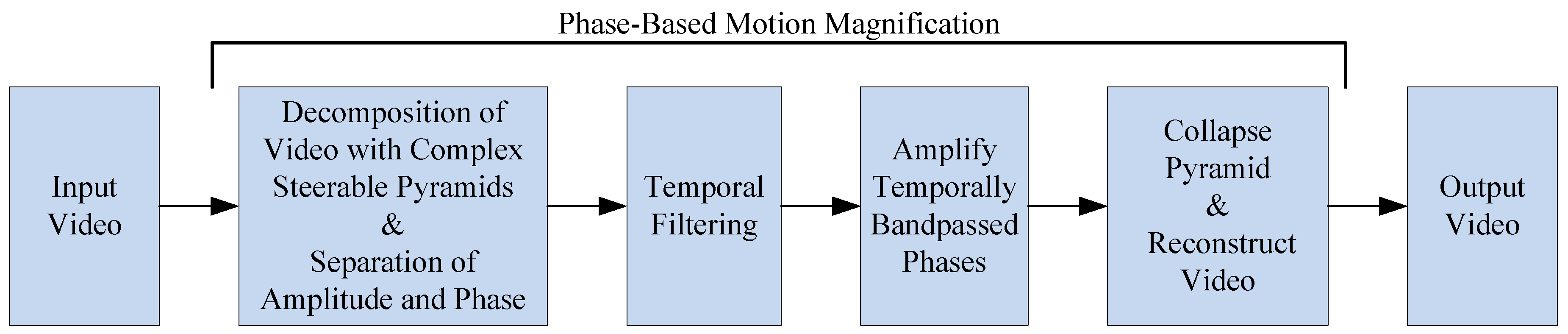
2.1.2. Phase-Based Motion Magnification
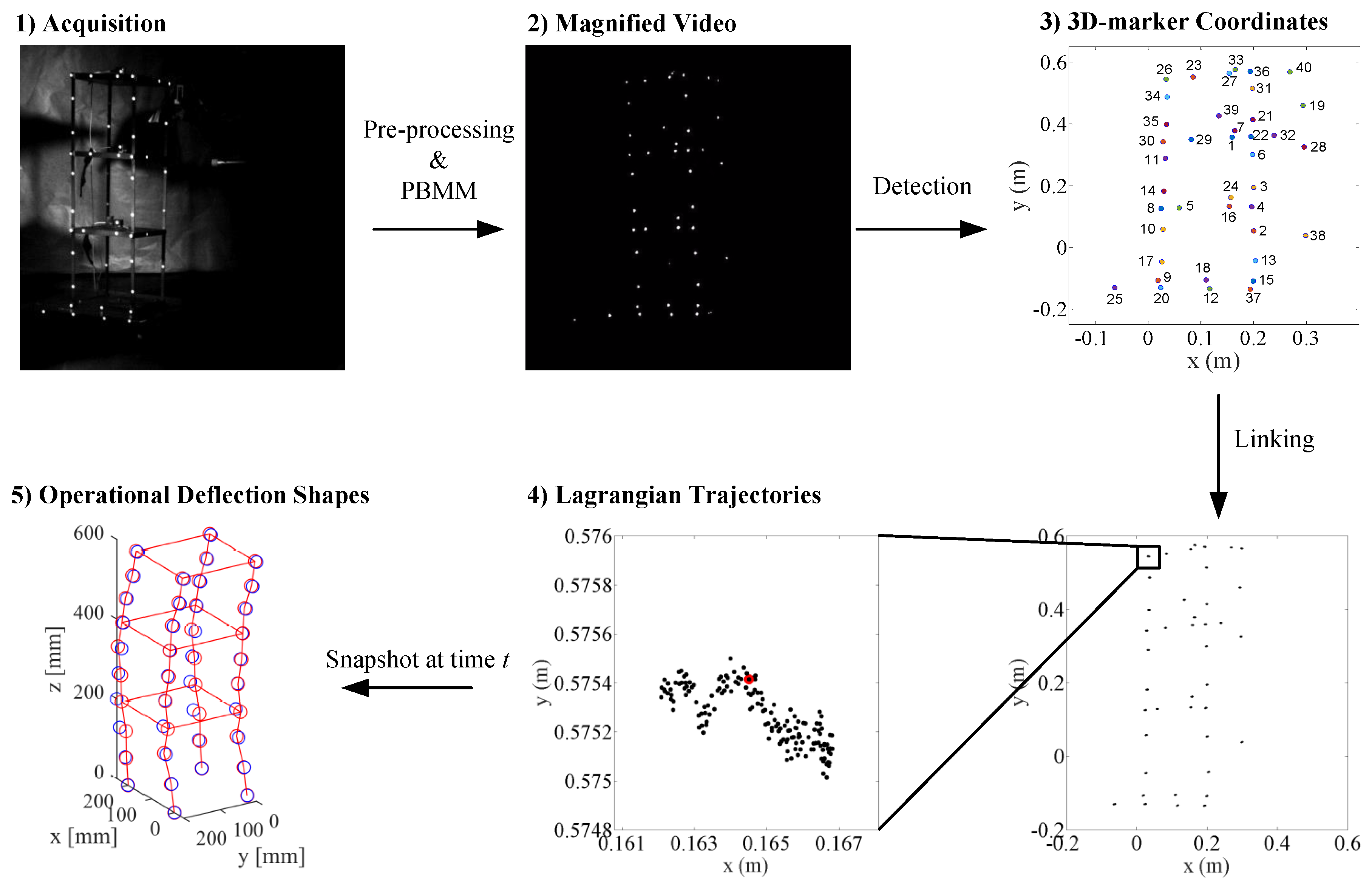
2.1.3. Magnified Tracking
2.2. Experimental Investigation
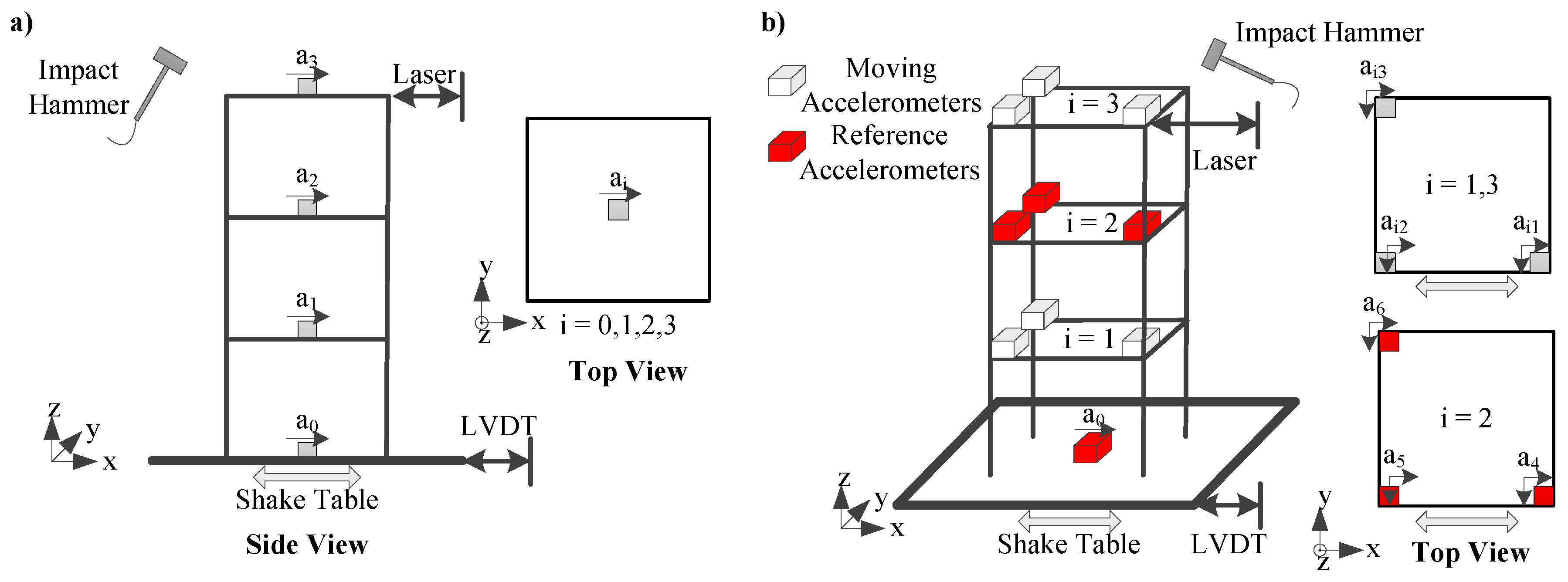
2.2.1. 2D Experimental Setup
2.2.2. 3D Experimental Setup
2.3. Numerical Modelling
3. Results and Discussion
3.1. 2D-PTV
3.2. 3D-PTV
3.3. Magnified Tracking
4. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DIC | Digital Image Correlation |
| MT | Magnified Tracking |
| PTV | Particle Tracking Velocimetry |
| PBMM | Phase-Based Motion Magnification |
| SSI | Stochastic Subspace Identification |
| ERA | Eigensystem Realization Algorithm |
References
- Sirca, G., Jr.; Adeli, H. System Identification in Structural Engineering. Sci. Iran. 2012, 19, 1355–1364. [Google Scholar] [CrossRef]
- Fuggini, C.; Chatzi, E.; Zangani, D. Combining Genetic Algorithms with a Meso-Scale Approach for System Identification of a Smart Polymeric Textile. Comput.-Aided Civ. Infrastruct. Eng. 2013, 28, 227–245. [Google Scholar] [CrossRef]
- Lozano-Galant, J.A.; Nogal, M.; Castillo, E.; Turmo, J. Application of Observability Techniques to Structural System Identification. Comput.-Aided Civ. Infrastruct. Eng. 2013, 28, 434–450. [Google Scholar] [CrossRef]
- Beck, J.L.; Au, S.K.; Vanik, M.W. Monitoring Structural Health using a Probabilistic Measure. Comput.-Aided Civ. Infrastruct. Eng. 2001, 16, 1–11. [Google Scholar] [CrossRef]
- Qarib, H.; Adeli, H. Recent Advances in Health Monitoring of Civil Structures. Sci. Iran. 2014, 21, 1733–1742. [Google Scholar]
- Lynch, J.P.; Farrar, C.R.; Michaels, J.E. Structural Health Monitoring: Technological Advances to Practical Implementations [Scanning the Issue]. Proc. IEEE 2016, 104, 1508–1512. [Google Scholar] [CrossRef]
- Cho, C.; Yi, X.; Li, D.; Wang, Y.; Tentzeris, M.M. Passive wireless frequency doubling antenna sensor for strain and crack sensing. IEEE Sens. J. 2016, 16, 5725–5733. [Google Scholar] [CrossRef]
- Klis, R.; Chatzi, E.N. Data recovery via hybrid sensor networks for vibration monitoring of civil structures. Int. J. Sustain. Mater. Struct. Syst. 2015, 2, 161–184. [Google Scholar] [CrossRef]
- Klis, R.; Chatzi, E.N. Vibration monitoring via spectro-temporal compressive sensing for wireless sensor networks. Struct. Infrastruct. Eng. 2017, 13, 195–209. [Google Scholar] [CrossRef]
- Lynch, J.P.; Loh, K.J. A Summary Review of Wireless Sensors and Sensor Networks for Structural Health Monitoring. Shock. Vib. Dig. 2006, 38, 91–130. [Google Scholar] [CrossRef]
- Wahbeh, A.M.; Caffrey, J.P.; Masri, S.F. A Vision-based Approach for the Direct Measurement of Displacements in Vibrating Systems. Smart Mater. Struct. 2003, 12, 785. [Google Scholar] [CrossRef]
- Yeum, C.M.; Dyke, S.J. Vision-based automated crack detection for bridge inspection. Comput.-Aided Civ. Infrastruct. Eng. 2015, 30, 759–770. [Google Scholar] [CrossRef]
- Nishikawa, T.; Yoshida, J.; Sugiyama, T.; Fujino, Y. Concrete crack detection by multiple sequential image filtering. Comput.-Aided Civ. Infrastruct. Eng. 2012, 27, 29–47. [Google Scholar] [CrossRef]
- Cha, Y.J.; Choi, W.; Suh, G.; Mahmoudkhani, S.; Büyüköztürk, O. Autonomous structural visual inspection using region-based deep learning for detecting multiple damage types. Comput.-Aided Civ. Infrastruct. Eng. 2017, 33, 731–747. [Google Scholar] [CrossRef]
- Ribeiro, D.; Calçada, R.; Ferreira, J.; Martins, T. Non-contact measurement of the dynamic displacement of railway bridges using an advanced video-based system. Eng. Struct. 2014, 75, 164–180. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J. Non-contact vibration measurement of cables in a cable-stayed bridge by consumer-grade camera. In Proceedings of the 4th Conference on Smart Monitoring, Assessment and Rehabilitation of Civil Structures (SMAR 2017), Zurich, Switzerland, 27–29 August 2017. [Google Scholar]
- Khuc, T.; Catbas, F.N. Computer vision-based displacement and vibration monitoring without using physical target on structures. Struct. Infrastruct. Eng. 2017, 13, 505–516. [Google Scholar] [CrossRef]
- Yoon, H.; Elanwar, H.; Choi, H.; Golparvar-Fard, M.; Spencer, B.F. Target-free approach for vision-based structural system identification using consumer-grade cameras. Struct. Control. Health Monit. 2016, 23, 1405–1416. [Google Scholar] [CrossRef]
- Harmanci, Y.E.; Lai, Z.; Gülan, U.; Holzner, M.; Chatzi, E. Computer Vision Aided Structural Identification: Feature Tracking Using Particle Tracking Velocimetry versus Optical Flow. In Proceedings of the 5th International Electronic Conference on Sensors and Applications, e-conference. 15–30 November 2018. [Google Scholar] [CrossRef]
- Wadhwa, N.; Rubinstein, M.; Durand, F.; Freeman, W.T. Phase-based video motion processing. ACM Trans. Graph. 2013, 32, 80. [Google Scholar] [CrossRef]
- Chen, J.G.; Wadhwa, N.; Cha, Y.J.; Durand, F.; Freeman, W.T.; Buyukozturk, O. Modal identification of simple structures with high-speed video using motion magnification. J. Sound Vib. 2015, 345, 58–71. [Google Scholar] [CrossRef]
- Cha, Y.J.; Chen, J.; Büyüköztürk, O. Output-only computer vision based damage detection using phase-based optical flow and unscented Kalman filters. Eng. Struct. 2017, 132, 300–313. [Google Scholar] [CrossRef]
- Yang, Y.; Dorn, C.; Mancini, T.; Talken, Z.; Kenyon, G.; Farrar, C.; Mascareñas, D. Blind identification of full-field vibration modes from video measurements with phase-based video motion magnification. Mech. Syst. Signal Process. 2017, 85, 567–590. [Google Scholar] [CrossRef]
- Yang, Y.; Dorn, C.; Mancini, T.; Talken, Z.; Nagarajaiah, S.; Kenyon, G.; Farrar, C.; Mascareñas, D. Blind identification of full-field vibration modes of output-only structures from uniformly-sampled, possibly temporally-aliased (sub-Nyquist), video measurements. J. Sound Vib. 2017, 390, 232–256. [Google Scholar] [CrossRef]
- Dasari, S.; Dorn, C.; Yang, Y.; Larson, A.; Mascareñas, D. A framework for the identification of full-field structural dynamics using sequences of images in the presence of non-ideal operating conditions. J. Intell. Mater. Syst. Struct. 2018, 29, 3456–3481. [Google Scholar] [CrossRef]
- Yang, Y.; Dorn, C.; Mancini, T.; Talken, Z.; Theiler, J.; Kenyon, G.; Farrar, C.; Mascareñas, D. Reference-free detection of minute, non-visible, damage using full-field, high-resolution mode shapes output-only identified from digital videos of structures. Struct. Health Monit. 2017, 17, 514–531. [Google Scholar] [CrossRef]
- Sarrafi, A.; Mao, Z.; Niezrecki, C.; Poozesh, P. Vibration-based damage detection in wind turbine blades using Phase-based Motion Estimation and motion magnification. J. Sound Vib. 2018, 421, 300–318. [Google Scholar] [CrossRef]
- Shang, Z.; Shen, Z. Multi-point vibration measurement and mode magnification of civil structures using video-based motion processing. Autom. Constr. 2018, 93, 231–240. [Google Scholar] [CrossRef]
- Fioriti, V.; Roselli, I.; Tati, A.; Romano, R.; De Canio, G. Motion Magnification Analysis for structural monitoring of ancient constructions. Measurement 2018, 129, 375–380. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J.M. Review of machine-vision based methodologies for displacement measurement in civil structures. J. Civ. Struct. Health Monit. 2017, 8, 91–110. [Google Scholar] [CrossRef]
- Park, S.; Park, H.; Kim, J.; Adeli, H. 3D Displacement Measurement Model for Health Monitoring of Structures using a Motion Capture System. Measurement 2015, 59, 352–362. [Google Scholar] [CrossRef]
- Baqersad, J.; Carr, J.; Lundstrom, T.; Niezrecki, C.; Avitabile, P.; Slattery, M. Dynamic Characteristics of a Wind Turbine Blade using 3D Digital Image Correlation. Proc. SPIE 2012, 8348, 83482I. [Google Scholar] [CrossRef]
- Patil, K.; Srivastava, V.; Baqersad, J. A multi-view optical technique to obtain mode shapes of structures. Measurement 2018, 122, 358–367. [Google Scholar] [CrossRef]
- Wang, W.; Mottershead, J.E.; Siebert, T.; Pipino, A. Frequency Response Functions of Shape Features from Full-Field Vibration Measurements using Digital Image Correlation. Mech. Syst. Signal Process. 2012, 28, 333–347. [Google Scholar] [CrossRef]
- Chesebrough, B.; Dasari, S.; Green, A.; Yang, Y.; Farrar, C.R.; Mascareñas, D. Light Field Imaging of Three-Dimensional Structural Dynamics. In Structural Health Monitoring, Photogrammetry & DIC; Springer: Berlin/Heidelberg, Germany, 2019; Volume 6, pp. 101–108. [Google Scholar]
- Molina-Viedma, A.; Felipe-Sesé, L.; López-Alba, E.; Díaz, F. 3D mode shapes characterisation using phase-based motion magnification in large structures using stereoscopic DIC. Mech. Syst. Signal Process. 2018, 108, 140–155. [Google Scholar] [CrossRef]
- Poozesh, P.; Sarrafi, A.; Mao, Z.; Avitabile, P.; Niezrecki, C. Feasibility of extracting operating shapes using phase-based motion magnification technique and stereo-photogrammetry. J. Sound Vib. 2017, 407, 350–366. [Google Scholar] [CrossRef]
- Zimmermann, M.; Gülan, U.; Harmanci, Y.E.; Chatzi, E.N.; Holzner, M. Structural Health Monitoring through Video Recording. In Proceedings of the 8th European Workshop On Structural Health Monitoring (EWSHM 2016), Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- Harmanci, Y.E.; Gülan, U.; Zimmermann, M.; Holzner, M.; Chatzi, E. High spatial density vibrational measurements via 3D-particle tracking velocimetry. In Proceedings of the 4th Conference on Smart Monitoring, Assessment and Rehabilitation of Civil Structures (SMAR 2017), Zurich, Switzerland, 27–29 August 2017. [Google Scholar]
- Harmanci, Y.E.; Gülan, U.; Holzner, M.; Chatzi, E. A comparative study on 2D and 3D tracking of vibration via motion magnified high-speed videos. In Proceedings of the 7th World Conference on Structural Control and Monitoring (7WCSCM), Qingdao, China, 22–25 July 2018. [Google Scholar]
- Maas, H.; Gruen, A.; Papantoniou, D. Particle tracking velocimetry in three-dimensional flows. Exp. Fluids 1993, 15, 133–146. [Google Scholar] [CrossRef]
- Holzner, M.; Liberzon, A.; Nikitin, N.; Luthi, B.; Kinzelbach, W.; Tsinober, A. A Lagrangian investigation of the small-scale features of turbulent entrainment through particle tracking and direct numerical simulation. J. Fluid Mech. 2008, 598, 465–475. [Google Scholar] [CrossRef]
- Gülan, U.; Lüthi, B.; Holzner, M.; Liberzon, A.; Tsinober, A.; Kinzelbach, W. An in vitro investigation of the influence of stenosis severity on the flow in the ascending aorta. Med. Eng. Phys. 2014, 36, 1147–1155. [Google Scholar] [CrossRef] [PubMed]
- Gülan, U.; Binter, C.; Kozerke, S.; Holzner, M. Shear-scaling-based approach for irreversible energy loss estimation in stenotic aortic flow: An in vitro study. J. Biomech. 2017, 56, 89–96. [Google Scholar] [CrossRef] [PubMed]
- Gülan, U.; Saguner, A.; Akdis, D.; Gotschy, A.; Manka, R.; Brunckhorst, C.; Holzner, M.; Duru, F. Investigation of Atrial Vortices Using a Novel Right Heart Model and Possible Implications for Atrial Thrombus Formation. Sci. Rep. 2017, 7, 16772. [Google Scholar] [CrossRef] [PubMed]
- Lundström, T.S.; Brynjell-Rahkola, M.; Ljung, A.L.; Hellström, J.G.I.; Green, T.M. Evaluation of Guiding Device for Downstream Fish Migration with in-Field Particle Tracking Velocimetry and CFD. J. Appl. Fluid Mech. 2015, 8, 579–589. [Google Scholar] [CrossRef]
- Cavagna, A.; Giardina, I. Bird Flocks as Condensed Matter. Annu. Rev. Condens. Matter Phys. 2014, 5, 183–207. [Google Scholar] [CrossRef]
- Ma, B.; Ruwet, V.; Corieri, P.; Theunissen, R.; Riethmuller, M.; Darquenne, C. CFD simulation and experimental validation of fluid flow and particle transport in a model of alveolated airways. J. Aerosol Sci. 2009, 40, 403–414. [Google Scholar] [CrossRef] [PubMed]
- Gallo, D.; Gülan, U.; Stefano, A.D.; Ponzini, R.; Lüthi, B.; Holzner, M.; Morbiducci, U. Analysis of thoracic aorta hemodynamics using 3D particle tracking velocimetry and computational fluid dynamics. J. Biomech. 2014, 47, 3149–3155. [Google Scholar] [CrossRef] [PubMed]
- Knobloch, V.; Binter, C.; Gülan, U.; Sigfridsson, A.; Holzner, M.; Lüthi, B.; Kozerke, S. Mapping mean and fluctuating velocities by Bayesian multipoint MR velocity encoding-validation against 3D particle tracking velocimetry. Magn. Reson. Med. 2014, 71, 1405–1415. [Google Scholar] [CrossRef] [PubMed]
- Virant, M.; Dracos, T. 3D PTV and its application on Lagrangian motion. Meas. Sci. Technol. 1997, 8, 1539. [Google Scholar] [CrossRef]
- Gülan, U.; Lüthi, B.; Holzner, M.; Liberzon, A.; Tsinober, A.; Kinzelbach, W. Experimental study of aortic flow in the ascending aorta via Particle Tracking Velocimetry. Exp. Fluids 2012, 53, 1469–1485. [Google Scholar] [CrossRef]
- Willneff, J.; Gruen, A. A new spatio-temporal matching algorithm for 3D-particle tracking velocimetry. In Proceedings of the 9th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, USA, 10–14 February 2002. [Google Scholar]
- Lüthi, B.; Tsinober, A.; Kinzelbach, W. Lagrangian measurement of vorticity dynamics in turbulent flow. J. Fluid Mech. 2005, 528, 87–118. [Google Scholar] [CrossRef]
- Wadhwa, N.; Chen, J.G.; Sellon, J.B.; Wei, D.; Rubinstein, M.; Ghaffari, R.; Freeman, D.M.; Büyüköztürk, O.; Wang, P.; Sun, S.; et al. Motion microscopy for visualizing and quantifying small motions. Proc. Natl. Acad. Sci. USA 2017, 114, 11639–11644. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, M. Analysis and Visualization of Temporal Variations in Video. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2014. [Google Scholar]
- Chen, J.G.; Davis, A.; Wadhwa, N.; Durand, F.; Freeman, W.T.; Büyüköztürk, O. Video camera–based vibration measurement for civil infrastructure applications. J. Infrastruct. Syst. 2016, 23, B4016013. [Google Scholar] [CrossRef]
- Hoyer, K.; Holzner, M.; Lüthi, B.; Guala, M.; Liberzon, A.; Kinzelbach, W. 3D scanning particle tracking velocimetry. Exp. Fluids 2005, 39, 923. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. Reference-based stochastic subspace identification for output-only modal analysis. Mech. Syst. Signal Process. 1999, 13, 855–878. [Google Scholar] [CrossRef]
- Reynders, E.; De Roeck, G. Reference-based combined deterministic–stochastic subspace identification for experimental and operational modal analysis. Mech. Syst. Signal Process. 2008, 22, 617–637. [Google Scholar] [CrossRef]
- CSI. SAP2000 Integrated Software for Structural Analysis and Design; Computers and Structures Inc.: Berkeley, CA, USA, 2000. [Google Scholar]
- Akutina, Y.; Mydlarski, L.; Gaskin, S.; Eiff, O. Error analysis of 3D-PTV through unsteady interfaces. Exp. Fluids 2018, 59, 53. [Google Scholar] [CrossRef]
- Reynders, E.; Schevenels, M.; De Roeck, G. MACEC 3.2: A Matlab Toolbox for Experimental and Operational Modal Analysis; Leuven University: Leuven, Belgium, 2011. [Google Scholar]

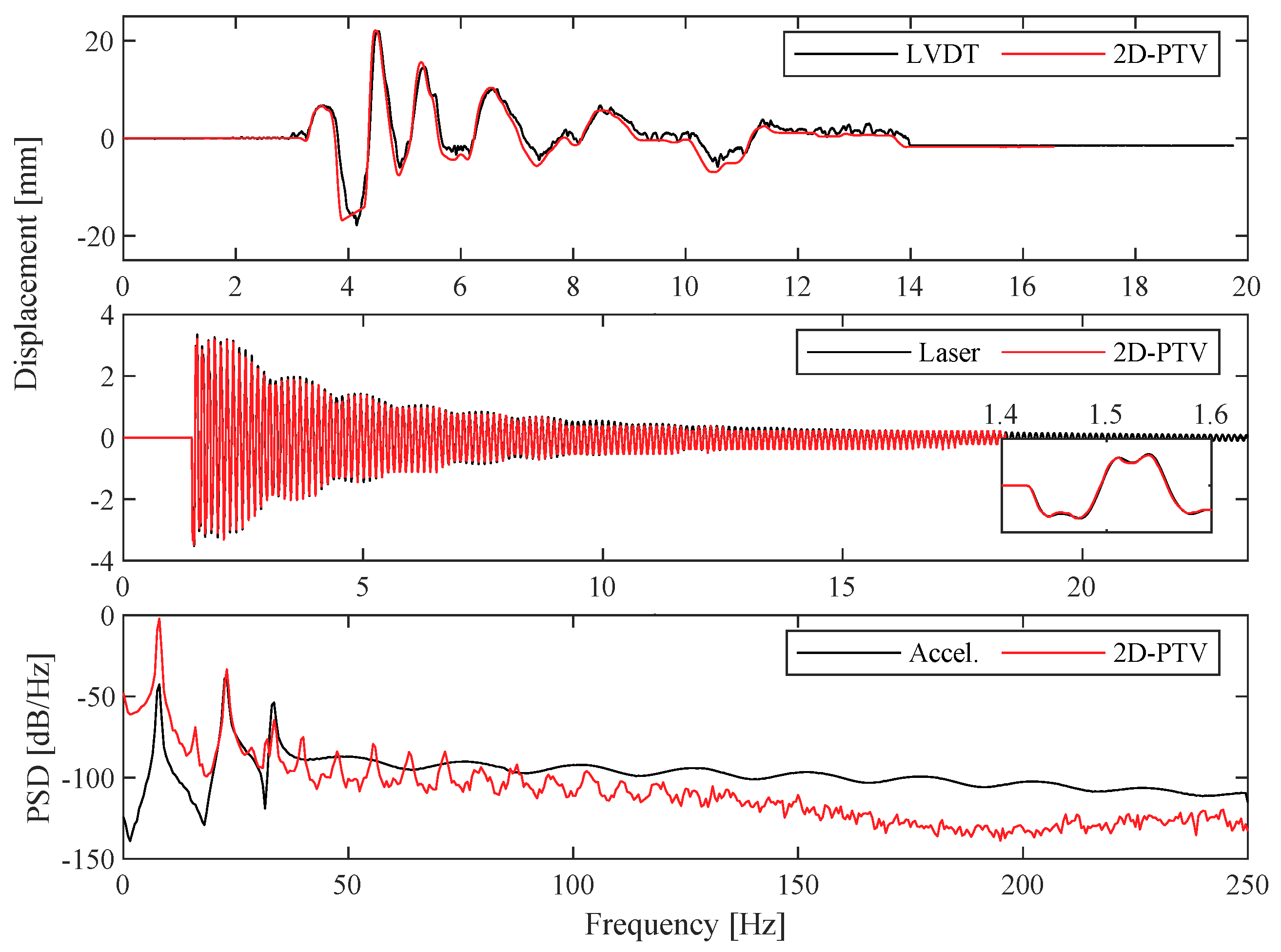
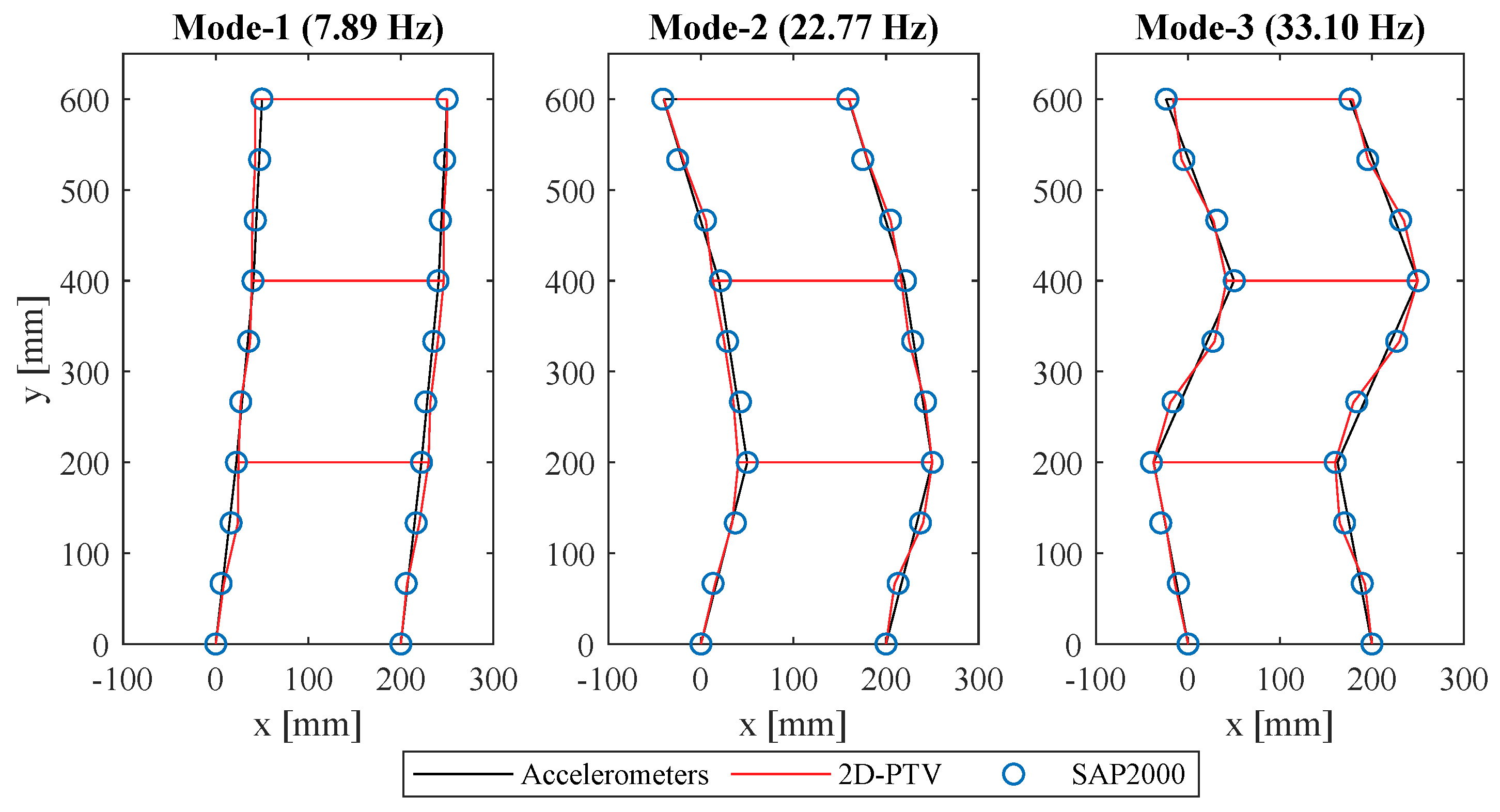
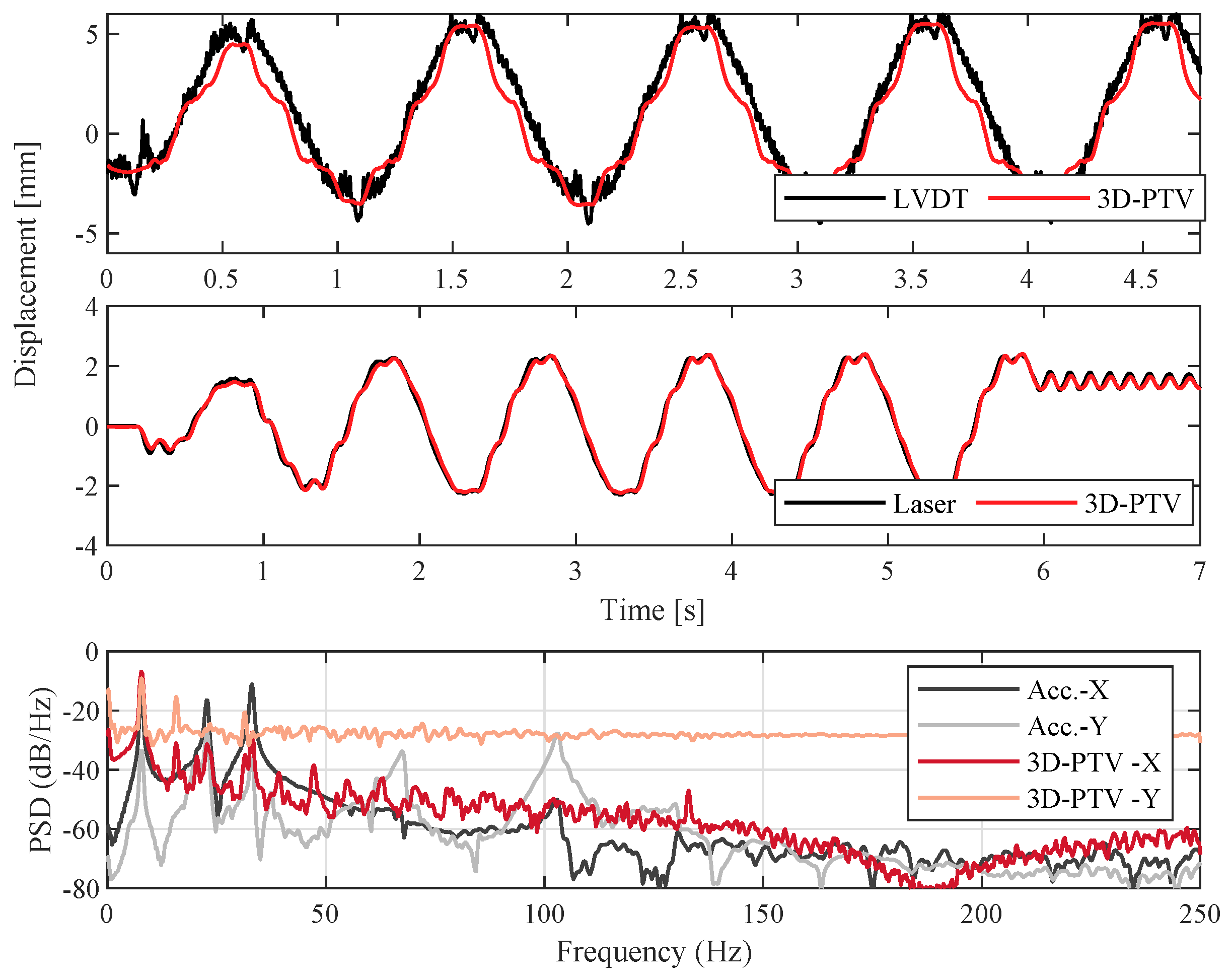
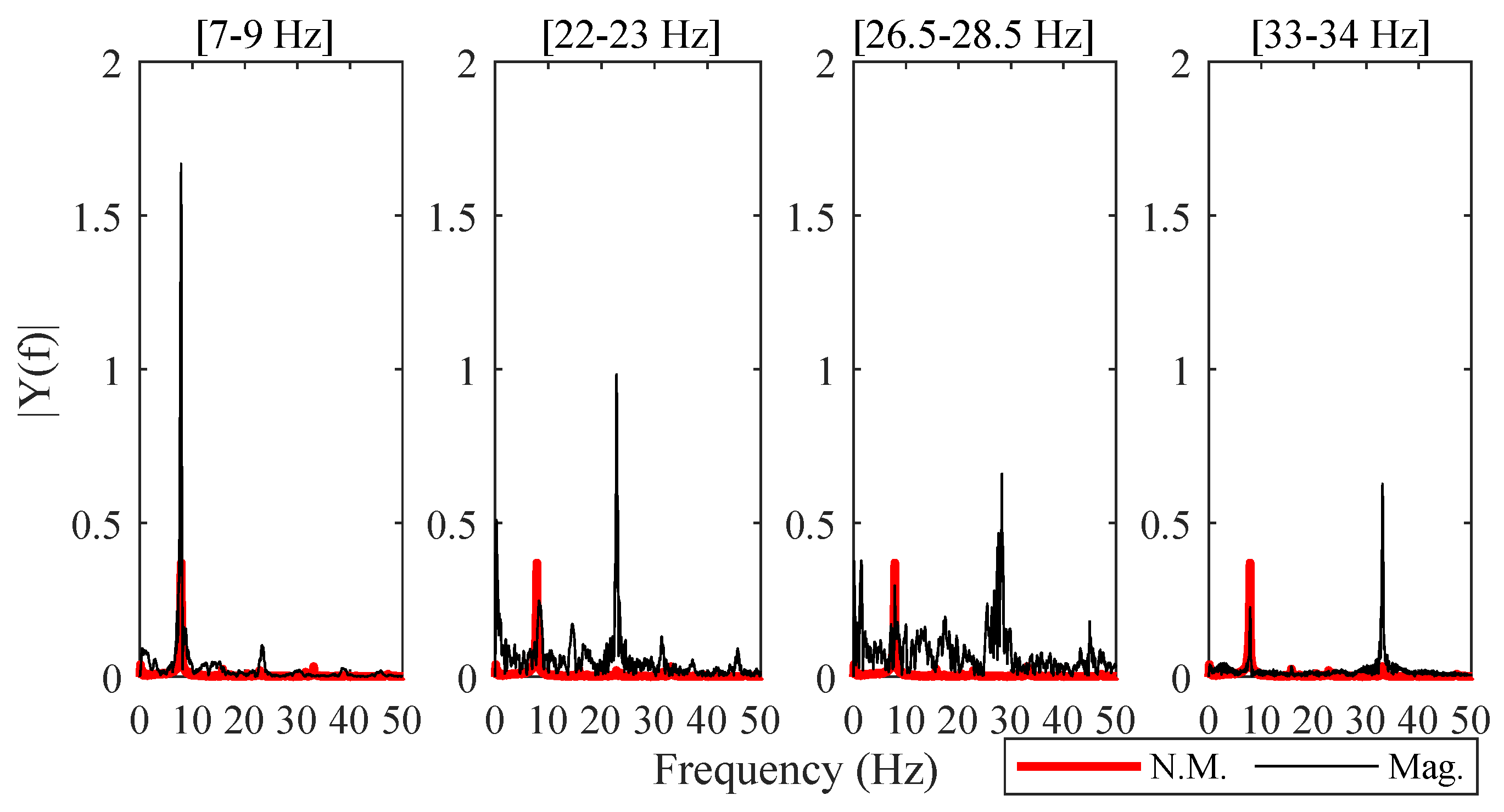
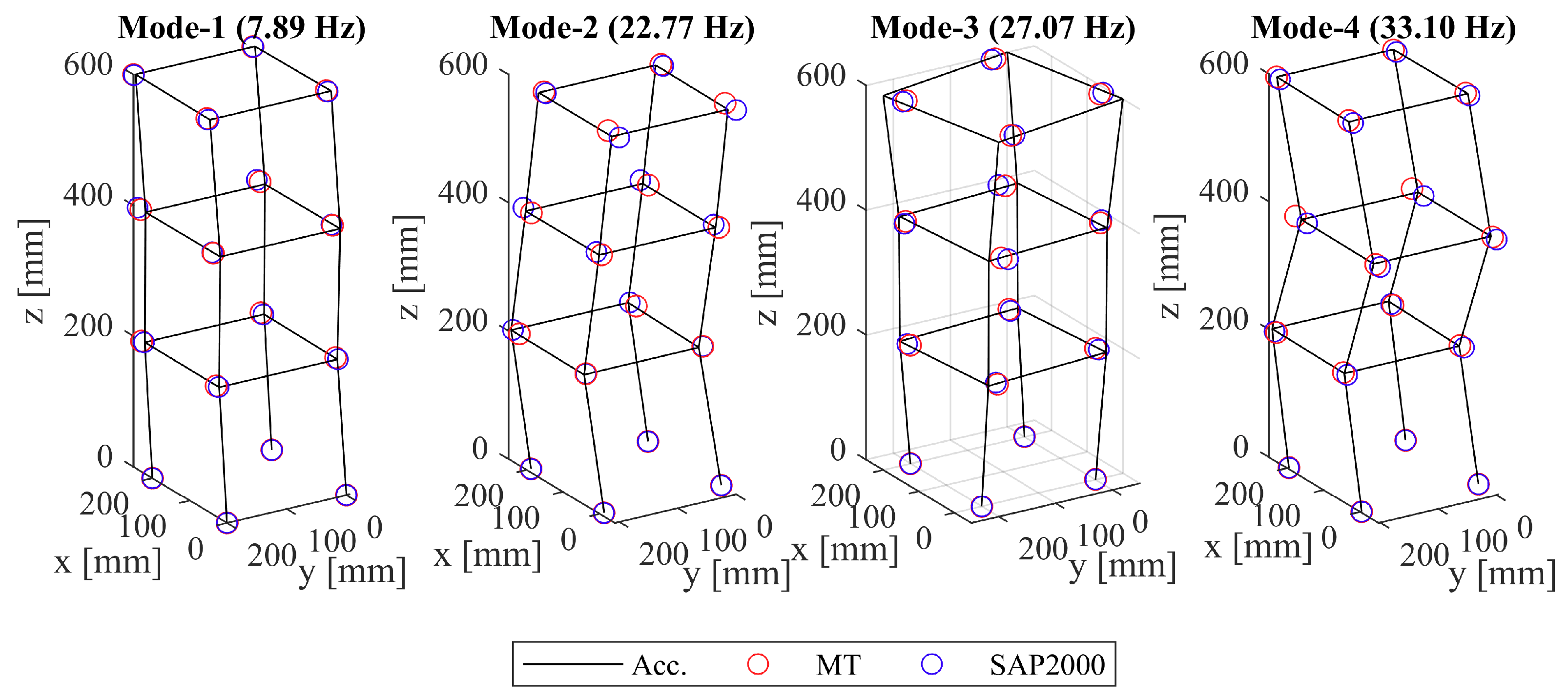
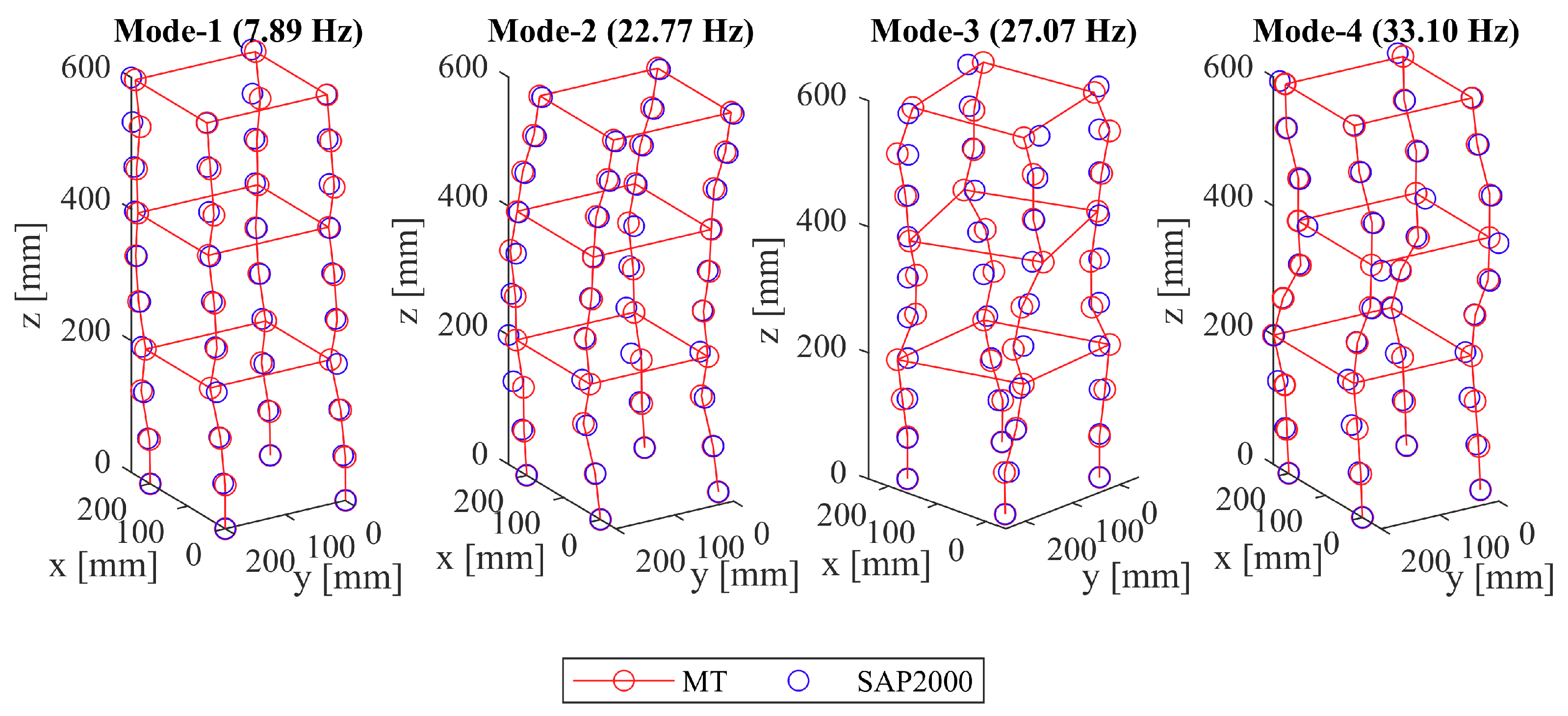
| Experiment No | Excitation | Dimension | Measurement Technique | Reference Technique |
|---|---|---|---|---|
| 1 | Northridge | 2D | 2D-PTV | Linear variable differential transformer (LVDT) |
| 2 | Hammer | 2D | 2D-PTV | Laser |
| 3 | Hammer | 2D | 2D-PTV | Accelerometers |
| 4 | Sinusoidal | 3D | 3D-PTV | Laser & LVDT |
| 5 | Hammer | 3D | 3D-PTV | Accelerometers |
| 6 | Hammer | 3D | 3D-MT | Accelerometers |
| Identified Frequencies [Hz] | ||||
|---|---|---|---|---|
| Acc. | 7.89 | 22.77 | 27.07 | 33.10 |
| 2D-PTV | 7.90 | 22.90 | - | 33.31 |
| 3D Magnified tracking (MT) | 7.86 | 22.90 | 27.15 | 33.01 |
| 2D-PTV | 3D-MT | ||||||
|---|---|---|---|---|---|---|---|
| Mode-1 | Mode-2 | Mode-3 | Mode-1 | Mode-2 | Mode-3 | Mode-4 | |
| Accelerometer | 0.9925 | 0.9855 | 0.9850 | 0.9641 | 0.9229 | 0.9535 | 0.9986 |
| SAP2000 | 0.9871 | 0.9883 | 0.9811 | 0.9388 | 0.9329 | 0.8862 | 0.9290 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harmanci, Y.E.; Gülan, U.; Holzner, M.; Chatzi, E. A Novel Approach for 3D-Structural Identification through Video Recording: Magnified Tracking. Sensors 2019, 19, 1229. https://doi.org/10.3390/s19051229
Harmanci YE, Gülan U, Holzner M, Chatzi E. A Novel Approach for 3D-Structural Identification through Video Recording: Magnified Tracking. Sensors. 2019; 19(5):1229. https://doi.org/10.3390/s19051229
Chicago/Turabian StyleHarmanci, Yunus Emre, Utku Gülan, Markus Holzner, and Eleni Chatzi. 2019. "A Novel Approach for 3D-Structural Identification through Video Recording: Magnified Tracking" Sensors 19, no. 5: 1229. https://doi.org/10.3390/s19051229
APA StyleHarmanci, Y. E., Gülan, U., Holzner, M., & Chatzi, E. (2019). A Novel Approach for 3D-Structural Identification through Video Recording: Magnified Tracking. Sensors, 19(5), 1229. https://doi.org/10.3390/s19051229






