Determination of Optimal Measurement Points for Calibration Equations—Examples by RH Sensors
Abstract
:1. Introduction
- The number and the location of the calibration points.
- The regression equations (linear, poly-nominal, non-linear).
- The regression techniques.
- The standard references and their uncertainties.
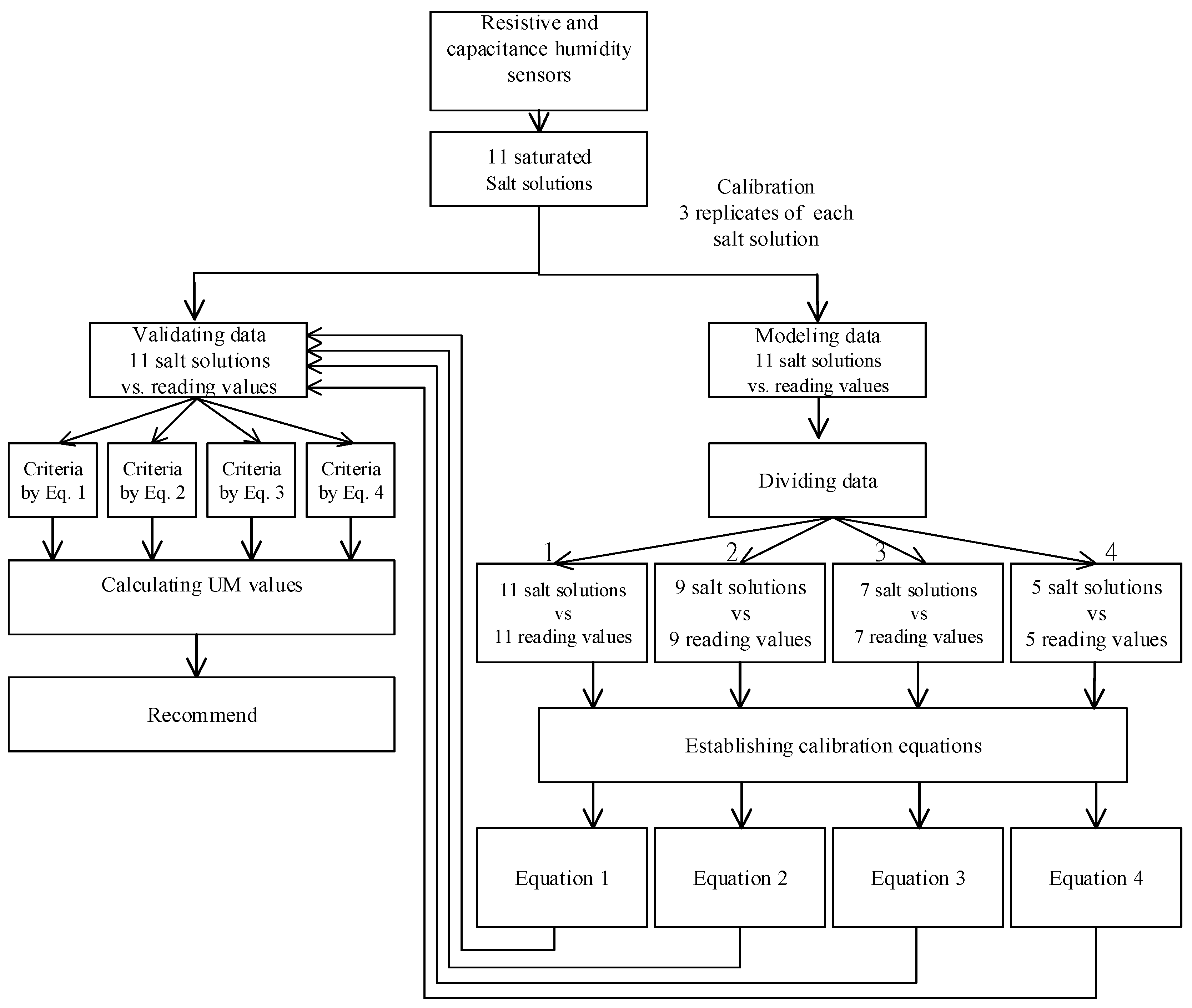
2. Materials and Methods
2.1. Relative Humidity (RH) and Temperature Sensors
2.2. Saturated Salt Solutions
2.3. Calibration of Sensors
2.4. Establish and Validate the Calibration Equation
2.5. Different Calibration Points
- Case 1: The data set is for 11 salt solutions and 11 calibration points
- Case 2: The data set is for 9 salt solutions and 9 calibration points
- Case 3: The data set is for 7 salt solutions and 7 calibration points
- Case 4: The data set is for 5 salt solutions and 5 calibration points
2.6. Data Analysis
2.6.1. Tests on a Single Regression Coefficient
2.6.2. The Estimated Standard Error of Regression
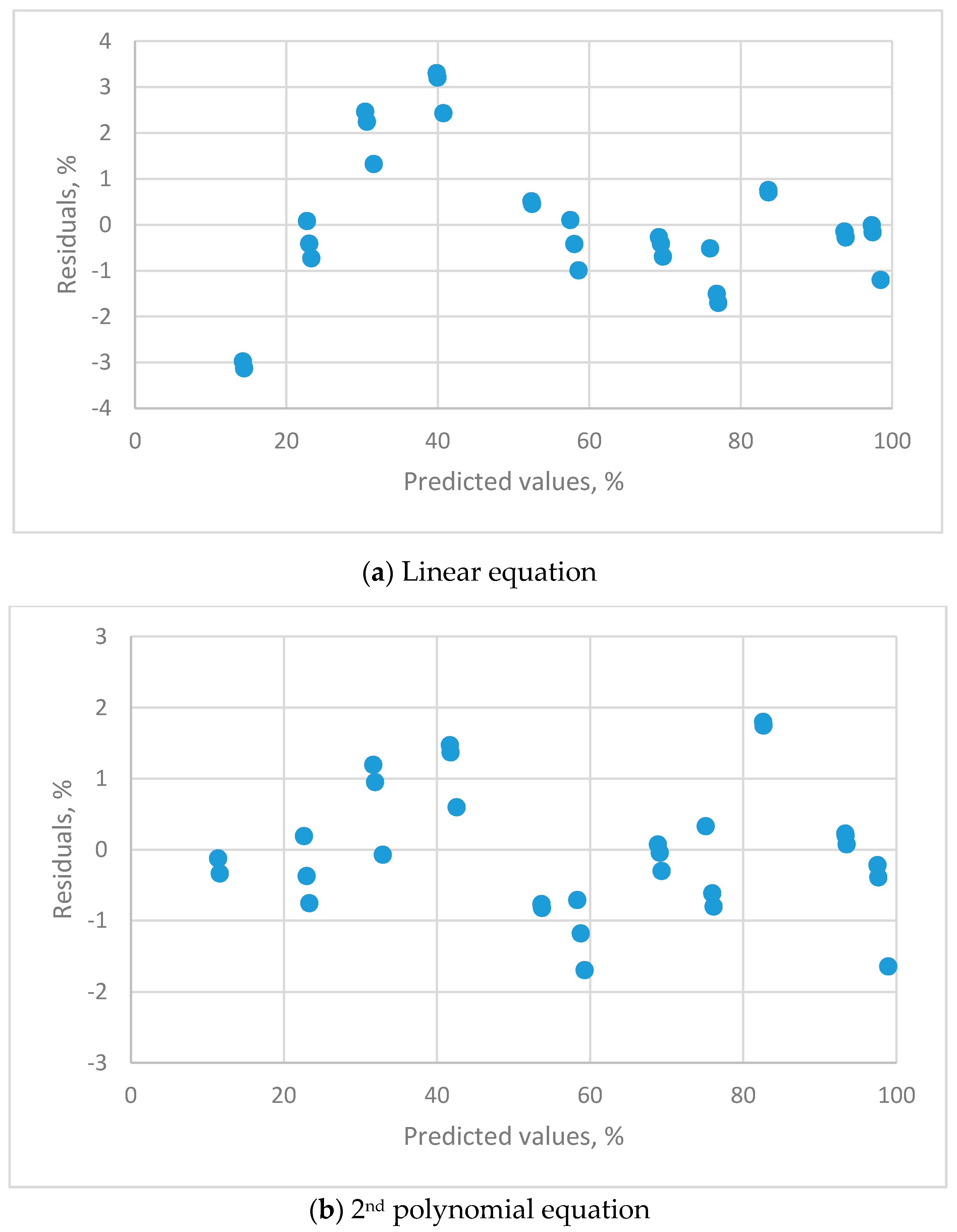
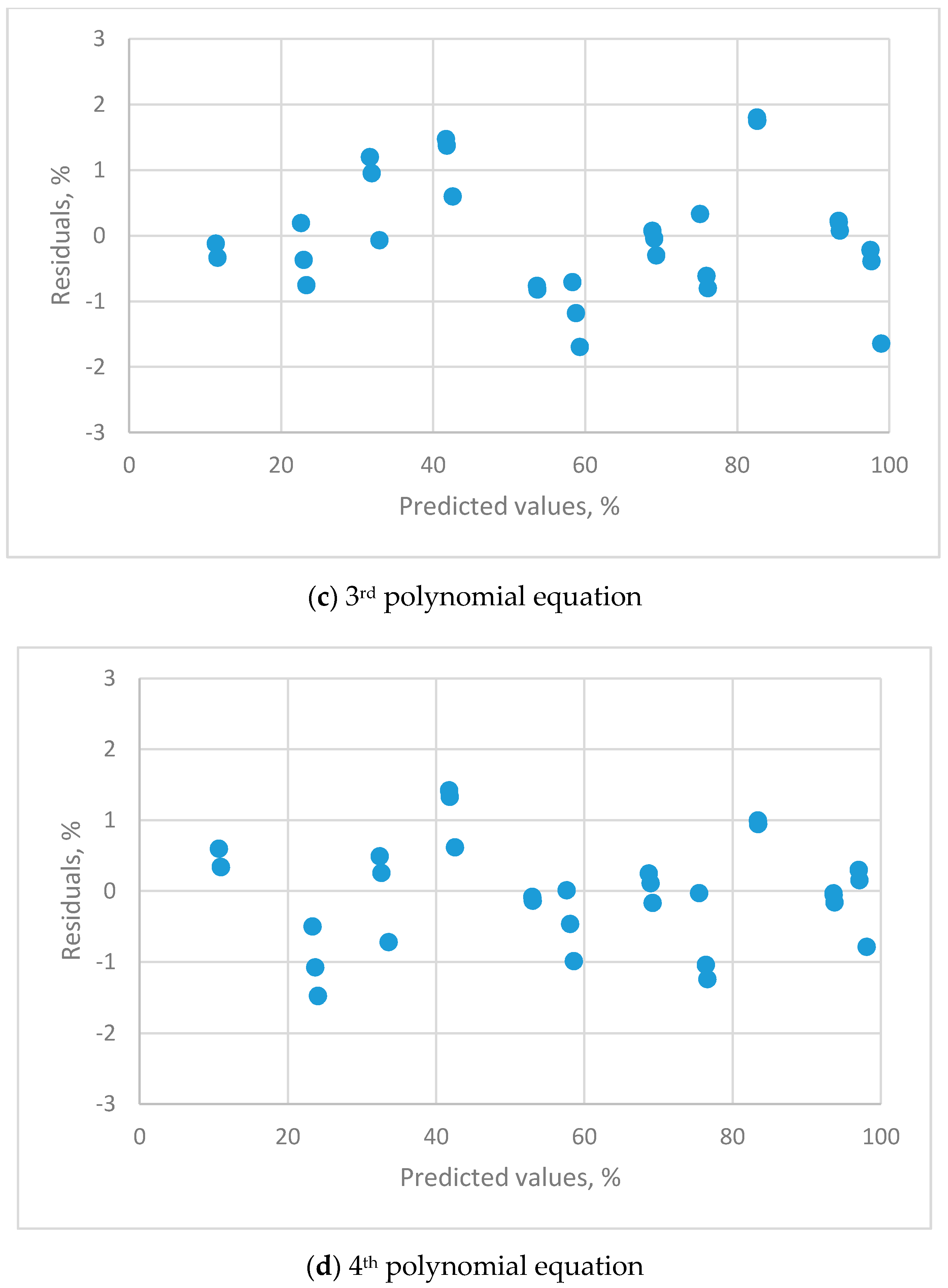
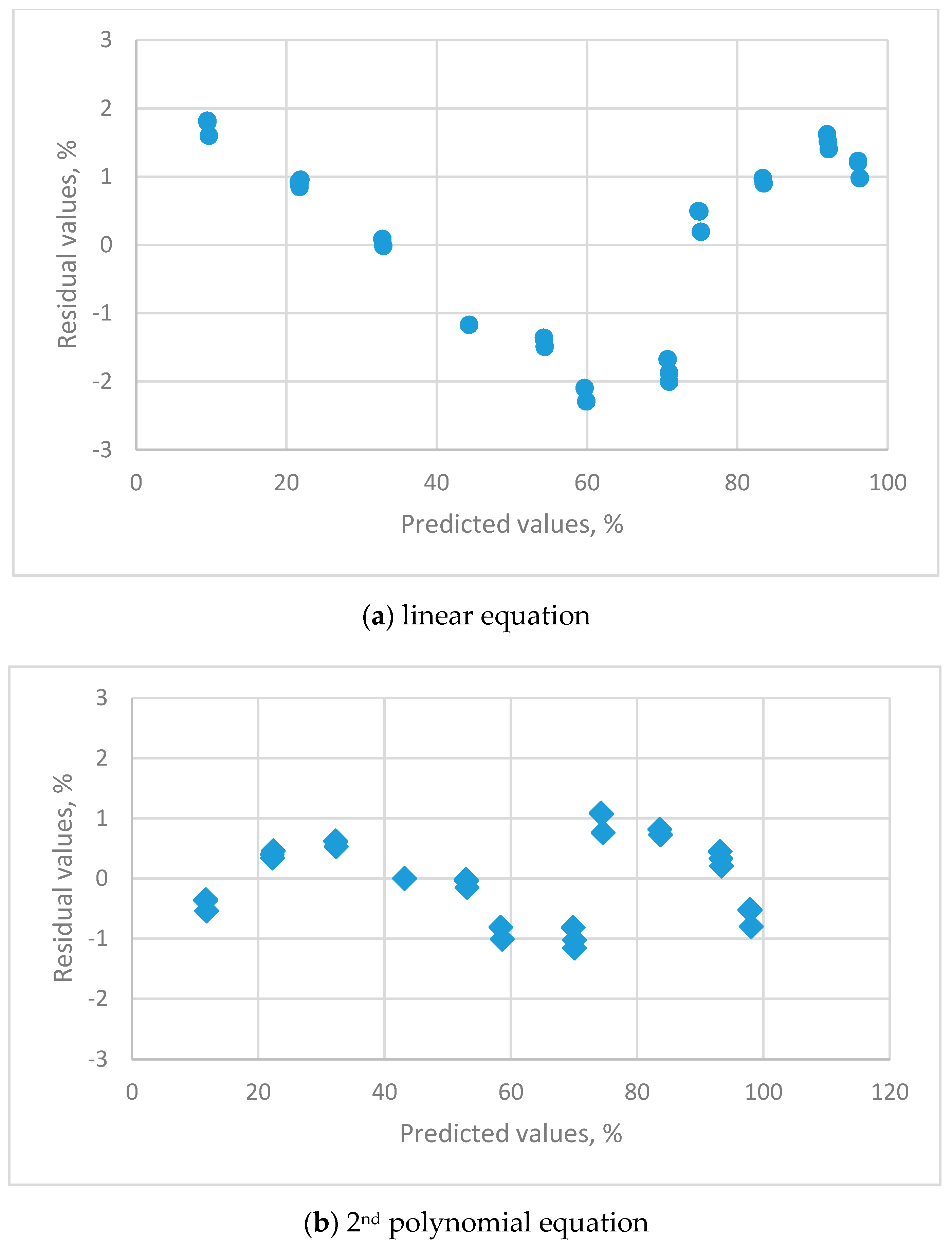
2.6.3. Residual Plots
2.7. Measurement Uncertainty for Humidity Sensors
3. Results and Discussion
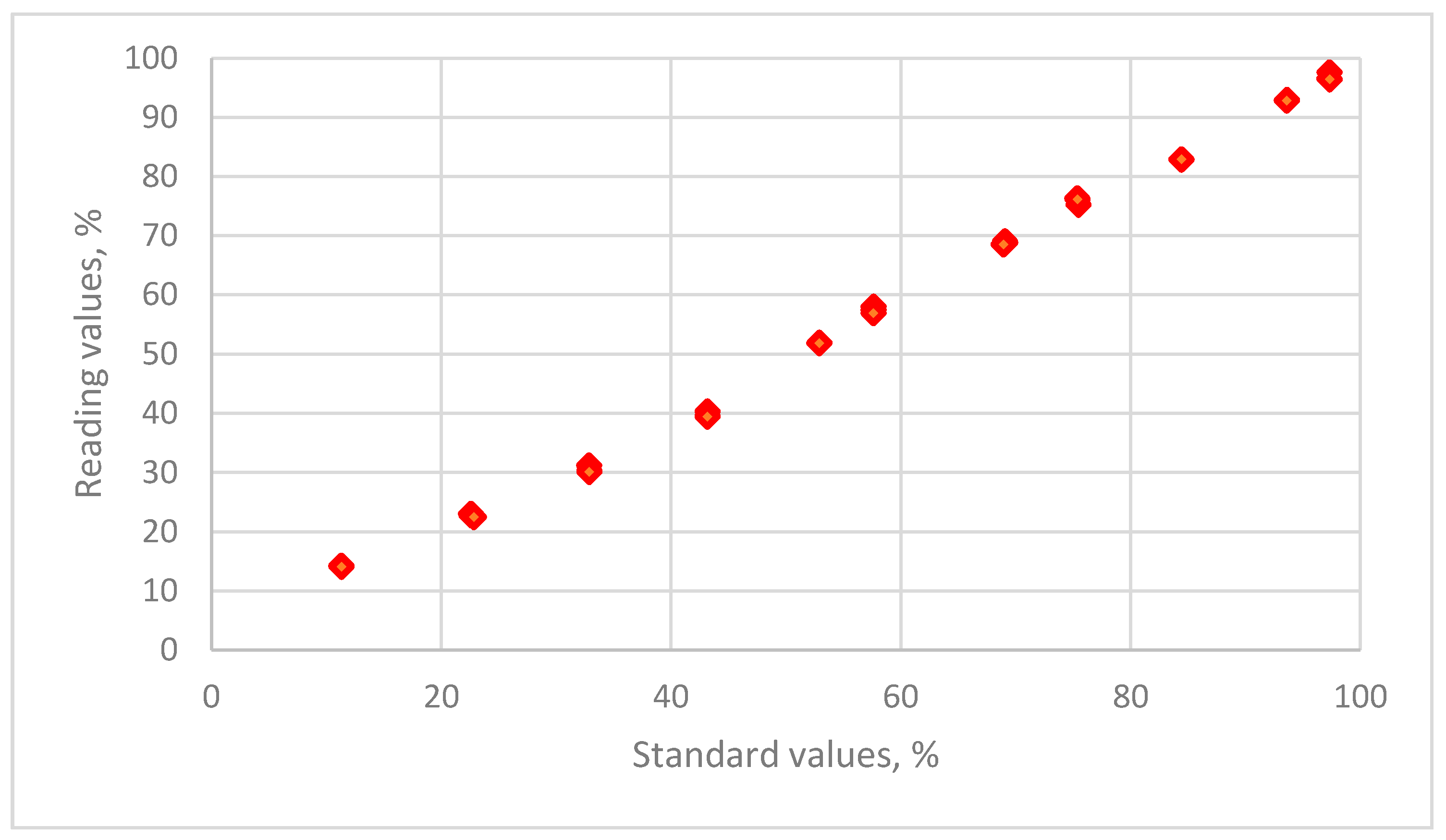
3.1. The Effect of the Accuracy of Different Calibration Points
3.1.1. THT-B121 Resistive Humidity Sensor
- y = −20.530298 + 2.805196x − 0.049153x2 + 0.000539x3 − 2.07539 × 10−6x4
- (sb = 2.5004 sb = 0.2590 sb = 0.0082 sb = 0.00016 sb = 4.770 × 10−7
- t = −8.2107 t = 11.181 t = −6.005 t = −5.0663 t = −4.3514)
- R2 = 0.992, s = 0.7719
- y = −19.471802 + 2.743833x − 0.047663x2 + 0.0005157x3 − 1.93676 × 10−6x4
- (sb = 2.2789 sb = 0.25086 sb = 0.00869 sb = 0.000117 sb = 5.360 × 10−7
- t = −8.5447 t = 10.9396 t = −5.4849 t = 4.3946 t = −3.6101)
- R2 = 0.991, s = 1.014
3.1.2. HMP 140A Capacitive Humidity Sensor
- y = 3.479518 + 0.833274x + 0.001867x2, R2 = 0.9994, s = 0.6837
- (sb = 0.4805 sb = 0.02028 sb = 0.000187
- t = 7.2408 t = 41.098 t = 10.004)
- y = 2.9113205 + 0.864217x + 0.0015542x2, R2 = 0.9995, s = 0.7890
- (sb = 0.63806 sb = 0.02925 sb = 0.000278
- t = 74.5628 t = 29.543 t = 5.5872)
3.1.3. Evaluation of Accuracy
3.2. The Effect of the Precision of Calibration Points
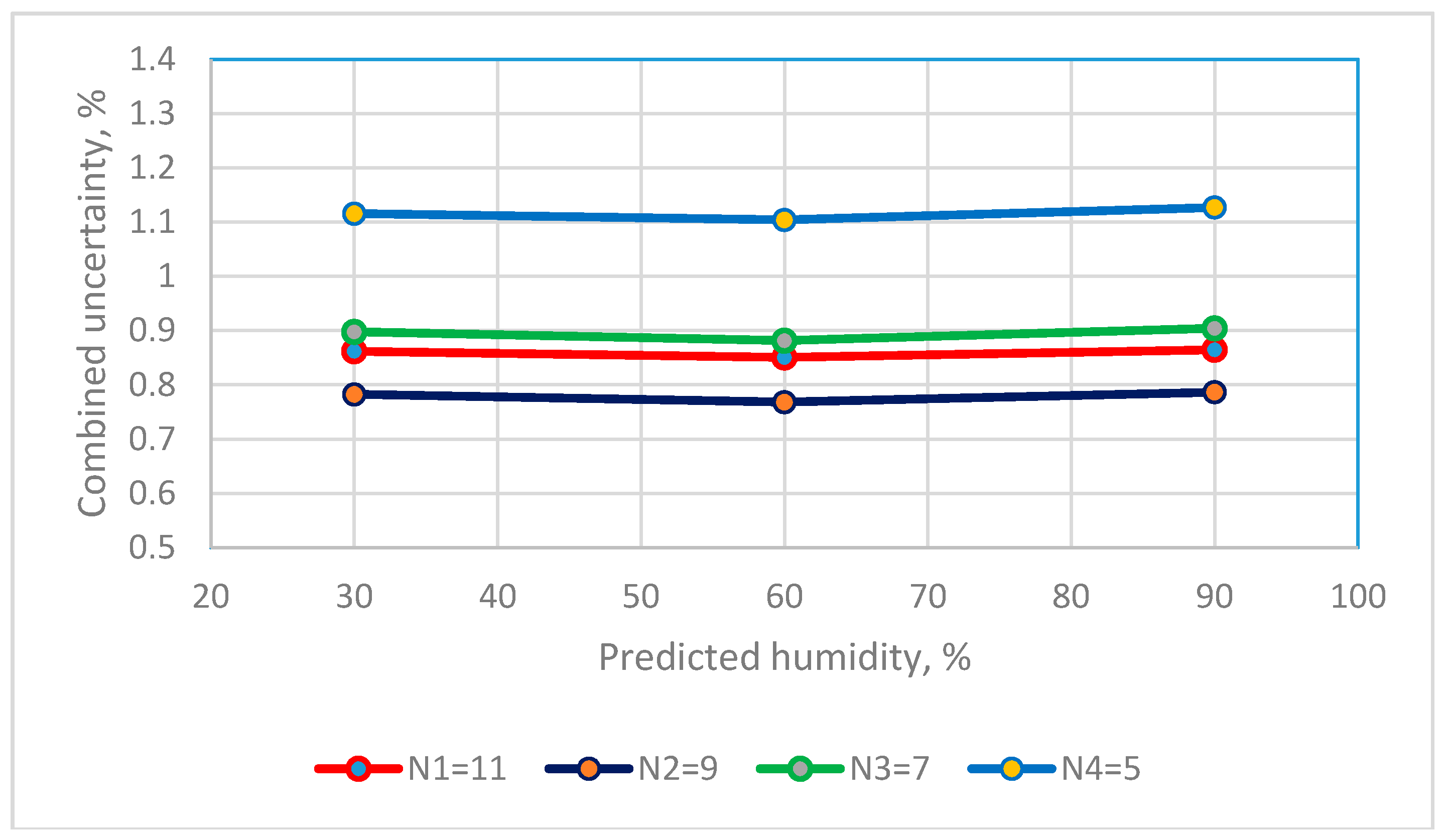
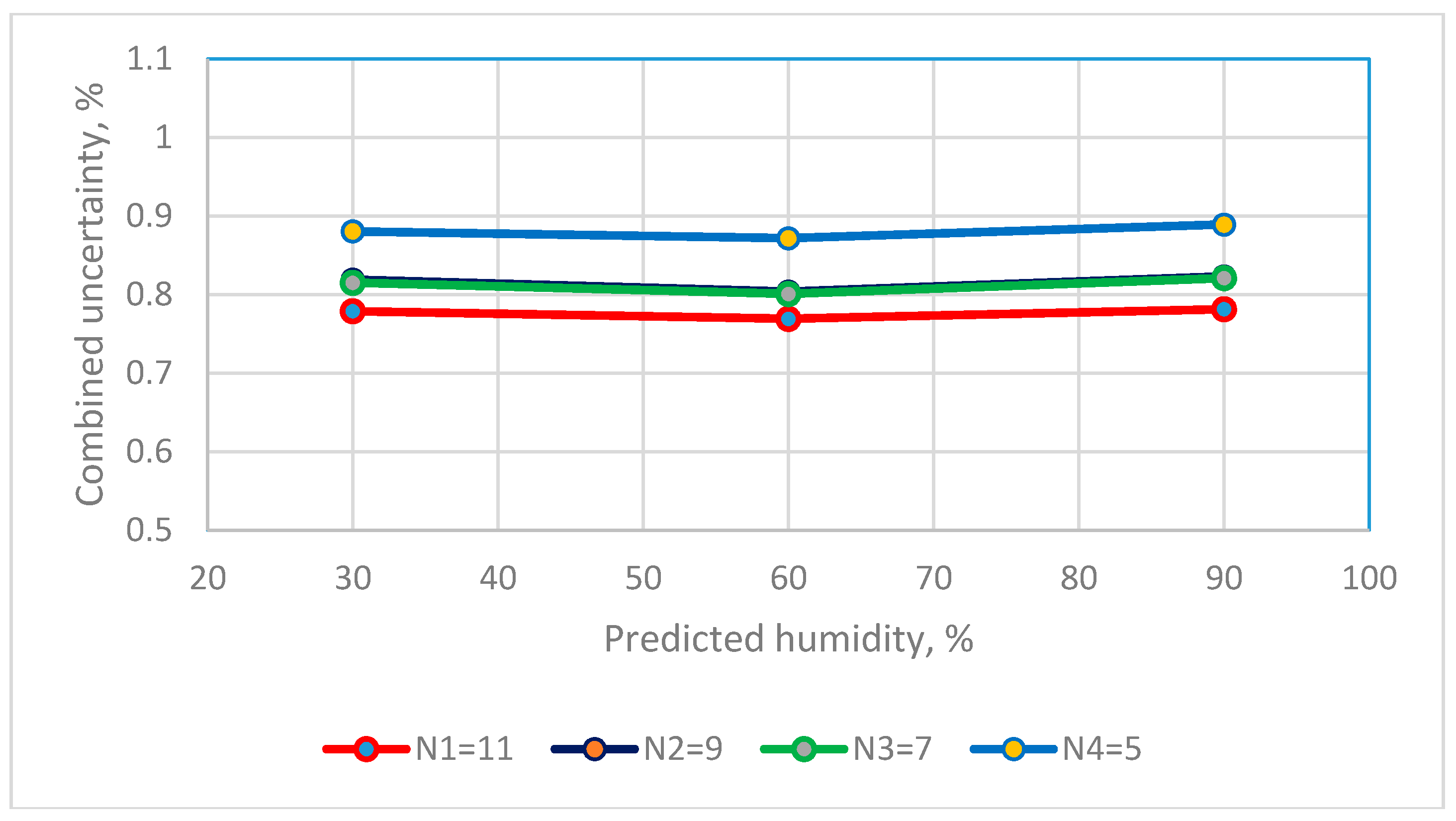
3.2.1. The Measurement Uncertainty for the Two Humidity Sensors
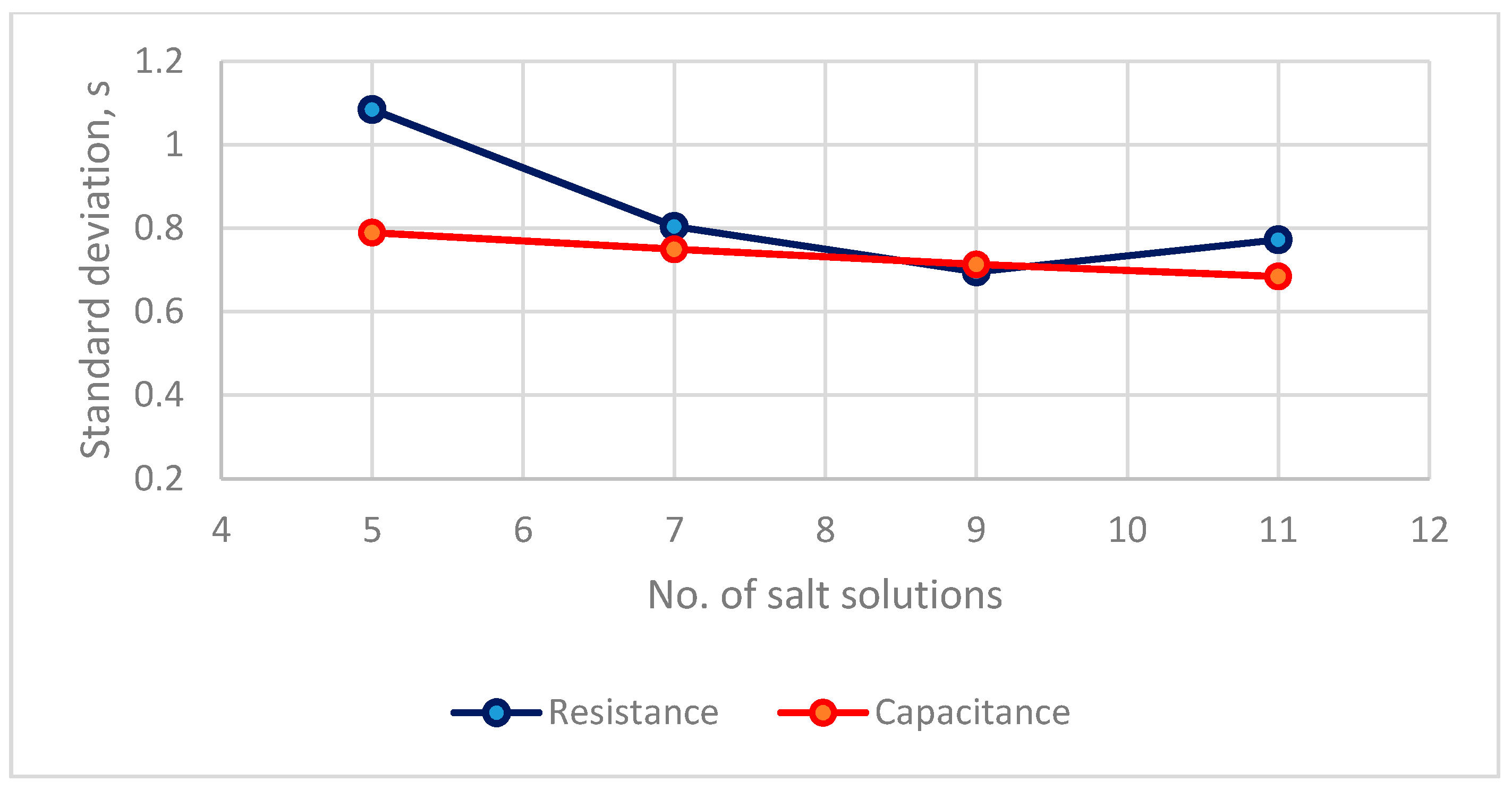
3.2.2. The Precision of the Two Types of RH Sensors
3.3. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Betta, G.; Dell’Isola, M. Optimum choice of measurement points for sensor calibration. Measurement 1996, 17, 115–125. [Google Scholar] [CrossRef]
- Betta, G.; Dell’Isola, M.; Frattolillo, A. Experimental design techniques for optimizing measurement chain calibration. Measurement 2001, 30, 115–127. [Google Scholar] [CrossRef]
- Hajiyev, C. Determination of optimum measurement points via A-optimality criterion for the calibration of measurement apparatus. Measurement 2010, 43, 563–569. [Google Scholar] [CrossRef]
- Hajiyev, C. Sensor Calibration Design Based on D-Optimality Criterion. Metrol. Meas. Syst. 2016, 23, 413–424. [Google Scholar] [CrossRef]
- Khan, S.A.; Shabani, D.T.; Agarwala, A.K. Sensor calibration and compensation using artificial neural network. ISA Trans. 2003, 42, 337–352. [Google Scholar] [CrossRef]
- Chen, C. Application of growth models to evaluate the microenvironmental conditions using tissue culture plantlets of Phalaenopsis Sogo Yukidian ‘V3’. Sci. Hortic. 2015, 191, 25–30. [Google Scholar] [CrossRef]
- Chen, H.; Chen, C. Use of modern regression analysis in liver volume prediction equation. J. Med. Imaging Health Inform. 2017, 7, 338–349. [Google Scholar] [CrossRef]
- Wang, C.; Chen, C. Use of modern regression analysis in plant tissue culture. Propag. Ornam. Plants 2017, 17, 83–94. [Google Scholar]
- Chen, C. Relationship between water activity and moisture content in floral honey. Foods 2019, 8, 30. [Google Scholar] [CrossRef]
- Chen, C. Evaluation of resistance-temperature calibration equations for NTC thermistors. Measurement 2009, 42, 1103–1111. [Google Scholar] [CrossRef]
- Chen, A.; Chen, C. Evaluation of piecewise polynomial equations for two types of thermocouples. Sensors 2013, 13, 17084–17097. [Google Scholar] [CrossRef] [PubMed]
- ISO/IEC 98–3. Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement; ISO: Geneva, Switzerland, 2010. [Google Scholar]
- National Aeronautics and Space Administration. Measurement Uncertainty Analysis Principles and Methods, NASA Measurement Quality Assurance Handbook—Annex 3; National Aeronautics and Space Administration: Washington, DC, USA, 2010. [Google Scholar]
- Chen, C. Evaluation of measurement uncertainty for thermometers with calibration equations. Accredit. Qual. Assur. 2006, 11, 75–82. [Google Scholar] [CrossRef]
- Myers, R.H. Classical and Modern Regression with Applications, 2nd ed.; Duxbury Press: Pacific Grove, CA, USA, 1990. [Google Scholar]
- Weisberg, S. Applied Linear Regression, 4th ed.; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Lu, H.; Chen, C. Uncertainty evaluation of humidity sensors calibrated by saturated salt solutions. Measurement 2007, 40, 591–599. [Google Scholar] [CrossRef]
- Greenspan, L. Humidity fixed points of binary saturated aqueous solutions. J. Res. Natl. Bur. Stand. 1977, 81A, 89–96. [Google Scholar] [CrossRef]
- OMIL. The Scale of Relative Humidity of Air Certified Against Saturated Salt Solutions; OMIL R 121; Organization Internationale De Metrologie Legale: Paris, France, 1996. [Google Scholar]
- Wernecke, R.; Wernecke, J. Industrial Moisture and Humidity Measurement: A Practical Guide; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Wiederhold, P.R. Water Vapor Measurement; Marcel Dekker, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Matko, V.; Đonlagić, D. Sensor for high-air-humidity measurement. IEEE Trans. Instrum. Meas. 1996, 4, 561–563. [Google Scholar] [CrossRef]
- Matko, V. Next generation AT-cut quartz crystal sensing devices. Sensors 2011, 5, 4474–4482. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.Y.; Fan, R.R.; Li, C.R.; Yang, X.Y.; Li, H.Z.; Lin, J.D.; Zhou, X.C.; Lv, R.X. A fast-response and highly linear humidity sensor based on quartz crystal microbalance. Sens. Actuator B Chem. 2019, 283, 659–665. [Google Scholar] [CrossRef]
- Wexler, A.; Hasegawa, S. Relative humidity-temperature relationships of some saturated salt solutions in the temperature range 0° to 50° C. J. Res. Natl. Bur. Stand. 1954, 53, 19–26. [Google Scholar] [CrossRef]
- Young, J. Humidity control in the laboratory using salt solutions—A review. J. Chem. Technol. Biotechnol. 1967, 17, 241–245. [Google Scholar] [CrossRef]
- Lake, B.J.; Sonya, M.N.; Noor, S.M.; Freitag, H.P.; Michael, J.; McPhaden, M.J. Calibration Procedures and Instrumental Accuracy Estimates of ATLAS Air Temperature and Relative Humidity Measurements; NOAA Pacific Marine Environmental Laboratory: Seattle, WA, USA, 2003. [Google Scholar]
- Wadsö, L.; Anderberg, A.; Åslund, I.; Söderman, O. An improved method to validate the relative humidity generation in sorption balances. Eur. J. Pharm. Biopharm. 2009, 72, 99–104. [Google Scholar] [CrossRef]
- Duvernoy, J.; Gorman, J.; Groselj, D. A First Review of Calibration Devices Acceptable for Metrology Laboratory. 2015. Available online: https://www.wmo.int/pages/prog/www/IMOP/publications/IOM-94-TECO2006/4_Duvernoy_France.pdf (accessed on 11 December 2018).
- Belhadj, O.; Rouchon, V. How to Check/Calibrate Your Hygrometer? J. Paper Conserv. 2015, 16, 40–41. [Google Scholar] [CrossRef]
- Japan Mechanical Society. The Measurement of Moisture and Humidity and Monitoring of Environment; Japan Mechanical Society: Tokyo, Japan, 2011. (In Japanese) [Google Scholar]
- Japan Industrial Standard Committee. Testing Methods of Humidity; JIS Z8866; JISC: Tokyo, Japan, 1998. [Google Scholar]
- Centre Microcomputer Application. Relative Humidity Sensor 025I. Available online: http://www.cma-science.nl/resources/en/sensors_bt/d025i.pdf (accessed on 2 December 2018).
- Delta Ohm Company. Calibration Instructions of Relative Humidity Sensors. 2012. Available online: http://www.deltaohm.com/ver2012/download/Humiset_M_uk.pdf (accessed on 10 December 2018).
- Omega Company. Equilibrium Relative Humidity Saturated Salt Solutions. 2013. Available online: https://www.omega.com/temperature/z/pdf/z103.pdf (accessed on 11 December 2018).
- TA Instruments. Humidity Fixed Points. 2016. Available online: http://www.tainstruments.com/pdf/literature/TN056.pdf (accessed on 10 December 2018).
- Vaisala Ltd. Vaisala Humidity Calibrator HMK 15 User’s Guide. 2017. Available online: www.vaisala.com/sites/default/files/documents/HMK15_User_Guide_in_English.pdf (accessed on 11 December 2018).
- Ellison, S.; Williams, A. Eurachem/CITAC Guide: Quantifying Uncertainty in Analytical Measurement, 3rd ed.; Eurachem: Torino, Italy, 2012. [Google Scholar]

| Salt Solutions | OIMI [19] | Lake [27] | Wadso [28] | Duvernoy [29] | Belhadj [30] | JMS [31] | JISC [32] | CMA [33] | Delta [34] | OMEGA [35] | TA [36] | Vaisala [37] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LiBr | * | |||||||||||
| LiCl | * | * | * | * | * | * | * | * | * | |||
| CH3COOK | * | * | * | * | ||||||||
| MgCl2·GH2O | * | * | * | * | * | * | * | * | * | * | ||
| K2CO3 | * | * | * | * | * | * | * | |||||
| Mg(NO3)2 | * | * | * | * | * | * | * | |||||
| NaBr | * | * | * | * | ||||||||
| KI | * | * | * | |||||||||
| SrCl2 | * | |||||||||||
| NaCl | * | * | * | * | * | * | * | * | * | * | * | * |
| (NH4)2SO4 | * | |||||||||||
| KCl | * | * | * | * | * | * | * | * | ||||
| KNO3 | * | * | * | * | ||||||||
| K2SO4 | * | * | * | * | * | * | * | * |
| Resistive Sensor | Capacitive Sensor | |
|---|---|---|
| Model 1 | THT-B121 | HMP 140A |
| Sensing element | Macro-molecule HPR-MQ | HUMICAP |
| Operating range | 0–60 °C | 0–50 °C |
| Measuring range | 10–99% RH | 0–100% |
| Nonlinear and repeatability | ±0.25% RH | ±0.2% RH |
| ResolutionTemperature effect | 0.1% RH (relative humidity)none | 0.1% RH0.005%/°C |
| Salt Solutions | (n1 = 11) Case 1 | (n2 = 9) Case 2 | (n3 = 7) Case 3 | (n4 = 5) Case 4 | uc |
|---|---|---|---|---|---|
| LiCl | * | * | * | * | 0.27 |
| CH3COOK | * | 0.32 | |||
| MgCl2 | * | * | * | * | 0.16 |
| K2CO3 | * | * | * | 0.39 | |
| Mg(NO3)2 | * | * | 0.22 | ||
| NaBr | * | * | * | * | 0.40 |
| KI | * | * | 0.24 | ||
| NaCl | * | * | * | * | 0.12 |
| KCl | * | * | * | 0.26 | |
| KNO3 | * | 0.55 | |||
| K2SO4 | * | * | * | * | 0.45 |
| Linear | 2nd Order | 3nd Order | 4th Order | |
|---|---|---|---|---|
| b0 | 0.028672 | −2.74999 | −11.0702 | −20.5303 |
| b1 | 1.008985 | 1.13766 | 1.780025 | 2.805196 |
| b2 | −0.0011437 | −0.01432 | −0.0491534 | |
| b3 | 7.81681 × 10−5 | 5.39281 × 10−4 | ||
| b4 | −2.07539 × 10−6 | |||
| R2 | 0.9967 | 0.9974 | 0.9987 | 0.9993 |
| s | 1.6098 | 1.4612 | 0.982 | 0.7719 |
| Residual plots | clear pattern | clear pattern | clear pattern | uniform distribution |
| Linear | 2nd Order | 3nd Order | 4th Order | |
|---|---|---|---|---|
| b0 | −0.970118 | −3.1191770 | −12.201481 | −19.471802 |
| b1 | 1.0155235 | 1.12632754 | 1.8869907 | 2.743833 |
| b2 | −0.001007316 | −0.01685101 | −0.04766345 | |
| b3 | 9.34623 × 10−5 | 5.15689 × 10−4 | ||
| b4 | −1.93676 × 10−6 | |||
| R2 | 0.9969 | 0.9974 | 0.9994 | 0.9991 |
| s | 1.8109 | 1.7146 | 0.7984 | 1.084 |
| Residual plots | clear pattern | clear pattern | clear pattern | uniform distribution |
| Case 1 (n1 = 11) | Case 2 (n2 = 9) | Case 3 (n3 = 7) | Case 4 (n4 = 5) | |
|---|---|---|---|---|
| b0 | −20.530297 | −23.41845561 | −23.904948 | −19.4718019 |
| b1 | 2.8051965 | 3.5861653 | 3.243023015 | 2.743832845 |
| b2 | −0.04915334 | −0.06230766 | −0.06426625 | −0.047663446 |
| b3 | 5.39281 × 10−4 | 7.0951 × 10−4 | 7.34202 × 10−4 | 5.15689 × 10−4 |
| b4 | −2.07539 × 10−6 | −2.81734 × 10−6 | −2.92042 × 10−6 | −1.93676 × 10−6 |
| R2 | 0.9993 | 0.9994 | 0.9994 | 0.9991 |
| s | 0.7719 | 0.6951 | 0.8039 | 1.084 |
| Linear | 2nd Order | |
|---|---|---|
| b0 | −0.414520 | 3.479518 |
| b1 | 1.031003 | 0.833274 |
| b2 | 0.00186718 | |
| R2 | 0.9975 | 0.9994 |
| s | 1.4002 | 0.6837 |
| Residual plots | clear pattern | Uniform distribution |
| Linear | 2nd Order | |
| b0 | 0.226512 | 2.911321 |
| b1 | 1.023088 | 0.814217 |
| b2 | 0.00155423 | |
| R2 | 0.9981 | 0.9995 |
| s | 1.4386 | 0.7890 |
| Residual plots | clear pattern | Uniform distribution |
| Case 1 (n1 = 11) | Case 2 (n2 = 9) | Case 3 (n3 = 7) | Case 4 (n4 = 5) | |
|---|---|---|---|---|
| b0 | 3.479580 | 3.156891 | 2.871078 | 2.9113205 |
| b1 | 0.833274 | 0.844157 | 0.862302 | 0.8142171 |
| b2 | 0.00186718 | 0.00176878 | 0.00161775 | 0.00155423 |
| R2 | 0.9975 | 0.9992 | 0.9994 | 0.9995 |
| s | 0.6837 | 0.7127 | 0.7490 | 0.7890 |
| Description | Estimate Value (%) | Standard Uncertainty u(x), (%) |
|---|---|---|
| Reference standard, Uref | N1 = 11, uref = 0.3311 N1 = 9, uref = 0.2983 N1 = 7, uref = 0.3151 N1 = 5, uref = 0.3084 | |
| Non-linear and repeatability, Unon | ±0.3 | 0.00866 |
| Resolution, Ures | 0.1 | 0.00290 |
| The combined standard uncertainty of Type B = 0.1926 | ||
| Description | Estimate Value (%) | Standard Uncertainty u(x), (%) |
|---|---|---|
| Reference standard, Uref | N1 = 11, uref = 0.3311 N1 = 9, uref = 0.2983 N1 = 7, uref = 0.3151 N1 = 5, uref = 0.3084 | |
| Nonlinear and repeatability, Unon | ±0.1 | 0.0058 |
| Resolution, Ures | ±0.1 | 0.0029 |
| Temperature effect, Utemp | ±0.005 | 0.0043 |
| The combined standard uncertainty of Type B = 0.1924 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.-Y.; Chen, C. Determination of Optimal Measurement Points for Calibration Equations—Examples by RH Sensors. Sensors 2019, 19, 1213. https://doi.org/10.3390/s19051213
Chen H-Y, Chen C. Determination of Optimal Measurement Points for Calibration Equations—Examples by RH Sensors. Sensors. 2019; 19(5):1213. https://doi.org/10.3390/s19051213
Chicago/Turabian StyleChen, Hsuan-Yu, and Chiachung Chen. 2019. "Determination of Optimal Measurement Points for Calibration Equations—Examples by RH Sensors" Sensors 19, no. 5: 1213. https://doi.org/10.3390/s19051213
APA StyleChen, H.-Y., & Chen, C. (2019). Determination of Optimal Measurement Points for Calibration Equations—Examples by RH Sensors. Sensors, 19(5), 1213. https://doi.org/10.3390/s19051213





