1. Introduction
With the explosive development of the Internet of Things (IoT), enormous sensors are connected through IoT techniques, and these sensors generate massive amounts of data and demand [
1,
2,
3,
4]. However, due to the limitations of size, battery life and heat dissipation in IoT sensors, severely constrained resources cannot meet the increasingly complex application requirements [
5]. Since the cloud has adequate computation resources, cloud computing [
6] has been proposed as an effective way to tackle the above challenges. By offloading computation tasks to cloud data centers, cloud computing can extend the computation power of IoT sensors.
However, cloud data centers are mostly far from IoT sensors, which causes significant communication overhead and severely lessens the offloading efficiency. They are usually unacceptable for some latency-sensitive IoT applications. Thus, edge computing [
7,
8], e.g., multi-access edge computing (MEC) [
9] and fog computing [
10,
11], as a complement and extension of the cloud computing paradigm, is a prospective solution that can overcome the aforementioned challenges. In edge computing, computation resources are deployed near devices, such as smart gateways, access points, base stations, etc., and integrated as edge servers. The resource-constrained device can offload the computing task to the edge server via single-hop wireless transmission. The edge server then performs the computation and returns the computation result. Different from cloud computing, edge computing can provide computing resources at the network edge. Therefore, it can reduce communication latency and network bandwidth requirement [
12,
13]. Furthermore, based on the advantages of edge computing, many efforts have explored its potential in practical applications, such as video analysis [
14], fault detection [
15] and vehicular networks [
16].
Computation offloading [
17,
18,
19] is a key technique of edge computing to efficiently enhance the computation capability of IoT sensors. In addition, computation offloading can save computation energy consumption of IoT sensors at the cost of additional transmission energy consumption. Therefore, balancing the tradeoff between computation and communication costs in order to optimize offloading strategies is a key challenge of computation offloading problem. Many previous studies on computation offloading in the field of edge computing have been proposed [
20]. Most of the literature optimize the offloading strategies under certain constraints, such as task completion deadline or bandwidth resource constraints, to achieve system performance gains, like reducing energy consumption or latency. To improve the system efficiency, Dinh et al. [
21] observed performance gain in energy and latency when offloading decisions, task assignment, and CPU frequency of the device were jointly considered. Ref. [
22] jointed optimization of the computation offloading decisions and the allocation of computation resources, transmission power, and radio bandwidth in a hybrid fog/cloud system. However, most works assume that computing tasks are independent. That is, computation offloading with inter-task dependency relationships, especially the task dependency among various devices, have seldom been considered and addressed. This kind of inter-task dependency is ubiquitous in the IoT environment such as smart home [
23], smart healthcare [
24], and smart city [
25,
26,
27]. For example, consider a scenario where multiple IoT sensors are combined to complete an IoT service. One of the sensors needs to combine the data processed by other sensors for calculation. There is data dependency between these IoT sensors, meaning that different tasks between IoT sensors need to exchange data to obtain the expected results. In general, making computation offloading strategies in the restriction of task dependency relationships is a challenging problem.
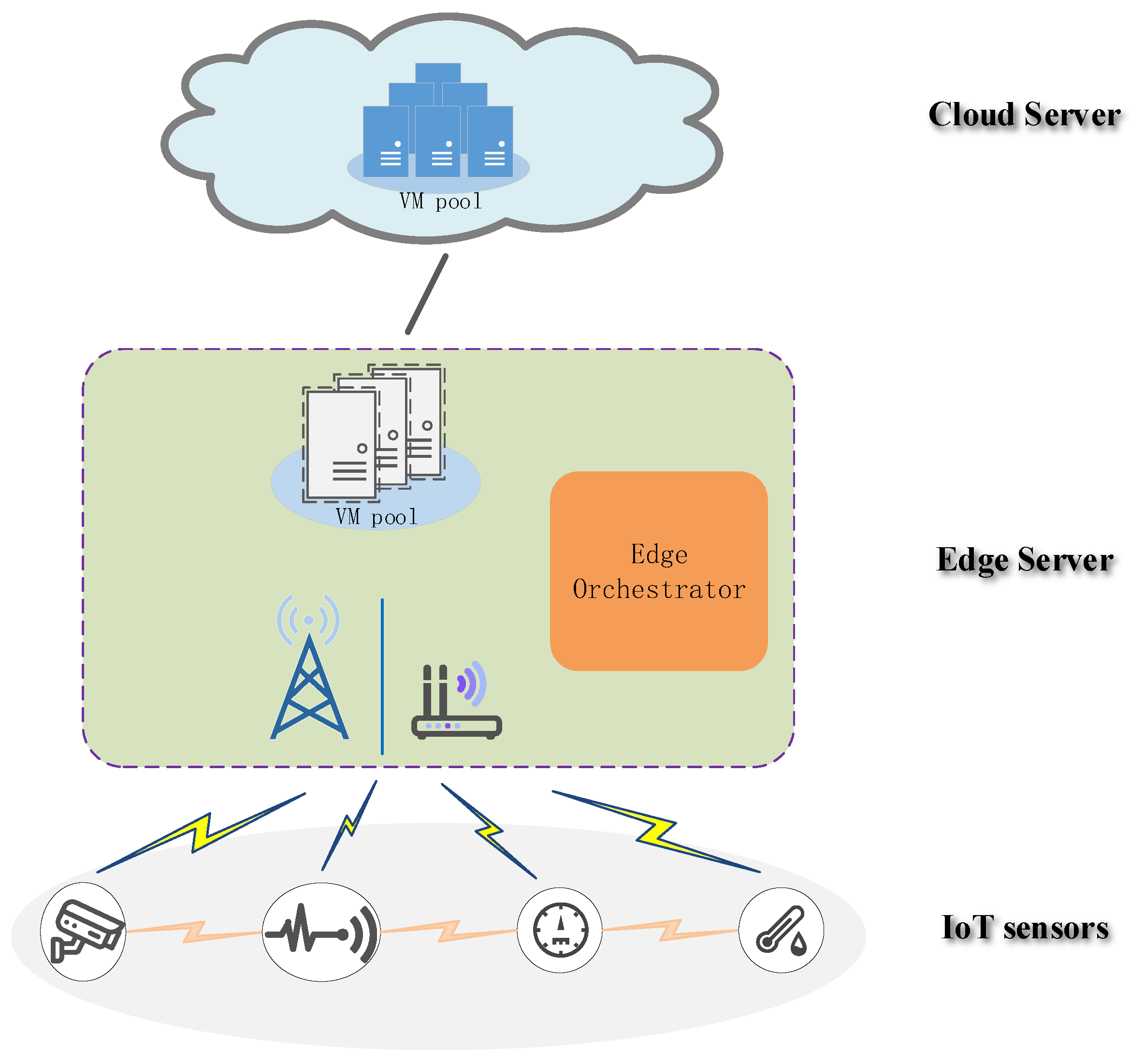
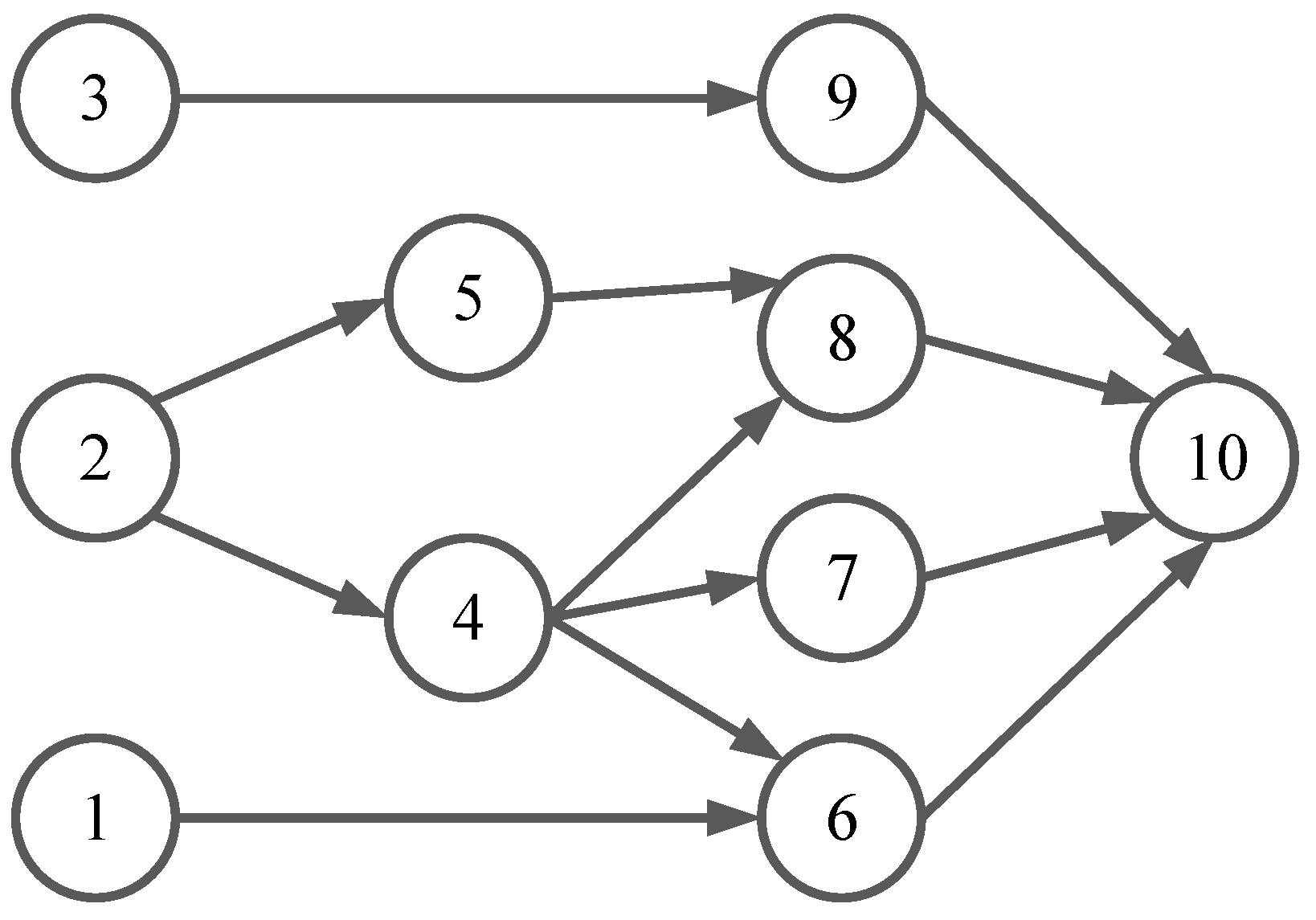
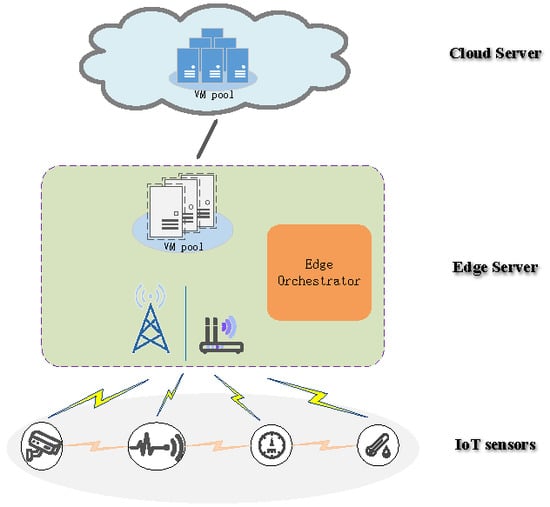
In this paper, to tackle the inter-task dependency problem mentioned above, we modeled the task computation offloading problem of IoT sensors as an energy optimization problem while satisfying inter-task dependency and service completion time constraint. Particularly, these tasks with dependency among various sensors were referred to as the collaborative task. Compared to the cloud data center, the computation capability and resources of the edge server are limited. Therefore, for the network architecture, similar to some previous works [
22,
28,
29], we described a cloud-assisted edge computing framework as a three-tier network architecture, which consisted of IoT sensors, an edge computing server, and a remote cloud server. The computing task of the IoT sensor could be performed locally, offloaded to the edge server, or further forwarded to the cloud server. The main contributions of this paper are summarized as follows:
Taking inter-task dependency and service completion time constraint into consideration, we formulated the computation offloading strategy problem as a mixed integer optimization problem on the cloud-assisted edge computing framework, aimed at minimizing the energy consumption of IoT sensors. Since the problem is a NP-hard problem, solving such problems is challenging.
Based on convex optimization theory, we proposed an Energy-efficient Collaborative Task Computation Offloading (ECTCO) algorithm to solve the optimization problem. The algorithm obtains computation offloading decisions through a semidefinite relaxation (SDR) [
30] approach and probability-based stochastic mapping method.
We performed extensive simulations to evaluate the proposed method. Simulation results showed that in the inter-task dependency scenario, the proposed ECTCO algorithm outperformed in terms of energy consumption compared to existing algorithms in computation offloading. Moreover, the performance evaluations verified the effectiveness and the adaptability of the proposed algorithm under different system parameters.
The remainder of this paper is organized as follows. Related works are reviewed in
Section 2.
Section 3 introduces the system model and formulates an optimization problem. In
Section 4, we present the SDR approach to solve the optimization problem and propose the ECTCO algorithm. Simulation results are presented and discussed in
Section 5. Finally,
Section 6 draws conclusions and discusses future work.
Notation: in this paper, the mathematical symbols follow the rules as follows. The italic letter denotes a variable, and the uppercase letter with calligraphic font denotes a set. The bold lowercase letter denotes a vector, while the bold uppercase letter denotes a matrix. and represent the transpose of vector and matrix , respectively. The trace function of matrix is denoted by Tr().
2. Related Works
Computation offloading is an attractive and challenging topic in edge computing. It has been extensively investigated with a variety of architectures and offloading schemes. Generally speaking, task computation offloading can be classified into two computing models [
17]: Binary offloading [
28,
29,
31,
32] and partial offloading [
33,
34,
35].
For binary offloading, the computation task is either executed locally or offloaded as a whole. We further divide the relevant researches into a two-tier network [
31,
32] and a three-tier network [
22,
28,
29]. In [
31], You et al., discussed the resource allocation problem based on TDMA and OFDMA in multi-user computation offloading system. The computation offloading strategy was obtained via the dynamic channel conditions. The results showed that OFDMA access enables higher energy savings compared to the TDMA system. Taking the scenario of edge caching into consideration, Hao et al. [
32] jointly optimized a task offloading and cache problem to improve energy efficiency. All of the studies above focus on a two-tier network consisting of devices and edge nodes only. In a three-tier network, the optimization problem of computation offloading strategy becomes more complicated. To achieve a higher energy efficiency, Ma et al. [
28] devised a distributed computation offloading algorithm in the cloud-edge interoperation system by utilizing game theory. Zhao et al. [
29] proposed a QoS guaranteed offloading policy by coordinating the edge cloud and the remote cloud under the delay bounded.
For partial offloading, the computation task is segmented into a set of sub-tasks. Some of the sub-tasks can be executed locally, and the rest are offloaded to the edge. In [
33], Wang et al. combined the dynamic voltage scaling technique with partial computation offloading and proposed a local optimal algorithm by using the univariate search technique to achieve the goal of reducing energy consumption and shortening the delay. In [
34], the authors integrated wireless power transfer (WPT) technology into the edge computing system to power the multi-user computation offloading. Ren et al. [
35] presented a novel partial computation offloading model to optimize the weighted-sum latency-minimization resource allocation problem of multi-user edge computing system. However, the aforementioned studies about computation offloading in edge computing including binary offloading and partial offloading do not consider the important inter-task dependency among various devices.
Recently, there have been some works on computation offloading with task dependency in the field of cloud computing [
36,
37]. In the single-user case, Zhang et al. [
36] modeled an application as general topology, and proposed the one-climb policy and Lagrange relaxation method to resolve the delay-constrained workflow scheduling problem. In [
37], Guo et al. investigated a multi-user scenario in the cloud computing environment, where each individual device had an application that could be partitioned into multiple sub-tasks with dependency, with the goal of optimizing the energy efficiency of the computation offloading. However, both of them divided a complex application into multiple sub-tasks by an individual device, taking into account the dependency between them. In contrast, we considered the inter-task dependency suitable to IoT scenario, that is, the inter-task dependency among IoT sensors. These tasks were simple computing tasks that can be fully offloading. Furthermore, different from the cloud computing field mentioned above, in this paper, we focused on cloud-assisted edge computing framework of the three-tier network architecture, in which the computation offloading decision considering the inter-task dependency was much more complicated.
6. Conclusions and Future Work
In this paper, we investigate an energy conservation problem of IoT sensors in cloud-assisted edge computing framework by optimization of the computation offloading strategy. The energy conservation problem was formulated as an energy consumption minimization problem while meeting the constraints of inter-task dependency relationships and service completion time. To solve the NP-hard problem, we proposed the ECTCO algorithm, employing the SDR approach and the probability-based stochastic mapping method to obtain the computation offloading strategy.
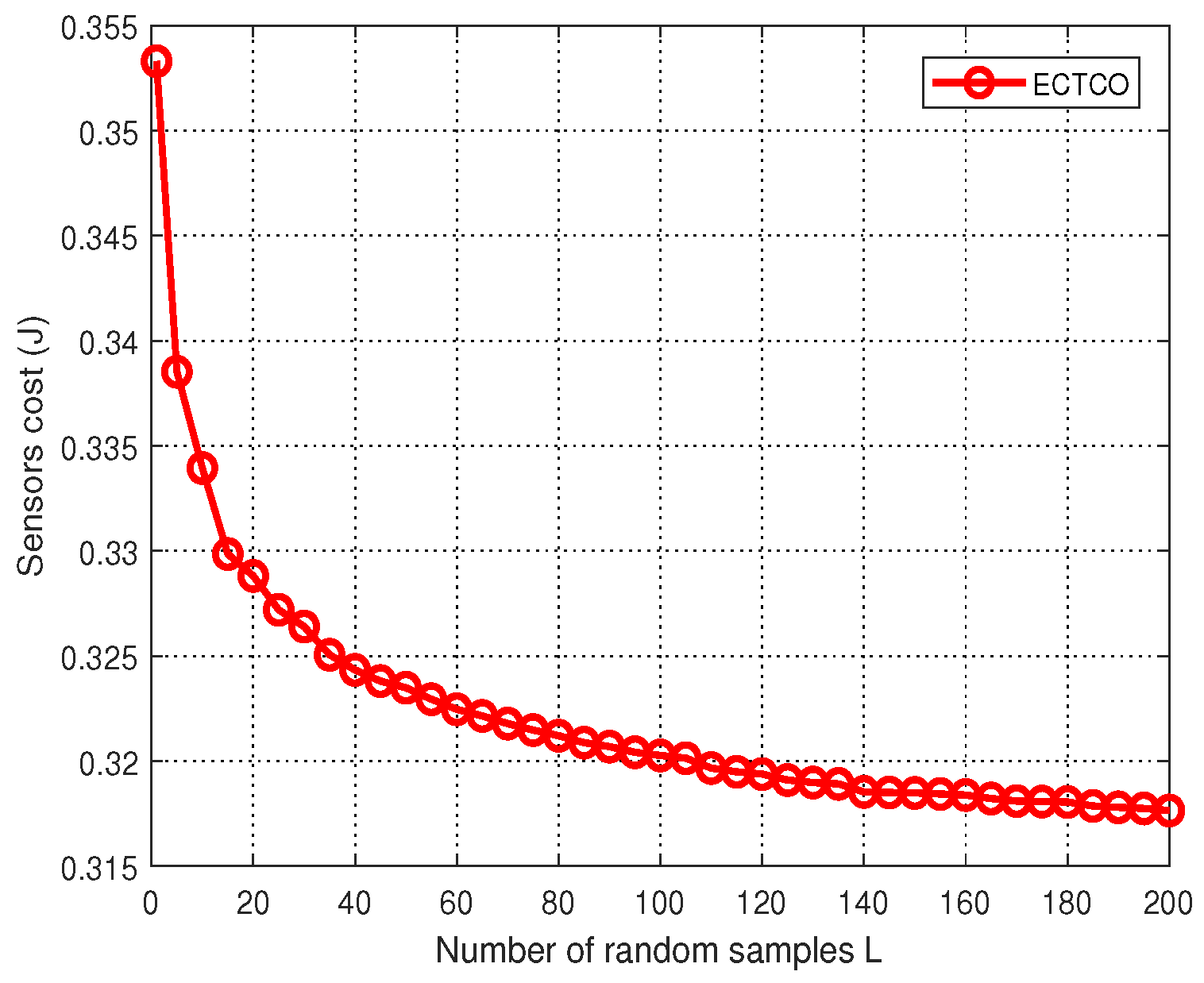
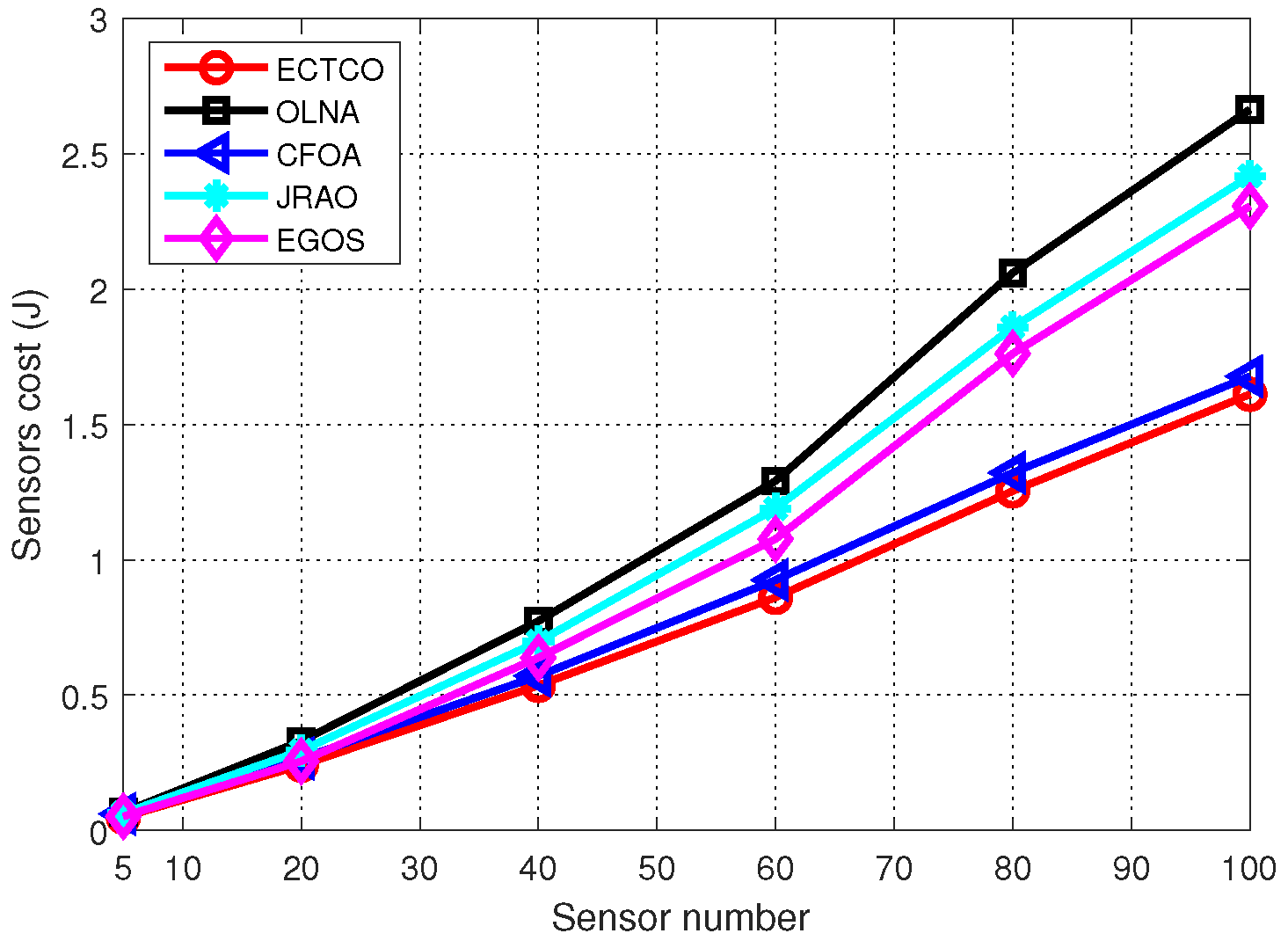
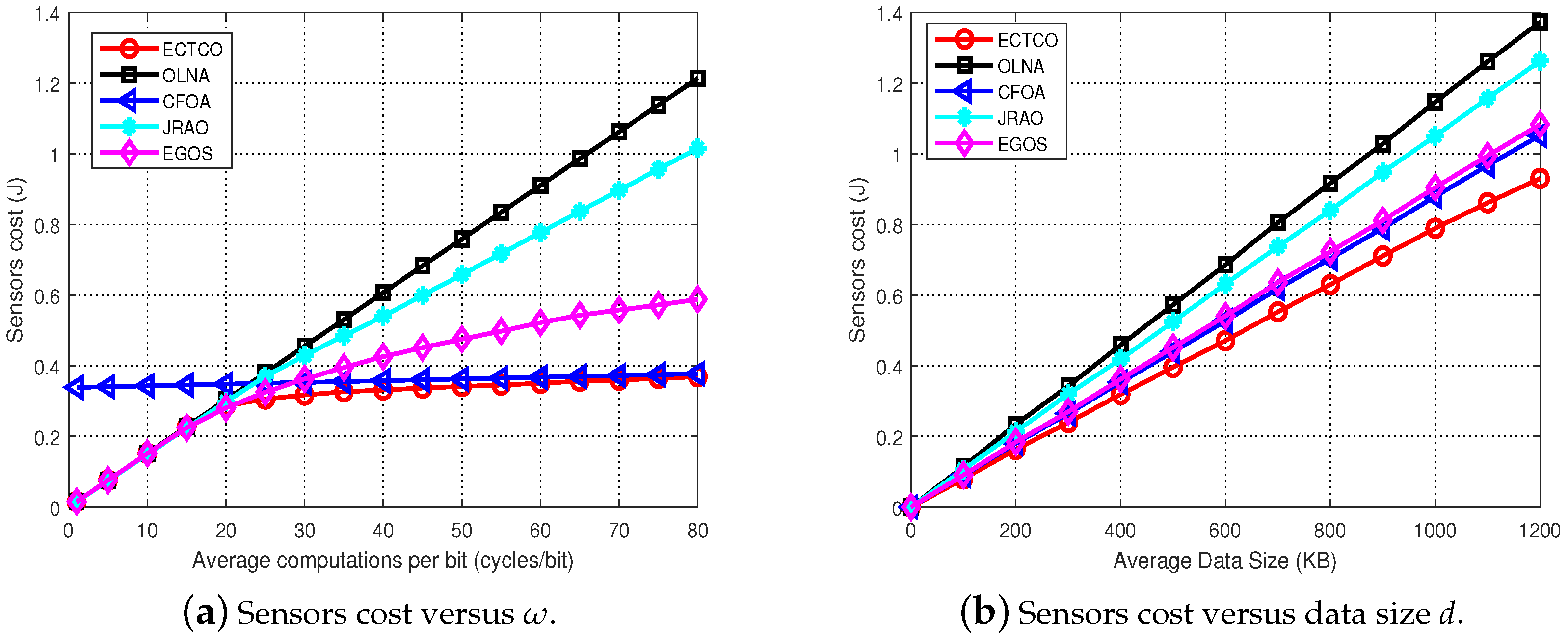
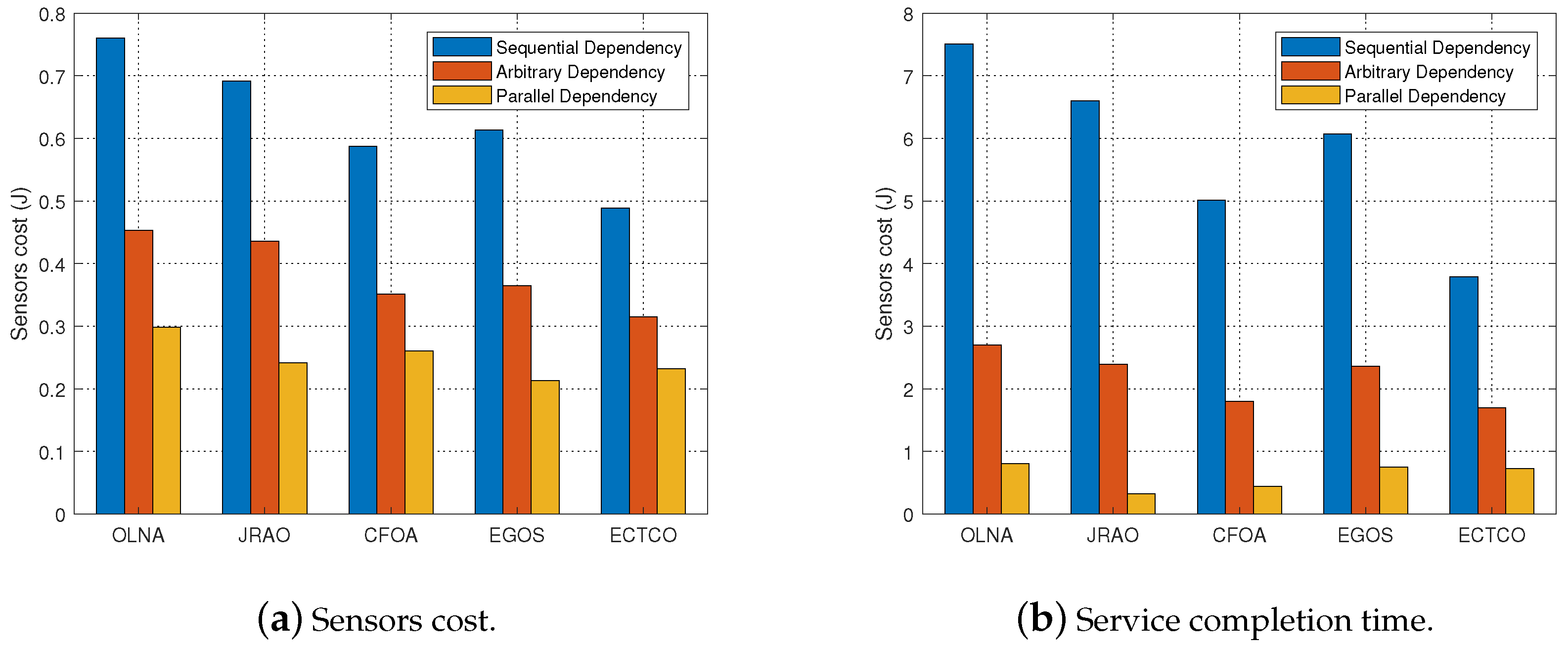
In the simulation section, we evaluated the performance of the proposed ECTCO algorithm by comparing it with existing algorithms. Simulation results demonstrated that in the inter-task dependency scenario, the proposed algorithm could balance the tradeoff between computation and communication overhead, and outperform the other four algorithms in computation offloading in terms of energy consumption. In addition, we studied the impact of different system parameters and dependencies. Performance evaluations showed that the proposed algorithm could effectively reduce the sensors cost under different system parameters and dependencies. These simulation results verified the effectiveness and adaptability of the ECTCO algorithm.
In future work, we plan to deploy the proposed framework to real-world IoT scenarios so as to further conduct practical evaluations of the proposed algorithm. We also expect to explore mobility management and the offloading problem of tasks for sensors with inter-task dependency in a dynamic moving environment.